Journal of Modern Physics
Vol.4 No.8(2013), Article ID:35810,6 pages DOI:10.4236/jmp.2013.48147
Generation and Shaping of Soliton-Like Pulses along Resonant Tunneling Diodes NMOS Varactors Lattice
1Department of Physics, Higher Teachers Training College, University of Maroua, Maroua, Cameroon
2Department of Physics, Faculty of Science, University of Yaounde 1, Yaounde, Cameroon
Email: bessimb@yahoo.fr
Copyright © 2013 Yerima Klofaï, Bernard Z. Essimbi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 10, 2013; revised June 14, 2013; accepted July 19, 2013
Keywords: Accumulation-Mode MOS; Soliton-Like Pulse Generation and Shaping; Resonant Tunneling Diode; Active Nonlinear Electrical Lattice; Expanded KdV Equation
ABSTRACT
The characteristics of N-type accumulation-mode MOS (NMOS) varactors line periodically loaded with resonant tunneling diodes (RTDs) are used for soliton-like pulses generation and shaping. The problem of wide pulse breaking up into multiple pulses rather than a single is solved. Applying perturbative analysis, we show that the dynamics of the nonlinear transmission line (NLTL) is reduced to expanded Korteweg-de Vries (KdV) equation. Moreover, numerical integration of nonlinear differential and difference equations that result from the mathematical analysis of the line is discussed. As results, NLTL can simultaneously sharpen both leading and trailing of pulse edges and one could obtain a rising and sharpening step pulse.
1. Introduction
Up to now, electrical systems in which travelling waves could be observed were merely studied. Systems operating in the millimeter wave frequency range are an example of a current niche market, with current research striving to fully integrate such systems using advanced semiconductor processing technology. Electromagnetic waves at these frequencies become comparable in size to the electronics circuits. This opens the possibility for novel design approaches that were traditionally not available to integrated circuit radio-frequency designers. In this frame the nonlinear transmission line (NLTL) stands as one of the most powerful vehicles to generate short electrical pulses [1,2]. NLTLs have broad applications in a variety of high-speed, wide bandwidth systems including mm-wave sources and frequency synthesizers. Many of these applications involve techniques for forming and sharpening a short electrical pulse, such ultrawideband (UWB) systems are for e.g., attractive for radar and wireless communication applications. Another application is pulse sharpening for the more traditional non return-to-zero (NRZ) data transmission in digital circuits by improving the edges of the pulses.
Moreover, among the very large number of guiding structures proposed and used in microwave applicationsplanar waveguides have proved to be the most successful solution to the problem of the interconnections in microwave and millimetre wave circuits. There are many reasons for this success; at first, it is apparent that planar waveguides are a “natural” solution in monolithic microwave integrated circuits (MMIC’s), being the direct evolution of classical interconnecting wires; hence microstrips as well as coplanar waveguides are completely compatible with the existing technological procedures for the metallization and passivation of monolithic integrated circuits. In this context, recent progresses in III-V semiconductor technology and in silicon-based CMOS process technologies have led to the development of NLTLs, as the key component for high-speed electronics [3-5]. Nonlinear transmission lines offer another advantage that they can be integrated with other electronic circuitry. The availability of dense integrated circuitry in CMOS offers an additional advantage for using CMOS based technologies even at very high-frequencies, as many integrated systems can greatly benefit from the availability of co-integrated baseband and digital back ends [6]. Essentially, a NLTL is a ladder network consisting of a high impedance propagating medium periodically loaded with nonlinear devices such as heterostructure barrier varactors, MOS varactors (MOSVARs) or RTDs. The underlying characteristic of the RTD is a nonlinear Nshaped current-voltage relationship with a negative differential resistance (NDR) in the active region even at millimetre wave frequencies. It is regarded as the most practical ultra high-speed quantum effect devices for ultrafast analogue and digital applications [7,8]. Besides, CMOS processes offer different characteristics for nonlinear capacitors that can be exploited to achieve simultaneous edge sharpening for both leading and trailing edges. In particular NMOS varactors exhibit non monotonic voltage dependence suitable for the shaping process. Let us recall that, recently we studied the generation of short electrical pulses based on nonlinear active wave propagation effects along RTD lines [9-11]. As will be shown, the coplanar waveguide (CPW) involving NMOS varactors and RTDs (hereafter, it is a resonant tunneling diode NMOS varactors lattice) can be utilized for the electrical short pulses generation and shaping in highspeed electronics.
The outline of the paper is as follows. In Section 2, we present the active nonlinear electrical lattice. In Section 3, within the perturbative method we analytically discuss the basic properties of this lattice. Section 4 is devoted to simulation results in the framework of the soliton-like pulses. Section 5 concludes the paper.
2. Fundamental Characteristics of the Active Nonlinear Electrical Lattice
The basic model of the active nonlinear electrical lattice is presented in Figure 1. Here, Figure 1(a) shows the equivalent circuit of the active NLTL where two sections are shown. This line consists of a shunt nonlinear conductance-capacitance 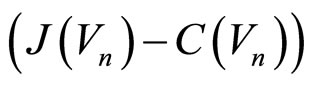 circuit, a series resistance-inductance (R-L) circuit. The nonlinear current-voltage characteristic of the RTD is shown in Figure 1(b) where a suitable dc current bias has been assumed [3,4]. For a capacitor with a positive voltage dependence as for an NMOS varactor in accumulationmode, one has [5],
circuit, a series resistance-inductance (R-L) circuit. The nonlinear current-voltage characteristic of the RTD is shown in Figure 1(b) where a suitable dc current bias has been assumed [3,4]. For a capacitor with a positive voltage dependence as for an NMOS varactor in accumulationmode, one has [5],
 (1)
(1)
where  denotes the voltage drop and
denotes the voltage drop and 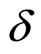 the nonlinearity parameter.
the nonlinearity parameter.
The current-voltage relationship of the nonlinear conductance of the RTD is taken as,
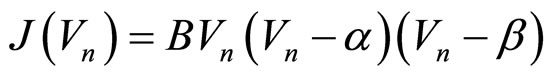 (2)
(2)
where α and β are positive constants and B is an amplitude factor.
By applying Kirchhoff laws, we obtain,
 (3a)
(3a)
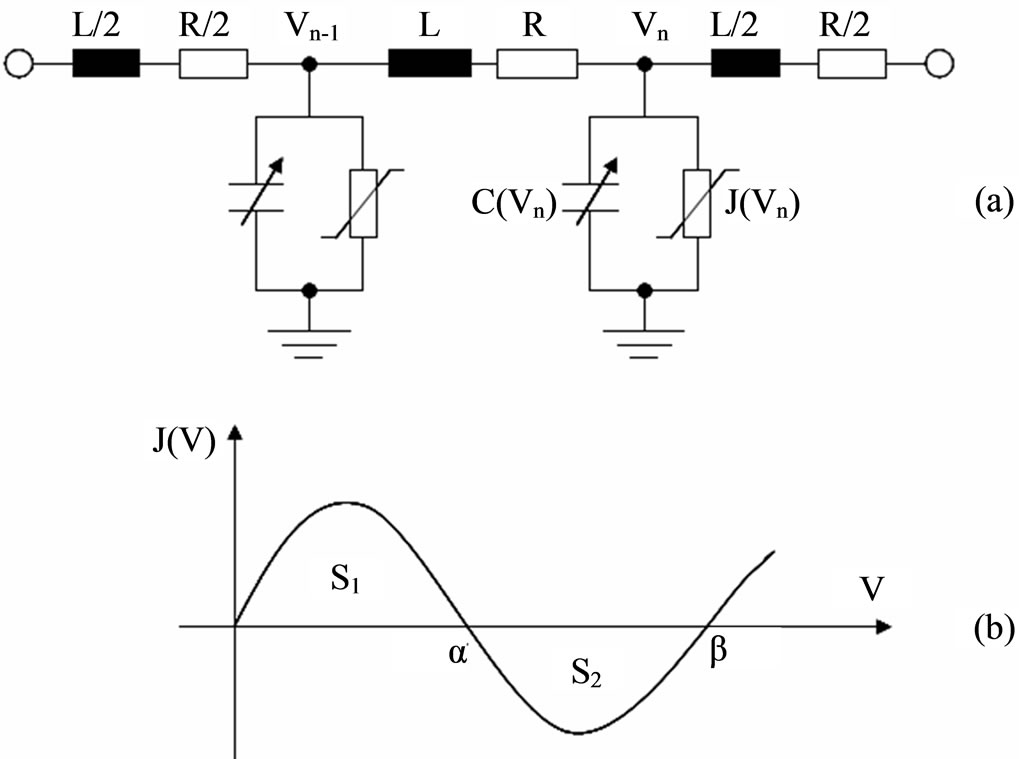
Figure 1. Active nonlinear transmission line: (a) Proposed NLTL; (b) RTD current-voltage characteristic at a dc bias circuit.
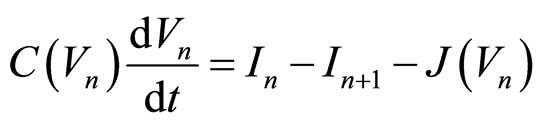 (3b)
(3b)
where 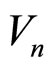 and
and  are the voltage and current at the
are the voltage and current at the 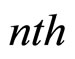 section, respectively.
section, respectively.
Therefore, from Equations (2) and (3), we obtain that voltages of the adjacent nodes on this lattice are related via partial differential equation as follows,
 (4)
(4)
Let us assume that the voltage varies slowly from one unit section to the other. The discrete index 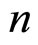 can be assumed to be a continuous variable and we can use the Taylor expansion for the left-hand side of Equation (4) to fourth order, to get
can be assumed to be a continuous variable and we can use the Taylor expansion for the left-hand side of Equation (4) to fourth order, to get
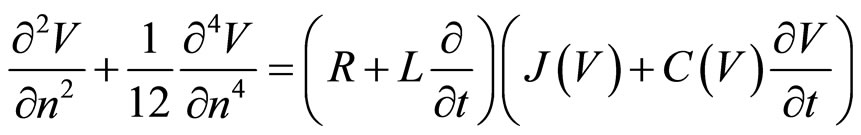 (5)
(5)
For our computer experiments, characteristic parameters of propagation media used are given by,
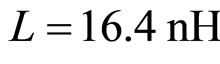 ,
, 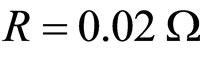 ,
, 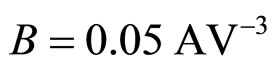 ,
, 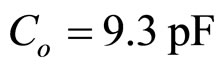 and
and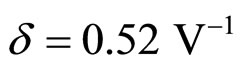 .
.
The others values the parameters α and β of the RTD will be set in Section 4 according to Figure (1)b.
3. A Perturbative Analysis of the Active Nonlinear Electrical Lattice
The problem studied in this paper deals with a NMOS varactor diode whose the nonlinear parameter in Equation (1) is positive. In a recent paper [10], we solved this problem analytically as well as numerically in the framework of a varactor diode with a negative nonlinear parameter. Therefore, for next investigations, we are going to follow the procedure presented in that reference.
Here, we first develop a perturbative analysis of Equation (5). In this equation, by setting a dimensionless voltage 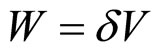 we get,
we get,
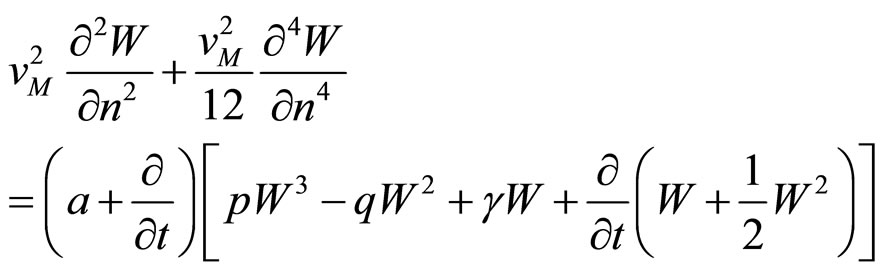 (6)
(6)
where
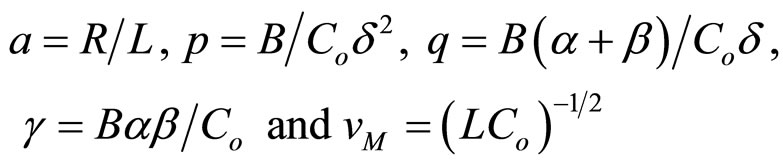
By applying the different transformations to Equation (6) for the space and time
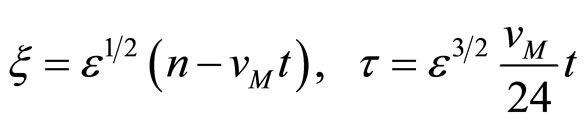 (7)
(7)
and for constants and variables,
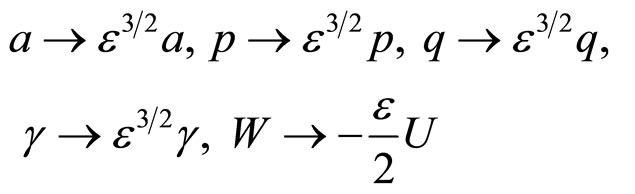 (8)
(8)
where 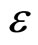 is an indicator of the slowness, we find that
is an indicator of the slowness, we find that  terms yield the following extended KdV equation
terms yield the following extended KdV equation
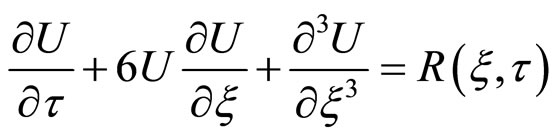 (9)
(9)
with
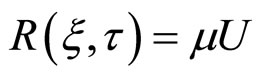 (10)
(10)
where  is a constant with
is a constant with 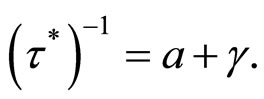
We recall that the fundamental properties of KdV solitons have extensively been studied and a survey of main results has recently been given in [2].
4. Computer Experiments and Discussions
Numerical evaluation of the proposed method is carried out in order to study the behaviour of the soliton-like pulse for a couple of parameter  of the nonlinear conductance. For integration of equation (9), we use the finite difference method under periodic boundary conditions and an input excitation as follows,
of the nonlinear conductance. For integration of equation (9), we use the finite difference method under periodic boundary conditions and an input excitation as follows,
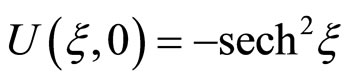 (11)
(11)
Figure 2 shows the result obtained from simulations. Here, one can see that the amplitude of the pulse is being amplified when travelling along the line. Therefore, this result agrees with the area condition in the current-voltage characteristic of the RTD. Let us recall that this behaviour is similar as the one observes in [10] in the case of a varactor diode with a negative nonlinear parameter.
Next, in order to discuss more realistic situations, we numerically solved Equation (3) using appropriate boundary conditions. The time integration of the equations is performed by means of the standard Runge-Kutta method of the fourth order with controlled time-steps in order to provide the prescribed accuracy. In the physical space, the unit time in our figures corresponds to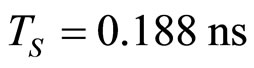 .
.
As indicated by Equation (11), we take an input excitation as,
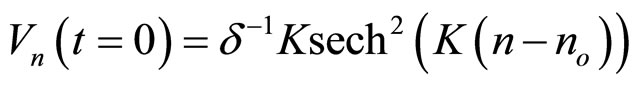 , (12)
, (12)
where 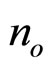 represents the initial cell excited in the lattice composed of
represents the initial cell excited in the lattice composed of  elementary sections. For these simulations,
elementary sections. For these simulations, 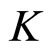 is a constant set to
is a constant set to .
.
Firstly, we set (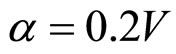 and
and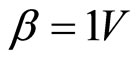 ), which corresponds to
), which corresponds to 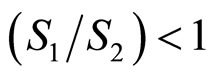 in Figure 1(b). The voltage distribution of the input signal is presented in Figure 3 (top), whereas the profiles of the wave at times
in Figure 1(b). The voltage distribution of the input signal is presented in Figure 3 (top), whereas the profiles of the wave at times 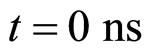 and
and  are depicted in Figure 3 (bottom). One sees that the amplitude of the pulse decreases from 150 mV to
are depicted in Figure 3 (bottom). One sees that the amplitude of the pulse decreases from 150 mV to
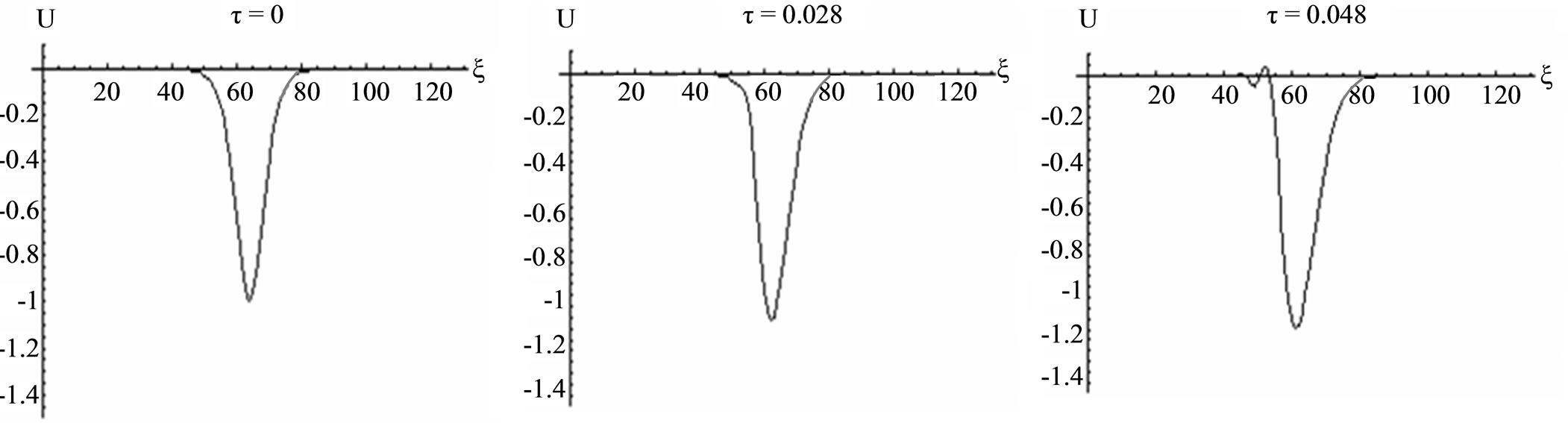
Figure 2. Numerical solution of the extended KdV equation for the initial condition, 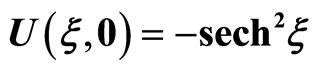 and, for
and, for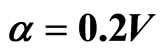 ,
,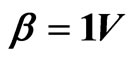 . The time points shown are
. The time points shown are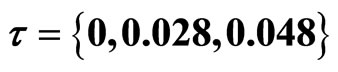 . The calculation is based on 128 points in the ξ domain corresponding to a step size of 0.175. The step in the time domain is 0.0001.
. The calculation is based on 128 points in the ξ domain corresponding to a step size of 0.175. The step in the time domain is 0.0001.

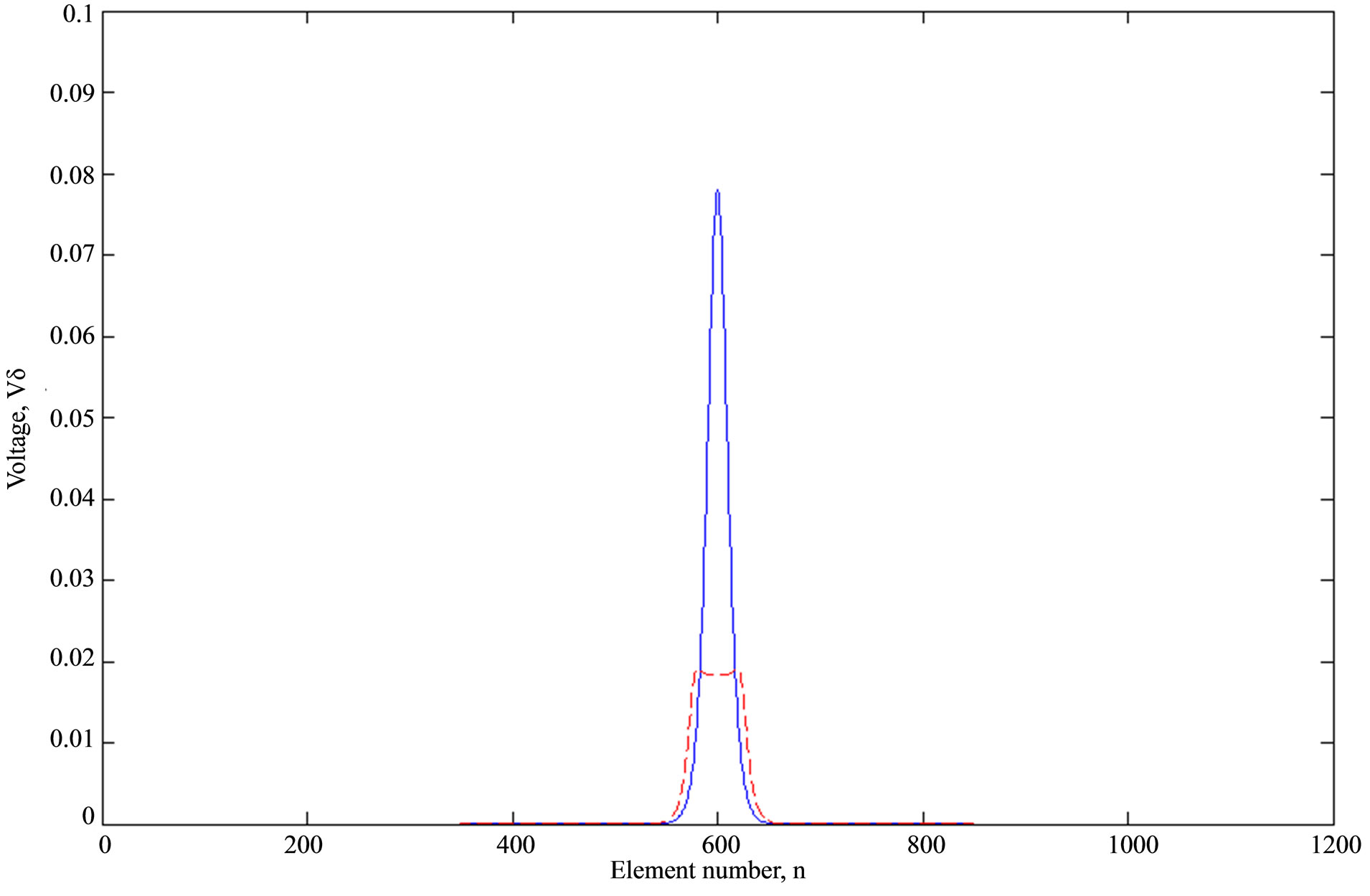
Figure 3. (top) Voltage distribution; (bottom) Profiles of the initial pulse at time t = 0 ns (solid line) and t1 = 940 ns (dashed line) for α = 0.2V and β = 1V with no = 600.
36.7 mV, rising and falling pulse edges are quite sharpened, and the pulse width grows.
Secondly, we set (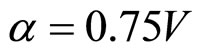 and
and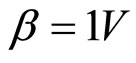 ), leading to
), leading to  in Figure 1(b). The numerical calculations are presented in Figure 4 (top) for the voltage distribution as well as the profiles of the pulse in Figure 4 (bottom). Here, the amplitude of the pulse decreases from 150 mV at time
in Figure 1(b). The numerical calculations are presented in Figure 4 (top) for the voltage distribution as well as the profiles of the pulse in Figure 4 (bottom). Here, the amplitude of the pulse decreases from 150 mV at time 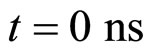 to 113.6 mV at time
to 113.6 mV at time 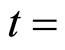
 as indicated in Figure 4 (bottom). Here, it appears that initially the amplitude of the wave decreased due to losses and after a short time, he reaches a steady state for which its amplitude remains constant. Let us pointed that, these behaviors are quite similar to those obtain in [10], excepted that here sharpened rising and
as indicated in Figure 4 (bottom). Here, it appears that initially the amplitude of the wave decreased due to losses and after a short time, he reaches a steady state for which its amplitude remains constant. Let us pointed that, these behaviors are quite similar to those obtain in [10], excepted that here sharpened rising and
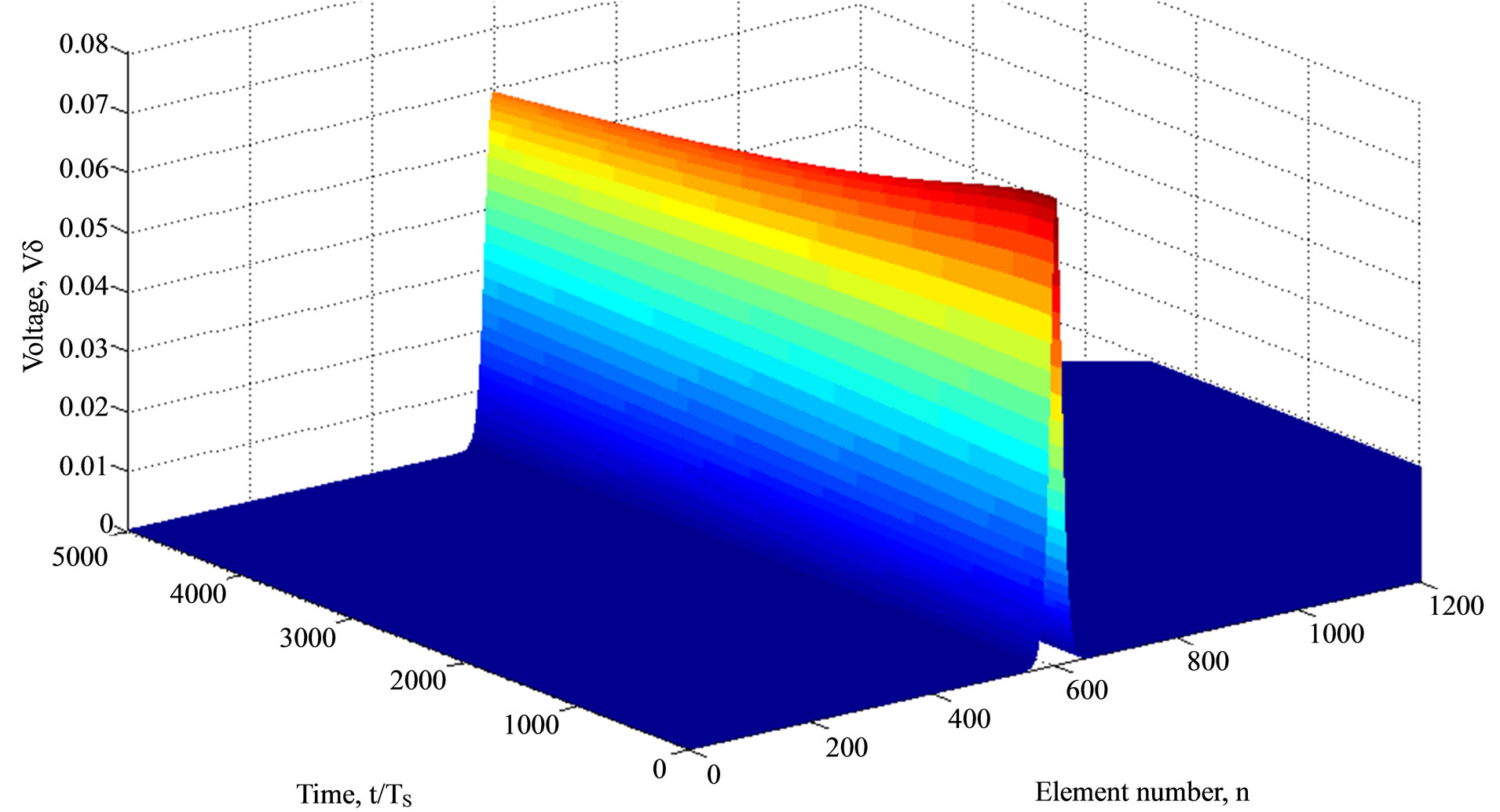
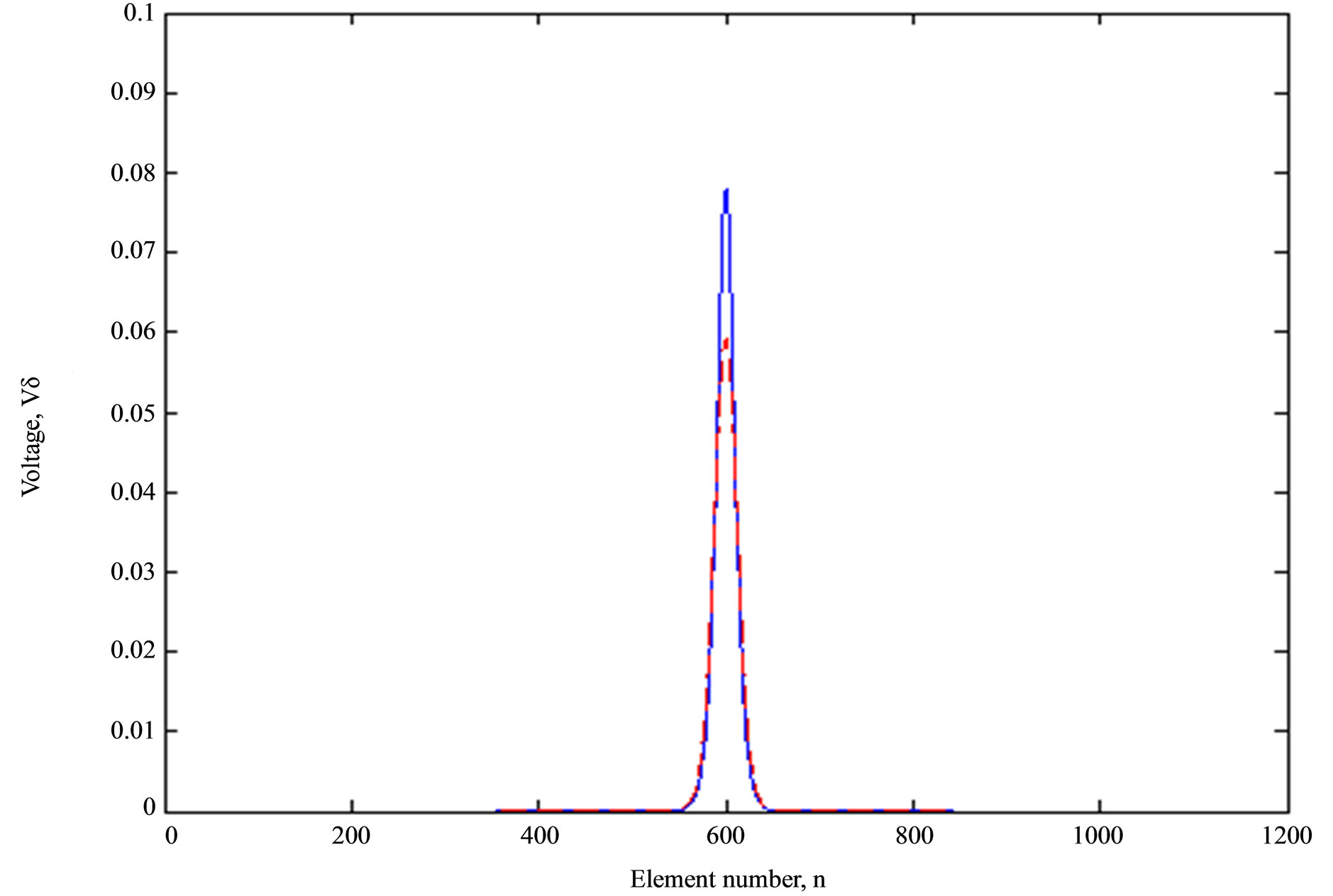
Figure 4. (top) Voltage distribution; (bottom) Profiles of the initial pulse at time t = 0 ns (solid line) and t1 = 940 ns (dashed line) for α = 0.2V and β = 1V with no = 600.
falling pulse edges are more pronounced.
Finally, to study the behaviour of the pulse along the lattice, we take an initial wave as,
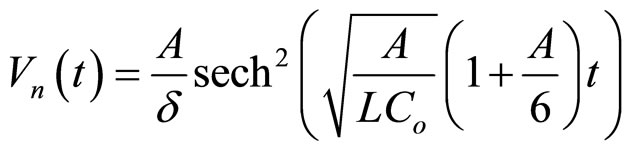
During these computer experiments, 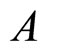 is kept fixed at 13, and
is kept fixed at 13, and 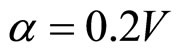 and
and 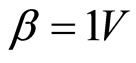 in Equation (2).
in Equation (2).
The simulated results (Figure 5) are taken at three distinct cells n = 500, 1000 and 1500 along the lattice having a total number of cells of 2000. Here one notices that the initial pulse when travelling along the line leads to arising and sharpening step pulse. This result differs from the one obtained in [10], when dealing with a varactor
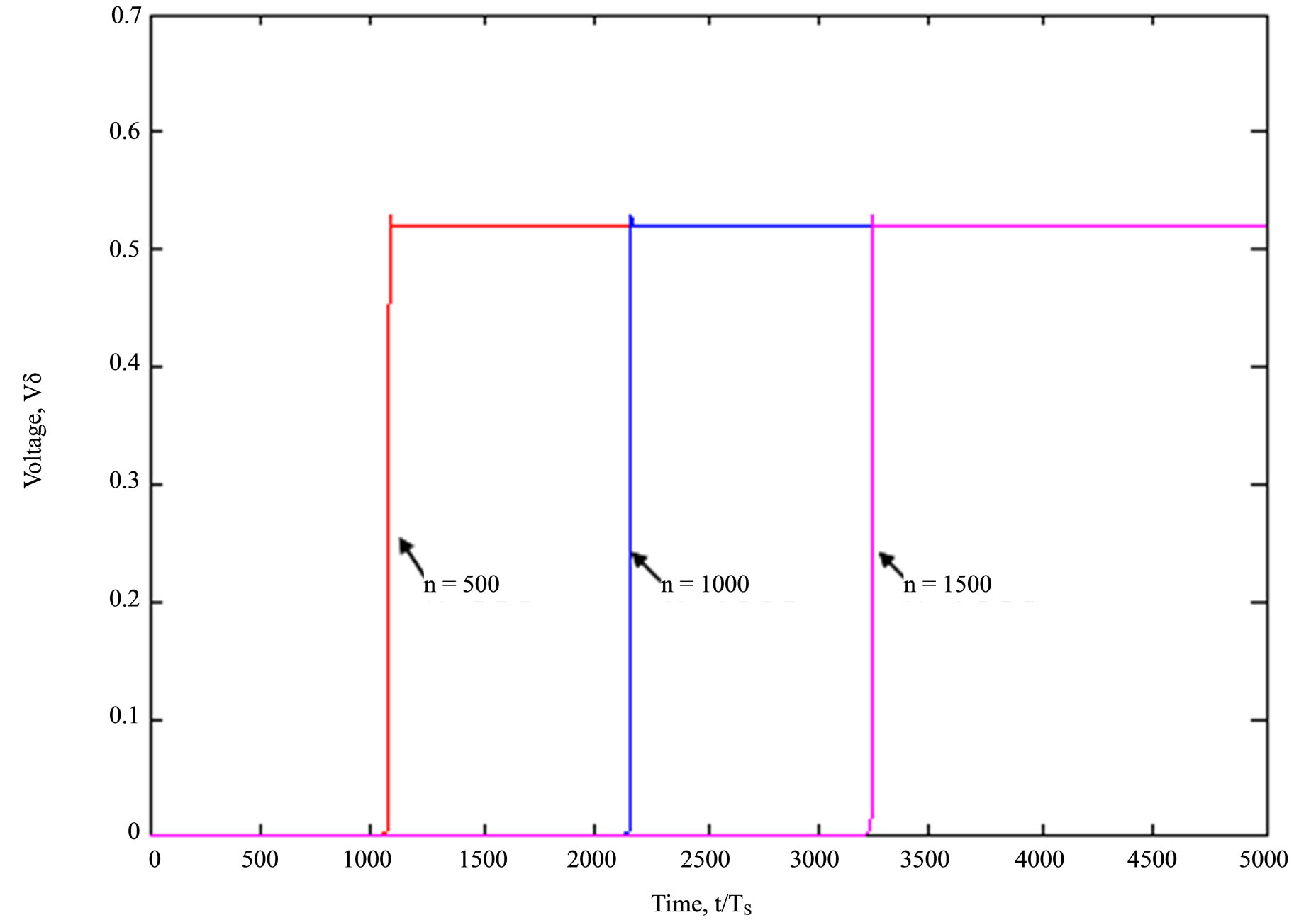
Figure 5. The space-time evolution of the input signal (16) monitored at three different nodes n = 500, 1000 and 1500.
diode. However, in order to achieve sharpened both rising and falling edges of the pulse a solution is proposed in [5] when using two N-type MOSVAR at each node of the lattice.
5. Conclusion
In this paper, we have analytically and numerically discussed soliton-like pulses generation and shaping in the active nonlinear electrical lattice in MMIC technology, using N-type accumulation-mode MOS varactors and RTDs. Such numerical solutions are probably the best way in which practical generation and sharpening circuits can be designed. Indeed, the transmission line elements are directly connected to the practical circuits elements in experiments. Such kind of lattices can be applied in broadband signal generations, and high-speed serial communications.
REFERENCES
- M. J. W. Rodwell, S. T. Allen, R. Y. Yu, M. G. Case, U. Bhattacharya, M. Reddy, E. Carman, M. Kamegawa, Y. Konishi, J. Pusl and R. Pullela, Proceedings of IEEE, Vol. 82, 1994, pp. 1037-1059. doi:10.1109/5.293161
- D. S. Ricketts and D. Ham, “Electrical Solitons: Theory, Design, and Applications,” 1st Edition, CRC Press, Boka Raton, 2010.
- I. V. Ryjenkova, V. K. Mezentsev, S. L. Musher, S. K. Turitsyn, R. Hu Hülsewede and D. Jaeger, Annals of telecommunications, Vol. 52, 1997, pp. 134-139.
- I. Jaeger, D. Kalinowski, A. Stöhr, J. Stiens, R. Vounckx and D. Jäger, Microwave and Optical Technology Letters, Vol. 49, 2007, pp. 2907-2909. doi:10.1002/mop.22902
- E. Afshari and A. Hajimiri, IEEE Journal of Solid-State Circuits, Vol. 40, 2005, pp. 744-752. doi:10.1109/JSSC.2005.843639
- E. Seok, D. Shim, C. Mao, R. Han, S. Sankaran, C. Cao, W. Knap and K. O. Kenneth, IEEE Journal of Solid-State Circuits, Vol. 45, No. 8, 2010, pp.1554-1564. doi:10.1109/JSSC.2010.2049793
- M. Asada, S. Suzuki and N. Kishimoto, Japanese Journal of Applied Physics, Vol. 47, 2008, pp. 4375-4384. doi:10.1143/JJAP.47.4375
- K. Narahara, “Nonlinear Waves in Transmission Lines Periodically Loaded with Tunneling Diodes,” In: A. Petrin, Ed., Wave Propagation in Materials for Modern Applications, INTECH, Croatia, 2010, pp. 437-454.
- B. Z. Essimbi and D. Jäger, Physica Scripta, Vol. 81, 2010, Article ID: 035801. doi:10.1088/0031-8949/81/03/035801
- B. Z. Essimbi and D. Jäger, Journal of Infrared, Millimeter and Terahertz Waves, Vol. 33, 2012, pp. 627-637. doi:10.1007/s10762-012-9895-9
- B. Z. Essimbi and D. Jäger, Physica Scripta, Vol. 85, 2012, Article ID: 035801. doi:10.1088/0031-8949/85/03/035801

