Journal of Modern Physics
Vol.4 No.8A(2013), Article ID:36094,6 pages DOI:10.4236/jmp.2013.48A009
Biefeld-Brown Effect and Space Curvature of Electromagnetic Field
Institute of Mechanical Sciences, Vilnius Gediminas Technical University, Vilnius, Lithuania
Email: Algirdas.maknickas@vgtu.lt
Copyright © 2013 Algirdas Antano Maknickas. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 29, 2013; revised July 3, 2013; accepted August 2, 2013
Keywords: Biefeld-Brown Effect; Space Curvature; Electromagnetic Gravity
ABSTRACT
With applying of new proposed electromagnetic gravity Lagrangian together with Einstein-Hilbert equation not zero space curvature was derived. The curvature gives “a priory” postulate of equivalence of mass and electro-magnetic field gravity properties. The non-zero trace of energy-stress tensor of electrical field changes space curvature of gravity mass, which yields to prediction of dependence of capacitor gravity mass from capacitor capacitance and voltage values, observed in Biefeld-Brown effect. The other, not observed prediction could be applied to coil gravity mass dependence from coil inductance and current values. New physical constant, electromagnetic field gravity constant αg, was introduced to conform with theoretical and experimental data.
1. Introduction
Biefeld-Brown’s [1-6] effect has been known since 1928. Christensen and Møller [7] built a Biefeld-Brown electrode setup and published measurements of the obtained thrust in ambient air. They also compared their results with theoretical predictions of electric wind effects. The agreement was very good and tended to explain the Biefeld-Brown effect as a purely electric wind phenomenon. The other try to verify the adequacy of BiefeldBrown effect with electric wind phenomena was made by Tajmar [8]. The author concluded in this article that electric wind phenomena can explain Biefeld-Brown effect. The results [8] suggest that corona wind effects were misinterpreted as a possible connection between gravitation and electromagnetism. Brown observed in [9] that thiseffect remained even if the ambient medium was a vacuum (up to 10−6 Torr). Talley [10,11] studied Brown’s electrode configurations in vacuum chambers up to 10−6 Torrin great detail. He found no thrust in the case of a static dc potential applied to the electrodes. However, he noticed an anomalous force during electrical breakdowns when the current was flowing. This force, the result of currents in divergent electric fields (due to the asymmetrical electrode configuration) finds further support in five-dimensional theories coupling the gravitational and electromagnetic field. Williams [12] integrated amass dependent fifth dimension into the relativistic Maxwell theory and predicted the coupling between both fields. The newest references of investigations of electrodynamic lifter propulsion could be found in [13]. However, ambiguity of explanation of Biefeld-Brown effect indicates that new theoretical and experimental researches are needed.
2. Einstein’s Field Equations
Suppose that the full action of the theory is given by the Einstein-Hilbert [14] term plus a term 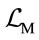 describing any matter fields appearing in the theory
describing any matter fields appearing in the theory
 . (1)
. (1)
The action principle then tells us that the variation of this action with respect to the inverse metric is zero, yielding
 (2)
(2)
Since this equation should hold for any variation δgμν, it implies that
 (3)
(3)
this equation of motion for the metric field could be found. The calculation of the left hand side of the equation for the variations of the Ricci scalar R and the determinant of the metric could be found in Carroll [15]. After having of all the necessary variations at our disposal, we can insert them into the equation of motion for the metric field to obtain
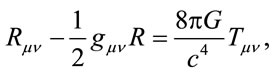 (4)
(4)
which is Einstein’s field equation [16,17] and constant
 (5)
(5)
has been chosen so that the non-relativistic limit yields the usual form of Newton’s gravity law, where 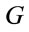 is the gravitational constant and
is the gravitational constant and 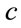 is speed of light in vacuum. The right hand side of this equation is (by definition) proportional to the energy-stress tensor
is speed of light in vacuum. The right hand side of this equation is (by definition) proportional to the energy-stress tensor
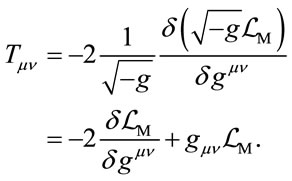 (6)
(6)
The Lagrangian of mater must be chosen so, that it satisfy conservation lows.
3. Einstein’s Field Equation for Gravity Mass in Electromagnetic Field
The electromagnetic tensor 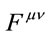 in Cartesian coordinates is commonly written as a matrix:
in Cartesian coordinates is commonly written as a matrix:
 (7)
(7)
or
 (8)
(8)
where 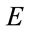 is the electric field,
is the electric field,  the magnetic field, and
the magnetic field, and 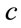 the speed of light. The signs in the tensor above depend on the convention used for the metric tensor. The convention used here is
the speed of light. The signs in the tensor above depend on the convention used for the metric tensor. The convention used here is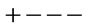 , corresponding to the metric tensor:
, corresponding to the metric tensor:
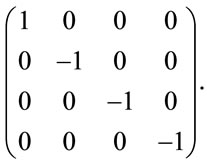 (9)
(9)
From the matrix form of the field tensor, it becomes clear that the electromagnetic tensor satisfies the following antisymmetry properties Fab = Fba (hence the name bi vector) of six independent components.
If one forms an inner product of the field strength tensor Lorentz invariant is formed:
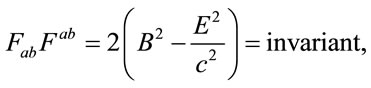 (10)
(10)
the Lagrangian of electromagnetic field in our model could be
 (11)
(11)
Lagrangian  differs from classic electromagnetic field Lagrangian just with constant αgc2, where αg is electromagnetic field gravity constant with dimension s2/m2, which could be calibrated on experiment data.
differs from classic electromagnetic field Lagrangian just with constant αgc2, where αg is electromagnetic field gravity constant with dimension s2/m2, which could be calibrated on experiment data.
According to [18], it is safer to rewrite inner product of field strength tensor as FabFcdgacgbd. This gives for the first term of sum of energy-stress tensor Equation (6).
 (12)
(12)
A different result could be obtained, if inner product of field strength tensor is leaving as FabFab. In this way result is:
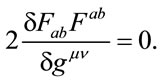 (13)
(13)
Let’s decide, that Equation (13) is true (discussion in Appendix), so the calculations of energy-stress tensor term of electromagnetic field give result:
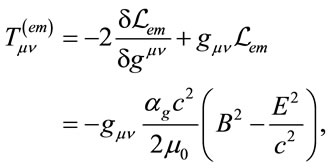 (14)
(14)
which is symmetric and satisfy rotation conservation low.
4. Einstein’s Field Equation for Gravity Mass in Electromagnetic Field
According to Equation (6) energy-stress tensor of gravity mass in electromagnetic field could be found with adding Lagrangian of gravitational and electromagnetic parts of Lagrangian
 (15)
(15)
After inserting of energy-stress tensor of Equation (15) into Equation (4) Einstein-Hilbert field equation looks like this
 (16)
(16)
Taking the trace of Equation (16) (contracting with gμν) and using the fact that gμνgμν = 4, we get for space curvature:
 (17)
(17)
yielding the equivalent form of Equation (16)
 (18)
(18)
Space curvature Equation (17) of spheric gravity mass with radius r in electromagnetic field could be rewritten as
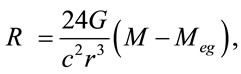 (19)
(19)
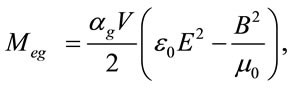 (20)
(20)
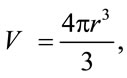 (21)
(21)
where Meg is electromagnetic mass and 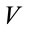 is volume of electromagnetic field and is equal to volume of devices, which is inside this electromagnetic field.
is volume of electromagnetic field and is equal to volume of devices, which is inside this electromagnetic field.
From Equation (19) assumption could be made, that summary curvature of the space generated by gravity mass should decrease in electric field and increase in magnetic field. If the mass of device M equals to absolute value of electromagnetic mass |Meg|, zero curvature of such device could be obtained, so gravity mass of this device stop interacting with the other gravity mass. Let’s prove it analytically.
The solution of Equation (19) in spheric coordinates (see for example [19]) is:
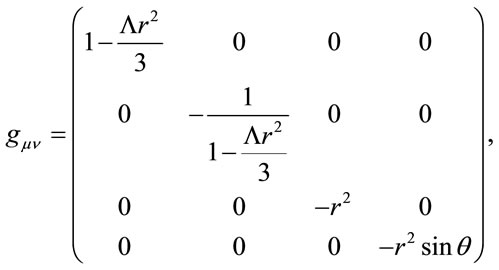 (22)
(22)
where Λ equals to
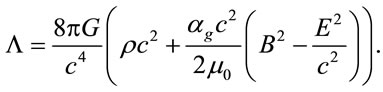 (23)
(23)
Thus, the gravitational potential of a point mass is
 (24)
(24)
 (25)
(25)
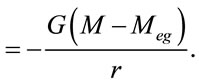 (26)
(26)
Equation (26) prove proposition, if the mass M equals to absolute value of |Meg|, we have zero gravitational gravity potential for gravity mass M and so such mass does not interact with external gravity field.
5. Biefeld-Brown Effect in Vacuum
Replacing of magnetic field B with B = 0 and replacing of electric field density with capacitor energy density multiplied by volume of electric field of capacitor in Equation (20) gives for electro gravity mass of capacitor
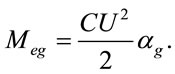 (27)
(27)
The simple capacitor of two parallel conductive plates describes as
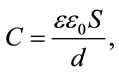 (28)
(28)
so Equation (27) could be rewritten as:
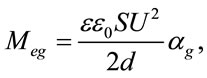 (29)
(29)
where ε is relative permittivity of material, ε0 is absolute permittivity of vacuum, S is the area of the capacitor and d is separation of the planes of the capacitor. Equation (29) explains all experimental data observed BiefeldBrown effect. The effect depends on the separation of the plates of the capacitor, the closer the plates, the greater the effect. The effect depends on the dielectric strength of the material between the electrodes, the higher the strength, the greater the effect. The effect depends on the area of the conductor, the greater the area, the greater the effect. The effect depends on the voltage difference between the plates, the greater the voltage, the greater effect. The effect depends on the volume of the dielectric material, the greater the volume, the greater part of electromagnetic energy concentrates in dielectric material, the greater the effect.
Electro-gravity constant αg could be found from Buehler [20] experiments. Author founds in their experiments with capacitor isolated from electronic wind, that lifting force of charged capacitor depends on energy of this capacitor is
 (30)
(30)
where ΔF is lifting force, m is device mass, M mass of earth, R earth radius and constant k equals to . The inserting of numeric values of given constants into Equation (30) results for numeric value of electro-gravity constant αg = 0.0479.
. The inserting of numeric values of given constants into Equation (30) results for numeric value of electro-gravity constant αg = 0.0479.
6. Biefeld-Brown Effect in Air
Lagrangian Equation (11) isn’t Gauge invariant and after adding of JμAμ term new lagrangian
 (31)
(31)
satisfy electromagnetic field’s equations of motion
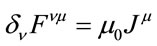 (32)
(32)
where Jμ is the four-current is the contravariant fourvector which combines electric current and electric charge density as follows
 (33)
(33)
and  is the electromagnetic four-potential is a covariant four-vector containing the electric potential and magnetic vector potential, as follows
is the electromagnetic four-potential is a covariant four-vector containing the electric potential and magnetic vector potential, as follows
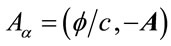 (34)
(34)
So Equation (15) must be rewritten as follow
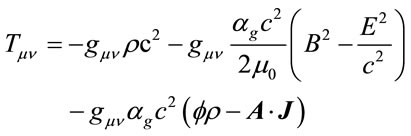 (35)
(35)
and Equation (20) transforms into
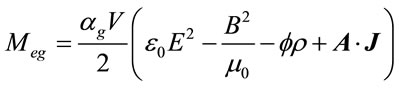 (36)
(36)
Equation (36) shows, that electromagnetic propulsion lifter acquire antigravity property through gravity shielding of A·J member, which describe ionic wind.
7. Mass Increasing Effect of Inductance Coil
If do not zero space curvature of electric field explains Biefeld-Brown effect excellently, the same effect, but with increasing of device mass, must be observed in a magnetic field. Analogically to Equation (29) electrogravity mass equation for inductance coil looks like this
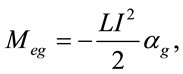 (37)
(37)
where L is the inductance, which depends on area and amount of windings and coil length, and I is the current. Equation (37) predict similar effects, observed in BiefeldBrown experiments with a capacitor, but in opposite direction of changing of coil mass: for the fixed inductance L increasing of current in coil must increase mass of the coil.
8. Conclusions
On the basis of the results obtained in this work the following conclusions have been made:
1) Electro gravity mass equation is in good agreement with Biefeld-Brown effect and fully explains all qualitative data observed in this effect;
2) Electromagnetic gravity model predicts decreasing of gravity mass effect in electric field and increasing of gravity mass in magnetic field;
3) Electromagnetic field gravity constant equals to αg = 0.0479 [s2/m2] and is the basic constant of proposed electromagnetic gravity model;
4) The total curvature of electromagnetic wave is zero, but separate curvatures of electric and magnetic components of the wave haven’t zero values.
9. Acknowledgements
I’d like to thank Gintaras Valiulis from Vilnius University and Algis Dziugys from Lithuanian Energy Institute for discussions and notes, which helps definitely understand problem of new proposed electro-gravity model.
REFERENCES
- T. T. Brown, “A Method of and an Apparatus or Machine for Producing Force or Motion,” UK Patent No. 00.311, 1928.
- T. T. Brown, Science and Invention (Reprinted in Psychic Observer), Vol. 37, 1929, pp. 66-67.
- T. T. Brown, “Electrostatic Motor,” US Patent No. 1.974.483, 1934.
- T. T. Brown, “Electrokinetic Apparatus,” US Patent No. 2.949.550, 1960.
- T. T. Brown, “Electrokinetic Transducer,” US Patent No. 3.018.394, 1962.
- T. T. Brown, “Electrokinetic Generator,” US Patent No. 3.022.430, 1962.
- P. S. Christensen and E. A. and Møller, AIAA Journal, Vol. 5, 1967, pp. 1768-1773. doi:10.2514/3.4302
- M. Tajmar, AIAA Journal, Vol. 42, 2004, pp. 315-318. doi:10.2514/1.9095
- T. T. Brown, “Electrokinetic Apparatus,” US Patent No. 3.187.206, 1965.
- R. L. Talley, “21st Century Propulsion Concept, US Air Force Astronautics Lab., Final Rept. AFAL-TR-88-031”.
- R. L. Talley, “Twenty First Century Propulsion Concept,” US Air Force Propulsion Directorate.
- P. E. Williams, “The Possible Unifying Effect of the Dynamic Theory,” Los Alamos Scientific Laboratory, Los Alamos.
- K. Masuyama, “Performance Characterization of Electrohydrodynamic Propulsion Devices,” Massachusetts Institute of Technology, Cambridge, 2012.
- D. Hilbert, Konigl. Gesell. d. Wiss. Gottingen, Nachr. Math.-Phys. Kl., 1915, pp. 395-407.
- S. M. Carroll, “Spacetime and Geometry,” Addison Wesley, Boston, 2004.
- A. Einstein, Annalen der Physik, Vol. 40, 1916, pp. 284- 337.
- A. Einstein, “Relativity: The Special and General Theory,” Crown, New York, 1961.
- S. W. Hawking and G. F. R. Ellis, “The Large Scale Structure of Space-Time,” Cambridge University Press, Cambridge, 1994.
- R. C. Tolman, “Relativity, Thermodynamics and Cosmology,” Clarendon Press, Oxford, 1934.
- D. R. Buehler, Journal of Space Mixing, Vol. 2, 2004, pp. 1-22.
- E. M. Landau and L. D. Lifshitz, “The Classical Theory of Fields : Volume 2,” Butterworth-Heinemann, Oxford, 1980.
Appendix: Discussion on Classic Derivation of Electromagnetic Energy-Stress Tensor
According to [21] energy-stress tensor Tik of electromagnetic field could be derived from action principle
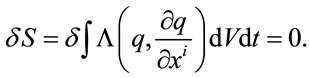 (38)
(38)
Variation of given action and determination it to zero leads to equation
 (39)
(39)
where
 (40)
(40)
Equation (39) is equivalent to proposition, that it is obtained conservation low of 4-momentum vector Pi
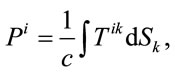 (41)
(41)
where integration is making in all hyperplane. Description of Tik, grounded on Equation (41) is ambiguous, because every tensor described as
 (42)
(42)
meets conservation low Equation (39). Trace of given energy-stress tensor with additional term
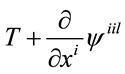 (43)
(43)
generally isn’t zero and must be calibrated with experiment.
The other rotational momentum conservation low specify energy-stress tensor to be symmetric
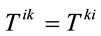 (44)
(44)
and it could be reached with choosing of Ψikl.
Now all this could be used to get Tik for Lagrangian of electromagnetic field
 (45)
(45)
which gives
 (46)
(46)
where Fkl is described as
 (47)
(47)
Tensor in Equation (46) isn’t symmetric. The trace calculation of energy-stress tensors Equation (46) gives
 (48)
(48)
which is true in electromagnetic field without charge, because δFil/δxi. Equation (48) satisfy Equation (43) transformation and finally the last equation could be rewritten as
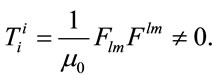 (49)
(49)
On the other hand symmetrization of 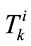 for indexes
for indexes  could be reached, if the term would be added
could be reached, if the term would be added
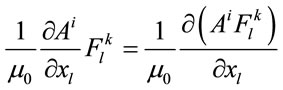 (50)
(50)
It could be made too, because it is Equation (42) transformation. The result of following transformations is new symmetric tensor
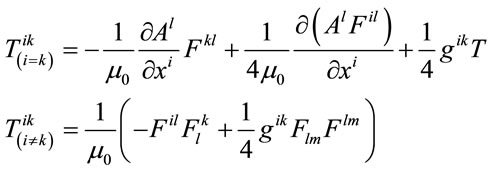 (51)
(51)
Transformations Equation (50) applied to whole  tensor change both not diagonal elements and diagonal elements of energy-stress tensor, which trace after transformation become zero
tensor change both not diagonal elements and diagonal elements of energy-stress tensor, which trace after transformation become zero
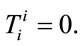 (52)
(52)
The answer to this question, which Equation (49) or Equation (52) is true, could be given just by experiments in a pure electric and magnetic fields. If gravity mass do not interact in both pure electric and magnetic fields, we must leave energy-stress tensor trace zero equality axiom. If interaction of gravity mass and pure electric and magnetic fields exist, there is sample explanation of this interaction within assumption of not zero trace of energystress tensor.

