Journal of Modern Physics
Vol.4 No.6(2013), Article ID:32994,6 pages DOI:10.4236/jmp.2013.46105
Positron-Excited Lithium Atom Collisions
1Department of Physics, Faculty of Science, Ain Shams University, Cairo, Egypt
2Egyptian E-Learning University (EELU), Giza, Egypt
Email: elbakry_salah@yahoo.com, e_eldahshan@yahoo.com
Copyright © 2013 Salah Y. El-Bakry et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 25, 2013; revised April 25, 2013; accepted May 16, 2013
Keywords: Positrons; Positronium Formation; Alkali Atoms; Collisions; Inelastic Scattering; Cross-Sections; Lithium; Polarization Potential
ABSTRACT
The inelastic scattering of positrons by excited lithium alkali atoms Li*(2p) have been investigated within the frame work of the coupled-static and frozen-core approximations with the assumption that the elastic and rearrangement channels are open. In the present work, a rather complicated computer code is developed based on the coupled-static, frozen-core and Green’s function partial wave expansion technique. The partial and total elastic and positronium (Ps) formation cross sections of e+-Li*(2p) are calculated through a wide range of incident energy of positrons ranging from 0.3 eV to 1000 eV. Also, we have calculated the partial and total elastic and rearrangement (reversal of the Ps formation) cross sections of Ps-Li+ collisions through the low, intermediate and high energy regions. The effect of polarization potential of the Ps atom is taken into our consideration. The total cross sections which corresponding to twelve partial cross sections (calculated at twelve values of the total angular momentum l = 0 to l = 11) are calculated for each channel. Our calculated total positronium formation cross sections are compared with experimental results and those calculated by other authors. The present calculations encourage the experimental physicists to carry out positron-lithium experiments by taking the excited lithium target into accounts in order to obtain more positronium especially in the low and intermediate energy regions.
1. Introduction
The importance of the study of positron-alkali atom collisions is the possibility of positronium (Ps) formation even at zero incident energy. This means that we are facing from the beginning a multi-channel collision problem in which at least two channels (elastic and positronium formation) are open. The positronium formation cross sections for the collision of positrons with lithium and sodium atoms are investigated using the hyperspherical close-coupling method [1] through the energy range 0.01 eV - 20 eV. The hyperspherical hidden crossing method (HHCM) is used to calculate the Ps formation cross section for positron-lithium collisions in the energy range 0 - 1.8 eV [2] as well as a correction term which includes the core polarization term in the model potential is added to the HHCM in the low-energy  scattering [3]. Three s-wave resonances in the positron-lithium system using the stabilization method are calculated [4]. The coupled-channel optical method [5] is used to study positron scattering by atomic lithium at energies ranging from the ionization threshold to 60 eV. The s-wave resonances in the positron-lithium system using the stabilization method are calculated [6] in the framework of hyperspherical coordinates. The positron-lithium collisions using two-center convergent closecoupling calculations are investigated [7]. On the theoretical and experimental levels, it has been shown [8,9] that Ps formation has an important contribution to the total collisional cross sections of positron alkali atom scattering at the low and intermediate energy regions. In the above mentioned work the lithium target atom is considered to be in the ground state.
scattering [3]. Three s-wave resonances in the positron-lithium system using the stabilization method are calculated [4]. The coupled-channel optical method [5] is used to study positron scattering by atomic lithium at energies ranging from the ionization threshold to 60 eV. The s-wave resonances in the positron-lithium system using the stabilization method are calculated [6] in the framework of hyperspherical coordinates. The positron-lithium collisions using two-center convergent closecoupling calculations are investigated [7]. On the theoretical and experimental levels, it has been shown [8,9] that Ps formation has an important contribution to the total collisional cross sections of positron alkali atom scattering at the low and intermediate energy regions. In the above mentioned work the lithium target atom is considered to be in the ground state.
This paper presents a trial to investigate the effect of the excited state of the target on the production of Ps formation through the inelastic collisions of positrons with initially excited lithium atoms. Section 2 of this work involves a brief theoretical treatment of our problem. Section 3 deals with the discussion of our results and the comparison with different authors.
2. Theoretical Formalism
The investigation of the two channel problem of 
 collisions with elastic and positronium formation channels are open and all other channels are closed, is subjected to the solution of the two coupled integro-differential equations (Equations (1) and (2)):
collisions with elastic and positronium formation channels are open and all other channels are closed, is subjected to the solution of the two coupled integro-differential equations (Equations (1) and (2)):
 (1)
(1)
where
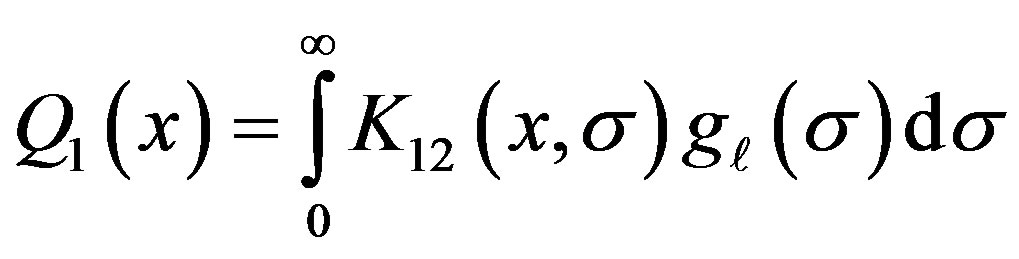
and
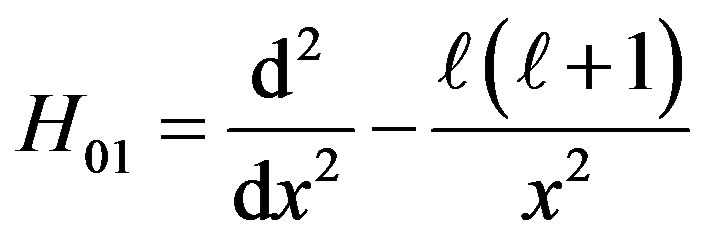
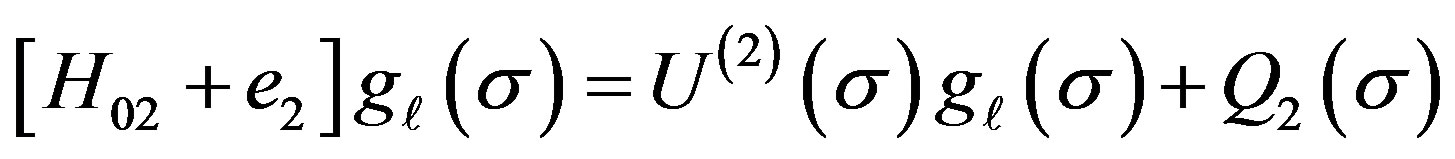 (2)
(2)
where

and
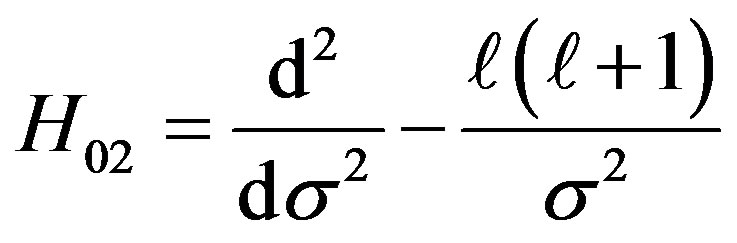 where
where 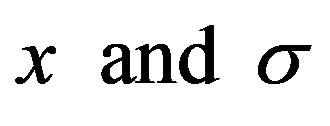 are the position vectors of the incident positron and the centre of mass of positronium, respectively, with respect to an infinitely heavy nucleus located at the origin of our configuration space. Correspondingly,
are the position vectors of the incident positron and the centre of mass of positronium, respectively, with respect to an infinitely heavy nucleus located at the origin of our configuration space. Correspondingly,  are the momenta and
are the momenta and 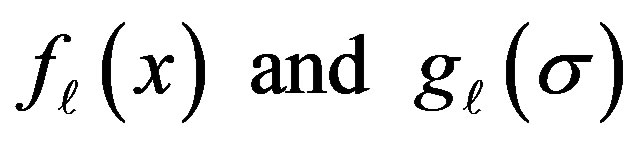 are the partial scattering wave functions of the first and second channels associated with the total angular momentum
are the partial scattering wave functions of the first and second channels associated with the total angular momentum .
. 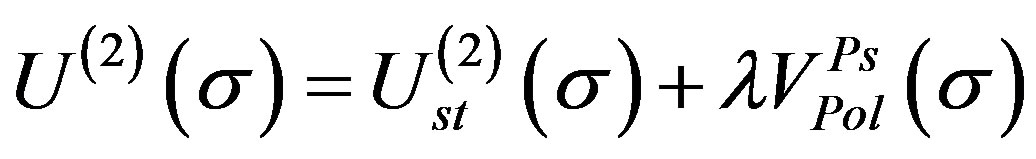 where
where 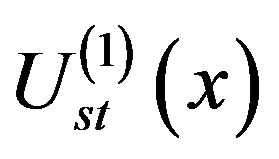 and
and 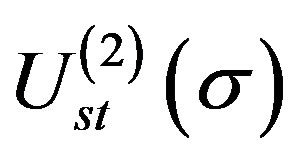 are the static potentials of the first and second channels, respectively, which are defined as:
are the static potentials of the first and second channels, respectively, which are defined as:  (3)
(3)
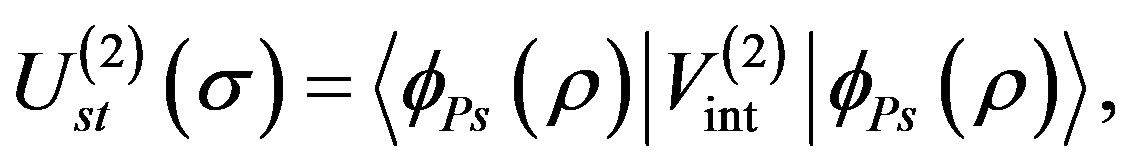 (4)
(4)
 and
and 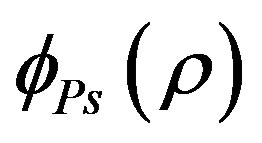 are the wave functions of the 2p-excited electron of the lithium target atom and positronium, respectively [10]. r is the position vector of the 2p-excited electron with respect to the origin of the scattering system at which an infinitely heavy nucleus of charge
are the wave functions of the 2p-excited electron of the lithium target atom and positronium, respectively [10]. r is the position vector of the 2p-excited electron with respect to the origin of the scattering system at which an infinitely heavy nucleus of charge  (
( , for Li) is located.
, for Li) is located. 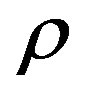 is the relative distances between the 2p-excited electron and the positron in the positronium.
is the relative distances between the 2p-excited electron and the positron in the positronium. 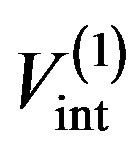 and
and 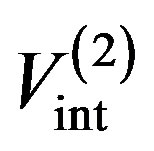 are the interaction potentials of the first and second channels, respectively.
are the interaction potentials of the first and second channels, respectively.  is the polarization potential of Ps and
is the polarization potential of Ps and 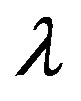 is a switching parameter (it is one if the polarization of the Ps is incorporated and zero otherwise). The coupling kernels
is a switching parameter (it is one if the polarization of the Ps is incorporated and zero otherwise). The coupling kernels 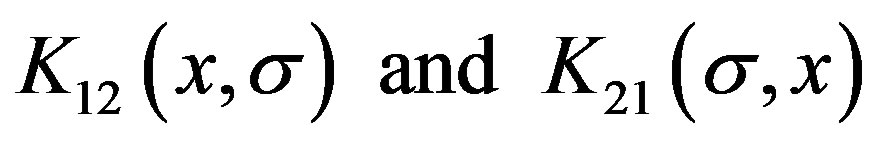 are given in terms of the positronium wave function and the excited target wave function (for more details see Ref.[10]).
are given in terms of the positronium wave function and the excited target wave function (for more details see Ref.[10]). In order to take the effect of the rest of the target on the positronium, we switch on the polarization potential of the positronium 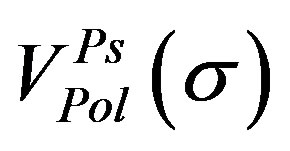 i.e. the polarization potential of the second channel. The Ps polarization potential [14] is defined by
i.e. the polarization potential of the second channel. The Ps polarization potential [14] is defined by
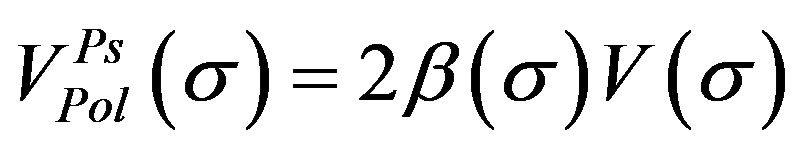 (5)
(5)
where 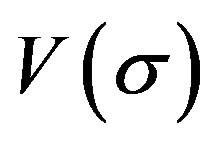 is a potential of the form
is a potential of the form
 (6)
(6)
The function 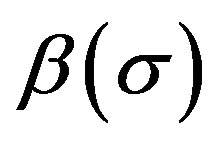 is calculated as follows:
is calculated as follows:
Let  (where
(where  is the ground state energy of the Ps and
is the ground state energy of the Ps and 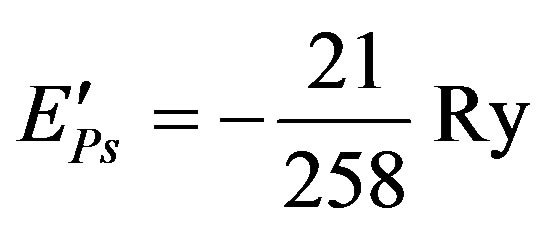 is the binding energy of the polarized positronium), and
is the binding energy of the polarized positronium), and
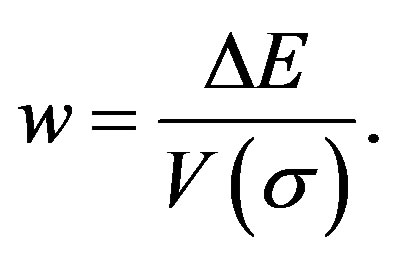 Also, we consider the two functions
Also, we consider the two functions 
such that
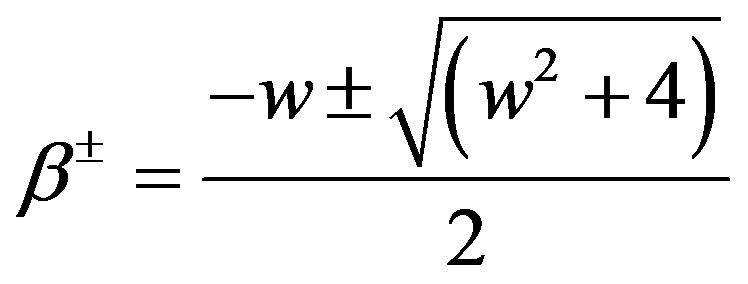 . (7)
. (7)
The adiabatic energy of the positronium within the field of a unit positive charge is found to be
 (8)
(8)
The proper 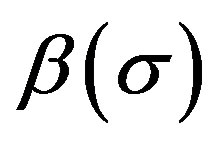 for calculating
for calculating 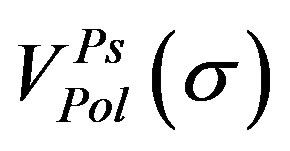 is that one of
is that one of 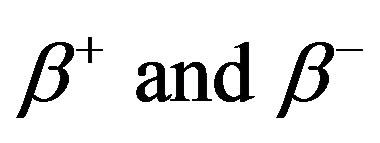 which yields a minimum value for
which yields a minimum value for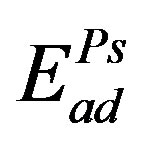 .
.
In order to calculate the reactance and transition matrices (R and T, respectively) required for the evaluation of the partial and total cross sections of the first and second channels we employed the numerical iterative Greenfunction partial-wave expansion technique [10] within the framework of the coupled-static approximation. The iterative solutions of Equations (1) and (2) are identified by:
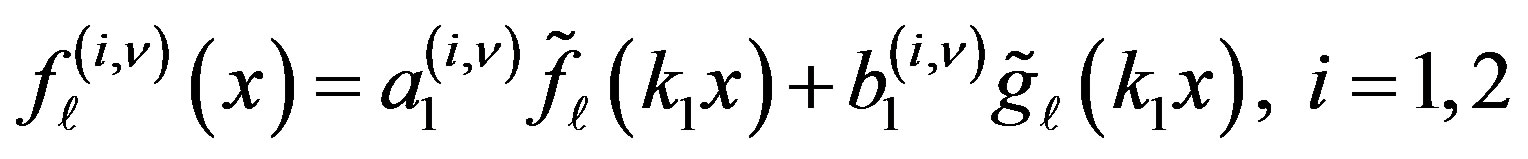 (9)
(9)
and
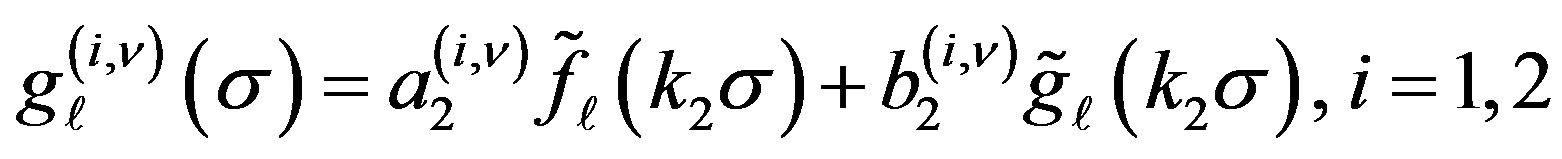 (10)
(10)
where 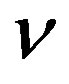 is the number of iterations and the functions
is the number of iterations and the functions  and
and 
 are related to the spherical Bessel functions of the first and second kinds,
are related to the spherical Bessel functions of the first and second kinds,  and
and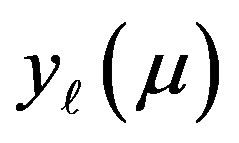 , respectively, by the relations
, respectively, by the relations 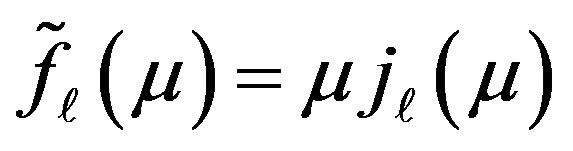 and
and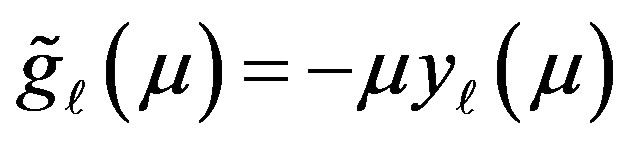 . Defining the two matrices
. Defining the two matrices
 (11)
(11)
where 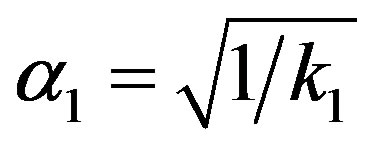 and
and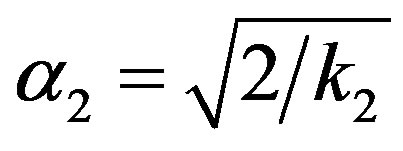 , we obtain the elements of the reactance matrix by applying the definitions
, we obtain the elements of the reactance matrix by applying the definitions
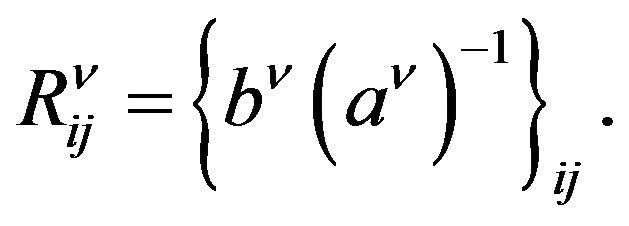 (12)
(12)
The iterative transition matrix,  , is related to the reactance matrix
, is related to the reactance matrix  by
by
 (13)
(13)
where  is
is  unit matrix and
unit matrix and . The elements of the transition matrix can be written as
. The elements of the transition matrix can be written as
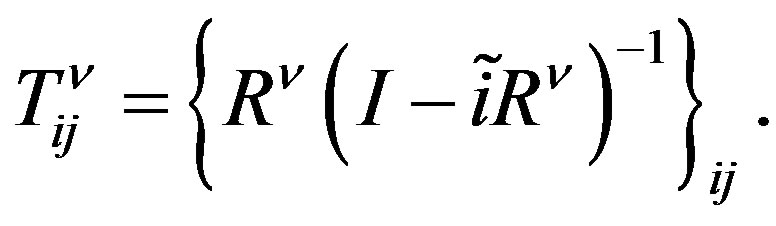 (14)
(14)
The iterative partial cross-sections corresponding to the total angular momentum , i.e.
, i.e. 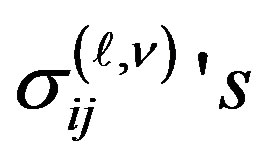 are determined ( in
are determined ( in 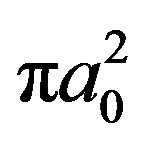 units ) by
units ) by
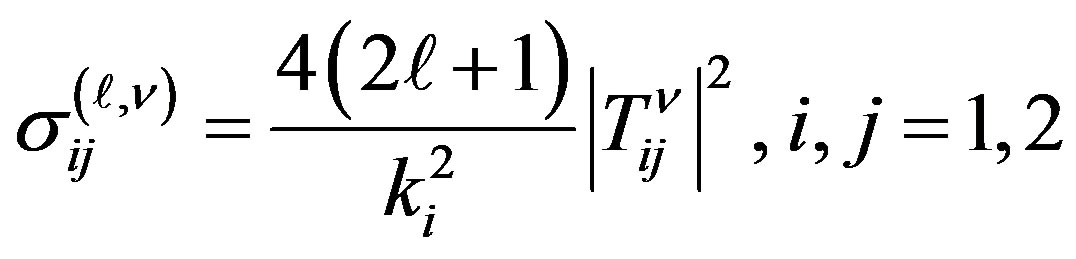 . (15)
. (15)
The total cross-sections in the 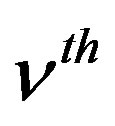 iteration are calculated by
iteration are calculated by
 , (16)
, (16)
where 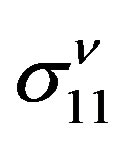 is the total elastic cross section of the positrons with momentum
is the total elastic cross section of the positrons with momentum 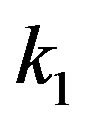 scattered from the excited lithium atoms
scattered from the excited lithium atoms 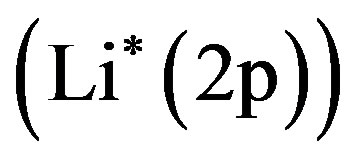 and
and 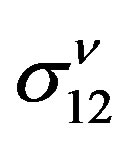 is the total positronium formation cross sections, respectively.
is the total positronium formation cross sections, respectively.
3. Results and Discussion
The mathematical formalism of the preceding section has been applied to the collisions of positrons with excited lithium atoms (Li*(2p)).
We started the computational process by testing the iterative solutions of the coupled integro-differential Equations (1) and (2). Two tests have been made: The first was concerned with the convergence of the elements of the reactance matrix Rν, Equation (12), and partial cross sections, Equation (15), when the number of iterations (ν) is increased and second was concentrated on the convergence when the integration range (IR) is increased (Physically IR represents the distance at which we assume that the scattered positrons are not affected by the excited lithium atoms with respect to the first channel as well as for the second channel IR represents the distance at which the Ps atom and the rest of the target are totally separated, i.e. IR is the range away from the target nucleus to which all radial integrals are calculated using Simpson expansions). We found out that the reactance matrix corresponding to a given integration range and total angular momentum  becomes almost symmetric after twenty iterations. Consequently, we fixed this value of ν in all further investigations.
becomes almost symmetric after twenty iterations. Consequently, we fixed this value of ν in all further investigations.
With regard to the second test, we put IR = nh, where n is the number of mesh points and h is the Simpson step used in the Simpson expansions of the integrals, and varied n and h in a very elaborate manner for all values  and
and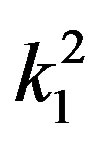 . The convergences of our results are found at h = 0.0625 and n = 768, i.e. IR = 48 a.u. Therefore, we fixed this value of IR in all other calculations.
. The convergences of our results are found at h = 0.0625 and n = 768, i.e. IR = 48 a.u. Therefore, we fixed this value of IR in all other calculations.
The final calculations were carried out for 12 partial waves corresponding to 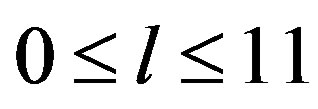 at 28 values of
at 28 values of  representing the low energy region
representing the low energy region  and the largely extend intermediate region
and the largely extend intermediate region 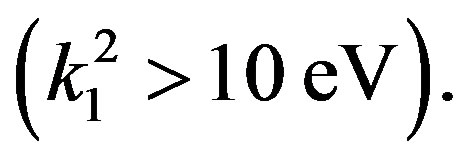 Let us consider that
Let us consider that  denotes the total cross section with polarization potential of the Ps atom and
denotes the total cross section with polarization potential of the Ps atom and 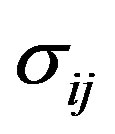 is the total cross section without polarization potential.
is the total cross section without polarization potential.
Figures 1 and 2 show the comparison between our calculated total elastic  and total Ps formation cross sections
and total Ps formation cross sections 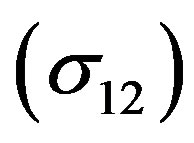 of e+-Li*(2p) without and with polarization potential. From these figures we conclude that:
of e+-Li*(2p) without and with polarization potential. From these figures we conclude that:
(a)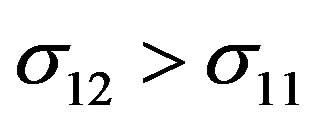 : at
: at  and at
and at 
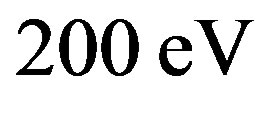 (b)
(b)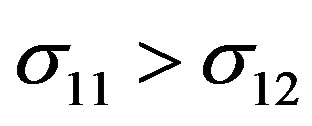 : at
: at  and at
and at 
 and this emphasizes the argument that the Ps formation is very important at very low energy region.
and this emphasizes the argument that the Ps formation is very important at very low energy region.
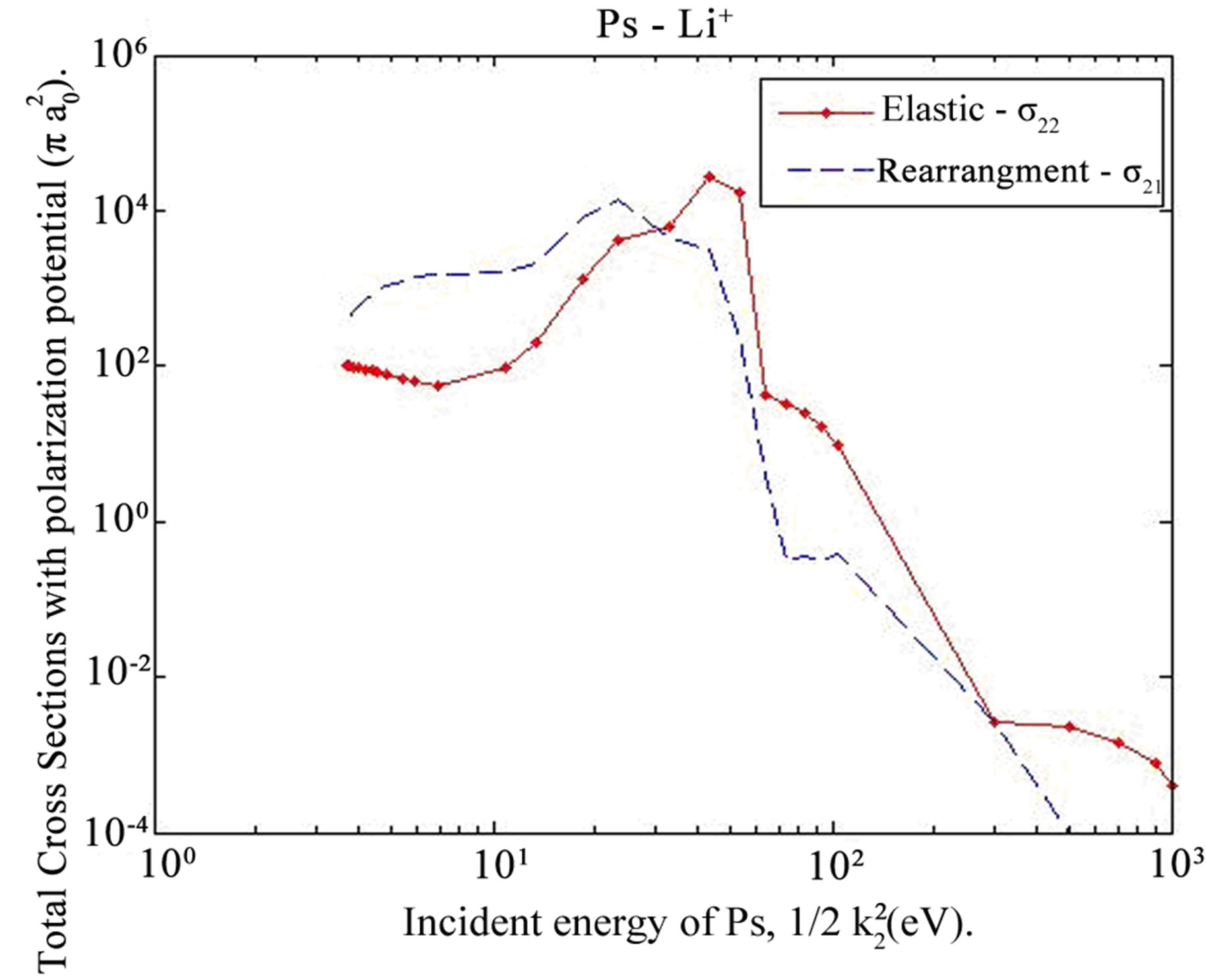
Figures 3 and 4 present a comparison between our calculated total rearrangement 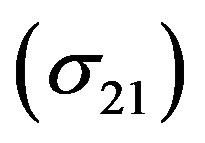 and total elastic
and total elastic

Figure 1. Comparison between our calculated total elastic  and total Ps formation cross sections
and total Ps formation cross sections  of e+- Li*(2p) scattering without polarization potential.
of e+- Li*(2p) scattering without polarization potential.
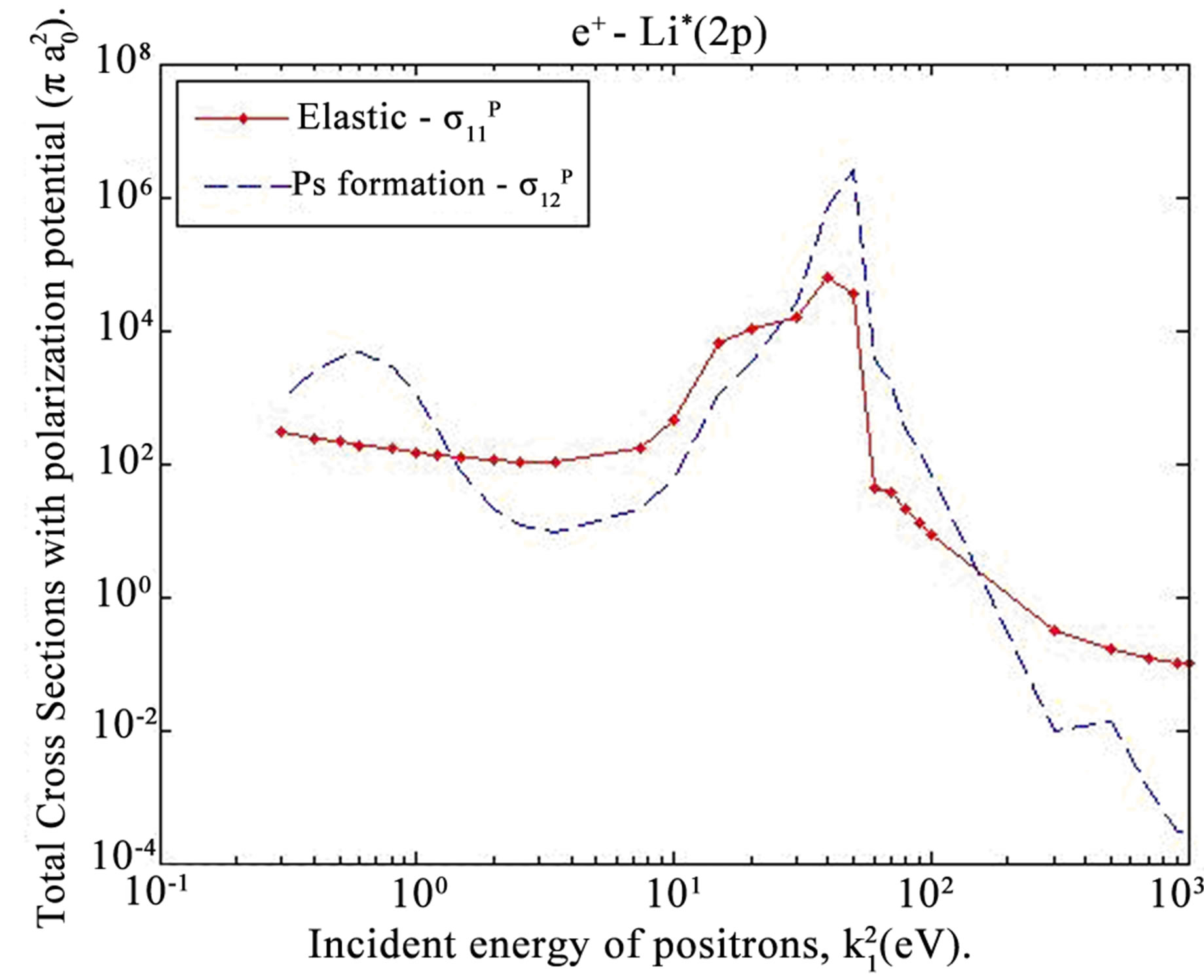
Figure 2. Comparison between our calculated total rearrangement (reversal of the positronium formation) cross sections  and total elastic cross sections
and total elastic cross sections  of PsLi+ scattering without polarization potential.
of PsLi+ scattering without polarization potential.
 cross sections of Ps-Li+ without and with polarization potential. These figures explore that:
cross sections of Ps-Li+ without and with polarization potential. These figures explore that:
(a) : at
: at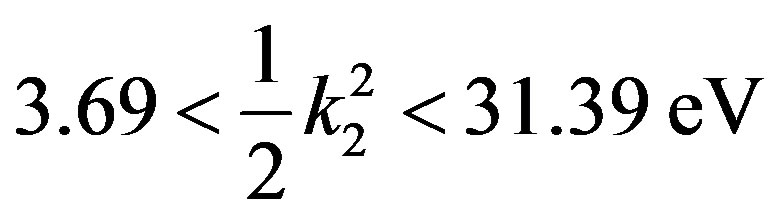 (b)
(b)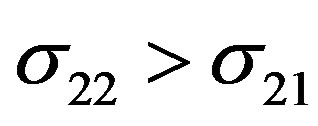 : at
: at .
.
From these figures we conclude that the reversals of Ps formation cross sections are more important than the elastic ones up to 31.39 eV of the incident energy of Ps. After 32 eV the total elastic cross sections of Ps-Li+ becomes more important.
Figure 5 shows the effect of adding the polarization potential of Ps atom in its ground state which is the increase of the total elastic cross sections (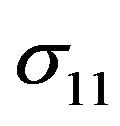 of e+- Li*(2p) scattering) through the low and intermediate energy regions and this demonstrates the importance of polarization potential especially at low energies. Figure 5 also shows the oscillating behavior of the total positronium formation cross sections
of e+- Li*(2p) scattering) through the low and intermediate energy regions and this demonstrates the importance of polarization potential especially at low energies. Figure 5 also shows the oscillating behavior of the total positronium formation cross sections 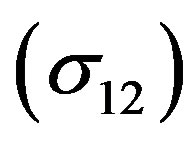 which supports the possible appearance of resonance. Beyond 100 eV we notice that the Ps formation does not play a fundamental role in the total collisional cross sections of e+-Li*(2p) inelastic scattering.
which supports the possible appearance of resonance. Beyond 100 eV we notice that the Ps formation does not play a fundamental role in the total collisional cross sections of e+-Li*(2p) inelastic scattering.
The effect of polarization potential on the total Ps formation cross sections of e+-Li*(2p) scattering is shown in Figure 6, from which we conclude that the total positronium formation cross sections 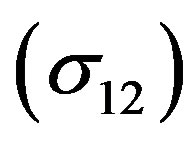 are increased. The effect of polarization potential on the total rearrangement cross sections
are increased. The effect of polarization potential on the total rearrangement cross sections  and the total elastic cross sections
and the total elastic cross sections  of Ps-Li+ scattering is shown in Figures 7 and 8, respectively.
of Ps-Li+ scattering is shown in Figures 7 and 8, respectively.
Comparison between various total positronium formation cross sections of positron-lithium scattering determined by different authors is presented in Figure 9. Also from Figure 9 we notice that: a) our  through the
through the
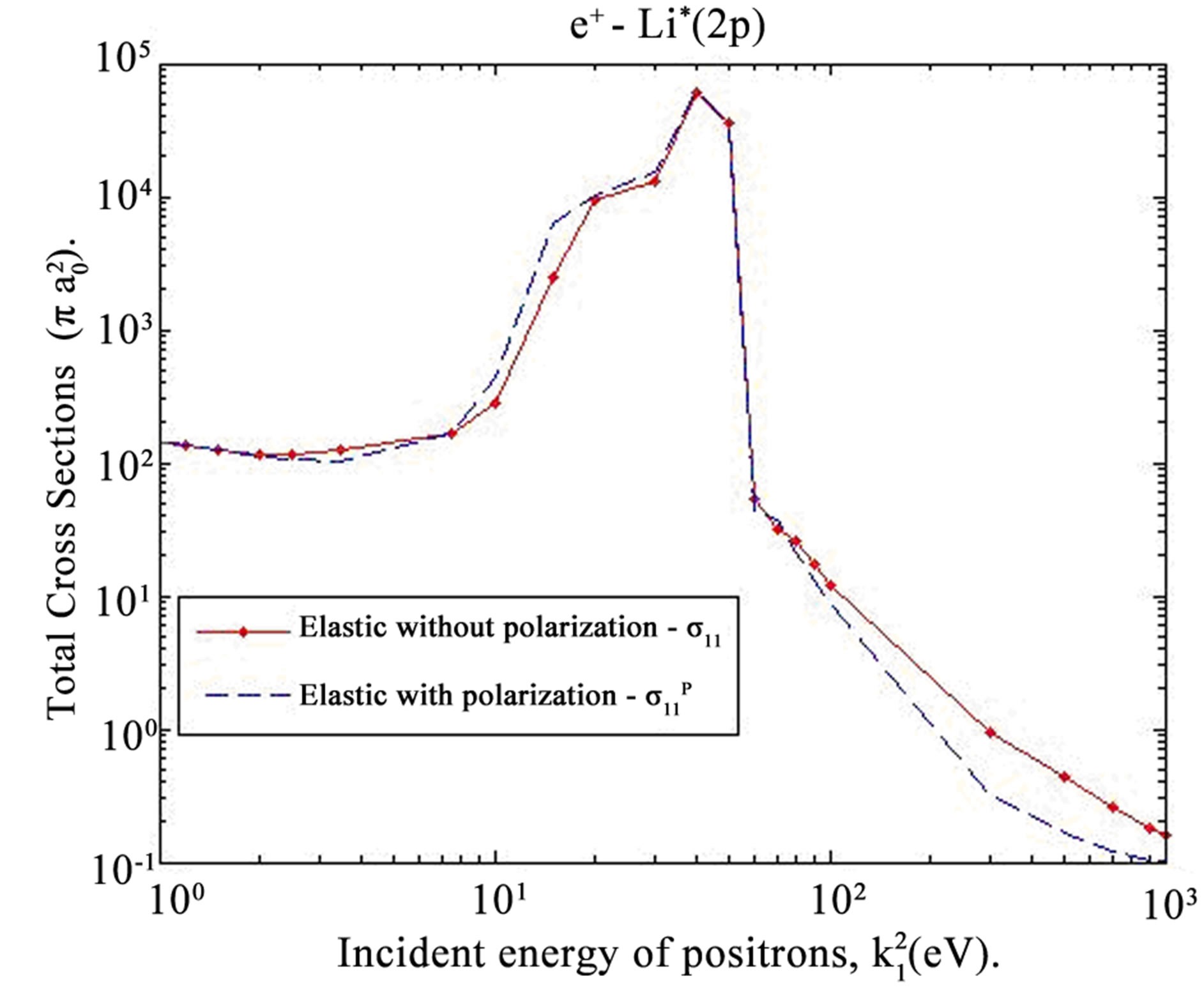
Figure 5. Shows the effect of polarization potential on the total elastic cross sections of e+-Li*(2p) scattering.
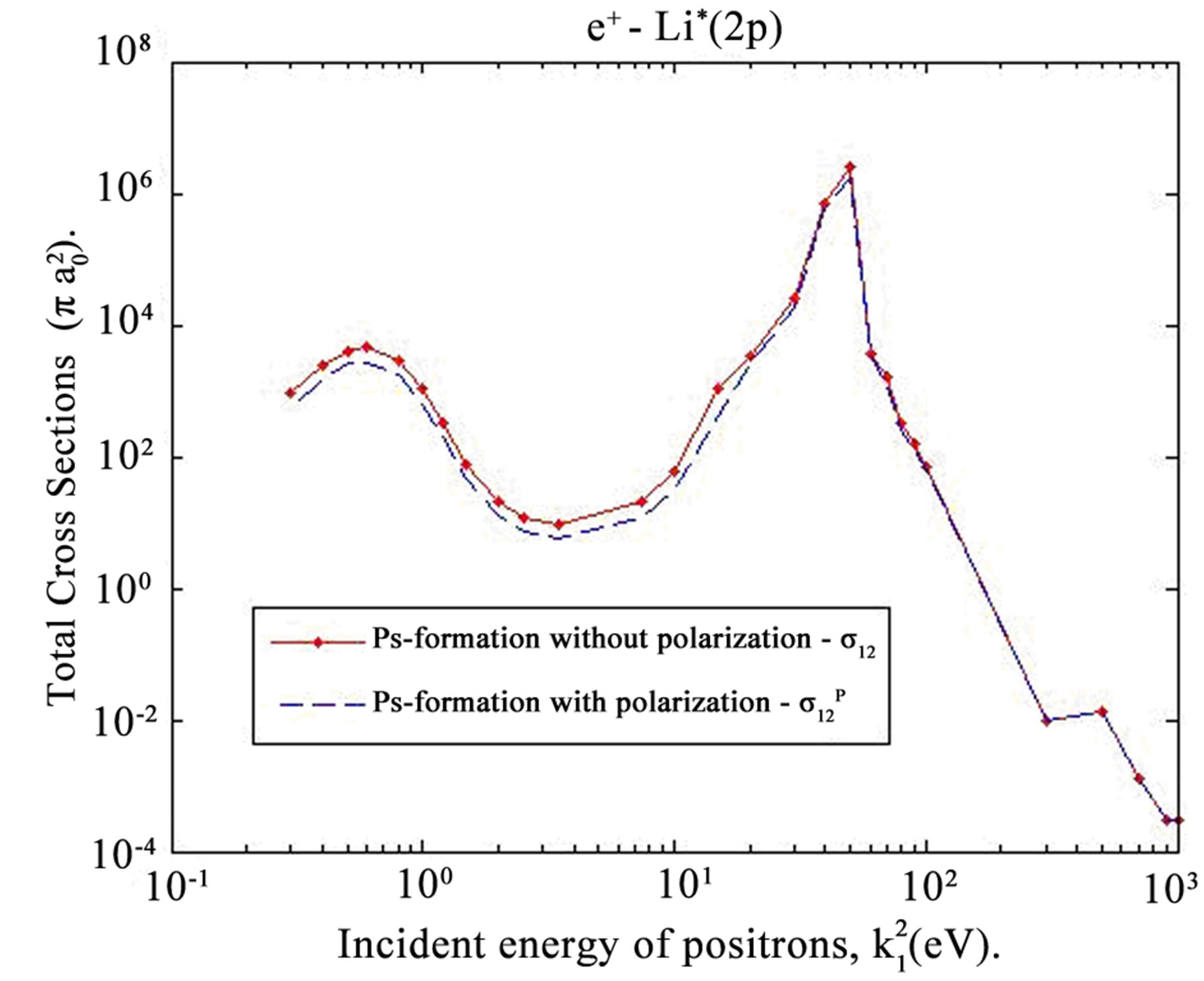
Figure 6. Shows the effect of polarization potential on the total Ps formation cross sections of e+-Li* (2p) scattering.
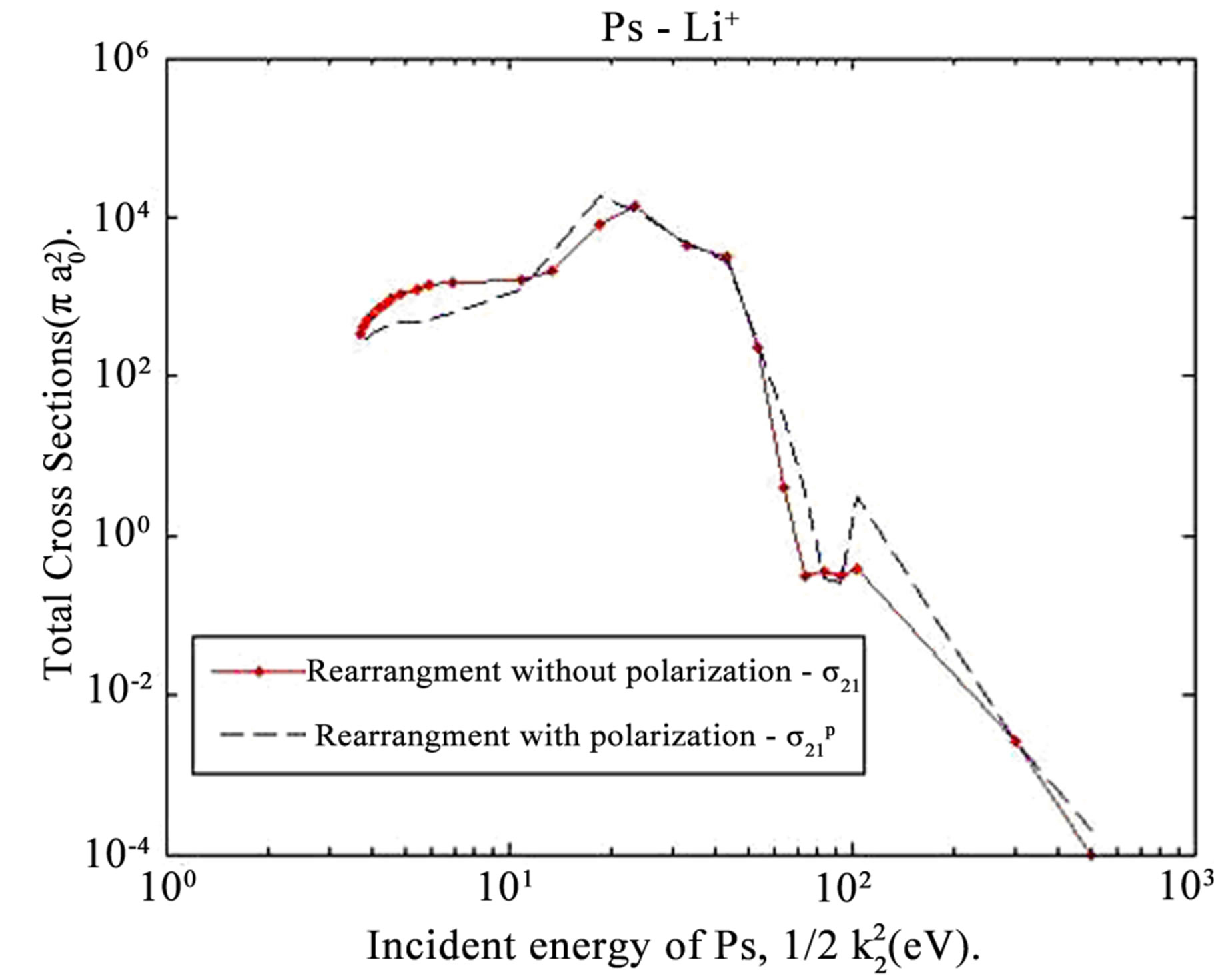
Figure 7. Shows the effect of polarization potential on the total rearrangement (reversal of the Ps formation) cross sections of Ps-Li+ scattering.

Figure 8. Shows the effect of polarization potential on the total elastic cross sections of Ps-Li+ scattering.

Figure 9. Comparison between various total positronium formation cross sections (in  ) of e+-Li scattering determined by different authors [8-13].
) of e+-Li scattering determined by different authors [8-13].
energy range 1.5 - 7.5 eV have the same order of magnitude as that determined experimentally. (b) our calculated Ps formation cross sections of e+-Li*(2p) scattering are greater than those of the experimental values of e+-Li (2s) scattering by: i) one order of magnitude at 0.3 eV and 1.2 eV, ii) two orders of magnitude at 0.4 eV - 0.8 eV, 15 eV.
The previous results of Ps formation cross sections emphasize that:
The positronium formation cross sections of e+-Li*(2p) scattering are considerably greater than those of e+-Li(2s) scattering, especially at low energy region.
Finally, we conclude that:
1) The effect of adding the polarization potential of Ps atom in its ground state is the increase of the total elastic cross-sections  through the low and intermediate energy regions as well as the increase of the total positronium formation cross-sections
through the low and intermediate energy regions as well as the increase of the total positronium formation cross-sections 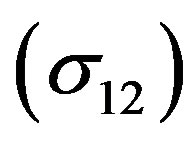 through the whole energy range except at 58 eV and 60 eV.
through the whole energy range except at 58 eV and 60 eV.
2) The existence of the oscillating behaviour of the total elastic cross-sections  supports the possible appearance of resonance.
supports the possible appearance of resonance.
3) For elastic channel of Ps-Li+ we have:
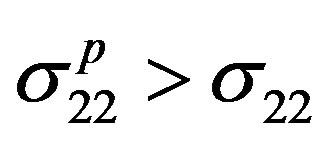 through the whole energy range except at: 10.89 eV, 47.39 eV, 51.39 eV, 53.39 eV and 57.39 eV.
through the whole energy range except at: 10.89 eV, 47.39 eV, 51.39 eV, 53.39 eV and 57.39 eV.
4) The present calculations of Ps formation cross sections emphasize that the positronium formation cross sections 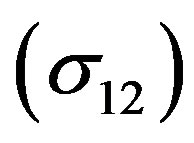 of e+-Li*(2p) scattering are considerably greater than those of e+-Li(2s) scattering, especially at low energy region.
of e+-Li*(2p) scattering are considerably greater than those of e+-Li(2s) scattering, especially at low energy region.
5) The present calculations encourage the experimental physicists to carry out positron-lithium experiments by taking the excited lithium target into accounts in order to obtain more positronium especially in the low and intermediate energy regions.
REFERENCES
- A.-T. Le, M. W. J. Bromley and C. D. Lin, Physical Review A, Vol. 71, 2005, Article ID: 032713.
- S. J. Ward and J. Shertzer, Nuclear Instruments and Methods in Physics Research Section B, Vol. 241, 2005, pp. 257-261.
- S. J. Ward and J. Shertzer, Nuclear Instruments and Methods in Physics Research Section B, Vol. 221, 2004, pp. 206-209.
- U. Roy and Y. K. Ho, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 35, 2002, pp. 2149- 2158.
- K. Ratnavelu and S. Y. Ng, Chinese Physics Letters, No. 723, 2006, pp. 1753-1957.
- H. Han, Z. Zhong, X. Zhang and T. Shi, Physical Review A, Vol. 78, 2008, Article ID: 044701.
- A. V. Lugovskoy, A. S. Kadyrov, I. Bray and A. T. Stelbovics, Physical Review A, Vol. 82, 2010, Article ID: 062 708.
- E. Surdutovich, J. M. Johnson, W. E. Kauppila, C. K. Kwan and T. S. Stein, Physical Review A, Vol. 65, 2002, Article ID: 032713. doi:10.1103/PhysRevA.65.032713
- T. S. Stein, M. Harte, J. Jiang, W. E. Kauppila, C. K. Kwan, H. Li and S. Zhou, Nuclear Instruments and Methods in Physics Research Section B, Vol. 143, 1998, pp. 68-80.
- S. Y. El-Bakry and M. A. Abdel-Raouf, IL Nuovo Cimento D, Vol. 19, 1997, pp. 637-664.
- M. A. Abdel-Raouf, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 21, 1988, pp. 2331-2352.
- P. S. Mazumdar and A. S. Ghosh, Physical Review A, Vol. 34, 1986, pp. 4433-4435.
- M. A. Abdel-Raouf, S. Y. El-Bakry, A. H. Moussa and M. El-Shabshiri, Czechoslovak Journal of Physics B, Vol. 39, 1989, pp. 1066-1088.
- M. A. Abdel-Raouf, Acta Physica Hungarica, Vol. 63, 1988, pp. 21-50.