Journal of Modern Physics
Vol.4 No.5(2013), Article ID:31599,4 pages DOI:10.4236/jmp.2013.45087
Band Structure of New ReFeAsO Superconductors
1Bogolyubov Institute for Theoretical Physics, NASU, Kiev, Ukraine
2Lashkaryov Institute of Semiconductor Physics, Kiev, Ukraine
3Metal-Insulator Transition Laboratory, Electronics and Telecommunications Research Institute, Daejeon, South Korea
Email: skruchin@i.com.ua
Copyright © 2013 Sergei P. Kruchinin et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 19, 2013; revised April 21, 2013; accepted May 20, 2013
Keywords: Iron-Based Superconductors; Band Structure; Density of State; Superconducting Critical Temperature
ABSTRACT
We investigate the band structure of Fe-based superconductors using the first-principle method of density-functional theory. We calculated the band structure and the density of states at the Fermi level for ReFeAsO (Re = Sm, Er) superconductors. Our calculations indicate that the maximum critical superconducting transition temperature Tc will be observed for compounds with Sm and Er at 55 and 46 K, respectively.
1. Introduction
The discovery of a new class of high-temperature superconductors—Fe-based layered compounds—aroused a significant interest at the beginning of 2008 and gave hope for a progress in the synthesis of novel high-temperature superconductors (HTSC) up to room-temperature superconductors [1,2]. The important role in the explanation of physical properties of superconductors is played by calculations of the electronic structure from the first principles. It is worth noting that one of the basic properties of high-temperature superconductors is the presence of many bands [3]. In the work [4], it was shown that the formation of a superconducting state depends essentially on the density of states near the Fermi surface.
In the present work, we investigate the band structure of some Fe-based compounds, by using the first-principle method of density-functional theory. Compound SmFeAsO showed the evidence of superconductivity at as high as 55 K. Also the superconducting ErFeAsO has recently been found [5].
These superconductors have a complicated multiband structure. We calculated the band structure and the density of states at the Fermi level. Our calculations indicate that the maximum critical superconducting transition temperature Tc will be observed for compounds with Sm. We obtain that Tc = 46 K for the compound ErFeAsO.
The novelty of this work is that we are having band calculations from first principles and using a magnetic pairing mechanism makes the assessment of the superconducting transition temperature Tc. We first present the band calculations of superconductor ErFeAsO, which isopened much later than other iron superconductors.
2. Methodology
We calculate the band structures of HTSC, by using the Band Lab program. This program is designed for Windows computer systems and performs calculations of the electronic structure of crystalline solids.
The bands are calculated using the method outlined by Pickett [6] within the density-functional scheme [7]. Since a summary of the method and its applications has been presented by Devreese and Van Camp [8], we outline the method here only in brief.
Starting with the N-electron problem in the field of ionic potentials
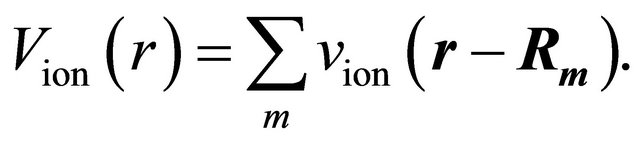 (1)
(1)
with the ions at static positions Rm, we have the Hamiltonian
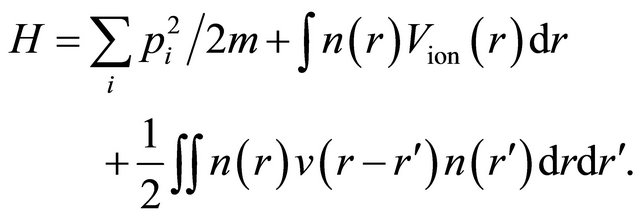 (2)
(2)
Here,  is the electron density operator at r, and
is the electron density operator at r, and 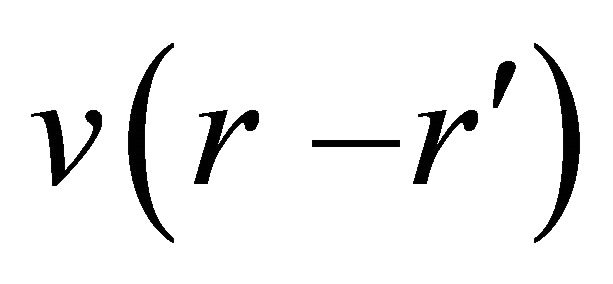 is the Coulomb interaction.
is the Coulomb interaction.
Hohenberg and Kohn established that there is a oneto-one correspondence between the ionic potential Vion (to within an arbitrary constant) and the ground state density n, so that the many-body problem can be considered as a functional of the density, rather than a functional of the potential [7].
Hohenberg and Kohn [9] established that, for variations δn of the energy density which conserve the particle number N, the ground-state energy functional 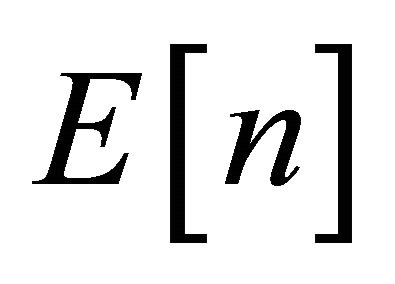 is minimized by the ground-state density, with corrections of the order of δn2. The resulting variational principle allows one to accurately obtain numerical results.
is minimized by the ground-state density, with corrections of the order of δn2. The resulting variational principle allows one to accurately obtain numerical results.
The energy functional has the form:
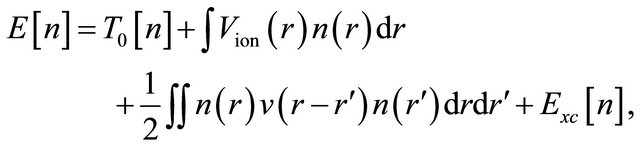 (2)
(2)
where 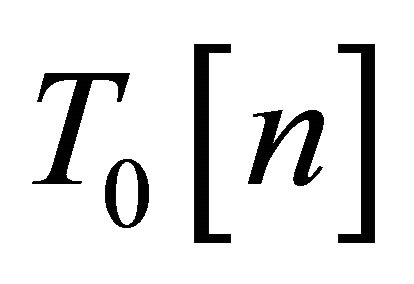 is the kinetic energy of the system of interacting electrons with the density
is the kinetic energy of the system of interacting electrons with the density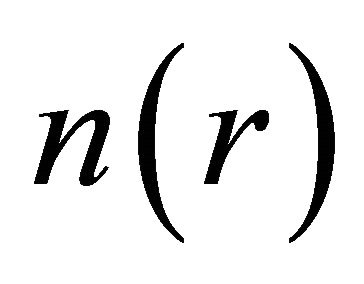 , and
, and  is the exchange-correlation energy. If one has adequate approximations for
is the exchange-correlation energy. If one has adequate approximations for 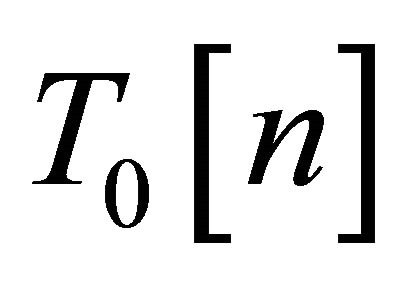 and
and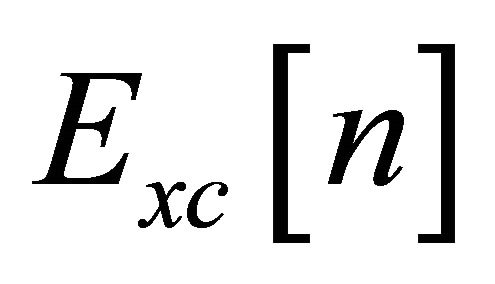 , the energy can be obtained directly from relation (3), by the minimization with respect to
, the energy can be obtained directly from relation (3), by the minimization with respect to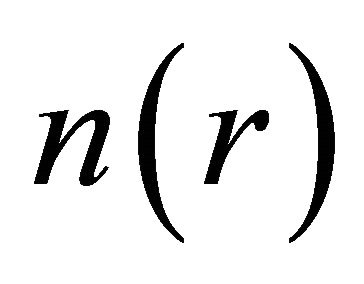 .
.
The energy functional is minimized by the density functional described by the above-presented relations, by performing iterations to attain the self-consistency.
Within the density-functional theory, the one-electron eigenvalues and eigenfunctions have no physical meaning and are not physically realizable. Some reviews containing discussions of applications of the density-functional theory, as well as the generalization to spin-polarized systems, are given, for example, in [10].
3. Band Structures of a Number of Oxypnictides ReFeAsO
The crystal structure of compound ReFeAsO is shown in Figure 1. Such substances possess the tetragonal structure at room temperature. The crystal structure is formed by alternating FeAs layers revealing antiferromagnetism which are separated by ReO layers. The results of calculations of the electronic spectrum can be found in [11]. It should be emphasized that the specific features of the electronic spectrum are related to the quasi-two-dimensional character of superconductivity in FeAs planes.
In many works, the increase in Tc which is caused by the replacement of La by other rare-earth elements is frequently named the “chemical” pressure [11]. A similar effect is characteristic of high-temperature superconductors [12]. The substitution of various rare-earth ions into the series of compounds ReFeAsO, as distinct from cuprate superconductors ReBaCuO, leads to a quite large dispersion of values of Tc. We may consider the magnetic mechanism of pairing in Fe-based superconductors. Spins of rare-earth ions interact strongly with spins of
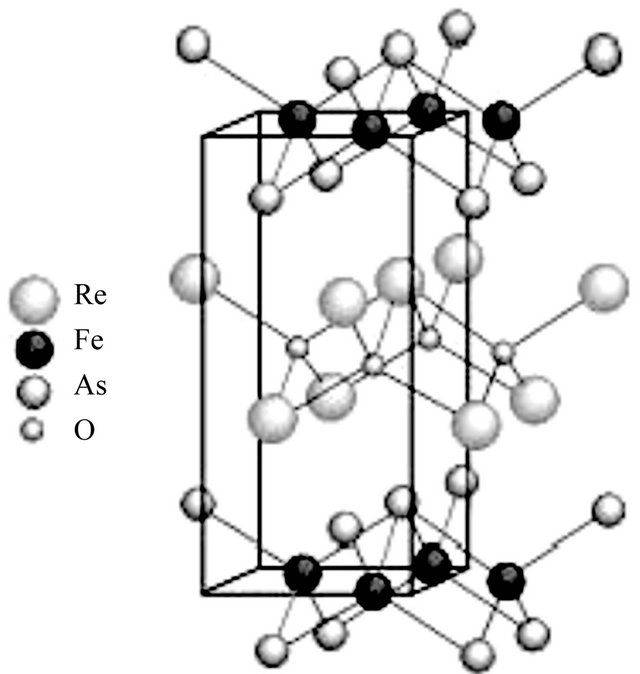
Figure 1. Crystalline structure of ReFeAsO.
iron and can essentially influence the spectrum of spin fluctuations in FeAS planes, which increases Tc if the magnetic mechanism of pairing is dominant.
We have carried out ab initio calculations for a number of oxyphictides ReFeAsO in the framework of an approach based on density-functional theory. The results of calculations are presented in Figures 2 and 3 for the band structure and the density of states in ReFeAsO. At a comprehensive study of the density of states, the relationship of the density of states at the Fermi level and the value of Tc is revealed. When comparing the band calculations Figures 2 and 3 shows that the density of states at the Fermi level is much higher in Figure 2 than in Figure 3, that is a superconductor SmFe AsO has a higher density of states than ErFeAsO. Therefore, the estimates for formula (4) give the above superconducting transition temperature for SmFe AsO. In Figure 4, we give the results of our theoretical calculations (circles) and experimental values (squares) of the critical supercondicting transition temperature. We indicate a good agreement with experimental data. In the calculations of Tc, we used the BCS-like formula for the magnetic mechanism [13]
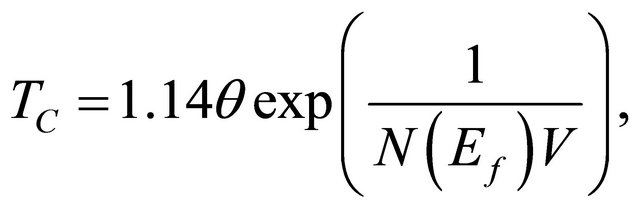 (4)
(4)
where θ-energy of spin fluctuations , V-attractive pairing potential acting between electrons, 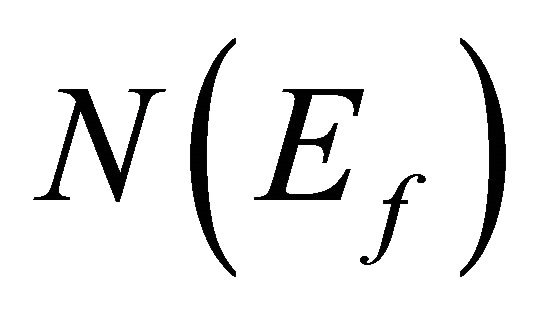 -density of states on the Fermi surface.
-density of states on the Fermi surface.
4. Summary
The discovery of a new type of high-temperature superconductivity in a FeAs system generates expectation of the appearance of novel superconductors with higher Tc by means of the doping that consists of the substitution of the atoms lying outside of the principal layers comprising FeAs. In FeAs, such a doping is favorable due to
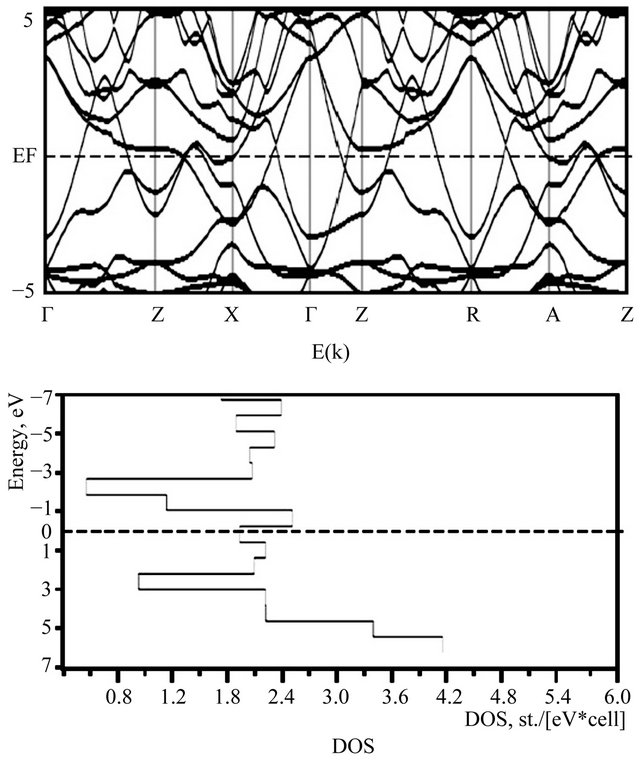
Figure 2. Results of our calculations of the band structure and the density of states for SmFeAsO with Tc = 55.0 K.
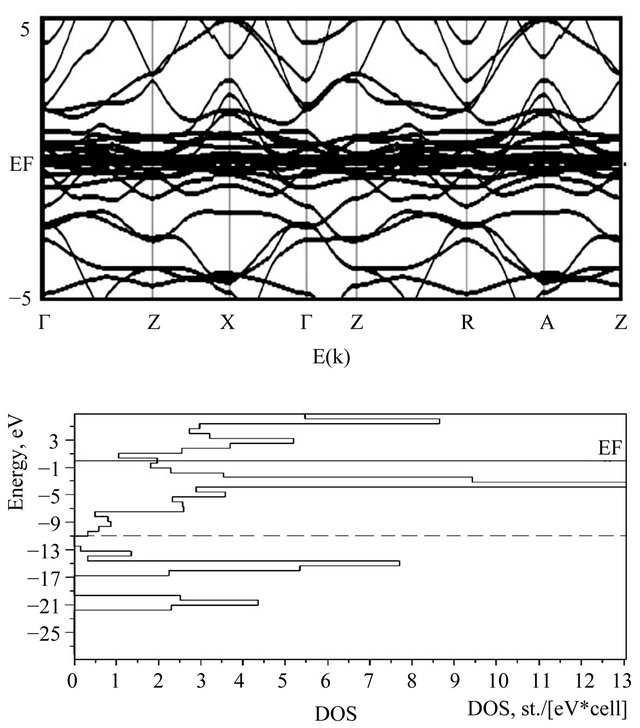
Figure 3. Results of our calculations of the band structure and the density of states for ErFeAsO with Tc = 46 K.
the easy replacement of chemical elements. In compounds ReFeAsO, the substitution of the rare-earth element is of special interest. We have carried out ab initio calculations for a number of oxypnictides ReFeAsO in
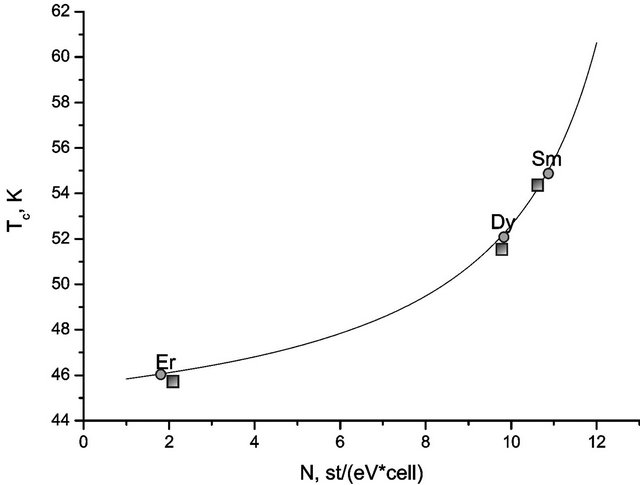
Figure 4. Dependence of Tc on the density of states on the Fermi surface N(Ef) for ReFeAsO [13] (○—theory, □—experiment).
the framework of density-functional theory. Our results indicate that the maximum critical superconducting transition temperature will be attained for compounds with Sm  and for ErFeAsO
and for ErFeAsO .
.
5. Acknowledgements
The authors thank Profs. Yu. Matsuda and K. Bennemann for their continued encouragement and helpful discussions. This paper is supported by Korea-Ukraine project of MEST in Korea, and MIT Creative Research Project in ETRI.
REFERENCES
- Y. Kamahira, T. Watanabe, M. Hirano and H. Hasono, Journal of the American Chemical Society, Vol. 139, 2008, pp. 3296-3297. doi:10.1021/ja800073m
- S. Kruchinin, H. Nagao and S. Aono, “Modern Aspects of Superconductivity: Theory of Superconductivity,” World Scientific, Singapore, 2010, p. 232.
- H. Nagao, S. P. Kruchinin, A. M. Yaremko and K. Yamaguchi, International Journal of Modern Physics B, Vol. 16, 2002, pp. 3419-3428. doi:10.1142/S0217979202012220
- S. P. Kruchinin and A. M. Yaremko, Superconductor Science and Technology, Vol. 11, 1998, pp. 4-8.
- P. Shirage, K. Miyazawa, K. Kihou, C.-H. Lee, H. Kito, K. Tokiwa, et al., Europhysics Letters, Vol. 92, 2010, pp. 57011-57015.
- S. P. Kruchinin and H. Nagao, Physics of Particles and Nuclei, Vol. 36, 2005, pp. 127-130.
- W. E. Pickett, Reviews of Modern Physics, Vol. 61, 1989, pp. 433-512. doi:10.1103/RevModPhys.61.433
- J. T. Devreese and P. Van Camp, Eds., “Electronic Structure, Dynamics, and Quantum Structural Properties of Condensed Matter,” Plenum, New York, 1985. doi:10.1007/978-1-4757-0899-8
- P. Hohenberg and W. Kohn, Physical Review B, Vol. 136, 1964, pp. 864-871. doi:10.1103/PhysRev.136.B864
- W. Kohn and L. J. Sham, Physical Review A, Vol. 140, 1965, pp. 1133-1138.
- Y. Mizuguchi, et al., Superconductor Science and Technology, Vol. 23, 2010, pp. 054013-0540018. doi:10.1088/0953-2048/23/5/054013
- A. S. Davydov and S. P. Kruchinin, Physics C, Vol. 179, 1991, pp. 461-468. doi:10.1016/0921-4534(91)92196-I
- P. Monthoux, A. Balatsky and D. Pines, Physical Review B, Vol. 46, 1992, pp. 14803-14812. doi:10.1103/PhysRevB.46.14803

