Journal of Modern Physics
Vol.4 No.1(2013), Article ID:26871,7 pages DOI:10.4236/jmp.2013.41009
Macroscopic Quantum Tunneling
1Physics Department, Wuhan University of Technology, Wuhan, China
2Institute of Space Medico-Engineering, Beijing, China
Email: biqiao@gmail.com
Received November 9, 2012; revised December 10, 2012; accepted December 18, 2012
Keywords: Quantum Tunneling; Soliton; Quantum Information Density
ABSTRACT
In this work, a mechanism of macroscopic quantum tunneling is studied, which shows this sort of phenomena may exist even in the bio-field system. The relevant Davydov solitons fields and the Feynman digraph have been constructed based on the nonlinear Green function theory, which allows one to get a synchronous resonance model to explain the macroscopic quantum tunneling, such as in double potential wells system. Furthermore, the functional of quantum information density can also be applied to drive the object into a type of soliton structure of quantum information density, which allows the system to possess property of the macroscopic quantum tunneling.
1. Introduction
Since quantum mechanics established a theory that the microscopic particles have certain probability to tunnel through a finite or infinity potential this issue has become a standard model described in the text book of quantum mechanics [1]. However, as development of recent years in many experiments for the Bose-Einstein condensation (BEC), nano-particle in quantum dots system, and somatic science, the phenomena of macroscopic quantum tunneling (MQT) have been discovered in many works [2-9]. These results motivate a strongly disputed question that macroscopic tunneling is possible, so that after many years the investigation of mechanism for MQT become more and more significant. In this work, we firstly study a model of MQT for BEC in double potential wells described by the Grosse-Pitaevskii equation, then extend the model to a general situation by introducing a nonlinear quantum field considering a sort of nonlinear Green functions and a Feynman digraph. This allows a mechanism of MQT for a bio-solitons system interaction with the object to be proposed. Moreover, a driven model which generalize the above process by quantum information density (QID) description is presented. We hope that the theory provided is useful to explain the phenomena of MQT, especially in the bio-solitons field system [10].
2. Macroscopic Quantum Tunneling of BEC
Let us consider two BEC systems are confined in the double potential wells, respectively. The BEC is described by the Grosse-Pitaevskii equation as
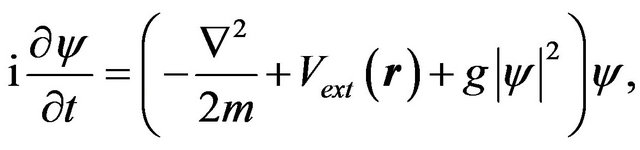 (1)
(1)
where
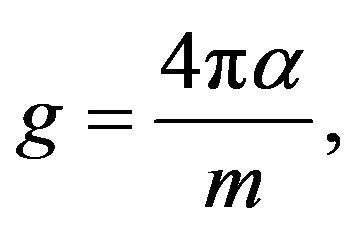 (2)
(2)
 is a
is a  wave scattering length among atoms. Then there exist MQT happening as type of Josephson oscillation for this system [3], so that a distribution of the wave functions between two well sides is supposed as
wave scattering length among atoms. Then there exist MQT happening as type of Josephson oscillation for this system [3], so that a distribution of the wave functions between two well sides is supposed as
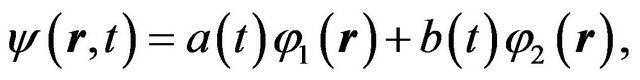 (3)
(3)
where  and
and 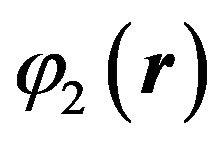 are the wave function of basic states, and
are the wave function of basic states, and  and
and  are the probability amplitudes in two wells, respectively. Then, by replacing this equation into the Grosse-Pitaevskii Equation (1), one gets
are the probability amplitudes in two wells, respectively. Then, by replacing this equation into the Grosse-Pitaevskii Equation (1), one gets
 (4)
(4)
where notice ,
, 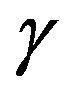 and
and 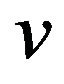 are defined by
are defined by
 (5)
(5)
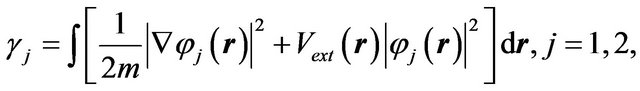 (6)
(6)
and
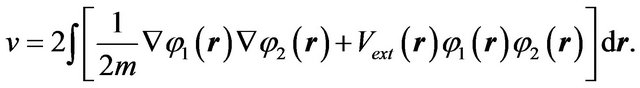 (7)
(7)
Since the solution for the equation
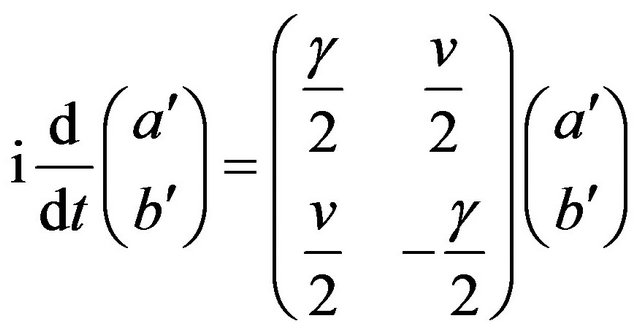 (8)
(8)
at the initial condition , is given by [4]
, is given by [4]
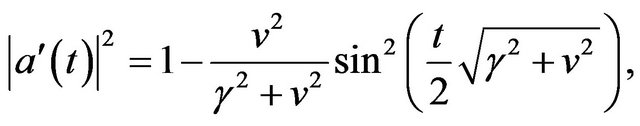 (9)
(9)
 (10)
(10)
hence a solution for Equation 4 is constructed as form
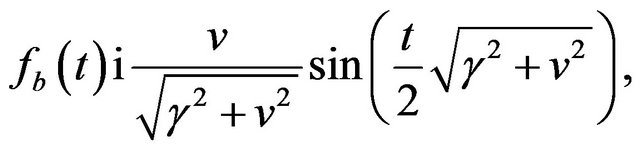 (11)
(11)
which satisfies
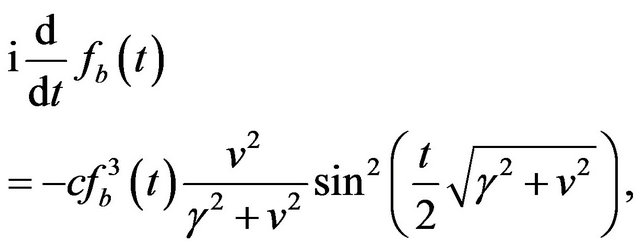 (12)
(12)
and gives
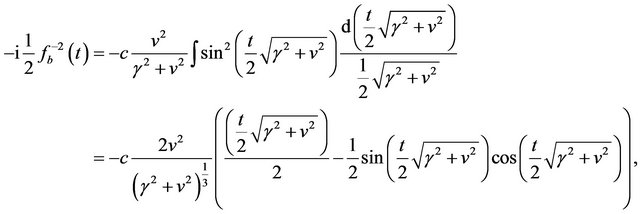 (13)
(13)
so that a solution 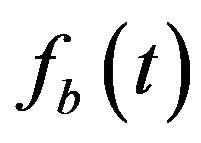 in Equation (11) is obtained as
in Equation (11) is obtained as
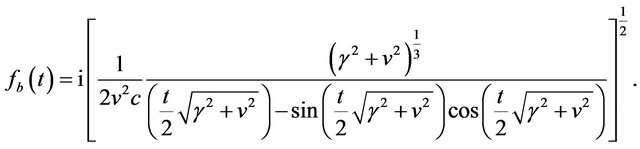 (14)
(14)
In the same way, one can get
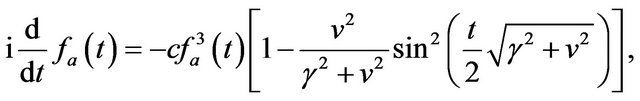 (15)
(15)
which gives
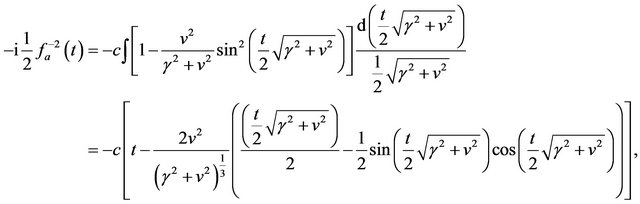 (16)
(16)
and allows one to obtain 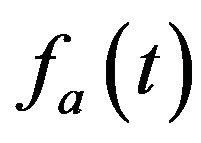 as
as
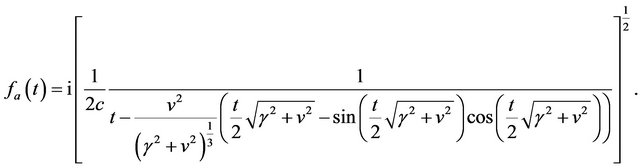 (17)
(17)
Therefore one has
 (18)
(18)
which proves that the solutions for Equation (4) are expressed by
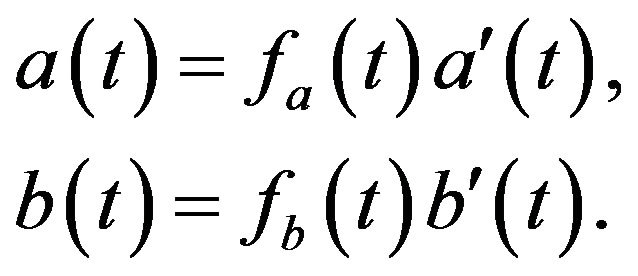 (19)
(19)
 From the solution
From the solution  we find that the nonlinear BEC tunneling oscillation is not like the linear Josephson sin oscillation because it contains kind of envelop functions
we find that the nonlinear BEC tunneling oscillation is not like the linear Josephson sin oscillation because it contains kind of envelop functions 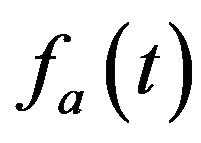 and
and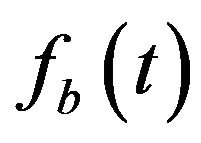 . This shows a soliton type of structure in the oscillation which may have self confinement phenomena appearance under strongly nonlinear situation as support from the experiments presented in Ref. [4].
. This shows a soliton type of structure in the oscillation which may have self confinement phenomena appearance under strongly nonlinear situation as support from the experiments presented in Ref. [4].
The above result explains that the system of EBC which satisfies the Grosse-Pitaevskii equation described micro-particles self confined as local solitons can be as the quasiparticles. Thus the symmetry of total system automatic broken and energy decrease to low level so that the particles together create coherence to condensate into the lower momentum state as solitons of BEC. These solitons can tunnel as sort of nonlinear oscillation through high potentials.
3. Nonlinear Quantum Field
The previously studied model can be extended as a general frame of biological quantum field to interact with object. This biological field assumed to consists of D-P solitons, nonlinear excitations, and so on [10] as mentioned in the previously works [11,12]. For simplicity, here we only call them as “soliton”. One of important techniques to study this quantum field needs to be able to handle operator series product. Although the Green function theory to describe quantum field have made plentiful progresses [13], however, it currently can only handle the linear operator series product, while the handling of the nonlinear operator series product remains great challenges. Actually, using the linear approximation methods lead to the relevant calculation procedures which is quit complicated and enables some information for new nonlinear biological excitation easily to be lost in the process. This provides an inspiration to search new nonlinear mathematical methods and establish nonlinear propagator theory [14,15]. Consequently, the nonlinear Green function and the slash product are introduced. For this let us second quantize a state of soliton as a nonlinear quantum field operator
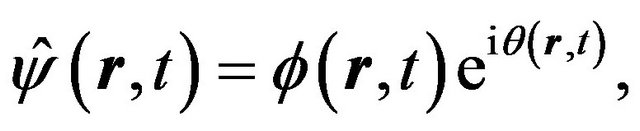 (20)
(20)
which satisfies a quantum nonlinear Schrödinger equation
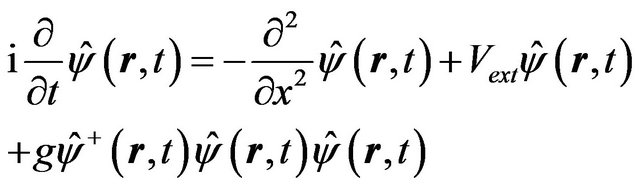 (21)
(21)
with the commutation relations
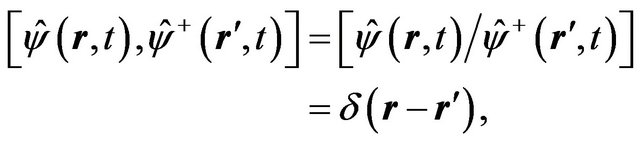 (22)
(22)
and
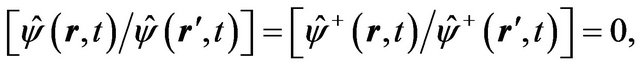 (23)
(23)
where 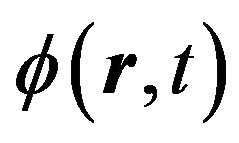 is an amplitude and
is an amplitude and 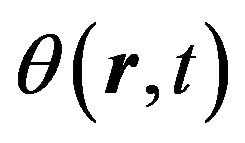 is a phase operator, and
is a phase operator, and ,
,  is defined as the slash product introduced by Charles Schwartz [12] between
is defined as the slash product introduced by Charles Schwartz [12] between  and
and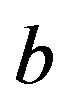 :
:
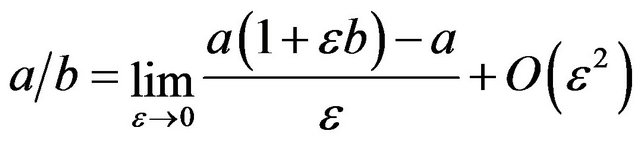 (24)
(24)
It can be proven that the slash product can keep linerarity for the nonlinear operator, this important property allows the most calculations in the linear quantum field theory can still remain the same forms in the nonlinear quantum field.
For example, if a creation operator (annihilation operator) is given by the Fourier transformation of 
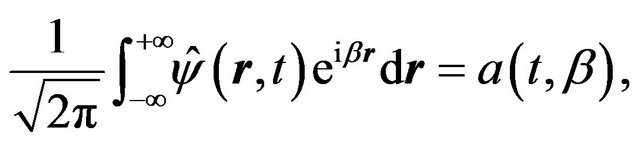 (25)
(25)
and
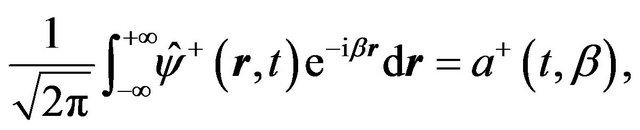 (26)
(26)
then the commutation relations are
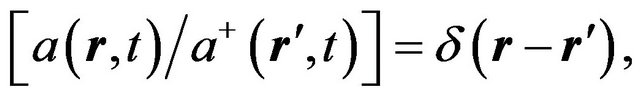 (27)
(27)
and
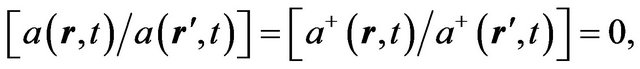 (28)
(28)
Thus in the Schrödinger picture, Equation (21) is expressed as
 (29)
(29)
where  is defined as
is defined as
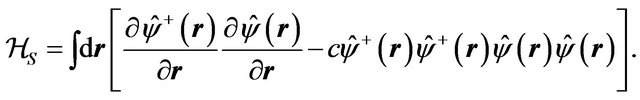 (30)
(30)
Furthermore, if Equation (29) can be written as
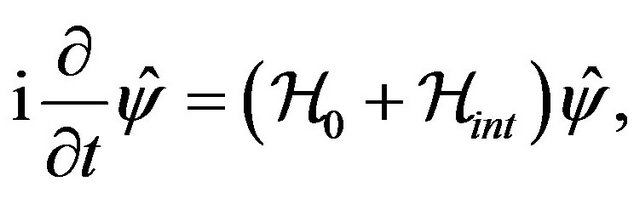 (31)
(31)
then a nonlinear propagator 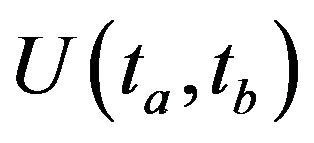 is constructed by
is constructed by
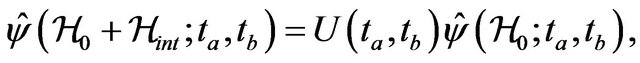 (32)
(32)
which gives
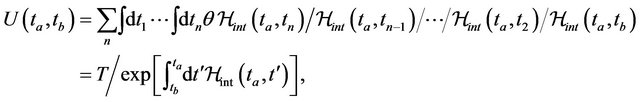 (33)
(33)
where  is defined as a time order operator for the slash product at
is defined as a time order operator for the slash product at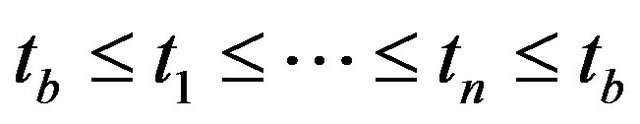 .
.  is defined as the Heaviside function. So, a
is defined as the Heaviside function. So, a 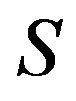 operator in the interaction picture can be introduced by
operator in the interaction picture can be introduced by
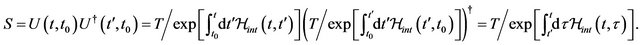 (34)
(34)
Thus, the various of Green functions can be introduced based on the above formalism, such as for any operator  and
and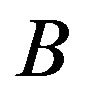 , the Bogoliubov retarded Green function is defined as
, the Bogoliubov retarded Green function is defined as
 (35)
(35)
where  represents expectation under the interaction picture in the statistical ensembles, i.e. in the canonical ensembles
represents expectation under the interaction picture in the statistical ensembles, i.e. in the canonical ensembles
 (36)
(36)
 (37)
(37)
with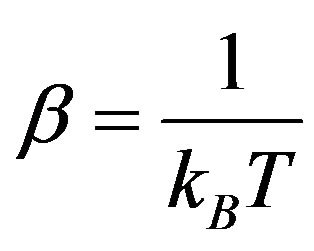 . Moreover, a n-points Green function can also be defined as
. Moreover, a n-points Green function can also be defined as
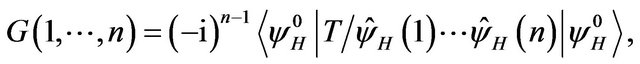 (38)
(38)
where  is a Heisenberg basic state; then a 2-point Green function is given by
is a Heisenberg basic state; then a 2-point Green function is given by
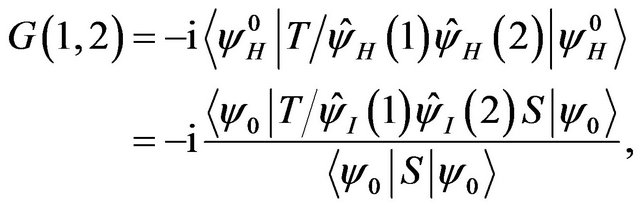 (39)
(39)
where  is introduced in the adiabatic hypothesis. Moreover, a spectral theorem in the form of the slash product is given by
is introduced in the adiabatic hypothesis. Moreover, a spectral theorem in the form of the slash product is given by
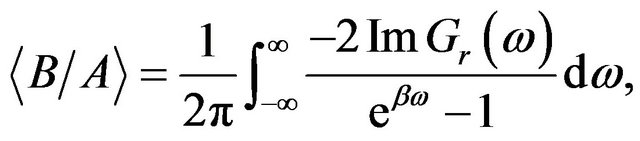 (40)
(40)
where 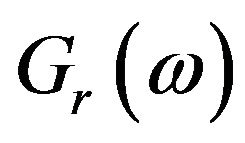 is the Fourier transformation of
is the Fourier transformation of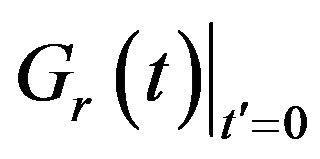 .
.
4. Nonlinear Synchronous Resonance
The above formalism of nonlinear quantum field allows us to postulate the D-P solitons interact with photons to form a nonlinear excitation field (NEF) around object. These D-P solitons in the biological system play basic role as a carrier of bio-information and bio-energy in the issues of organization [10,11]. The object which has sort of solitons by micro-vibration of its atoms or molecules is emerged in the nonlinear excitation field. The surround NEF can interact with the solitons in the object by adjusting its solitons to have almost the same state, energy, information and shape as that of the object through “breath” virtual Bose (such as phonon). This process is shown in Figure 1. When the solitons from NEF propagate to the range of the solitons of object, the solitons of NEF emit quanta as imaginary Bose (such as phonon) into the solitons of the object, so that the both soliton amplitudes and velocities appear to have strong coherence. This virtual phonon exchange constitutes a similar “breathing” of the interaction. In this process, the synchronous resonance among them happen. Consider the above assumption of model, here we firstly define the soliton in the object as  -soliton and the solitons in NEF as
-soliton and the solitons in NEF as 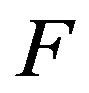 -soliton. Since the surround
-soliton. Since the surround  -solitons are highly coherent with
-solitons are highly coherent with 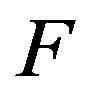 -soliton in the local position, the
-soliton in the local position, the  -soliton can easily absorb quanta from the surround
-soliton can easily absorb quanta from the surround  -soliton field, and then emit quanta to return the
-soliton field, and then emit quanta to return the 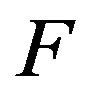 -soliton field, as “breath”. When the quanta from
-soliton field, as “breath”. When the quanta from  - soliton field transmit into a
- soliton field transmit into a  -soliton, it allows the
-soliton, it allows the  -soliton to expand and re-excit the weak part with
-soliton to expand and re-excit the weak part with 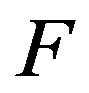 -soliton. In fact, it is known that the vibration of the D-P soliton in local position is as kind of electromagnetic wave in the sub-millimeter wave or far-infrared wave whose frequency change with the composition change of the frequency of partial chain of protein. If the frequency of the quanta is the same as the frequency in partial chain of protein, then there is a resonance to excite the partial chain of solitons in the object. Hence, the exchange process of the quanta allows
-soliton. In fact, it is known that the vibration of the D-P soliton in local position is as kind of electromagnetic wave in the sub-millimeter wave or far-infrared wave whose frequency change with the composition change of the frequency of partial chain of protein. If the frequency of the quanta is the same as the frequency in partial chain of protein, then there is a resonance to excite the partial chain of solitons in the object. Hence, the exchange process of the quanta allows  -soliton to have the same status with the
-soliton to have the same status with the 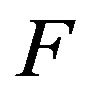 -soliton in NEF. The interaction Hamiltonian of the system in the momentum (wave vector
-soliton in NEF. The interaction Hamiltonian of the system in the momentum (wave vector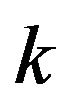 , or
, or ) space is supposed to be given by
) space is supposed to be given by
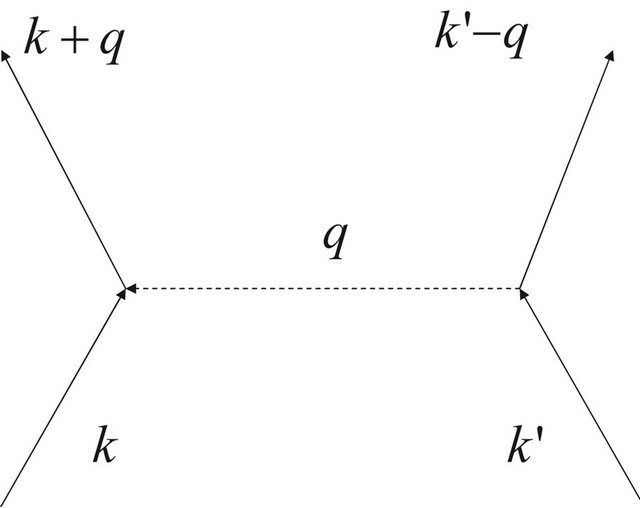
Figure 1. The exchange of a virtual quanta q between soliton k and soliton k’.
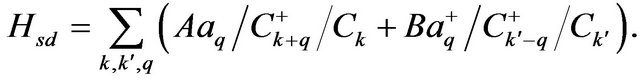 (41)
(41)
The exchange interaction can be described by the Figure 1, which shows, in the microscopic level, it is possible by adjusting 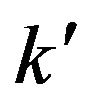 represented a wave vector of the soliton from NEF emits a
represented a wave vector of the soliton from NEF emits a , to permit the wave vector of soliton from the object to be equal to
, to permit the wave vector of soliton from the object to be equal to  after absorption of a
after absorption of a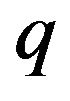 , so that
, so that
 (42)
(42)
This allows the solitons in the object are strongly correlated with NEF and having synchronous resonances with NEF, which enable the object possibly to enter a kind of status of condensation or coherence as NEF. Then a macroscopic quantum tunneling for the object becomes possible.
This can still be described by the above double potential wells model as the distribution of the wave functions appear in two potential wells, e.g.
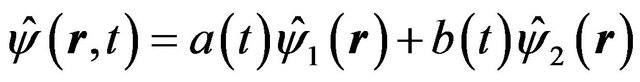 (43)
(43)
where  represents a wave function of the soliton in NEF, and
represents a wave function of the soliton in NEF, and  represents a wave function of soliton in the object. Then, by using quantum nonlinear Schrodinger equation again, one gets the solution being similar to Equation (19), thus we obtain
represents a wave function of soliton in the object. Then, by using quantum nonlinear Schrodinger equation again, one gets the solution being similar to Equation (19), thus we obtain
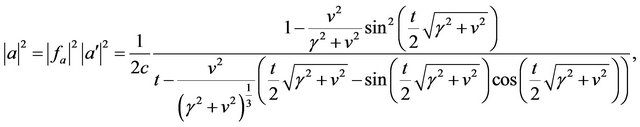 (44)
(44)
and
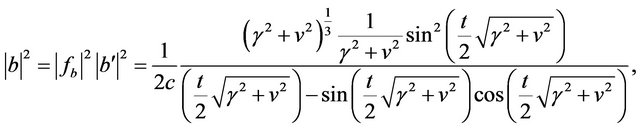 (45)
(45)
which shows it is a complicated anharmonic oscillation with many frequencies. One amplitude is
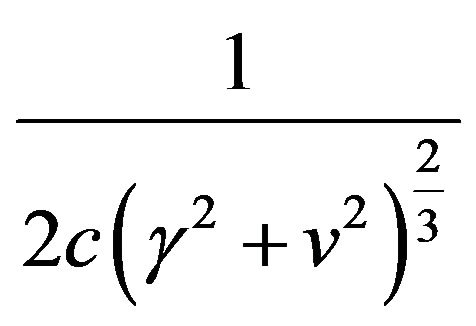 (46)
(46)
showing ,
,  , and
, and 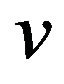 increase with the amplitude decrease. Where notice here
increase with the amplitude decrease. Where notice here 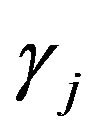 and
and  may be not related to
may be not related to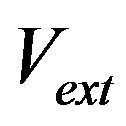 ,
,
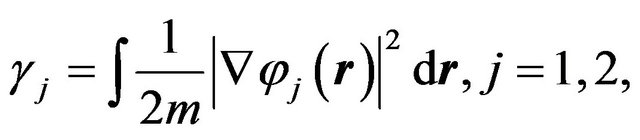 (47)
(47)
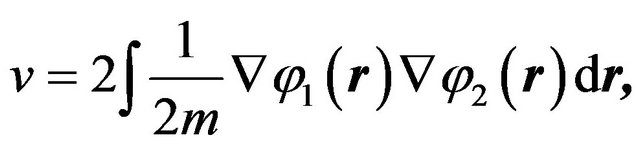 (48)
(48)
and  reflects a nonlinear coupling. This means an object with small mass finally will be easier to confine in another well (or tunneling out of its original well) by a strong nonlinear interaction (from NEF) under the condition of the double potential wells distribution of the solitons plus NEF. This is supposed by the phenomena of the self-trapping in BEC experiments as mentioned before. While here we want to emphasize that this model is also supported by many phenomena from experiments of the somatic science, such as Refs. [7,8,16].
reflects a nonlinear coupling. This means an object with small mass finally will be easier to confine in another well (or tunneling out of its original well) by a strong nonlinear interaction (from NEF) under the condition of the double potential wells distribution of the solitons plus NEF. This is supposed by the phenomena of the self-trapping in BEC experiments as mentioned before. While here we want to emphasize that this model is also supported by many phenomena from experiments of the somatic science, such as Refs. [7,8,16].
5. QID Driving
Generally, the above model can be extended by using of the concept of quantum information density described by the Liouville equation [12]. Indeed, the Liouville equation for quantum information can be derived by directly starting from quantum Liouville equation: by using power series of expansion of the density operator , one gets a Liouville equation for the general functional of
, one gets a Liouville equation for the general functional of , such as
, such as  constructed by
constructed by
 (49)
(49)
The physical meaning of the above equation can be explained as “a QID representation of Liouville equation”, where 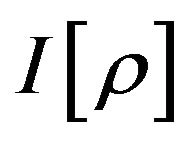 corresponding to a sort of general QID, especially
corresponding to a sort of general QID, especially 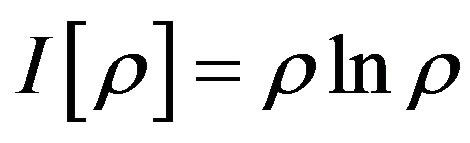 [17]. In this sense
[17]. In this sense  can be considered as a minimum unit of the quantum information density. Besides, the classical situation can also be proved by using the same way.
can be considered as a minimum unit of the quantum information density. Besides, the classical situation can also be proved by using the same way.
The above derived QID representation of Liouville equation coincides with the traditional Liouville equation, therefore it can not describe an irreversible process since its time evolution is symmetric by inheriting from the Liouville equation [13], however, from the point of view of thermodynamical second law we can introduce a difference (or gradient) of QID to allow
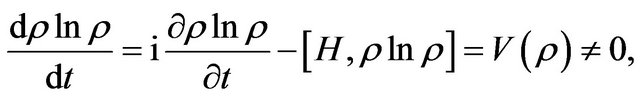 (50)
(50)
where 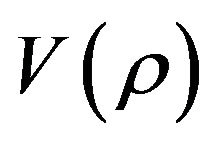 is assumed to be introduced by a difference (or gradient) of QID.
is assumed to be introduced by a difference (or gradient) of QID.
Because QID is just the negative entropy density, the above expression is like a microscopic representation of thermodynamical second law: when the QID in the two coupled systems are not equal to each other, then there exists a difference (or gradient) of QID will spontaneously drive the higher QID to transmit to the lower QID until the both arriving at equilibrium. Moreover, if 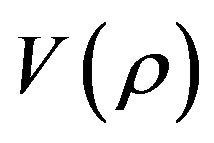 is a functional of
is a functional of  of the object, (such as) through a mechanism of synchronous resonance proposed above, then it can drive the object to enter kind of soliton status so that MQT is possible. In fact for a quantum system, if one supposes a non-equilibrium Liouville equation is expressed as
of the object, (such as) through a mechanism of synchronous resonance proposed above, then it can drive the object to enter kind of soliton status so that MQT is possible. In fact for a quantum system, if one supposes a non-equilibrium Liouville equation is expressed as
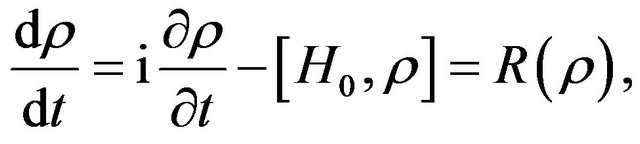 (51)
(51)
where the density operator given by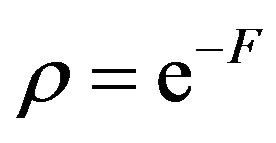 , then using the Baker-Hausdorf formula and applying the Magnus lemma [13] gives
, then using the Baker-Hausdorf formula and applying the Magnus lemma [13] gives
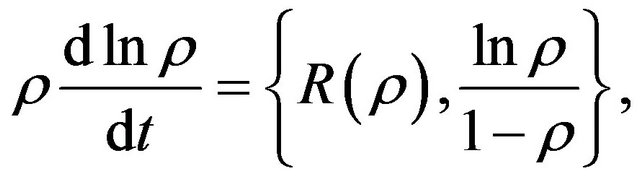 (52)
(52)
where
 (53)
(53)
This allows one to gain
 (54)
(54)
where 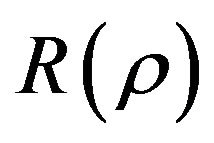 is chosen to satisfy
is chosen to satisfy
 (55)
(55)
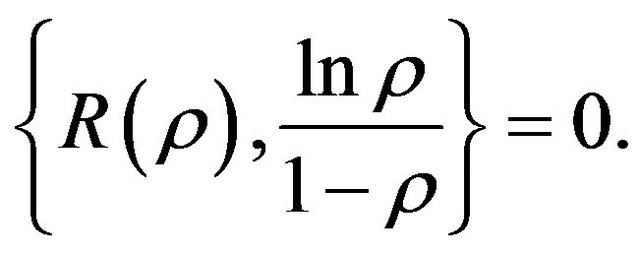
Then a nonlinear Liouville equation is obtained as
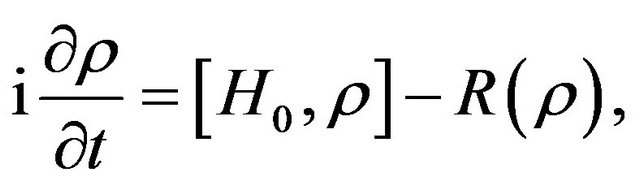 (56)
(56)
where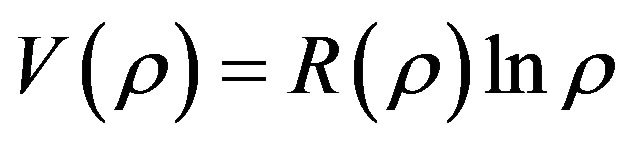 , such as, if
, such as, if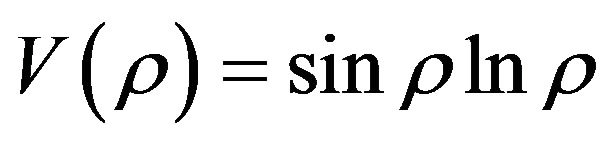 , then
, then
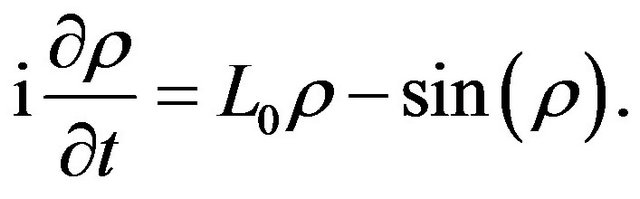 (57)
(57)
This sort of nonlinear Liouville equation may have soliton type of solution. In this sense, the influence of NEF to the object can be realized through an information density driving . This arises a possibility: using functional of
. This arises a possibility: using functional of  as nonlinear driving,
as nonlinear driving, 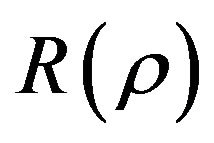 , from certain natural or artificial source of NEF, then an object will enter sort of macroscopic quantum status to have possible MQT. This even can be realized by a series of nonlinear pules of
, from certain natural or artificial source of NEF, then an object will enter sort of macroscopic quantum status to have possible MQT. This even can be realized by a series of nonlinear pules of . For instance, if a series of multiplied pulses series can be transmitted from a source of NEF [18,19],
. For instance, if a series of multiplied pulses series can be transmitted from a source of NEF [18,19],
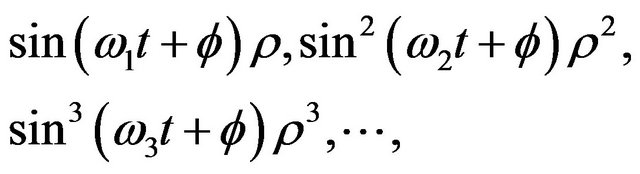 (58)
(58)
which allows a driving 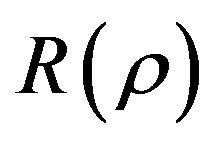 expressed by
expressed by
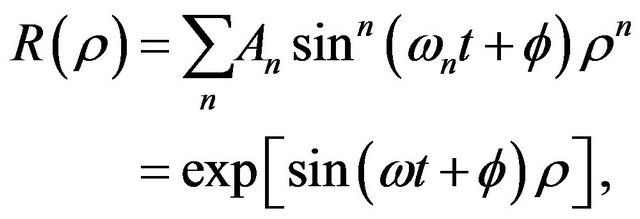 (59)
(59)
where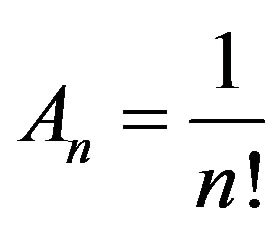 ,
, 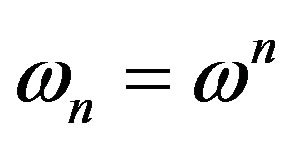 is adjusted by NEF. This makes a complicated nonlinear oscillation of the QID to drive the original object probably to have soliton type of structure, hence the MQT is possible.
is adjusted by NEF. This makes a complicated nonlinear oscillation of the QID to drive the original object probably to have soliton type of structure, hence the MQT is possible.
6. Conclusion
In conclusions, the macroscopic quantum tunneling (MQT) for the BEC system or solitons system are possible. One possible mechanism of MQT orientates from the synchronous resonance between the NEF and the object as the two potential wells system. This MQT shows complicated anharmonic oscillations and to have many different frequencies. Moreover, the model can be extended as QID representation. The functional of nonlinear QID can be applied to drive the object into a type of soliton structure of QID, so that the MQT is possible.
REFERENCES
- D. J. Griffiths, “Introduction to Quantum Mechanics,” 2nd Edition, Addison-Wesley Press, Boston, 2004.
- A. Smerzi, S. Fantoni, S. Giovanazzi, et al., “Quantum Coherent Atomic Tunneling between Two Trapped Bose-Einstein Condensates,” Physical Review Letters, Vol. 79, No. 25, 1997, pp. 4950-4953.
- M. Albiez, R. Gati, J. Fölling, et al., “Direct Observation of Tunneling and Nonlinear Self-Trapping in a Double Bosonic Josephson Junction,” Physical Review Letters, Vol. 95, No. 1, Article ID: 010402.
- J. Liu, “Dynamics for the Bose-Einstein Condensation,” Science Press, Bejing, 2009.
- Z. L. Duan, B. X. Fan, et al., “Quantum Tunneling Time of a Bose-Einstein Condensate Traversing through a Laser-Induced Potential Barrier,” Physical Review A, Vol. 81, No. 5, 2010, Article ID: 055602.
- G. Dekela, O. V. Farberovichb, A. Sofferc and V. Fleurov, “Nonlinear Dynamic Phenomena in Macroscopic Tunneling,” Physica D, Vol. 238, No. 15, 2009, pp. 1475- 1481. doi:10.1016/j.physd.2008.06.013
- K. Z. Song, “The Existence and Significance of Parapsychological Function,” Journal of International Society of Life Information Science (ISLIS), Vol. 17, No 1, 1999, pp. 198-214.
- K. Z. Song, R. L. Lan, X. G. Li and L. Z. Zhou, “The Research of the Break through Spacial Obstacle Function, Create Somatic Science, 705-717,” Sichuan Educate Publisher, Beijing, 1989.
- K. D. Sattler, “Handbook of Nanophysics 3: Nanoparticles and Quantum Dots, Volume 3,” Taylor & Francis Group, CRC Press, New York, 2011.
- X. F. Pang and Y.-P. Feng, “Quantum Mechanics in Nonlinear Systems,” World Scientific Publishing, Singapore City, 2005.
- Q. Bi, “Bio-Solitons Return Life,” International Review of Physics, Vol. 3, No. 5, 2009, pp. 278-288.
- Q. Bi, K. Z. Song and H. E. Ruda, “Characteristics of Coherence and Information for the Davydov Soliton Field,” Journal of Modern Physics, Vol. 3, No. 12, 2012, pp. 1907-1913.
- S. Doniach and E. H. Sondheimer, “Green’s Functions for Solid State Physicists,” The Benjamin/Cummings Company, Inc., London, 1982.
- Q. Bi and H. E. Ruda, “Green Functions for Nonlinear Operators and Application to Quantum Computing,” Physica A, Vol. 334, No. 3, 2004, pp. 459-476. doi:10.1016/j.physa.2003.10.077
- Charles Schwartz, “Nonlinear Operators and Their Propagators,” Journal of Mathematical Physics, Vol. 38, No. 1, 1997, pp. 484-500. doi:10.1063/1.531829
- B. H. Wu, et al., “Introduction to Science of Human Body,” Sichuan University Publishing House, Chengdu, 1998.
- Q. Bi, X. S. Xing and H. E. Ruda, “Dynamical Equations for Quantum Information and Application in Information Channel,” Chinese Physics Letters, Vol. 7, No. 7, 2005, pp. 1618-1621.
- S. G. Schirmer, A. D. Greentree, V. Ramakrishna and H. Rabitz, “Quantum Control Using Sequences of Simple Control Pulses,” quant-ph/0105155.
- V. Ramakrishna, R. Ober, X. Sun, O. Steuernagel, J. Botina and H. Rabitz, “Explicit Generation of Unitary Transformations in a Single Atom or Molecule,” Physical Review A, Vol. 61, No. 3, 2000, Article ID: 032106.

