Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21680,7 pages DOI:10.4236/jmp.2012.38095
Exact Projective Excitations of Nonautonomous Nonlinear Schrödinger System in (1 + 1)-Dimensions
1Department of Physics, Shaoguan University, Shaoguan, China
2Department of Information Engineering, College of Lishui Professional Technology, Lishui, China
Email: *clzheng@yahoo.cn
Received May 8, 2012; revised June 1, 2012; accepted June 28, 2012
Keywords: Nonautonomous NLS System; Projective Approach; Exact Solution; Localized Excitation
ABSTRACT
With the aid of a direct projective approach, a general transformation solution for the nonautonomous nonlinear Schrödinger (NLS) system is derived. Based on certain known exact solutions of the projective equation, some periodic and localized excitations with novel properties are correspondingly revealed by entrancing appropriate system parameters. The integrable constraint conditions for the nonautonomous NLS system derived naturally here are consistent with the compatibility condition via the Painlevé analysis in other literatures.
1. Introduction
Nonlinear science is believed, by many outstanding scientists, to be the most deeply important frontier for understanding nature and applications in reality. For example, nonlinear optical solitons are regarded as the natural data bits and an important alternative for the next generation of ultrahigh speed optical telecommunication systems. It is known that the propagation of electromagnetic waves in nonlinear optical waveguides and the ground state wave functions of Bose-Einstein condenstates (BECs) can be described by nonlinear Schrödinger (NLS) system [1], which is actually one of the fundamental dynamical models in nonlinearity [2,3]. The nonautonomous NLS system in (1 + 1)-dimensional form is
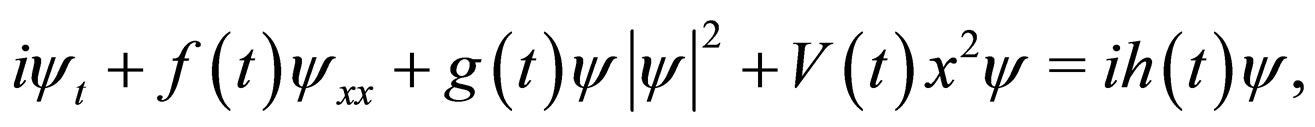 (1)
(1)
where 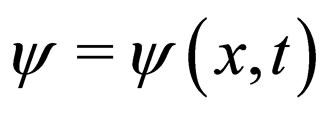 is the complex wave envelope in a comoving frame, with time-modulated dispersion
is the complex wave envelope in a comoving frame, with time-modulated dispersion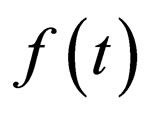 , nonlinearity
, nonlinearity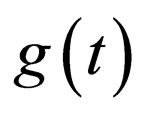 , net gain (>0) or loss (<0)
, net gain (>0) or loss (<0)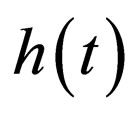 , and external harmonic trap potential
, and external harmonic trap potential 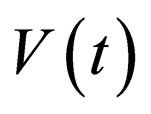 in BECs, which is usually absent in nonlinear optical transmission aspect [4]. The subscripts x and t denote the spatial and temporal partial derivatives. These coefficients are often assumed to be real. In the contexts of many physical fields, the BECs and nonlinear optics provide excellent proving grounds for exploring nonlinear systems with distributed coefficients. It has been reported that specific dependencies of the equation coefficients on time variables can enhance the stabilities of the solutions [5,6]. Moreover, timemodulated nonlinearities and/or dispersions can facilitate the manipulation of the soliton behaviors. These facts have greatly enlarged our knowledge on nonlinear excitations and given an origin to some important concepts such as nonautonomous soliton [7], and Feschbach resonance, which has been used to control some nonlinearities of matter waves by manipulating the scattering length either in time or space, and have led to certain proposals of many novel nonlinear phenomena. Dispersion management (DM) for BBCs has also proposed recently and has induced plenty of consequent studies. In nonlinear optics, nonlinear management (NM) and DM are also both used for experiments and theories with temporal or spatial optical solitons, soliton lasers, ultrafast soliton switches [7]. Furthermore, some recent progresses on inhomogeneous nonlinear media have generated novel concepts such as the optical similariton [8]. However, the nonautonomous NLS system (1) and/or its similar versions are very difficult to be solved because of the presence of the time-dependent dispersion, nonlinear interaction managements and external potential. Up to now, a general exact solution to the nonautonomous NLS system (1) has been rarely found although the knowledge of such exact solutions is very valuable for various purposes. Certainly, some special exact solutions have been obtained by the Lax par method [7], the similarity transformation [8] and so on. In the short note, we try to give a general exact solution to the nonautonomous NLS system via a selfsimilarity projective approach (SPA), which can convert all exact solutions of selfsimilar well-known models to corresponding solutions of the nonautonomous NLS system. In the following section, we first briefly describe the projective approach. In Section 3, a general exact solution to the nonautonomous NLS system will be derived via the SPA. A brief summary and discussion is given in the last section.
in BECs, which is usually absent in nonlinear optical transmission aspect [4]. The subscripts x and t denote the spatial and temporal partial derivatives. These coefficients are often assumed to be real. In the contexts of many physical fields, the BECs and nonlinear optics provide excellent proving grounds for exploring nonlinear systems with distributed coefficients. It has been reported that specific dependencies of the equation coefficients on time variables can enhance the stabilities of the solutions [5,6]. Moreover, timemodulated nonlinearities and/or dispersions can facilitate the manipulation of the soliton behaviors. These facts have greatly enlarged our knowledge on nonlinear excitations and given an origin to some important concepts such as nonautonomous soliton [7], and Feschbach resonance, which has been used to control some nonlinearities of matter waves by manipulating the scattering length either in time or space, and have led to certain proposals of many novel nonlinear phenomena. Dispersion management (DM) for BBCs has also proposed recently and has induced plenty of consequent studies. In nonlinear optics, nonlinear management (NM) and DM are also both used for experiments and theories with temporal or spatial optical solitons, soliton lasers, ultrafast soliton switches [7]. Furthermore, some recent progresses on inhomogeneous nonlinear media have generated novel concepts such as the optical similariton [8]. However, the nonautonomous NLS system (1) and/or its similar versions are very difficult to be solved because of the presence of the time-dependent dispersion, nonlinear interaction managements and external potential. Up to now, a general exact solution to the nonautonomous NLS system (1) has been rarely found although the knowledge of such exact solutions is very valuable for various purposes. Certainly, some special exact solutions have been obtained by the Lax par method [7], the similarity transformation [8] and so on. In the short note, we try to give a general exact solution to the nonautonomous NLS system via a selfsimilarity projective approach (SPA), which can convert all exact solutions of selfsimilar well-known models to corresponding solutions of the nonautonomous NLS system. In the following section, we first briefly describe the projective approach. In Section 3, a general exact solution to the nonautonomous NLS system will be derived via the SPA. A brief summary and discussion is given in the last section.
2. A Brief Review on the Projective Approach
In recent decades, many powerful approaches have been devised, such as inverse scattering theory, Bäcklund transformation, Hirota’s bilinear method, Darboux transformation, the hyperbola function method, the mixed exponential method, homogeneous balance method, and multilinear variable separation approach et al. [9]. Besides these methods, one can also obtain solutions of a nonlinear partial differential equations (NLPDEs) by the technical of establishing and making full advantage of a direct projective relation between the given NLPDE and other NLPDE and its known solutions sometimes. For example, using a deformation projective method first presented by Lou and his coworkers [10], some scholars [11-13] obtained many soliton solutions and periodic solutions of nonlinear models through finding some relations between the exact solutions of the given models and those of the cubic nonlinear Klein-Gordon (NKG) system which has been studied widely in the previous literature [10]. The basic idea of the algorithm is as follows: For a general nonlinear physical system
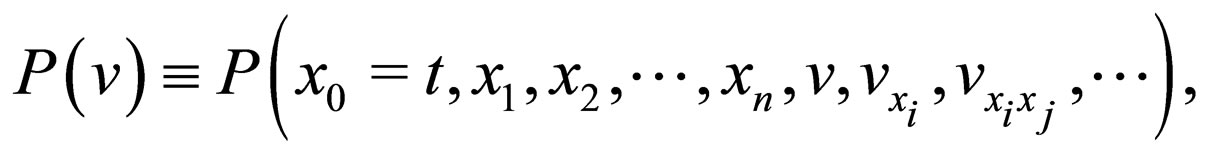 (2)
(2)
where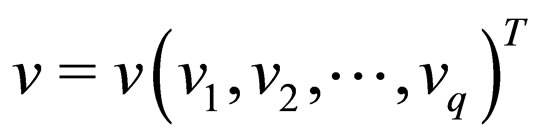 ,
,
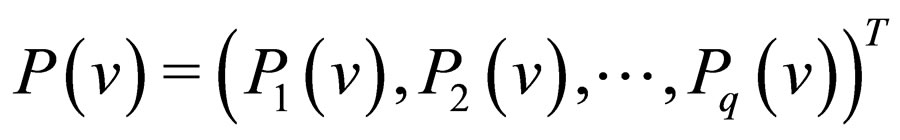 ,
,
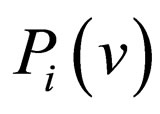 are polynomials of
are polynomials of 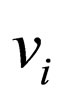 and their derivatives, (T indicates the transposition of a matrix). By using a travelling wave transformation based on the following ansatz
and their derivatives, (T indicates the transposition of a matrix). By using a travelling wave transformation based on the following ansatz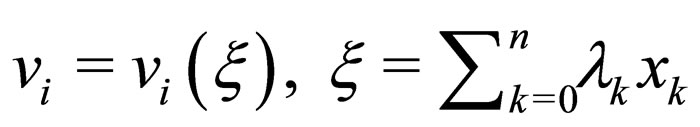 , where
, where 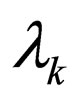 are real arbitrary constants, and substituting the ansatz into Equation (2) yields an ordinary differential equation system. Then
are real arbitrary constants, and substituting the ansatz into Equation (2) yields an ordinary differential equation system. Then 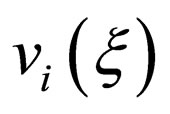 is expanded into a polynomial in
is expanded into a polynomial in 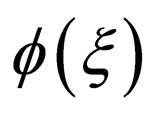
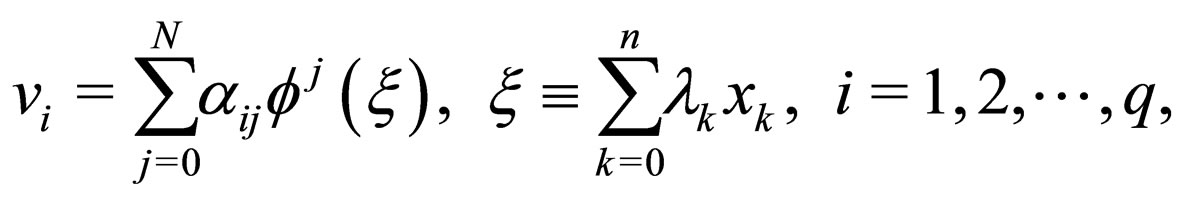 (3)
(3)
where 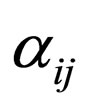 are constants to be determined and N is fixed by balancing the linear term of the highest order with the nonlinear term in Equation (2). If we suppose
are constants to be determined and N is fixed by balancing the linear term of the highest order with the nonlinear term in Equation (2). If we suppose 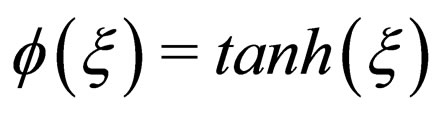 ,
, 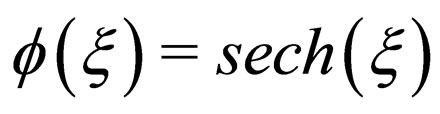 and
and 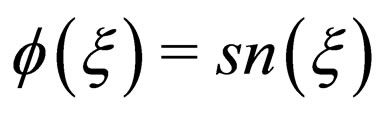 or
or 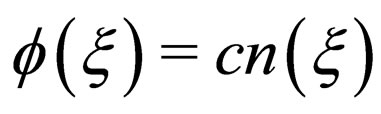 respectively, then the corresponding approaches are usually called the tanh-function method, the sech-function method and the Jacobian-function method. Although the Jacobian elliptic function method is more improved than the tanh-function method and the sech-function method, the repeated calculations are often tedious since the different function
respectively, then the corresponding approaches are usually called the tanh-function method, the sech-function method and the Jacobian-function method. Although the Jacobian elliptic function method is more improved than the tanh-function method and the sech-function method, the repeated calculations are often tedious since the different function 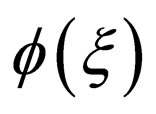 should be treated in a repeated way. The idea of deformation projective approach is that,
should be treated in a repeated way. The idea of deformation projective approach is that, 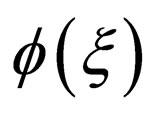 is not assumed to be a specific function, such as tanh, sech, sn and cn, etc., but a solution of the projective equation, such as the Riccati equation
is not assumed to be a specific function, such as tanh, sech, sn and cn, etc., but a solution of the projective equation, such as the Riccati equation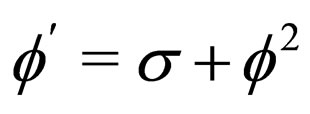 , (
, ( is a constant and the prime denotes differentiation with respect to
is a constant and the prime denotes differentiation with respect to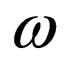 ), the cubic nonlinear KG equation
), the cubic nonlinear KG equation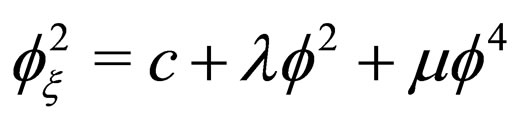 , (here c,
, (here c, 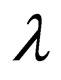 and
and 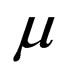 are all arbitrary constants), or the Jacobian elliptic equation. Using the projective relation (3) and the solutions of the related projective equations, one can obtain many explicit and exact travelling wave solutions of system (2). Along with this line, some scholars further assume that the projective function
are all arbitrary constants), or the Jacobian elliptic equation. Using the projective relation (3) and the solutions of the related projective equations, one can obtain many explicit and exact travelling wave solutions of system (2). Along with this line, some scholars further assume that the projective function 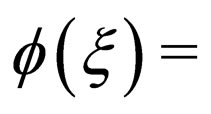 is an exact excitation of the generalized Jacobian elliptic equation
is an exact excitation of the generalized Jacobian elliptic equation 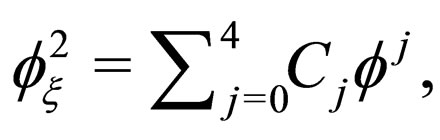 where
where 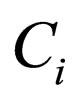 are all arbitrary constants. Because the generalized Jacobian elliptic equation possesses more exact solutions [14], one may derive more travelling wave solutions of system (2) than previous ones.
are all arbitrary constants. Because the generalized Jacobian elliptic equation possesses more exact solutions [14], one may derive more travelling wave solutions of system (2) than previous ones.
Recently, the above projective transformation approach is further extended for finding novel localized excitations of a physical model [15-17]. With the help of projective transformation idea and based on the general reduction theory, the projective algorithm is extended that: For the system (2) we assume its solution in an extended symmetric form
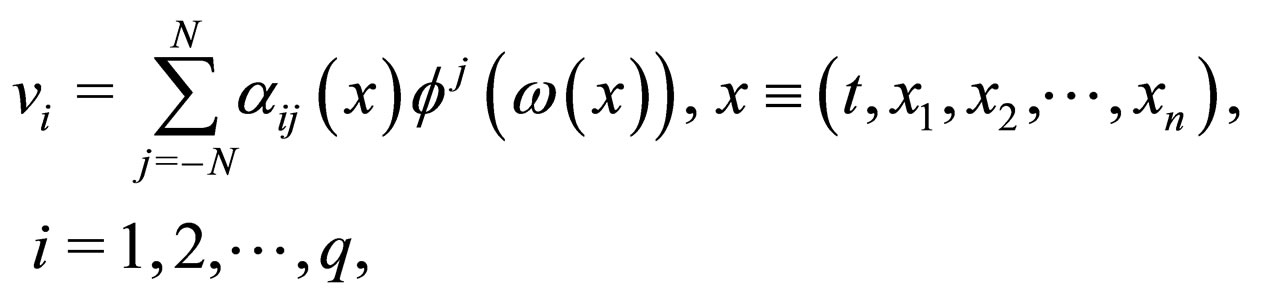 (4)
(4)
where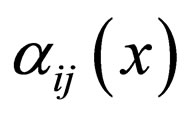 ,
, 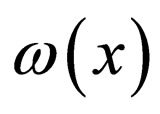 are arbitrary functions to be determined,
are arbitrary functions to be determined, 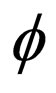 is a solution of the Riccati equation or the generalized Jacobian elliptic equation. N is also determined by balancing the highest nonlinear terms and the highest-order partial terms in the given nonlinear system. Substituting the ansatz (4) together with the related projective equations into Equation (2), collecting coefficients of polynomials of
is a solution of the Riccati equation or the generalized Jacobian elliptic equation. N is also determined by balancing the highest nonlinear terms and the highest-order partial terms in the given nonlinear system. Substituting the ansatz (4) together with the related projective equations into Equation (2), collecting coefficients of polynomials of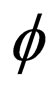 , then setting each coefficient to zero, yields a set of partial differential equations concerning
, then setting each coefficient to zero, yields a set of partial differential equations concerning 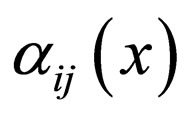 and
and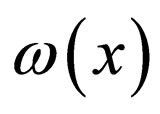 . Solving the system of partial differential equations to obtain
. Solving the system of partial differential equations to obtain 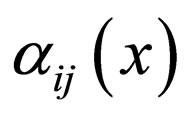 and
and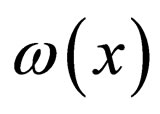 , substituting the derived results and the solutions of the related projective equations into Equation (4), one can derive many exact solutions to the given nonlinear system.
, substituting the derived results and the solutions of the related projective equations into Equation (4), one can derive many exact solutions to the given nonlinear system.
Motivated by the above ideas, one may assume a selfsimilar family model as the projective equation, which has been extensively studied in other literature [18,19]. For instant, when discussing a nonautonomous Korteweg-de Vries (KdV) system, we may use the classical (1 + 1)- dimensional KdV equation as a projective equation since the autonomous KdV equation has been widely explored. In the following part of the paper, the (1 + 1)-dimensional nonautonomous NLS system is selected to illustrate the selfsimilarity projective approach, and a general exact solution to the nonautonomous NLS system is derived, which can convert all exact solutions of self-similar well-known standard nonlinear Schröding equation to the corresponding exact solutions of the nonautonomous NLS system.
3. An Exact Projective Solution to the Nonautonomous NLS System
The standard nonlinear Schrödinger (NLS) equation can be used as a self-similar projective equation of the nonautonomous NLS system assumed, the dimensionless autonomous NLS form is
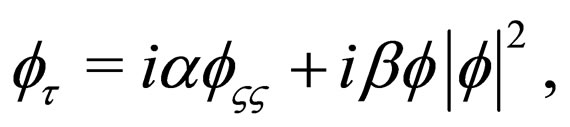 (5)
(5)
where 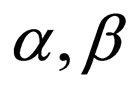 are system parameters,
are system parameters, 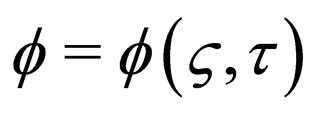 is a complex wave function of related system dynamics in physical fields such as BBCs and nonlinear optics. As is known, the nature of NLS equation has been widely explored via different approaches before, and its exact solutions are vast in related literature. For example, when
is a complex wave function of related system dynamics in physical fields such as BBCs and nonlinear optics. As is known, the nature of NLS equation has been widely explored via different approaches before, and its exact solutions are vast in related literature. For example, when 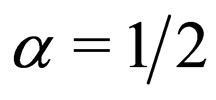 and
and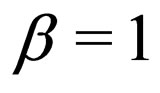 , the NLS equation possesses a canonical bright soliton solution
, the NLS equation possesses a canonical bright soliton solution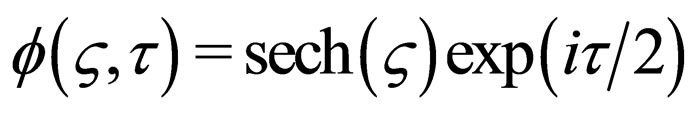 , while
, while 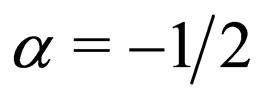 and
and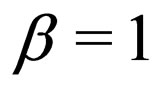 , the NLS equation has a fundamental dark soliton solution
, the NLS equation has a fundamental dark soliton solution
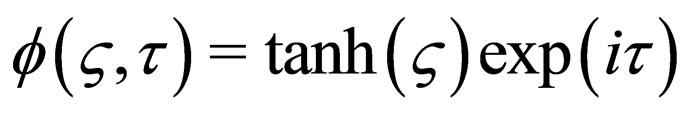 .
.
For more detailed information, one may refer to a review in reference [20]. Actually, in (1 + 1) dimensions, it has been proven when a physical system can be expressed by a partial differential equation, then under some suitable approximations, one can always find nonlinear Schrödinger type equation [21,22]. This is why the (1 + 1)-dimensional nonlinear Schrödinger system can be successfully used in almost all the physical branches.
In order to build a direct projective relation between the nonautonomous NLS system (1) and the standard NLS Equation (5), we construct an ansatz to the nonautonomous NLS system as follows
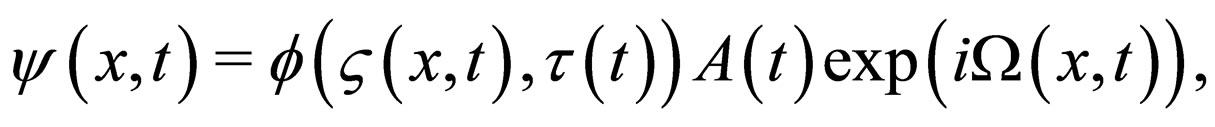 (6)
(6)
where 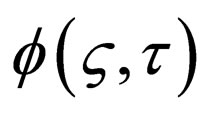 is an exact complex solution to the standard NLS Equation (5),
is an exact complex solution to the standard NLS Equation (5), 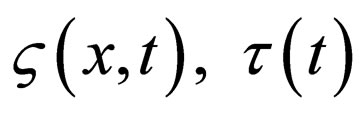 are similarity variables,
are similarity variables, 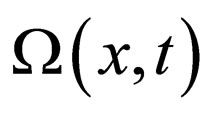 is a similarity wave phase, and
is a similarity wave phase, and 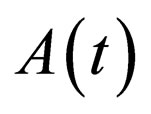 is a time-dependent function to modulate the wave amplitude to be determined. The reason for
is a time-dependent function to modulate the wave amplitude to be determined. The reason for 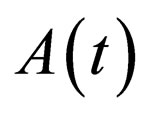 to be factored out of
to be factored out of 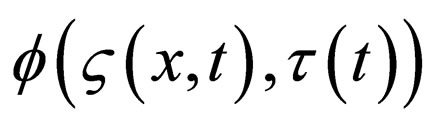 in format (6) is the existence of the coefficients functions of time t in Equation (1). All the parameters all real differential functions, and should be well chosen to avoid some singularity of the complex wave function
in format (6) is the existence of the coefficients functions of time t in Equation (1). All the parameters all real differential functions, and should be well chosen to avoid some singularity of the complex wave function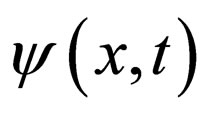 . Substituting Equation (6) together with Equation (5) into the nonautonomous NLS system (1), collecting coefficients of polynomials of
. Substituting Equation (6) together with Equation (5) into the nonautonomous NLS system (1), collecting coefficients of polynomials of 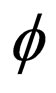 and its derivatives, then setting each coefficient to zero, yields a set of partial differential equations
and its derivatives, then setting each coefficient to zero, yields a set of partial differential equations
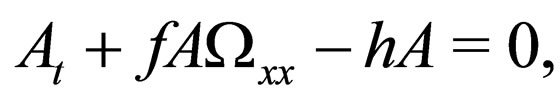 (7)
(7)
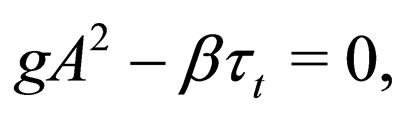 (8)
(8)
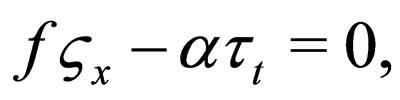 (9)
(9)
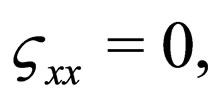 (10)
(10)
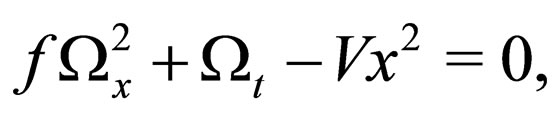 (11)
(11)
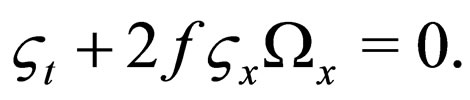 (12)
(12)
After some careful and direct algebra, one can obtains the amplitude, self-similarity variables and phase of the complex wave pulse
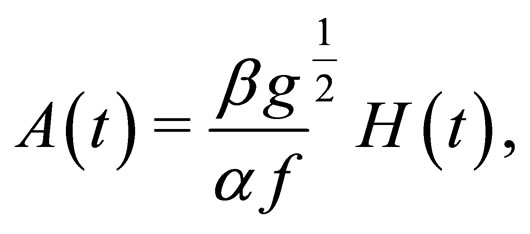 (13)
(13)
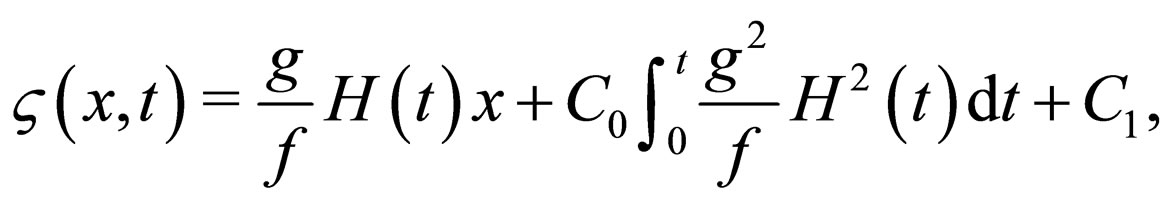 (14)
(14)
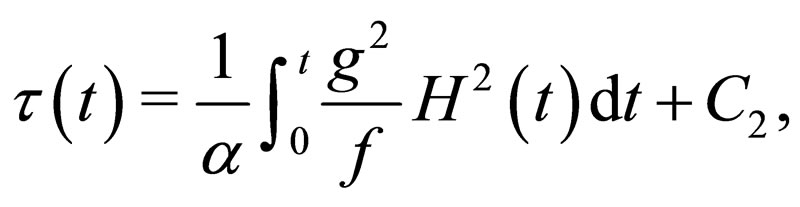 (15)
(15)
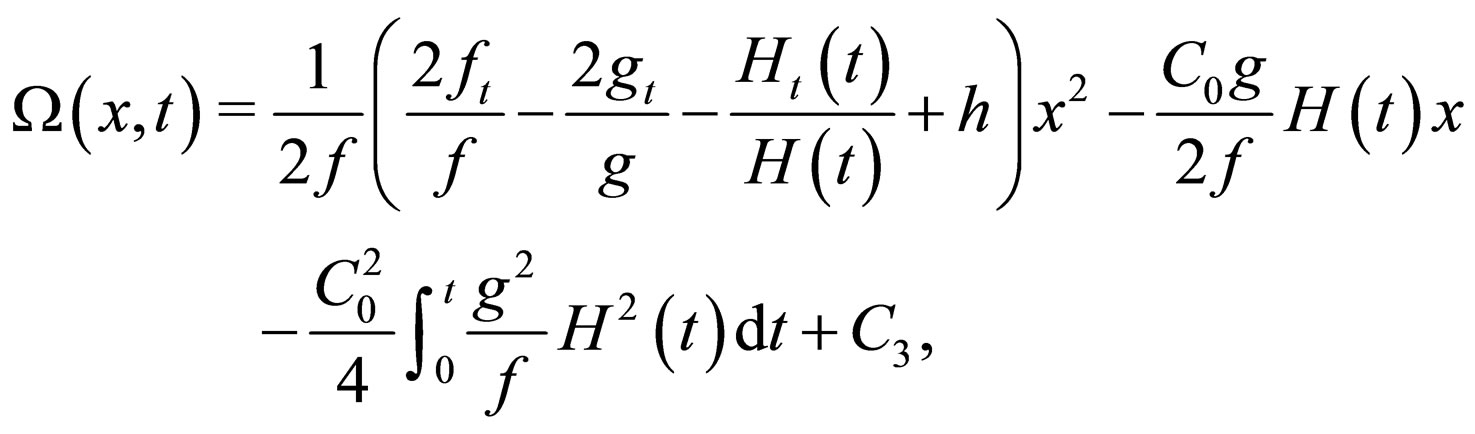 (16)
(16)
where 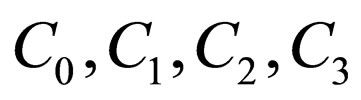 are integrable constants,
are integrable constants,  is defined by
is defined by
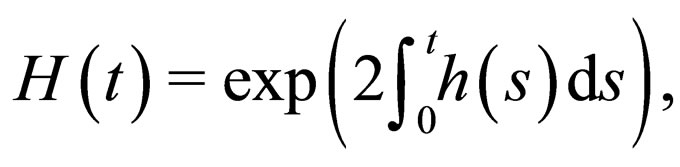 (17)
(17)
and with a constraint condition
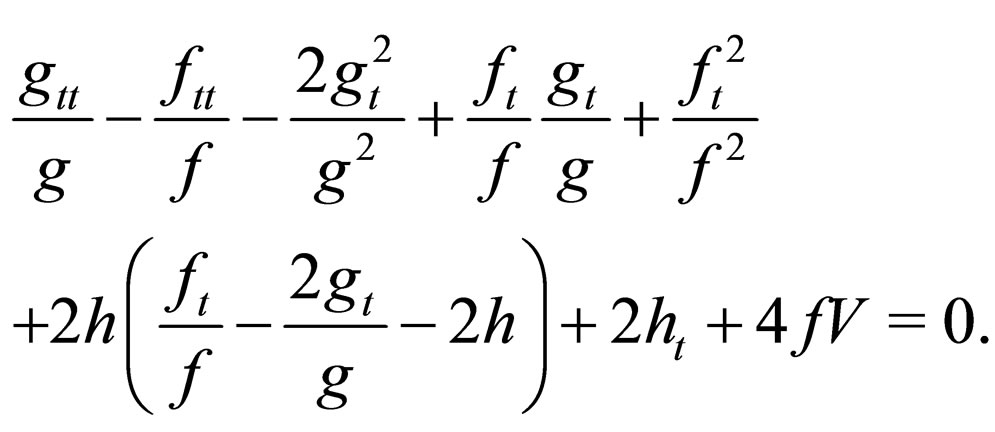 (18)
(18)
It is interesting to note that when the net gain coefficient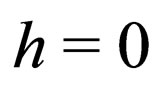 , the constraint condition (18) becomes
, the constraint condition (18) becomes
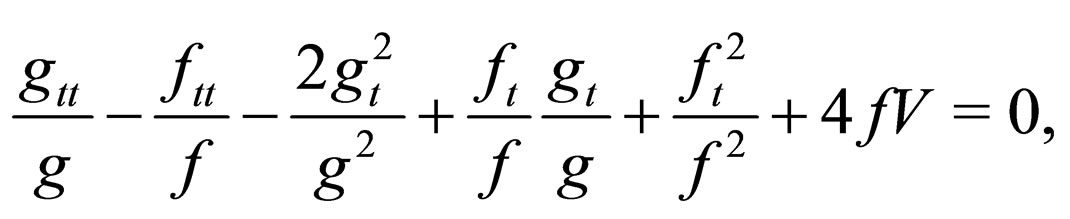 (19)
(19)
which is just the completely integrable compatibility condition via the Painlevé analysis [4,7], i.e., a subtle balance condition to keep the nonautonomous NLS system integrable.
From the management viewpoint of the solitons, Equation (18) provides an effectively way to manipulate soliton dynamics. When any three parameters among 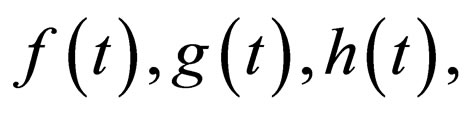 and
and 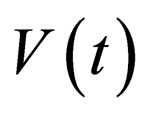 are set, the remaining one can be tuned correspondingly via Eqaution (18) to control the coherent dynamics of solitons. Actually, some special applications of equation (18) have been explored in reference [7]. However, the general selfsimilarity projective transformations (13)-(16) were not reported in the previous literature. Such transformations are quite systematic in obtaining the exact solutions of the nonautonomous NLS system. For a given nonautonomous NLS system or its similar versions, we first check if the coefficients satisfy the constrain condition Equation (18). If it is true, then the nonautonomous NLS system can be reduced to the standard NLS Equation (5). All allowed exact solutions, including canonical solitons, of the standard NLS Equation (5) can be converted into the corresponding exact solutions of the nonautonomous NLS system. In the sense, the canonical soliton of the standard NLS equation can be naturally viewed as a seed solution of the corresponding localized solutions of Equation (1) under the compatibility condition Equation (18). For example, when
are set, the remaining one can be tuned correspondingly via Eqaution (18) to control the coherent dynamics of solitons. Actually, some special applications of equation (18) have been explored in reference [7]. However, the general selfsimilarity projective transformations (13)-(16) were not reported in the previous literature. Such transformations are quite systematic in obtaining the exact solutions of the nonautonomous NLS system. For a given nonautonomous NLS system or its similar versions, we first check if the coefficients satisfy the constrain condition Equation (18). If it is true, then the nonautonomous NLS system can be reduced to the standard NLS Equation (5). All allowed exact solutions, including canonical solitons, of the standard NLS Equation (5) can be converted into the corresponding exact solutions of the nonautonomous NLS system. In the sense, the canonical soliton of the standard NLS equation can be naturally viewed as a seed solution of the corresponding localized solutions of Equation (1) under the compatibility condition Equation (18). For example, when 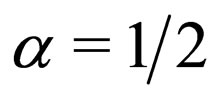 and
and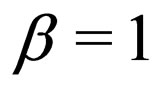 , a simple exact solution of the NLS Equation (5) is given by
, a simple exact solution of the NLS Equation (5) is given by
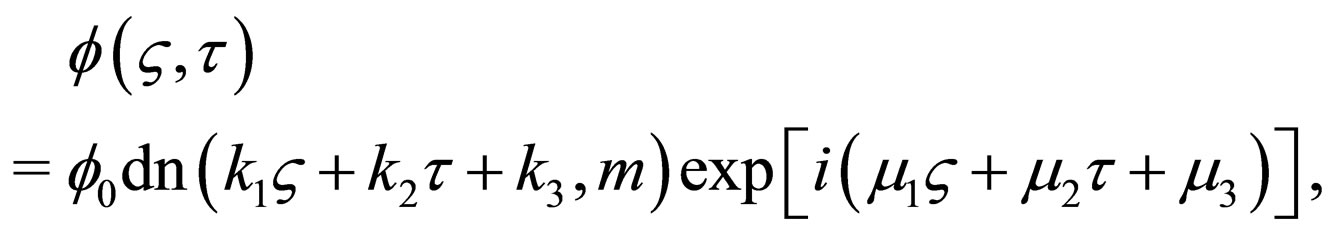 (20)
(20)
where
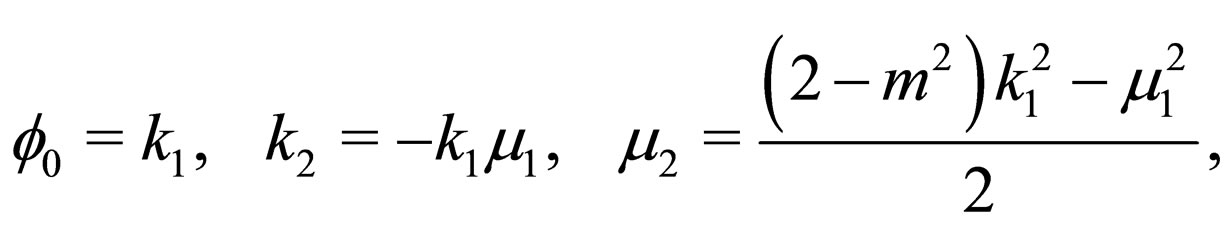 (21)
(21)
and 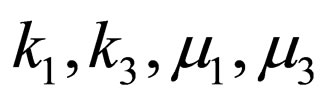 are arbitrary constants, dn(·, m) denotes the dn type Jacobian elliptic function with
are arbitrary constants, dn(·, m) denotes the dn type Jacobian elliptic function with 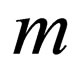 being its modulus. This leads to the following family of double periodic wave solutions to the nonautonomous NLS system (1)
being its modulus. This leads to the following family of double periodic wave solutions to the nonautonomous NLS system (1)
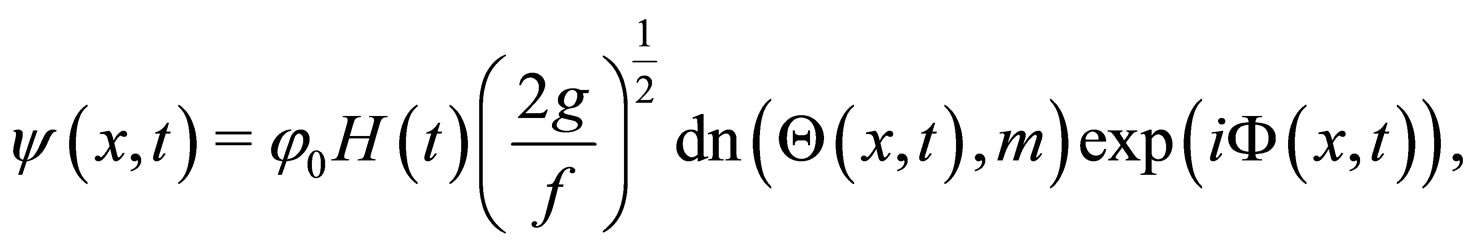 (22)
(22)
where
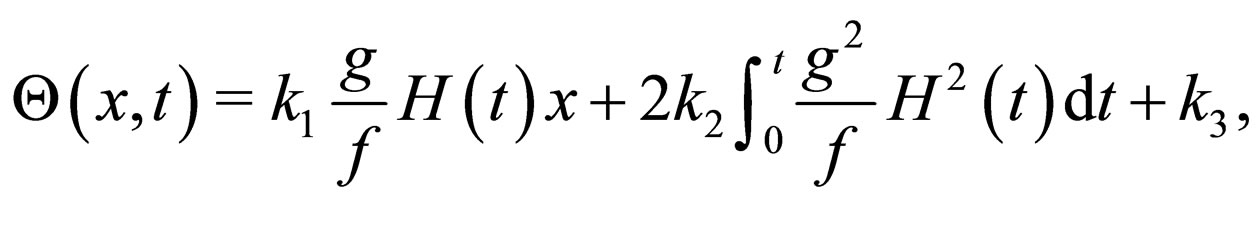 (23)
(23)
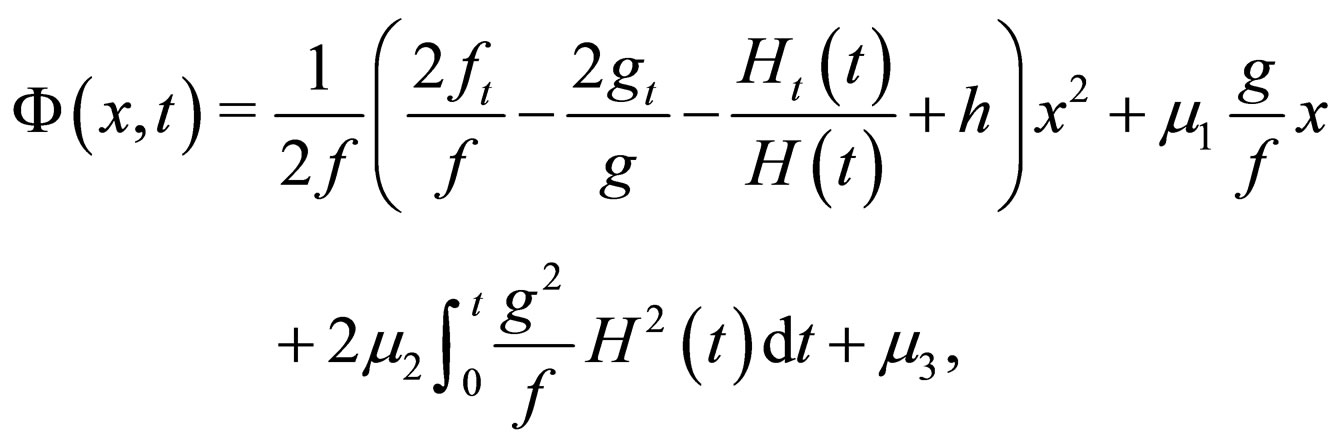 (24)
(24)
and the integrable constants 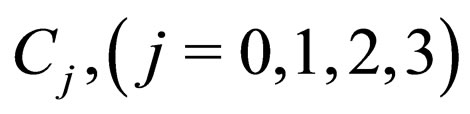 in Equations (13)-(16) are set to be zero for simplicity. In the limit case
in Equations (13)-(16) are set to be zero for simplicity. In the limit case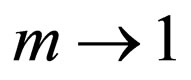 , the above double periodic wave solution (22) will be reduced to a solitary wave solution
, the above double periodic wave solution (22) will be reduced to a solitary wave solution
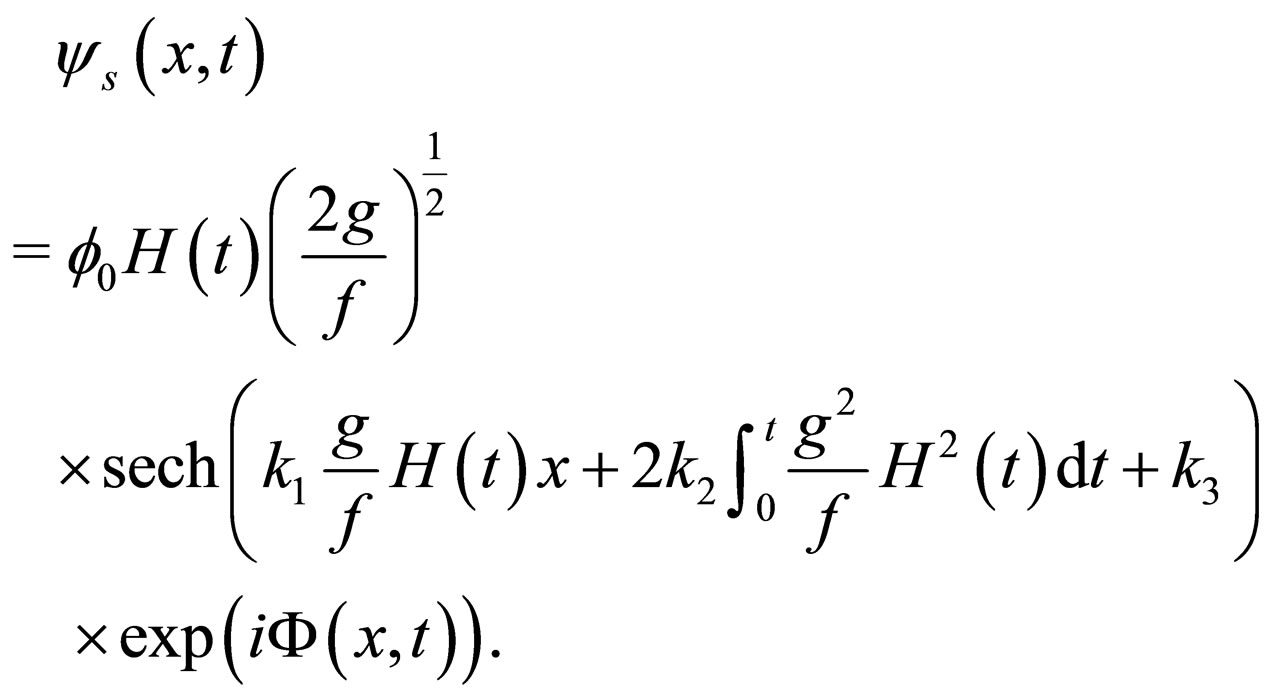 (25)
(25)
with the constraint condition (18). As a special case, if 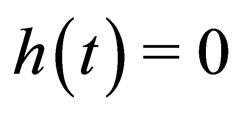 and
and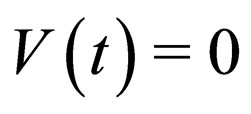 , the constrain condition (18) becomes
, the constrain condition (18) becomes
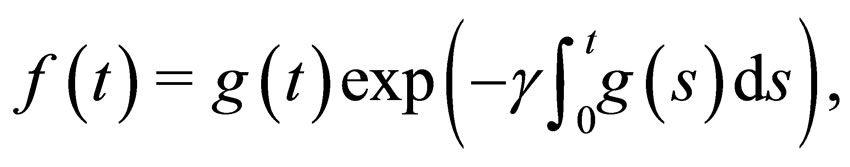 (26)
(26)
where 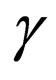 is a integrable constant, then the above corresponding exact solutions read
is a integrable constant, then the above corresponding exact solutions read
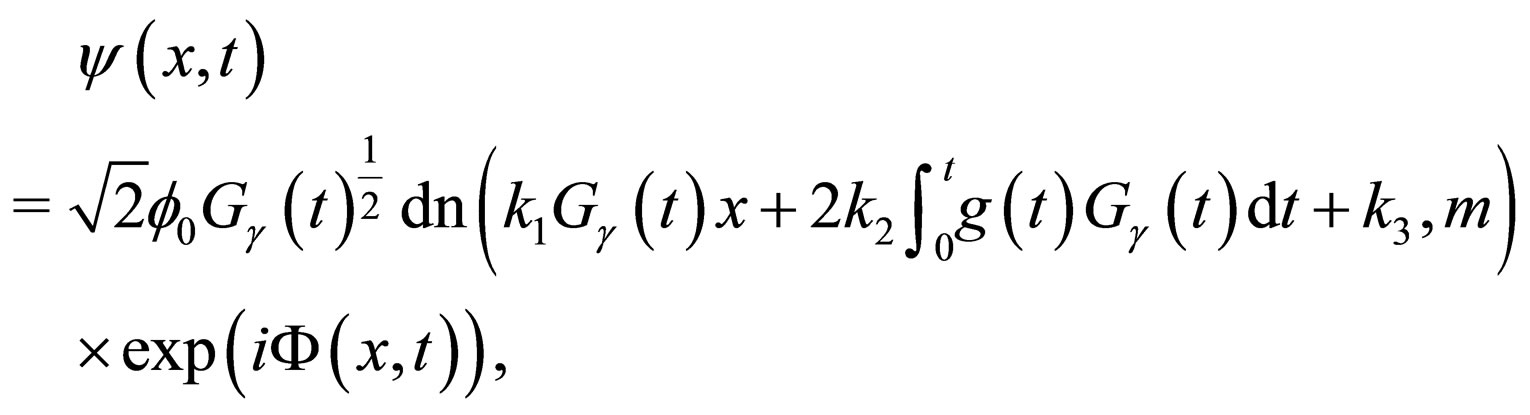 (27)
(27)
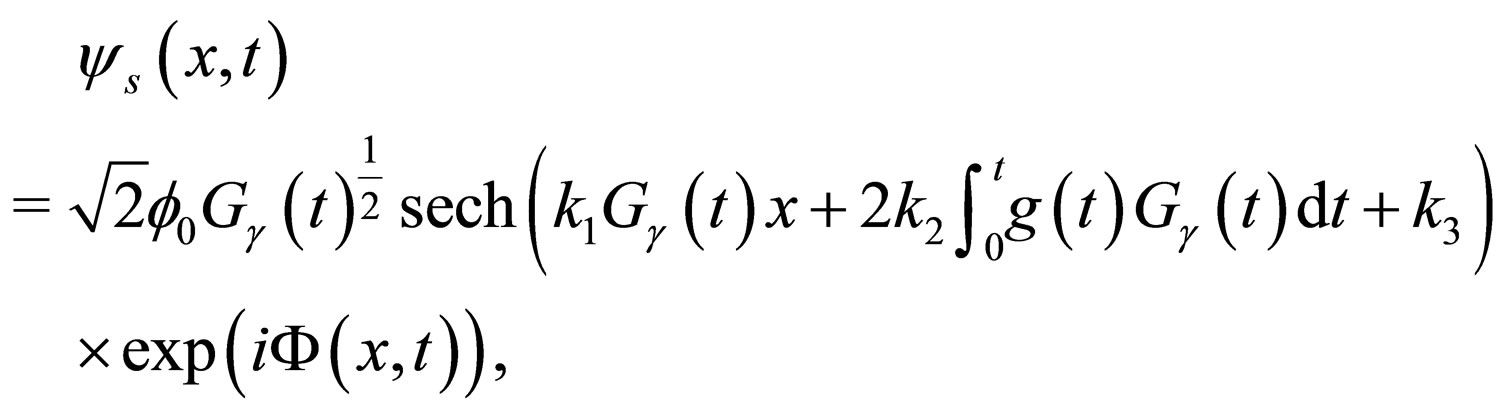 (28)
(28)
where
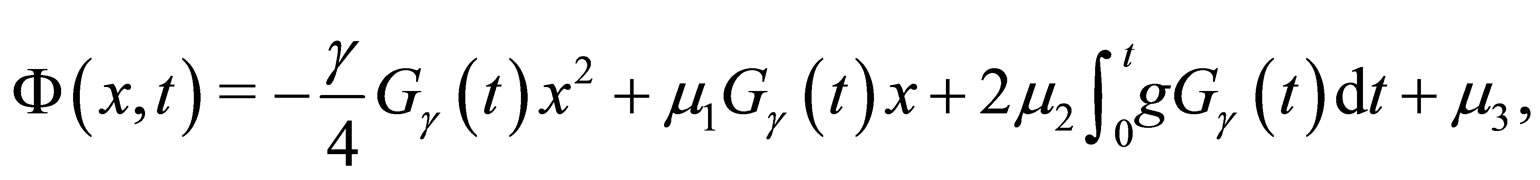 (29)
(29)
with
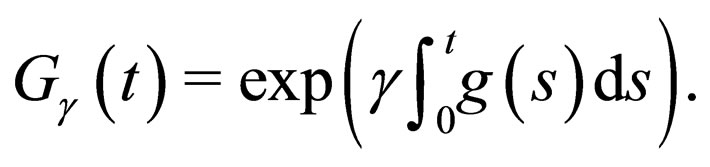 (30)
(30)
Once the nonlinear parameter 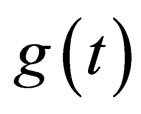 is explicitly given, then all the exact solutions and their related dynamic behaviors of the nonautonomous NLS system are correspondingly determined. For integrality and readability, some remarks are given as follows:
is explicitly given, then all the exact solutions and their related dynamic behaviors of the nonautonomous NLS system are correspondingly determined. For integrality and readability, some remarks are given as follows:
Firstly, as a special situation, if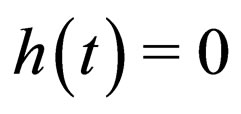 ,
, 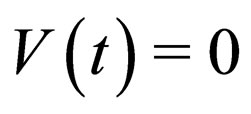 and
and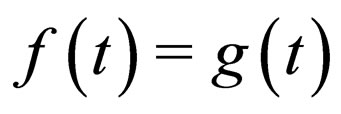 , i.e.,
, i.e., 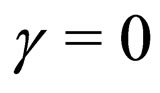 in Equation (26), the nonautonomous NLS system (1) has the canonical soliton solutions regardless of the explicit form of the timedependent nonlinearity and dispersion. This is because in this case the the constraint condition is identified and the scale factor
in Equation (26), the nonautonomous NLS system (1) has the canonical soliton solutions regardless of the explicit form of the timedependent nonlinearity and dispersion. This is because in this case the the constraint condition is identified and the scale factor 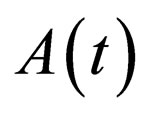 is a constant
is a constant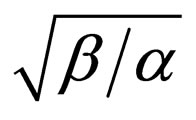 . In this sense the soliton solution of Equation (1) is a fundamental canonical soliton. While
. In this sense the soliton solution of Equation (1) is a fundamental canonical soliton. While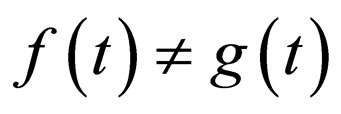 , i.e.,
, i.e., 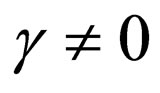 in Equation (26), the original balance between nonlinearity and dispersion is broken down. In the case the canonical soliton must deform itself to build new balance between nonlinearity and dispersion, and the soliton-like solution of Equation (1) is a deformed canonical soliton or a similariton due to the amplitude of the soliton scaled by the factor
in Equation (26), the original balance between nonlinearity and dispersion is broken down. In the case the canonical soliton must deform itself to build new balance between nonlinearity and dispersion, and the soliton-like solution of Equation (1) is a deformed canonical soliton or a similariton due to the amplitude of the soliton scaled by the factor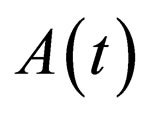 . And it actually means that if
. And it actually means that if 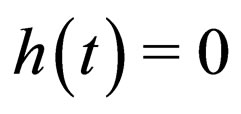 and
and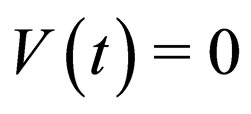 , the exact solitons of the nonautonomous NLS system (1) are quasi-canonical or deformed solitons depending on if
, the exact solitons of the nonautonomous NLS system (1) are quasi-canonical or deformed solitons depending on if 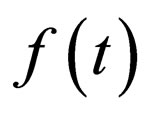 is equal to
is equal to 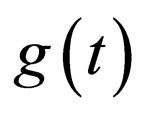 or not as mentioned above.
or not as mentioned above.
Secondly, for more general cases, if 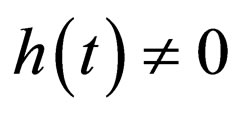 and
and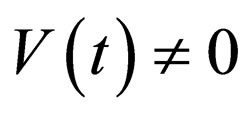 , the constraint condition (18) indicates that
, the constraint condition (18) indicates that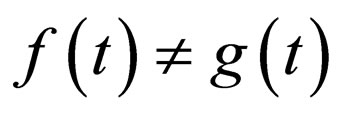 , which means the amplitude of the soliton must vary with factor
, which means the amplitude of the soliton must vary with factor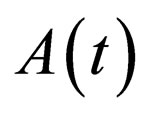 . This leads to an important and a novel phenomenon that there does not exist the canonical and even quasi-canonical matter-wave solitons under the constraint condition (18). However, when we set
. This leads to an important and a novel phenomenon that there does not exist the canonical and even quasi-canonical matter-wave solitons under the constraint condition (18). However, when we set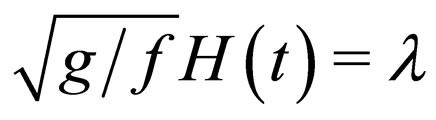 , (
, (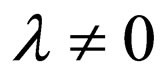 is an arbitrary constant), i.e.,
is an arbitrary constant), i.e., 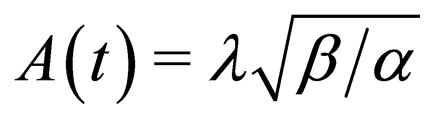 ,
,
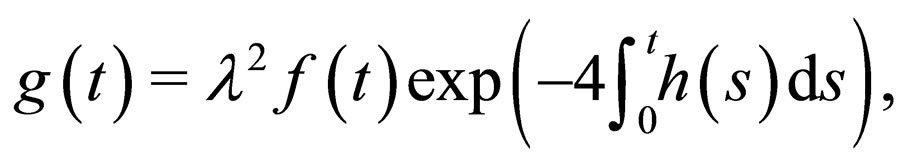 (31)
(31)
and 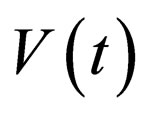 is tuned by the constraint condition (18) as follows
is tuned by the constraint condition (18) as follows
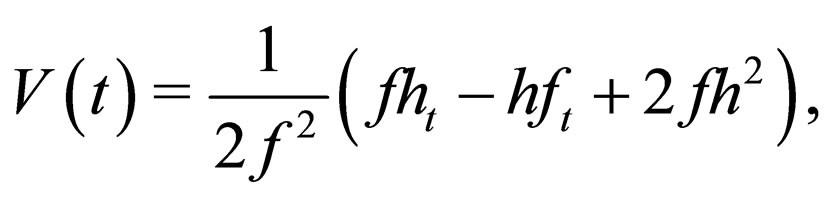 (32)
(32)
then we can rederive fundamental canonical solitons, which distinctly indicates the influence of the dispersion, nonlinear managements and net gain to the localized excitation behaviors.
Finally, it is also interesting to mention that the external trap potential 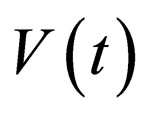 is absent in the selfsimilarity projective transformations (13)-(16). However, the presence of the potential affects the balance between nonlinearity, dispersion and net gain via the constraint condition (18), and builds a deep relation between the optical solitons and the matter-waves.
is absent in the selfsimilarity projective transformations (13)-(16). However, the presence of the potential affects the balance between nonlinearity, dispersion and net gain via the constraint condition (18), and builds a deep relation between the optical solitons and the matter-waves.
4. Summary and Discussion
In summary, the direct self-similarity projective approach is successfully applied to the nonautonomous nonlinear Schrödinger system. In terms of the known exact solutions of the self-similarity projective equation, i.e., the standard nonlinear Schröding equation, some significant types of localized excitations with novel properties are correspondingly revealed by entrancing appropriate system parameters. The present analysis can be applied to all exact solutions of the nonautonomous nonlinear Schrödinger system. The self-similarity projective approach provides an effective and a systematical way to investigate the nonlinear dynamics of the nonautonomous nonlinear Schrödinger system. By the way, as a comparison it is helpful to mention some techniques to find the localized excitation solutions of the nonautonomous NLS equation in previous literature. The Lax pair analysis is very useful in discussing integrability conditions. And a widely used approach is the deformation projective method, which introduces some explicit transformation parameters. These parameters are determined by a set of partial differential equations, which in general case are little solved analytically as emphasized in reference [23]. Another similarity transformation reducing the nonautonomous nonlinear Schrödinger equation to a stationary NLS one has also been introduced [24]. Alternatively, by the Lie point symmetry group analysis, the nonautonomous nonlinear Schrödinger system or its similar versions can be classified into different classes and each one can be converted into the corresponding representative equation by some allowed transformations. As a result, some exact solutions of the representative equation can be transformed into the corresponding solutions of the equations in the same class. However, it was also pointed out in [25] that in most cases it is still difficult to obtain the exact solutions of these representative equations and the integrability of certain representative equations is not clear. Quite different from the above mentioned techniques, the present work builds a direct connection between the nonautonomous NLS equation and its autonomous counterpart, which provides a more systematical way to find exact solutions of the nonautonomous NLS equation. The corresponding transformation formulas are explicit and straightforward. Furthermore, one can naturally derive the integrable constrain condition (18) via the SPA rather than some integrable conditions via Painlevé analysis first in previous discussions. From the control viewpoint, the self-similarity projective approach provides an effective and a powerful way to control the soliton dynamics as mentioned above. In addition, the SPA that we use to solve the nonautonomous nonlinear Schrödinger system will pave the way to new methods for solving high-dimensional partial differential equations.
5. Acknowledgements
The authors are in debt to Professors Y. M. Liu and J. F. Zhang, Doctors C. Q. Dai and T. T. Jia for their fruitful discussions. The work was supported by the National Natural Science Foundation of China under Grant No.11172181, the Natural Science Foundation of Guangdong Province of China under Grant No. 101512005- 01000008, the Special Foundation of Talent Engineering of Guangdong Province of China, and the Scientific Research Foundation of Key Discipline of Guangdong Shaoguan University.
REFERENCES
- K. E. Strecker, G. B. Partridge, A. G. Truscott and R. G. Hulet, “Formation and Propagation of Matter-Wave Soliton Trains,” Nature, Vol. 417, 2002, pp. 150-153. doi:10.1038/nature747
- L. F. Mollenauer, R. H. Stolen and J. P. Gordon, “Experimental Observation of Picosecond Pulse Narrowing and Solitons in Optical Fibers,” Physics Review Letter, Vol. 45, No. 13, 1980, pp. 1095-1098. doi:10.1103/PhysRevLett.45.1095
- C. Q. Dai, X. G. Wang and J. F. Zhang, “Nonautonomous Spatiotemporal Localized Structures in the Inhomogeneous Optical Fibers: Interaction and Control,” Annals of Physics, Vol. 326, No. 3, 2011, pp. 645-656. doi:10.1016/j.aop.2010.11.005
- D. Zhao, X. G. He and H. G. Luo, “Transformation from the Nonautonomous to Standard NLS Equations,” Physics and Astronomy, Vol. 53, No. 2, 2009, pp. 213-216. doi:10.1140/epjd/e2009-00051-7
- I. Towers and B. A. Malomed, “Stable (2+1)-dimensional Solitons in a Layered Medium with Sign-Alternating Kerr Nonlinearity,” Journal of the Optical Society of America B, Vol. 19, 2002, pp. 537-543. doi:10.1364/JOSAB.19.000537
- Y. Gao and S. Y. Lou, “Analytical Solitary Wave Solutions to a (3+1)-Dimensional Gross-Pitaevskii Equation with Variable Coefficients,” Communications in Theoretical Physics, Vol. 52, 2009, pp. 1030-1035.
- V. N. Serkin, A. Hasegawa and T. L. Belyaeva, “Nonautonomous Solitons in External Potentials,” Physics Review Letter, Vol. 98, No. 7, 2007, Article ID: 074102. doi:10.1103/PhysRevLett.98.074102
- S. A. Ponomarenko and G. P. Agrawal, “Do Solitonlike Self-Similar Waves Exist in Nonlinear Optical Media?” Physics Review Letter, Vol. 97, No. 1, 2006, Article ID: 013901. doi:10.1103/PhysRevLett.97.013901
- S. Y. Lou, H. C. Hu and X. Y. Tang, “Interactions among Periodic Waves and Solitary Waves of the (N+1)-Dimensional Sine-Gordon Field,” Physics Review E, Vol. 71, No. 3, 2005, Article ID: 036604. doi:10.1103/PhysRevE.71.036604
- S. Y. Lou and G. J. Ni, “The Relations among a Special Type of Solutions in Some (D+1)-Dimensional Nonlinear Equations,” Journal of Mathematical Physics, Vol. 30, No. 7, 1989, pp. 1614-1620. doi:10.1063/1.528294
- H. M. Li, “Searching for (3+1)-Dimensional Painlevé Integrable Model and Its Solitary Wave Solution,” Chinese Physics Letters, Vol. 19, No. 6, 2002, pp. 745-747. doi:10.1088/0256-307X/19/6/301
- C. L. Zheng, H. P. Zhu and L. Q. Chen, “Exact Solution and Semifolded Structures of Generalized BroerKaup System in (2+1)-Dimensions,” Chaos, Solitons & Fractals, Vol. 26, No. 1, 2004, pp. 181-194. doi:10.1016/j.chaos.2004.12.017
- Sirendaoreji and S. Jiong, “Auxiliary Equation Method for Solving Nonlinear Partial Differential Equations,” Physics Letters A, Vol. 309, No. 5-6, 2003, pp. 387-396. doi:10.1016/S0375-9601(03)00196-8
- E. G. Fan, “An Algebraic Method for Finding a Series of Exact Solutions to Integrable and Nonintegrable Nonlinear Evolution Equations,” Journal of Physics A: Mathematical and General, Vol. 36, No. 25, 2003, p. 7009. doi:10.1088/0305-4470/36/25/308
- C. L. Zheng and L. Q. Chen, “Some Novel Evolutional Behaviors of Localized Excitations in the Boiti-LeonMartina-Pempinelli System,” International Journal of Modern Physics B, Vol. 22, No. 6, 2008, pp. 671-682. doi:10.1142/S0217979208038879
- H. Y. Wu, J. X. Fei and C. L. Zheng, “Self-Similar Solutions of Variable-Coefficient Cubic-Quintic Nonlinear Schrödinger Equation with an External Potential,” Communications in Theoretical Physics, Vol. 54, 2010, pp. 55-59.
- J. X. Fei and C. L. Zheng, “Chirped Self-Similar Solutions of a Generalized Nonlinear Schrödinger Equation,” Verlag der Zeitschrift für Naturforschung, Vol. 66, 2011, pp. 1-5.
- C. Q. Dai, Y. Y. Wang and X. G. Wang, “Ultrashort Self-Similar Solutions of the Cubic-Quintic Nonlinear Schrödinger Equation with Distributed Coefficients in the Inhomogeneous Fiber,” Journal of Physics A: Mathematical and Theoretical, Vol. 44, No. 15, 2011, Article ID: 155203. doi:10.1088/1751-8113/44/15/155203
- C. Q. Dai, R. P. Chen and G. Q. Zhou, “Spatial Solitons with the Odd and Even Symmetries in (2+1)-Dimensional Spatially Inhomogeneous Cubic-Quintic Nonlinear Media with Transverse W-Shaped Modulation,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 44, No. 14, 2011, Article ID: 145401. doi:10.1088/0953-4075/44/14/145401
- C. Sulem and P. L. Sulem, “The Nonlinear Schrödinger Equation: Self-Focusing and Wave Collapse,” SpringerVerlag, New York, 1991.
- F. Calogero, A. Degasperis and J. Xiaoda, “Nonlinear Schrödinger-Type Equations from Multiscale Reduction of PDEs. I. Systematic Derivation,” Journal of Mathematical Physics, Vol. 41, No. 9, 2000, p. 6399. doi:10.1063/1.1287644
- F. Calogero and A. Degasperis, “Nonlinear Schrödingertype Equations from Multiscale Reduction of PDEs. II. Necessary Conditions of Integrability for Real PDEs,” Journal of Mathematical Physics, Vol. 42, No. 6, 2001, pp. 2635-2652. doi:10.1063/1.1366296
- J. He and Y. Li, “Designable Integrability of the Variable Coefficient Nonlinear Schrödinger Equations,” Studies in Applied Mathematics, Vol. 126, No. 1, 2011, pp. 1-15. doi:10.1111/j.1467-9590.2010.00495.x
- J. B. Beitia, V. M. Perez-Garcia and V. Brazhnyib, “Solitary Waves in Coupled Nonlinear Schrödinger Equations with Spatially Inhomogeneous Nonlinearities,” Communications in Nonlinear Science and Numerical Simulation, Vol. 16, No. 1, 2011, Article ID: 158172. doi:10.1016/j.cnsns.2010.02.024
- L. Gagnon and P. Winternitz, “Symmetry Classes of Variable Coefficient Nonlinear Schrödinger Equations,” Journal of Physics A: Mathematical and General, Vol. 26, No. 23, 1993, p. 7061. doi:10.1088/0305-4470/26/23/043
NOTES
*Corresponding author.

