Journal of Modern Physics
Vol.3 No.7(2012), Article ID:21083,11 pages DOI:10.4236/jmp.2012.37078
The Quaternion Structure of Space-Time and Arrow of Time
Fudan University, Shanghai, China
Email: yqgu@fudan.edu.cn
Received April 6, 2012; revised May 8, 2012; accepted June 1, 2012
Keywords: Arrow of time; Invariance; The principle of relativity; Quaternion structure of space-time; simultaneity
ABSTRACT
In fundamental theories of physics, the dynamical equations all have time inversion invariance. Except for the evolution of some simple system which has realistic inverse processes, but for a slightly more complicated system, the evolution processes are irreversible. This is the problem of arrow of time, which is always warmly debated. In different point of view, we find there may have some conceptual misunderstanding in the controversy: 1) The realization of an inverse process does not mean the time of the system goes backward; 2) The principles of relativity and covariance are the constraints to physical laws, but not constraints to specific solutions. The equations must be covariant, but the solutions are not definitely symmetric; 3) Time is a global property of the universe, which is a measurement of the evolution process of the universe. The internal time of a matter system reflecting its internal evolution speed also takes this cosmic time as a unified background and standard of measurement; 4) The universe has a unified cosmic time T and a cosmic space related to this cosmic time. They are objective and absolute; 5) The eigensolution of a spinor is a critical state losing time concept, which responses the interaction of environment with some uncertainty, then the evolution process of the world is not uniquely determined; 6) The non-uniqueness of the evolution process means that the inverse process is absent. So for a world including spinors, the evolution is essentially irreversible. In this paper, according to the widely accepted principles and direct calculations of transformation, we reveal the misunderstandings in the usual controversy, and then give more natural and reasonable explanations for structure of space-time and arrow of time.
1. Introduction
In fundamental theories of physics such as Newtonian mechanics, electrodynamics, quantum mechanics, the dynamical equations all have time inversion invariance. But except for the evolution of some simple system which has realistic inverse processes, such as swing of a pendulum, dissolution and crystallization of crystal, emission and absorption of photons, for a slightly more complicated system, the evolution processes are essentially irreversible. This is the problem of arrow of time, which is always warmly debated [1-9].
In different point of view, we find there may have some conceptual misunderstanding in the controversy:
1) The realization of an inversion process does not mean that time of the system goes backward. We make two clocks with mirror image. One rotates clockwise, and the other rotates anticlockwise. But this does not mean time of the clockwise one goes forward, and time of the other goes backward. Similarly, the expansion of the universe does not mean the cosmic time goes forward, and the contraction does not mean the cosmic time goes backward. The expansion or contraction is just a dynamical effect of the space-time.
2) The principles of relativity and covariance are the constraints to physical laws, but not constraints to concrete solutions. The specific matter system is only a special solution of physical laws, so the equations must be covariant, but the solutions are not definitely symmetric.
3) Time is a global property of the universe, which is a measurement of the evolution process of the universe. The universe has a unique and unified cosmic time, and it always goes unidirectionally forward. Related to this cosmic time we have the specific state of universe at some time, which forms the cosmic space and the existences. There is an internal time to reflect the evolution process of a system, just like the history and lifetime of a man, which is the proper time 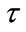 of the system. However, this proper time also takes the cosmic time as a unified background and a measuring standard.
of the system. However, this proper time also takes the cosmic time as a unified background and a measuring standard.
4) The universe has a unified cosmic time 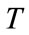 and a cosmic space related to this cosmic time. The cosmic space is the total space described by the coordinate system relatively at rest to the cosmic background radiation. The cosmic space and time are objective and absolute. Since the total universe is also a realistic solution of all physical laws. So this solution is objective, and it does not definitely have the symmetry of the equations.
and a cosmic space related to this cosmic time. The cosmic space is the total space described by the coordinate system relatively at rest to the cosmic background radiation. The cosmic space and time are objective and absolute. Since the total universe is also a realistic solution of all physical laws. So this solution is objective, and it does not definitely have the symmetry of the equations.
5) The eigensolution of spinor is a critical state losing time concept, which responses the interaction of environment with some uncertainty, then the evolution process of the world is not uniquely determined and has some randomness. The evolution of the world is not uniquely determined.
6) The non-uniqueness of the evolution process means that the inverse process is absent. So for a world including spinors, the evolution is essentially irreversible.
These opinions have been discussed in other papers [10-12]. In what follows, we give some detailed discussion for the structure of the space-time and relative symmetries of the transformation through specific calculations and explanations.
2. The Quaternion Structure of Space-Time
Relativity is a theory of space-time of the universe, which is based on the principle of constant vacuum light speed and the principles of relativity and generalized covariance. Though this treatment is reasonable is physics, there is an underlying risk in epistemology. Because the structure of space-time is a problem involving much broader contents than the vacuum light speed [13], and we can't accurately measure light speed in true vacuum. Using the property of a specific matter system to describe general concepts, it is easy to fall into the trap of language. The logical procedure should be to establish the geometry of space-time at first, and then to use the geometry and electrodynamics explaining the invariance of the vacuum light speed. In this way, a lot of plausible paradoxes will disappear, and one will not be puzzled by superluminal neutrino phenomena and problems of the time’s arrow [11,12]. The theory of space-time is a geometry, so like the Euclidian geometry, it will be more effective and convenient to describe the structure of space-time by the method of geometry, and then explain the corresponding relations between realistic world and geometric concepts. In this way, the problems become simple and clear in logic. In a sense, the principle of constant light speed is a constraint for the metric of the space-time, and the principles of relativity and covariance explain the rules of transformation between coordinate systems.
A point or event in the space-time can be labeled by 3 independent spatial coordinates  and one temporal coordinate
and one temporal coordinate , that is to say the space-time is 3 + 1 dimensional. This is a basic fact, which can only be accepted as a fundamental postulate. The selection of coordinate system and the local reference frame or tetrad at each event is subjective and arbitrary. However, the event and the 4 dimensional distance or interval between two events are objective. For the same physical system, different researchers can choose quite different coordinate system and local tetrad, but their coordinates and physical parameters should be in one-to-one correspondence, and the equations should take the same structure. This is the essential meaning of the principles of relativity and covariance. However, the usual understanding and explanations in textbooks have some problems.
, that is to say the space-time is 3 + 1 dimensional. This is a basic fact, which can only be accepted as a fundamental postulate. The selection of coordinate system and the local reference frame or tetrad at each event is subjective and arbitrary. However, the event and the 4 dimensional distance or interval between two events are objective. For the same physical system, different researchers can choose quite different coordinate system and local tetrad, but their coordinates and physical parameters should be in one-to-one correspondence, and the equations should take the same structure. This is the essential meaning of the principles of relativity and covariance. However, the usual understanding and explanations in textbooks have some problems.
Spinor equation is the most basic equation to describe matter. Detailed analysis shows that, to this kind of equation, the relativity principle is valid only if the space-time has 3 + 1 dimensions and has a quadratic interval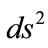 . In this case, the space-time has elegant quaternion structure, and the physical fields and their dynamic equations can be expressed in quaternion form. Their transformation laws can be realized only for such quaternion differential operator. This feature can be found in the following calculations. Further more, for this first order differential field equation system, the solutions evolve in one direction in time.
. In this case, the space-time has elegant quaternion structure, and the physical fields and their dynamic equations can be expressed in quaternion form. Their transformation laws can be realized only for such quaternion differential operator. This feature can be found in the following calculations. Further more, for this first order differential field equation system, the solutions evolve in one direction in time.
In this paper, we use notations 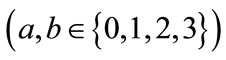 stands for the indexes in flat space-time and
stands for the indexes in flat space-time and 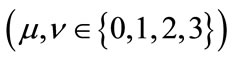 stands for the indexes in the curved space-time, but
stands for the indexes in the curved space-time, but 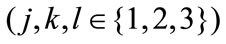 for the indexes in space. Let
for the indexes in space. Let 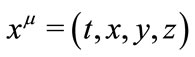 be a smooth enough coordinate system labeled in the space-time and
be a smooth enough coordinate system labeled in the space-time and 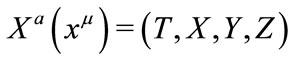 is an orthogonal reference system in the tangent space-time at given event
is an orthogonal reference system in the tangent space-time at given event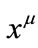 . This tetrad can be represented by the basis of Clifford algebra
. This tetrad can be represented by the basis of Clifford algebra  which is isomorphic to the quaternion basis. The usual Dirac matrix is a realization. Denote
which is isomorphic to the quaternion basis. The usual Dirac matrix is a realization. Denote
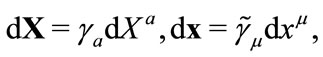 (2.1)
(2.1)
in which coordinate increments 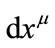 and
and  are vectors satisfying linear transformation law.
are vectors satisfying linear transformation law.  and
and  are time-like vectors.
are time-like vectors. 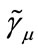 is a set of quaternion basis in curvilinear coordinate system. They are not definitely orthogonal, but satisfy the following relation
is a set of quaternion basis in curvilinear coordinate system. They are not definitely orthogonal, but satisfy the following relation
 (2.2)
(2.2)
where  is Minkowski metric, and
is Minkowski metric, and  is the metric in curvilinear coordinate system,
is the metric in curvilinear coordinate system,
 (2.3)
(2.3)
The calculation and explanation for the tetrad coefficients  refer to [14,15].
refer to [14,15].
The interval between two infinitely adjacent events 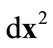 or
or 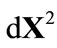 is an objective quantity independent of coordinate system, we have
is an objective quantity independent of coordinate system, we have
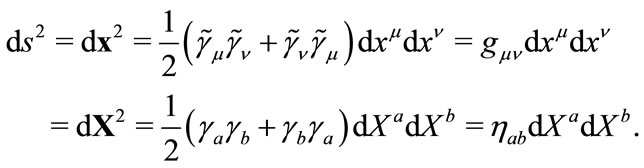 (2.4)
(2.4)
(2.1) and (2.4) are the fundamental postulates on the space-time, and all results of the special relativity can be derived from them [12].
The properties of a fundamental physical system can be described by fields and interactive coefficients. For example, a particle can be described by spinor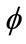 , electromagnetic field by vector potential
, electromagnetic field by vector potential  and field intensity
and field intensity , and gravitational field by metric
, and gravitational field by metric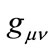 . For a relatively isolated system, we can express all fields to describe the system by a column vector
. For a relatively isolated system, we can express all fields to describe the system by a column vector 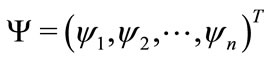 , then the dynamical equation of the system certainly take the following form [16],
, then the dynamical equation of the system certainly take the following form [16],
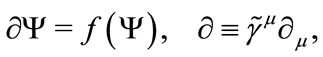 (2.5)
(2.5)
in which 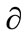 is a quaternion differential operator,
is a quaternion differential operator, 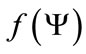 consists of some tensorial products of
consists of some tensorial products of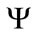 , such that the total equation satisfies covariance. The following calculations show that, the principles of relativity and covariance completely depend on the perfect and marvellous quaternion structure of (2.5). The covariance is invalid in other dimensional space-time.
, such that the total equation satisfies covariance. The following calculations show that, the principles of relativity and covariance completely depend on the perfect and marvellous quaternion structure of (2.5). The covariance is invalid in other dimensional space-time.
The quaternion basis 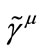 in operator
in operator  can be represented by matrices. The minimum order is 4, and the usual Dirac matrices are a specific realization. It can be proved that the order of the matrices is an integral multiple of 4, so the dimension
can be represented by matrices. The minimum order is 4, and the usual Dirac matrices are a specific realization. It can be proved that the order of the matrices is an integral multiple of 4, so the dimension 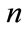 of field
of field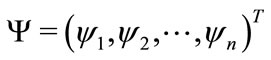 is also the integral multiple of 4. In fact, all physical phenomena we have observed can be described by spinor
is also the integral multiple of 4. In fact, all physical phenomena we have observed can be described by spinor 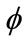 with 4 components and spin
with 4 components and spin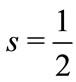 , vector
, vector 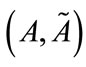 with 8 components and spin
with 8 components and spin and tensor
and tensor  with 32 components and spin
with 32 components and spin 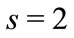 together with their combinations. These fields all exist in couples form. Between different representations, the operator
together with their combinations. These fields all exist in couples form. Between different representations, the operator  and
and  should make a double linear transformation. This transformation reflects the different selection of coordinates and measuring methods of fields.
should make a double linear transformation. This transformation reflects the different selection of coordinates and measuring methods of fields.
Denote the Pauli matrices by
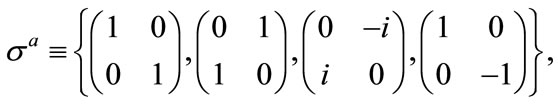 (2.6)
(2.6)
 (2.7)
(2.7)
then the base vector 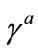 of 4 order can be represented by the following matrices with symmetry,
of 4 order can be represented by the following matrices with symmetry,
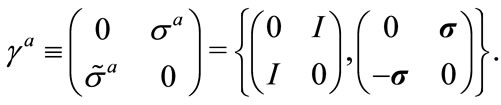 (2.8)
(2.8)
This representation is equivalent to the usual Dirac matrix. But in contrast with Dirac matrix, (2.8) can display the symmetry of the fields. The coefficient matrix of (2.5) can be constructed by the block matrix of (2.8).
Dynamical equation (2.5) is a first order symmetric hyperbolic evolution equation system. Its general solution can be expressed by the following integral,
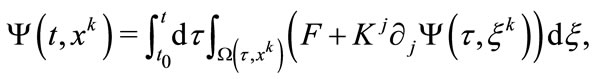 (2.9)
(2.9)
where 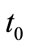 is any given time smaller than the present time
is any given time smaller than the present time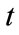 ,
,  ,
,  is the dependent domain of
is the dependent domain of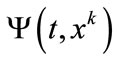 , which is included in the light cone with vertex
, which is included in the light cone with vertex , and
, and

The representation (2.9) is solved by characteristic cone method. The geometrical meaning is shown in Figure 1. The representation (2.9) manifestly reveals some philosophical features such as the arrow of time, causal and historical connection. This is the reason why to choose the formula as a fundamental physical postulate to replace (2.5) [16].
In Figure 1, the cosmic space is absolute space of the universe, which is described by the coordinate system relatively rest to the cosmic background radiation. Cosmic time is the absolute time. The absolute space is a simultaneous hyperplane relative to the cosmic time. The cosmic time has unitarity and uniqueness. 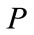 stands for a particle moving in the cosmic space, but
stands for a particle moving in the cosmic space, but  stand for points relatively rest to the cosmic space. The coordinates
stand for points relatively rest to the cosmic space. The coordinates  is not definitely orthogonal, but we can establish orthogonal local tetrad
is not definitely orthogonal, but we can establish orthogonal local tetrad 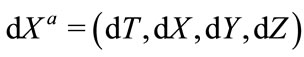 at each event
at each event , and (3) gives the relation between
, and (3) gives the relation between 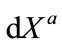 and
and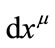 .
. 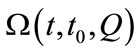 stands for dependent domain of point
stands for dependent domain of point 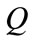 from time
from time 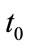 to
to , which means the state and physical parameters at point
, which means the state and physical parameters at point  is determined by the historical data in this domain.
is determined by the historical data in this domain.  is the dependent domain of region
is the dependent domain of region 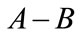 from
from  to
to . Due to the local correlation of interaction,
. Due to the local correlation of interaction,  can be any given time smaller than present time
can be any given time smaller than present time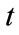 , such as
, such as 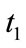 or
or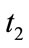 .
.
From the space-time diagram, we can get the following conclusions:
1) the unidirectionality of time: The general solution (2.9) reflects the causal connections between parameters in field equation (2.5). It evidently shows the unidirectionality and sequentiality of time. The future is always

Figure 1. Space-time diagram: The cosmic space is the absolute space of the universe, which is describe by the coordinate system relatively at rest to the cosmic background radiation. Cosmic time is the absolute time. The absolute space is a simultaneous hyperplane relative to the cosmic time. The cosmic time has unitarity and uniqueness. P stands for a mass point moving in the cosmic space, but A, B, O, Q stand for points relatively at rest to the cosmic space. The coordinates 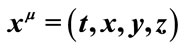 is not definitely orthogonal, but we can establish orthogonal local tetrad
is not definitely orthogonal, but we can establish orthogonal local tetrad 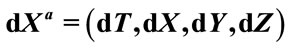 at each event
at each event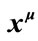 , and (3) gives the relation between
, and (3) gives the relation between 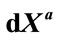 and
and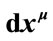 .
. 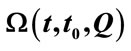 stands for dependent domain of point Q from time
stands for dependent domain of point Q from time  to
to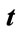 , and
, and 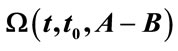 for dependent domain of region
for dependent domain of region  from
from  to
to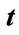 .
.
determined by the past. The fields of 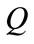 at time
at time 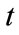 are only determined by the history in the backward characteristic cone. Future and past can not be mixed. The particle
are only determined by the history in the backward characteristic cone. Future and past can not be mixed. The particle 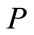 moves in left direction at
moves in left direction at 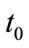 and
and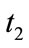 , and in right direction at
, and in right direction at 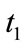 and
and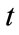 . The motion can be reversed, but the cosmic time
. The motion can be reversed, but the cosmic time  goes always unidirectionally forward. The inversion of process just means the reflection of motion, rather than inversion of time. The arrow of time has nothing to do with the expansion or contraction of the universe, which is just a dynamical effect of the space-time. The unidirectionality of time is an objective property of the universe.
goes always unidirectionally forward. The inversion of process just means the reflection of motion, rather than inversion of time. The arrow of time has nothing to do with the expansion or contraction of the universe, which is just a dynamical effect of the space-time. The unidirectionality of time is an objective property of the universe.
Since the eigen state of a spinor is a critical state without unique evolutionary direction, the non-uniqueness of the process makes the inverse of evolution become impossible. A thermodynamics system consists of a tremendous number of microscopic particles all described by spinors. And the evolution of each particle has some uncertainty or randomness, so the thermodynamic process is essentially irreversible. Entropy can be only clearly defined for a system satisfying large number statistical assumption. But for a system with internal structure, the entropy can not be defined. It is the randomness of a statistical system which defines the entropy, rather than the entropy decides the irreversible process [11].
2) the absoluteness of space-time: By Figure 1 we learn, the evolution of the universe has globality and synchronism. There exists a global cosmic time scale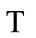 , whose meaning is close to the concept of Newtonian absolute time. When
, whose meaning is close to the concept of Newtonian absolute time. When 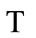 evolves to some specific moment
evolves to some specific moment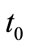 , it corresponds to the fact that universe evolves to a specific state. This specific state is a simultaneous hyperplane which defines the cosmic space. The meaning of the cosmic space is close to the concept of Newtonian absolute space. The space-time itself and the matter inside it all evolve from one hyperplane to next hyperplane. The cosmic time can neither go back, nor be transcended.
, it corresponds to the fact that universe evolves to a specific state. This specific state is a simultaneous hyperplane which defines the cosmic space. The meaning of the cosmic space is close to the concept of Newtonian absolute space. The space-time itself and the matter inside it all evolve from one hyperplane to next hyperplane. The cosmic time can neither go back, nor be transcended.
3) the subjectivity of choice coordinate and tetrad system: Does the absoluteness of the space-time contradicts relativity? The answer is NO. Different from the usually understanding that the relativity denied the objectivity of time and space, the significance of relativity theory is that it emphasizes the correlation between space and time, and the universality of the principle of relativity and covariance. To understand this, we must firstly understand “The realistic world is just a solution of physical laws, and this solution is objective existence”. The laws of physics can also have many other reasonable and realizable solutions, but they are not objective existence. What the covariance emphasizes is that, the coordinate system is just an identification system which can be quite arbitrary chosen. Between different coordinate systems there is 1-1 corresponding transformation. Only in the coordinate system relatively rest to the cosmic background radiation we have objective simultaneous hyperplane and realistic global simultaneity. In the local frame and curvilinear coordinate system moving relative to the cosmic background radiation, the simultaneous hyperplane is only of theoretical sense, rather than objective existence.
4) the uniqueness of simultaneity: This problem has been explained in [11,12], which can be illustrated by Figure 2.
Assume that we have realistic simultaneous hyperplane in the static reference frame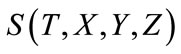 , and at moment
, and at moment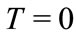 , we have simultaneous hyperplane (i.e. the space of the world)
, we have simultaneous hyperplane (i.e. the space of the world)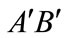 , which evolves into
, which evolves into  at moment
at moment 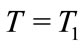 and
and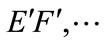 . By Lorentz transformation, this real space corresponds to the inclined plane
. By Lorentz transformation, this real space corresponds to the inclined plane  respectively in
respectively in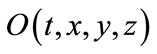 . The simultaneous hyperplane in
. The simultaneous hyperplane in 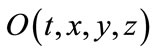 is the dash lines. The dash lines can not be realistic simultaneous hyperplane, because the part with
is the dash lines. The dash lines can not be realistic simultaneous hyperplane, because the part with 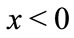 has become history in view of
has become history in view of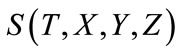 , but not yet been determined in view of
, but not yet been determined in view of 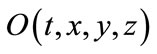 and could be designed and chosen. On the other hand, the part
and could be designed and chosen. On the other hand, the part 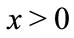 in
in 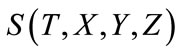 does not take place yet, but it has become history in
does not take place yet, but it has become history in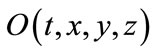 . The situation is absurd, because the evolution of the universe is not uniquely determined. The simultaneous hyperplane in
. The situation is absurd, because the evolution of the universe is not uniquely determined. The simultaneous hyperplane in 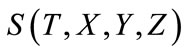 and
and 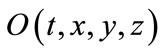 describe two different worlds. In this sense, the proposition “all inertial frames of reference are equivalent” is invalid.
describe two different worlds. In this sense, the proposition “all inertial frames of reference are equivalent” is invalid.
5) the internal time of matter system: To understand time, we should distinguish the different meanings of cosmic time 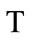 and the internal time or proper time
and the internal time or proper time 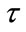 of a specific matter system.
of a specific matter system. 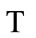 is a measurement for the evolution process of the whole universe, and it is objective and acts as a global standard of time. But
is a measurement for the evolution process of the whole universe, and it is objective and acts as a global standard of time. But 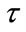 is a measurement of the evolution speed of a specific matter system. Relativity provides the method to treat the relationship between
is a measurement of the evolution speed of a specific matter system. Relativity provides the method to treat the relationship between 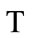 and
and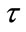 , that is,
, that is,
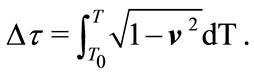 (2.10)
(2.10)
3. Transformation Law and the Physical Meaning
Dynamical equation (2.5) simultaneously has general covariance under curvilinear coordinate transformation and Lorentz invariance under transformation of local frame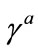 . For vectors and tensors, since they can be directly projected to the natural basis of the coordinate system
. For vectors and tensors, since they can be directly projected to the natural basis of the coordinate system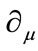 , the representation is simple. It is enough that the equation takes tensorial form. However, for the spinors the problem becomes complicated and abstruse, because the spinor is related to concrete local tetrad. In what follows, we examine the physical meaning of the transformation and the quaternion structure of spinor and space-time via specific calculation.
, the representation is simple. It is enough that the equation takes tensorial form. However, for the spinors the problem becomes complicated and abstruse, because the spinor is related to concrete local tetrad. In what follows, we examine the physical meaning of the transformation and the quaternion structure of spinor and space-time via specific calculation.
3.1. Dirac Equation in Spherical Coordinate System
In [15], we derived the covariant form of the spinor equation in spherical coordinate system,

Figure 2. The real space is an evolution simultaneous hyperplane: In the static reference frame s, the simultaneous hyperplane is A'B', C'D', E'F' etc. But in moving reference frame o, it corresponds to inclined hyperplane AB, CD, EF. The simultaneous hyperplane in reference frame o is the dash lines. The simultaneous hyperplanes in two reference frame can not be all realistic for a world.
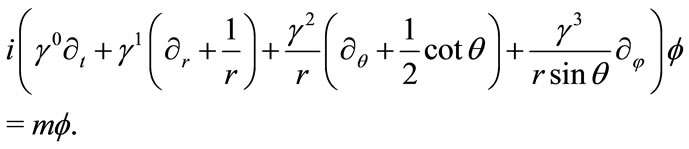 (3.1)
(3.1)
But some readers told that it is different from the equation directly transformed from the Cartesian Coordinate system. They felt that it is not understandable and even doubted whether there is error. Now we derive the covariant equation by direct calculation, and show the meaning of tetrad basis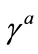 . We represent the bispinor
. We represent the bispinor  in the Weyl form
in the Weyl form 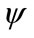 and
and . This is the so called chiral form. Then the Dirac equation in Cartesian coordinate system becomes,
. This is the so called chiral form. Then the Dirac equation in Cartesian coordinate system becomes,
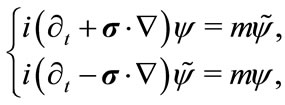 (3.2)
(3.2)
in which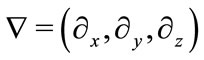 . Transform the Cartesian coordinates
. Transform the Cartesian coordinates 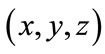 into spherical coordinates
into spherical coordinates , by straightforward calculation we have
, by straightforward calculation we have
 (3.3)
(3.3)
where  reads
reads
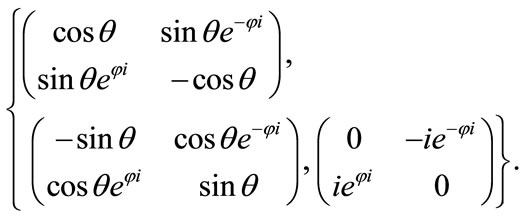 (3.4)
(3.4)
Then the dynamical equation (3.2) becomes
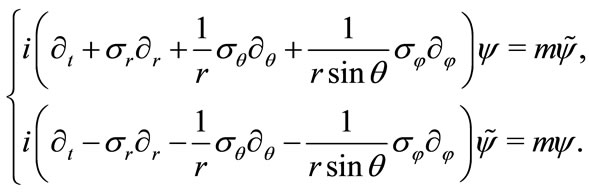 (3.5)
(3.5)
We usually solve the Dirac equation with central potential in this form (3.5). However, this form is not covariant, because the tetrad is transformed following the coordinate system, but the spinor still remains the original without transformation. The covariant form should be
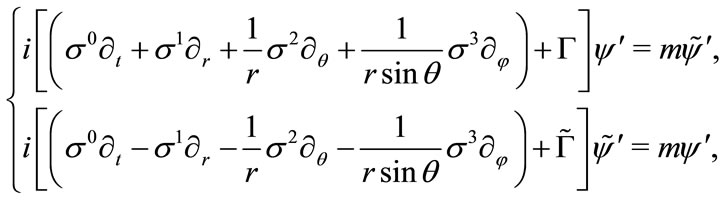 (3.6)
(3.6)
in which  and
and 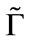 is the spinor connection.
is the spinor connection.
When making tetrad transformation, the spinor also needs a linear transformation,
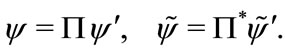 (3.7)
(3.7)
Then the equation can keep covariance. For pure space coordinate transformation, we have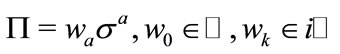 and
and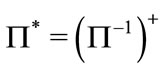 , where the superscript
, where the superscript  stands for the transposed conjugate matrix. Substituting (3.7) into (3.5), and then compared it with (3.6), we get
stands for the transposed conjugate matrix. Substituting (3.7) into (3.5), and then compared it with (3.6), we get
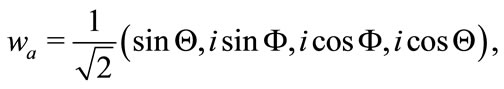 (3.8)
(3.8)
in which
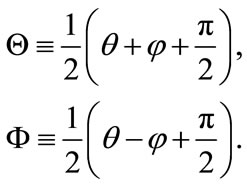 (3.9)
(3.9)
Then we get
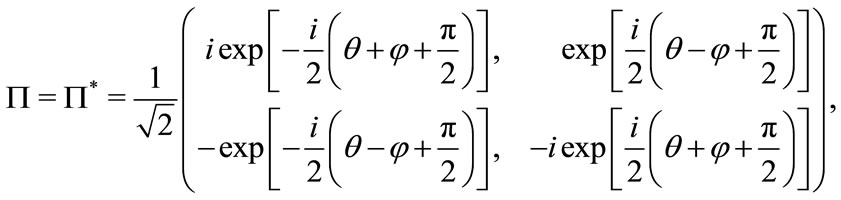 (3.10)
(3.10)
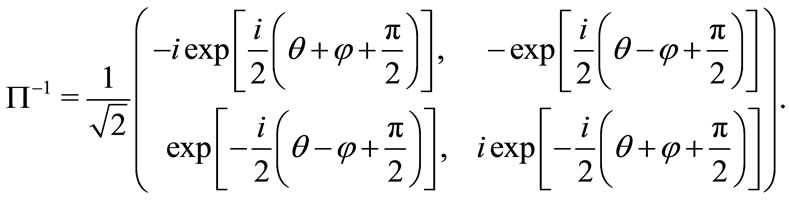 (3.11)
(3.11)
Substituting (3.7)-(3.11) into original equation (3.5), we can get the following form by some arrangement.
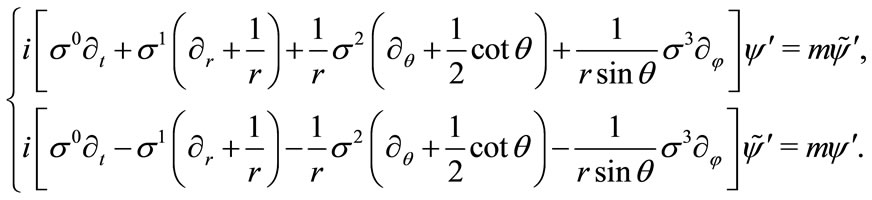 (3.12)
(3.12)
(3.12) is just the same equation calculated in [15]. The above calculation and equation show that
1) The tetrad coefficient matrix is given by
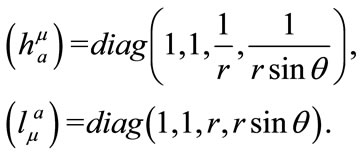 (3.13)
(3.13)
The following vectors are orthogonal,
 (3.14)
(3.14)
2) By spinor transformation (3.7), the direction of the tetrad basis turns into: 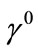 along
along ,
,  along
along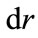 ,
,  along
along , and
, and 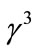 along
along 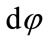 direction, because in the tangent space
direction, because in the tangent space
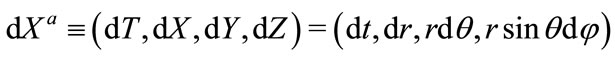 and (3.12) becomes
and (3.12) becomes
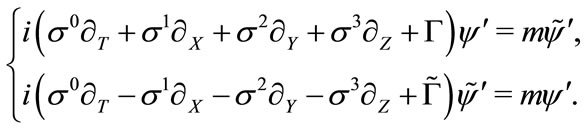 (3.15)
(3.15)
3) The transformation law between displacement vector 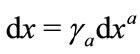 and
and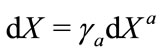 , and between the differential operators
, and between the differential operators 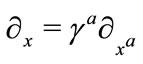 and
and 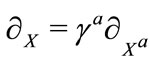 is given by [12],
is given by [12],
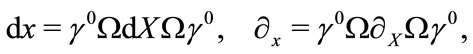 (3.16)
(3.16)
where , and the operator
, and the operator 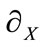 does not make derivatives on
does not make derivatives on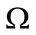 .
.
3.2. Transformation Law under the Reflection of Tetrad
Under curvilinear coordinate transformation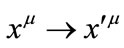 , the transformation of tetrad
, the transformation of tetrad 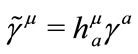 is realized via the index
is realized via the index  of coefficient matrix
of coefficient matrix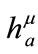 , but the spinor does not transform in form. However, the definition of covariant derivative of spinor actually implies a transformation like (3.7). Under proper Lorentz transformation of tetrad, the transformation of spinor is similar to (3.7), and can be easily derived. In what follows, we check the invariance and transformation laws of the spinor equation with interactions under the tetrad reflection transformation.
, but the spinor does not transform in form. However, the definition of covariant derivative of spinor actually implies a transformation like (3.7). Under proper Lorentz transformation of tetrad, the transformation of spinor is similar to (3.7), and can be easily derived. In what follows, we check the invariance and transformation laws of the spinor equation with interactions under the tetrad reflection transformation.
Denote  Hermitian matrices by
Hermitian matrices by
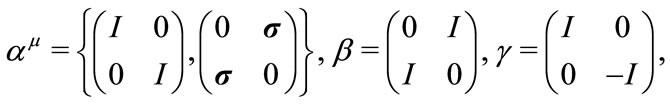 (3.17)
(3.17)
we examine the following Lagrangian
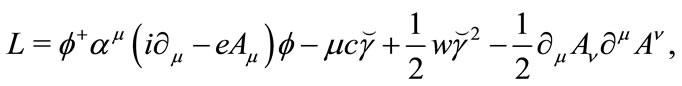 (3.18)
(3.18)
in which  is the electromagnetic potential,
is the electromagnetic potential,
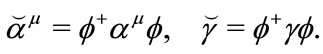 (3.19)
(3.19)
According to the transformation of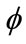 , it is easy to prove that,
, it is easy to prove that, 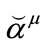 is a contravariant vector, and
is a contravariant vector, and  a true scalar. The corresponding dynamical equation is given by,
a true scalar. The corresponding dynamical equation is given by,
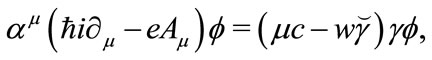 (3.20)
(3.20)
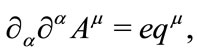 (3.21)
(3.21)
in which 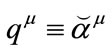 is the current of spinor. The Hamiltonian form of (3.20) is given by,
is the current of spinor. The Hamiltonian form of (3.20) is given by,
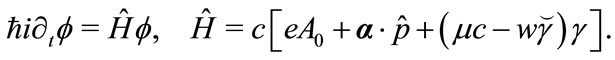 (3.22)
(3.22)
where  is the momentum operator. For (3.22) we have normalizing condition,
is the momentum operator. For (3.22) we have normalizing condition,
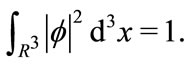 (3.23)
(3.23)
Now we check the invariance of (3.22) under space reflection transformation. Making double linear transformation
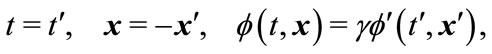 (3.24)
(3.24)
where an indeterminate gauge factor 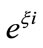 is ignored. Easy to check
is ignored. Easy to check 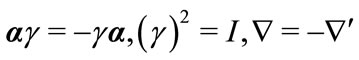 and
and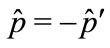 ,
,
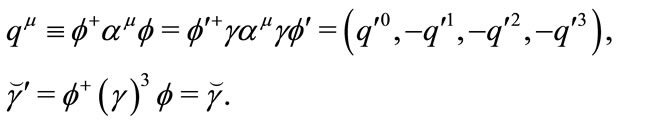 (3.25)
(3.25)
That is 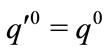 and
and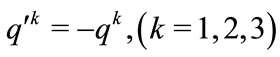 . Substituting (3.25) into (3.21) we get the transformation of
. Substituting (3.25) into (3.21) we get the transformation of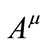 ,
,
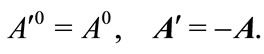 (3.26)
(3.26)
Of course, (3.25) and (3.26) are just the transformation of a contravariant vector under space reflection.
Substituting the above relations into (3.22), we get
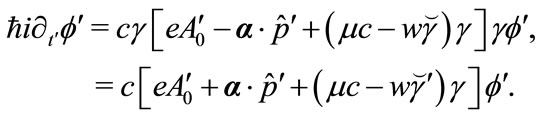 (3.27)
(3.27)
The equation (3.27) takes the same form of (3.22). This means the law for this spinor is independent of reference frame  or
or , and the transformation for field satisfies invertible linear relation (3.24). This is true meaning of principle of relativity.
, and the transformation for field satisfies invertible linear relation (3.24). This is true meaning of principle of relativity.
Now we check the invariance under time inversion transformation. Making double linear transformation,
 (3.28)
(3.28)
Easy to prove
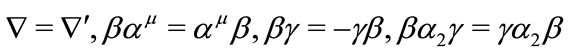
and
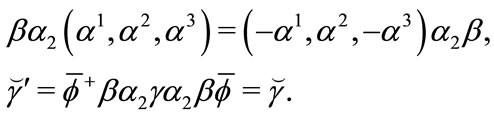 (3.29)
(3.29)
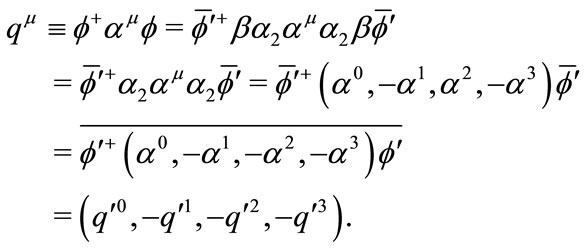 (3.30)
(3.30)
From (3.30) we learn, the transformation law of contravariant vector  under time inversion is different from that under curvilinear coordinate transformation
under time inversion is different from that under curvilinear coordinate transformation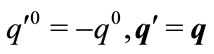 . It takes the same form under space reflection transformation.
. It takes the same form under space reflection transformation.
Substituting (3.30) into (3.21) we get the transformation law of potential . For operator
. For operator 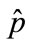 we have
we have
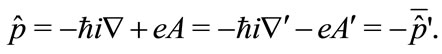 (3.31)
(3.31)
Substituting the above relations into (3.22), we get
 (3.32)
(3.32)
Take the complex conjugate of (3.32), we get
 (3.33)
(3.33)
(3.33) also takes the same form of (3.22), so the spinor and vector equations all keep the invariance under the space-time inversion transformation.
From the above calculations we learn
1) For the first order equation (2.5), the principle of relativity and covariance is a strong constraints, which can be realized only in 3 + 1 dimensional space-time due to the quaternion structure. In this point of view, the theories with other dimensions are almost impossible in physics. The fact that the unverse chooses the 3 + 1 dimensional space-time with elegant quaternion structure has profound philosophical implications, which is the sapiential design of the Creator.
2) The philosophical reason of the principle of relativity and covariance is the arbitrariness and subjectiveness to choose the coordinates and measurement method of fields. Charge is a property of a specific matter system. One particle carries a positive or a negative charge or even no charge is an objective fact, which can not be transformed. In this point of view, the so called  invariance theorem is simply not a physical law, but a result due to misusing concepts. For a specific spinor equation, the change of charge means the object being described also changed, and the equation is describing another system. Of course, as a mathematical theorem to show the relation between solutions and coefficients is reasonable.
invariance theorem is simply not a physical law, but a result due to misusing concepts. For a specific spinor equation, the change of charge means the object being described also changed, and the equation is describing another system. Of course, as a mathematical theorem to show the relation between solutions and coefficients is reasonable.
3) The function of quaternion basis is similar to the unit of imaginary number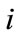 . They are concrete numbers, so they can not be transformed under coordinate or tetrad transformation. In quantum field theory we have transformations such as
. They are concrete numbers, so they can not be transformed under coordinate or tetrad transformation. In quantum field theory we have transformations such as . These relations should be a results of misunderstanding the meaning of principle of relativity and misusing concepts. The reason why we have such transformations seems to be we need them. Nobody can really understand such illegal relations [17].
. These relations should be a results of misunderstanding the meaning of principle of relativity and misusing concepts. The reason why we have such transformations seems to be we need them. Nobody can really understand such illegal relations [17].
The tetrad coefficients 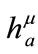 or
or 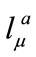 is different from
is different from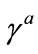 . They are fields similar to metric
. They are fields similar to metric , so
, so 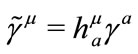 is transformed under curvilinear coordinate transformation. However in this case the transformation of spinors is implicit, and the possible transformation is included in the definition of spinor covariant derivative [15].
is transformed under curvilinear coordinate transformation. However in this case the transformation of spinors is implicit, and the possible transformation is included in the definition of spinor covariant derivative [15].
4) Chiral equation (3.2) is equivalent to the usual Dirac equation, and the transformation just means the method of measuring field is different. Just like changing coordinates does not influence the property of space-time, the transformation of field also does not influence the property of this concrete particle. The representation  and
and  only needs an invertible linear transformation,
only needs an invertible linear transformation,
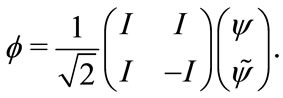 (3.34)
(3.34)
Such transformation can not increase any new phenomenon. For the same equation, it is impossible that the equation describes electron if the spinor is denoted by , and describes neutrino when
, and describes neutrino when 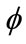 is transformed into
is transformed into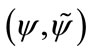 . Because physical phenomenon is objective, but the description is subjective. Electrons and neutrino have different internal structure, they should be described by different equations with different interacting coefficients.
. Because physical phenomenon is objective, but the description is subjective. Electrons and neutrino have different internal structure, they should be described by different equations with different interacting coefficients.
4. Some Problems Relative to the Structure of Space-Time
4.1. Hyperdrive Neutrino
It was reported that the hyperdrive neutrino phenomenon was observed in supernova explosion and OPERA experiment [18]. This leads to the doubt of the effectiveness of the theory of relativity. However, the problem may be not in the foundation of relativity, but in the expression of the theory. From the above calculation we find that, the 3 + 1 dimensional space-time has special advantages, which should be described by quaternion geometry. The traditional theory of relativity starts from the principle of constant vacuum speed of light. This isn’t illegal in principle. But for the following reasons it is easy to cause difficulty in understanding: 1) The electromagnetic interaction is of “viscosity”. The light always slows down when it goes through medium due to the internal dielectric constant of the medium. Since we can never really get the absolute vacuum for electromagnetic field, we can not get exact vacuum speed of light. The measured speed of light is always less than the theoretical vacuum light speed. 2) Except for the electromagnetic field, we have a lot of other fields such as spinors, gravitational field and strong interaction field in the space-time. Their propagating speed is also vacuum speed of light determined by the quaternion differential operator . So it is more natural to establish geometry of the space-time at first, and then explain the speed of light according to geometry and electrodynamics. Otherwise, we may fall into the trap of language.
. So it is more natural to establish geometry of the space-time at first, and then explain the speed of light according to geometry and electrodynamics. Otherwise, we may fall into the trap of language.
To explain the electromagnetic “viscosity” in vacuum, we must make clear the annihilation and creation of particle and anti-particle at first [19,20]. We know that positrons and electrons are all described by spinors, which all satisfy the normalization condition. So the spinors can never be really annihilated. The encounter of particle and anti-particle is different from the summation of their electromagnetic interaction coefficients . They are encounter of spinors, and for spinors we always have
. They are encounter of spinors, and for spinors we always have . The encounter of particle and anti-particle, like the encounter of electron and proton, will form a tight neutral core. Such neutral core only has extremely weak interaction with other particles, which forms a kind of pseudo dark matter dispersed in the universe. In appropriate conditions and interacted by high-energy photons, the neutral core will be broken again. So for electromagnetic interaction we can never get the absolute vacuum. How can we get the accurate vacuum speed of light?
. The encounter of particle and anti-particle, like the encounter of electron and proton, will form a tight neutral core. Such neutral core only has extremely weak interaction with other particles, which forms a kind of pseudo dark matter dispersed in the universe. In appropriate conditions and interacted by high-energy photons, the neutral core will be broken again. So for electromagnetic interaction we can never get the absolute vacuum. How can we get the accurate vacuum speed of light?
4.2. The Fine Structure of Mass-Energy Relation
Only in Newtonian mechanics, mass is a basic concept, and the value is determined by empirical data. However, mass is not a basic concept in other fundamental theory of physics, which must be derived from other equations or relations, and the value depends on the context theory. This problem leads to a lot of misunderstanding and controversy. In the author's point of view, only fields are the basic concept for elementary particles, and other properties and relations should be derived from the dynamical equation of fields. In [20-22] we found the mass-speed relation for a spinor with interaction potential is not the simple Einstein mass-energy relation , which has fine structure,
, which has fine structure,
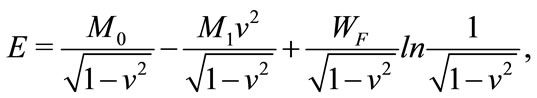 (4.1)
(4.1)
where 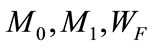 are positive constants with mass dimension, and
are positive constants with mass dimension, and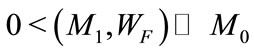 . These parameters reflect the internal structure of a particle.
. These parameters reflect the internal structure of a particle.
The current derivation and understanding of massenergy relation is mainly limited to the Lorentz transformation of parameters of motion, but does not go deep into the dynamical structure of particles. Therefore the relation only reflects the main part, and does not reveal the rich contents. For the following reasons: 1) This is a universal relation obeyed by all matter; 2) It associates with the inner connection between particles and fields; 3) It associates with the relationship between space-time and motion; 4) It associates with classical and quantum opinions; 5) The relation occupies the core of fundamental physics with clear physical meanings. Therefore, how to accurately measure the relation may be a breakthrough to discover new physical phenomena and internal structure of space-time and elementary particles.
4.3. The Quaternion Form of Other Field Equations
From the above calculations we learn that, the quaternion form of coordinate increment and spinor equation can simultaneously display coordinates and tetrad, and this form is more convenient for understanding and calculations. In fact, other physical fields also can be expressed in quaternion form.
For vector field with spin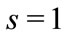 , we have the first order field equation in quaternion form,
, we have the first order field equation in quaternion form,
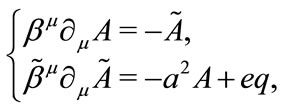 (4.2)
(4.2)
where  is a source term,
is a source term, 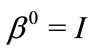 and
and
 (4.3)
(4.3)
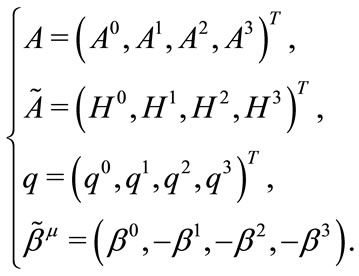 (4.4)
(4.4)
By current conservation or normalizing condition we have
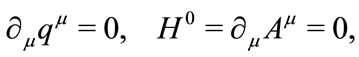 (4.5)
(4.5)
Expanding (4.2), we get the total Maxwell equation system in 3 dimensional vector form,
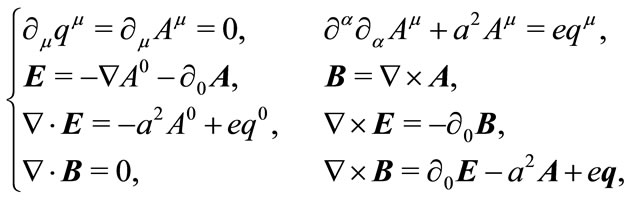 (4.6)
(4.6)
in which
 (4.7)
(4.7)
For long distance interaction such as electromagnetic field, the distance factor 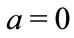 in (4.6). From (4.2), we find magnetic charge should be the imaginary part of electric charge. Unfortunately, this part leads to the violation of normalizing condition, that is to say, the charge conservation is broken. This is absurd, so the monopole can not exist in the nature.
in (4.6). From (4.2), we find magnetic charge should be the imaginary part of electric charge. Unfortunately, this part leads to the violation of normalizing condition, that is to say, the charge conservation is broken. This is absurd, so the monopole can not exist in the nature.
The strong interaction also should be described by (4.2). In this case, we should have .
.
The transformation law of the complex field 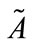 is interesting. Make boosting transformation along
is interesting. Make boosting transformation along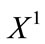 , we have Lorentz transformation
, we have Lorentz transformation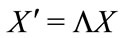 ,
,
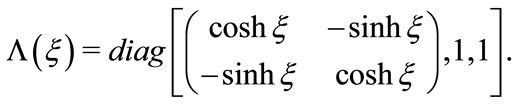 (4.8)
(4.8)
Then the transformation of 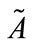 becomes
becomes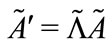 , where
, where
 (4.9)
(4.9)
When making space rotation transformation,  has the same transformation law of coordinate system, that is
has the same transformation law of coordinate system, that is .
.
Similar to (4.2), for tensor field with spin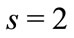 , we have dynamics
, we have dynamics
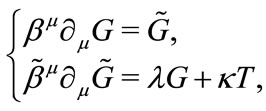 (4.10)
(4.10)
in which  is contravariant tensor in matrix form,
is contravariant tensor in matrix form, 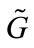 is the complex field intensity, and
is the complex field intensity, and 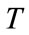 is source term.
is source term.
Obviously, (3.2), (4.2) and (4.10) all take the form of (2.5). Almost all known physical laws and relations can be derived from some combination of these equations, so (2.5) is the most fundamental and universal law of physics, and it actually forms a kind of unified field theory.
In (4.2) and (4.10), the components of fields are projected to the orthogonal tetrad. How to transform the equation into curved space-time and establish the relation between the components is still an open problem. Of course, the transformation is just a choice of description. We can make deep understanding into the structure of space-time and fields, and find new internal symmetries. However, like the chiral transformation, the transformation can not produce new physical phenomenon, because the physical phenomenon is objective, but the transformation is subjective.
5. Conclusions
From the above specific discussion and calculation, we can get the following conclusions:
1) The space-time has a quaternion structure, which should be naturally described by the basic relations (2.1)- (2.4).
2) The evolution of a given physical system is governed by the universal dynamical equation (2.5), and in principle, all properties of the system can be logically derived from the dynamical equation together with the concrete initial and boundary conditions. The solution of the first order dynamics (2.5) determines the arrow of time, and the non-uniqueness of evolution of spinor fields breaks the reversibility of the process.
3) The invariance and covariance of the dynamics are different concepts from the symmetry of the solutions, although there are some connections between them. The physical laws must be invariant and covariant, but the solutions or the configurations of concrete matter system are not definitely symmetric.
REFERENCES
- S. F. Savitt, “Time’s Arrows Today,” Cambridge University Press, Cambridge, 1995. doi:10.1017/CBO9780511622861
- J. L. Lebowitz, “Boltzmann’s Entropy and Time’s Arrow,” Physics Today, Vol. 46, No. 9, 1993, pp. 32-38.
- P. M. Harman, “The Natural Philosophy of James Clerk Maxwell,” Cambridge University Press, Cambridge, 1998.
- D. Ruelle, “Chance and Chaos,” Princeton University Press, New Jersey, 1991.
- D. Albert, “Time and Chance,” Harvard University Press, Cambridge, 2000.
- H. D. Zeh, “The Physical Basis of the Direction of Time,” Springer-Verlag, Berlin, 2001.
- S. W. Hawking, R. Laflamme and G. W. Lyons, “The Origin of Time Asymmetry,” arXiv:gr-qc/9301017.
- J. W. Moffat, “Quantum Gravity, the Origin of Time and Time’s Arrow,” arXiv:gr-qc/9209001.
- I. Dincer and Y. A. Cengel, “Energy, Entropy and Exergy Concepts and Their Roles in Thermal Engineering,” Entropy, Vol. 3, No. 3, 2001, pp. 116-149. doi:10.3390/e3030116
- G. F. R. Ellis, “On the Flow of Time,” arXiv:0812.0240.
- Y. Q. Gu, “Some Subtle Concepts in Fundamental Physics,” arXiv:0901.0309v1
- Y. Q. Gu, “Some Paradoxes in Special Relativity and the Resolutions,” Advances in Applied Clifford Algebras, Vol. 21, No. 1, 2011, pp. 103-119. doi:10.1007/s00006-010-0244-6
- G. F. R. Ellis and J.-Ph. Uzan, “c Is the Speed of Light, Isn’t It?” American Journal of Physics, Vol. 73, No. 3, 2005, pp. 240-247. doi:10.1119/1.1819929
- Y. Q. Gu, “The Vierbein Formalism and Energy-Momentum Tensor of Spinors,” arXiv:gr-qc/0612106.
- Y. Q. Gu, “The Spinor Connection and Its Dynamical Effects,” arXiv:gr-qc/0610001v3.
- Y. Q. Gu, “A Canonical Form for Relativistic Dynamic Equation,” Advances in Applied Clifford Algebras, Vol. 7, No. 1, 1997, pp. 13-24. doi:10.1007/BF03041212
- G. F. R. Ellis, “On the Limits of Quantum Theory: Contextuality and the Quantum-Classical Cut,” arXiv:1108.5261.
- OPERA Collaboration, “Measurement of the Neutrino Velocity with the OPERA Detector in the CNGS Beam,” arXiv:1109.4897v2.
- Y. Q. Gu, “Some Properties of the Spinor Soliton,” Advances in Applied Clifford Algebras, Vol. 8, No. 1, 1998, pp. 17-29. doi:10.1007/BF03041923
- Y. Q. Gu, “The Characteristic Functions and Their Typical Values for the Nonlinear Spinors,” arXiv:hep-th/0611210.
- Y. Q. Gu, “New Approach to N-body Relativistic Quantum Mechanics,” International Journal of Modern Physics, Vol. A22, 2007, pp. 2007-2020. doi:10.1142/S0217751X07036233
- Y. Q. Gu, “A Sensitive Test of Mass-Energy Relation,” arXiv:hep-th/0610189.

