Journal of Modern Physics
Vol.2 No.11(2011), Article ID:8634,5 pages DOI:10.4236/jmp.2011.211161
Magnetic Field Induction and Time Intervals of the Electron Transitions Approached in a Classical and Quantum-Mechanical Way
Institute of Physical Chemistry, Polish Academy of Sciences, Warsaw, Poland
E-mail: olsz@ichf.edu.pl
Received July 27, 2011; revised August 29, 2011; accepted September 13, 2011
Keywords: Lorentz Force and Magnetic Induction, Electron Wave Packets, Changes of the Electron Momentum, Transition Time between Quantum States
ABSTRACT
The motion of electron wave packets of a metal is examined classically in the presence of the magnetic field with the aim to calculate the time intervals between two states lying on the same Fermi surface. A lower limiting value of the transition time equal to about 10–18 sec is estimated as an average for the case when the states are lying on the Fermi surface having a spherical shape. Simultaneously, an upper limit for the electron circular frequency in a metal has been also derived. A formal reference of the classical transition time to the time interval entering the energy-time uncertainty relations known in quantum mechanics is obtained.
1. Introduction
In general, any progress in foundations of quantum mechanics, on one side, and in an analysis of the time problem on another side, represent not an easy task. Nevertheless, some new views concerning both these domains could be reported [1,2]. Another situation does exist in a rather elementary physics which is usually treated as a source of well-established statements and ideas. However, one of the aims of the present paper is to demonstrate, with a reference to the time problem, that there exist some connections between the classical physics and quantum theory which seemed to escape till present from our knowledge.
The Lorentz force of the magnetic field acting on a charged particle gives regularly the particle rotation in a plane normal to that field. For an ensemble of electrons present on the metal Fermi surface taken as an example the effect is represented by rotation of the electron states in the momentum space. The Lorentz force limited to the action of a constant magnetic field does not change the electron energy, so the gyrating electrons remain in fact in each instant of time on the same Fermi surface. A separate problem concerns anisotropic Fermi surfaces for which the frequency of gyration is influenced by the surface shape as well as the direction of the field with respect the crystallographic axes. But in a simple case represented by free electrons the Fermi surface is a sphere and gyration frequency 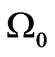 remains practically the same for all electrons on that sphere:
remains practically the same for all electrons on that sphere:
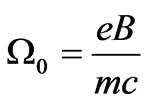 (1)
(1)
B in (1) is the magnetic induction of the applied field; see e.g. [3]. Beyond of the electron gyration, another effect of B is a splitting of a quasi-continuous ensemble of the electron states filling the Fermi sphere into discrete levels called the Landau levels [3,4]. However, for not very strong magnetic fields, the Landau levels become so numerous that their mutual distances are very small, therefore a new quasi-continuous ensemble of states filling the Fermi sphere formed in the presence of B does not differ much from the ensemble in the absence of B. In the present paper the discrete structure of the electron states due to the Landau degeneracy has been neglected.
Another point is that the Fermi surface is not necessarily an ensemble of completely filled electron states. Some of states can be empty and a transition of an electron from a filled state on the Fermi surface to an empty state on the same surface can take place practically with no expense of the electron energy. In principle, the probability and time necessary for such a transition can be provided by a time-dependent quantum theory. This applies equally to the cases of the absence, or presence, of the magnetic field. But the aim of the paper is to approach, in the first step, the electron transitions on the Fermi surface in a semiclassical way. We shall see (Section 5) that the action of an external magnetic field simplifies much the problem of the electron transitions. In the next step, we demonstrate that the same method gives an easy insight into the time limitations associated with the transition process.
2. Energy Balance for the Electron Transitions
The Fermi surface is a convenient idea because it puts an order in a huge amount of electron states in a metal having the same energy. The states are defined in the momentum space of the vector k: for free electrons the surface becomes a sphere and the states located on it have the same amount of the electron momentum. If one state k on the surface, called further for convenience the hole state, is shifted to another state k + q, called the electron state, and this second state is located on the same surface of the Fermi sphere as the k state, the requirement of a constant energy 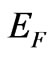 on the surface, where
on the surface, where
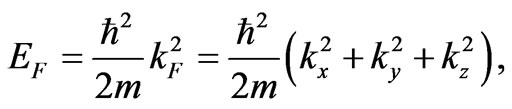 (2)
(2)
gives the equation
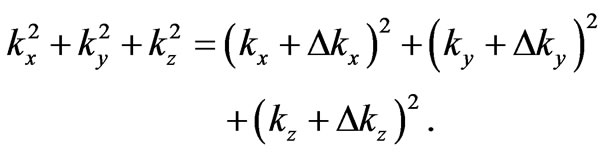 (3)
(3)
This equation is equivalent to
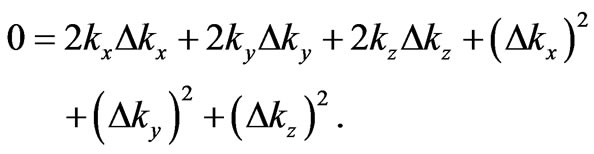 (3a)
(3a)
The notation

for the vector q has been applied in (3) and (3a), and the subscript F in (2) is henceforth omitted for the sake of simplicity.
Equations (3), or (3a), represent rather complicated relations between six parameters ,
, 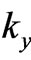 ,
, 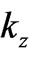 and
and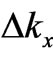 ,
, 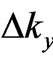 ,
, 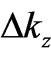 , among which for the moment no time parameter is involved.
, among which for the moment no time parameter is involved.
3. Physical Example of the Energy Balance Represented in Section 2
Physically, a typical example of the electron-hole pair is given in semiconductors: for an electron state lying on the Fermi surface near a narrow energy gap an absorption of a low-frequency photon having the wave vector q can take place leading to the momentum balance [3]
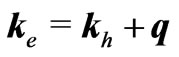 (4)
(4)
between the electron ![]() and the hole
and the hole ![]() momenta. For an idealized situation of the energy of transition equal to zero, and the Fermi surface not completely filled, an electron can be scattered elastically to another state on the same Fermi surface. Assuming that only perfectly free electrons are present on the surface, the relation
momenta. For an idealized situation of the energy of transition equal to zero, and the Fermi surface not completely filled, an electron can be scattered elastically to another state on the same Fermi surface. Assuming that only perfectly free electrons are present on the surface, the relation
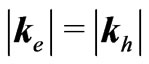 (4a)
(4a)
satisfied for the electron and hole momenta is, in this case, equivalent to the effect of the principle of the conservation of energy.
A creation of the electron-hole pair can be followed by a recombination of that pair. In this way a situation on the Fermi surface becomes equal to that from before the scattering process. Necessarily, the recombination process should occupy some time. Usually this time is tried to be estimated by applying the quantum-mechanical timedependent perturbation theory. In such a theory a reference is made to an energy-absorption process leading to a filling of the hole state by an electron. In this case the hole state, which is assumed to be lower, is recombined with an electron state of a higher energy. The electron transitions of this kind lead to the well-known luminescence processes associated with emission of a rather small amount of energy involved in a single transition [5-8], whereas higher amounts of energy accompany the recombinations due to the electrons entering transitions characteristic for the Auger effect, or the X-ray emission.
In the first step, our aim is to present an approach to the time intervals between electron and hole states within a framework which is outside the quantum theory, so the approach is of a classical kind.
4. Effect of the Magnetic Field on the Electron Wave Packets
First we demonstrate that an external magnetic field acting on the electon states simplifies the energy balance of Section 2. Classically, when the electric field is neglected and only the magnetic field is present, the motion of the electron wave packet is governed by the Lorentz equation (see e.g. [9]):
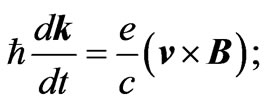 (5)
(5)
v is a classical velocity of the electron motion in the ordinary space. Since the Fermi energy in a metal is about 103 times smaller than the rest energy of an electron, no relativistic effects seem to be of importance for the motion described by the Equation (5).
Moreover, the magnetic field can be assumed so weak that the spherical shape of the Fermi surface remains practically unchanged. This means that so many Landau levels are below the Fermi energy that the circles representing the cross-sections of the cylinders of the Landau levels with the Fermi surface cover quasicontinuously that surface [3,4].
For the magnetic field B assumed along the coordinate axis z, so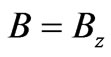 , and small intervals
, and small intervals 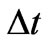 and
and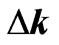 , the Lorentz Equation (5) can be simplified to the equations pair
, the Lorentz Equation (5) can be simplified to the equations pair
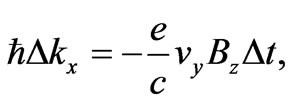 (5a)
(5a)
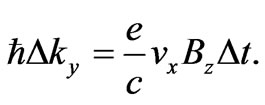 (5b)
(5b)
The sign of 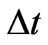 in (5a) and (5b) is changed in comparison to that entering (5) because the travelling of an electron to a hole is going from
in (5a) and (5b) is changed in comparison to that entering (5) because the travelling of an electron to a hole is going from 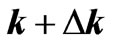 to k, therefore the time interval associated with the travelling process should be of an opposite sign to the time interval connected with transitions from k to
to k, therefore the time interval associated with the travelling process should be of an opposite sign to the time interval connected with transitions from k to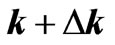 . In fact, the choice of sign of
. In fact, the choice of sign of 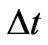 becomes immaterial because the calculation of
becomes immaterial because the calculation of 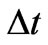 defines only the absolute value of that interval; see Section 5.
defines only the absolute value of that interval; see Section 5.
The third equation descending from the Lorentz Formula (5) for 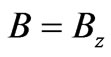 is
is
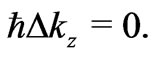 (5c)
(5c)
This formula is valid in a free space, similarly to a precise meaning of (5a) and (5b). But, in the present case, the space is constrained to a surface of a Fermi sphere, so we assume that, excepting for a stationary motion along an orbit localized in a plane normal to the magnetic field, the interval 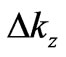 satisfies (5c) only at
satisfies (5c) only at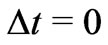 ; see Section 5.
; see Section 5.
5. A Coupling of the Classical Momentum with an Interval of Time
The wave-packet velocities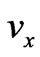 ,
, 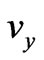 entering (5a), (5b) can be represented by the well-known formulae [3,4,9]:
entering (5a), (5b) can be represented by the well-known formulae [3,4,9]:
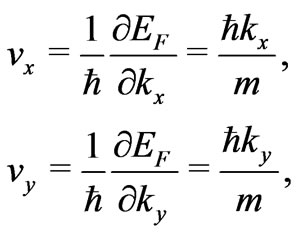 (6)
(6)
specialized here for the energy (2) of the free-electron states. It should be noted that Formulae (6) are valid also in the presence of the magnetic field [9].
In effect of a substitution of (6) into (5a) and (5b), the expression dependent on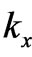 ,
, 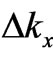 ,
, 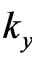 ,
, 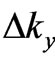 , being a component of the energy balance in (3a), vanishes:
, being a component of the energy balance in (3a), vanishes:
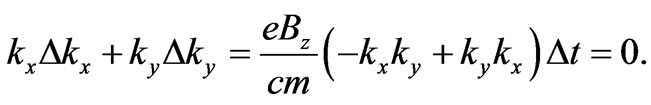 (7)
(7)
This result reduces (3a) to a simple relation between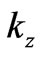 ,
, 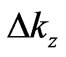 and
and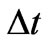 .
.
For, a substitution of the result of (7) together with (6) into Equation (3) of the energy balance gives:
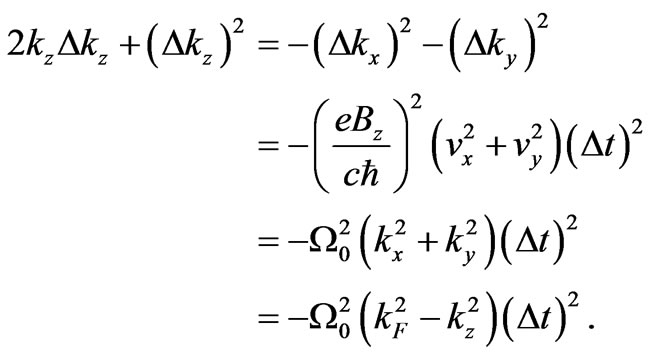 (8)
(8)
In (8) the expressions for the frequency 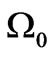 [see (1)], as well as (2), have been applied.
[see (1)], as well as (2), have been applied.
In effect, only the terms
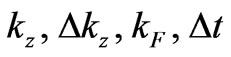 (8a)
(8a)
are coupled by the Formula (8) in its final step. This reduces the momentum problem in four dimensions (x, y, z, t) to that in only two dimensions (z, t).
Evidently, a substitution of  in (8) implies the time interval
in (8) implies the time interval
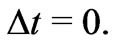 (9)
(9)
6. Discussion of the Equation (8)
Since necessarily 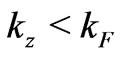 (see (2)), the difference
(see (2)), the difference 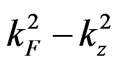 is a positive number, or zero. For
is a positive number, or zero. For  chosen as an example, a compact form of (8) equal to
chosen as an example, a compact form of (8) equal to
![]() (10)
(10)
implies that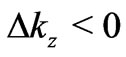 . We obtain in this case from (10)
. We obtain in this case from (10)
![]() (11)
(11)
where instead of 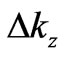 its absolute value
its absolute value 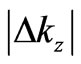 is substituted.
is substituted.
As far as 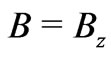 in (1) does not vanish, we find from (11) that for any
in (1) does not vanish, we find from (11) that for any 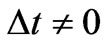 the interval
the interval 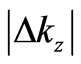 cannot be equal to zero. In fact, since
cannot be equal to zero. In fact, since 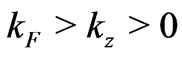 and
and 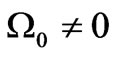 the interval
the interval 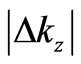 should be a non-vanishing positive number for any
should be a non-vanishing positive number for any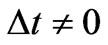 . Therefore, a finite transition time provides us with
. Therefore, a finite transition time provides us with 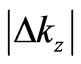 equal to a positive number which cannot be made arbitrarily small.
equal to a positive number which cannot be made arbitrarily small.
Another property is obtained when (11) is divided by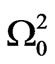 . This gives:
. This gives:
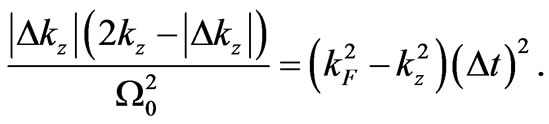 (12)
(12)
Since![]() ,
, 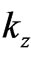 , and
, and 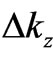 are proportional to cm–1, and
are proportional to cm–1, and 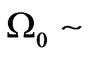 sec–1, both sides of (12) represent a reciprocal value of the velocity square. According to a special theory of relativity such expressions should not become smaller than
sec–1, both sides of (12) represent a reciprocal value of the velocity square. According to a special theory of relativity such expressions should not become smaller than
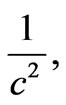 (13)
(13)
where c is a speed of light. For the left-hand side of (12) this condition means that 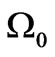 cannot be an arbitrarily large number. In reality, however, in calculating
cannot be an arbitrarily large number. In reality, however, in calculating 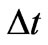 we are not so much interested in a definite size of
we are not so much interested in a definite size of 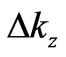 or
or , or the size of B entering
, or the size of B entering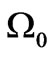 , but rather in a basic inequality coming from (12) and (13):
, but rather in a basic inequality coming from (12) and (13):
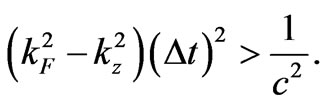 (14)
(14)
The average value of 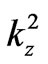 in (14) is
in (14) is
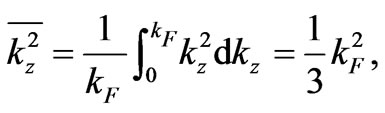 (15)
(15)
therefore, by substituting 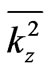 instead of
instead of  in (14) we obtain for
in (14) we obtain for 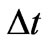 the relation
the relation
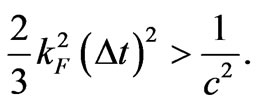 (16)
(16)
For numerous metals 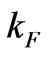 is equal to about 108 cm–1, or not much above this value [10]. This means that the lower limit of the classical interval
is equal to about 108 cm–1, or not much above this value [10]. This means that the lower limit of the classical interval 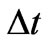 is equal approximately to
is equal approximately to
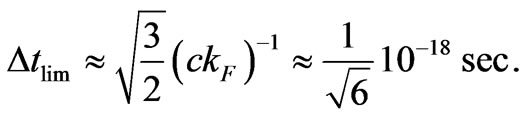 (17)
(17)
Beyond of (14), another combination of (12) and (13) gives:
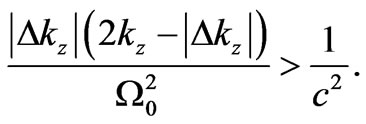 (14a)
(14a)
For small 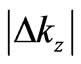 we have the change of the Bloch’s wave vector:
we have the change of the Bloch’s wave vector:
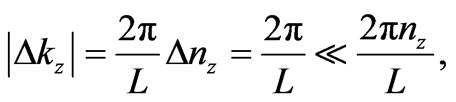 (15a)
(15a)
on condition the change of the quantum number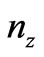 , which is assumed to be a large number, is equal to
, which is assumed to be a large number, is equal to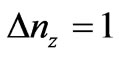 ; symbol L in (15a) represents the length of the edge of the metal sample. The interval
; symbol L in (15a) represents the length of the edge of the metal sample. The interval 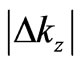 in (15a) substituted to (14a) gives approximately the condition
in (15a) substituted to (14a) gives approximately the condition
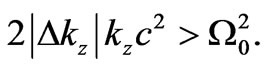 (16a)
(16a)
For 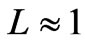 cm and
cm and 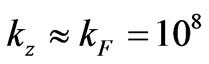 cm–1, we obtain the following requirement giving a limit of the size of
cm–1, we obtain the following requirement giving a limit of the size of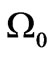 :
:
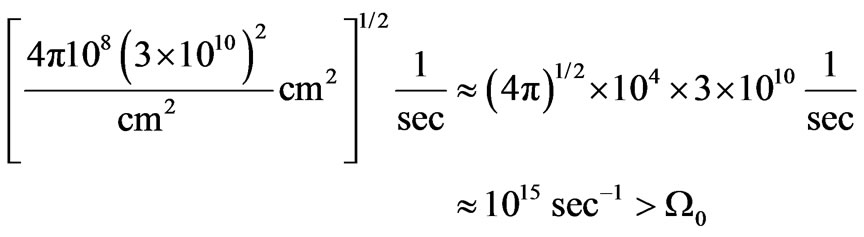 (17a)
(17a)
since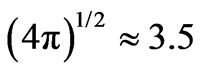 .
.
7. Quantum-Mechanical Approach to the Interval Δt
An interesting point is a formal reference of a classical relation (14) to the quantum-mechanical uncertainty principle coupling time and energy; see e.g. [11]. Consequently to their classical behaviour, 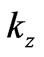 and
and 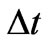 in (14) can be continuous parameters having no reference to the Planck constant
in (14) can be continuous parameters having no reference to the Planck constant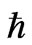 . However, the behavior characteristic for quantum mechanics is obtained when both sides of (14) are multiplied by the term
. However, the behavior characteristic for quantum mechanics is obtained when both sides of (14) are multiplied by the term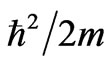 . This gives in place of (14) the formula
. This gives in place of (14) the formula
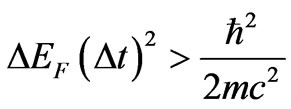 (18)
(18)
in which 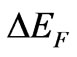 is a quantum-mechanical energy difference between the Fermi energy at the momentum
is a quantum-mechanical energy difference between the Fermi energy at the momentum 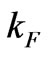 and the energy of electron having the momentum
and the energy of electron having the momentum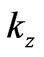 :
:
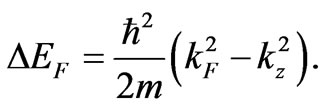 (19)
(19)
Another transformation of (18) gives:
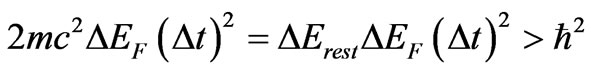 (20)
(20)
where on the left-hand side we have a product of  with another energy difference
with another energy difference
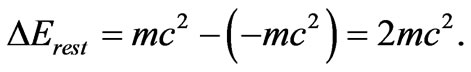 (21)
(21)
Expression (21) is the change of the electron energy from a set of negative values equal approximately to 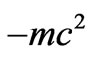 to a set of energies above the rest electron energy
to a set of energies above the rest electron energy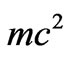 ; see e.g. [9] .
; see e.g. [9] .
Formally (20) becomes a product of two uncertainty relations, one containing the energy interval 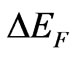 and the other containing the interval
and the other containing the interval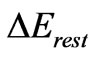 :
:
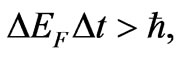 (20a)
(20a)
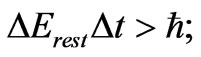 (20b)
(20b)
both relations are based on the same time interval 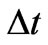 entering (14). Because we have regularly
entering (14). Because we have regularly , a satisfied relation (20a) implies immediately fullfillment of (20b).
, a satisfied relation (20a) implies immediately fullfillment of (20b).
8. Concluding Remarks
The time interval of a transition between two electron states lying on the same spherical Fermi surface is calculated, in the first step, in a classical approximation as a function of: 1) the change of the electron wave vector, 2) the actual component value of that vector, and 3) the size of the magnetic induction, all quantities were taken along the direction of the magnetic field. In the next step, a lower boundary for the length of this time interval is obtained in effect of an application of the special theory of relativity.
But the same result for the size of the time interval can be approached also on a quantum-mechanical footing. To this purpose a product of two uncertainty relations for time and energy should be taken into account. In each of these relations the size of the time interval is assumed to be the same, only the intervals of energy entering the uncertainty relations are different. One of these intervals is equal to the Fermi energy minus the actual component of the electron kinetic energy taken along the magnetic field, the other interval, however, amounts twice the rest energy of the electron.
REFERENCES
- B. d’Espagnat, “Veiled Reality: An Analysis of PresentDay Quantum Mechanical Concepts,” Westview Press, Boulder, 2003.
- R. J. Cook, “Physical Time and Physical Space in General Relativity,” American Journal of Physics, Vol. 72, 2004, pp. 214-219. doi:10.1119/1.1607338
- C. Kittel, “Quantum Theory of Solids,” 2nd Edition, Wiley, New York, 1987.
- C. Kittel, “Introduction to Solid State Physics,” 7th Edition, Wiley, New York, 1996.
- S. S. De, A. K. Ghosh and M. Bera, “On Some Physical Characteristics of Ga,As-(Ga,Al)As Quantum-Well Photoluminescence,” Canadian Journal of Physics, Vol. 76, No. 2, 1998, pp. 105-110. doi:10.1139/cjp-76-2-105
- S. T. Perez-Merchancano, M. de Dios-Leyva and L. E. Oliveira, “Photoluminescence under Quasistationary Excitation Conditionsin Quantum Wells and Quantum-Well Wires,” Journal of Luminescence, Special Issue: Proceedings of the International Conference on Luminescence and Optical Spectroscopy of Condensed Matter, Vol. 72-74, 1997, pp. 389-390.
- S. T. Perez-Merchancano, M. de Dios-Leyva and L. E. Oliveira, “Radiative Recombination in Cylindrical GaAs- (Ga,Al)As Quantum-Well Wires under Quasistationary Excitation Conditions,” The Physical Review B, Vol. 53, No. 19, 1996, pp. 12985-12989. doi:10.1103/PhysRevB.53.12985
- L. E. Oliveira and M. de Dios-Leyva, “Radiative Lifetimes, Quasi-Fermi-Levels and Carrier Densities in GaAs- (Ga,Al))As Quantum-Well Photoluminescence under Steady State Excitation Conditions,” The Physical Review B, Vol. 48, No. 20, 1993, pp. 15092-15102. doi:10.1103/PhysRevB.48.15092
- J. C. Slater, “Quantum Theory of Molecules and Solids,” Vol. 3, McGraw-Hill, New York, 1967.
- N. W. Ashcroft and N. D. Mermin, “Solid State Physics,” Holt, Rinehart and Winston, New York, 1976.
- L. I. Schiff, “Quantum Mechanics,” 3rd Edition, McGrawHill, New York, 1968.

