Journal of Modern Physics
Vol. 2 No. 10 (2011) , Article ID: 8054 , 5 pages DOI:10.4236/jmp.2011.210143
Well Behaved Class of Charge Analogue of Durgapal’s Relativistic Exact Solution
1Department or Physics, Kumaun University, S.S.J.Campus, Almora, India
2Department of Mathematics, Kumaun University, S.S.J.Campus, Almora, India
3Department or Physics, Kumaun University, S.S.J.Campus, Almora, India
E-mail: p.fuloria@yahoo.com, drbctewari@yahoo.co.in
Received July 12, 2011; revised August 26, 2011; accepted September 6, 2011
Keywords: Charged Fluids, Reissener-Nordstom Metric, General Relativity
ABSTRACT
We obtain a new class of charged super-dense star models after prescribing particular Forms of the metric potential and electric intensity. The metric describing the superdense stars joins smoothly with the Reissner-Nordstrom metric at the pressure free boundary. The interior of the stars possess their energy density, pressure, pressure density ratio and velocity of sound to be monotonically decreasing towards the pressure free interface. In view of the surface density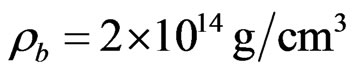 , the heaviest star occupies a mass 5.523 MQ with its radius 13.98 km. In absence of the charge we are left behind with the regular and well behaved fifth model of Durgapal [1].
, the heaviest star occupies a mass 5.523 MQ with its radius 13.98 km. In absence of the charge we are left behind with the regular and well behaved fifth model of Durgapal [1].
1. Introduction
Exact interior solutions of the Einstein-Maxwell field equations joining smoothly to the Nordstrom solution at the pressure free interface are gathering big applause due to some of the following reasons: 1) Gravitational collapse of a charged fluid sphere to a point singularity may be avoided. 2) Solutions of Einstein-Maxwell equations are useful in the study of cosmic sensership. 3) Chargeddust models and electromagnetic mass models are expected to provide some clue about structure of an electron . In the present paper our aim is to obtain a class of regular and well behaved charged fluid models whose neutral analogues are also regular and well behaved. Here we consider a spherically symmetric metric which shares its metric potential with one of the Durgapal’s interior metric [1].
On account of the nonlinearity of Einstein-Maxwell field equations, not many realistic well behaved, analytic solutions are known for the description of relativistic charge fluid spheres. For well behaved model of relativistic star with charged and perfect fluid matter, following conditions should be satisfied (Pant et al. [2]):
1) The solution should be free from physical and geometrical singularities i.e. finite and positive values of central pressure, central density and non zero positive values of  and
and .
.
2) The solution should have positive and monotonically decreasing expressions for pressure and density (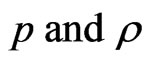 ) with the increase of r. The solution should have positive value of ratio of pressure-density and less than 1(weak energy condition) and less than 1/3(strong energy condition) throughout within the star.
) with the increase of r. The solution should have positive value of ratio of pressure-density and less than 1(weak energy condition) and less than 1/3(strong energy condition) throughout within the star.
3) The solution should have positive and monotonically decreasing expression for fluid parameter 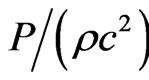 with the increase of r.
with the increase of r.
4) The solution should have positive and monotonically decreasing expression for velocity of sound 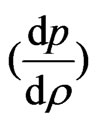 with the increase of r and causality condition should be obeyed at the centre, i.e.,
with the increase of r and causality condition should be obeyed at the centre, i.e.,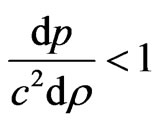 .
.
5) The red shift Z should be positive, finite and monotonically decreasing in nature with the increase of r.
Electric intensity E is positive and monotonically increasing from centre to boundary and at the centre the Electric intensity is zero.
Under these well behaved conditions, one has to assume the gravitational potential and electric field intensity in such a way that the field equation can be integrated and solution should be well behaved. Keeping in view of this aspect ,several authors obtained the parametric class of exact solutions Pant et al. [3,4], GuptaMaurya [5-7], Pant [8,9], N. Bijalwan [10] etc. These coupled solutions are well behaved with some positive values of charge parameter K and completely describe interior of the super-dense astrophysical object with charge matter. Further, The mass of the such modeled super dense object can be maximized by assuming surface density is . In the present paper we have obtained yet another new parametric class of well behaved exact solutions of Einstein-Maxwell field equations, which is compatible within the range of Neutron star and quark star.
. In the present paper we have obtained yet another new parametric class of well behaved exact solutions of Einstein-Maxwell field equations, which is compatible within the range of Neutron star and quark star.
2. Einstein’s-Maxwell Equation for Charged Fluid Distribution
Let us consider a spherical symmetric metric in curvature coordinates
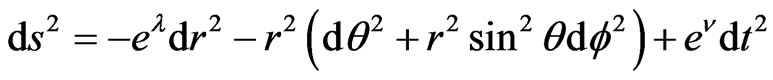 (1)
(1)
where the functions 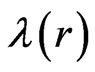 and
and 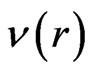 satisfy the Einstein-Maxwell equations
satisfy the Einstein-Maxwell equations
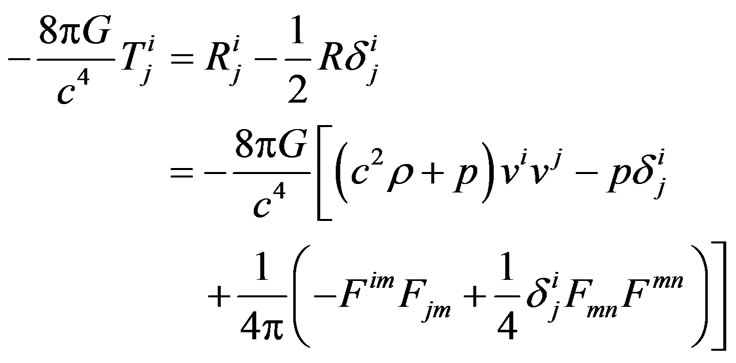 (2)
(2)
where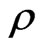 , p,
, p, ![]() , Fij denote energy density, fluid pressure, velocity vector and skew-symmetric electromagnetic field tensor respectively.
, Fij denote energy density, fluid pressure, velocity vector and skew-symmetric electromagnetic field tensor respectively.
In view of the metric (1), the field Equation (2) gives Dionysiou [11]
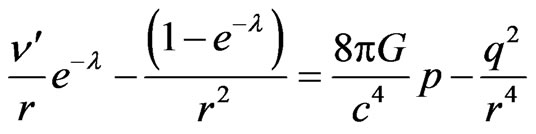 (3)
(3)
 (4)
(4)
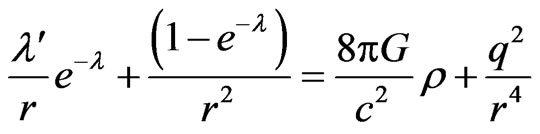 (5)
(5)
where prime ( ' ) denotes the differentiation with respect to r and 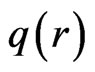 represents the total charge contained with in the sphere of radius r.
represents the total charge contained with in the sphere of radius r.
By using the transformation
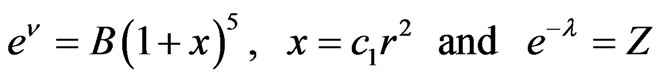 (6)
(6)
where B being the positive constants. Now putting (6) into (3)-(5), we have
 (7)
(7)
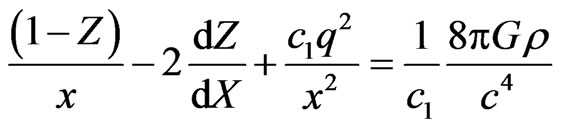 (8)
(8)
and Z satisfying the equation
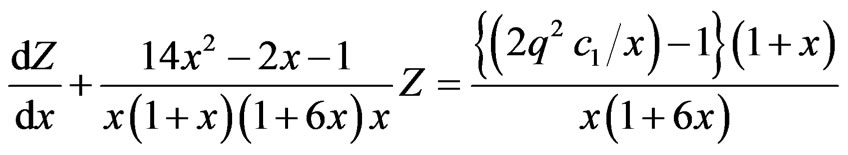 (9)
(9)
where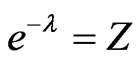
 .
.
3. New Class of Solutions
In order to solve the differential Equation (9) let us consider the electric intensity E of the following form
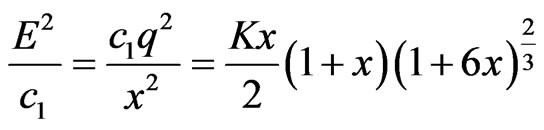 (10)
(10)
where K is a positive constant. The electric density is so assumed that the model is physically significant and well behaved, i.e., E remains regular and positive throughout the sphere.
In view of (10) differential Equation (9) yields the following solution
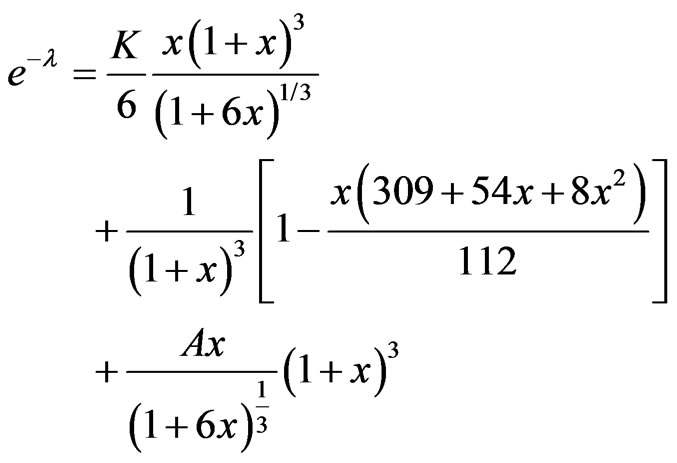 (11)
(11)
where A is an arbitrary constant of integration.
4. Properties of the New Class of Solutions
Using (11), into (7) and (8), we get the following expressions for pressure and energy density
 (12)
(12)
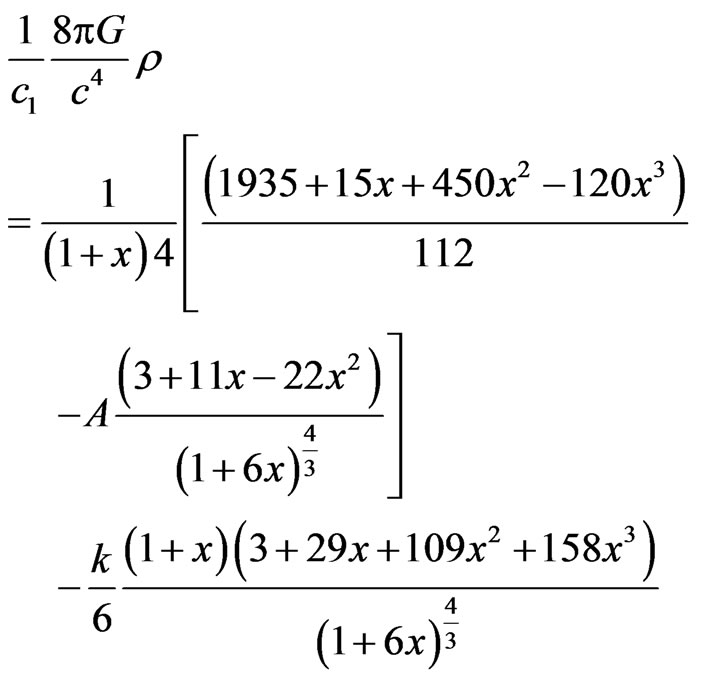 (13)
(13)
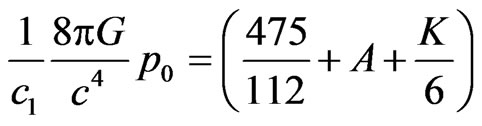 (14)
(14)
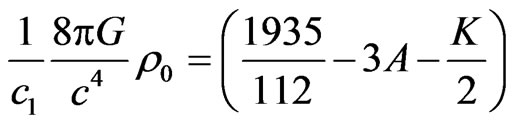 (15)
(15)
Differenting (12) and (13) w.r.t. x, we get:
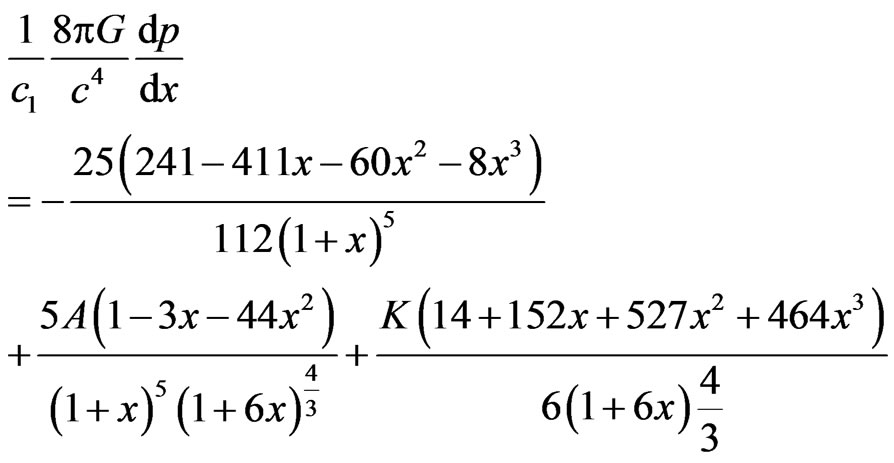 (16)
(16)
 (17)
(17)
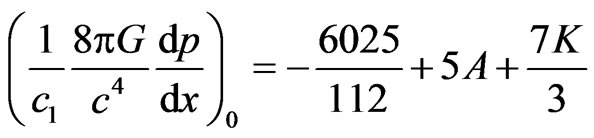 (18)
(18)
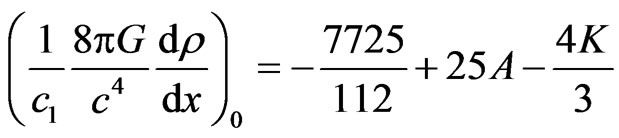 (19)
(19)
The velocity of sound is given by the following expression (20)-(21)

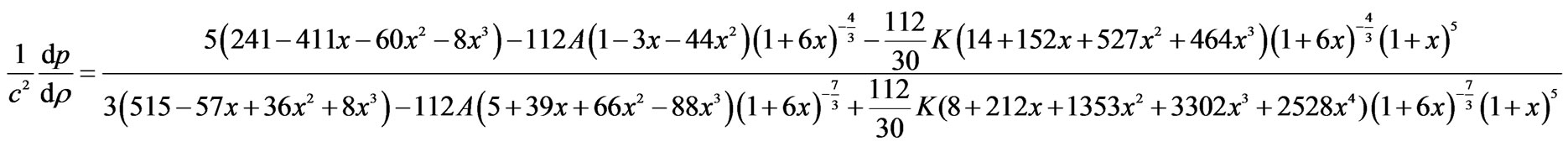 (20)
(20)
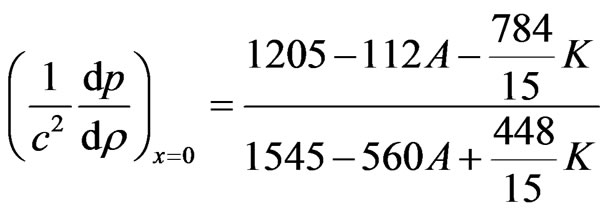 (21)
(21)
The expression for gravitational red-shift (z) is given by
 (22)
(22)
The central value of gravitational red shift to be non zero positive finite, we have
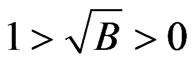 (22a)
(22a)
Differenting (22) w.r.t. x, we get,
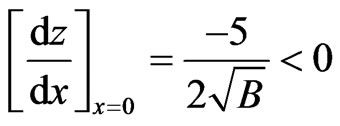 (22b)
(22b)
the expression of right hand side of (22b) is negative, thus the gravitational red-shift is maximum at the center and monotonically decreasing.
5. Boundary Conditions
The solutions so obtained are to be matched over the boundary with Reissner-Nordstrom metric:
 (23)
(23)
which requires the continuity of 
 and q across the boundary r = rb
and q across the boundary r = rb
 (24)
(24)
 (25)
(25)
 (26)
(26)
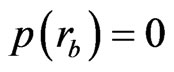 (27)
(27)
The condition (27) can be utilized to compute the values of arbitrary constants A as follows:
Pressure at p(r = rb) = 0 gives
 (28)
(28)
In view of (24) and (25) we get
 (29)
(29)
The expression for mass can be written as
 (30)
(30)
The expression for surface density is given by
 (31)
(31)
6. Discussion
In view of Table 1 it has been observed that all the physical parameters (p, 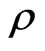 ,
,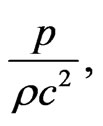
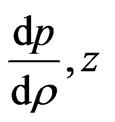 and E) are positive at the centre and within the limit of realistic equation of state and well behaved conditions for all values of K satisfying the inequalities
and E) are positive at the centre and within the limit of realistic equation of state and well behaved conditions for all values of K satisfying the inequalities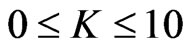 . However, corresponding to any value of K > 10, there exist no value of X for which surface density is positive .From Table 2 we observe that for K = 2 we obtain increasing mass with increasing values of X and central redshift also increases. We have taken a different expression for elec-
. However, corresponding to any value of K > 10, there exist no value of X for which surface density is positive .From Table 2 we observe that for K = 2 we obtain increasing mass with increasing values of X and central redshift also increases. We have taken a different expression for elec-
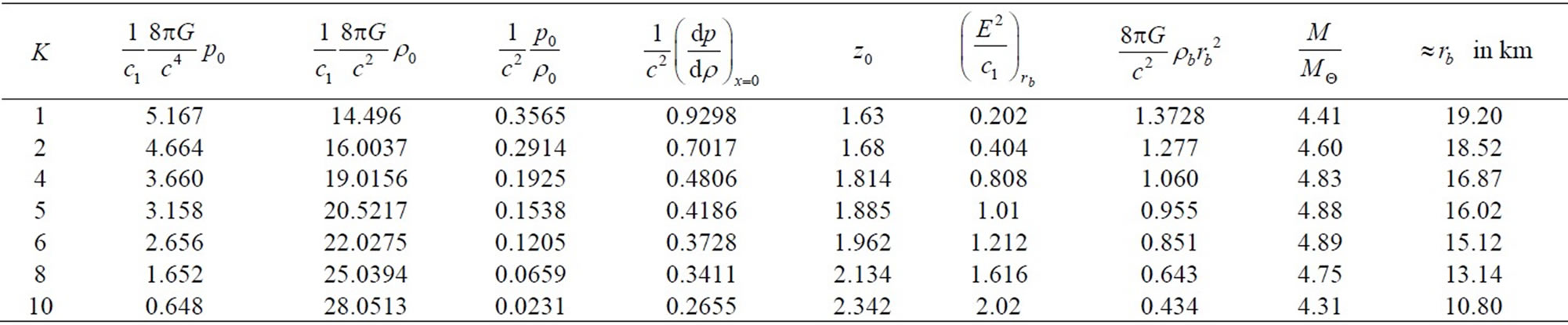
Table 1. The variation of various physical parameters at the center,surface density, electric field intensity on the boundary, mass and radius of stars with different values of K and X = 0.2.

Table 2. The variation of various physical parameters at the center,surface density, electric field intensity on the boundary, mass and radius of stars with different values of X and K = 2.
tric intensity as compared to that of Gupta and Mauraya’s solution [5]. Our solution satisfies all the necessary physical conditions giving us a possibitity for different charge variations within the fluid sphere. Owing to the various conditions that we obtain here we arrive at the conclusion that under well behaved conditions this class of solutions gives us the mass of super dense object within the range of neutron star and quark star.
We now present here a model of super dense star based on the particular solution discussed above corresponding to K = 0.35 with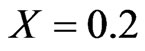 , by assuming surface density;
, by assuming surface density;  The resulting well behaved model has the heaviest star occupying a mass 5.523 M with its radius 13.98 km. In absence of the charge we are left behind with the regular and well behaved fifth model of Durgapal [1].
The resulting well behaved model has the heaviest star occupying a mass 5.523 M with its radius 13.98 km. In absence of the charge we are left behind with the regular and well behaved fifth model of Durgapal [1].
REFERENCES
- M. C. Durgapal, “A Class of New Exact Solutions in General Relativity,” Journal of Physics A: Mathematical and General, Vol. 15, August 1982, pp. 2637-2644.
- N. Pant, “Some New Exact Solutions with Finite Central Parameters and Uniform Radial Motion of Sound,” Astrophysics and Space Science, Vol. 331, No. 2, 2011, pp. 633-644. doi:10.1007/s10509-010-0453-4
- N. Pant, et al., “Well Behaved Class of Charge Analogue of Heintzmann’s Relativistic Exact Solution,” Astrophysics and Space Science, Vol. 332, No. 2, 2011, pp. 473- 479. doi:10.1007/s10509-010-0509-5
- N. Pant, et al., “Variety of Well Behaved Parametric Classes of Relativistic Charged Fluid Spheres in General Relativity,” Astrophysics and Space Science, Vol. 333, No. 1, 2011, pp. 161-168.
- Y. K. Gupta and S. K. Maurya, “A Class of Regular and Well Behaved Relativistic Super Dense Star Models,” Astrophysics and Space Science, Vol. 334, No. 1, 2011, pp. 155-162. doi:10.1007/s10509-010-0503-y
- S. K. Maurya and Y. K. Gupta, “A Family of Well Behaved Charge Analogue of a Well Behaved Neutral Solution in Genetral Relativity,” Astrophysics and Space Science, Vol. 332, No. 2, 2011, pp. 481-490. doi:10.1007/s10509-010-0541-5
- S. K. Maurya and Y. K. Gupta, “Charged Analogue of Vlasenko-Pronin Super Dense Star in General Relativity,” Astrophysics and Space Science, Vol. 333, No. 1, 2011, pp. 149-160. doi:10.1007/s10509-011-0616-y
- N. Pant, “Well Behaved Parametric Class of Relativistic in Charged Fluid Ball General Relativity,” Astrophysics and Space Science, Vol. 332, No. 2, 2011, pp. 403-408. doi:10.1007/s10509-010-0521-9
- N. Pant, “New Class of Well Behaved Exact Solutions of Relativistic Charged White-Dwarf Star with Perfect Fluid,” Astrophysics and Space Science, Vol. 334, No. 2, 2011, pp. 267-271. doi:10.1007/s10509-011-0720-z
- N. Bijalwan, “Static Electrically Charged Fluids in Terms Pressure: General Relativity,” Astrophysics and Space Science, Vol. 334, No. 1, 2011, pp.139-143. doi:10.1007/s10509-011-0691-0
- D. D. Dionysiou, “Equilibrium of a Static Charged Perfect Fluid Sphere,” Astrophysics and Space Science, Vol. 85, No. 1-2, 1982, pp. 331-343. doi:10.1007/BF00653455

