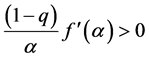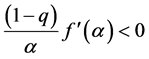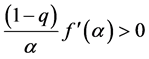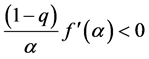Applied Mathematics
Vol.07 No.18(2016), Article ID:73034,17 pages
10.4236/am.2016.718188
The Convergences Comparison between the Halley’s Method and Its Extended One Based on Formulas Derivation and Numerical Calculations
Shunji Horiguchi
Department of Economics, Niigata Sangyo University, Niigata, Japan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 22, 2016; Accepted: December 24, 2016; Published: December 27, 2016
ABSTRACT
The purpose of this paper is that we give an extension of Halley’s method (Section 2), and the formulas to compare the convergences of the Halley’s method and extended one (Section 3). For extension of Halley’s method we give definition of function by variable transformation in Section 1. In Section 4 we do the numerical calculations of Halley’s method and extended one for elementary functions, compare these convergences, and confirm the theory. Under certain conditions we can confirm that the extended Halley’s method has better convergence or better approximation than Halley’s method.
Keywords:
Recurrence Formula, Newton’s Method, Halley’s Method, Extension of Halley’s Method, Third-Order Convergence

1. Introduction
In 1673, Yoshimasu Murase [1] made a cubic equation to obtain the thickness of a hearth. He introduced two kinds of recurrence formulas of square  and the deformation. We find that the three formulas lead to a Horner’s method (Horiguchi, [2] ) and an extension of Newton’s method (Horiguchi, [3] ). This shows originality of Wasan (mathematics developed in Japan) in the Edo era (1603-1868). We do research similar to Horiguchi, [3] against the Halley’s method. We give function
and the deformation. We find that the three formulas lead to a Horner’s method (Horiguchi, [2] ) and an extension of Newton’s method (Horiguchi, [3] ). This shows originality of Wasan (mathematics developed in Japan) in the Edo era (1603-1868). We do research similar to Horiguchi, [3] against the Halley’s method. We give function 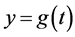 defined from
defined from 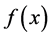 for extension of Halley’s method.
for extension of Halley’s method.
From now on, let  be a real number, and a function
be a real number, and a function 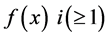 times differentiable if necessary, and
times differentiable if necessary, and 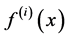 continuous.
continuous.
Definition 1.1. Let  where
where 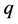 is a real number that is not 0. We define the function g(t) such as
is a real number that is not 0. We define the function g(t) such as
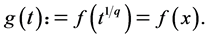 (1)
(1)
Because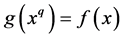 , the graph of
, the graph of 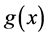 extends or contracts by
extends or contracts by 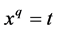 in the
in the  -axis, without changing the height of
-axis, without changing the height of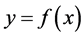 . Expansion and contraction come to object in
. Expansion and contraction come to object in 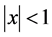 and
and .
.
Theorem 1.2. The formulas
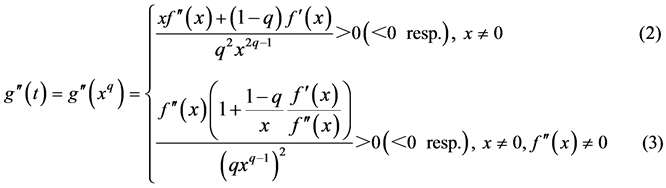
give the convex upward (the convex downward resp.) at the point 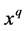 of graph of
of graph of
Proof. It is proved by the next calculations.


□
From the formulas (4), (5), we obtain the next theorem.
Theorem 1.3. The curvature of the cure 

These become the curvature 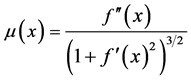


Proof. Formula (6) is obtained by substituting the formulas (4) and (5) for 

Theorem 1.4. A necessary and sufficient condition for

is that formula (9) holds.

Proof. Formula (9) is obtained from (8). □
Proposition 1.5. If 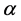


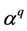


2. Halley’s Method and Extension of Halley’s Method
Definition 2.1. The recurrence formula to approximate a root of the equation

is called Halley’s method1.
Halley’s method is obtained by improving the Newton’s method (11) (Ref. [5] ).

They are methods of giving the initial value

From now on we omit the notation 

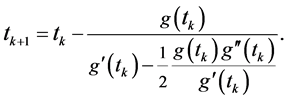
If we express this by formula (1) in
Definition 2.2. Let α be a root of the equation
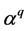


Here, if 
Calculation formula of 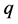
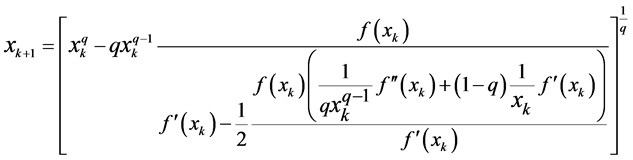
3. Formulas to Compare the Convergences for Extensions of Halley’s Method
Theorem 3.1. Let 
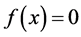


If 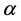



Proof. There is a brief proof of (15) in wikipedia [4] . Therefore we go to the proof of (16).
We merely sketch 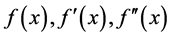



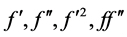

From these formulas, we obtain the following linearly convergence.

Lemma 3.2. In the sequence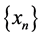
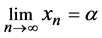




Proof. Applying L’Hospital’s rule to
□
Theorem 3.3. Let the condition be the same as Theorem 3.1. If 



If 



Proof. If 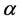
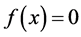
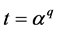
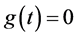


Here 

Therefore we obtain
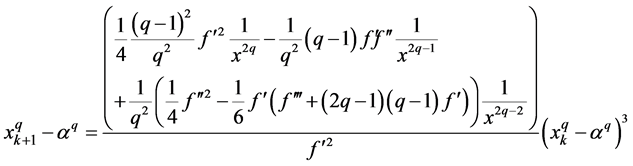
By lemma 3.2, we get

Therefore, formula (25) becomes

By changing the independent variable 

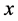

In case that 


□
Theorem 3.4. Let 





That is

Proof. Compare the coefficient of 


The formula (29) is obtained from this. □
Corollary 3.5. (1) If 

(2) If 
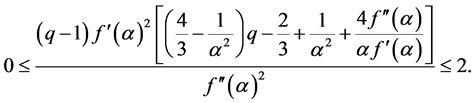
We transform the equation 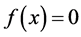




and if 

We get the following by comparing the coefficient of 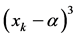
Proposition 3.6. Let


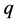






Theorem 3.7. Let 



which distinguishes the convex-concave of the curve
(i)

(ii)

Proof. We lead inequalities (38), (39) from (29). Let
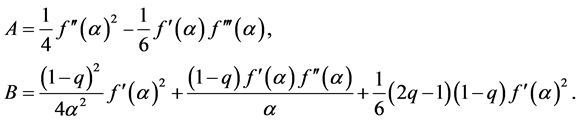
Then inequality (29) becomes


We transform the formula B.

Therefore inequality (29) becomes (44).

Furthermore, we transform the inequality.

From (45), we get (38), (39) according to plus, minus number of 
Theorem 3.8. Let the condition be the same as the above Theorem. Inequality (29) is represented by the curvature
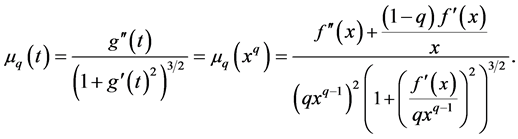
Those are the next complicated inequalities (47) and (48).
(i)
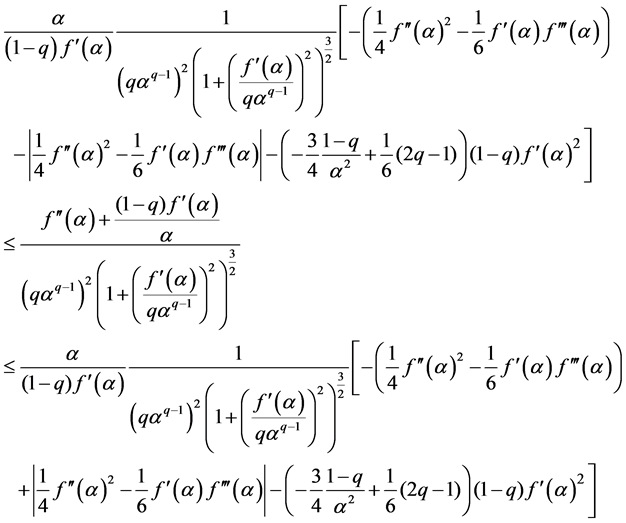
(ii)
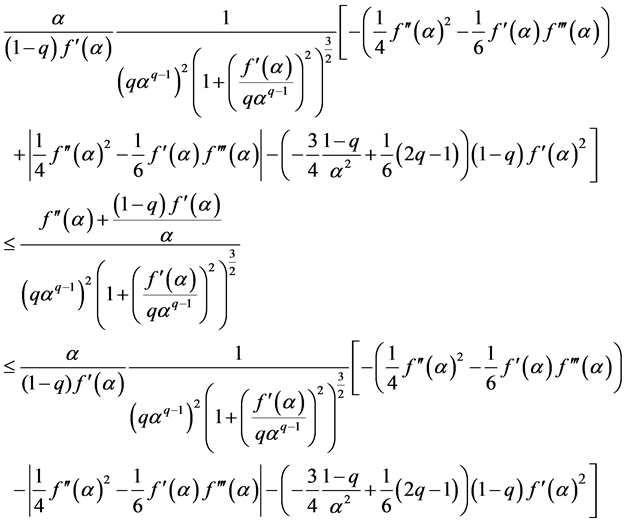
Proof. We get (47), (48) by dividing formula (38), (39) in
4. Convergence Comparisons by the Numerical Calculations of Halley’s Method and Extensions of Halley’s Method
We perform numerical calculations by the calculation formula (14) in the standard format in Excel 2013 of Microsoft. We perform numerical calculations for various equations such as 

In the examples of the followings, there are cases where some numerical calculations do not fit in with the inequality (30) a little. Those are probably due to the formula (21) the approximate formula, choosing the initial value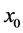
Example 4.1. A quadratic equation

The roots of (49) are
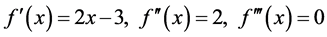


We choose real numbers 
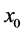



Two numbers 1 and 1.11022E−16 of intersection of two row and two column mean the following.
Number 1 indicates the number of iterations that Halley’s method 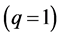

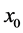


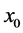
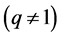

We confirm Theorem 3.7. Because 

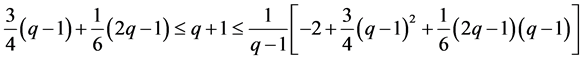
The results are Table 3. The range of 
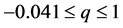
Example 4.2. A cubic equation
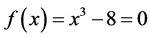
Because the root of (52) is 2, the condition (30) becomes

We choose real numbers 

Table 1. Calculations of (14) for root 1, −0.041 ≤ q ≤ 1.
Table 2. Calculations of (14) for root 1, 23 ≤ q ≤ 24.042.
Table 3. Calculations of (51) for root 1, −0.041 ≤ q ≤ 1.
Table 4. Calculations of (14) for root 2, −1.8875 ≤ q ≤ −1.462.
Table 5. Calculations of (14) for root 2, 1 ≤ q ≤ 1.4262.
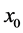

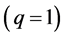
Example 4.3. A cubic equation
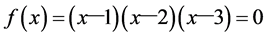
In case of the root 1, the condition (30) becomes

We choose real numbers 


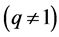




Example 4.4.
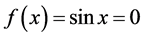
The roots of (56) are 

If we take the root in

We do numerical computations for the real numbers 
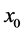
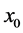



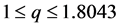
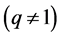
Table 6. Calculations of (14) for root 1, −0.1934 ≤ q ≤ 1.
Table 7. Calculations of (14) for root 1, 35 ≤ q ≤ 36.
Table 8. Calculations of (14) for root π, −0.3455 ≤ q ≤ 0.458.
Example 4.5.

The roots of (59) are 

If we take the root in

Table 10 gives numerical computations. In case of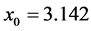



Example 4.6.
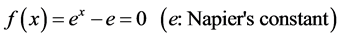
The root of (62) is 1. The condition (30) becomes

Table 11 and Table 12 give the numerical values to almost adapt to Theorem 3.4.
Example 4.7.

The root of (64) is 1. The condition (30) becomes

Table 13 and Table 14 give the numerical values to almost adapt to Theorem 3.4.
Table 9. Calculations of (14) for root π, 1 ≤ q ≤ 1.8043.
Table 10. Calculations of (14) for root π, 0.46 ≤ q ≤ 1.
Table 11. Calculations of (14) for root 1, −13.14142 ≤ q ≤ −13.
Table 12. Calculations of (14) for root 1, 1 ≤ q ≤ 1.14142.
Table 13. Calculations of (14) for root 1, 1 ≤ q ≤ 1.2041684.
Table 14. Calculations of (14) for root 1, 10.795834 ≤ q ≤ 11.
Acknowledgements
Dr. Hideko Nagasaka (Nihon University former professor) taught me numerical computations. I am deeply grateful to her.
Cite this paper
Horiguchi, S. (2016) The Convergences Comparison between the Halley’s Method and Its Extended One Based on Formulas Derivation and Numerical Cal- culations. Applied Mathematics, 7, 2394- 2410. http://dx.doi.org/10.4236/am.2016.718188
References
- 1. Murase, Y. (1673) Sanpoufutsudankai. In: Nishida, T., Ed., Kenseisha Co., Ltd., Tokyo. (In Japanese)
- 2. Horiguchi, S. (2014) On Relations between the General Recurrence Formula of the Extension of Murase-Newton’s Method (the Extension of Tsuchikura-Horiguchi’s Method) and Horner’s Method. Applied Mathematics, 5, 777-783.
https://doi.org/10.4236/am.2014.54074 - 3. Horiguchi, S (2016) The Formulas to Compare the Convergences of Newton’s Method and the Extended Newton’s Method (Tsuchikura-Horiguchi Method) and the Numerical Calculations. Applied Mathematics, 7, 40-60.
https://doi.org/10.4236/am.2016.71004 - 4. http://en.wikipedia.org/wiki/Halley’s_method
- 5. Nagasaka, H. (1980) Computer and Numerical Analysis (Japanese Title Keisanki to suuchikaiseki). Asakura Publishing Co., Ltd., Tokyo. (In Japanese)
NOTES
1Edmond Halley (1656-1742) is the British astronomer, and famous for Halley’s comet of research.