Received 25 June 2016; accepted 21 August 2016; published 24 August 2016

ABSTRACT

We study a Dirichlet optimal design problem for a quasi-linear monotone p-biharmonic equation with control and state constraints. We take the coefficient of the p-biharmonic operator as a design variable in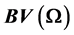. In this article, we discuss the relaxation of such problem.

Keywords:

p-Biharmonic Problem, Optimal Design, Relaxation, Henig Dilating Cone, Existence Result

1. Introduction

The aim of this article is to analyze the following optimal design problem (OCP), which can be regarded as an optimal control problem, for quasi-linear partial differential equation (PDE) with mixed boundary conditions

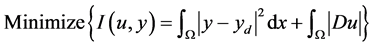(1)

subject to the quasi-linear equation

(2)

(3)

the pointwise state constraints

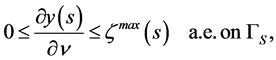(4)

and the design (control) constraints

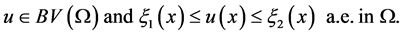(5)

Here, 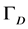and are the disjoint part of the boundary 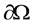(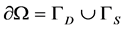),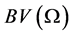stands for the control space, 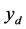, f, and 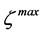are given distributions. Problems of this type appear for p-power-like elastic isotropic flat plates of uniform thickness, where the design variable u is to be chosen such that the deflection of the plate matches a given profile. The model extends the classical weighted biharmonic equation, where the weight 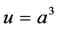involves the thickness a of the plate, see e.g. [1] - [3] , or u can be regarded as a rigidity parameter. The OCP (1)-(4) can be considered as a prototype of design problems for quasilinear state equations. For an interesting exposure to this subject we can refer to the monographs [4] - [6] .

A particular feature of OCP (1)-(4) is the restriction by the pointwise constraints (4) in 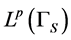-space. In fact, the ordering cone of positive elements in -spaces is typically non-solid, i.e. it has an empty topological interior. Following the standard multiplier rule, which gives a necessary optimality condition for local solutions to state constrained OCPs, the constraint qualifications such as the Slater condition or the Robinson condition should be applied in this case. However, these conditions cannot be verified for cones such as due to the fact that, where stands for the topological interior of the set A. Therefore, our main intention in this article is to propose a suitable relaxation of the pointwise state constraints in the form of some inequality conditions involving a so-called Henig approximation of the ordering cone of positive elements. Here, B is a fixed closed base of. Due to fact that for all, we can replace the cone by its approximation. As a result, it leads to some relaxation of the inequality constraints of the considered problem, and, hence, to the approximation of the feasible set to the original OCP. Hence, the solvability of a given class of OCPs can be characterized by solving the corresponding Henig relaxed problems in the limit.

As was shown in the recent publication [7] , the proposed approach is numerically viable for state-constrained optimal control problems with the state equation given by linear partial differential equations. In particular, using the finite element discretization of the Henig dilating cone of positive functions, it has been shown in [7] that the above approximation scheme, called conical regularization, where the regularization is done by replacing the ordering cone with a family of dilating cones, leads to a finite-dimensional optimization problem which can conveniently be treated by known numerical techniques. The non-emptiness of the feasible set for the state- constrained OCPs is an open question even for the simplest situation. Therefore, we consider a more flexible notion of solution to the boundary value problem (2)-(3). With that in mind we discuss a variant of the penalization approach, called the “variational inequality (VI) method”. Following this approach we weaken the requirements on admissible solutions to the original OCP and consider instead the family of penalized OCPs for appropriate variational inequalities

where the sets are defined in a special way. As a result, we show that each of new penalized OCP is solvable for each and their solutions can be used for approximation of optimal pairs to the original problem.

The outline of the paper is the following. In Section 2 we report some preliminaries and notation we need in the sequel. In Sections 3, we give a precise statement of the state constrained optimal control (or design) problem and describe the main assumptions on the initial data and control functions. In Section 4, we provide the results concerning solvability of the original problem with control and state constraints. We show that this problem admits at least one solution if and only if the corresponding set of feasible solutions is nonempty. In Section 5 we show that the pointwise state constraints can be replaced by the weakened conditions coming from Henig relaxation of ordering cones. As a result, we give a precise definition of the relaxed optimization problems and show that the solvability of the original OCP can be characterized by the associated relaxed problems. In particular, we prove that the optimal solution to the original problem can be attained in the limit by the optimal solution of the relaxed problem. We consider in Section 6 the “variational inequality method” as an approximation of the OCPs. Following this approach, we weaken the requirements on feasible solutions to the original OCP. In contrast to the Henig relaxation approach, the penalized optimal control problem for indicated variational inequality has a non-empty feasible set and this problem is always solvable. In conclusion, we show that some of the optimal solutions to the original problem can be attained in the limit by optimal solutions of the penalized problem. However, it is unknown whether the entire set of the optimal solutions can be attained in such way.

2. Definitions and Basic Properties

Let be a bounded open connected subset of (). We assume that the boundary is Lip- schitzian so that the unit outward normal is well-defined for a.e., where the abbreviation ‘a.e.’ should be interpreted here with respect to the -dimensional Hausdorff measure. We also assume that the boundary consists of two disjoint parts, where the sets and have positive -dimensional measures, and is of.

Let p be a real number such that. By we denote the Sobolev space as the subspace of of functions y having generalized derivatives up to order in. We note that thanks to interpolation theory, see ( [8] , Theorem 4.14), is a Banach space with respect to the norm

where

For any we define the traces

By ( [9] , Theorem 8.3), these linear operators can be extended continuously to the whole of space. We set

as closed subspaces of and, respectively. Moreover, the injections

(6)

are compact.

Let. We define the Banach space

as the closure of with respect to the norm. Let be the dual space to, where is the conjugate of p. We also define the space as the closure

of with respect to the norm.

Throughout this paper, we use the notation. Let us notice that equipped with the norm

(7)

is a uniformly convex Banach space [10] . Moreover, the norm is equivalent on to the usual norm of. Indeed, since the Laplace operator acts from in and the Dirichlet boundary value problem

(8)

is uniquely solvable in for all, it follows that the inverse operator is well defined and satisfies the following elliptic regularity estimate [11]

This allows us to conclude the following. If and are such that on

and y is a solution of (8), then, on the boundary, and, therefore,. Hence,

(9)

for a suitable positive constant independent of f. On the other hand, it is easy to see that

Thus, by the Closed Graph Theorem, we can conclude that is equivalent to the norm induced by (for the details we refer to [12] [13] ).

By we denote the space of all functions in for which the norm

is finite.

We recall that a sequence converges weakly-* to f in if and only if the two following conditions hold (see [14] ): strongly in and weakly-* in the space of Radon measures, i.e.

It is well-known also the following compactness result for BV-spaces (Helly’s selection theorem, see [15] ).

Theorem 1. If and, then there exists a subsequence of

strongly converging in to some such that weakly-* in the space of Radon measures. Moreover, if strongly converges to some f in and satisfies

, then

(10)

3. Setting of the Optimal Control Problem

Let, be fixed elements of satisfying the conditions

(11)

where is a given positive value.

Let be a nonlinear mapping such that F is in the space of Carathéodory functions on, i.e.

1) the function is continuous in for almost all;

2) the function is measurable for each.

In addition, the following conditions of subcritical growth, monotonicity, and non-negativity are fulfilled:

(12)

(13)

(14)

for some, where

is the critical exponent for the Sobolev imbedding, and. In particular, conditions (13) - (14) imply that is monotonically increasing on and for almost all.

Let, , and be given distributions. The optimal control pro- blem we consider in this paper is to minimize the discrepancy between and the solutions of the following state-constrained boundary valued problem

(15)

(16)

(17)

by choosing an appropriate function as control. Here,

is the operator of fourth order called the generalized p-biharmonic operator, and the class of admissible controls we define as follows

(18)

It is clear that is a nonempty convex subset of with an empty topological interior.

More precisely, we are concerned with the following optimal control problem

(19)

Before we will discuss the question of existence of admissible pairs to the problem (19), we note that the function can be associated with operator defined by the rule

(20)

Moreover, taking into account the growth condition (12) and the compactness of the Sobolev imbedding for it is easy to show that operator is compact.

Definition 3.1. We say that an element is the weak solution (in the sense of Minty) to the boundary value problem (15) - (16), for a given admissible control, if

(21)

Remark 3.1. Since the set is dense in, it follows that the element with an arbitrary and can be taken as a test function in (21). As a result, (21) implies that

Passing to the limit as (because), we get

Hence,

(22)

and we arrive at the standard definition of weak solution to the boundary value problem (15)-(16). However, in order to avoid some mathematical difficulties, we will mainly use the Minty inequality in our further analysis. It is

worth to note that having applied Green’s formula twice to operator tested by,

we arrive at the identity

Hence, if y as an element of is the weak solution of the boundary value problem (15) - (16) in the sense of Definition 3.1, then relations (15)-(16) are fulfilled as follows (for the details, we refer to ( [16] , Section 2.4.4) and ( [4] , Section 2.4.2))

In particular, taking in (22), this yields the relation

(23)

As a result, conditions (11), (18), and inequalities (14) and (9) lead us to the following a priori estimate

(24)

The existence of a unique weak solution to the boundary value problem (15)-(16) in the sense of Definition 3.1 follows from an abstract theorem on monotone operators.

Theorem 2 ( [17] ) Let V be a reflexive separable Banach space. Let V^* be the dual space, and let be a bounded, hemicontinuous, coercive and strictly monotone operator. Then the equation has a unique solution for each.

Here, the above mentioned properties of the strict monotonicity, hemicontinuity, and coercivity of the operator A have respectively the following meaning:

(25)

(26)

(27)

(28)

In our case, we can define the operator as a mapping by

(29)

In view of the properties (12)-(14) and compactness of the Sobolev imbedding for, it is easy to show that and satisfies all assumptions of Theorem 2 (for the details we refer to [16] [17] ). Hence, the variational problem

(30)

for which is its operator form, has a unique solution. We note that the duality pairing in the right hand side of (30) makes a sense for any distribution because. It remains to show that the solution y of (30) satisfies the Minty relation (21). Indeed, in view of the monotonicity of A, we have

Thus,

and, hence, in view of Remark 3.1, the Minty relation (21) holds true.

Taking this fact into account, we adopt the following notion.

Definition 3.2. We say that is a feasible pair to the OCP (19) if, , the pair is related by the Minty inequality (21), , and

(31)

where stands for the natural ordering cone of positive elements in, i.e.

(32)

We denote by the set of all feasible pairs for the OCP (19). We say that a pair is an optimal solution to problem (19) if

Remark 3.2. Before we proceed further, we need to make sure that minimization problem (19) is meaningful, i.e. there exists at least one pair such that satisfying the control and state constraints (16)-(18), , and would be a physically relevant solution to the boundary value problem (15)-(16). In fact, one needs the feasible set to be nonempty. But even if we are aware that, this set must be suf- ficiently rich in some sense, otherwise the OCP (19) becomes trivial. From a mathematical point of view, to deal directly with the control and especially state constraints is typically very difficult [18] - [20] . Thus, the non- emptiness of feasible set for OCPs with control and state constraints is an open question even for the simplest situation.

It is reasonably now to make use of the following Hypothesis.

(H₁) There exists at least one pair such that.

4. Existence of Optimal Solutions

In this section we focus on the solvability of optimal control problem (15)-(19). Hereinafter, we suppose that the

space is endowed with the norm. Let be the to-

pology on the set which we define as the product of the weak-* topology of and the weak topology of.

We begin with a couple of auxiliary results.

Lemma 1. Let be a sequence such that in. Then we have

(33)

Proof. Since in L¹(W) and is bounded in, we get that strongly in L^r(W) for every. In particular, we have that in and in. Hence, it is immediate to pass to the limit and to deduce (33).

As a consequence, we have the following property.

Corollary 1. Let and be sequences such that

in and in. Then

Our next step concerns the study of topological properties of the feasible set to problem (19).

The following result is crucial for our further analysis.

Theorem 3. Let be a bounded sequence in. Then there is a pair

such that, up to a subsequence, and.

Proof. By Theorem 1 and compactness properties of the space, there exists a subsequence of, still denoted by the same indices, and functions and such that

(34)

Then by Lemma 1, we have

It remains to show that the limit pair is related by inequality (21) and satisfies the state constraints (31). With that in mind we write down the Minty relation for:

(35)

In view of (34) and Lemma 1, we have

Moreover, due to the compactness of the Sobolev imbedding for, we have

where Hölder’s inequality yields

We, thus, can pass to the limit in relation (35) as and arrive at the inequality (21), which means that is a weak solution to the boundary value problem (15)-(16). Since the injections (6) are compact

and the cone is closed with respect to the strong convergence in, it follows that

strongly in and, hence,

This fact together with leads us to the conclusion:, i.e. the limit pair is feasible to optimal control problem (19). The proof is complete.

In conclusion of this section, we give the existence result for optimal pairs to problem (19).

Theorem 4. Assume that, for given distributions, , and, the Hypothesis (H₁) is valid. Then optimal control problem (19) admits at least one solution .

Proof. Since the set is nonempty and the cost functional is bounded from below on, it follows that there exists a minimizing sequence to problem (19). Then the inequality

implies the existence of a constant such that

Hence, in view of the definition of the class of admissible controls and a priori estimate (24), the se-

quence is bounded in. Therefore, by Theorem 3, there exist functions

and such that and, up to a subsequence, weakly-* in BV(W) and weakly in. To conclude the proof, it is enough to show that the cost functional I is lower semicontinuous with respect to the t-convergence. Since strongly in by Sobolev embedding theorem, it follows that

Thus,

Hence, is an optimal pair, and we arrive at the required conclusion.

5. Henig Relaxation of State-Constrainted OCP (19)

The main goal of this section is to provide a regularization of the pointwise state constraints by replacing the ordering cone (see (32)) by its solid Henig approximation (see [21] - [24] ) and show that the conical regularization approach leads to a family of optimization problems such that their solutions can be obtained by solving the corresponding optimality system and the regularized solution t-converge in the limit as to a solution of the original problem.

We begin with some formal descriptions and abstract results. Let Z be a real normed space, and let be a closed ordering cone in Z.

Definition 5.1. A nonempty convex subset B of a nontrivial ordering cone (i.e., where is the zero element in Z) is called base of if for each element there is a unique repre- sentation where and.

In what follows, we always assume that the ordering cone has a closed base. We note that, in general, bases are not unique. We denote the norm of Z by and for arbitrary elements we define

In order to introduce a representation for a base of, let be the topological dual space of Z, and let be the dual pairing. Moreover, by

and

we define the dual cone and the quasi-interior of the dual cone of, respectively. Using the definition of the dual cone, the ordering cone can be characterized as follows (see [25] , Lemma 3.21):

Due to Lemma 1.28 in [25] , we can give the following result.

Lemma 2. Let be a nontrivial ordering cone in a Banach space Z. Then the set

is a base of for every. Moreover, if is reproducing in Z, i.e. if

, and if B is a base of, then there is an element satisfying.

Remark 5.3. As follows from Lemma 2, the set

(36)

is a closed base of ordering cone.

Now, we are prepared to introduce the definition of a so-called Henig dilating cone (see Zhuang, [24] ) which is based on the existence of a closed base of ordering cone.

Definition 5.2. Let Z be a normed space, and let be a closed ordering cone with a closed base B. Choosing arbitrarily, the corresponding Henig dilating cone is defined by

where is the closed unit ball in Z centered at the origin.

It is clear that depends on the particular choice of B. As follows from this definition, for every, i.e. Henig dilating cone is proper solid. Moreover, we have the following properties of such cones (see [24] [26] ).

Proposition 5. Let Z be a normed space, and let be a closed ordering cone with a closed base B. Choosing, where

(37)

the following statements hold true.

1) is pointed, i.e.;

2);

3);

4);

5) the implication

(38)

holds true with.

In the context of constraint qualifications problem, the following result plays an important role.

Proposition 6. Let Z be a normed space, and let be a closed ordering cone with a closed base B. Choosing arbitrarily, where is defined by (37), the inclusion

(39)

holds true.

Proof. Let be chosen arbitrarily. By the definition of a base there is a unique representation with and. Obviously,

holds true. Let’s assume for a moment that

(40)

Then we obtain

which completes the proof. In order to show (40), let be chosen arbitrarily, i.e.

Then

yields

As a result, (40) is satisfied.

Remark 5.2. The following property, coming from Proposition 6, turns out rather useful: in order to prove, it is sufficient to check whether.

The following result shows that Henig dilating cones possess good approximation properties.

Proposition 7. Let be a closed ordering cone in a normed space Z, and let B be an arbitrary closed base of. Let parameter be defined as in (37), and let be a monotonically decreasing sequ-

ence such that. Then the sequence of cones converges to in Kuratowski sense

with respect to the norm topology of Z as k tends to infinity, that is

where

Proof. Let be chosen arbitrarily. Then holds true for every neighborhood N of z, and due to the inclusions , we see that for all. Hence,

(41)

Taking into account the inclusion (41) and the fact that

we get

(42)

To show that the sequence converges to in Kuratowski sense, it remains to show

(43)

However, the inclusion (43) is equivalent to

(44)

Let be an arbitrarily element. Since is closed, there is an open neighborhood of with respect to the norm topology of Z such that. By Proposition 5 (see item (4)), there is a sufficiently large index such that

This implies

Combining (42), (43), and (44), we arrive at the relation

Thus, and the proof is complete.

Taking these results into account, we associate with OCP (19) the following family of Henig relaxed pro- blems

(45)

subject to the constraints

(46)

or in a more compact form each of these problems can be stated as follows

(47)

where

(48)

the base B takes the form (36), and the feasible set we define as follows: if and only if, , , the pair is related by the Minty inequality (21), and

(49)

Here, stands for the corresponding Henig dilating cone.

Since, by Proposition 6, the inclusion holds true for all e > 0, it is reasonable to call the OCP (47) a Henig relaxation of OCP (19). Moreover, as obviously follows from Proposition 7, the convergence in Kuratowski sense holds true with respect to the t-topology on.

We are now in a position to show that using the relaxation approach we can reduce the main suppositions of Theorem 4. In particular, we can characterize Hypothesis () by the non-emptiness properties of feasible sets for the corresponding Henig relaxed problems.

Theorem 8. Let be a monotonically decreasing sequence converging to 0 as. Then,

for given distributions, , and, the Hypothesis (H₁) implies that

the Henig relaxed problem (47) has a nonempty set of feasible solutions for all,. And vice versa, if there exists a sequence satisfying conditions

(50)

then the sequence s is t-compact and each of its t-cluster pairs is a feasible solution to the original OCP (19).

Proof. Since the implication is obvious by Proposition 7, we concentrate on the proof of the inverse statement―property (50) implies the existence of at least one pair such that.

Let be an arbitrary sequence with property: for all. Since the set and a priory estimate (24) do not depend on parameter and the condition (50)₂ implies,

it follows by compactness arguments (see the proof of Theorem 4) that there exist a subsequence of

(still denoted by the same index) and a pair such that

Closely following the proof of Theorem 3, it can be shown that the limit pair is such that, , and function is a weak solution to the boundary value problem (15) - (16). Moreover, in view of the compactness properties of injections (6), we may suppose that

(51)

It remains to establish the inclusions

(52)

By contraposition, let us assume that. Since the cone is closed, it follows that there is a neighborhood of in such that. Using the fact that

by Proposition 7 and definition of the Kuratowski limit, it is easy to conclude the existence of an index such that

(53)

However, in view of the strong convergence property (51), there is an index satisfying

(54)

Combining (53) and (54), we finally obtain

This, however, is a contradiction to

Thus,. In the same manner it can be shown that. Hence, the pair is feasible for OCP (19).

As an obvious consequence of this Theorem and Theorem 4, we have the following noteworthy property of the Henig relaxed problems (47).

Corollary 2. Let, , and be given distribution. Then the Henig relaxed problem (47) is solvable for each provided Hypothesis () is satisfied.

The next result is crucial in this section. We show that some optimal solutions for the original OCP (19) can be attained by solving the corresponding Henig relaxed problems (45)-(46). However, we do not claim that the entire set of the solutions to OCP (19) can be restored in such way.

Theorem 9. Let, , and be given distributions. Let be a monotonically decreasing sequence such that as, where is de- fined by (48). Let be a sequence of optimal solutions to the Henig relaxed problems (45)- (46) such that

(55)

Then there is a subsequence of and a pair such that

(56)

(57)

Proof. In view of a priory estimate (24), the uniform boundedness of optimal controls with respect to BV-norm (55) implies the fulfilment of condition (50)₂. Hence, the compactness property (56) and the inclusion are a direct consequence of Theorem 8. It remains to show that the limit pair is a solution to OCP (19). Indeed, the condition implies the fulfilment of Hypothesis (). Hence, by Theorem 4, the original OCP (19) has a nonempty set of solutions. Let be one of them. Then the following inequality is obvious

(58)

On the other hand, by Proposition 5 (see property (4)), we have for every. Since are the solutions to the corresponding relaxed problems (47), it follows that

(59)

As a result, taking into account the relations (58) and (59), and the lower semicontinuity property of the cost functional I with respect to the t-convergence, we finally get

Thus,

and we arrive at the desired property (57)₂. The proof is complete.

Remark 5.3. It is worth to note that condition (55) can be omitted if the original OCP (19) is regular, that is when Hypothesis () is valid. Indeed, let us assume that and is an arbitrary pair. Then is feasible to each Henig relaxed problems (45)-(46), and, hence,

(60)

Since, by Proposition 6, the inclusion holds true for all, and the sequence is monotone in the following sense (because of the property (2) of Proposition 5)

it follows that

As a result, (60) leads to the estimate

As was mentioned at the beginning of this section, the main benefit of the relaxed optimal control problems (45)-(46) comes from the fact that the Henig dilating cone has a nonempty topological interior. Hence, it gives a possibility to apply the Slater condition or the Robinson condition in order to characterize the optimal solutions for the state constrained OCP (19). On the other hand, this approach provides nice convergence properties for the solutions of relaxed problems (45)-(46). However, as follows from Theorems 8 and 9 (see also Remark 5.5), the most restrictive assumption deals with the regularity of the relaxed problems (45)-(46) for all. So, if we reject the Hypothesis (), it becomes unclear, in general, whether the relaxed sets of feasible solutions are nonempty for all. In this case it makes sense to provide further relaxation for each of Henig problems (45)-(46). In particular, using the methods of variational inequalities, we show in the next section that original OCP (19) may admit the existence of the so-called weakened approximate solution which can be interpreted as an optimal solution to some optimization problem of a special form.

6. Variational Inequality Approach to Regularization of OCP (19)

As follows from Theorem 4, the existence of optimal solutions to the problem (19) can be obtained by using compactness arguments and the Hypothesis (). However, because of the state constraints (17) the fulfilment of Hypothesis () is an open question even for the simplest situation. Nevertheless, in many applications it is an important task to find a feasible (or at least an approximately admissible, in a sense to be made precise) solution when both control and state constraints for the OCP are given. Thus, if the set of feasible solutions is rather “thin”, it is reasonable to weaken the requirements on feasible solutions to the original OCP. In particular, it would be reasonable to assume that we may satisfy the state equation

and the corresponding state constraint

with some accuracy. Here, the operator is defined by the left-hand side of relation (29). For this purpose, we make use of the following observation: If a pair is feasible to the original problem, i.e., then this pair satisfies the relation

(61)

for each, where is defined as follows

(62)

Here, is the corresponding Henig dilating cone.

Note that the reverse statement is not true in general. In fact, we discuss a variant of the penalization approach, called the “variational inequality (VI) method”. This idea was first studied in [27] . Thus, if a pair is related by variational inequality (61), then it is not necessary to suppose that satisfy the operator

equation. In view of this, we can use the penalized term as a deviation

measure in an associated cost functional. As a result, we arrive at the following penalized OCP:

(63)

subject to the constraints

(64)

or in a more compact form this problem can be stated as follows

(65)

where is given by (48), the set is defined in (62), and the set of feasible solutions we describe as follows:

In this section we show that penalized OCP (65) is solvable for each without any assumption about ful- filment of Hypothesis (H₁). We also study the asymptotic properties of sequences of optimal pairs to problem (65) when the small parameter varies in a strictly decreasing sequence of positive numbers converging to zero. We begin with the following result.

Lemma 3. Under assumptions (11)-(14), for every fixed and, the variational inequality (61) admits at least one solution such that.

Proof. Let be a fixed value. As follows from definition of the set (see (62) and Remark 5.1), is a nonempty convex closed subset of with respect to the -norm topology. Due to the assumptions (11)-(14), we have the following estimates

(66)

where is the norm of the embedding operator. Hence, for every fixed, the operator is bounded and coercive. Moreover, it is shown in [16, Proposition 2.42], the properties (11)-(14) ensure the following implication

Thus, the operator is pseudo-monotone for each. Hence, following the well-know existence result (see, for instance, [28] [29] ), there exists at least one solution of variational inequality (61) such that.

As an obvious consequence of Lemma 3, we have the following noteworthy property of penalized OCP (63) - (64).

Corollary 3 For each the feasible set is nonempty.

To proceed further, we introduce the following notion.

Definition 6.1. An operator is said to be quasi-monotone if for any sequence

such that and in, the condition

(67)

implies the relation

(68)

for all.

Definition 6.2. We say that an operator possesses the property, if for

any sequence such that and in, the conditions

imply the relation.

Our next intention is to prove the following crucial result.

Theorem 10. The operator, given by formula (29), is quasi-monotone pro- vided assumptions (11)-(14) hold true.

Proof. Let be a sequence such that and in

. We assume that inequality (67) holds true. Our aim is to establish the relation (68). With that in mind, we set

(69)

and divide our proof onto several steps.

Step 1. We show that, for each,

(70)

Indeed, since in, it follows by the Sobolev embedding theorem that in for all. Hence, making use of the subcritical growth condition (12), we get

(71)

As for the first term in (70), we note that in for every, because for all by the initial assumptions. Hence,

(72)

by the Lebesgue Dominated Theorem. Since the sequence is bounded in and

it follows from (72) that strongly in. Therefore, the first term in (70) tends to zero as as the product of strongly and weakly convergent sequences. Combining this fact with (71), we arrive at the desired property (70).

Step 2. Let us show that

(73)

By analogy with the previous step, we note that in for every. In particular, this yields strongly in . In view of this, we infer

This means that

But we also have that the sequence is bounded in. Hence, in

for each. Since for any, it follows that

(74)

by definition of the weak convergence in. Thus, in order to conclude the equality (73), it remains to show that

(75)

In view of the subcritical growth condition (12), we have the following estimate

where is the norm of the embedding operator. Hence, we may suppose that the se- quence is compact with respect to the weak convergence in and, therefore, there exists an element such that, up to a subsequence,

(76)

Thus, to conclude this step, we have to show that. By monotonicity property (13), it follows that for every and every positive function, we have

So, taking into account (76) and the fact that strongly in by Sobolev embedding theorem, we can pass to the limit in this inequality as. As a result, we get

for all positive. After localization, we have

Since the function is strictly monotone, it follows that. Thus, the relation (75) is a direct consequence of the convergence (76).

Step 3. This is the final step of our proof. As follows from (69), for every element and each index, we have the estimate

(77)

Let be a fixed element. We put for all. Taking into account the monotonicity condition (77), we see that

(78)

Since, it follows from (78) that

(79)

Passing to the limit in (79) as, we obtain

(80)

where

and

Hence, for each, we have the inequality

(81)

Since the convergence is strong in, it follows that strongly in, and therefore,

(82)

As a result, we deduce from (81) and (82) that

that is, the inequality (68) is valid.

Remark 6.1. In fact (see [19] , Remark 3.13), we have the following implication:

Hence, in view of Theorem 10, we can claim that the operator, which is defined by relation (29), possesses the property.

We are now in a position to show that the penalized optimal control problem in the coefficient of variational inequality (63)-(64) is solvable for each value.

Lemma 4 If the assumptions (11)-(14) are valid, then the OCP (63)-(64) admits at least one solution for every fixed and any, , and.

Proof. Let be a minimizing sequence to problem (63)-(64). The coerciveness pro- perty (66) and estimate

(83)

immediately imply that the sequence is bounded in. Indeed, using the notations and, we have

On the other hand, from (83) it follows that

So, comparing these two chains of relations, we arrive at the existence of a constant such that C is independent of and as far as is a solution to (63).

Since

and the set is sequentially closed with respect to the t-convergence, we may assume by Theroem 1 that there exists a pair such that. Then passing to the limit in

as, we obtain

(84)

Having put here, we arrive at the inequality

Hence,

by the quasi-monotonicity property of the operator A. Combining this inequality with (84), we come to the re- lation

Thus, is a feasible pair to the problem (63)-(64).

Let us show that is an optimal pair to this problem. As follows from (83), the sequence is bounded in. Let d be its weak limit in as. Then

Substituting for in the last inequality, we get

Since the quasi-monotone operator possesses the -property (see Remark 6.6), it follows that. As a result, using the t-lower semicontinuity property of the cost functional (63), we finally obtain

Thus, is an optimal pair to the penalized problem (63)-(64).

The next step of our analysis is to consider a sequence of optimal pairs in the limit as tends to 0.

Theorem 11. Let be a sequence of optimal pairs to penalized problems (63) - (64). In addition to the assumptions of Lemma 4, assume that there exists a constant such that

(85)

Then the sequence is relatively compact with respect to the t-convergence and each of its t-cluster pair is such that (up to a subsequence)

(86)

(87)

i.e. is an optimal pair to the original OCP (19).

Proof. Let be a given sequence of optimal pairs to penalized problems (63)-(64). Since each of the set contains zero, we have

Hence, the following estimate for the optimal states takes place

(88)

Let us show that the sequence of corresponding optimal controls is BV-bounded. Indeed, due to the estimate (85), the numerical sequence is uniformly bounded with respect to. Hence, in view of the structure of the cost functional (63), we deduce

(89)

From this, we immediately conclude that, and, hence, due to Theorem 1, Proposition 7,

and estimate (88), we may assume that there exists a pair such that as in (here, we have used the fact that the sets converge in Kuratowski sense to K, see the proof of Theorem 8).

Let us show that the pair is feasible to the original problem (19). Using the arguments of the proof of Lemma 4, we have in and. Then, as follows from (89), we have

Thus, as elements of and, hence,.

It remains to prove that is an optimal pair. If, on the contrary, we assume that the exists a pair such that, then

Therefore, passing to the limit in this inequality as and using the w-lower semicontinuity property of the cost functional, we finally get

This contradiction immediately leads us to the conclusion: The is an optimal pair to the OCP (19).

Remark 6.2. As follows from the proof of Theorem 11, whatever the sequence of optimal solutions to the penalized problems (63)-(64) has been chosen, if this sequence satisfies condition (85), then it always gives in the limit as some optimal pair to the original OCP (19). However, it is unknown whether the entire set of the solutions to OCP (19) can be attained in such way.

Remark 6.3. It is easy to see that in the case if the feasible set to the original OCP is nonempty, it suffices to guarantee the fulfilment of assumption (85). Indeed, let be any feasible pair to the original OCP (19). Then for each. Since is an optimal pair to problem (63)-(64), this yields

and we arrive at the inequality (85).

Acknowledgements

Research is funded by DFG-Excellence Cluster Engineering for Advanced Materials.

Cite this paper

Peter Kogut,Günter Leugering,Ralph Schiel, (2016) On Henig Regularization of Material Design Problems for Quasi-Linear p-Biharmonic Equation. Applied Mathematics,07,1547-1570. doi: 10.4236/am.2016.714134

References