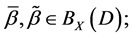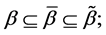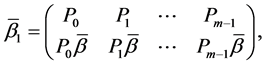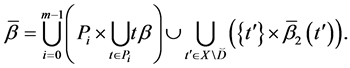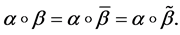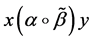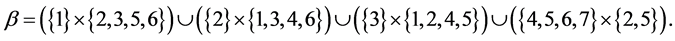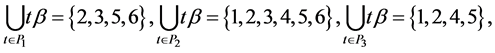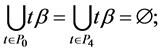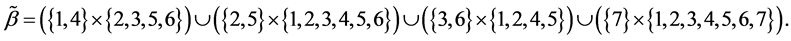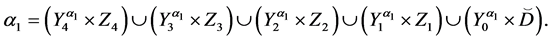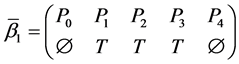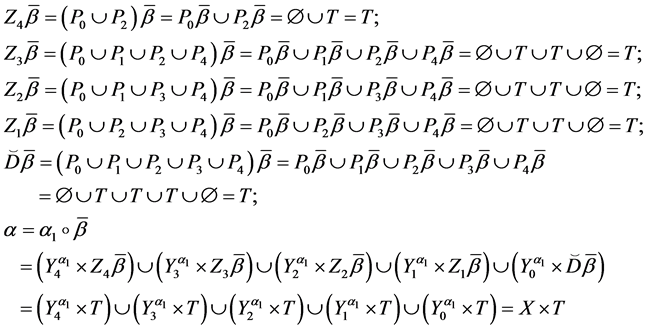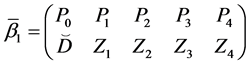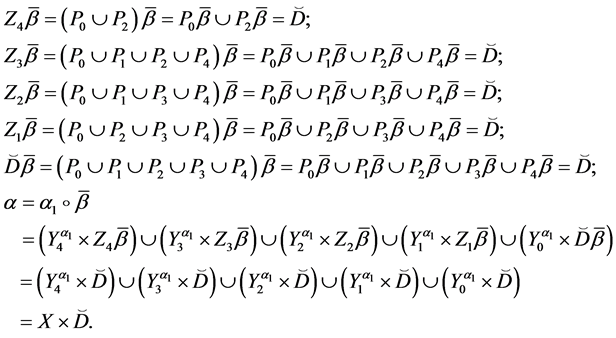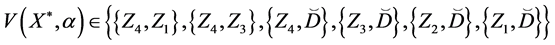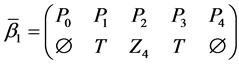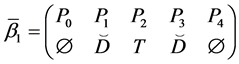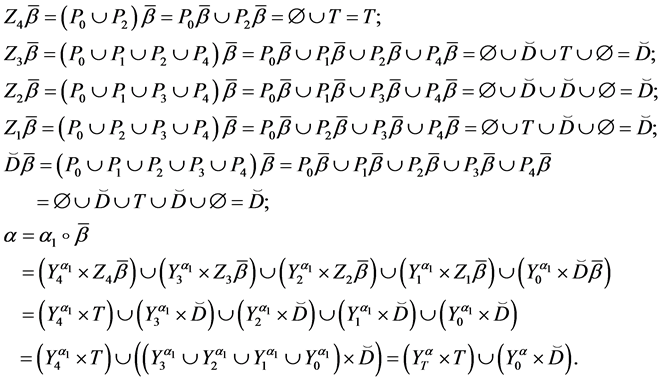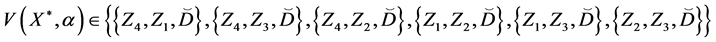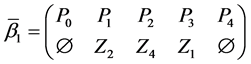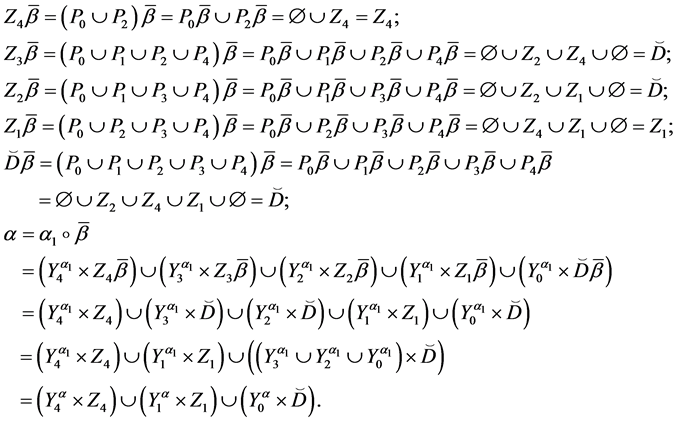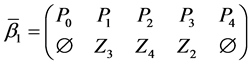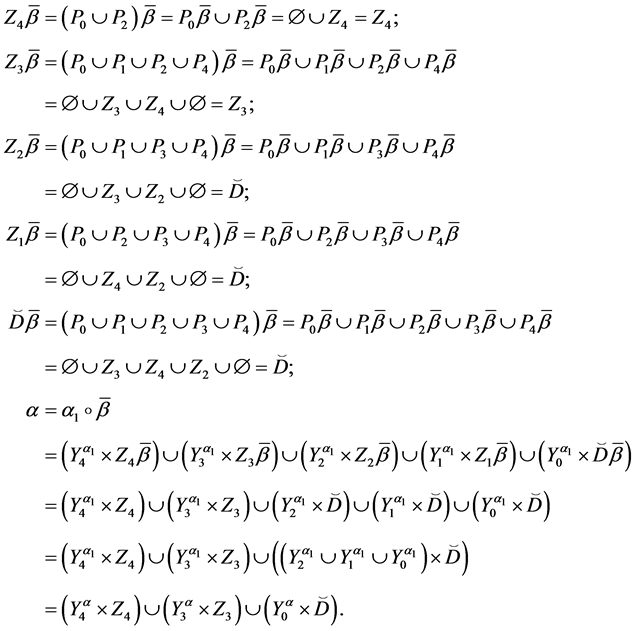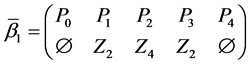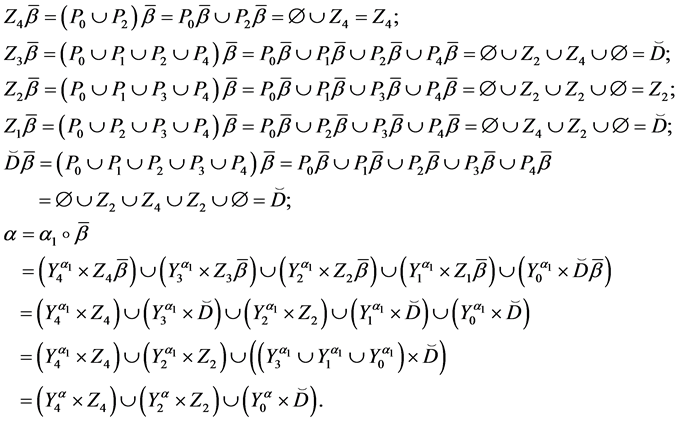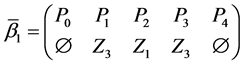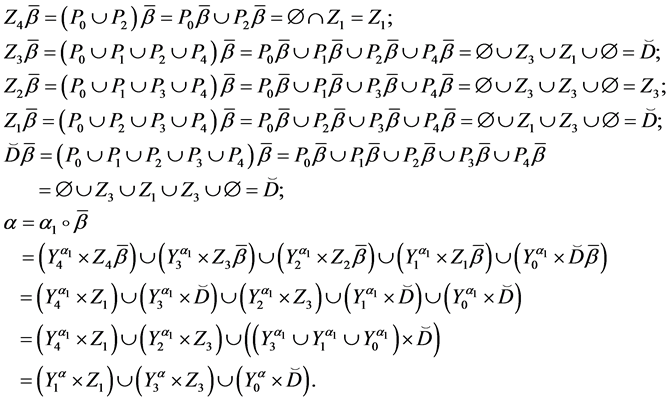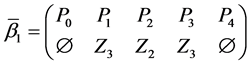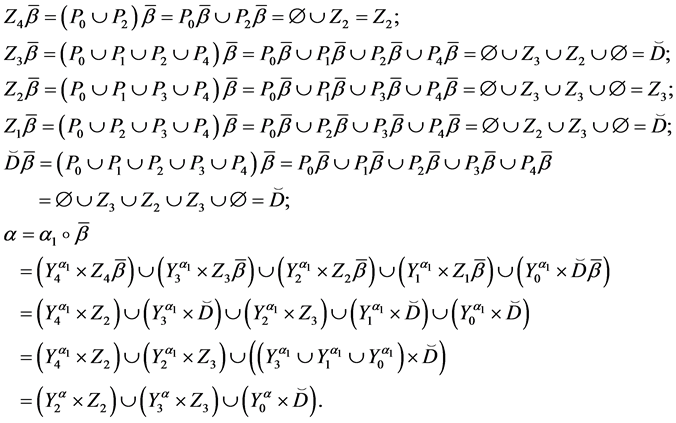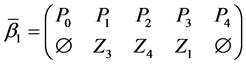Applied Mathematics
Vol.07 No.01(2016), Article ID:63138,10 pages
10.4236/am.2016.71009
Generating Set of the Complete Semigroups of Binary Relations
Yasha Diasamidze1, Neset Aydin2, Ali Erdoğan3
1Shota Rustavelli University, Batumi, Georgia
2Çanakkale Onsekiz Mart University, Çanakkale, Turkey
3Hacettepe University, Ankara, Turkey

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 December 2015; accepted 25 January 2016; published 28 January 2016
ABSTRACT
Difficulties encountered in studying generators of semigroup  of binary relations defined by a complete X-semilattice of unions D arise because of the fact that they are not regular as a rule, which makes their investigation problematic. In this work, for special D, it has been seen that the semigroup
of binary relations defined by a complete X-semilattice of unions D arise because of the fact that they are not regular as a rule, which makes their investigation problematic. In this work, for special D, it has been seen that the semigroup , which are defined by semilattice D, can be generated by the set
, which are defined by semilattice D, can be generated by the set  .
.
Keywords:
Semigroups, Binary Relation, Generated Set, Generators

1. Introduction
Theorem 1. Let 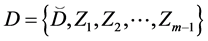 be some finite X-semilattice of unions and
be some finite X-semilattice of unions and
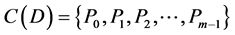
be the family of sets of pairwise nonintersecting subsets of the set X.
If φ is a mapping of the semilattice D on the family of sets  which satisfies the condition
which satisfies the condition 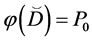 and
and 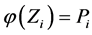 for any
for any  and
and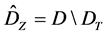 , then the following equalities are valid:
, then the following equalities are valid:
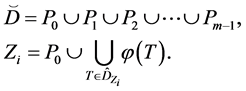 (1)
(1)
In the sequel these equalities will be called formal.
It is proved that if the elements of the semilattice D are represented in the form 1, then among the parameters Pi 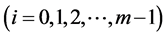 there exist such parameters that cannot be empty sets for D. Such sets Pi
there exist such parameters that cannot be empty sets for D. Such sets Pi 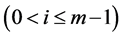 are called basis sources, whereas sets Pi
are called basis sources, whereas sets Pi 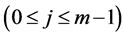 which can be empty sets too are called completeness sources.
which can be empty sets too are called completeness sources.
It is proved that under the mapping 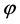 the number of covering elements of the pre-image of a basis source is always equal to one, while under the mapping
the number of covering elements of the pre-image of a basis source is always equal to one, while under the mapping 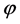
Let 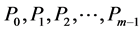
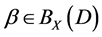
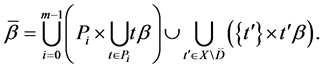

The representation of the binary relation 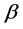

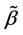
If 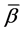
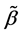
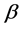
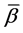
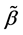
a)
b)
c) the subquasinormal representation of the binary relation 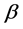
d) if
then 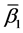
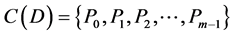
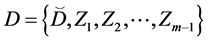
e) if 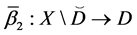
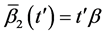
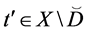
2. Results
Proposition 2. Let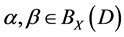
Proof. It is easy to see the inclusion 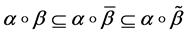
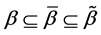


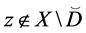
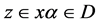
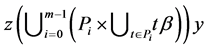
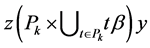
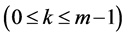
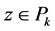
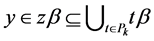
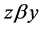

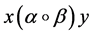

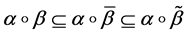

Corollary 1. If 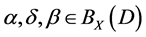
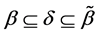

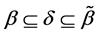
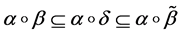
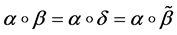
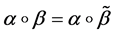
Let the X-semilattice 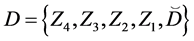
Figure 1. Diagram of D.
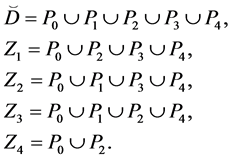
The parameters P1, P2, P3 are basis sources and the parameters 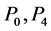

Example 3. Let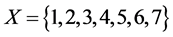
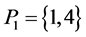
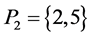

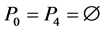
mal equalities of the semilattice D follows that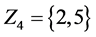

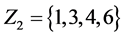
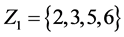
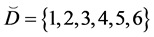
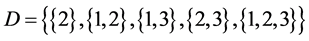
Then we have:
Theorem 4. Let the X-semilattice 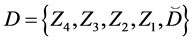
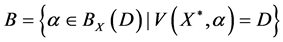
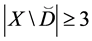
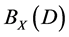
Proof. It is easy to see that 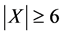
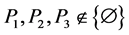
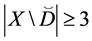
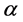
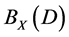
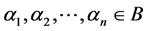
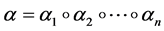

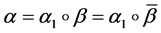
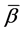
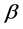
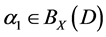
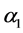
Of this follows that

For the binary relation 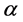
a) Let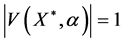
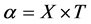
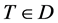
1.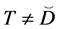
and 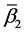

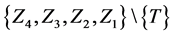
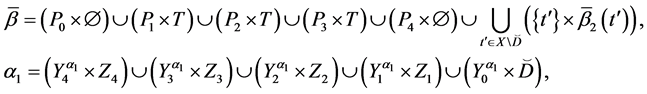
where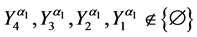
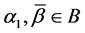
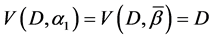
since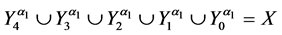
2.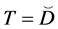
and 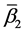
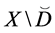
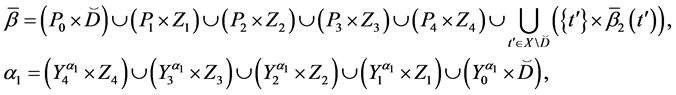
where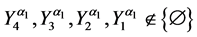
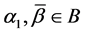
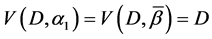
b)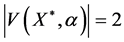
since 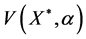
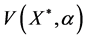
1. Let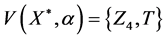
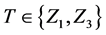
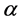
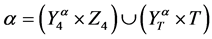
and 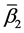
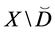
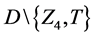
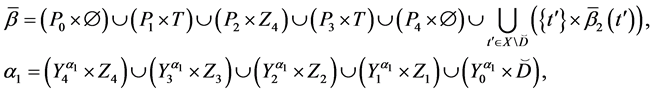
where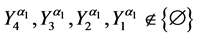
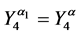
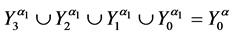

2. Let
form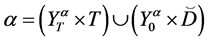
and 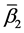

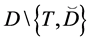
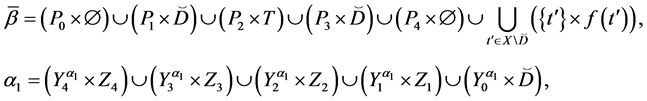
where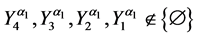
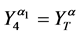
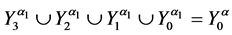

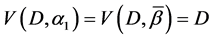
c)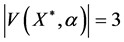
since 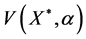
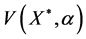
1. Let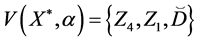
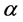
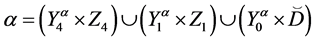
and 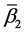
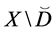
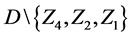
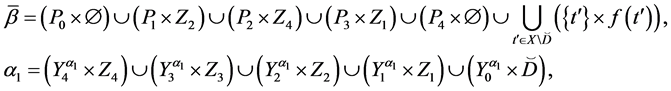
where

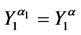
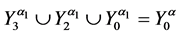
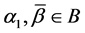
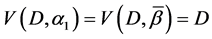
2. Let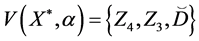
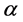
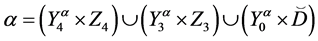
and 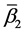


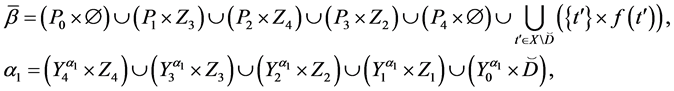
where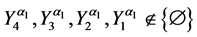
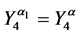
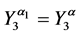
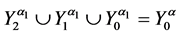
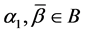
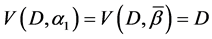
3. Let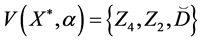
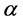
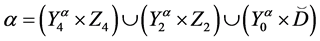
and 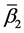

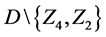
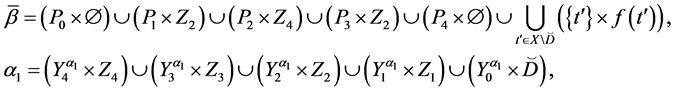
where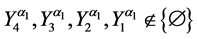
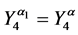
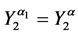


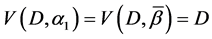
4. Let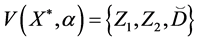
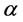

and 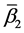

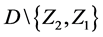
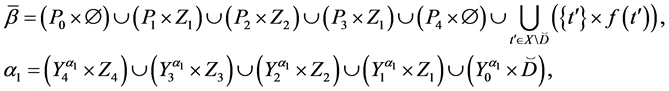
where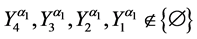
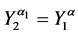
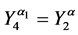
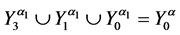
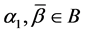
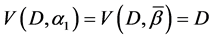
5. Let
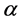
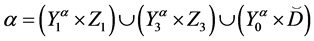
and 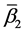
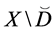
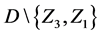
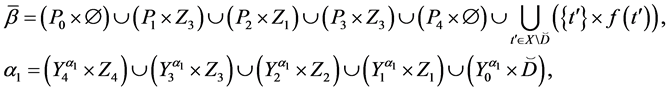
where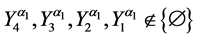
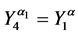
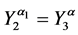
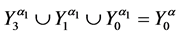
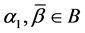
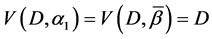
6. Let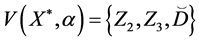
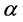

and 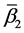
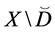
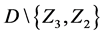
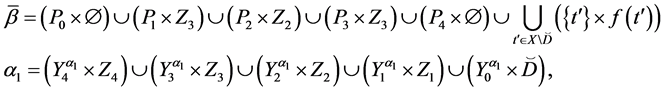
where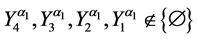
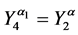


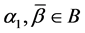
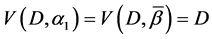
7. Let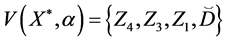

and 

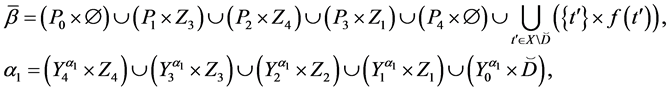
where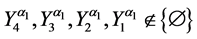

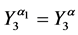
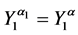
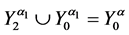

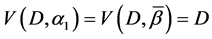
,
Cite this paper
YashaDiasamidze,NesetAydin,AliErdoğan, (2016) Generating Set of the Complete Semigroups of Binary Relations. Applied Mathematics,07,98-107. doi: 10.4236/am.2016.71009
References
- 1. Diasamidze, Ya. and Makharadze, Sh. (2013) Complete Semigroups of Binary Relations. Cityplace Kriter, Country-Region Turkey, 520 p.
- 2. Davedze, M.Kh. (1968) Generating Sets of Some Subsemigroups of the Semigroup of All Binary Relations in a Finite Set. Proc. A. I. Hertzen Leningrad State Polytechn. Inst., 387, 92-100. (In Russian)
- 3. Davedze, M.Kh. (1971) A Semigroup Generated by the Set of All Binary Relations in a Finite Set. XIth All-Union Algebraic Colloquium, Abstracts of Reports, Kishinev, 193-194. (In Russian)
- 4. Davedze, M.Kh. (1968) Generating Sets of the Subsemigroup of All Binary Relations in a Finite Set. Doklady AN BSSR, 12, 765-768. (In Russian)
- 5. Givradze, O. (2010) Irreducible Generating Sets of Complete Semigroups of Unions Defined by Semilattices of Class . Proceedings of the International Conference “Modern Algebra and Its Aplications”, Batumi.
- 6. Givradze, O. (2011) Irreducible Generating Sets of Complete Semigroups of Unions Defined by Semilattices of Class in Case, When and . Proceedings of the International Conference “Modern Algebra and Its Aplications”, Batumi.