Applied Mathematics
Vol.06 No.12(2015), Article ID:61467,12 pages
10.4236/am.2015.612181
Existence and Stability Analysis of Fractional Order BAM Neural Networks with a Time Delay
Yuping Cao1, Chuanzhi Bai2
1Department of Basic Courses, Lianyungang Technical College, Lianyungang, China
2Department of Mathematics, Huaiyin Normal University, Huaian, China

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 25 September 2015; accepted 22 November 2015; published 25 November 2015

ABSTRACT
Based on the theory of fractional calculus, the contraction mapping principle, Krasnoselskii fixed point theorem and the inequality technique, a class of Caputo fractional-order BAM neural networks with delays in the leakage terms is investigated in this paper. Some new sufficient conditions are established to guarantee the existence and uniqueness of the nontrivial solution. Moreover, uniform stability of such networks is proposed in fixed time intervals. Finally, an illustrative example is also given to demonstrate the effectiveness of the obtained results.
Keywords:
BAM Neural Networks, Caputo Fractional-Order, Existence, Fixed Point Theorems, Uniform Stability

1. Introduction
Fractional order calculus was firstly introduced 300 years ago, but it did not attract much attention for a long time since it lack of application background and the complexity. In recent decades, the study of fractional-order calculus has re-attracted tremendous attention of much researchers because it can be applied to physics, applied mathematics and engineering [1] -[6] . We know that the fractional-order derivative is nonlocal and has weakly singular kernels. It provides an excellent instrument for the description of memory and hereditary properties of dynamical processes where such effects are neglected or difficult to describe to the integer order models.
We know that the next state of a system not only depends upon its current state but also upon its history information. Since a model described by fractional-order equations possesses memory, it is precise to describe the states of neurons. Moreover, the superiority of the Caputo’s fractional derivative is that the initial conditions for fractional differential equations with Caputo derivatives take on the similar form as those for integer-order differentiation. Therefore, it is necessary and interesting to study fractional-order neural networks both in theory and in applications.
Recently, some important and interesting results on fractional-order neural networks have been obtained and various issues have been investigated [7] -[14] by many authors. In [11] , the authors proposed a fractional-order Hopfield neural network and investigated its stability by using energy function. In [12] , the authors investigated stability, multistability, bifurcations, and chaos for fractional-order Hopfield neural networks. In [13] , Chen et al. obtained a sufficient condition for uniform stability of a class of fractional-order delayed neural networks. In [14] , we investigated the finite-time stability for Caputo fractional-order BAM neural networks with distributed delay and established a delay-dependent stability criterion by using the theory of fractional calculus and generalized Gronwall-Bellman inequality approach. In [15] , Song and Cao considered the existence, uniqueness of the nontrivial solution and also uniform stability for a class of neural networks with a fractional-order derivative, by using the contraction mapping principle, Krasnoselskii fixed point theorem and the inequality technique.
The integer-order bidirectional associative memory (BAM) neural networks models, first proposed and studied by Kosko [16] . This neural network has been widely studied due to its promising potential for applications in pattern recognition and automatic control. In recent years, integer-order BAM neural networks have been extensively studied [17] -[21] . Recently, some authors considered the uniform stability of delayed neural networks; for example, see [22] -[24] and references therein. However, to the best of our knowledge, there are few results on the uniform stability analysis of fractional-order BAM neural networks.
Motivated by the above-mentioned works, this paper considers the uniform stability of a class of fractional-order BAM neural networks with delays in the leakage terms described by
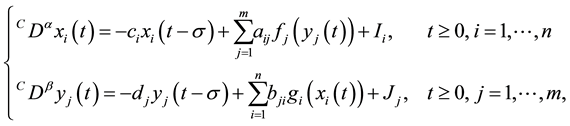 (1)
(1)
where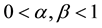 ,
,
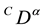 and
and
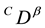 denote the Caputo fractional derivative of order
denote the Caputo fractional derivative of order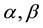 , respectively;
, respectively;

 and
and
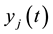
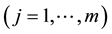 are the activations of the ith neuron in the neural field
are the activations of the ith neuron in the neural field
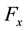 and the jth neuron in in the neural field
and the jth neuron in in the neural field
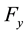 at time t, respectively;
at time t, respectively;
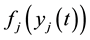 denotes the activation function of the jth neuron from the neural field
denotes the activation function of the jth neuron from the neural field
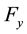 at time t and
at time t and
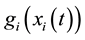 denotes the activation function of the ith neuron from the neural field
denotes the activation function of the ith neuron from the neural field
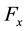 at time t;
at time t;











This paper is organized as follows. In Section 2, some definitions of fractional-order calculus and some necessary lemmas are given. In Section 3, some new sufficient conditions to ensure the existence, uniqueness of the nontrivial solution and also uniform stability of the fractional-order BAM neural networks 1 is obtained. Finally, an example is presented to manifest the effectiveness of our theoretical results in Section 4.
2. Preliminaries
For the convenience of the reader, we first briefly recall some definitions of fractional calculus, for more details, see [1] [2] [5] , for example.
Definition 1. The Riemann-Liouville fractional integral of order


provided the right side is pointwise defined on

Definition 2. The Caputo fractional derivative of order


Let





The initial conditions associated with system (1) are of the form

where
To prove our results, the following lemmas are needed.
Lemma 1. ([25] ). Let
has solutions
where

Lemma 2. ([26] ). Let D be a closed convex and nonempty subset of a Banach space X. Let

1)


2)

3)

Then, there exists


In order to obtain main result, we make the following assumptions.
(H1) The neurons activation functions





(H2) For





3. Main Results
For convenience, let



Theorem 3. Under assumption (H1), the system (1) has a unique solution on


Proof. Define

where
By Lemma 1, we know that the fixed point of (F, G) is a solution of system (1) with initial conditions (2). In the following, we will using the contraction mapping principle to prove that the operator (F, G) has a unique fixed point.
Firstly, we prove


where

and

By Minkowski inequality, we have

By direct computation, we obtain by (3) that

Similar to (11) and the proof of Theorem 1 in [15] , we have by (H1), (4) and (5) that


and

Substitute (11)-(14) into (10), we get

Similarly, we obtain

Thus, from (15), (16) and (7), we have
Secondly, we prove that


By (6), we conclude that

Theorem 4. Assume that (H2) holds. If there exist real numbers


then the system (1) has at least one solution on
Proof. Let

Define two operators



where
Firstly, we will prove
Thus, we conclude that
Secondly, for any
which implies that

Thirdly, we prove that






which implies that





as


Theorem 5. Assume that (H1) and condition (6) hold. Then the solution of system (1) is uniformly stable on
Proof. Assume that


ditions


that is,
which implies
Hence, we have

For any

which implies that the solution of system (1) is uniformly stable on
4. An Illustrative Example
In this section, we give an example to illustrate the effectiveness of our main results.
Consider the following two-state Caputo fractional BAM type neural networks model with leakage delay

with the initial condition
where








Thus,
that is, condition (6) holds. By utilizing Theorems 3.1 and 3.3, we can obtain that the system (20) has a unique solution which is uniformly stable on
In the following, we show the simulation result for model (20). We consider four cases:
Case 1 with the initial values


Case 2 with the initial values


Case 3 with the initial values


Case 4 with the initial values


The time responses of state variables are shown in Figure 1.


Figure 1. Transient states of the fractional-order BAM neural networks (20) with


Acknowledgements
This work is supported by Natural Science Foundation of Jiangsu Province (BK2011407) and Natural Science Foundation of China (11571136 and 11271364).
Cite this paper
YupingCao,ChuanzhiBai, (2015) Existence and Stability Analysis of Fractional Order BAM Neural Networks with a Time Delay. Applied Mathematics,06,2057-2068. doi: 10.4236/am.2015.612181
References
- 1. Miller, K.S. and Ross, B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley & Sons, New York.
- 2. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- 3. Soczkiewicz, E. (2002) Application of Fractional Calculus in the Theory of Viscoelasticity. Molecular and Quantum Acoustics, 23, 397-404.
- 4. Kulish, V. and Lage, J. (2002) Application of Fractional Calculus to Fluid Mechanics. Journal of Fluids Engineering, 124, 803-806.
http://dx.doi.org/10.1115/1.1478062 - 5. Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, Vol. 24, Elsevier Science B.V., Amsterdam.
- 6. Sabatier, J., Agrawal, Om.P. and Machado, J. (2007) Theoretical Developments and Applications. Advance in Fractional Calculus. Springer, Berlin.
- 7. Arena, P., Caponetto, R., Fortuna, L. and Porto, D. (1998) Bifurcation and Chaos in Noninteger Order Cellular Neural Networks. International Journal of Bifurcation and Chaos, 8, 1527-1539.
http://dx.doi.org/10.1142/S0218127498001170 - 8. Arena, P., Fortuna, L. and Porto, D. (2000) Chaotic Behavior in Noninteger Order Cellular Neural Networks. Physical Review E, 61, 776-781.
http://dx.doi.org/10.1103/PhysRevE.61.776 - 9. Yu, J., Hu, C. and Jiang, H. (2012) α-Stability and α-Synchronization for Fractional-Order Neural Networks. Neural Networks, 35, 82-87.
http://dx.doi.org/10.1016/j.neunet.2012.07.009 - 10. Wu, R., Hei, X. and Chen, L. (2013) Finite-Time Stability of Fractional-Order Neural Networks with Delay. Communications in Theoretical Physics, 60, 189-193.
http://dx.doi.org/10.1088/0253-6102/60/2/08 - 11. Boroomand, A. and Menhaj, M.B. (2009) Fractional-Order Hopfield Neural Networks. In: Köppen, M., Kasabov, N. and Coghill, G., Eds., Advances in Neuro-Information Processing, Springer, Berlin, 883-890.
- 12. Kaslik, E. and Sivasundaram, S. (2012) Nonlinear Dynamics and Chaos in Fractional-Order Neural Networks. Neural Networks, 32, 245-256.
http://dx.doi.org/10.1016/j.neunet.2012.02.030 - 13. Chen, L., Chai, Y., Wu, R., Ma, T. and Zhai, H. (2013) Dynamic Analysis of a Class of Fractional-Order Neural Networks with Delay. Neurocomputing, 111, 190-194.
http://dx.doi.org/10.1016/j.neucom.2012.11.034 - 14. Cao, Y. and Bai, C. (2014) Finite-Time Stability of Fractional-Order BAM Neural Networks with Distributed Delay. Abstract and Applied Analysis, 2014, Article ID: 634803.
- 15. Song, C. and Cao, J. (2014) Dynamics in Fractional-Order Neural Networks. Neurocomputing, 142, 494-498.
http://dx.doi.org/10.1016/j.neucom.2014.03.047 - 16. Kosto, B. (1988) Bi-Directional Associative Memories. IEEE Transactions on Systems, Man, and Cybernetics, 18, 49-60.
http://dx.doi.org/10.1109/21.87054 - 17. Cao, J. and Wang, L. (2002) Exponential Stability and Periodic Oscillatory Solution in BAM Networks with Delays. IEEE Transactions on Neural Networks, 13, 457-463.
http://dx.doi.org/10.1109/72.991431 - 18. Arik, S. and Tavsanoglu, V. (2005) Global Asymptotic Stability Analysis of Bidirectional Associative Memory Neural Networks with Constant Time Delays. Neurocomputing, 68, 161-176.
http://dx.doi.org/10.1016/j.neucom.2004.12.002 - 19. Park, J. (2006) A Novel Criterion for Global Asymptotic Stability of BAM Neural Networks with Time Delays. Chaos, Solitons and Fractals, 29, 446-453.
http://dx.doi.org/10.1016/j.chaos.2005.08.018 - 20. Bai, C. (2008) Stability Analysis of Cohen-Grossberg BAM Neural Networks with Delays and Impulses. Chaos, Solitons and Fractals, 35, 263-267.
http://dx.doi.org/10.1016/j.chaos.2006.05.043 - 21. Raja, R. and Anthoni, S.M. (2011) Global Exponential Stability of BAM Neural Networks with Time-Varying Delays: The Discrete-Time Case. Communications in Nonlinear Science and Numerical Simulation, 16, 613-622.
http://dx.doi.org/10.1016/j.cnsns.2010.04.022 - 22. Meyer-Base, A., Roberts, R. and Thummler, V. (2010) Local Uniform Stability of Competitive Neural Networks with Different Timescales under Vanishing Perturbations. Neurocomputing, 73, 770-775.
http://dx.doi.org/10.1016/j.neucom.2009.10.003 - 23. Arbi, A., Aouiti, C. and Touati, A. (2012) Uniform Asymptotic Stability and Global Asymptotic Stability for Time-Delay Hopfield Neural Networks. IFIP Advances in Information and Communication Technology, 381, 483-492.
http://dx.doi.org/10.1007/978-3-642-33409-2_50 - 24. Rakkiyappan, R., Cao, J. and Velmurugan, G. (2014) Existence and Uniform Stability Analysis of Fractional-Order Complex-Valued Neural Networks with Time Delays. IEEE Transactions on Neural Networks and Learning Systems, 26, 84-97.
- 25. Zhang, S. (2006) Positive Solutions for Boundary Value Problems of Nonlinear Fractional Differential Equations. Electronic Journal of Differential Equations, 2006, 1-12.
- 26. Krasnoselskii, M. (1964) Topological Methods in the Theory of Nonlinear Integral Equations. Pergamon, Elmsford.


































