Received 17 June 2015; accepted 18 August 2015; published 21 August 2015

ABSTRACT

The paper deals with the estimation of parameters of multidimensional diffusion processes that are discretely observed. We construct estimator of the parameters based on the minimum Hellinger distance method. This method is based on the minimization of the Hellinger distance between the density of the invariant distribution of the diffusion process and a nonparametric estimator of this density. We give conditions which ensure the existence of an invariant measure that admits density with respect to the Lebesgue measure and the strong mixing property with exponential rate for the Markov process. Under this condition, we define an estimator of the density based on kernel function and study his properties (almost sure convergence and asymptotic normality). After, using the estimator of the density, we construct the minimum Hellinger distance estimator of the parameters of the diffusion process and establish the almost sure convergence and the asymptotic normality of this estimator. To illustrate the properties of the estimator of the parameters, we apply the method to two examples of multidimensional diffusion processes.

Keywords:

Hellinger Distance Estimation, Multidimensional Diffusion Processes, Strong Mixing Process, Consistence, Asymptotic Normality

1. Introduction

Diffusion processes are widely used for modeling purposes in various fields, especially in finance. Many papers are devoted to the parameter estimation of the drift and diffusion coefficients of diffusion processes by discrete observation. As a diffusion process is Markovian, the maximum likelihood estimation is the natural choice for parameter estimation to get consistent and asymptotical normally estimator when the transition probability density is known [1] . However, in the discrete case, for most diffusion processes, the transition probability density is difficult to calculate explicitly which prevents the use of this method. To solve this problem, several methods have been developed such as the approximation of the likelihood function [2] [3] , the approximation of the transition density [4] , schemes of approximation of the diffusion [5] or methods based on martingale estimating functions [6] .

In this paper, we study the multidimensional diffusion model

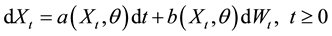
under the condition that 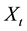is positive recurrent and exponentially strong mixing. We assume that the diffusion process is observed at regular spaced times 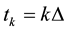where is a positive constant. Using the density of the invariant distribution of the diffusion, we construct an estimator of θ based on minimum Hellinger distance method.

Let 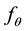denote the density of the invariant distribution of the diffusion. The estimator of 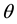is that value (or values) 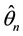in the parameter space which minimizes the Hellinger distance between 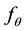and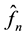, where 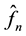is a nonparametric density estimator of.

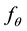The interest for this method of parametric estimation is that the minimum Hellinger distance estimation method gives efficient and robust estimators [7] . The minimum Hellinger distance estimators have been used in parameter estimation for independent observations [7] , for nonlinear time series models [8] and recently for univariate diffusion processes [9] .

The paper is organized as follows. In Section 2, we present the statistical model and some conditions which imply that 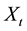is positive recurrent and exponentially strong mixing. Consistence and asymptotic normality of the kernel estimator of the density of the invariant distribution are studied in the same section. Section 3 defines the minimum Hellinger distance estimator of 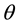and studies its properties (consistence and asymptotic normality). Section 4 is devoted to some examples and simulations. Proofs of some results are presented in Appendix.

2. Nonparametric Density Estimation

We consider the d-dimensional diffusion process solution of the multivariate stochastic differential equation:

(1)

where 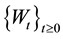is a standard l-dimensional Wiener process, is an unknown parameter which varies in a compact subset of, is the drift coefficient and is the diffusion coefficient.

We assume that the functions a and b are known up to the parameter and b is bounded.

We denote by the unknown true value of the parameter.

For a matrix, the notation denote the transpose of the matrix A. We will use the notation to denote a vectorial norm or a matricial norm.

The process is observed at discrete time where is a positive constant.

We make the following assumptions on the model:

(A₁): there exists a constant C such that

(A₂): there exist constants and such that

(A₃): the matrix function is non degenerate, that is

Assumptions (A₁)-(A₃) ensure the existence of a unique strong solution for the Equation (1) and an invariant measure for the process that admits a density with respect to the Lebesgue measure and the strong mixing property for with exponential rate [10] -[12] . We denote by the strong mixing coefficient.

In the sequel, we assume that the initial value follows the invariant law; which implies that the process is strictly stationary.

We consider the kernel estimator of that is,

where is a sequence of bandwidths such that and as and is a non negative kernel function which satisfies the following assumptions:

(A₄)

(1) There exists such that,

(2) and as,

(A₅) and for.

We finish with assumptions concerning the density of the invariant distribution:

(A₆) is twice continuously differentiable with respect to.

(A₇) implies that for all.

Properties (consistence and asymptotic normality) of the kernel density estimator are examined in the following theorems. The proof of the two theorems can be found in the Appendix.

Theorem 1. Under assumptions (A₁)-(A₄), if the function is continuous with respect to x for all, then for any positive sequence such that and as, almost surely.

Theorem 2. Under assumptions (A₁)-(A₆), if is such that as then the limiting

distribution of is where

3. Estimation of the Parameter

The minimum Hellinger distance estimator of is defined by:

where

Let denote the set of squared integrable functions with respect to the Lebesgue measure on.

Define the functional as follows: let and denote:

where is the Hellinger distance.

If is reduced to an unique element, then is defined as the value of this element. Elsewhere, we choose an arbitrary but unique element of and call it.

Theorem 3. (almost sure consistency)

Assume that assumptions (A₁)-(A₄) and (A₇) hold. If for all, is continuous at, then for any positive sequence such that and, converges almost surely to as.

Proof. By Theorem 1, almost surely.

Using the inequality for, we get

Since

almost surely [13] [14] .

By theorem 1 [7] , uniquely on; then the functional T is continuous at in the Hellin-

ger topology. Therefore almost surely.

This achieves the proof of the theorem.

Denote

when these quantities exist. Furthermore, let

To prove asymptotic normality of the estimator of the parameter, we begin with two lemmas.

Lemma 1. Let be a subset of and denote the complementary set of. Assume that

(1) assumptions (A₁)-(A₅) are satisfied,

(2) is twice continuously differentiable with respect to and

(3)

(4)

then for any positive sequence such that, the limiting distribution of

The proof can be found in the Appendix.

Remark 1. The two dimensional stochastic process (see Section 4) with invariant density

, ,

where, satisfies the conditions of Lemma 1 with for example a subset of where.

Lemma 2. Let be a compact set of and denote by the complementary set of. Suppose that assumptions (A₁)-(A₆) are satisfied and:

(1)

(2), and are such that and

(3)

(4)

(5)

then

The proof can be found in the Appendix.

Remark 2. Let a compact set of where is a sequence of positive

numbers diverging to infinity. Let, and, , then the two dimensional stochastic process with invariant density, ,

where, satisfies the conditions of Lemma 2.

Theorem 4. (asymptotic normality)

Under assumption (A₇) and conditions of Lemma 1 and Lemma 2, if

(1) for all, is twice continuously differentiable at,

(2) the components of and belong to and if the norms of these components are continuous functions at,

(3) is in the interior of and is a non-singular matrix, then the limiting distribution of is where

Proof. From Theorem 2 [7] , we have:

where is a (m ´ m) matrix which tends to 0 as.

We have

Denote

We have

where

By Lemma 2, in probability as; then, the limiting distribution of is reduced to that of

since. But

Therefore the limiting distribution of

where

This completes the proof of the theorem.

4. Examples and Simulations

4.1. Example 1

We consider the two-dimensional Ornstein-Uhlenbeck process solution of the stochastic differential equation

(2)

where

Let and, we have:

Ÿ and satisfy assumptions (A₁)-(A₃). Therefore, is exponentially strong mixing and the invariant distribution admits a density with respect to the Lebesgue measure.

Furthermore [15] , , the Gaussian distribution on with the unique symmetric solution of the equation is

(3)

The solution of the Equation (3) is.

Therefore [16] , the density of the invariant distribution is

Ÿ The minimum Hellinger distance estimator of is defined by:

where

with

where is a kernel function which satisfies conditions (A₄) and (A₅) such that.

Let, we can write Equation (2) as follows:

which gives the the following system

Thus, and are two independent univariate Ornstein-Uhlenbeck processes of parameters and respectively.

We now give simulations for different parameter values using the R language. For each process, we generate sample paths using the package “sde” [17] and to compute a value of the estimator, we use the function “nlm” [18] of the R language. The kernel function is the density of the standard normal distribution. We use the

bandwidth according to conditions on the bandwidth in the paper.

Simulations are based on 1000 observations of the Ornstein-Uhlenbeck process with 200 replications.

Simulation results are given in the Table 1.

In Table 1, denotes the true value of the parameter and denotes an estimation of given by the minimum Hellinger distance estimator. Simulation results illustrate the good properties of the estimator. Indeed, the means of the estimator are quite close to the true values of the parameter in all cases and the standard errors are low.

4.2. Example 2

We consider the Homogeneous Gaussian diffusion process [19] solution of the stochastic differential equation

(4)

where is known, W is a two-dimensional Brownian motion, B is a matrix with eigenvalues with strictly negative parts and A is a matrix. By condition on the matrix B, X has an invariant probability where and is the unique symetric solution of the equation

(5)

Let

As in [19] , we suppose that. In the following, we suppose that.

Then we have

Let, we have.

Let and, we have; is invertible and we have

is invertible and we have. Hence, the invariant density of is

For simulation, we must write the stochastic differential Equation (4) in matrix form as follows:

As in [19] , the true values of the parameter are and. Then, we have

Now, we can simulate a sample path of the Homogeneous Gaussian diffusion using the “yuima” package of R language [20] . We use the function “nlm” to compute a value of the estimator.

We generate 500 sample paths of the process, each of size 500. The kernel function and the bandwidth are those of the previous example.

We compare the estimator obtained by the minimum Hellinger distance method (MHD) of this paper and the estimator obtained in [19] by estimating function. Table 2 summarizes results of simulation of means and standard errors of the different estimators.

Table 2 shows that the two estimators have good behavior. For the two methods, the means of the estimators are close to the true values of the parameter. But the standard errors of the MHD estimator are lower than those of the estimating function estimator.

Cite this paper

Julien ApalaN’drin,OuagninaHili, (2015) From Nonparametric Density Estimation to Parametric Estimation of Multidimensional Diffusion Processes. Applied Mathematics,06,1592-1610. doi: 10.4236/am.2015.69142

References

Appendix

A1. Proof of Theorem 1

Proof.

We have:

Step 1:

by Theorem 2.1 [21] .

Hence

(6)

Step 2:

where

Ÿ

Ÿ

Then by theorem 2.1 [9] , we have for all

We have

where

Then

Therefore

(7)

by the Borel-Cantelli’s lemma.

(6) and (7) imply that

This achieves the proof of the theorem.

A2. Proof of Theorem 2

Proof.

(1)

By making the change of variable and using assumptions (A₄) and (A₅), we get:

(2)

where

We have and.

Let, and be positive integers which tend to infinity as such that.

Define and by

and

We have

Step 1: We prove that in probability.

By Minkowski’s inequality, we have

(1) Using Billingsley’s inequality [22] ,

(2)

Hence,

Therefore, choosing and such that

(8)

we get

which implies that

Step 2: asymptotic normality of.

, have the same distribution; so that

From Lemma 4.2 [23] , we have

Setting. If and are chosen such that

(9)

the charasteristic function of is which is the charasteristic function of where, are independent random variables with distribution that of.

We have and

(1)

(2) Note that with.

(10)

Therefore

Since the random variables have the same distribution, then by Lyapunov’s theorem [24] ,

the limiting distribution of is where

The condition (8), (9) and (10) are satisfied, for example, with

This achieves the proof of the theorem.

A3. Proof of Lemma 1

Proof. The proof of the lemma is done in two steps.

Step 1: we prove that

With assumptions (A₄) and (A₅), we have

Furthermore,

Therefore

Step 2: asymptotic normality of, ,

(1)

Proof is similar to that of theorem 2; we use the inequality of Davidov [22] instead of that of Billingsley.

Note that:

and

(2),

Recall that if and only if for all.

Let, and, the real random variables are

strongly mixing with mean zero and variance where is the covariance matrix of;.

From (1),.

Therefore,

This completes the proof of the lemma.

A4. Proof of Lemma 2

Proof.

We have,

Now,

(1)

Using Davidov’s inequality for mixing processes, we get

Choose and, we obtain

Hence,

(2)

Therefore,

The last relation implies that

(11)

Furthermore,

We have,

Therefore, if

then

(12)

(11) and (12) imply that