Received 5 June 2015; accepted 10 July 2015; published 14 July 2015

ABSTRACT

We show how to use the Lucas polynomials of the second kind in the solution of a homogeneous linear differential system with constant coefficients, avoiding the Jordan canonical form for the relevant matrix.

Keywords:

Homogeneous Linear Differential Systems with Constant Coefficients, Exponential Matrix, Lucas Polynomials of the Second Kind

1. Introduction

It is well known that an analytic function f of a matrix, i.e. 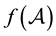is the matrix polynomial obtained from the scalar polynomial interpolating the function f on the eigenvalues of 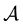(see e.g. the Gantmacher book [1] ), however, in many books (see e.g. [2] ), the series expansion

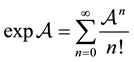(1.1)

is assumed for defining (and computing)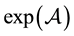. So, apparently, the series expansion for the exponential of a matrix is “hard to die”.

Let 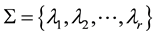be the spectrum of. Denoting by

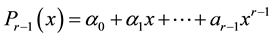
the polynomial interpolating on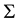, i.e. such that: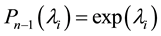, , 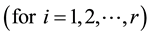then

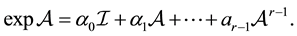(1.2)

If the eigenvalues are all distinct, 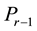coincides with the Lagrange interpolation polynomial and (1.2) is the Lagrange-Sylvester formula. In case of multiple eigenvalues, 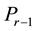is the Hermite interpolation polynomial, and (1.2) reduces to Arthur Buchheim’s formula, generalizing the preceding one.

This avoids the use of higher powers of in the Taylor expansion (1.1). In any case, the possibility to write, , in an easy block form, requires not only the knowledge of the spectrum, but even the Jordan canonical form of. It is necessary to compute the eigenvectors and moreover the principal vectors, if is defective. A known machinery which implies a lot of computations.

In the following, we show how to proceed in connections with the matrix, which appears in the solution of the vectorial Cauchy problem

We propose an alternative method, based on recursion, using the functions, which are essentially linked to Lucas polynomials of the second kind (i.e. the basic solution of a homogeneous linear recurrence relation with constant coefficients [3] [4] ), and to the multi-variable Chebyshev polynomials [5] .

Another Taylor series will be used, but using only functions of the invariants of, not explicitly all powers of.

It is worth to recall that the knowledge of eigenvalues is equivalent to that of invariants, since the latter are the elementary symmetric functions of the former (with alternate sign).

Up to our knowledge, this is the first time that polynomials are used to solve this kind of differential problems, furthermore our method has the advantage to avoid computation of higher powers of the matrix. The solution of the considered problem is given in terms of the functions of the invariants of. These functions are polynomials, independent of the Jordan canonical form of, and can be computed recursively, avoiding the knowledge of eigenvectors and principal vectors. Moreover, if the matrix is real, the functions are real as well, and possible complex eigenvalues does not affect the form of solution.

2. Homogeneous Linear Differential Systems with Constant Coefficients

It is well-known that a higher order differential system can be always be reduced to a first order system, hence we will limit ourselves to considering such type of systems.

For simplicity, we start off with the system

(2.1)

with matrix:

assuming, (otherwise the system is trivial), and put by definition:

In the following, consider the Cauchy problem with initial conditions:

(2.2)

Looking at the first equation in (2.1), we note that since the right hand side is (real or) complex analytic, the solution is (real or) complex analytic as well. Deriving side by side, we find

(2.3)

Eliminating between the first equation in (2.1) and (2.3), since, we find

(2.4)

This procedure can be iterated, obtaining, for example

In general we find the same recursion satisfied by the powers of the matrix [6] , i.e.

(2.5)

where the coefficients are essentially Lucas polynomials of the second kind (see [3] -[5] [7] ), defined by the recurrence relation:

(2.6)

and the initial conditions:

(2.7)

It is easily shown that the second function satisfies the same recursion (2.5).

As a consequence, putting

(2.8)

and using Taylor expansion, the solution of the Cauchy problem (2.1) - (2.2), can be found in the form:

(2.9)

The above result can be put in vectorial form, in order to be generalized.

Let, ,.

Introduce the matrix and define

then, the solution in vectorial form reads

Note that the convergence of the vectorial series in any compact set K of the space is guaranteed, since the components of are polynomials of weight not exceeding, and consequently are bounded in K.

In the following section, we will extend this solution to the general vectorial case.

Remark 2.1 Note that Equation (9) does not use all powers of matrix, but only the functions of its invariants, which are simply computed by recursion, a worthwhile improvement of the computing cost.

3. The 3D Case

Now, we consider also the case of the system

(3.1)

with matrix:

we suppose, , (so that the system cannot be reduced to a or trivial system), and put by definition:

We consider, the Cauchy problem with initial conditions:

(3.2)

By using the same technique as in the case, we find

(3.3)

and by iterating the procedure we obtain, for example,

and so on. In general we find the same recursion satisfied by the powers of the matrix [6] , i.e.

(3.4)

where the coefficients are the generalized Lucas polynomials [4] , defined by the recurrence relation:

(3.5)

and the initial conditions:

(3.6)

The second and third function and satisfy the same recursion (3.4).

As a consequence, putting

and

and using Taylor expansion, the solution of the Cauchy problem (3.1) - (3.2), can be found in the form:

The above result can be put in the following vectorial form.

Let, , ,

.

Introduce the matrix and define

then, the solution in vectorial form reads

Remark 3.1 Even in this case, the considerations of Rem. 2.1 still hold, showing a more convenient form of computing solutions of the Cauchy problem (3.1) - (3.2), with respect to traditional methods, as reported e.g. in [2] .

4. The General Result

Theorem 4.1 Consider the Cauchy problem for a homogeneous linear differential system

(4.1)

where

denote by the invariants of, and recall the generalized Lucas polynomials , defined in [4] .

Suppose that the system cannot be reduced to a lower order system, so that

,.

Introduce the matrix and define

then, the solution of problem (3.1) takes the form

(4.2)

Proof―The proof can be found by induction, considering the r vector

composed of its first component and a second component given by the vector, and applying the result from Section 2.

Note that the convergence of the vectorial series in any compact set K of the space is guaranteed, since the components of are polynomials of weight not exceeding, and consequently are bounded in K.

5. Conclusions

We have recalled that the exponential of a matrix can be written as a matrix polynomial, obtained from the scalar polynomial interpolating on the spectrum of, and then avoiding the Taylor expansion for the exponential matrix.

Furthermore, by using the functions, and in particular the fundamental solution of a homogeneous linear recurrence relation, i.e. the generalized Lucas polynomials of the second kind, we have shown how to obtain the solution of the vectorial Cauchy problem (1) in terms of functions of the invariants of, instead of powers of. These functions are independent of the Jordan canonical form of, and can be computed recursively, avoiding the knowledge of eigenvectors and principal vectors. Moreover, if the matrix is real, the functions are real as well, and complex eigenvalues do not affect the form of the solution.

Therefore, this is, in our opinion, a more convenient technique for solving problem (4.1).

Cite this paper

PierpaoloNatalini,Paolo E.Ricci, (2015) A “Hard to Die” Series Expansion and Lucas Polynomials of the Second Kind. Applied Mathematics,06,1235-1240. doi: 10.4236/am.2015.68116

References

NOTES

^*Corresponding author.