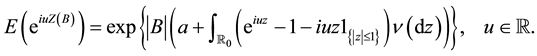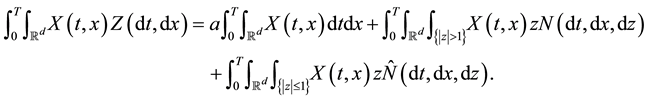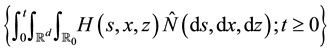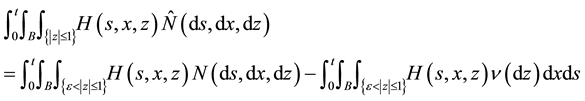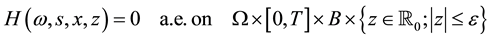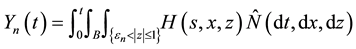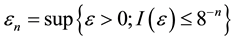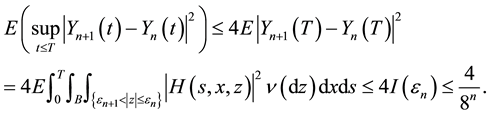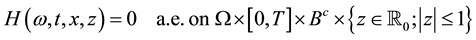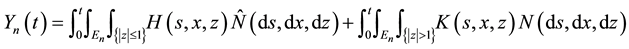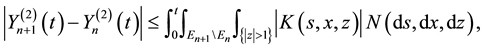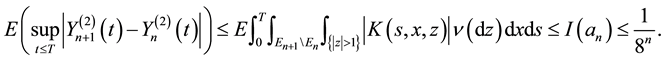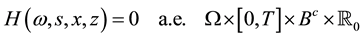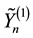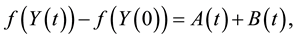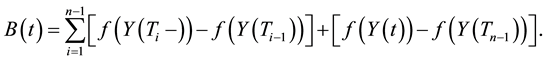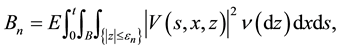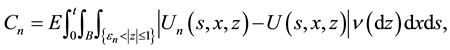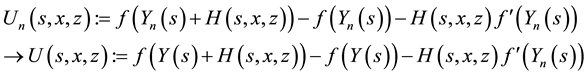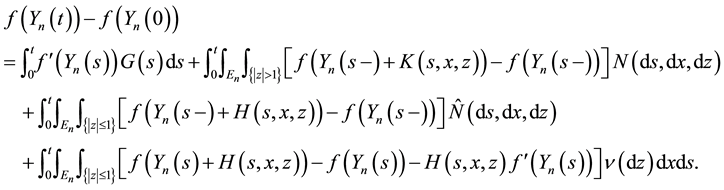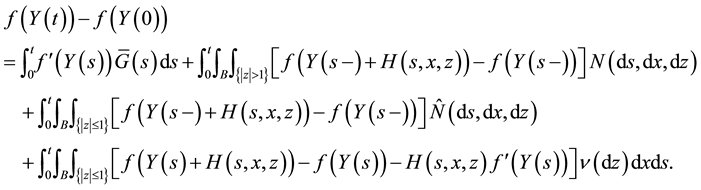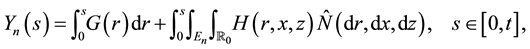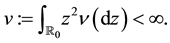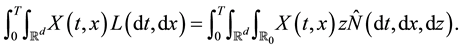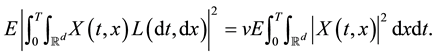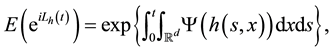Applied Mathematics
Vol.06 No.10(2015), Article ID:59834,13 pages
10.4236/am.2015.610156
Itô Formula for Integral Processes Related to Space-Time Lévy Noise
Raluca M. Balan*, Cheikh B. Ndongo
Department of Mathematics and Statistics, University of Ottawa, Ottawa, Canada
Email: *rbalan@uottawa.ca, cndon072@uottawa.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2015; accepted 20 September 2015; published 23 September 2015
ABSTRACT
In this article, we give a new proof of the Itô formula for some integral processes related to the space-time Lévy noise introduced in [1] [2] as an alternative for the Gaussian white noise perturbing an SPDE. We discuss two applications of this result, which are useful in the study of SPDEs driven by a space-time Lévy noise with finite variance: a maximal inequality for the p-th moment of the stochastic integral, and the Itô representation theorem leading to a chaos expansion similar to the Gaussian case.
Keywords:
Lévy Processes, Poisson Random Measure, Stochastic Integral, Itô Formula, Itô Representation Theorem

1. Introduction
Random processes indexed by sets in the space-time domain are useful objects in stochastic analysis, since they can be viewed as mathematical models for the noise perturbing a stochastic partial differential equation (SPDE). In the recent years, a lot of effort has been dedicated to studying the behaviour of the solution of basic equations (like the heat or wave equations), driven by a Gaussian white noise. This type of noise was introduced by Walsh in [3] and is defined as a zero-mean Gaussian process , with covariance
, with covariance
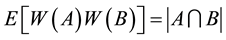 , where
, where
 denotes the Lebesgue measure and
denotes the Lebesgue measure and
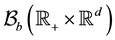 is the class of bounded
is the class of bounded
Borel sets in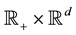 .
.
In the recent articles [1] [2] , a new process has been introduced as an alternative for the Gaussian white noise perturbing an SPDE, which has a structure similar to a Lévy process. We introduce briefly the definition of this process below.
Let N be a Poisson random measure (PRM) on
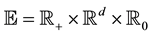 of intensity
of intensity
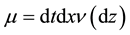 where
where
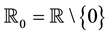 and
and
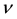 is a Lévy measure on
is a Lévy measure on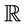 :
:
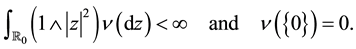
We denote by
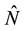 the compensated PRM defined by
the compensated PRM defined by
 for any Borel set A in
for any Borel set A in
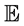 with
with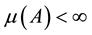 . The Lévy-type noise process mentioned above is defined as
. The Lévy-type noise process mentioned above is defined as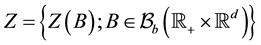 , where
, where
for some
(In particular, Z can be an a-stable random measure with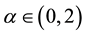
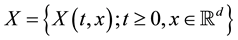
The stochastic integral with respect to

Assume that N is defined on a probability space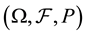
where

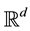

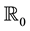
An elementary process on
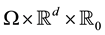
where

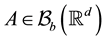



As in the classical theory, for any predictable process H such that
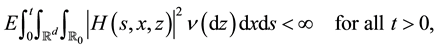
we can define the stochastic integral of H with respect to

is a zero-mean square-integrable martingale which satisfies

On the other hand, for any predictable process K such that
we can define the integral of K with respect to N and this integral satisfies
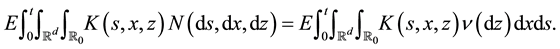
In this article, we work with processes whose trajectories are right-continuous with left limits. If x is a right
continuous function with left limits, we denote by


Theorem 1 (Ito Formula I). Let
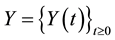

where G, K and H are predictable processes which satisfy
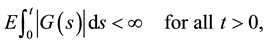


Then there exists a modification of Y (denoted also by Y) whose sample paths are right-continuous with left limits, such that for any function
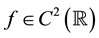


Note that since the first two terms on the right-hand side of (4) are processes of finite variation and the last term is a square-integrable martingale, Y is a semimartingale. Therefore, the Itô formula given by Theorem 1 can be derived from the corresponding result for a general semimartingale, assuming that Y has sample paths which are right-continuous with left limits (see e.g. Theorem 2.5 of [7] ).
The goal of the present article is to give an alternative proof of this result which contains the explicit construction of the modification of Y for which the Itô formula holds.
We will also give the proof of the following variant of the Itô formula, which will be useful for the applications related to the (finite-variance) Lévy white noise, discussed in Section 4.
Theorem 2 (Ito Formula II). Let


where G and H are predictable processes which satisfy (5), respectively (1). Then there exists a càdlàg modification of Y (denoted also by Y) such that for any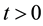
The method that we use for proving Theorems 1 and 2 is similar to the one described in Section 4.4.2 of [6] in the case of classical Lévy processes, the difference being that in our case, N is a PRM on
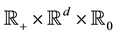

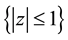
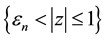
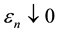



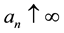
2. Approximation by Right-Continuous Processes with Left Limits
In this section, we show that the Lévy-type integral processes given by (4) and (9) have right-continuous modifications with left limits, which are constructed by approximation. These modifications will play an important role in the proof of Itô’s formula. Since the process
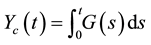

We consider first processes of the form (4). We start by examining the case when both integrands H and K
vanish outside a set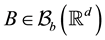

(the integral being a sum with finitely many terms), we need to consider only the integral process which depends on H.
Note that if H vanishes a.e. on


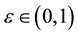
is a process whose sample paths are right-continuous with left limits (the first term is a sum with finitely many terms and the second term in continuous). Therefore, we will suppose that H satisfies the following assumption:
Assumption A. It is not possible to find
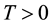

with respect to the measure
Lemma 1. Let

where
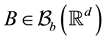
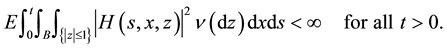
Then, there exists a càdlàg modification


where
for some sequence


Proof: We use the same argument as in the proof of Theorem 4.3.4 of [6] . Fix
where
Note that
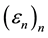

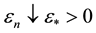
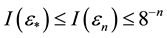

Note that

By Chebyshev’s inequality,

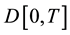

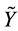



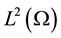





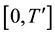

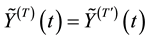


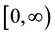
We consider now the case when the at least one of the integrands H and K do not vanish outside a set
Assumption B. It is not possible to find
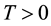

with respect to the measure
Assumption

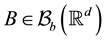
with respect to the measure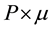
We consider bounded Borel sets in
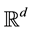

Theorem 3 (Interlacing I). Let
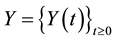

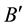
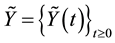

where

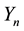
with



Proof: Fix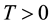

Note that

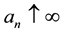
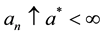
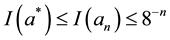
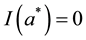
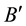



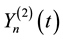
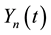
We denote by
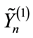

By Chebyshev’s inequality,
Note that
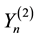
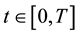
and hence, using relation (3),
By Markov’s inequality,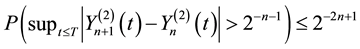
Let

We consider next processes of the form (9) with G = 0. Note that if H vanishes a.e. outside a set

where the first term has a càdlàg modification given by Lemma 1, the second term is càdlàg, and the third term is continuous. Therefore, we will suppose that H satisfies the following assumption:
Assumption C. It is not possible to find


with respect to the measure
Theorem 4 (Interlacing II). Let Y be a process given by (9) with



with
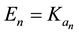


Proof: We proceed as in the proof of Theorem 3. Fix

By Assumption C,

and
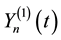


be the càdlàg modification of
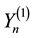
Let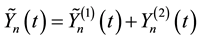
and the conclusion follows as in the proof of Lemma 1. ,
3. Proof of Itô Formula
In this section, we give the proofs of Theorem 1 and Theorem 2.
We start with the simpler case when there are no small jumps (the analogue of Lemma 4.4.6 of [6] ).
Lemma 2. Let
where G is a predictable process which satisfies (5),
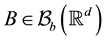

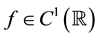
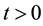
Proof: We denote
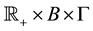


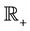
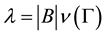




Case 1: G = 0. By the representation of N,




and the conclusion follows since N has points


Case 2: G is arbitrary. The map






where A and B are defined as follows: if
Note that
It remains to prove that

For this, we assume that

So it suffices to prove that

for all
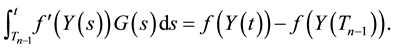
We first prove (13). Fix


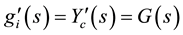
We extend

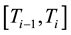
where for the last equality we used the fact that


This proves (13).
Next, we prove (14). Note that if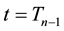
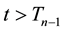


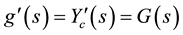
Arguing as above, we see that
where for the last equality we used the fact that
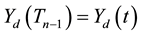

This concludes the proof of (14). ,
Proof of Theorem 1: We fix
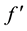


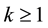
Case 1: H and K vanish outside a fixed set
If H vanishes a.e. on

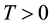

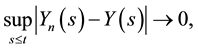
where the process

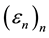


Note that
where
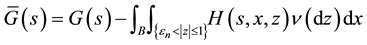

Cauchy-Schwarz inequality,


After using the definitions of


we obtain that:
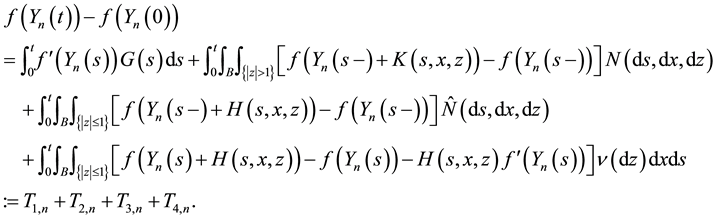
We denote by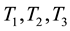
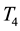

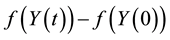
We treat separately the four terms in the right-hand side. By the dominated convergence theorem,
Since
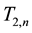
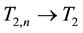

and

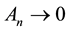
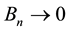

and the fact that
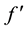


Finally,

and
a.s., by (16) and the continuity of f. By the dominated convergence theorem,



and the fact that
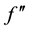
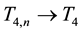
Case 2. H satisfies Assumption B or K satisfies Assumption
By Theorem 3, there exists a càdlàg approximation of Y (denoted also by Y) such that (15) holds, where




The conclusion follows letting

Proof of Theorem 2: We assume that


Case 1. H vanishes outside a set
where

is a bounded set). By Theorem 1, there exists a càdlàg modification of Y (denoted also by Y) such that
We add and subtract
ranging the terms.
Case 2. H satisfies Assumption C.
By Theorem 4, there exists a càdlàg modification of Y (denoted also by Y) such that (15) holds, where
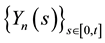




4. Applications
In this section, we assume that the Lévy measure

As in [1] , we consider the process

For any predictable process
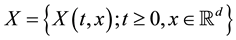
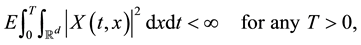
we can define the stochastic integral of X with respect to L and this integral satisfies:
By (2), this integral has the following isometry property:
When used as a noise process perturbing an SPDE, L behaves very similarly to the Gaussian white noise. For this reason, L was called a Lévy white noise in [1] .
4.1. Kunita Inequality
The following maximal inequality is due to Kunita (see Theorem 2.11 of [7] ). In problems related to SPDEs with noise L, this result plays the same role as the Burkholder-Davis-Gundy inequality for SPDEs with Gaussian white noise.
Theorem 5 (Kunita Inequality). Let

where X is a predictable process which satisfies (20).
If
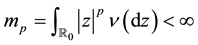

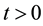
where


Proof: We apply Theorem 2 with
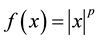

Remark 1. Kunita’s constant

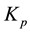
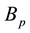
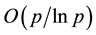
4.2. Itô Representation Theorem and Chaos Expansion
In this section, we give an application to Theorem 2 to exponential martingales, which leads to Itô representation theorem and a chaos expansion (similarly to Sections 5.3 and 5.4 of [6] ).
For any

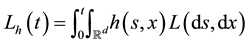
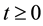
fication of the process
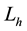
where
Hence


The following result is the analogue of Lemma 5.3.3 of [6] .
Lemma 3. For any


Proof: We apply Theorem 2 to the function

Hence,


Since the sum of the last two integrals is 0, the conclusion follows. ,
We fix

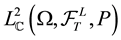
of C-valued square-integrable random variables which are measurable with respect to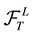
Lemma 4. The linear span of the set

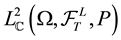
Proof: The proof is similar to that of Lemma 5.3.4 of [6] . We omit the details. ,
Theorem 6 (Ito Representation Theorem). For any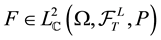

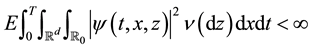
such that
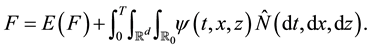
Proof: By Lemma 3, relation (22) holds for
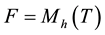

The multiple (and iterated) integral with respect
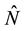
More precisely, we consider the Hilbert space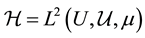

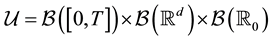
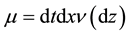
For any integer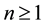
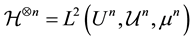
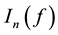


Moreover, if



We have the following result.
Theorem 7 (Chaos Expansion). For any

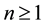
In particular,
Proof: We use the same argument as in the classical case, when

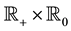
is a square-integrable Lévy process (see Theorem 5.4.6 of [6] or Theorem 10.2 of [10] ). By Theorem 6, there exists a predictable process


By (21),


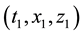
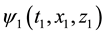
Satisfying
such that
We substitute this into (23) and iterate the procedure. We omit the details. ,
Acknowledgements
Research of R. M. Balan is funded by a grant from the Natural Sciences and Engineering Research Council of Canada.
Cite this paper
Raluca M.Balan,Cheikh B.Ndongo, (2015) Itô Formula for Integral Processes Related to Space-Time Lévy Noise. Applied Mathematics,06,1755-1768. doi: 10.4236/am.2015.610156
References
- 1. Balan, R.M. (2015) Integration with Respect to Lévy Colored Noise, with Applications to SPDEs. Stochastics, 87, 363- 381.
http://dx.doi.org/10.1080/17442508.2014.956103 - 2. Balan, R.M. (2014) SPDEs with α-Stable Lévy Noise: A Random Field Approach. International Journal of Stochastic Analysis, 2014, Article ID: 793275.
http://dx.doi.org/10.1155/2014/793275 - 3. Walsh, J.B. (1989) An Introduction to Stochastic Partial Differential Equations. Ecole d’Eté de Probabilités de Saint- Flour XIV. Lecture Notes in Math, 1180, 265-439.
http://dx.doi.org/10.1007/BFb0074920 - 4. Rajput, B.S. and Rosinski, J. (1989) Spectral Representations of Infinitely Divisible Processes. Probability Theory and Related Fields, 82, 451-487.
http://dx.doi.org/10.1007/BF00339998 - 5. Samorodnitsky, G. and Taqqu, M.S. (1994) Stable Non-Gaussian Random Processes. Chapman and Hall, New York.
- 6. Applebaum, D. (2009) Lévy Processes and Stochastic Calculus. 2nd Edition, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511809781 - 7. Kunita, H. (2004) Stochastic Differential Equations Based on Lévy Processes and Stochastic Flows of Diffeomorphisms. In: Rao, M.M., Ed., Real and Stochastic Analysis, New Perspectives, Birkhaüser, Boston, 305-375.
http://dx.doi.org/10.1007/978-1-4612-2054-1_6 - 8. Resnick, S.I. (2007) Heavy Tail Phenomena: Probabilistic and Statistical Modelling. Springer, New York.
- 9. Balan, R.M. and Ndongo, C.B. (2015) Intermittency for the Wave Equation with Lévy White Noise. Arxiv: 1505.04167.
- 10. Di Nunno, G., Oksendal, B. and Proske, F. (2009) Malliavin Calculus for Lévy Processes with Applications to Finance. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-540-78572-9
NOTES
*Corresponding author.