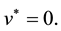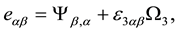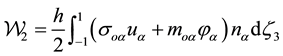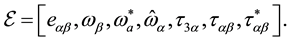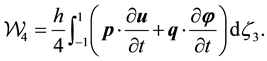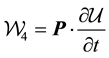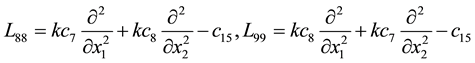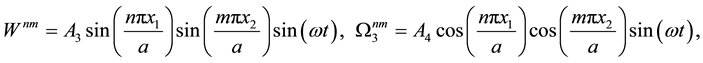Received 9 April 2015; accepted 15 May 2015; published 18 May 2015

ABSTRACT

This paper presents an extension of mathematical static model to dynamic problems of micropolar elastic plates, recently developed by the authors. The dynamic model is based on the generalization of Hellinger-Prange-Reissner (HPR) variational principle for the linearized micropolar (Cosserat) elastodynamics. The vibration model incorporates high accuracy assumptions of the micropolar plate deformation. The computations predict additional natural frequencies, related with the material microstructure. These results are consistent with the size-effect principle known from the micropolar plate deformation. The classic Mindlin-Reissner plate resonance frequencies appear as a limiting case for homogeneous materials with no microstructure.

Keywords:

Cosserat Materials, Plate Vibration, Frequencies of Transverse Micro-Vibration, Variational Principle

1. Introduction

Classical theory of elasticity ignores the size effects of the particles and their mutual rotational interactions, thus considering the material particles to have only three degrees of freedom that represent their macrodisplacements. The stress tensor is symmetric and the surface loads are assumed to be solely determined by the force vector. Classical theory of elasticity is widely used in engineering and is successfully applied under small deformations to such linear elastic materials as stainless steel, concrete, plastic, aluminium, etc. Many modern engineering materials, however, contain fibers, grains, pores or macromolecules, which in turn make them exhibit the defor- mation that cannot be adequately described by the classical elasticity (see, for example, the studies of a low- density polymeric foam in [1] [2] ). The microstructure of the body also has an impact on the elastic vibrations with high frequencies and short wavelengths. The dynamic problems describe the appearance of the new types of waves that are not predicted by the classical elasticity [3] . Micropolar theory of elasticity describes the deformation of the materials with internal microstructure. The material particles have six degrees of freedom (macrodisplacements and microrotations) and the surface loads are assured by the force and moment vectors. This assumption leads to the introduction of the couple stress tensor and the asymmetry of the stress tensor. The examples of the materials that consider micropolar and exhibit nonclassical behavior include platelet and particulate composites, sandwich and grid structures, honeycombs, concrete with sand, ferroelectric and pho- nonic crystals, polyfoams, and human bones [1] [4] - [12] .

The first theory of elasticity that took into account the microstructure of the material was developed in 1909 by Cosserat brothers. They presented the equations of local balance of momenta for stress and couple stress, and the expressions for surface tractions and couples [13] . Many significant contributions were made by Eringen, who developed micromorphic and micropolar theories of solids, fluids, memory-dependent media, micro stretch solids and fluids and solved several problems in these fields [14] . In 1967, Eringen introduced a theory of plates in the framework of micropolar elasticity [15] . Eringen’s theory assumes constant transverse variation of micro- polar rotations and is based on a direct integration of the Cosserat elasticity equations. The micropolar plate theory based on the Reissner plate theory [16] - [18] is developed by the authors in [19] - [21] . The results of the preliminary computations for the micropolar plate theory based on the Reissner plate are compatible with the precision of the Reissner plate theory [22] .

In this paper, we present an extension of our static approach to the dynamics of micropolar elastic plates. We reformulate a generalization of Hellinger-Prange-Reissner (HPR) variational principle [23] for elastodynamics of micropolar materials, and then, using our assumptions, we postulate the variational principle for the Cosserat plate dynamics. This principle allows us to obtain dynamic equilibrium equations and constitutive relations. We present our preliminary study of the influence of plate size effect on the natural frequencies in comparison with Mindlin-Reissner plates and perform the computations for different levels of the asymmetric microstructure.

2. Micropolar (Cosserat) Linear Elastodynamics

2.1. Fundamental Equations

Throughout this paper we will use the Einstein summation notation. The Latin subindices take values in the set, while the Greek letters take the values 1 or 2.

The Cosserat linear elasticity balance equations without body forces represent the balance of linear and angular momentums of micropolar elastodynamics and have the following form:

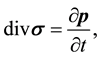(1)

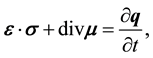(2)

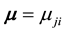where the quantity is the stress tensor, the couple stress tensor, and 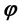the are displace-

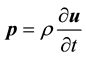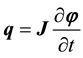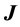ment and rotation vectors, and are the linear and angular momenta, and are the

material density and the rotatory inertia characteristics, 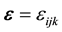is the Levi-Civita tensor. In the linearized theory 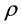and are assumed to be constant [3] [14] . For simplicity we consider the case.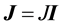

The linearized constitutive equations are given in the form [3] :

(3)

(4)

and the strain-displacement and torsion-rotation relations

(5)

where, are the symmetric and, , , the asymmetric Cosserat elasticity constants.

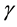
The constitutive equations in the reverse form can be written as

(6)

(7)

where, , , , and.

We consider a Cosserat elastic body. The equilibrium Equations (1) and (2) with constitutive formulas (3)-(4) and kinematics formulas (5) should be accompanied by the following mixed boundary conditions

(8)

(9)

and initial conditions

(10)

(11)

where and are prescribed on, and on, and denotes the outward unit normal vector to.

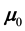
2.2. Cosserat Elastic Energy

The strain stored energy of the body is defined by the integral [3] :

(12)

where non-negative

(13)

then the constitutive relations (3)-(4) can be written in the form:

(14)

For future convenience, we present the stress energy

where

(15)

The constitutive relations in the reverse form (6)-(7) can be also written in form:

(16)

The total internal work done by the stresses and over the strains and for the body [3] is

(17)

and

provided the constitutive relations (3)-(4) hold.

We also consider the stored kinetic energy of the body defined by the integral

We also present the kinetic energy as

where

(18)

or

and

(19)

The internal work done by the inertia forces over displacement and microrotation is

Using the integration by parts

and taking into account the zero variation of and at the end points of the time interval we obtain

Note that since the variations and at and points and are zeros then

(20)

2.3. Hellinger-Prange-Reissner (HPR) Principle for Elastodynamics

We modify the HPR principle [23] for the case of Cosserat elastodynamics in the following way. Now it states, that for any set of all admissible states that satisfy the strain-displacement and torsion-rotation relations (5), the zero variation

of the functional

(21)

at is equivalent of to be a solution of the system of equilibrium Equations (1) and (2), constitutive relations (6)-(7), which satisfies the mixed boundary conditions (8)-(9).

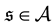
Proof of the Principle

Let us consider the variation of the functional:

Taking into account (5), we can perform the integration by parts

and based on (16)-(19)

Then, keeping in mind and (20), we can rewrite the expression for the variation of the functional in the following form

The latter expression provides the proof of the principle.

3. Review of Cosserat Plate Assumptions

In this section we review our stress, couple stress and kinematic assumptions of the Cosserat plate [20] . We consider the thin plate P, where h is the thickness of the plate and contains its middle plane. The sets T and B are the top and bottom surfaces contained in the planes, respectively and the curve is the boundary of the middle plane of the plate.

The set of points forms the entire surface of the plate and is the

lateral part of the boundary where displacements and microrotations are prescribed. The notation

of the remainder we use to describe the lateral part of the boundary edge where stress and

couple stress are prescribed. We also use notation for the middle plane internal domain of the plate.

In our case we consider the vertical load and pure twisting momentum boundary conditions at the top and bottom of the plate, which can be written in the form:

(22)

(23)

(24)

(25)

where

Some basic stress and kinematic assumptions are similar to the Reissner plate theory [16] and other chosen to be consistent with the micropolar elasticity equilibrium equations.

3.1. Stress and Couple Stress Assumptions

We reproduce the main micropolar plate assumptions presented in [20] . The variation of stress and couple stress components across the thickness is represented by means of polynomials of

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

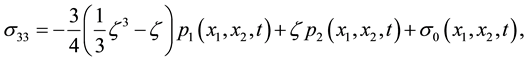
where, is the splitting parameter, the

functions and are defined as and

, , and. In the future consideration

and

We also will use the notation of the normalized components of the micropolar plate stress set

are defined as

(35)

(36)

(37)

(38)

(39)

(40)

(41)

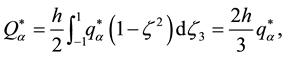
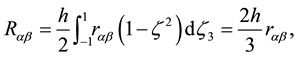
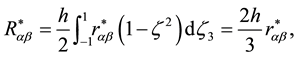
Here, and are the bending moments, and―the twisting moments,―the shear forces, and―the transverse shear forces,―the micropolar bending moments,―the micropolar twisting moments,―the micropolar couple moments, all defined per unit length.

3.2. Kinematics Assumptions

(42)

(43)

(44)

(45)

where

(46)

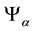
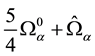
The terms represent the rotations, vertical displacement, describe microrotation

components, and 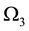the slope at the middle plane of the plate. Thus, the transverse variation effect of micro- rotations is not neglected in our kinematic assumptions.

The components of the corresponding micropolar plate strain set are defined as

(47)

(48)

(49)

(50)

(51)

(52)

(53)

The components of Cosserat plate strain can also be represented in terms of the components of set 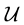by the following formulas:

(54)

The formulas (54) are called the Cosserat plate strain-displacement relation.

We also assume that the initial condition can be presented in the similar form:

4. Specification of HPR Variational Principle for the Cosserat Plate Dynamics

The HPR variational principle for a Cosserat plate dynamics is most appropriately expressed in terms of corres- ponding integrands calculated across the whole thickness. We also introduce the weighted characteristics of dis- placements, microrotations, strains and stresses of the plate, which will be used to produce the explicit forms of these integrands.

4.1. The Cosserat Plate Elastic Stress Energy Density

We define the plate stress energy density by the formula [20] ;

(55)

(56)

Then the stress energy of the plate P

(57)

where is the internal domain of the middle plane of the plate P.

4.2. The Cosserat Plate kinetic Energy Density

We define the plate stress energy density by the formula;

(58)

Taking into account the kinematics assumptions and integrating 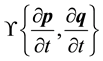with respect in we obtain the explicit plate stress energy density expression in the form:

Then the kinetic energy of the plate can be written

(59)

4.3. The Density of the Work Done over the Cosserat Plate Boundary

In the following consideration we also assume that the proposed stress, couple stress, and kinematic assumptions are valid for the lateral boundary of the plate P as well.

We evaluate the density of the work over the boundary.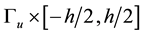

(60)

Taking into account the stress and couple stress assumptions (26)-(34) and kinematic assumptions (42)-(45) we are able to represent by the following expression:

(61)

where the sets and are defined as

and

In the above is the outward unit normal vector to

The density of the work over the boundary

can be presented in the form

where

(62)

Now is the outward unit normal vector to and

(63)

We are able to evaluate the work done at the top and bottom of the Cosserat plate by using boundary con- ditions (22) and (24)

4.4. The Cosserat Plate Internal Work Density

Here we define the density of the work done by the stress and couple stress over the Cosserat strain field:

(64)

Substituting stress and couple stress assumptions and integrating the expression (64) we obtain the following expression:

(65)

where is the Cosserat plate strain set of the the weighted averages of strain and torsion tensors

4.5. The Alternate Density Form of the Kinetic Energy

Here we define the density of the kinetic energy:

which can be presented in the form

where

5. Cosserat Plate HPR Dynamic Principle

Let denote the set of all admissible states that satisfy the Cosserat plate strain-displacement relation (54) and let be a HPR functional on defined by

(66)

for every Here and.

Then

is equivalent to the plate bending system of equations (A) and constitutive formulas (B) mixed problems.

A. The bending equilibrium system of equations:

(67)

(68)

(69)

(70)

(71)

(72)

where and, with the resultant traction boundary conditions:

(73)

(74)

at the part and the resultant displacement boundary conditions

(75)

at the part

The constitutive formulas have the following reverse form¹:

(76)

(77)

(78)

(79)

(80)

(81)

(82)

(83)

(84)

(85)

(86)

(87)

(88)

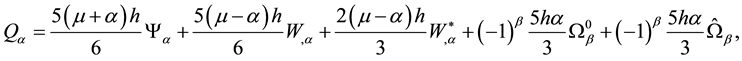
Proof of the principle. The variation of

where

where we call the compliance Cosserat plate tensor.

We apply Green’s theorem and integration by parts for and [23] to the expression:

Then based on the fact that and satisfy the Cosserat plate strain-displacement relation (54), we obtain

If s is a solution of the mixed problem, then

On the other hand, some extensions of the fundamental lemma of calculus of variations [23] together with the fact that and satisfy the Cosserat plate strain-displacement relation (54) imply that is a solution of the A and B mixed problems. The uniqueness proof is similar to [20] .

Remark. The above equilibrium equations and boundary conditions for the Cosserat plate can also be obtained by substituting polynomial approximations of stress and couple stress directly to the elastic equilibrium (1)-(2) and the boundary conditions (22)-(25) and collecting and equating to zero all coefficients of the resulting poly- nomials with respect to variable.

6. Micropolar Plate Dynamic Field Equations

In order to obtain the micropolar plate bending field equations in terms of the kinematic variables, we substitute the constitutive formulas in the reverse form (76)-(88) into the bending system of Equations (67)-(72). The micropolar plate bending field equations can be written in the following form:

(89)

where

The operators are defined as follows

where

The right-hand side, and therefore the solution are the functions of the splitting parameter. The opti- mal value of the parameter corresponds to the minimum of elastic energy over the micropolar strain field. The algorithm was described in [21] . The system (89) should be complemented with the boundary conditions. We describe the case of the hard simply supported boundary conditions in the numerical simulation section.

Numerical Simulation

Let us consider a square plate of thickness h. In our numerical computations we will consider a plate of thickness h = 0.1 m made of polyurethane foam, and the ratio varying from 5 to 30. The values of the technical elastic parameters for the polyurethane foam are reported in [1] :, , l_t = 0.62 mm, ,. These values correspond to the following values of Lamé and asymmetric para- meters:, , , , , (the ratio is equal to 1 for the bending).

The boundary is given by

and the hard simply supported boundary conditions can be represented in the following mixed Dirichlet- Neumann form [21] :

By applying the method of separation of variables for the two-dimensional eigenvalue problem (89) with the hard simply supported boundary conditions we obtain the kinematic variables in the following form:

(90)

and a standard eigenvalue problem for a system of 9 algebraic equations. Thus the model produces a spectrum of 9 infinite sequences of eigenfrequencies, which are related to the rotatory and flexural vibrations, particularly and correspond to the rotatory vibration of the middle plane,―flexural vibration,―transverse variation of flexural vibration, , ,―microrotatory vib- ration, and,―transverse variation of microrotatory vibration.

Preliminary computations show that only eigenfrequencies remain nonzero when asymmetric constants of Cosserat elasticity tend to zero. These frequencies corresponds to the free oscillation of the case of Mindlin-Reissner Plate. We can see that for the case the first iegenfrequencies in Figures 1-3.

We perform computations for different levels of the asymmetric microstructure by reducing the values of the elastic asymmetric parameters. Figure 4 illustrates the typical size effect of micropolar dynamic plate theory that predicts that micropolar plates made of smaller thickness has higher eigenfrequencies that would be expected on the basis of the Midlin-Reissner plate theory. Similar experimental behavior was reported in [1] for

torsion and bending of cylindrical rods of a Cosserat solid.

We also check how the total energy of the free oscillation depends of the value of the shear correction factor in the constitutive formulas:

(91)

(92)

We consider a rectangular plate of thickness. As we can see from Figure 5, the minimum value of the shear correction factor is shifted to the left by 4% - 5% depending on the geometry of the

plates. This result is consistent with the changes of this factor used in the Mindlin-Reissner plate theory.

7. Conclusion

This paper presents a mathematical model for the vibration of micropolar elastic plates. This model is based on the proposed generalization of Hellinger-Prange-Reissner (HPR) variational principle for the linearized micro- polar (Cosserat) elastodynamics. The modeling of the plate vibration is based on the HPR variational principle for the dynamics of Cosserat plates, which incorporates most of assumptions of the authors’ enhanced mathe- matical model for Cosserat plate deformation. The dynamic theory of the plates obtained from the dynamic

variational principle includes a system of dynamics equations and the constitutive relations. The preliminary computations of the rectangular plate vibration predict additional natural frequencies, which are related with the material microstructure and obey the size-effect principle similar to the known from the micropolar plate de- formation. The computations also show how natural frequencies of micropolar plate converge to classic Mindlin-Reissner plates and the total vibration energy can get 4% - 5% smaller depending on a parameter in the constitutive formulas and the geometry of the plates. These result are consistent with the modification (from 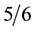to) of the similar parameter used in the Mindlin-Reissner plate theory.

References

NOTES

¹In the following formulas a subindex β = 1 if α = 2 and β = 2 if α = 1.