Applied Mathematics
Vol.06 No.03(2015), Article ID:54629,20 pages
10.4236/am.2015.63050
Viscous Dissipation and Radiation Effects on MHD Boundary Layer Flow of a Nanofluid Past a Rotating Stretching Sheet
M. Wahiduzzaman1*, Md. Shakhaoath Khan2, P. Biswas1, Ifsana Karim2, M. S. Uddin1
1Mathematics Discipline, Khulna University, Khulna, Bangladesh
2Discipline of Chemical Engineering, The University of Newcastle, Callaghan, Australia
Email: *wahidmathku@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 February 2015; accepted 12 March 2015; published 13 March 2015
ABSTRACT
Viscous dissipation and radiative heat transfer in nanofluid with the influence of magnetic field over a rotating stretching surface has been investigated numerically. The steady laminar boun- dary layer flow is considered in this study. The governing boundary-layer equations are formu- lated and transformed into nonlinear ordinary coupled differential equations by using similarity variables. The governing equations are solved numerically using the Nactsheim-Swigert Shooting iteration technique together with the Runge-Kutta six order iteration schemes with the help of a computer programming language Compaq Visual Fortran 6.6a. The simulation results are presented graphically to illustrate influence of well-known parameters on the velocity, temperature and concentration distributions as well as skin-friction coefficient, Nusselt and Sherwood number at the sheet.
Keywords:
Nanofluid, Viscous Dissipation, Thermal Radiation, Stretching Sheet, Nactsheim-Swigert Shooting Iteration Technique

1. Introduction
Crane [1] first obtained an elegant analytical solution to the boundary layer equations for the problem of steady two-dimensional flow due to a stretching surface in a quiescent incompressible fluid. Carragher and Crane [2] studied the heat transfer in the flow over a stretching surface in the case when the temperature difference between the surface and the ambient fluid is proportional to the power of distance from fixed point. Na and Pop [3] studied an unsteady flow past a stretching sheet. The thermal radiation effect is a new dimension added to the study of stretching surface has important applications in physics and engineering particularly in space technology and high temperature process. It plays an important role in controlling the heat transfer process in polymer processing industry. The study of radiative heat transfer within the influence of magnetic field over a stretching surface has newly arrived. Pop et al. [4] investigated the flow over stretching sheet near a stagnation point taking the effect of thermal radiation. The research of nanofluids has gained huge attention in recent years. Jang and Choi [5] investigated the analysis of convective instability and heat transfer characteristics of the nanofluids. Jang and Choi [6] studied the effect of various parameters on nanofluid thermal conductivity. Kumar [7] inves- tigated the radiative heat transfer with the viscous dissipation effect in the presence of transverse magnetic field. Khan and Pop [8] have investigated boundary layer flow of a nanofluid past a stretching sheet. Very recently a number of studies of MHD boundary layer fluid (e.g., nanofluid) flow with the effects of thermal radiation, vis- cous dissipation and Nanofluid were reported in the literature [9] - [25] . But the effect of rotation is still not get- ting promising attraction to the researchers.
Our prime objective is to extend analysis of Khan and Pop [8] . This study finds the effect of rotation, thermal radiation and viscous dissipation on boundary layer flow of nanofluid past a stretching sheet of a rotating sys- tem.
2. Methods: Mathematical Model
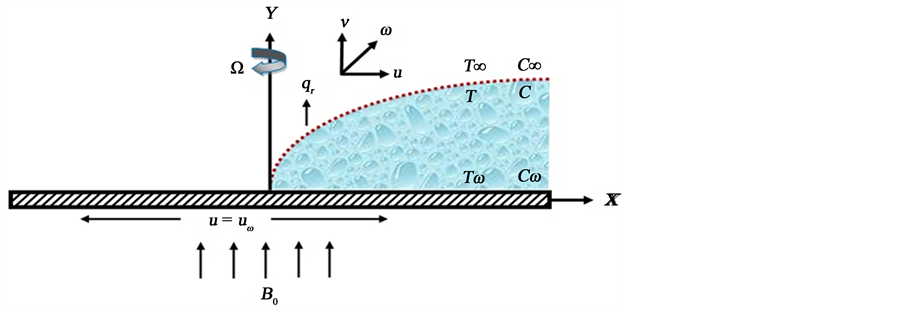
The steady two dimensional boundary layer flow of a nanofluid past a stretching surface of a rotating system is considered with the linear stretching velocity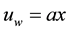 , where
, where 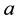 constant and x is coordinate measured along the stretching surface. The flow takes place at
constant and x is coordinate measured along the stretching surface. The flow takes place at 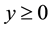 where y is the coordinate measured normal to the stretch- ing surface. A steady uniform stress leading to equal and opposite forces is applied along the x-axis, so that the sheet is stretched keeping the origin fixed. The sketch of the physical configuration and coordinate system are shown in Figure 1 by following Khan and Pop [8] .
where y is the coordinate measured normal to the stretch- ing surface. A steady uniform stress leading to equal and opposite forces is applied along the x-axis, so that the sheet is stretched keeping the origin fixed. The sketch of the physical configuration and coordinate system are shown in Figure 1 by following Khan and Pop [8] .
It is assumed that at the stretching surface, the temperature  and the concentration
and the concentration 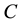 takes constant value
takes constant value  and
and 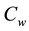 respectively. The ambient values attained as
respectively. The ambient values attained as  tends to infinity of
tends to infinity of  and
and 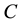 are denoted by
are denoted by 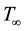 and
and 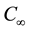 respectively. A uniform magnetic field B is imposed to the plate. The magnetic vector
respectively. A uniform magnetic field B is imposed to the plate. The magnetic vector 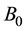 can be taken as
can be taken as 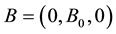 and
and  is the radiative heat flux in the y-direction. The velocity of the plate (uniform velocity) considered as
is the radiative heat flux in the y-direction. The velocity of the plate (uniform velocity) considered as . Also a and b are the linear constant parameter, l is the characteristics length and
. Also a and b are the linear constant parameter, l is the characteristics length and



Figure 1. Physical configuration of the flow.



and the boundary condition for the model is

where, 




In order to find a similarity solution to the Equations (2) to (5) with boundary conditions (6), the following similarity transformations, dimensionless variables are used in the rest of analysis:

From the above transformations the non-dimensional, nonlinear, coupled ordinary differential equations are obtained as:




The transformed boundary conditions are as follows:

where the notation primes denote differentiation with respect to 



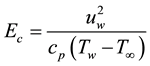
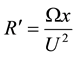

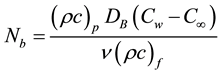



The physical quantities of importance in stretching sheet transport modeling [10] [11] are the skin friction coefficient, the reduced Nusselt number, and reduced Sherwood number, which are calculated respectively by the following equations:
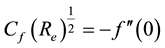
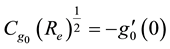

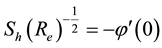
where 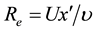

The governing equations are transformed into nonlinear ordinary differential equations which depends on the Magnetic parameter, the Radiation parameter, the Prandtl number, the Eckert number, the Rotational parameter, the Lewis number, the Brownian motion parameter, the Thermophoresis parameter, Stretching parameter and constant parameter respectively.
3. Numerical Technique
The obtained non-linear coupled ordinary differential Equations (8)-(11) with boundary condition (12) are solved numerically using Nactsheim-Swigert shooting technique together with Runge-Kutta six order iteration schemes [26] . For the purpose of this method, the Nactsheim-Swigert shooting iteration technique [26] together with Runge-Kutta six order iteration scheme is taken and determines the temperature and concentration as a function of the coordinate
4. Results and Discussion
The heat and mass transfer problem associated with laminar flow of the nanofluids past a stretching surface of a rotating system has been studied. In order to investigated the physical representation of the problem, the numeri- cal values of primary velocity, secondary velocity, temperature and species concentration with the boundary layer have been computed for different parameters as the Magnetic parameter


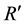






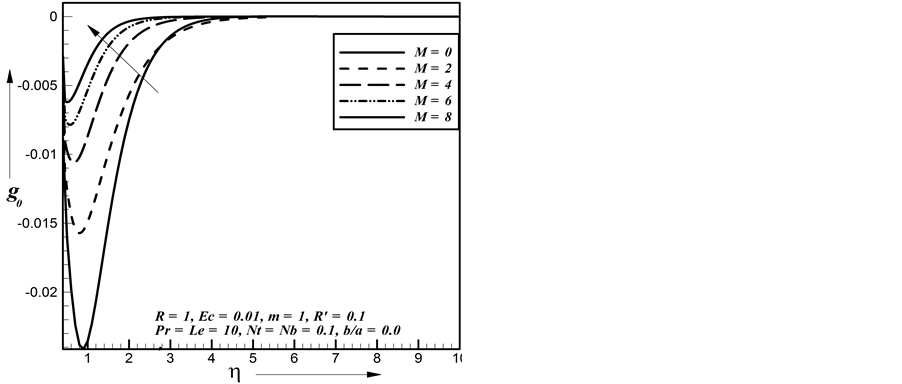
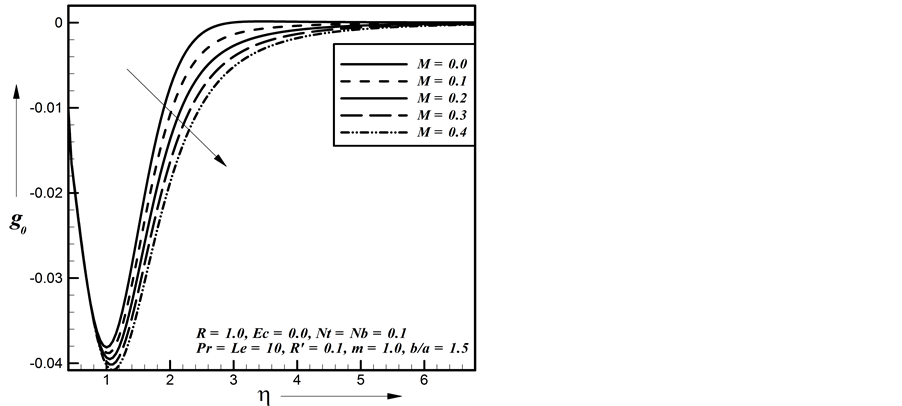
In Figures 3-6, dimensionless secondary velocity distribution is plotted for different values of Magnetic pa- rameter M, Here consider the values of Stretching parameter
Figure 2. Effect of M on primary velocity profiles.
Figure 3. Effect of M on secondary velocity profiles.
Figure 4. Effect of M on secondary velocity profiles when b/a = 0.5.
Figure 5. Effect of M on secondary velocity profiles when b/a = 1.0.
Figure 6.Effect of M on secondary velocity profiles when b/a = 1.5.
Magnetic parameter increases the secondary velocity increases gradually when 




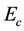


Figure 7. Effect of R’ on secondary velocity profiles.
Figure 8. Effect of b/a on temperature profiles.
Figure 9. Effect of Nb on temperature profiles.
Figure 10. Effect of m on temperature profiles.
Figure 11. Effect of Ec on temperature profiles
Figure 12. Effect of Le on temperature profiles.
Figure 13. Effect of Leon temperature profiles.
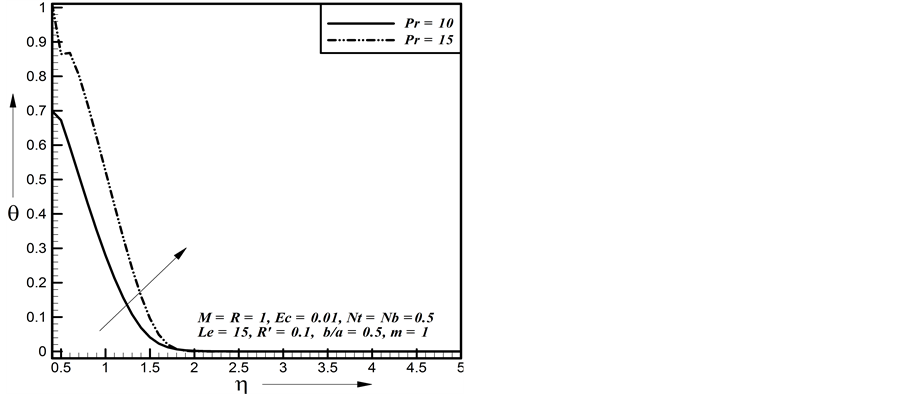
the Lewis number increases the temperature decreases gradually. In Figure 14, the dimensionless temperature distribution is plotted for different values of Magnetic parameter M. It is observed that as the Magnetic parameter increases the temperature increases gradually. In Figure 15, the dimensionless temperature distribution is plotted for different values of Prandtl number


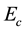



For the physical interest of the problem, the dimensionless skin-friction coefficient 
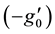
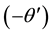


Figure 26 represents the primary shear stress 


Figure 27 represents the primary shear stress 


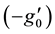

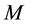
Figure 14. Effect of M on temperature profiles.
Figure 15. Effect of Pr on temperature profiles.
Figure 16. Effect of R on temperature profiles.
Figure 17. Effect of R’ on temperature profiles.
Figure 18. Effect of b/a on concentration profiles.
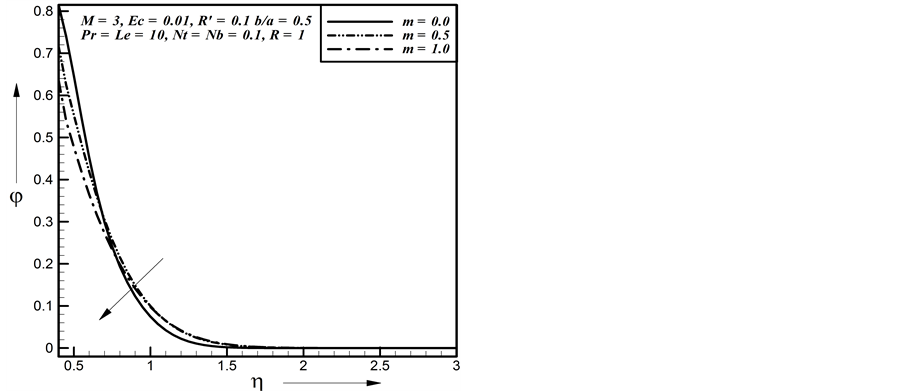
Figure 19. Effect of m on concentration profiles.
Figure 20. Effect of Ec on concentration profiles.
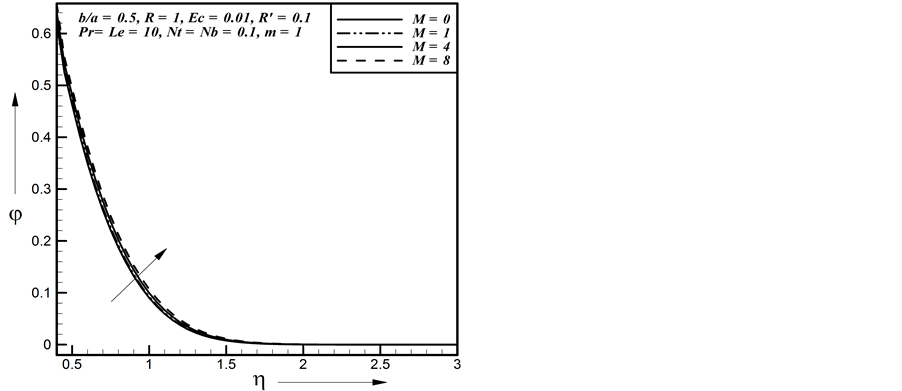
Figure 21. Effect of M on concentration profiles.
Figure 22. Effect of R on concentration profiles.
Figure 23. Effect of Le on concentration profiles.
Figure 24. Effect of Nt on concentration profiles.
Figure 25. Effect of Nb on concentration profiles.
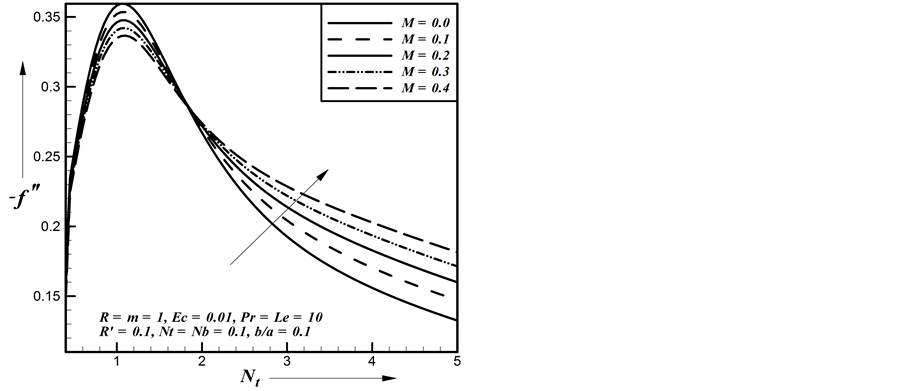
Figure 26. Effect of M on primary shear stress.
Figure 27. Effect of M on primary shear stress.
Figure 28. Effect of M on secondary shear stress.
Figure 29. Effect of M on secondary shear stress.
Figure 30. Effect of M on secondary shear stress.
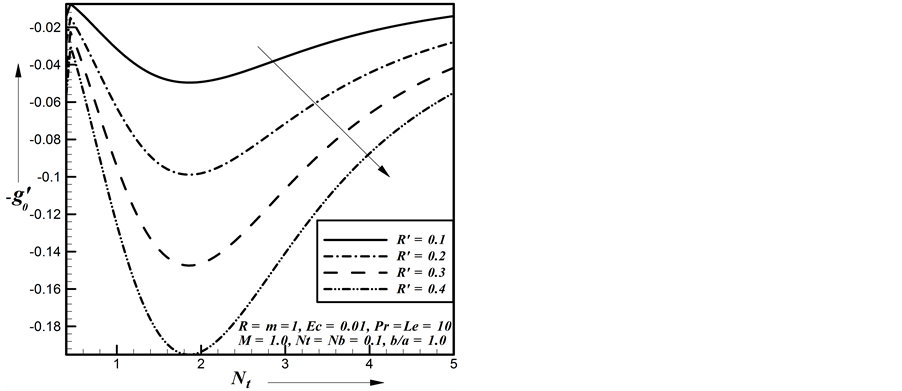
Figure 31. Effect of R’ on secondary shear stress.
Figure 32. Effect of m on heat transfer rate.
Figure 33. Effect of Ec on heat transfer rate.
Figure 34. Effect of Nb on heat transfer rate.
Figure 35. Effect of Pr on heat transfer rate.
Figure 36. Effect of R on heat transfer rate.
Figure 37. Effect of Le on mass transfer rate.
Figure 38. Effect of Nb on mass transfer rate.
Magnetic parameter increases the secondary shear stress increases gradually. Figure 29 represents the se- condary shear stress 




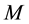
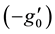
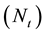

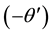





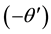
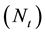
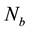




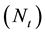




Figure 38 represents the dimensionless mass transfer rate 


The performances of the dimensionless skin-friction coefficient, dimensionless heat transfer rate and dimen- sionless mass transfer rate with the function of Thermophoresis parameter are concluded in Table 1.
5. Conclusions
Laminar boundary layer flow of a nanofluid has been investigated for steady flow past a stretching surface of rotating system with the influence of magnetic field and thermal radiation. The results are presented for various parameters. The velocity, temperature and concentration distributions for different parameters are shown graphically. The important findings of the investigation from graphical representation are listed below:
Table 1. Different behavior of the skin-friction coefficient, heat transfer rate, dimensionless mass transfer rate.
a) The temperature and concentration boundary layer thickness increases due to increase of magnetic parameter for nanofluids.
b) The temperature boundary layer thickness increases due to increase of Brownian motion parameter. Also the heat transfer rate at the sheet increases for increasing value of Brownian motion parameter and Thermophoresis parameter. The concentration boundary layer thickness increases due to increase of Thermophoresis parameter and concentration boundary layer thickness decreases due to increase of Brownian motion parameter. Also the mass transfer rate at the sheet decreases due to decrease of Brownian motion parameter.
c) The temperature and concentration boundary layer thickness decreases due to increase of stretching parameter.
d) The temperature boundary layer thickness increases due to increase of constant parameter and concentration boundary layer thickness decreases due to increase of constant parameter. Also the surface heat transfer rate is decreased.
e) The temperature boundary layer thickness increases due to increase of Radiation parameter whereas concentration boundary layer thickness decreases due to increase of Radiation parameter. Also the surface heat transfer rate is increased.
f) The temperature boundary layer thickness increases due to increase of Eckert number where as concentration boundary layer thickness decreases due to increase of Eckert number. Also the surface heat transfer rate is increased.
g) The temperature boundary layer thickness increases due to increase of Rotational parameter for nanofluids.
h) The temperature boundary layer thickness as well as the concentration boundary layer thickness decreases due to increase of Lewis number. Also the mass transfer rate at the sheet decreases.
i) The primary velocity profiles decreases for increasing Magnetic parameter when the stretching parameter takes the value zero but when the Stretching parameter takes value 0.1 then the primary velocity profiles increases. The secondary velocity profiles increase for increasing Magnetic parameter when the stretching parameter takes the value zero, but when the Stretching parameter takes the value (0.5 to 1.5 in present study) then the secondary velocity profiles decreases.
References
- Crane, L.J. (1970) Flow Past a Stretching Plate. Journal of Applied Mathematics and Physics, 21, 645-647. http://dx.doi.org/10.1007/BF01587695
- Carragher, P. and Crane, L. (1982) Heat Transfer on Continuous Stretching Sheet. Journal of Applied Mathematics and Mechanics, 62, 564-565. http://dx.doi.org/10.1002/zamm.19820621009
- Na, T.Y. and Pop, I. (1996) Unsteady Flow Past a Stretching Sheet. Mechanics Research Communications, 23, 413- 422. http://dx.doi.org/10.1016/0093-6413(96)00040-7
- Pop, S.R., Grosan, T. and Pop, I. (2004) Radiation Effects on the Flow near the Stagnation Point of a Stretching Sheet. Technische Mechanik, 25, 100-106.
- Kim, J., Kang, Y.T. and Choi, C.K. (2004) Analysis of Convective Instability and Heat Transfer Characteristics of Nanofluids. Physics of Fluids, 16, 2395-2401. http://dx.doi.org/10.1063/1.1739247
- Jang, S.P. and Choi, S.U.S. (2007) Effects of Various Parameters on Nanofluid Thermal Conductivity. Journal of Heat Transfer, 129, 617-623. http://dx.doi.org/10.1115/1.2712475
- Kumar, H. (2009) Radiative Heat Transfer with Hydromagnetic Flow and Viscous Dissipation over a Stretching Surface in the Presence of Variable Heat Flux. Thermal Science, 13, 163-169.
- Khan, W.A. and Pop, I. (2010) Boundary-Layer Flow of a Nanofluid Past a Stretching Sheet. International Journal of Heat and Mass Transfer, 53, 2477-2483. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.01.032
- Bég, O.A., Khan, M.S., Karim, I., Alam, M.M. and Ferdows, M. (2013) Explicit Numerical Study of Unsteady Hydro- magnetic Mixed Convective Nanofluid Flow from an Exponentially Stretching Sheet in Porous Media. Applied Nanoscience, 4, 943-957. http://dx.doi.org/10.1007/s13204-013-0275-0
- Ferdows, M., Khan, M.S., Alam, M.M. and Sun, S. (2012) MHD Mixed Convective Boundary Layer Flow of a Nanofluid through a Porous Medium Due to an Exponentially Stretching Sheet. Mathematical Problems in Engineering, 2012, Article ID: 408528. http://dx.doi.org/10.1155/2012/408528
- Ferdows, M., Khan, M.S., Bég, O.A., Azad, M.A.K. and Alam, M.M. (2013) Numerical Study of Transient Magnetohydrodynamic Radiative Free Convection Nanofluid Flow from a Stretching Permeable Surface. Journal of Process Mechanical Engineering, 228, 181-196. http://dx.doi.org/10.1177/0954408913493406
- Karim, I., Alam, M.M. and Khan, M.S. (2012) Effects of Heat Generation on Salt Water Flow through in an Ocean by Inclined Angle. 5th BSME International Conference on Thermal Engineering, Paper No. 208, IUT, Dhaka, 1-6.
- Khan, M.S., Karim, I., Islam, M.S. and Wahiduzzaman, M. (2014) MHD Boundary Layer Radiative, Heat Generating and Chemical Reacting Flow Past a Wedge Moving in a Nanofluid. Nano Convergence, 1, 20. http://dx.doi.org/10.1186/s40580-014-0020-8
- Khan, M.S., Alam, M.M. and Ferdows, M. (2011) Finite Difference Solution of MHD Radiative Boundary Layer Flow of a Nanofluid Past a Stretching Sheet. Proceeding of the International Conference of Mechanical Engineering 2011 (ICME 11), FL-011, BUET, Dhaka, 1-7.
- Khan, M.S., Alam, M.M. and Ferdows, M. (2011) MHD Radiative Boundary Layer Flow of a Nanofluid Past a Stretching Sheet. Proceeding of the International Conference of Mechanical Engineering and Renewable Energy (ICMERE 11), PI-105, CUET, Chittagong, 1-6.
- Khan, M.S., Alam, M.M. and Ferdows, M. (2013) Effects of Magnetic Field on Radiative Flow of a Nanofluid Past a Stretching Sheet. Procedia Engineering, 56, 316-322. http://dx.doi.org/10.1016/j.proeng.2013.03.125
- Khan, M.S., Alam, M.M. and Ferdows, M. (2015) Rotationg Fluid Flow on MHD Radiative Nanofluid Past a Stretching Sheet. Archives Des Sciences, Accepted.
- Khan, M.S., Karim, I., Ali, L.E. and Islam, A. (2012) Unsteady MHD Free Convection Boundary-Layer Flow of a Nano- fluid along a Stretching Sheet with Thermal Radiation and Viscous Dissipation Effects. International Nano Letters, 2, 24. http://dx.doi.org/10.1186/2228-5326-2-24
- Khan, M.S., Karim, I. and Biswas, H.A. (2012) Heat Generation, Thermal Radiation and Chemical Reaction Effects on MHD Mixed Convection Flow over an Unsteady Stretching Permeable Surface. International Journal of Basic and Applied Science, 1, 363-377.
- Khan, M.S., Karim, I. and Biswas, H.A. (2012) Non-Newtonian MHD Mixed Convective Power-Law Fluid Flow over a Vertical Stretching Sheet with Thermal Radiation, Heat Generation and Chemical Reaction Effects. Academic Research International, 3, 80-92.
- Khan, M.S., Karim, I. and Islam, M.S. (2014) MHD Buoyancy Flows of Cu, Al2O3 and TiO2 Nanofluid near Stagnation-Point on a Vertical Plate with Heat Generation. Physical Science International Journal, 4, 754-767. http://dx.doi.org/10.9734/PSIJ/2014/9074
- Khan, M.S., Karim, I. and Islam, M.S. (2014) Possessions of Chemical Reaction on MHD Heat and Mass Transfer Nanofluid Flow on a Continuously Moving Surface. American Chemical Science Journal, 4, 401-415. http://dx.doi.org/10.9734/ACSJ/2014/5422
- Khan, M.S., Wahiduzzaman, M., Karim, I., Islam, M.S. and Alam, M.M. (2014) Heat Generation Effects on Unsteady Mixed Convection Flow from a Vertical Porous Plate with Induced Magnetic Field. Procedia Engineering, 90, 238- 244. http://dx.doi.org/10.1016/j.proeng.2014.11.843
- Khan, M.S., Wahiduzzaman, M., Sazad, M.A.K. and Uddin, M.S. (2012) Finite Difference Solution of MHD Free Convection Heat and Mass Transfer Flow of a Nanofluid along a Stretching Sheet with Heat Generation Effects. Indian Journal of Theoretical Physics, 60, 285-306.
- Wahiduzzaman, M., Khan, M.S. and Karim, I. (2015) MHD Convective Stagnation Flow of Nanofluid over a Shrinking Surface with Thermal Radiation, Heat Generation and Chemical Reaction. Procedia Engineering, Accepted.
- Nachtsheim, P.R. and Swigert, P. (1965) Satisfaction of the Asymptotic Boundary Conditions in Numerical Solution of the System of Non-Linear Equations of Boundary Layer Type. NASA, TND-3004, Washington DC.
NOTES
*Corresponding author.