Applied Mathematics
Vol.06 No.01(2015), Article ID:53062,16 pages
10.4236/am.2015.61009
Symmetry Analysis for MHD Viscous Flow and Heat Transfer over a Stretching Sheet
Hossam S. Hassan
Department of Basic and Applied Science, Arab Academy for Science, Technology and Maritime Transport, Alexandria, Egypt
Email: hossams@aast.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 October 2014; revised 22 November 2014; accepted 10 December 2014
ABSTRACT
This work deals with the boundary layer flow and heat transfer of an electrically conducting viscous fluid over a stretching sheet. Lie-group method is applied for determining the symmetry reductions for the governing equations by reducing the number of independent variables in the given system of partial differential equations by one, leading to a system of non-linear ordinary differential equation. The resulting system is then solved numerically using shooting method coupled with Runge-Kutta scheme. Effects of various values of physical parameters on the horizontal and vertical velocities, temperature profiles, wall heat transfer and the wall shear stress (skin friction), have been studied and the results are plotted. Furthermore, a comparison between the present results with existing numerical and homotopy methods has been reported and we found that they are in a good agreement.
Keywords:
MHD Flow, Viscous Flow, Stretching Sheet, Lie-Group, Similarity Solution

1. Introduction
The boundary layer flow and heat transfer of an incompressible viscous fluid over a stretching sheet appear in several manufacturing processes of industry such as the aerodynamic extrusion of plastic sheets, the extrusion of polymers, hot rolling, the cooling of metallic plates, glass-fiber production, etc., [1] .
Sakiadis [2] presented the pioneering work in this field. He investigated the flow induced by a semi-infinite horizontally moving wall in an ambient fluid.
Crane [3] studied the flow over a linearly stretching sheet in an ambient fluid and gave a similarity solution in closed analytical form for the steady two-dimensional problem. He presented a closed form exponential solution for the planar viscous flow of linear stretching case.
Gupta and Gupta [4] investigated the effect of mass transfer on the Crane flow. They analyzed the viscous flow and heat transfer by an isothermal stretching sheet with suction/injection.
Chiam [5] studied the boundary layer flow due to a plate stretching with a power-low velocity distribution in presence of a magnetic field. To yield similarity equations, a special form of the magnetic field is chosen. He presented linearized solutions for the case of large magnetic parameters and derived an expression for the skin friction coefficient using Crocco’s transformation and compared it numerically using Runge-Kutta shooting algorithm with Newton iteration.
Vajravelu [6] studied flow and heat transfer in a viscous fluid over a non-linear stretching sheet. In his study, the heat transfer is analyzed when the sheet is maintained at a constant temperature and the viscous dissipation is neglected. He used a fourth-order Runge-Kutta integration scheme to solve the resulting nonlinear differential equations.
Cortell [7] presented a numerical analysis for the flow and heat transfer in a viscous fluid over a nonlinear stretching sheet by employing a novel numerical procedure. In his work, he studied two cases for the nonlinear stretching sheet, with constant surface temperature and with prescribed surface temperature. The resulting nonlinear ordinary differential equations after converting the governing partial differential equations by a similarity transformation are solved using Runge-Kutta scheme.
Abbas and Hayat [8] studied the radiation effects on the magnetohydrodynamic (MHD) flow of an incompressible viscous fluid in a porous space. In their study, they extended the analysis of Cortell [7] by considering a MHD flow, analyzed the flow in a porous medium, included the radiation effects and provided analytic solution namely homotopy analysis method (HAM) instead of numerical technique applied in [7] . Hayat et al. [9] investigated the magnetohydrodynamic (MHD) boundary layer flow by employing the modified Adomian decomposition method and the Padé approximation and developed the series solution of the governing non-linear problem.
Ghotbi [10] considered the problem of the boundary layer flow of an incompressible viscous fluid over a non- linear stretching sheet. In order to obtain analytical solution of the governing nonlinear differential equations, HAM is applied.
Mehmood et al. [11] reported the corrections to HAM results presented in [10] . A comparison between their HAM solution and the exact solution obtained by Pavlov [12] was made and it was in a good agreement.
Javed et al. [13] investigated the boundary layer flow and heat transfer analysis of electrically conducting viscous fluid over a nonlinearly shrinking sheet. They used a similarity transformation to reduce the governing partial differential equations to a set of nonlinear ordinary differential equations. The resulting system of equations is then solved numerically using an implicit finite difference scheme known as Keller-box method.
Fathizadeh et al. [14] employed the modification of the homotopy perturbation method to solve the MHD boundary-layer equations. In their work, the viscous fluid is electrically conducting in the presence of a uniform applied magnetic field and the induced magnetic field is neglected for small magnetic Reynolds number. They obtained the similarity solutions of ordinary differential equation resulting from the momentum equation. Some numerical comparisons among the new modified homotopy perturbation method, the standard homotopy perturbation, the exact solution and the shooting method are obtained.
In this paper, we shall investigate the solution of the MHD boundary layer flow for an incompressible viscous fluid over a sheet stretching according to a power-law velocity. Lie-group theory is applied to the equations of motion for determining symmetry reductions of partial differential equations [15] - [30] . The resulting system of nonlinear differential equations is then solved numerically using shooting method coupled with Runge-Kutta scheme. Our results are compared with the work of [5] - [14] .
2. Mathematical Formulation of the Problem
We consider the MHD flow over a flat plate coinciding with the plane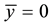 , of an incompressible viscous fluid with heat transfer. The wall is stretched horizontally by applying on both sides two equal and opposite forces along the
, of an incompressible viscous fluid with heat transfer. The wall is stretched horizontally by applying on both sides two equal and opposite forces along the 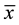 -axis to keep the origin fixed. The fluid is electrically conducting under the influence of an applied magnetic field
-axis to keep the origin fixed. The fluid is electrically conducting under the influence of an applied magnetic field 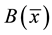 in the
in the 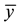 -direction normally to the stretching sheet, Figure 1.
-direction normally to the stretching sheet, Figure 1.
The induced magnetic field is neglected. Under these assumptions, the continuity, momentum and energy equations become
Figure 1. Physical model and coordinate system.
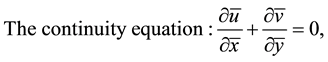 (2.1)
(2.1)
 (2.2)
(2.2)
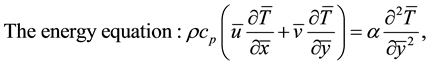 (2.3)
(2.3)
where  and
and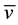 , are the velocity components in the
, are the velocity components in the  and
and 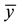 directions, respectively,
directions, respectively, 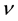 is the kinematic viscosity,
is the kinematic viscosity, 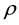 is the fluid density,
is the fluid density, 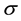 is the electrical conductivity of the fluid,
is the electrical conductivity of the fluid, 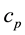 is the specific heat of the fluid at constant pressure,
is the specific heat of the fluid at constant pressure, 

The magnetic field is defined by

where 

The boundary conditions are

where 



The variables in Equations (2.1)-(2.5) are dimensionless according to

where 
Substitution from Equation (2.6) into Equations (2.1)-(2.3) gives



where, 



The boundary conditions Equation (2.5) will be

From the continuity Equation (2.7) there exist stream function 

which satisfies Equation (2.7) identically.
Substituting from Equation (2.11) into Equations (2.8)-(2.9), yields


where subscripts denote partial derivatives.
The boundary conditions Equation (2.8) will be

3. Solution of the Problem
Firstly, we derive the similarity solutions using Lie-group method under which Equations (2.12)-(2.13) and the boundary conditions Equation (2.14) are invariant, and then we use these symmetries to determine the similarity variables.
Consider the one-parameter 


where “
A system of partial differential Equations (2.12)-(2.13) is said to admit a symmetry generated by the vector field
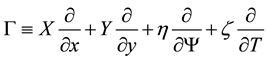
if it is left invariant by the transformation
The solutions 

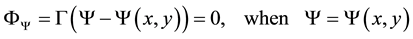
and

Assume,


A vector 

where,

is the third prolongation of
To calculate the prolongation of the given transformation, we need to differentiate Equation (3.1) with respect to each of the variables, 

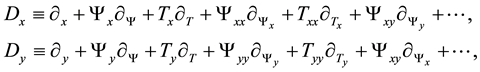
Equation (3.7) gives the following linear partial differential equation


The components

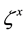






where 



Invariance of the boundary conditions Equation (2.14i), yields

Substitution from Equations (3.12)-(3.13) into Equation (3.11) will lead to a large expression, then, equating to zero the coefficients of






Substitution from Equation (3.14) into Equation (3.11) will remove many terms. Then, equating to zero the coefficients of 



Again, substitution from Equations (3.12)-(3.16) into Equation (3.10) will remove many terms. Then, equating to zero the coefficients of






and

Solving the system of Equations (3.14)-(3.18) in view of the invariance of the boundary conditions Equation (2.14), yields

The system of nonlinear Equations (2.12)-(2.13) has the three-parameter Lie group of point symmetries generated by

The one-parameter group generated by 



The finite transformations corresponding to the symmetries



where


We look for solutions that invariant under the linear combination of the operators given by Equation (3.20). By determine the one-dimensional optimal system of subalgebras of the given partial differential equation, all of these solutions can be obtained. Olver’s approach given in [17] starts out by computing the commutators of the
Table 1. Table of commutators of the basis operators.
symmetry Lie algebra Equation (3.20) and then obtaining the adjoint representations. The adjoint action on Lie algebras is defined by the adjoint operator given by

where, 
In terms of Lie brackets using Campbell-Baker-Hausdorff theorem [31] , this operator can be rewritten as

In our problem, 
To construct the one-dimensional optimal system of


for some constants






Let,
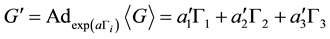
We make appropriate choice of 


By substitution 

Now, Equation (3.26) prompts the consideration of the cases 

Case (1):
By choosing 


We can further consider the subcases 



Case (2):
Using repeatedly the adjoint operation to simplify


In summary, the optimal system of one-dimensional subalgebras of the symmetry Lie algebra is

Table 3 shows the solution of the invariant surface conditions associated with the optimal system.
(i) Solutions invariant under
The characteristic
Table 2. Table of adjoint representations.
Table 3. Solutions of the invariant surface conditions associated with the optimal system.
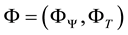
has the components

Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are

where 
Substitution from Equation (3.31) into Equations (2.12)-(2.13), yields


where, 


The boundary conditions Equation (2.14) will be

(ii) Solutions invariant under
The characteristic Equation (3.29) has the components

Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are

Practically, Equation (3.36) is a solution of Equations (2.12)-(2.13), even though it is not a particularly interesting one which contradicts the boundary conditions Equation (2.14). So, no solutions are invariant under the group generated by
(iii) Solutions invariant under
The characteristic Equation (3.29) has the components

Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are

where 

(iv) Solutions invariant under
The characteristic Equation (3.29) has the components

Therefore, the general solutions of the invariant surface conditions Equations (3.3)-(3.4) are

This contradicts the boundary conditions Equation (2.14). So, no solutions are invariant under the group generated by
4. Results and Discussion
The system of non-linear differential Equations (3.32)-(3.33) with the boundary conditions Equation (3.34) is solved numerically using the shooting method, coupled with Runge-Kutta scheme. From Equations (2.11) and (3.31), we get

The effects of the parameter 





4.1. The Horizontal Velocity
Figure 2 illustrates the effect of 






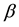
Figure 3 describes the effect of 



4.2. The Vertical Velocity
Figure 4 shows the behaviour of the vertical velocity 



Figure 5 illustrates the behaviour of the vertical velocity 




Figure 2. Horizontal velocity profiles over a range of 




Figure 3. Horizontal velocity profiles over a range of 



4.3. The Temperature
Figure 6 illustrates the variation of the temperature profiles 




Figure 7 describes the distribution of the temperature 




Figure 8 shows the variation of the temperature profiles 




4.4. Wall Shear Stress
The dimensionless wall shear stress 







Figure 4. Vertical velocity profiles over a range of 


Figure 5. Vertical velocity profiles over a range of 


the layer thickness decreases with an increase in the skin friction at the wall which may cause to lose the smoothness of the stretching wall. So, by increasing the value of
Tables 5-8 show the numerical values of 











Figure 6. Temperature profiles over a range of 


Figure 7. Temperature profiles over a range of 


Figure 8. Temperature profiles over a range of 


Table 4. Comparison between the values of 


Table 5. Comparison between the values of 


Table 6. Comparison between the values of 


Table 7. Comparison between the values of 


Table 8. Comparison between the values of 



Table 9. Comparison between the values of 



Table 10. Comparison between the values of 



Table 11. Numerical values of 



4.5. Wall Shear Stress
Table 9 illustrates the numerical values of the surface heat flux 






Also, from Table 9, it is noticed that, for fixed value of




Another comparison between the present work with the work of Vajravelu [6] is made, see Table 10.
Table 11 illustrates the numerical values of the surface heat flux 





5. Conclusion
We have used Lie-group method to obtain the similarity reductions of the MHD boundary-layer equations. By determining the transformation group under which the given system of partial differential equations and its boundary conditions are invariant, we obtained the invariants and the symmetries of these equations. In turn, we used these invariants and symmetries to determine the similarity variables that reduced the number of independent variables. The resulting system of ordinary differential equations was solved numerically using shooting method coupled with Runge-Kutta scheme and the results were plotted. The numerical values of the wall shear stress (skin friction) and surface heat flux were compared with those obtained by other works and they were found in a good agreement.
Acknowledgements
The author would like to express his appreciations for the potential reviewers for their valuable comments that improved the paper and enhanced the results.
References
- Pop, S.R., Grosan, T. and Pop, I. (2004) Radiation Effects on the Flow near the Stagnation Point of a Stretching Sheet. Technische Mechanik, 25, 100-106.
- Sakiadis, B.C. (1961) Boundary Layer Behaviour on Continuous Solid Surfaces, II. The Boundary Layer on a Continuous Flat Surface. AIChE Journal, 7, 221-225. http://dx.doi.org/10.1002/aic.690070211
- Crane, L.J. (1970) Flow past a Stretching Plate. Journal of Applied Mathematics and Physics (ZAMP), 21, 645-647. http://dx.doi.org/10.1007/BF01587695
- Gupta, P.S. and Gupta, A.S. (1977) Heat and Mass Transfer on a Stretching Sheet with Suction or Blowing. Canadian Journal of Chemical Engineering, 55, 744-746. http://dx.doi.org/10.1002/cjce.5450550619
- Chaim, T.C. (1995) Hydromagnetic Flow over a Surface Stretching with a Power-Law Velocity. International Journal of Engineering Science, 33, 429-435. http://dx.doi.org/10.1016/0020-7225(94)00066-S
- Vajravelu, K. (2001) Viscous Flow over a Nonlinearly Stretching Sheet. Applied Mathematics and Computation, 124, 281-288. http://dx.doi.org/10.1016/S0096-3003(00)00062-X
- Cortell, R. (2007) Viscous Flow and Heat Transfer over a Nonlinearly Stretching Sheet. Applied Mathematics and Computation, 184, 864-873. http://dx.doi.org/10.1016/j.amc.2006.06.077
- Abbas, Z. and Hayat, T. (2008) Radiation Effects on MHD Flow in a Porous Space. International Journal of Heat and Mass Transfer, 51, 1024-1033. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.05.031
- Hayat, T., Hussain, Q. and Javed, T. (2009) The Modified Decomposition Method and Padé Approximants for the MHD Flow over a Non-Linear Stretching Sheet. Nonlinear Analysis: Real World Applications, 10, 966-973. http://dx.doi.org/10.1016/j.nonrwa.2007.11.020
- Ghotbi, A.R. (2009) Homotopy Analysis Method for Solving the MHD Flow over a Non-Linear Stretching Sheet. Communications in Nonlinear Science and Numerical Simulation, 14, 2653-2663.
- Mehmood, A., Munawar, S. and Ali, A. (2010) Comments to: ‘‘Homotopy Analysis Method for Solving the MHD Flow over a Non-Linear Stretching Sheet (Commun. Nonlinear Sci. Numer. Simul. 14 (2009) (2653-2663)”. Communications in Nonlinear Science and Numerical Simulation, 15, 4233-4240. http://dx.doi.org/10.1016/j.cnsns.2009.12.039
- Pavlov, K.B. (1974) Magnetohydrodynamic Flow of an Incompressible Viscous Fluid Caused by Deformation of a Surface. Magnitnaya Gidrodinamika, 4, 146-147.
- Javed, T., Abbas, Z., Sajid, M. and Ali, N. (2011) Heat Transfer Analysis for a Hydromagnetic Viscous Fluid over a Non-Linear Shrinking Sheet. International Journal of Heat and Mass Transfer, 54, 2034-2042. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.12.025
- Fathizadah, M., Madani, M., Khan, Y., Faraz, N., Yıldırım, A. and Tutkun, S. (2013) An Effective Modification of the Homotopy Perturbation Method for MHD Viscous Flow over a Stretching Sheet. Journal of King Saud University- Science, 25, 107-113. http://dx.doi.org/10.1016/j.jksus.2011.08.003
- Hill, J.M. (1982) Solution of Differential Equations by Means of One-Parameter Groups. Pitman Publishing Company, Boston.
- Seshadri, R. and Na, T.Y. (1985) Group Invariance in Engineering Boundary Value Problems. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-5102-6
- Olver, P.J. (1986) Applications of Lie Groups to Differential Equations. Springer-Verlag, New York.
- Ibragimov, N.H. (1999) Elementary Lie Group Analysis and Ordinary Differential Equations. Wiley, New York.
- Boutros, Y.Z., Abd-el-Malek, M.B., Badran, N.A. and Hassan, H.S. (2006) Lie-Group Method for Unsteady Flows in a Semi-Infinite Expanding or Contracting Pipe with Injection or Suction through a Porous Wall. Journal of Computational and Applied Mathematics, 197, 465-494. http://dx.doi.org/10.1016/j.cam.2005.11.031
- Boutros, Y.Z., Abd-el-Malek, M.B., Badran, N.A. and Hassan, H.S. (2007) Lie-Group Method of Solution for Steady Two-Dimensional Boundary-Layer Stagnation-Point Flow towards a Heated Stretching Sheet Placed in a Porous Medium. Meccanica, 41, 681-691. http://dx.doi.org/10.1007/s11012-006-9014-x
- Boutros, Y.Z., Abd-el-Malek, M.B., Badran, N.A. and Hassan, H.S. (2007) Lie-Group Method Solution for Two-Di- mensional Viscous Flow between Slowly Expanding or Contracting Walls with Weak Permeability. Applied Mathematical Modelling, 31, 1092-1108. http://dx.doi.org/10.1016/j.apm.2006.03.026
- Abd-el-Malek, M.B., Badran, N.A. and Hassan, H.S. (2007) Lie-Group Method for Predicting Water Content for Immiscible Flow of Two Fluids in a Porous Medium. Applied Mathematical Sciences, 1, 1169-1180.
- Abd-el-Malek, M.B. and Hassan, H.S. (2010) Symmetry Analysis for Steady Boundary-Layer Stagnation-Point Flow of Rivlin-Ericksen Fluid of Second Grade Subject to Suction. Nonlinear Analysis: Modelling and Control, 15, 379-396.
- Abd-el-Malek, M.B. and Hassan, H.S. (2010) Solution of Burgers’ Equation with Time-Dependent Kinematic Viscosity via Lie-Group Analysis. Proceedings of the 5th International Workshop “Group Analysis of Differential Equations & Integrable Systems”, Protaras-Cyprus, 6-10 June 2010, 6-14.
- Abd-el-Malek, M.B., Badran, N.A., Hassan, H.S. and Abbas, H.H. (2013) New Solutions for Solving the Problem of Particle Trajectories in Linear Deep-Water Waves via Lie-Group Method. Applied Mathematics and Computation, 219, 11365-11375. http://dx.doi.org/10.1016/j.amc.2013.05.059
- Abd-el-Malek, M.B. and Hassan, H.S. (2014) Lie Group Method for Solving the Problem of Fission Product Behavior in Nuclear Fuel. Mathematical Methods in the Applied Sciences, 37, 420-427. http://dx.doi.org/10.1002/mma.2802
- Hassan, H.S., Mahrous, S.A., Sharara, A. and Hassan, A. (2014) A Study for MHD Boundary Layer Flow of Variable Viscosity over a Heated Stretching Sheet via Lie-Group Method. Applied Mathematics & Information Sciences, in Press.
- Abd-el-Malek, M.B., Badran, N.A., Hassan, H.S. and Abbas, H.H. (2015) New Solutions for Solving Boussinesq Equation via Potential Symmetries Method. Applied Mathematics and Computation, 251, 225-232. http://dx.doi.org/10.1016/j.amc.2014.11.055
- Abd-el-Malek, M.B., Badran, N.A., Hassan, H.S. and Abbas, H.H. (2014) Lie Group Method for Studying the Thermophoresis and Heat Generation Effect on Free-Convection Laminar Boundary-Layer Flow over a Vertical Flat Plate. Submitted for Publication.
- Abd-el-Malek, M.B. and Hassan, H.S. (2014) Solution of N-Dimensional Radially Symmetric Non-Linear Diffusion Equation via Symmetry Analysis. Submitted for Publication.
- Jacobson, N. (1979) Lie Algebras. Dover, New York.
- WafoSoh, C. (2005) Invariant Solutions of the Unidirectional Flow of an Electrically Charged Power-Law Non-New- tonian Fluid over a Flat Plate in Presence of a Transverse Magnetic Field. Communications in Nonlinear Science and Numerical Simulation, 10, 537-548. http://dx.doi.org/10.1016/j.cnsns.2003.12.008













