Received 13 January 2015; accepted 1 February 2015; published 5 February 2015

ABSTRACT

In this paper, we take Q₁₆ subsemilattice of D and we will calculate the number of right unit, idem- potent and regular elements α of B_X (Q₁₆) satisfied that V (D, α) = Q₁₆ for a finite set X. Also we will give a formula for calculate idempotent and regular elements of B_X (Q) defined by an X-semilattice of unions D.

Keywords:

Semilattice, Semigroup, Binary Relation

1. Introduction

Let X be a nonempty set and B_X be semigroup of all binary relations on the set X. If D is a nonempty set of subsets of X which is closed under the union then D is called a complete X-semilattice of unions.

Let f be an arbitrary mapping from X into D. Then one can construct a binary relation 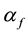on X by

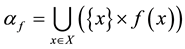. The set of all such binary relations is denoted by 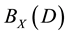and called a complete semi- group of binary relations defined by an X-semilattice of unions D.

We use the notations, , , ,.

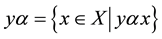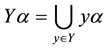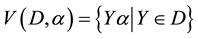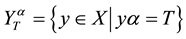A representation of a binary relation of the form 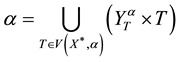is called quasinormal. Note that, if 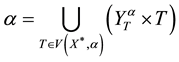is a quasinormal representation of the binary relation, then 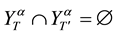for T,

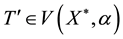and.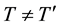

A complete X-semilattice of unions D is an XI-semilattice of unions if 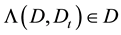for any 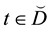and

for any nonempty element Z of D.

Now, is said to be right unit if for all. Also, is idempotent if. And is said to be regular if for some.

Let D', D'' be complete X-semilattices of unions and be a one-to-one mapping from D' to D''. A mapping

is a complete isomorphism provided for all nonempty subset D₁ of the se-

milattice D'. Besides that, if is a complete isomorphism where, for all, is said to be a complete -isomorphism.

Let Q and D' be respectively some XI and X-subsemilattices of the complete X-semilattice of unions D. Then

where complete isomorphism and. Besides, let us denote

and

where

This structure was comprehensively investigated in Diasamidze [1] .

Lemma 1. [1] If Q is complete X-semilattice of unions and is the set all right units of the semigroup then.

Lemma 2. [2] Let X be a finite set, D be a complete X-semilattice of unions and be X-subsemilattice of unions of D satisfies the following conditions

Q is XI-semilattice of unions.

Theorem 1. [2] Let X be a finite set and Q be XI-semilattice. If is -iso- morphic to Q and, then

Theorem 2. [2] Let be a quasinormal representation of the form such that

. is a regular iff for some complete -isomorphism, the following conditions are satisfied:

Let X be a finite set and be a complete X-semilattice of unions which satisfies the following conditions

The diagram of the D is shown in Figure 1. By the symbol we denote the class of all complete X- semilattice of unions whose every element is isomophic to an X-semilattice of the form D.

All subsemilattice of are given in Figure 2.

In Diasamidze [1] , it has shown that subsemilattices 1 - 15 are XI-semilattice of unions and subsemilattices 17 - 24 are not XI-semilattice of unions. In Yeşil Sungur [3] and Albayrak [4] , they have shown that subsemilattices 25 and 26 are XI-semilattice of unions if and only if”. Also they found that number of right unit, idempotent and regular elements in subsemilattices.

In this paper, we take in particular, subsemilattice of D. We will calculate the number of right unit, idempotent and regular elements of satisfied that for a finite set X. Also we will give a formula for calculate idempotent and regular elements of defined by an X-semilattice of unions.

2. Results

Let be complete X-subsemilattice of D satisfies the following conditions

The diagram of the Q₁₆ is shown in Figure 3. From Lemma 2 Q₁₆ is XI-semilattice of unions.

Let denote the set of all XI-subsemilattice of the semilattice D which are isomorphic of the X-semi- lattice Q₁₆. Then we get

Let be a idempotent element having a quasinormal representation of the form

, such that. First we calculate number of this idempotent elements in.

Lemma 3. If X is a finite set and is the set all right units of the semigroup, then the number may be calculated by formula:

Proof. From Lemma 1 we have where is identity mapping of the set Q₁₆.

For this reason in Theorem 1. Then we obtain

Theorem 3. If X is a finite set and is the set all idempotent elements of the semigroup, then the number may be calculated by formula:

Proof. By using Lemma 3 we have number of right units of the semigroup defined by

for. Then number of idempotent elements of calculated

by formula. By using

we obtain above formula.

Now we will calculate number of regular elements having a quasinormal representation of the

form such that. Let be the set all regular elements of the

semigroup. By using we get . The number of all automorphisms of the semilattice Q₁₆ is q = 4. These are

Then. Also by using

we get.

Theorem 4. If X is a finite set and is the set all regular elements of the semigroup, then the number may be calculated by formula:

Proof. To account for the elements that are in, we first subtract out intersection of’s. Let. By using Theorem 2 and

We get which is a contradiction with, , , are dis- joint sets. Then. Smilarly for. Thus we obtain

From Theorem 1 we get above formula.

Corollary 1. If X is a finite set, I_D is the set all idempotent elements of the semigroup and R_D is the set all regular elements of the semigroup, then the number and may be calculated by formula:

Proof. Let I_D be the set of all idempotent elements of the semigroup. Then number of idempotent element of is equal to sum of idempotent elements of the subsemigroup defined by XI-subsemilattice of D. is given in Diasamidze [1] for. From Theorem 3 we have number of idempotent elements of the subsemigroup. Then the number may be calculated by formula

. Similarly the number may be calculated by formula.

References