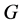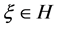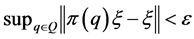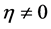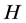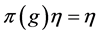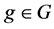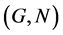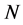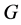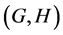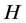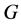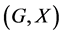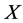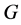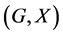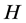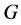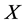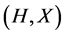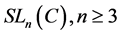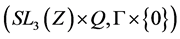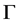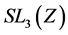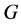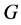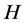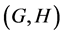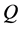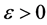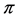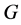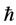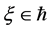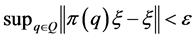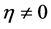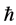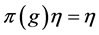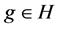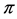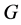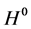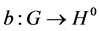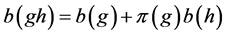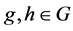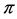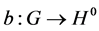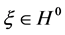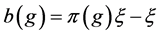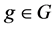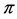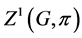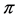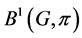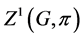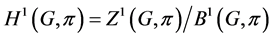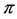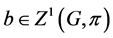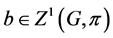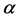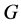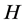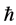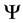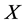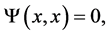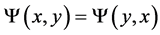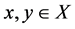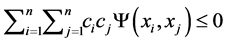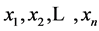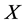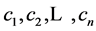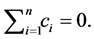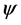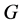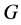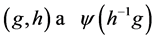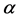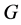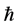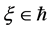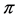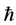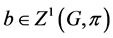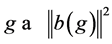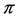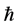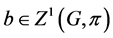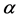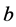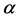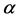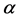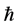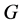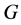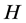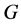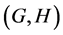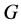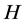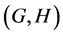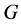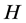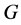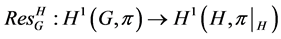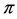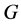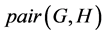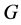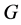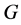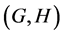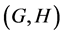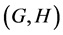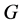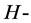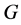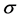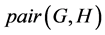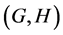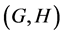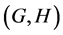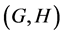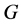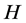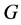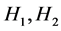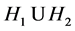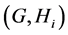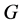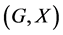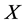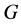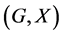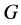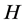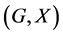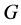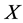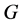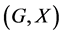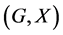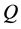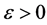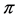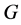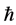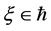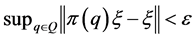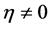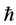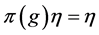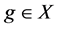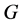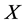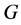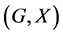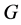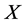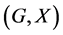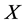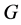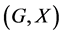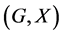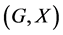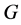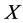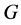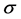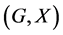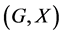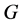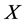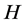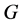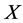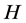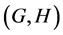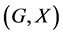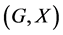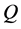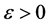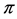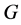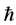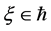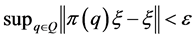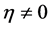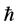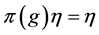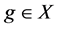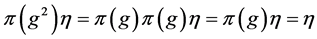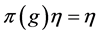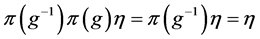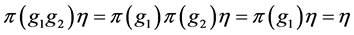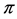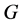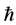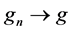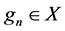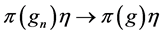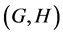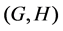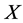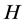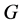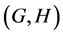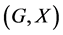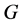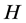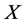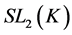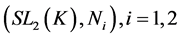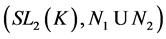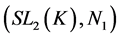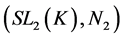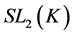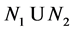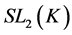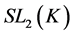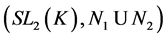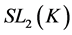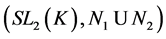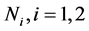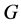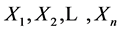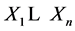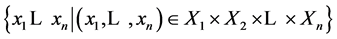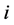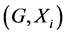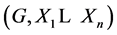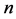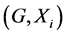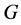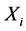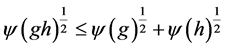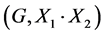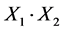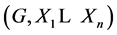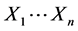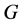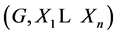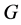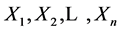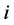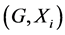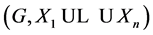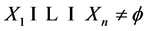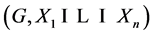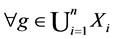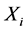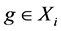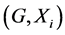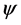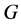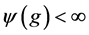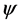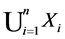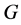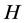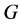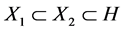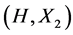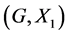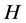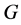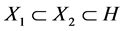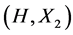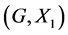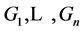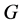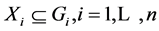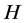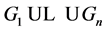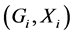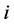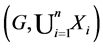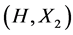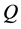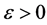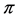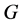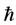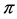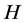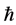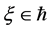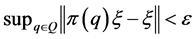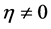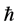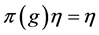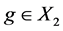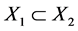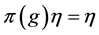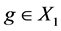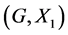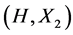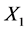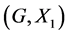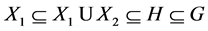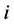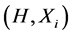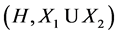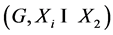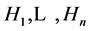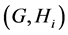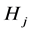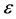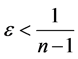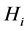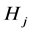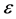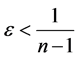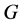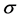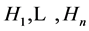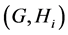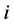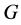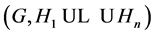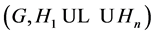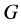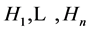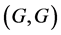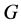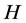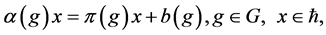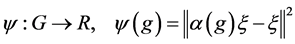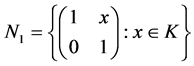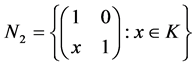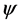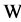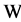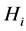Applied Mathematics
Vol.05 No.19(2014), Article ID:51232,5 pages
10.4236/am.2014.519285
Relative Property (T) for Topological Groups
Jicheng Tao1, Wen Yan2
1Department of Mathematics, China Jiliang University, Hangzhou, China
2Department of Mathematics, Tuskegee University, Tuskegee, USA
Email: taojc@cjlu.edu.cn, wenyanmath@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 August 2014; revised 16 September 2014; accepted 6 October 2014
ABSTRACT
In this paper, we investigate Kazhdan’s relative Property (T) for pairs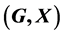 , where
, where  is a topological group and
is a topological group and 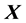 is any subset of
is any subset of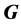 . We show that the pair
. We show that the pair 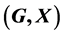 has Property (FH) and every function conditionally of negative type on
has Property (FH) and every function conditionally of negative type on  is X-bounded if the pair
is X-bounded if the pair  has relative Property (T). We also prove that
has relative Property (T). We also prove that  has Property (T) when
has Property (T) when 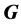 is a s-compact locally compact group generated by its subgroups
is a s-compact locally compact group generated by its subgroups 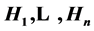 and the pair
and the pair 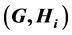 has relative Property (T) for all
has relative Property (T) for all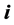 .
.
Keywords:
Relative Property (T) of Topological Group, Function Conditionally of Negative Type, Property (FH)

1. Introduction
In the mid 60’s, Kazhdan defined the following Property (T) for locally compact groups and used this to prove that a large class of lattices are finitely generated.
Definition 1.1. [1] A topological group 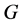 has Property (T) if there exist a compact subset
has Property (T) if there exist a compact subset 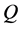 and a real number
and a real number 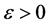 such that, whenever
such that, whenever 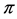 is a continuous unitary representation of
is a continuous unitary representation of ![]() on a Hilbert space
on a Hilbert space ![]()
for which there exists a vector ![]() of norm 1 with
of norm 1 with![]() , then there exists an invariant
, then there exists an invariant
vector, namely a vector ![]() in
in ![]() such that
such that ![]() for all
for all![]() .
.
Since then, Property (T) has been studied extensively and there are a lot of publications. One can see [2] - [5] .
The notion of relative Property (T) for a pair![]() , where
, where ![]() is a normal subgroup of
is a normal subgroup of![]() , was implicit in Kazhdan’s paper [5] , and later made explicit by Margulis [6] . The definition of relative Property (T) has been extended in [7] to pairs
, was implicit in Kazhdan’s paper [5] , and later made explicit by Margulis [6] . The definition of relative Property (T) has been extended in [7] to pairs ![]() with
with ![]() not necessarily normal in
not necessarily normal in![]() . In order to obtain more information about the unitary dual of locally compact group, Cornulier in [3] extended the definition of relative Property (T) to pairs
. In order to obtain more information about the unitary dual of locally compact group, Cornulier in [3] extended the definition of relative Property (T) to pairs![]() , where
, where ![]() is any subset of the locally compact group
is any subset of the locally compact group![]() .
.
We know that if the pair ![]() has relative Property (T), then there exists an open, compactly generated subgroup
has relative Property (T), then there exists an open, compactly generated subgroup ![]() of
of![]() , containing
, containing![]() , such that
, such that ![]() has relative Property (T). Shalom [8] generalizes Kazhdan’s definition of Property (T) to topological groups that are not locally compact. There are many natural examples such as the loop group of all continuous functions from a circle to
has relative Property (T). Shalom [8] generalizes Kazhdan’s definition of Property (T) to topological groups that are not locally compact. There are many natural examples such as the loop group of all continuous functions from a circle to ![]() and the pair
and the pair
![]() (
(![]() is a subgroup of
is a subgroup of![]() ), which both have Property (T).
), which both have Property (T).
Inspired by the work of Cornulier and Shalom, in this paper, we go further in this direction and try to extend Cornulier’s result from locally compact groups to topological groups. The motivation for this is that, given a topological group![]() , the knowledge of the family of subsets X such that has relative Property (T) contains much more precise information than the bare information whether G has Property (T). On the other hand, relative Property (T) for topological groups is very important to discuss Haagerup Property.
, the knowledge of the family of subsets X such that has relative Property (T) contains much more precise information than the bare information whether G has Property (T). On the other hand, relative Property (T) for topological groups is very important to discuss Haagerup Property.
2. Preliminaries
We first introduce some of basic notations and terminologies, the details can be found in [1] .
Definition 2.1. [1] Let ![]() be a topological group, and
be a topological group, and ![]() be a closed subgroup. The pair
be a closed subgroup. The pair ![]() has Property (T) if there exist a compact subset
has Property (T) if there exist a compact subset ![]() and a real number
and a real number ![]() such that, whenever
such that, whenever ![]() is a continuous unitary representation of
is a continuous unitary representation of ![]() on a Hilbert space
on a Hilbert space ![]() for which there exists a vector
for which there exists a vector ![]() of norm
of norm
1 with![]() , then there exists an invariant vector, namely a vector
, then there exists an invariant vector, namely a vector ![]() in
in ![]() such that
such that ![]() for all
for all![]() .
.
Definition 2.2. Let ![]() be an orthogonal representation of the topological group
be an orthogonal representation of the topological group ![]() on a real Hilbert space
on a real Hilbert space![]() .
.
1) A continuous mapping ![]() such that
such that![]() , for all
, for all ![]() is called a 1- cocycle with respect to
is called a 1- cocycle with respect to![]() .
.
2) A 1-cocycle ![]() for which there exists
for which there exists ![]() such that
such that![]() , for all
, for all ![]() is called a 1-coboudary with respect to
is called a 1-coboudary with respect to![]() .
.
3) The space ![]() of all 1-cocycles with respect to
of all 1-cocycles with respect to ![]() is a real vector space under the pointwise operations, and the set
is a real vector space under the pointwise operations, and the set ![]() of all 1-coboundaries is a subspace of
of all 1-coboundaries is a subspace of![]() . The quotient vector space
. The quotient vector space
![]() is called the first cohomology group with coefficients in
is called the first cohomology group with coefficients in![]() .
.
4) Let![]() . The affine isometric action associated to a cocycle
. The affine isometric action associated to a cocycle ![]() is the affine isometric action
is the affine isometric action ![]() of
of ![]() on
on ![]() defined by
defined by
![]()
where ![]() is the canonical affine Hilbert space associated with
is the canonical affine Hilbert space associated with ![]()
Definition 2.3. A continuous real valued kernel ![]() on a topological space
on a topological space ![]() is conditionally of negative
is conditionally of negative
type if ![]()
![]() , for all
, for all![]() , and
, and![]() , for any elements
, for any elements ![]() in
in![]() , and any real numbers
, and any real numbers ![]() with
with ![]() A continuous real value function
A continuous real value function ![]() on a topological group
on a topological group ![]() is conditionally of negative type if the kernel on
is conditionally of negative type if the kernel on ![]() defined by
defined by ![]() is conditionally of negative type.
is conditionally of negative type.
Example 2.4. Let ![]() be a topological group, and let
be a topological group, and let ![]() be an affine isometric action of
be an affine isometric action of ![]() on a real Hilbert space
on a real Hilbert space![]() , according to Example C. 2.2 ii in [1] , for any
, according to Example C. 2.2 ii in [1] , for any![]() , the function
, the function
![]()
is conditionally of negative type.
In particular, for any orthogonal representation ![]() on
on ![]() and for any
and for any![]() , the function
, the function ![]() is conditionally of negative type.
is conditionally of negative type.
Theorem 2.5. [1] Let ![]() be an orthogonal representation of the topological group G on a real Hilbert space
be an orthogonal representation of the topological group G on a real Hilbert space![]() . Let
. Let![]() , with associated affine isometric action
, with associated affine isometric action![]() . The following statements are equivalent:
. The following statements are equivalent:
1) ![]() is bounded;
is bounded;
2) all the orbits of ![]() are bounded;
are bounded;
3) some orbit of ![]() is bounded;
is bounded;
4) ![]() has a fixed point in
has a fixed point in![]() .
.
Definition 2.6. A topological group ![]() has Property (FH) if every affine isometric action of
has Property (FH) if every affine isometric action of ![]() on a real Hilbert space has a fixed point. Let
on a real Hilbert space has a fixed point. Let ![]() be a closed subgroup of
be a closed subgroup of![]() . The pair
. The pair ![]() has Property (FH) if every affine isometric action of
has Property (FH) if every affine isometric action of ![]() on a real Hilbert space has an
on a real Hilbert space has an ![]() -fixed point.
-fixed point.
The following theorem describes connection among bounded functions conditionally of negative type, Property (FH) and cohomology groups pair![]() .
.
Theorem 2.7. [1] Let ![]() be a topological group,
be a topological group, ![]() be a closed subgroup of
be a closed subgroup of![]() . The following statements are equivalent:
. The following statements are equivalent:
1) ![]() is the zero mapping, for every orthogonal representation
is the zero mapping, for every orthogonal representation ![]() of
of![]() ,
,
2) ![]() has Property (FH),
has Property (FH),
3) every function conditionally of negative type on ![]() is H-bounded.
is H-bounded.
Theorem 2.8. [1] ![]() be a topological group, H be a closed subgroup of
be a topological group, H be a closed subgroup of![]() .
.
1) If Pair ![]() has relative Property (T), then pair
has relative Property (T), then pair ![]() has Property (FH).
has Property (FH).
2) If Pair ![]() has relative Property (T), then every function conditionally of negative type on
has relative Property (T), then every function conditionally of negative type on ![]() is
is ![]() bounded.
bounded.
3) Assume that ![]() is a
is a ![]() -compact locally compact group and that
-compact locally compact group and that ![]() has Property (FH), then pair
has Property (FH), then pair ![]() has relative Property (T).
has relative Property (T).
Proof. By virtue of [1] Remark 2.12.5: if the pair ![]() has relative Property (T), then
has relative Property (T), then ![]() has Property (FH) and Theorem 2.7 1), 2) is obvious and 3) is the Delorme-Guichardet Theorem applied to the pair
has Property (FH) and Theorem 2.7 1), 2) is obvious and 3) is the Delorme-Guichardet Theorem applied to the pair![]() , consisting of a group
, consisting of a group ![]() and a subgroup
and a subgroup ![]() (see [1] , Exercise 2.14.9).
(see [1] , Exercise 2.14.9). ![]()
Theorem 2.9. [4] Let ![]() be a topological group and
be a topological group and ![]() be subgroups of
be subgroups of ![]() such that
such that ![]() is generated by
is generated by![]() . Each pair
. Each pair ![]() has relative Property (T). Then G has Property (T).
has relative Property (T). Then G has Property (T).
3. Relative Property (T) of Pairs for Topological Groups and Subsets
When ![]() be a locally compact group, Cornulier extended the definition of relative Property (T) to pairs
be a locally compact group, Cornulier extended the definition of relative Property (T) to pairs![]() , where
, where ![]() is any subset of
is any subset of![]() , and then established various characterizations of relative Property (T) for the pair
, and then established various characterizations of relative Property (T) for the pair![]() , which were already known in [1] [9] for the case that
, which were already known in [1] [9] for the case that ![]() is a topological group,
is a topological group, ![]() is a closed subgroup. We extend the definition of relative Property (T) to pairs
is a closed subgroup. We extend the definition of relative Property (T) to pairs![]() , where
, where ![]() is a topological group,
is a topological group, ![]() is any subset of
is any subset of![]() , and then established similar characterizations of relative Property (T) for the pair
, and then established similar characterizations of relative Property (T) for the pair![]() .
.
Definition 3.1. Let ![]() be a topological group, and
be a topological group, and ![]() is any subset of G. The pair
is any subset of G. The pair ![]() has relative Property (T) if there exist a compact subset
has relative Property (T) if there exist a compact subset ![]() and a real number
and a real number ![]() such that, whenever
such that, whenever ![]() is a continuous unitary representation of
is a continuous unitary representation of ![]() on a Hilbert space
on a Hilbert space ![]() for which there exists a vector
for which there exists a vector ![]() of norm
of norm
1 with![]() , then there exists an invariant vector, namely a vector
, then there exists an invariant vector, namely a vector ![]() in
in ![]() such that
such that ![]() for all
for all![]() .
.
Definition 3.2. Let ![]() be a topological group, and
be a topological group, and ![]() is any subset of
is any subset of![]() . The pair
. The pair ![]() has Property (FH) if every affine isometric action of
has Property (FH) if every affine isometric action of ![]() on a real Hilbert space has an
on a real Hilbert space has an ![]() -fixed point.
-fixed point.
The following theorem will establish some characterizations of relative Property (T) for a pair![]() .
.
Theorem 3.3. Let ![]() be a topological group and
be a topological group and ![]() be any subset of
be any subset of![]() .
.
1) If pair ![]() has relative Property (T), then pair
has relative Property (T), then pair ![]() has Property (FH).
has Property (FH).
2) If pair ![]() has relative Property (T), every function conditionally of negative type on
has relative Property (T), every function conditionally of negative type on ![]() is
is ![]() - bounded.
- bounded.
3) Assume that ![]() is a
is a ![]() -compact locally compact group and that pair
-compact locally compact group and that pair ![]() has Property (FH), then the pair
has Property (FH), then the pair ![]() has relative Property (T).
has relative Property (T).
We will apply the following lemma to prove above theorem:
Lemma 3.4. Let ![]() be a topological group,
be a topological group, ![]() be any subset and
be any subset and ![]() be a close subgroup of
be a close subgroup of![]() , where
, where ![]() generates
generates![]() . Then the pair
. Then the pair ![]() has relative Property (T) if and only if the pair
has relative Property (T) if and only if the pair ![]() has relative Property (T).
has relative Property (T).
Proof. Necessity. Since the pair ![]() has relative Property (T), there exist a compact subset
has relative Property (T), there exist a compact subset ![]() and a real number
and a real number ![]() such that whenever
such that whenever ![]() is a continuous unitary representation of
is a continuous unitary representation of ![]() on a Hilbert space
on a Hilbert space ![]() for which there exists a vector
for which there exists a vector ![]() of norm 1 with
of norm 1 with![]() , then there exists an invariant vector
, then there exists an invariant vector ![]() in
in ![]() such that
such that ![]() for all
for all![]() . Hence
. Hence
1)![]() .
.
2) Since![]() ,
,![]() .
.
3)![]() .
.
4) According to ![]() is a continuous unitary representation of
is a continuous unitary representation of ![]() on a Hilbert space
on a Hilbert space![]() , if
, if![]() , where
, where![]() , then
, then![]() .
.
According to 1), 2), 3) and 4), pair ![]() has relative Property (T).
has relative Property (T).
Sufficiency. It follows from definition of relative Property (T).
Proof of Theorem 3.3. According to Lemma 3.4, the pair ![]() has relative Property (T), where
has relative Property (T), where ![]() generate
generate![]() , then by Theorem 2.8, every function conditionally of negative type on
, then by Theorem 2.8, every function conditionally of negative type on ![]() is H-bounded.
is H-bounded.
1) By Theorem 2.7, the pair ![]() has Property (FH), hence the pair
has Property (FH), hence the pair ![]() has Property (FH).
has Property (FH).
2) Since every function conditionally of negative type on ![]() is
is ![]() -bounded, it is
-bounded, it is ![]() -bounded too.
-bounded too.
3) According to [3] (Theorem 1.1), the result holds. ![]()
Example 3.5 Let K be a any non-archimedean local field, we consider the following subgroups of![]() :
:
![]()
![]()
Then the pair![]() ,
, ![]() do not have relative Property (T) .
do not have relative Property (T) .
In fact, if ![]() has relative Property (T), then
has relative Property (T), then ![]() has relative Property. Since the group
has relative Property. Since the group ![]() is generated by
is generated by![]() , by Theorem 2.9,
, by Theorem 2.9, ![]() has Property (T). This contradicts the fact that
has Property (T). This contradicts the fact that ![]() does not have Property (T). By Lemma 3.4,
does not have Property (T). By Lemma 3.4, ![]() do not have relative Property (T).
do not have relative Property (T).
Remark 3.6. By Theorem 3.3, ![]() does not have Property (FH).
does not have Property (FH). ![]() do not have relative Property (FH). According to [1] (remark: 1.4.4 (iii) on Page 47), groups
do not have relative Property (FH). According to [1] (remark: 1.4.4 (iii) on Page 47), groups ![]() do not have Property (T), hence do not have Property (FH).
do not have Property (T), hence do not have Property (FH).
Theorem 3.7. Let ![]() be a topological group,
be a topological group, ![]() be subsets. Denote by
be subsets. Denote by ![]() the point- wise product
the point- wise product![]() . Suppose that, for every
. Suppose that, for every![]() ,
, ![]() has relative Property (T). Then pair
has relative Property (T). Then pair ![]() has Property (FH).
has Property (FH).
Proof. It suffices to prove the case when n = 2, since the result follows by induction on![]() . By Theorem 3.3,
. By Theorem 3.3, ![]() has Property (FH), and every function conditionally of negative type on
has Property (FH), and every function conditionally of negative type on ![]() is
is ![]() -bounded. Let
-bounded. Let ![]()
be any conditionally negative definite function on G. According to the inequality, ![]() ,
,
the pair ![]() is
is ![]() -bounded. Hence, pair
-bounded. Hence, pair ![]() is
is ![]() -bounded.
-bounded.
Remark 3.8. In [3] , Cornulier show when ![]() be a locally compact group for above theorem, then pair
be a locally compact group for above theorem, then pair ![]() has relative Property (T).
has relative Property (T).
Theorem 3.9. Let ![]() be a topological group,
be a topological group, ![]() be subsets. Suppose that, for every
be subsets. Suppose that, for every![]() ,
, ![]() has relative Property (T), then we have:
has relative Property (T), then we have:
1) the pair ![]() has Property (FH).
has Property (FH).
2) if![]() , then the pair
, then the pair ![]() has Property (FH).
has Property (FH).
Proof. 1)![]() , then there exists a
, then there exists a ![]() such that
such that![]() . Since pair
. Since pair ![]() has relative Property
has relative Property
(T), let ![]() be any function conditionally of negative type on
be any function conditionally of negative type on![]() , then
, then![]() , that is,
, that is, ![]() is an
is an ![]() - bounded function. Similarly, we can easily prove result 2).
- bounded function. Similarly, we can easily prove result 2). ![]()
Theorem 3.10. Let ![]() be a topological group.
be a topological group.
1) Let ![]() be a subgroup of
be a subgroup of![]() ,
,![]() . If the pair
. If the pair ![]() has relative Property (T), then
has relative Property (T), then ![]() has relative Property (T).
has relative Property (T).
2) Let ![]() be a subgroup of
be a subgroup of![]() ,
,![]() . If the pair
. If the pair ![]() has Property (FH), then
has Property (FH), then ![]() has Property (FH).
has Property (FH).
3) Let ![]() be subgroups of
be subgroups of![]() ,
,![]() . Let
. Let ![]() be a topological group generated by
be a topological group generated by
![]() . If
. If ![]() has relative Property (T) for every
has relative Property (T) for every![]() , then the pair
, then the pair ![]() has Property (FH).
has Property (FH).
Proof. 1) Since ![]() has relative Property (T), if there exist a compact subset
has relative Property (T), if there exist a compact subset ![]() and a real number
and a real number ![]() such that,
such that, ![]() is a continuous unitary representation of
is a continuous unitary representation of ![]() on a Hilbert space
on a Hilbert space![]() , then
, then ![]() is a continuous unitary representation of
is a continuous unitary representation of ![]() on a Hilbert space
on a Hilbert space ![]() for which there exists a vector
for which there exists a vector ![]() of norm
of norm
1 with![]() , there exists an invariant vector, namely a vector
, there exists an invariant vector, namely a vector ![]() in
in ![]() such that
such that
![]() for all
for all![]() . According to
. According to![]() ,
, ![]() for all
for all![]() . Hence
. Hence ![]() has relative Property (T).
has relative Property (T).
2) Since ![]() has Property (FH), every affine isometric action of
has Property (FH), every affine isometric action of ![]() on a real Hilbert space is an affine isometric action of
on a real Hilbert space is an affine isometric action of![]() , and thus it has an
, and thus it has an ![]() -fixed point. Hence, it has an
-fixed point. Hence, it has an ![]() -fixed point. That is,
-fixed point. That is, ![]() has Property (FH).
has Property (FH).
3) It suffices to prove the case when n = 2, since then the result follows by induction. According to 1) and Theorem 3.9, ![]() , for every
, for every![]() , the pair
, the pair ![]() has relative Property (T), then the pair
has relative Property (T), then the pair ![]() has Property (FH). By using the result in 2), the pair
has Property (FH). By using the result in 2), the pair ![]() has Property (FH).
has Property (FH). ![]()
In [4] , M.Ershov and A. Jaikin-Zapirain showed the following facts: Suppose G be a group generated by subgroups![]() , and the pair
, and the pair ![]() has relative Property (T) for each i, and any two subgroups
has relative Property (T) for each i, and any two subgroups ![]()
and ![]() are
are ![]() -orthogonal for some
-orthogonal for some![]() . Then G has Property (T).
. Then G has Property (T).
We will naturally ask: Can we remove the hypothesis “any two subgroups ![]() and
and ![]() are
are ![]() -orthogonal for some
-orthogonal for some![]() ”?
”?
The following Theorem solves the above problem partially:
Theorem 3.11. Let ![]() be a
be a ![]() -compact locally compact group generated by subgroups
-compact locally compact group generated by subgroups![]() . Suppose that the pair
. Suppose that the pair ![]() has relative Property (T) for each
has relative Property (T) for each![]() . Then
. Then ![]() has Property (T).
has Property (T).
Proof. According to Theorem 3.9, the pair ![]() has Property (FH). Then by Theorem 3.3, the pair
has Property (FH). Then by Theorem 3.3, the pair ![]() has relative Property (T). Since
has relative Property (T). Since ![]() is a group generated by subsets
is a group generated by subsets![]() , according to Lemma 3.4, the pair
, according to Lemma 3.4, the pair ![]() has relative Property (T), then
has relative Property (T), then ![]() has Property (T).
has Property (T). ![]()
Acknowledgements
The work is finished during the first author visiting Auburn University. He thanks Professor Tin-Yau Tam for his invitation to visit Auburn University and participate the Linear Algebra Seminar.
References
- Kekka, B., Harpe, P.D.L. and Valette, A. (2008) Kazhdan’s Property T. Cambridge University Press, Cambridge.
- Chifan, I. and Ioana, A. (2011) On Relative Property (T) and Haagerup’s Property. Transactions of the American Mathematical Society, 363, C6407-C6420. http://dx.doi.org/10.1090/S0002-9947-2011-05259-1
- Cornulier, Y. (2006) Relative Kazhdan Property. Annales Scientifiques de1’École Hormale Supérieure, 39, 301-333.
- Ershov, M. and Jaikin-Zapirain, A. (2010) Property (T) for Noncommutative Universal Lattices. Inventiones Mathematicae, 179, 303-347. http://dx.doi.org/10.1007/s00222-009-0218-2
- Kazhdan, D. (1967) Connection of Dual Space of Group with the Structure of Its Closed Subgroups. Functional Analysis and Its Applications, 1, 63-65. http://dx.doi.org/10.1007/BF01075866
- Margulis, G. (1982) Finitely-Additive Invariant Measures on Euclidean Spaces. Ergodic Theory and Dynamical Systems, 2, 383-396. http://dx.doi.org/10.1017/S014338570000167X
- Harpe, P.D.L., Valette, A. and Marc, B. (1989) La Propriété (T) de Kazhdan pour les groups localement compacts. Astérisque 175, Société mathématique de France (SMF).
- Shalom, Y. (1999) Bounded Generation and Kazhdan’s Property (T). Publications Mathématiques de l’Institut des Hautes Études Scientifiques, 90, 145-168. http://dx.doi.org/10.1007/BF02698832
- Jolissaint, P. (2005) On Property (T) for Pairs of Topological Groups. L’Enseignement Mathématique, 51, 31-45.



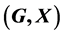 , where
, where  is a topological group and
is a topological group and 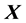 is any subset of
is any subset of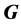 . We show that the pair
. We show that the pair 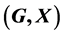 has Property (FH) and every function conditionally of negative type on
has Property (FH) and every function conditionally of negative type on  is X-bounded if the pair
is X-bounded if the pair  has relative Property (T). We also prove that
has relative Property (T). We also prove that  has Property (T) when
has Property (T) when 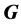 is a s-compact locally compact group generated by its subgroups
is a s-compact locally compact group generated by its subgroups 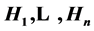 and the pair
and the pair 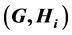 has relative Property (T) for all
has relative Property (T) for all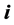 .
.
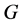 has Property (T) if there exist a compact subset
has Property (T) if there exist a compact subset 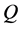 and a real number
and a real number 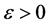 such that, whenever
such that, whenever 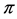 is a continuous unitary representation of
is a continuous unitary representation of