Applied Mathematics
Vol.5 No.16(2014), Article
ID:49430,25
pages
DOI:10.4236/am.2014.516241
Compound Means and Fast Computation of Radicals
Jan Šustek
Department of Mathematics, Faculty of Science, University of Ostrava, Ostrava, Czech Republic
Email: jan.sustek@osu.cz
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 June 2014; revised 2 August 2014; accepted 16 August 2014
ABSTRACT
In last decades, several algorithms were developed for fast evaluation of some elementary functions with very large arguments, for example for multiplication of million-digit integers. The present paper introduces a new fast iterative method for computing values 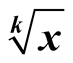 with high accuracy, for fixed
with high accuracy, for fixed 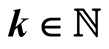 and
and . The method is based on compound means and Padé approximations.
. The method is based on compound means and Padé approximations.
Keywords:Compound Means, Padé Approximation, Computation of Radicals, Iteration

1. Introduction
In last decades, several algorithms were developed for fast evaluation of some elementary functions with very large arguments, for example for multiplication of million-digit integers. The present paper introduces a new iterative method for computing values 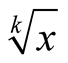 with high accuracy, for fixed
with high accuracy, for fixed 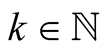 and
and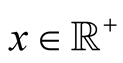 .
.
The best-known method used for computing radicals is Newton’s method used to solve the equation
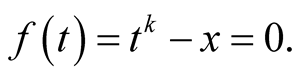
Newton’s method is a general method for numerical solution of equations and for particular choice of the equation it can lead to useful algorithms, for example to algorithm for division of long numbers. This method converges quadratically. Householder [1] found a generalization of this method. Let 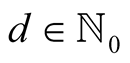 be a parameter of the method. When solving the equation
be a parameter of the method. When solving the equation 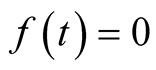 the iterations converging to the solution are
the iterations converging to the solution are
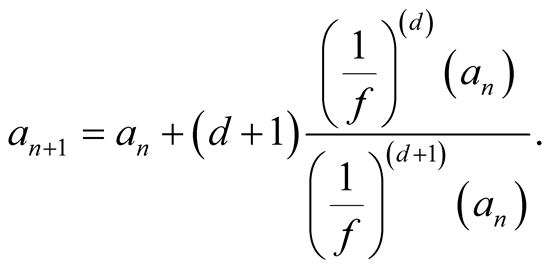 (1.1)
(1.1)
The convergence has order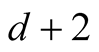 . The order of convergence can be made arbitrarily large by the choice of
. The order of convergence can be made arbitrarily large by the choice of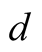 . But for larger values of
. But for larger values of 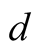 it is necessary to perform too many operations in every step and the method gets slower.
it is necessary to perform too many operations in every step and the method gets slower.
The method (3.4) presented in this paper involves compound means. It is proved that this method performs less operations and is faster than the former methods.
Definition 1. A function 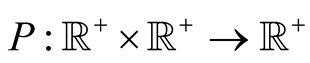 is called mean if for every
is called mean if for every 

A mean 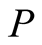 is called strict if
is called strict if
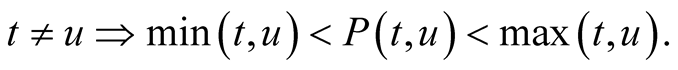
A mean 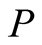 is called continuous if the function
is called continuous if the function 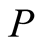 is continuous.
is continuous.
A known class of means is the power means defined for 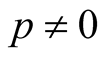 by
by

for 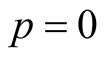 we define
we define
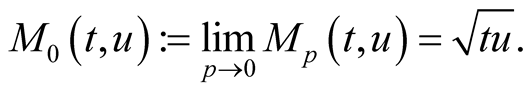
The most used power means are the arithmetic mean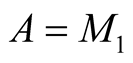 , the geometric mean
, the geometric mean 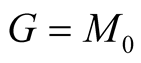 and the harmonic mean
and the harmonic mean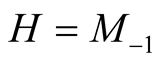 . All power means are continuous and strict. There is a known inequality between power means
. All power means are continuous and strict. There is a known inequality between power means
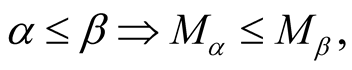
see e.g. [2] . From this one directly gets the inequality between arithmetic mean and geometric mean. For other classes of means see e.g. [3] .
Taking two means, one can obtain another mean by composing them by the following procedure.
Definition 2. Let  be two means. Given two positive numbers
be two means. Given two positive numbers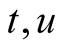 , put
, put

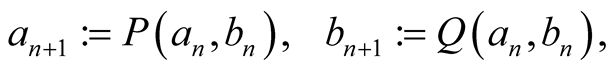
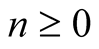 . If these two sequences converge to a common limit then this limit is denoted by
. If these two sequences converge to a common limit then this limit is denoted by

The function 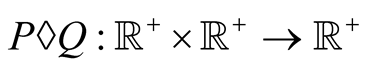 is called compound mean.
is called compound mean.
The best known application of compound means is Gauss’ arithmetic-geometric mean [4]
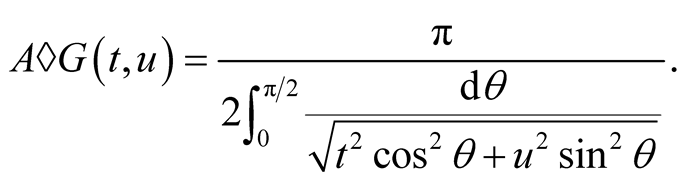 (1.2)
(1.2)
Iterations of the compound mean then give a fast numerical algorithm for computation of the elliptic integral (1.2).
Matkowski [5] proved the following theorem on existence of compound means.
Theorem 1. Let 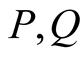 be continuous means such that at least one of them is strict. Then the compound mean
be continuous means such that at least one of them is strict. Then the compound mean 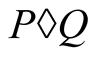 exists and is continuous.
exists and is continuous.
2. Properties
We call a mean 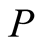 homogeneous if for every
homogeneous if for every 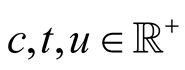

All power means are homogeneous. If two means are homogeneous then their compound mean is also homogeneous.
Homogeneous mean 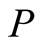 can be represented by its trace
can be represented by its trace
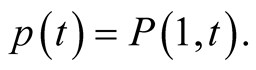
Conversely, every function 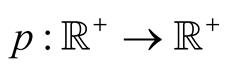 with property
with property
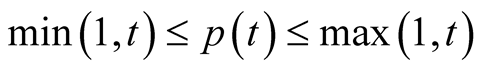 (2.1)
(2.1)
represents homogeneous mean
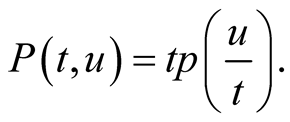
Theorem 2. If the compound mean 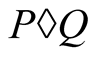 exists then it satisfies the functional equation
exists then it satisfies the functional equation
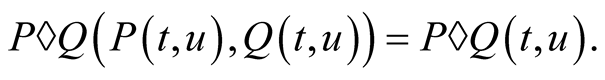 (2.2)
(2.2)
On the other hand, there is only one mean 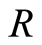 satisfying the functional equation
satisfying the functional equation
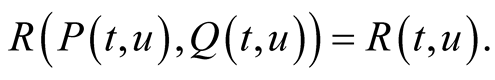
Easy proofs of these facts can be found in [5] .
Example 1. Take the arithmetical mean  and the harmonic mean
and the harmonic mean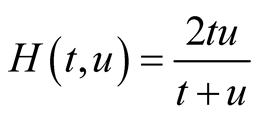 . The arithmetic-harmonic mean
. The arithmetic-harmonic mean 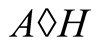 exists by Theorem 1 and Theorem 2 implies that
exists by Theorem 1 and Theorem 2 implies that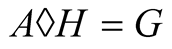 . Hence the iterations of the arithmetic-harmonic mean
. Hence the iterations of the arithmetic-harmonic mean  can be used as a fast numerical method of computation of
can be used as a fast numerical method of computation of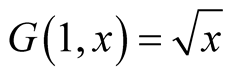 . This leads to a well known Babylonian method
. This leads to a well known Babylonian method
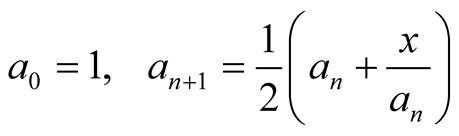
with a quadratical convergence to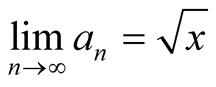 .
.
The Babylonian method is in fact Newton’s method used to solve the equation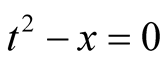 . Using Newton’s method to solve the equation
. Using Newton’s method to solve the equation 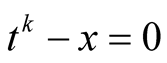 leads to iterations
leads to iterations
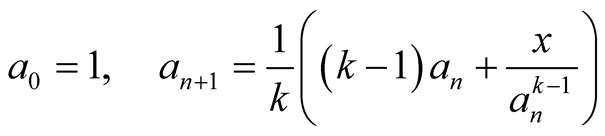 (2.3)
(2.3)
with a quadratical convergence to .
.
3. Our Method
In the present paper we will proceed similarly as in Example 1. For a fixed integer 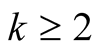 and a positive real number
and a positive real number 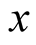 we will find a sequence of approximations converging fast to
we will find a sequence of approximations converging fast to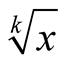 .
.
We need the following lemma.
Lemma 1. Let function 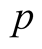 satisfy
satisfy 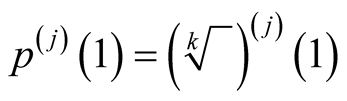 for
for 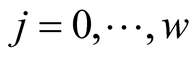 and let
and let 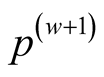 be bounded. Let
be bounded. Let
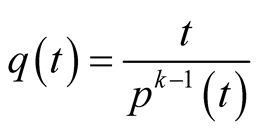 . Assume that
. Assume that 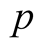 and
and 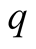 satisfy (2.1) strictly if
satisfy (2.1) strictly if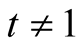 . Then the function
. Then the function 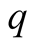 satisfies
satisfies
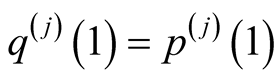 for
for 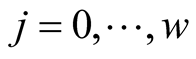 and
and 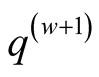 is bounded. Let
is bounded. Let 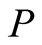 and
and 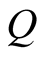 be the homogeneous means corresponding to traces
be the homogeneous means corresponding to traces 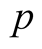 and
and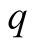 , respectively. Then the compound mean
, respectively. Then the compound mean 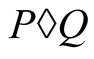 exists and its convergence has order
exists and its convergence has order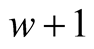 .
.
Proof. The assumption implies that
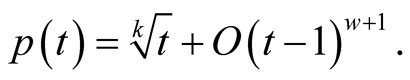
Then
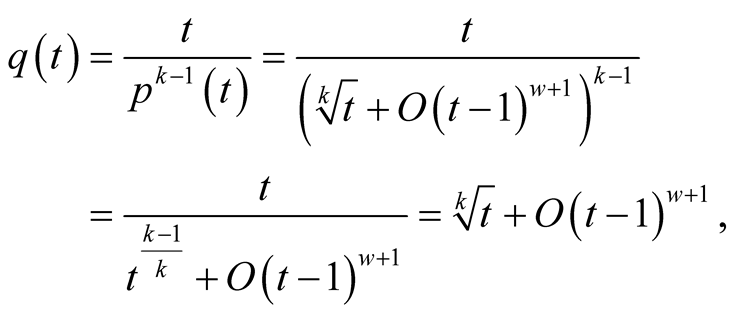
hence  for
for  and
and 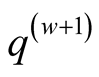 is bounded.
is bounded.
The compound mean  exists by Theorem 1. Let
exists by Theorem 1. Let 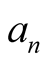 and
and  be the iterations of
be the iterations of . To find the order of convergence put
. To find the order of convergence put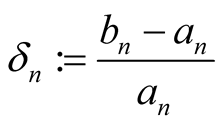 . Then
. Then
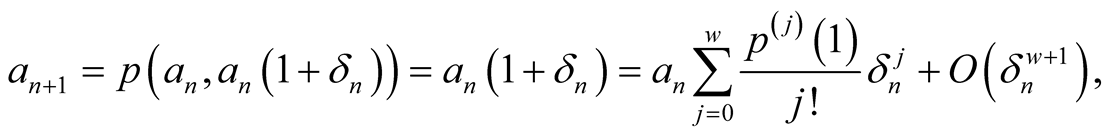
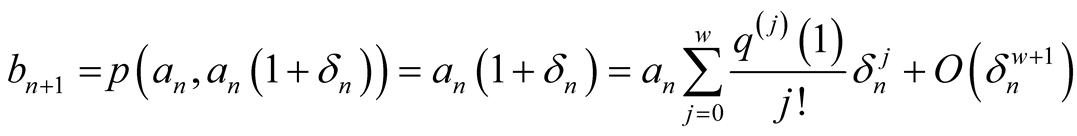
and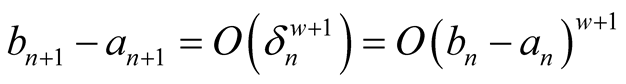 . □
. □
Take the mean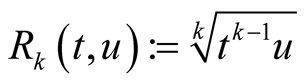 . This mean is strict, continuous and homogeneous and it has the property
. This mean is strict, continuous and homogeneous and it has the property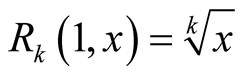 . We will construct two means
. We will construct two means 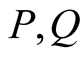 such that
such that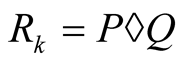 .
.
Let 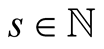 and let
and let 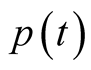 be the Padé approximation of the function
be the Padé approximation of the function  of order
of order 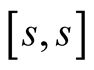 around
around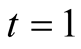 ,
,
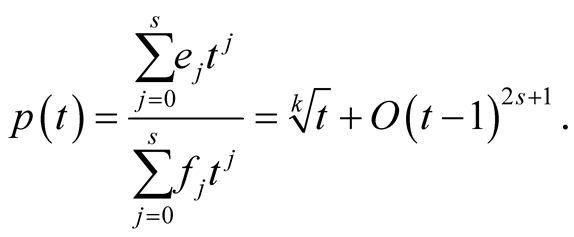 (3.1)
(3.1)
The exact formula for 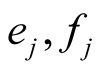 will be derived in Lemma 15. In Lemma 20 we will prove that
will be derived in Lemma 15. In Lemma 20 we will prove that 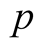 satisfies
satisfies
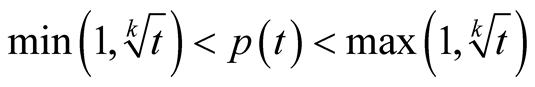 (3.2)
(3.2)
for every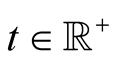 . Hence it is a trace of a strict homogeneous mean
. Hence it is a trace of a strict homogeneous mean
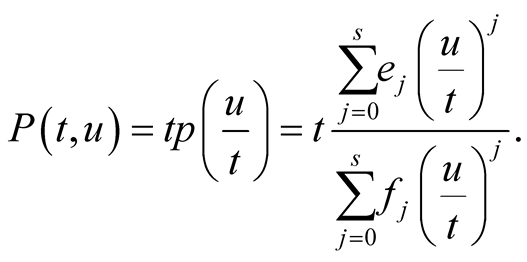
Relation 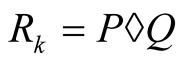 and Theorem 2 imply that
and Theorem 2 imply that
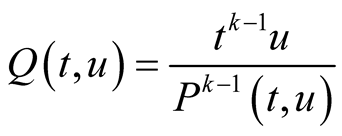 (3.3)
(3.3)
and its trace is
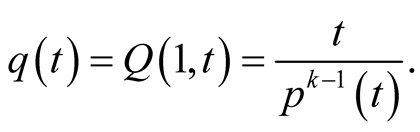
Inequalities (3.2) imply that 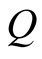 is a strict homogeneous mean too.
is a strict homogeneous mean too.
As in Definition 2, denote the sequences given by the compound mean 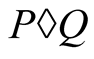 by
by , starting with
, starting with 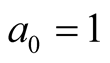 and
and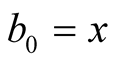 . From (3.3) we obtain that
. From (3.3) we obtain that
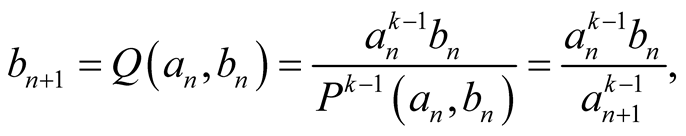
hence 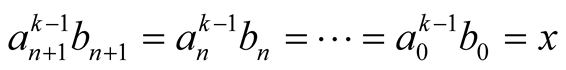 and
and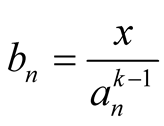 . So the iterations of the compound mean
. So the iterations of the compound mean  are
are
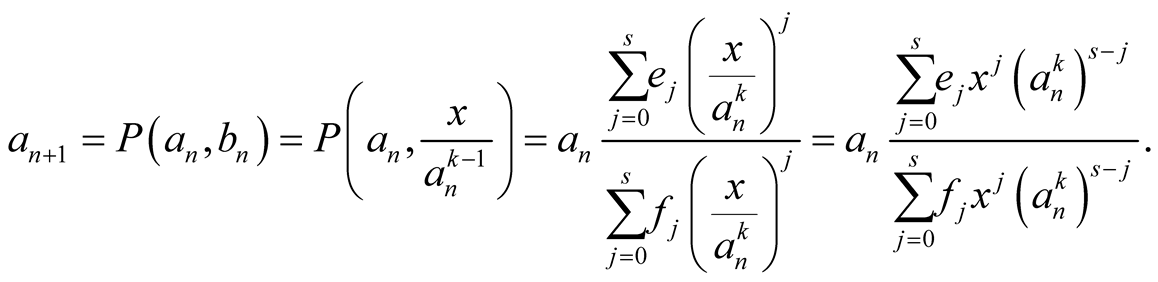 (3.4)
(3.4)
Note that we don’t have to compute the sequence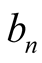 .
.
According to (3.1) and Lemma 1 the convergence of the sequence (3.4) to its limit 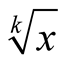 has order
has order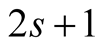 .
.
4. Complexity
Let 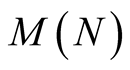 denote the time complexity of multiplication of two N-digit numbers. The classical algorithm of multiplication has asymptotic complexity
denote the time complexity of multiplication of two N-digit numbers. The classical algorithm of multiplication has asymptotic complexity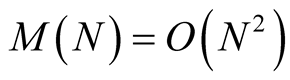 . But there are also algorithms with asymptotic complexity
. But there are also algorithms with asymptotic complexity
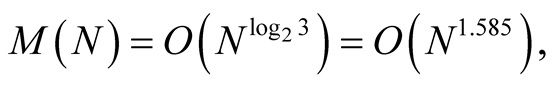
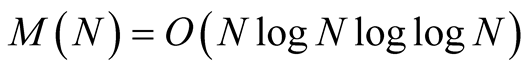
or
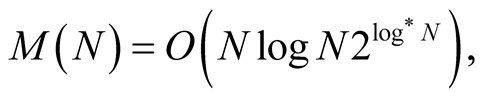
see Karatsuba [6] , Schönhage and Strassen [7] or Fürer [8] , respectively. The fastest algorithms have large asymptotic constants, hence it is better to use the former algorithms if the number 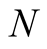 is not very large.
is not very large.
The complexity of division of two N-digit numbers differs from the complexity of multiplication only by some multiplicative constant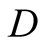 . Hence the complexity of division is
. Hence the complexity of division is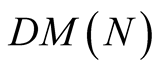 . Analysis in [9] shows that this constant can be as small as
. Analysis in [9] shows that this constant can be as small as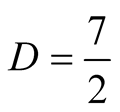 .
.
We will denote by 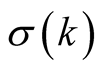 the minimal number of multiplications necessary to compute the power
the minimal number of multiplications necessary to compute the power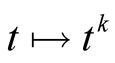 . See [10] for a survey on known results about the function
. See [10] for a survey on known results about the function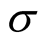 .
.
Before the main computation of complexity we need this auxiliary lemma.
Lemma 2. Assume that 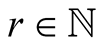 and that
and that  is a function such that for some
is a function such that for some 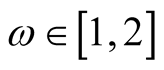 the function
the function
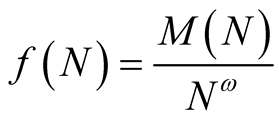 is nondecreasing with
is nondecreasing with
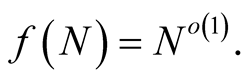 (4.1)
(4.1)
For every 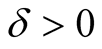 put
put 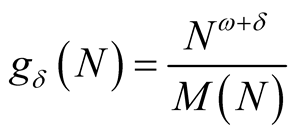 and assume that 1) for every
and assume that 1) for every 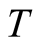 the image set
the image set  is bounded and 2) there is
is bounded and 2) there is 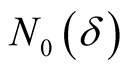 with
with 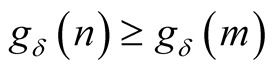 for every
for every .
.
Then

Proof. From the monotonicity of 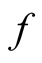 we have for every
we have for every 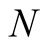
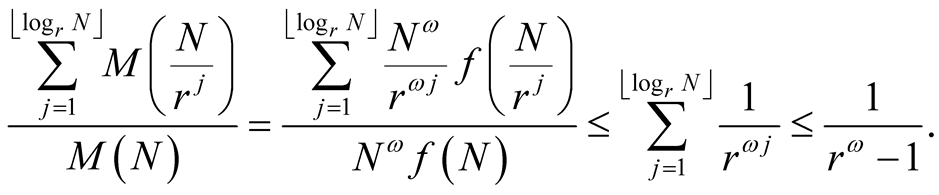 (4.2)
(4.2)
Let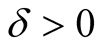 . Then (4.1) implies
. Then (4.1) implies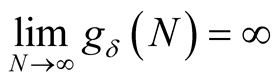 . From this and properties 1 and 2 we deduce that there exists a number
. From this and properties 1 and 2 we deduce that there exists a number 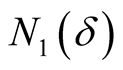 such that
such that 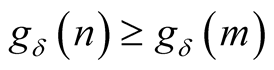 for every
for every 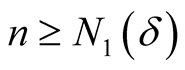 and every
and every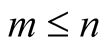 . This implies for every
. This implies for every 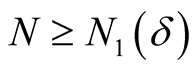
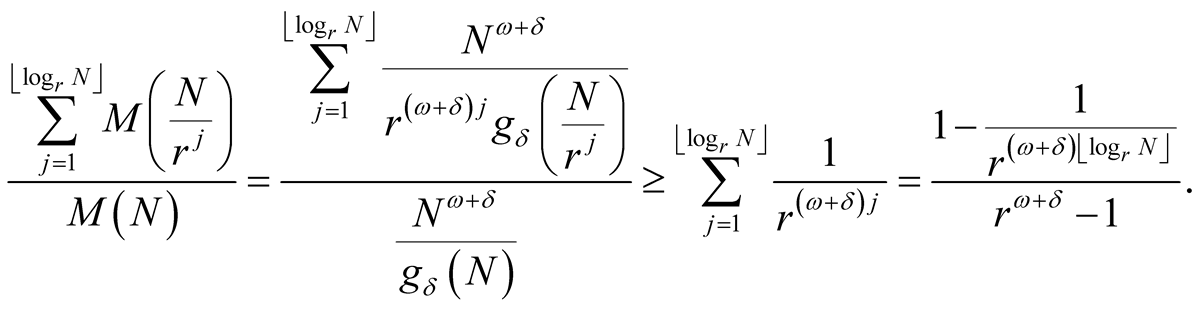 (4.3)
(4.3)
Inequalities (4.2) and (4.3) yield
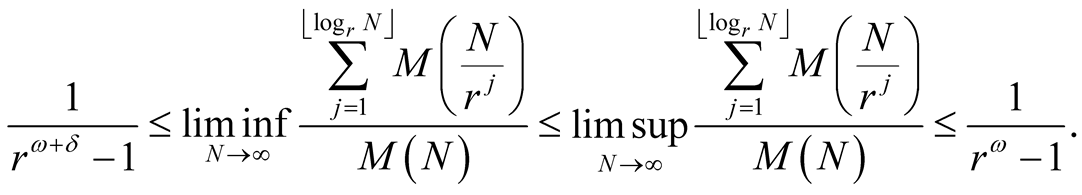
Passing to the limit 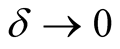 implies the result. □
implies the result. □
Note that all the above mentioned functions 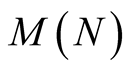 satisfy all assumptions of Lemma 2 with
satisfy all assumptions of Lemma 2 with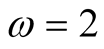 ,
, 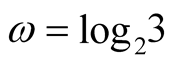 ,
, 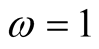 and
and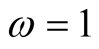 , respectively.
, respectively.
Now we compute the complexity 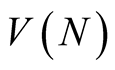 of algorithm computing
of algorithm computing 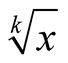 to within
to within 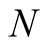 digits. The functions
digits. The functions  and
and 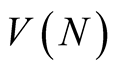 have asymptotically the same order as
have asymptotically the same order as , see for instance Theorem 6.3 in [3] . Hence all fast algorithms for computing
, see for instance Theorem 6.3 in [3] . Hence all fast algorithms for computing 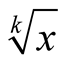 differ only in the asymptotic constants.
differ only in the asymptotic constants.
Let the algorithm for computing 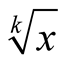
• performs 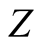 multiplications of two N-digit numbers before the iterations• performs
multiplications of two N-digit numbers before the iterations• performs 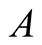 multiplications and
multiplications and 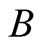 divisions of two long numbers in every step• has order of convergence
divisions of two long numbers in every step• has order of convergence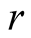 .
.
The accuracy to within 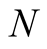 digits is necessary only in the last step. In the previous step we need accuracy only to within
digits is necessary only in the last step. In the previous step we need accuracy only to within 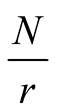 digits and so on. Hence
digits and so on. Hence
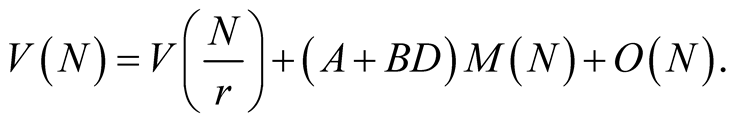
The error term 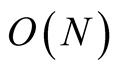 corresponds to additions of N-digit numbers. This and Lemma 2 imply that1
corresponds to additions of N-digit numbers. This and Lemma 2 imply that1
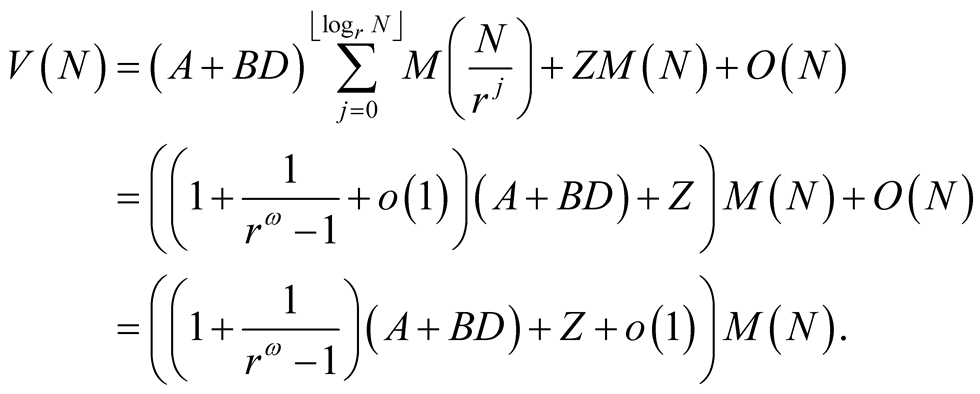
4.1. Complexity of Newton’s Method
Newton’s method (2.3) has order 2 and in every step it performs 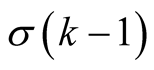 multiplications (evaluation of
multiplications (evaluation of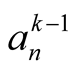 ) and 1 division. So the complexity is
) and 1 division. So the complexity is
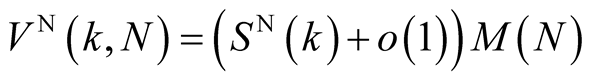
where
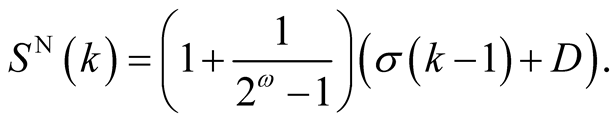
For the choice of multiplication and division algorithms with  and
and 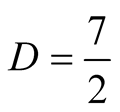 we have
we have
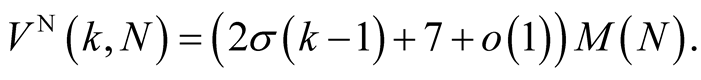
4.2. Complexity of Householder’s Method
Consider Householder’s method (1.1) applied to the equation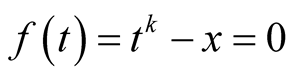 . Let
. Let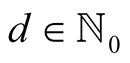 . An easy calculation (see [11] for instance) leads to iterations
. An easy calculation (see [11] for instance) leads to iterations
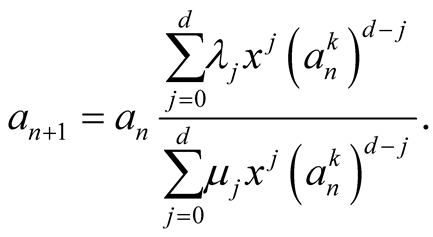
where 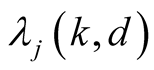 and
and 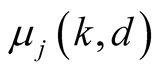 are suitable constants. The method has order
are suitable constants. The method has order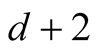 , before the iterations it performs
, before the iterations it performs 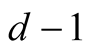 multiplications of N-digit numbers (evaluation of
multiplications of N-digit numbers (evaluation of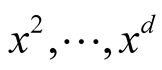 ) and in every step it performs
) and in every step it performs 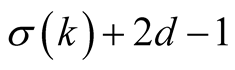 multiplications (evaluation of
multiplications (evaluation of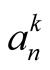 , then evaluations of numerator and denominator by Horner’s method, and then the final multiplication) and 1 division. So the complexity of Householder’s algorithm is
, then evaluations of numerator and denominator by Horner’s method, and then the final multiplication) and 1 division. So the complexity of Householder’s algorithm is

where
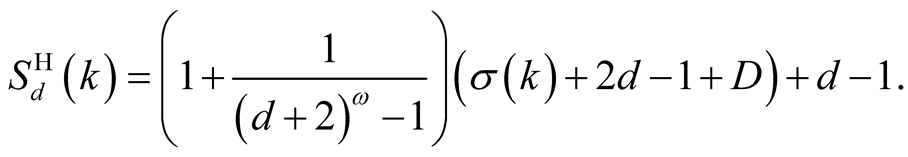
For the choice of multiplication and division algorithms with  and
and  we have
we have
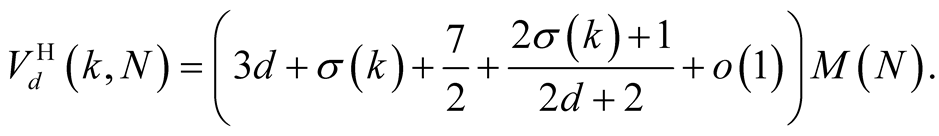
The optimal value of  which minimizes the complexity is in this case
which minimizes the complexity is in this case
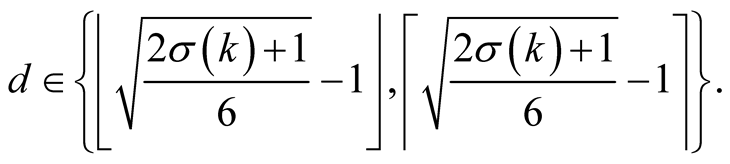
4.3. Complexity of Our Method
Given , our method (3.4) has order
, our method (3.4) has order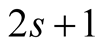 , before the iterations it performs
, before the iterations it performs  multiplications of N-digit numbers (evaluation of
multiplications of N-digit numbers (evaluation of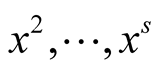 ) and in every step it performs
) and in every step it performs 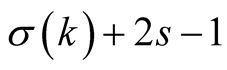 multiplications (evaluation of
multiplications (evaluation of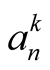 , then evaluations of numerator and denominator by Horner’s method2, and then the final multiplication) and
, then evaluations of numerator and denominator by Horner’s method2, and then the final multiplication) and 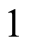 division. So the complexity of our algorithm is
division. So the complexity of our algorithm is
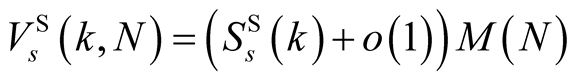
where
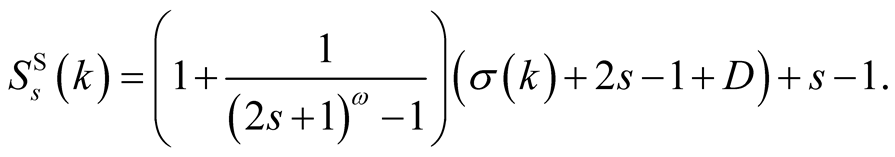
For the choice of multiplication and division algorithms with  and
and 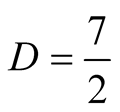 we have
we have
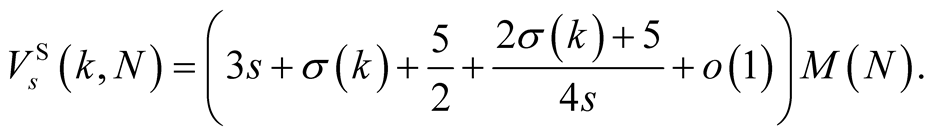 (4.4)
(4.4)
The optimal value of 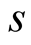 which minimizes the complexity is in this case
which minimizes the complexity is in this case
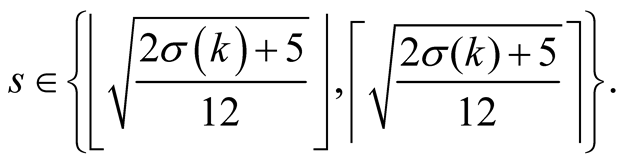
5. Examples
Example 2. Compare the algorithms for computation of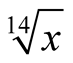 . For
. For  we have
we have 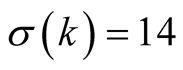 and, according to (4.4), the optimal value of
and, according to (4.4), the optimal value of 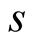 for our algorithm is
for our algorithm is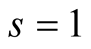 . Padé approximation of the function
. Padé approximation of the function 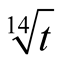 around
around 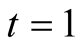 is
is
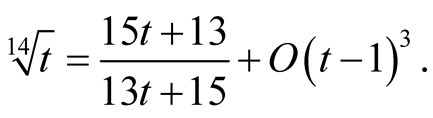
Hence the iterations of our algorithm are
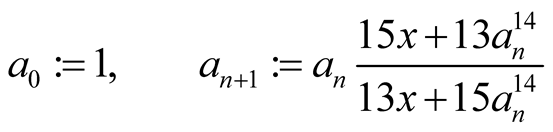 (5.1)
(5.1)
with convergence of order 3. For computation of 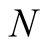 digits of
digits of 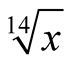 we need to perform
we need to perform
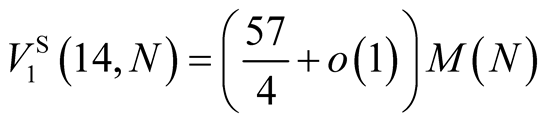
operations.
Newton’s method
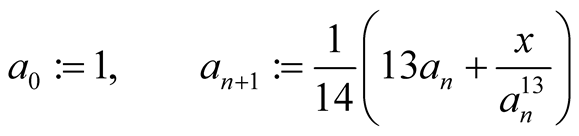
has order 2 and for computation of 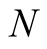 digits it needs
digits it needs 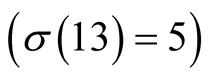
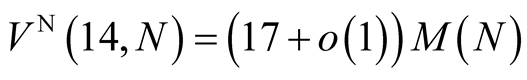
operations. Hence our method saves 16% of time compared to Newton’s method.
For Householder’s method the optimal value is 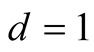 and it leads to the same iterations (5.1) as our method.
and it leads to the same iterations (5.1) as our method.
Example 3. Compare the algorithms for computation of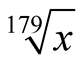 . For
. For 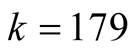 we have
we have 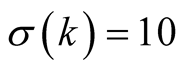 and, according to (4.4), the optimal value of
and, according to (4.4), the optimal value of  for our algorithm is
for our algorithm is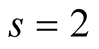 . Padé approximation of the function
. Padé approximation of the function 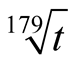 around
around 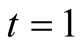 is
is
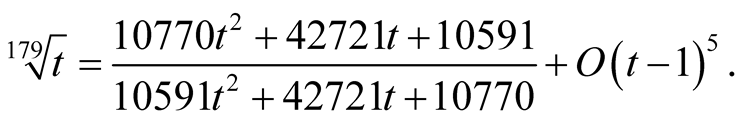
Hence the iterations of our algorithm are
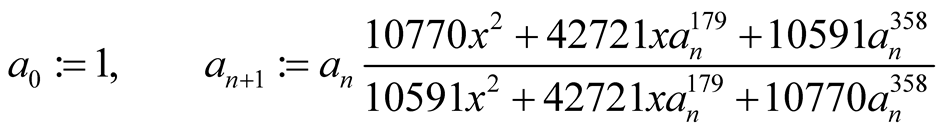
with convergence of order 5. For computation of  digits of
digits of  we need to perform
we need to perform
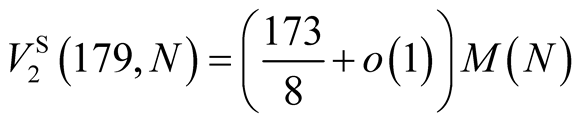
operations.
Newton’s method
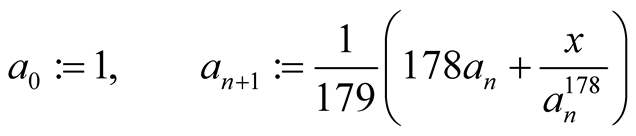
has order 2 and for computation of 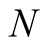 digits it needs
digits it needs
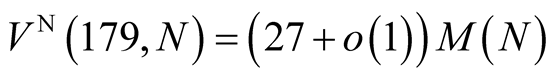
operations.
For Householder’s method the optimal value is 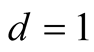 and it leads to iterations
and it leads to iterations
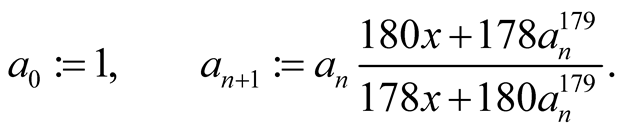
This method has order 3 and for computation of 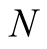 digits it needs
digits it needs
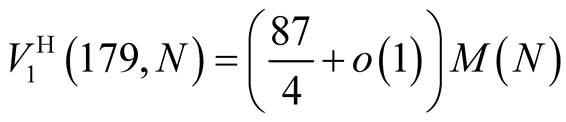
operations.
Hence our method saves 20% of time compared to Newton’s method and saves 0.6% of time compared to Householder’s method.
Example 4. Compare the algorithms for computation of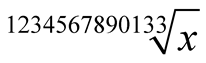 . For
. For 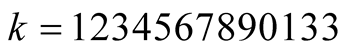 the exact value of
the exact value of 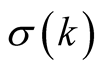 is not known. We assume that
is not known. We assume that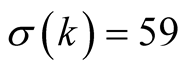 . According to (4.4), the optimal value of
. According to (4.4), the optimal value of 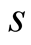 for our algorithm is
for our algorithm is . The iterations of our algorithm are
. The iterations of our algorithm are
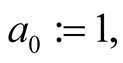

with convergence of order 7. For computation of  digits of
digits of  we need to perform
we need to perform
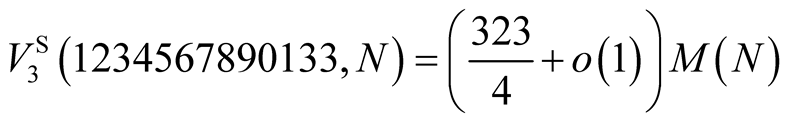
operations.
For Householder’s method the optimal value is 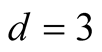 and it leads to iterations
and it leads to iterations
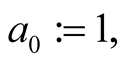

This method has order 5 and for computation of 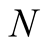 digits it needs
digits it needs
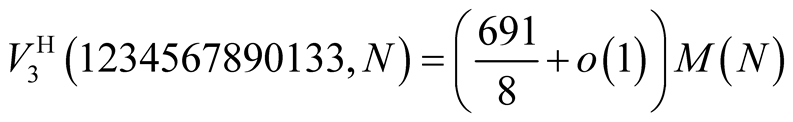
operations.
Newton’s method
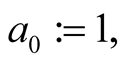

has order 2 and for computation of 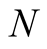 digits it needs (assuming that
digits it needs (assuming that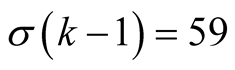 )
)
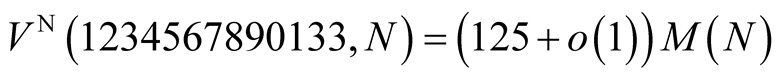
operations.
Hence our method saves 35% of time compared to Newton’s method and saves 7% of time compared to Householder’s method.
6. Proofs
In this section we will prove that function 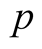 defined by (3.1) satisfies inequalities (3.2). For the sake of brevity, will use the symbol
defined by (3.1) satisfies inequalities (3.2). For the sake of brevity, will use the symbol 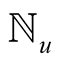 for the set
for the set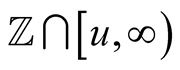 .
.
6.1. Combinatorial Identities
First we need to prove several combinatorial identities. Our notation will be changed in this subsection. Here, 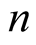 will be a variable used in mathematical induction,
will be a variable used in mathematical induction, 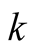 will be a summation index, and
will be a summation index, and  will be additional parameters. The change of notation is made because of easy application of the following methods based on [14] . For a function
will be additional parameters. The change of notation is made because of easy application of the following methods based on [14] . For a function 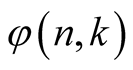 we will denote its differences by
we will denote its differences by
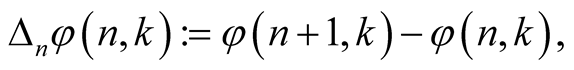
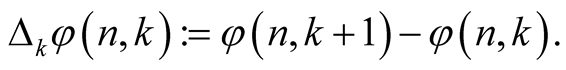
Given a function , there is some function
, there is some function  satisfying some relation between
satisfying some relation between  and
and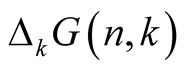 . This new function is then used for easier evaluation of sums containing
. This new function is then used for easier evaluation of sums containing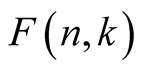 . Recall that
. Recall that
 for negative integer
for negative integer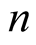 .
.
For 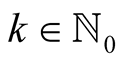 and
and 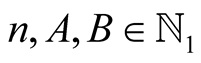 with
with 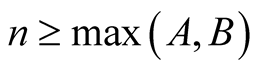 put
put
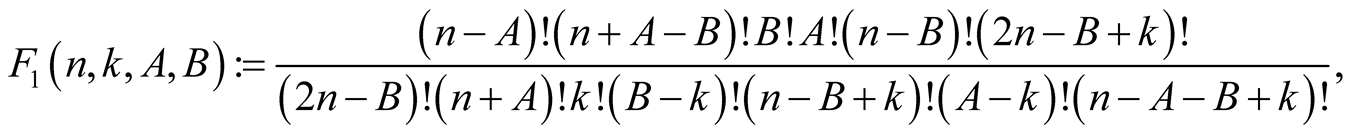

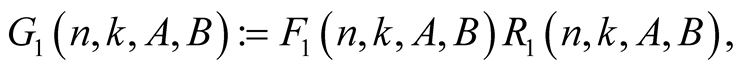

Lemma 3. For every 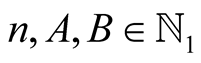 satisfying
satisfying 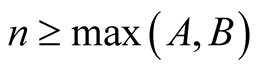 we have
we have
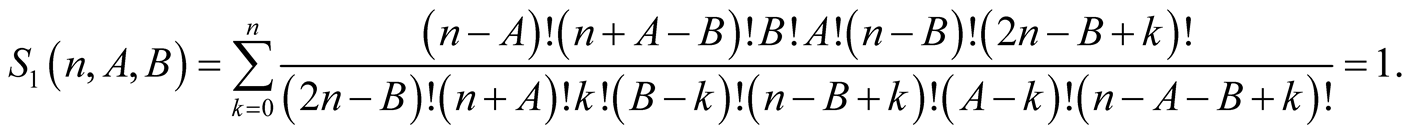
Proof. From the polynomial identity

we immediately obtain
 (6.1)
(6.1)
For fixed  we have
we have 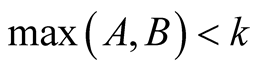 and hence
and hence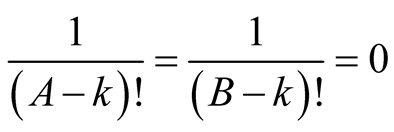 . Thus
. Thus
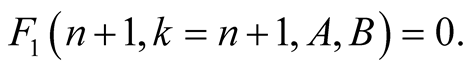 (6.2)
(6.2)
Similarly for 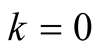 and
and 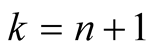 we have
we have
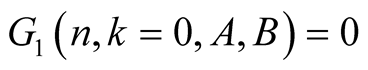 (6.3)
(6.3)
and
 (6.4)
(6.4)
Then (6.1), (6.2), (6.3) and (6.4) imply
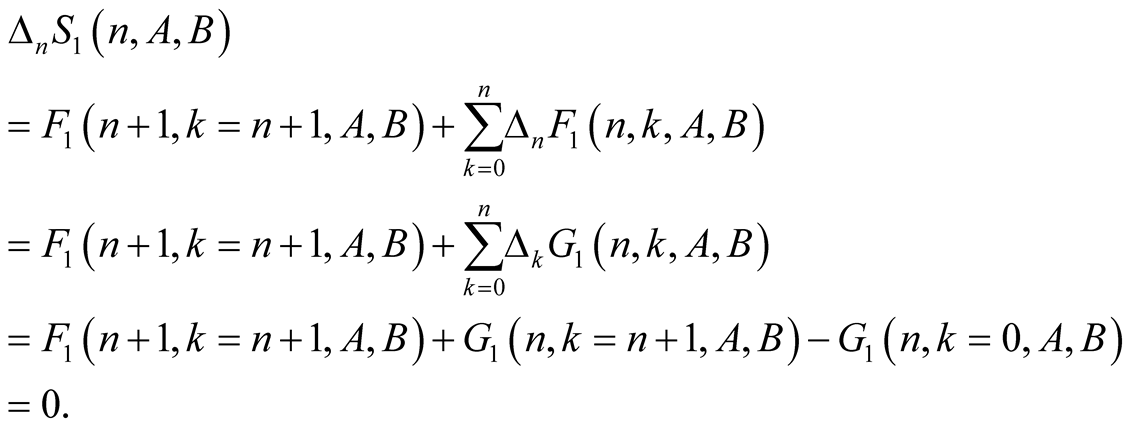 (6.5)
(6.5)
If 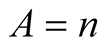 and
and 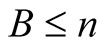 then
then  for
for 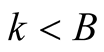 and
and 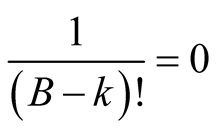 for
for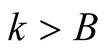 . Hence the only nonzero summand in
. Hence the only nonzero summand in 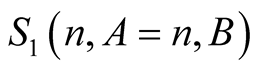 is the one for
is the one for 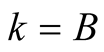 and
and
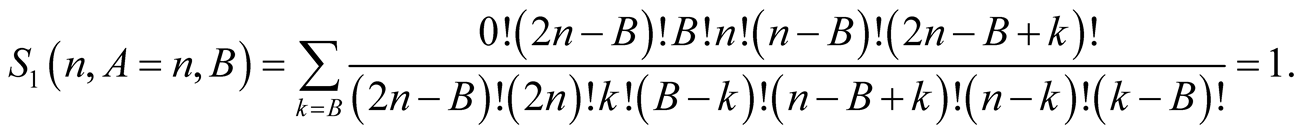 (6.6)
(6.6)
Similarly for 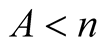 and
and 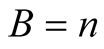 we obtain
we obtain
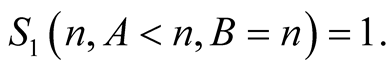
From this and (6.6) we obtain that
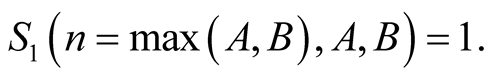
Equation (6.5) implies that 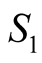 will not change for greater
will not change for greater . □
. □
For 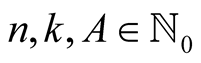 with
with 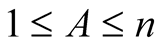 and
and 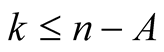 put
put

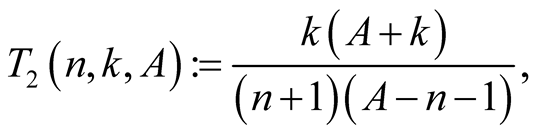
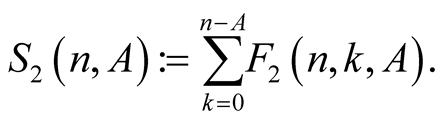
Lemma 4. For every 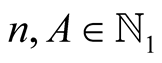 with
with 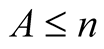
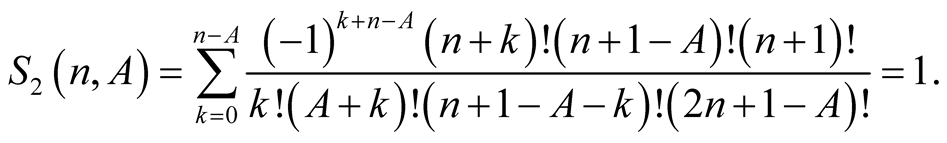
Proof. From the polynomial identity
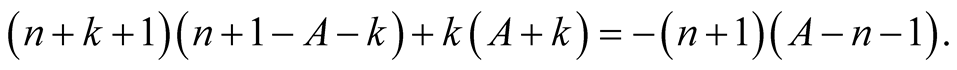
we obtain for 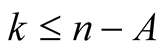 that
that
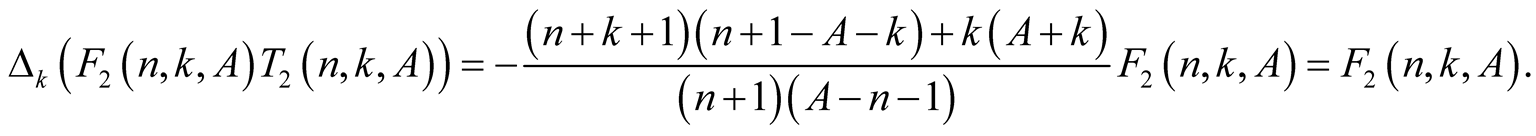
This and the fact that 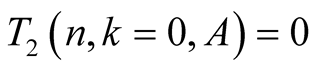 imply
imply
 □
□
For 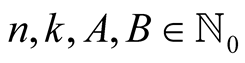 with
with 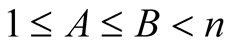 and
and  put
put
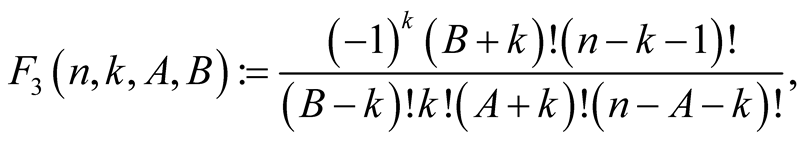
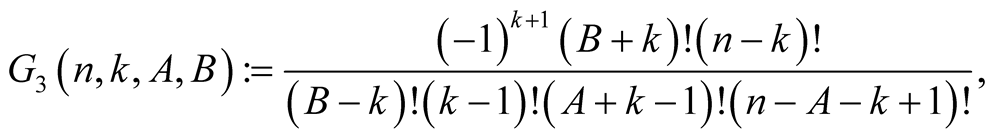
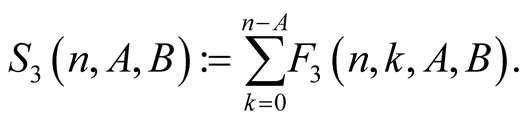
Lemma 5. For every 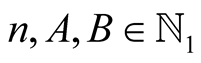 with
with 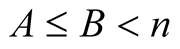
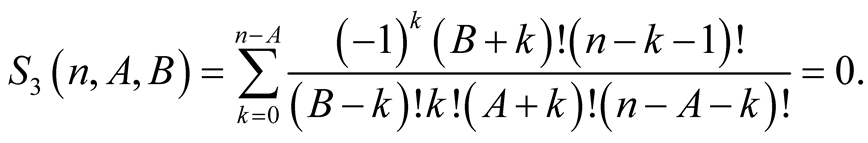
Proof. From the polynomial identity
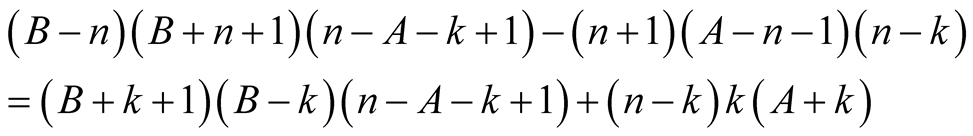
we obtain for 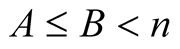 and
and 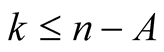 that
that
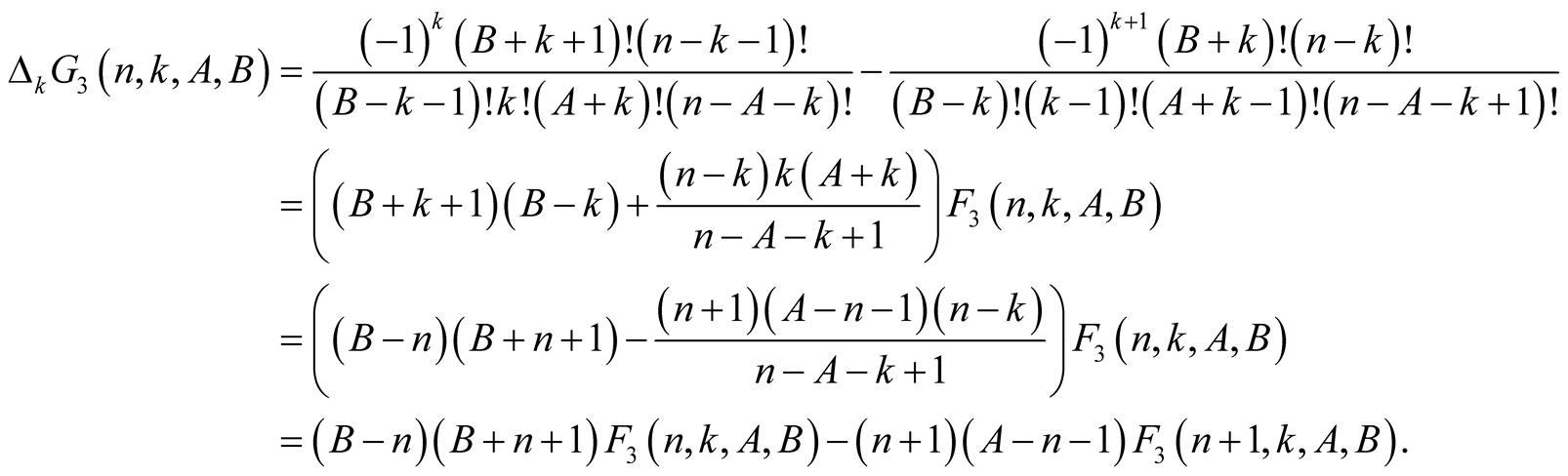 (6.7)
(6.7)
For 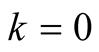 we have
we have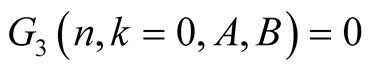 . This and (6.7) imply
. This and (6.7) imply
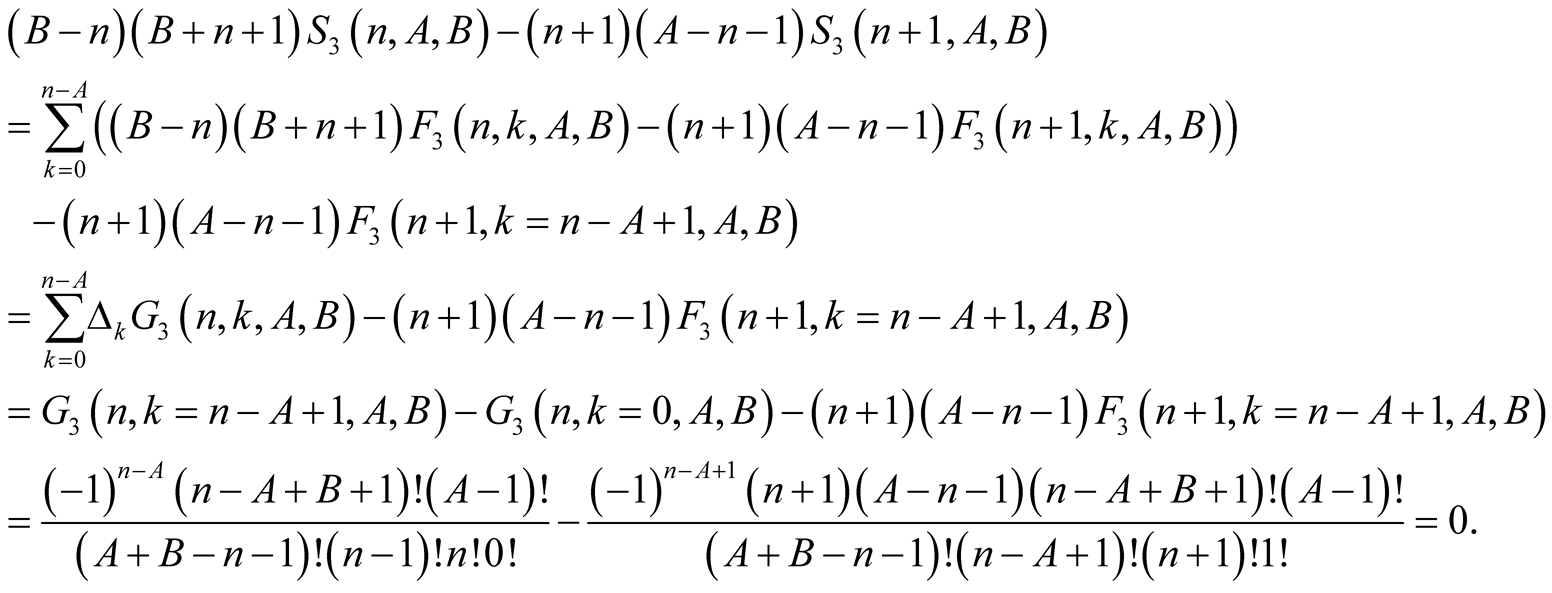 (6.8)
(6.8)
Lemma 4 for 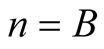 implies
implies
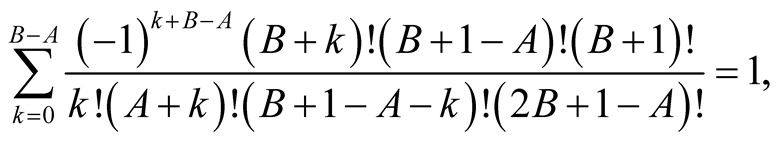
hence
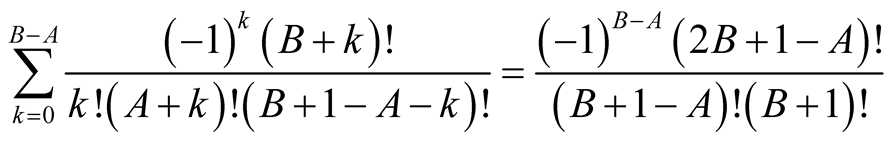
and
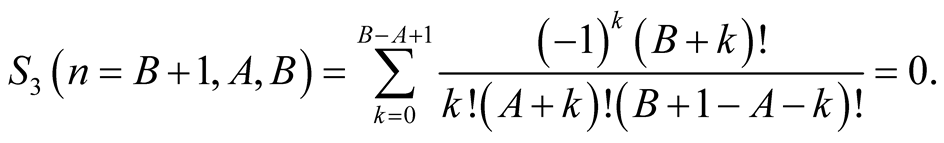 (6.9)
(6.9)
For 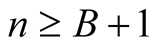 we have
we have  and (6.8) yields
and (6.8) yields
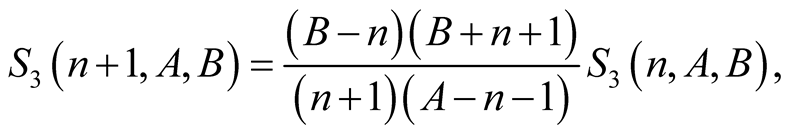
This with (6.9) implies the result for every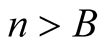 . □
. □
For 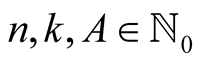 with
with 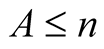 put
put
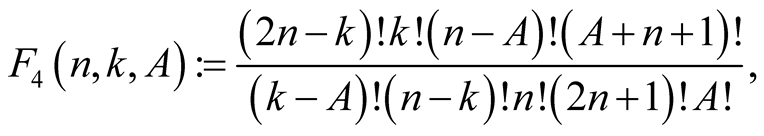
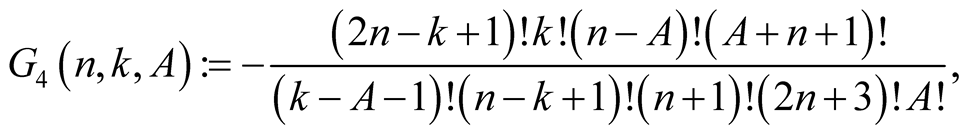
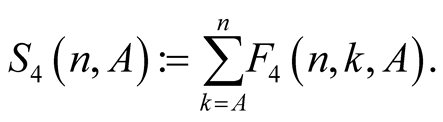
Lemma 6. For every 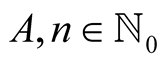 with
with 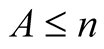
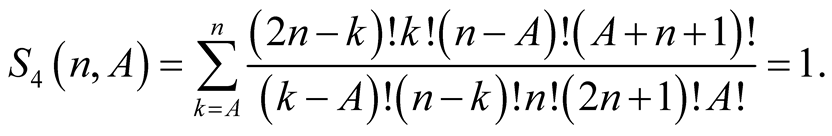
Proof. From the polynomial identity
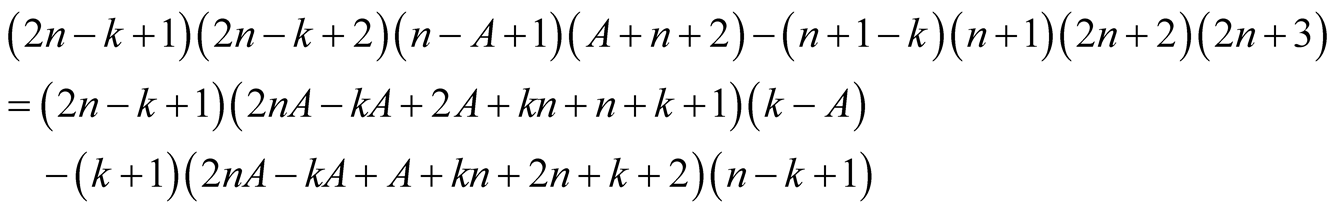
we obtain for 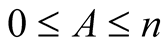 and
and  that
that
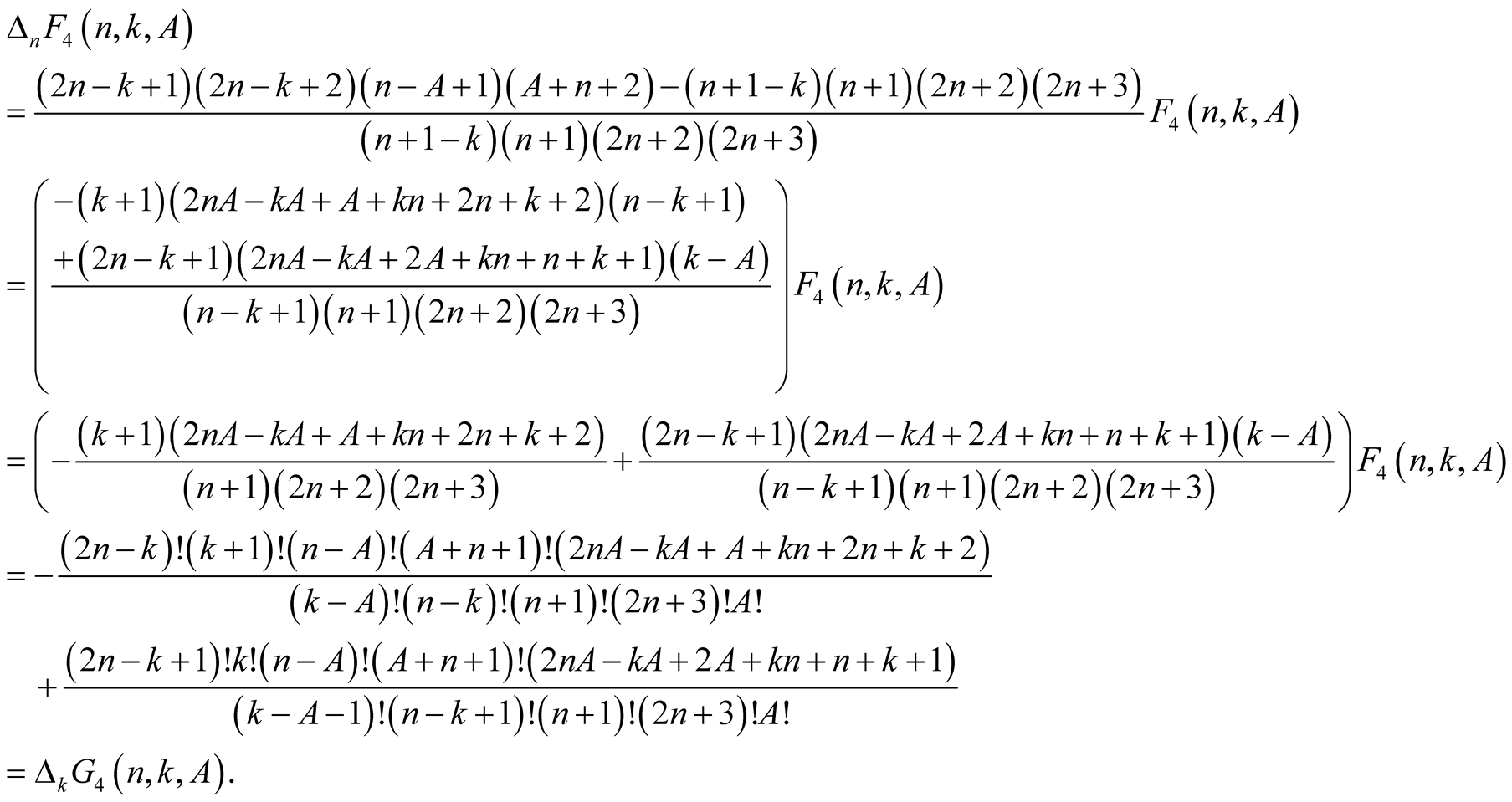
(6.10)
For 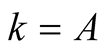 we have
we have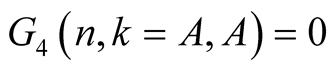 . From this, (6.10) and the polynomial identity
. From this, (6.10) and the polynomial identity
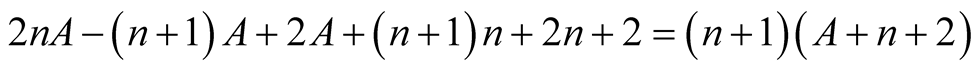
we obtain
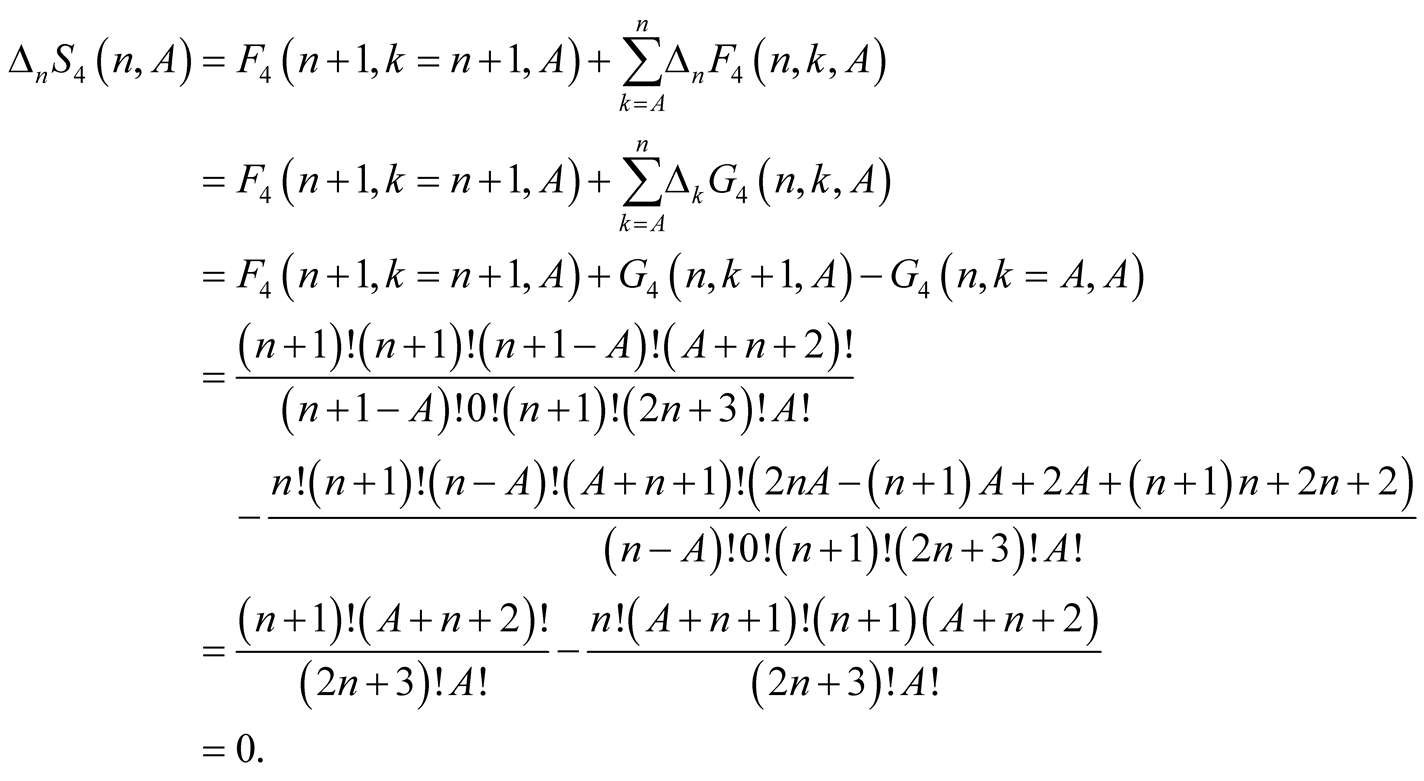 (6.11)
(6.11)
For n = A the sum  contains only one nonzero summand for
contains only one nonzero summand for 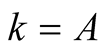 and we have
and we have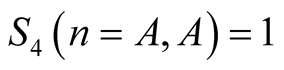 . Equation (6.11) implies that
. Equation (6.11) implies that 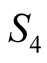 will not change for greater
will not change for greater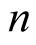 . □
. □
For 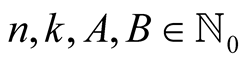 with
with 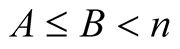 put
put
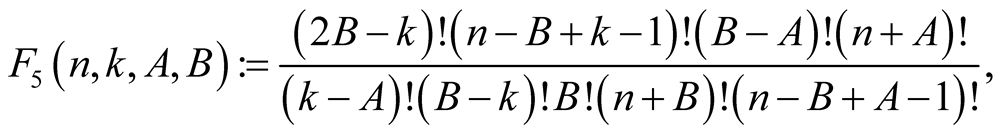
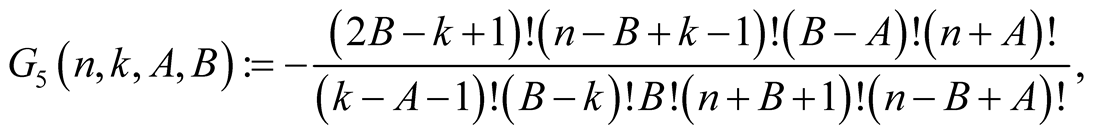
Lemma 7. For every 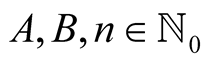 with
with 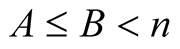
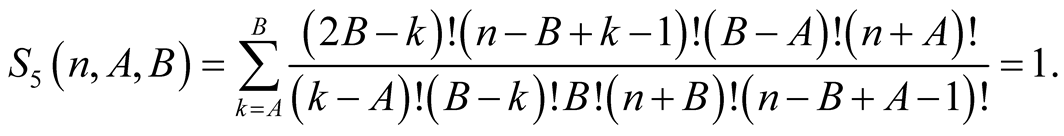
Proof. From the polynomial identity
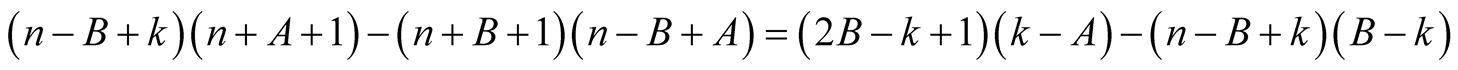
we obtain for 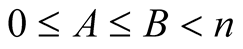 and
and 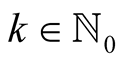
 (6.12)
(6.12)
For 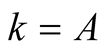 and
and 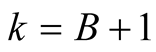 we have
we have

and
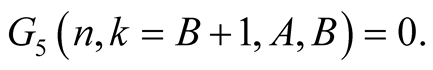
From this and (6.12) we obtain
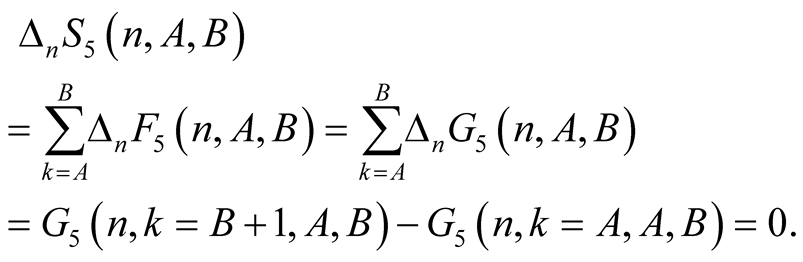 (6.13)
(6.13)
Lemma 6 for 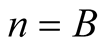 yields
yields
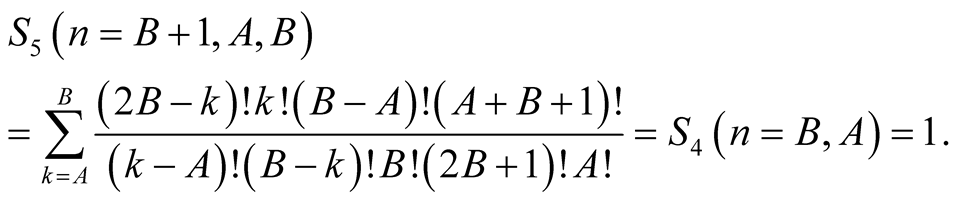
Equation (6.13) implies that 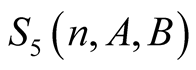 has the same value for greater
has the same value for greater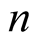 . □
. □
For 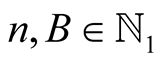 and
and 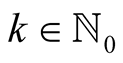 put
put
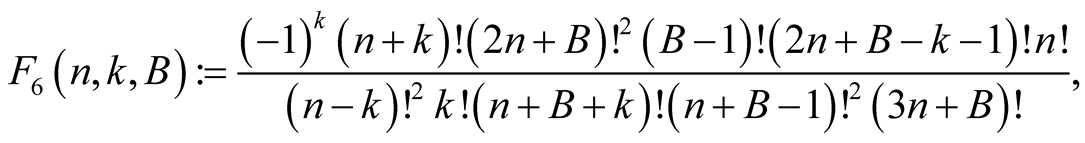
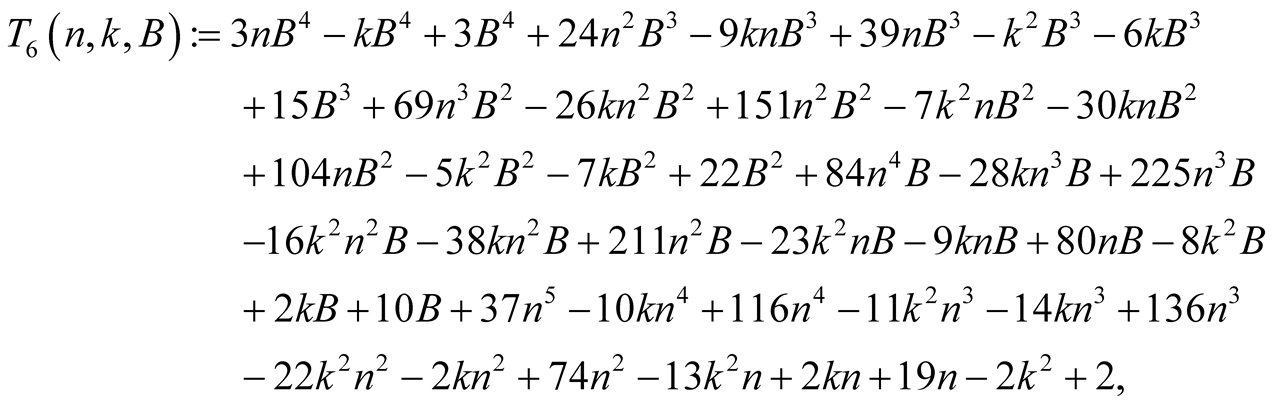
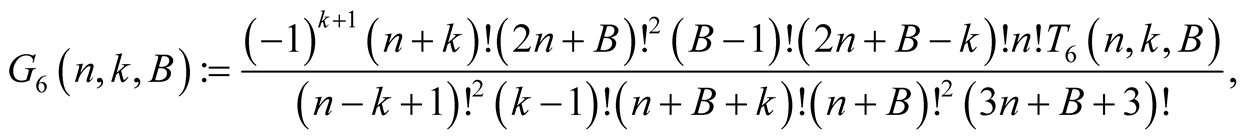
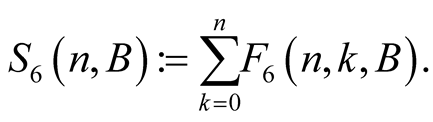
Lemma 8. For every 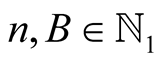
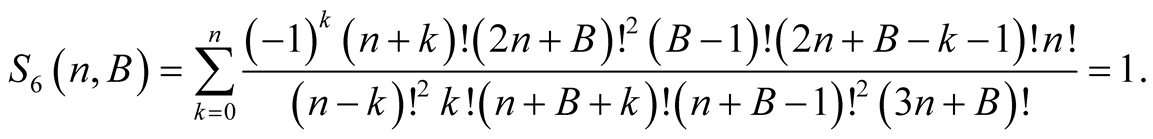
Proof. From the polynomial identity
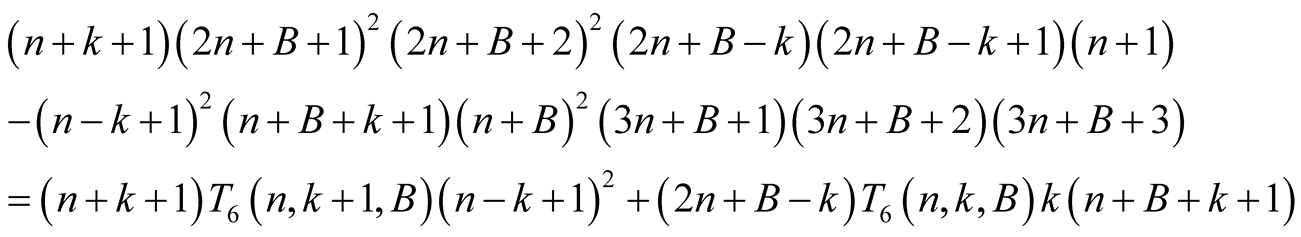
we obtain
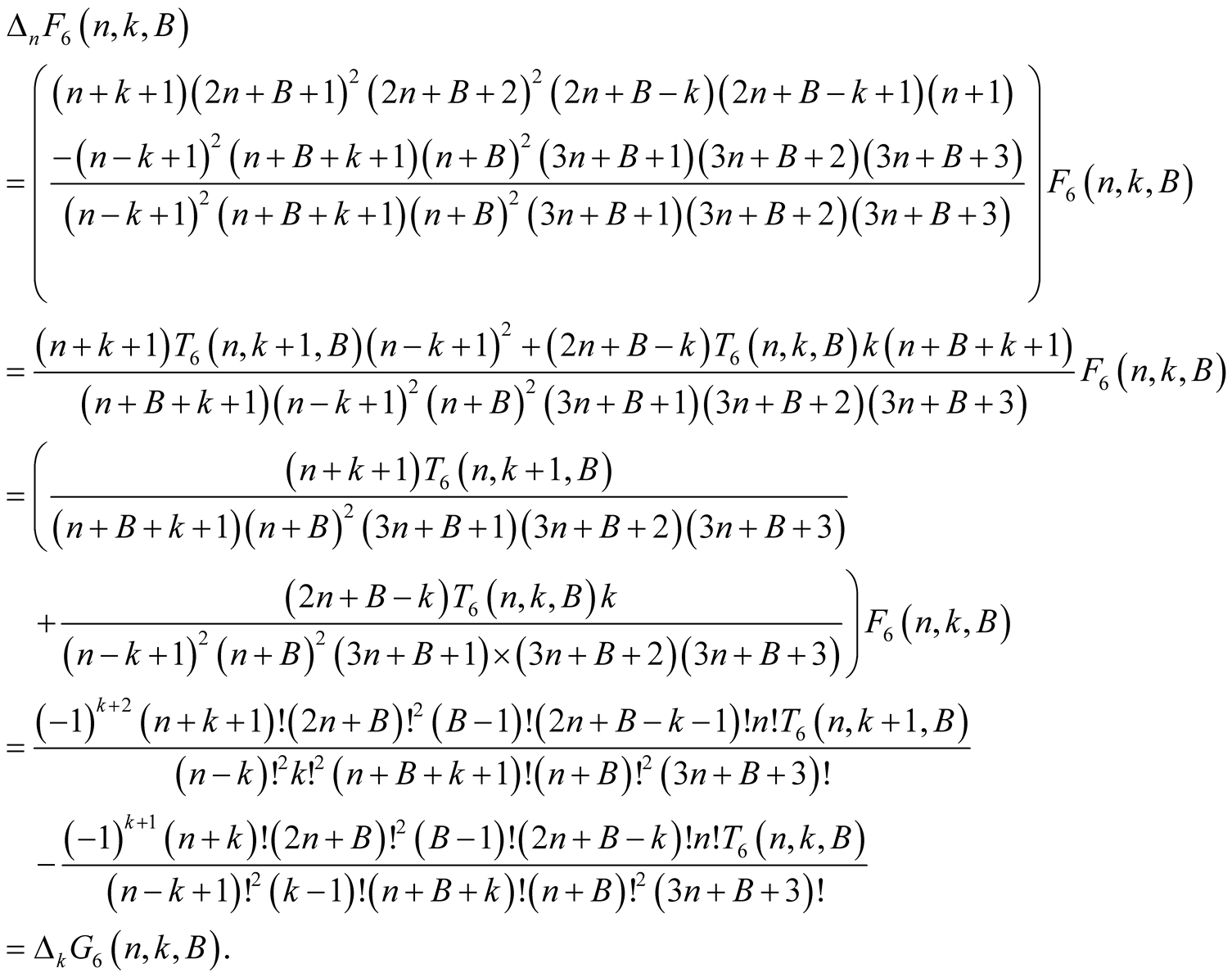 (6.14)
(6.14)
For 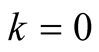 we have
we have . From this, (6.14) and the polynomial identity
. From this, (6.14) and the polynomial identity
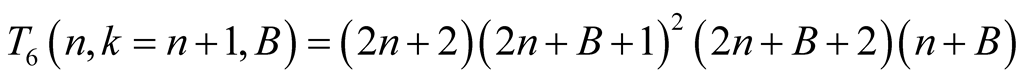
we obtain
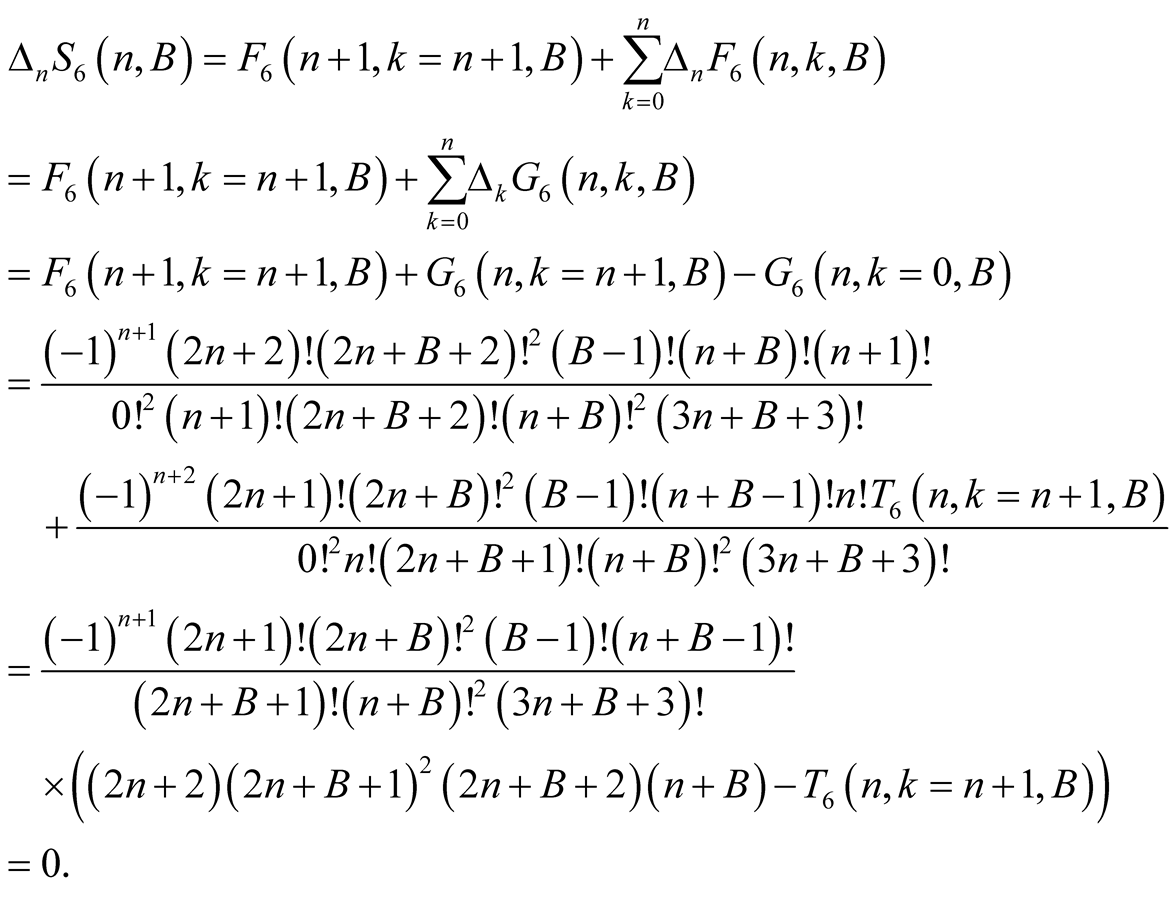 (6.15)
(6.15)
For 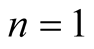 we have
we have
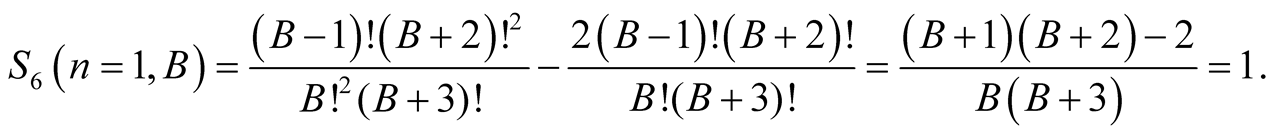
Equation (6.15) implies that 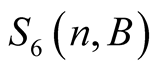 has the same value for greater
has the same value for greater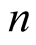 . □
. □
For 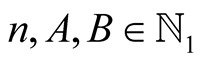 and
and 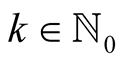 with
with 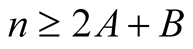 put
put
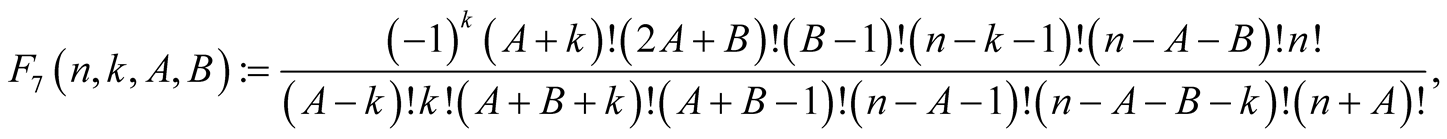

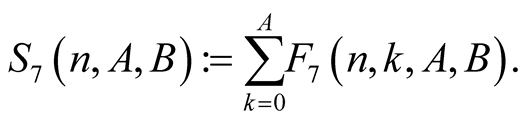
Lemma 9. For every 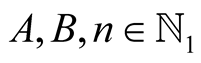 with
with 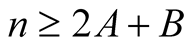
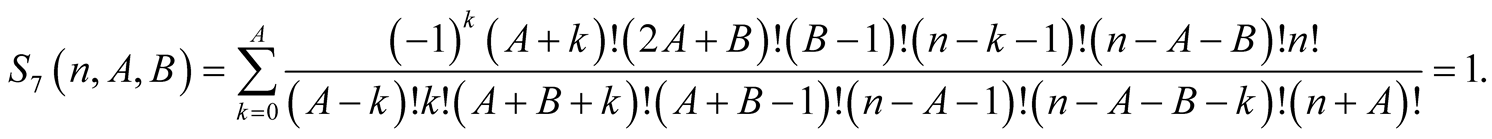
Proof. From the polynomial identity
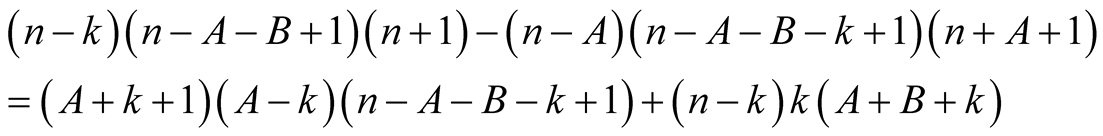
we obtain for 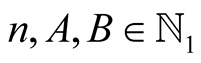 and
and 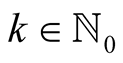 with
with 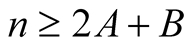
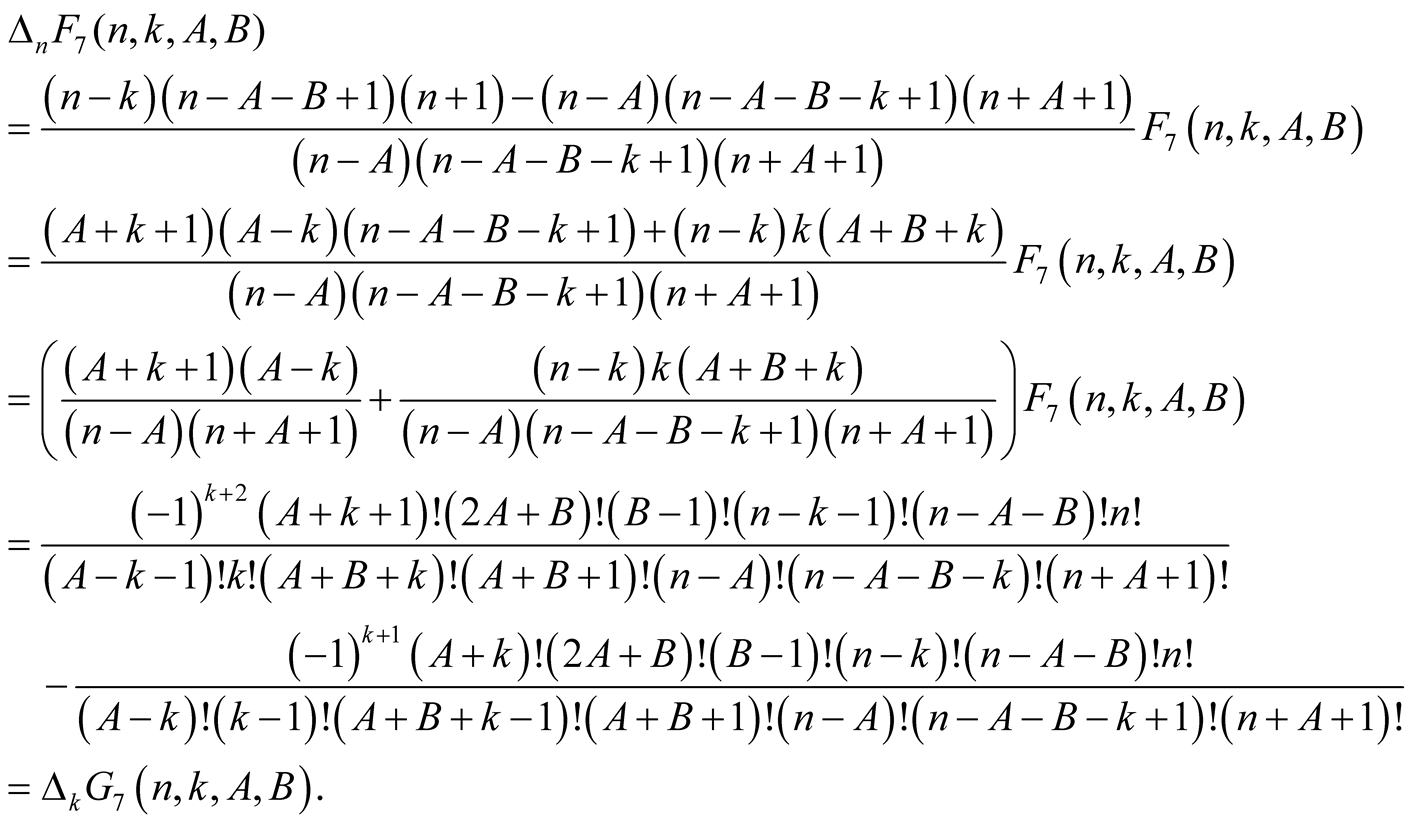 (6.16)
(6.16)
For 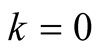 and
and 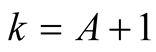 we have
we have
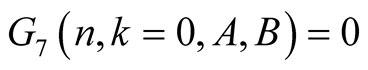
and
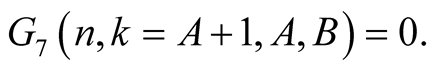
From this and (6.16) we obtain
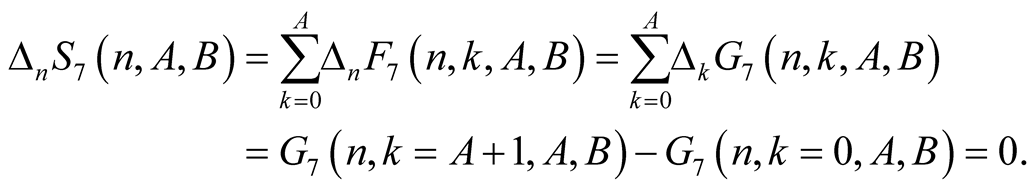 (6.17)
(6.17)
For 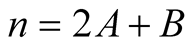 Lemma 8 implies
Lemma 8 implies
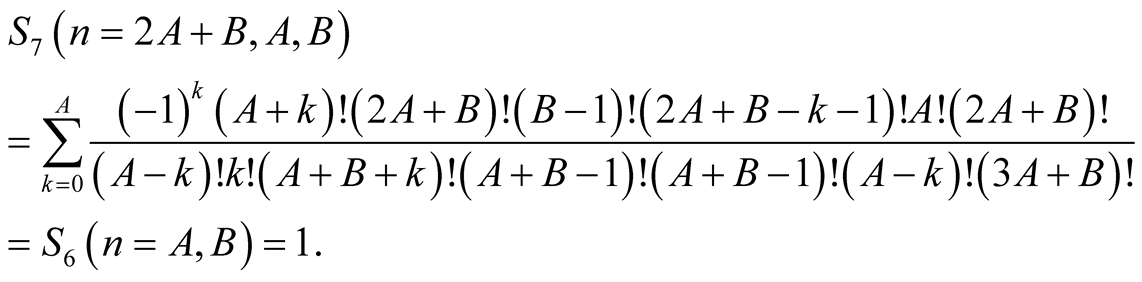
Equation (6.17) implies that 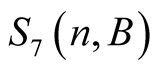 has the same value for greater
has the same value for greater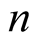 . □
. □
6.2. Formulas
Now the symbol 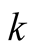 again has its original meaning.
again has its original meaning.
For 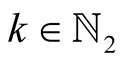 and
and 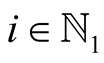 put
put
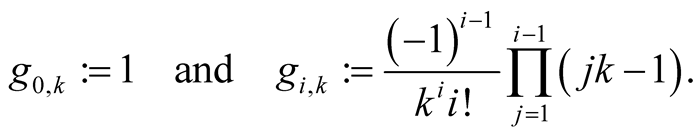
The numbers 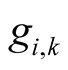 are the coefficients of Taylor’s polynomial of the function
are the coefficients of Taylor’s polynomial of the function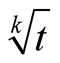 .
.
Lemma 10. For 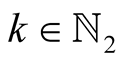 and
and 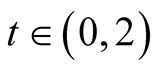
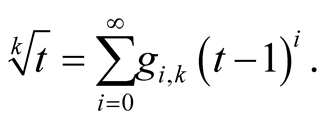
Proof. See for instance Theorem 159 in [15] . □
Now we prove a technical lemma that we need later.
Lemma 11. For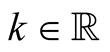 ,
, 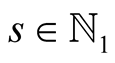 and
and 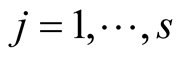
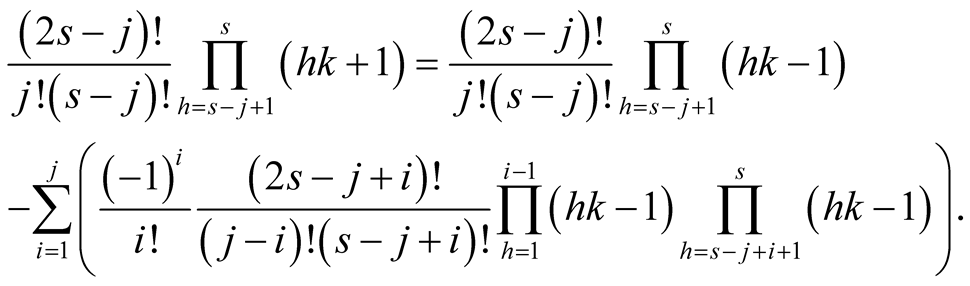 (6.18)
(6.18)
Proof. On both sides of (6.18) there are polynomials of degree 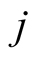 in variable
in variable . Therefore it suffices to prove the equality for
. Therefore it suffices to prove the equality for 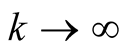 and for
and for 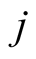 values
values 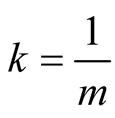 with
with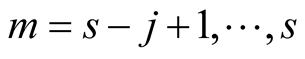 .
.
For 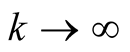 we immediately have
we immediately have
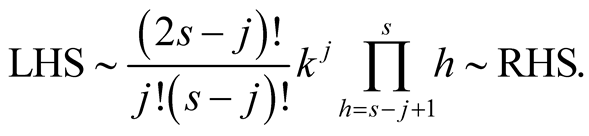
For  with
with 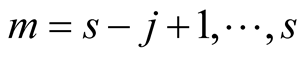 we obtain on the left-hand side of (6.18)
we obtain on the left-hand side of (6.18)
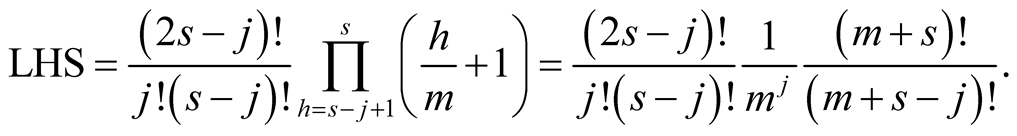
For such numbers  we have
we have
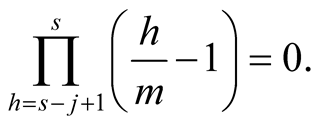
Therefore we obtain on the right-hand side of (6.18)
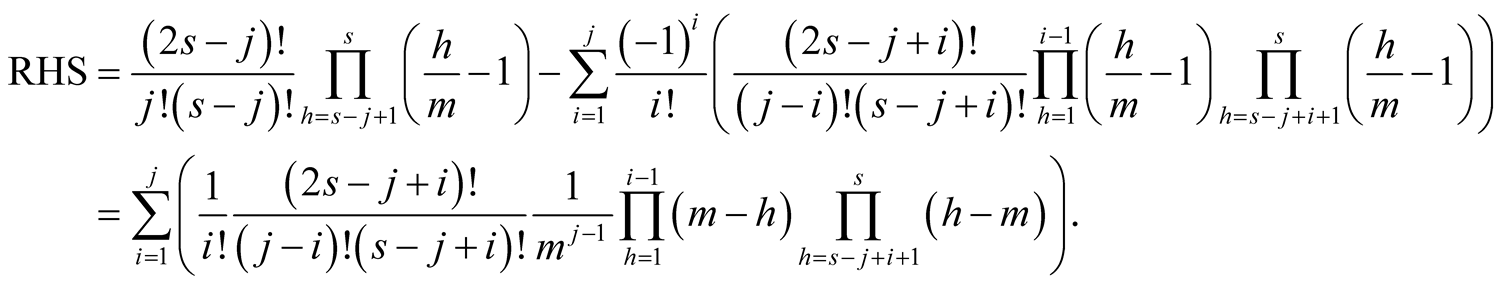
The first product on the last line is equal to zero for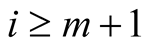 , the second product on the last line is equal to zero for
, the second product on the last line is equal to zero for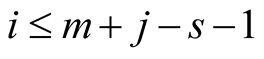 . For other values of
. For other values of 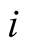 both products contain only positive terms. Hence
both products contain only positive terms. Hence
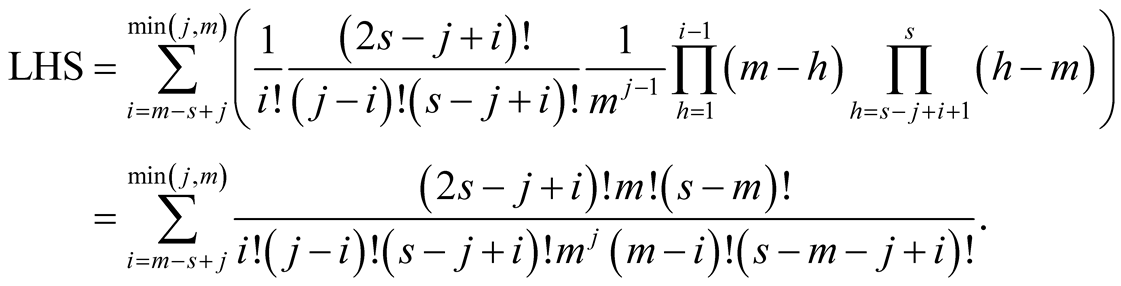
This implies that
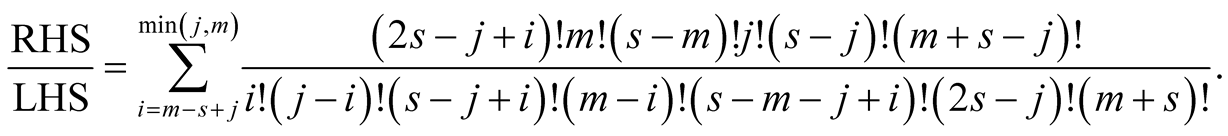
For 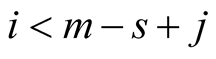 we have
we have , for
, for 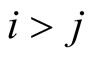 we have
we have  and for
and for 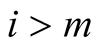 we have
we have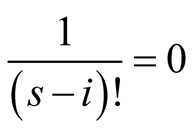 . Then Lemma 3 implies
. Then Lemma 3 implies
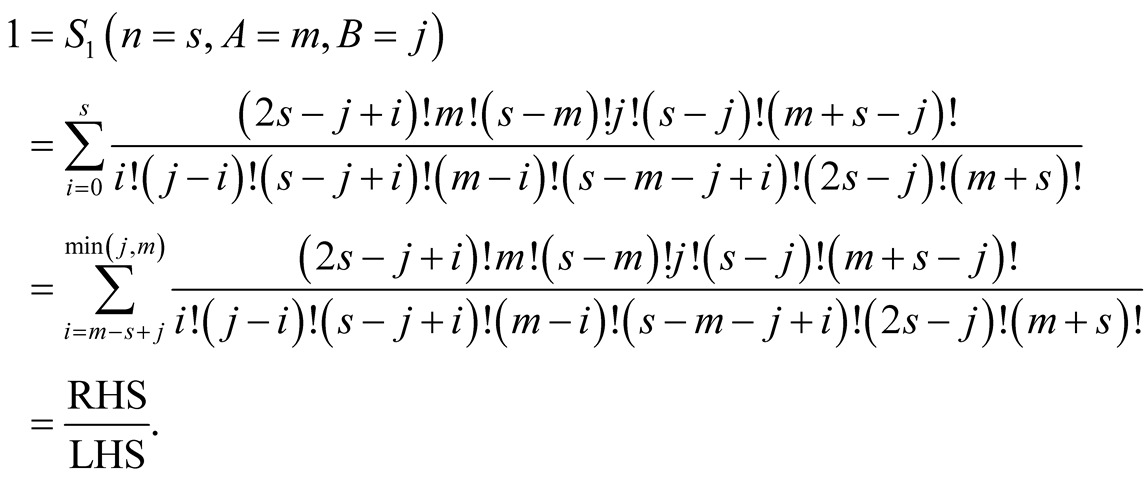
Hence equality (6.18) follows for 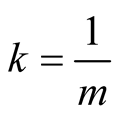 with
with . □
. □
For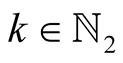 ,
, 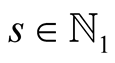 and
and 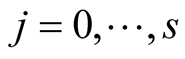 put
put


For 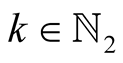 and
and 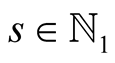 put
put
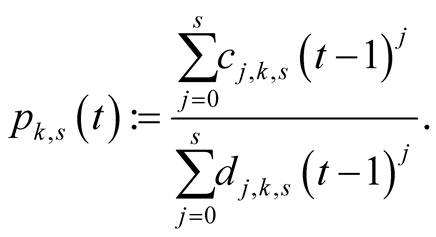 (6.19)
(6.19)
We will prove that (6.19) is Padé approximation of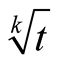 .
.
Lemma 12. For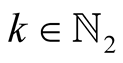 ,
, 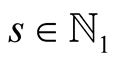 the numbers
the numbers 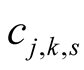 and
and 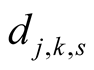 satisfy the system of equations
satisfy the system of equations
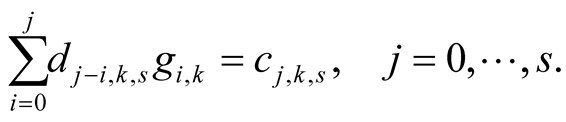
Proof. Lemma 11 implies
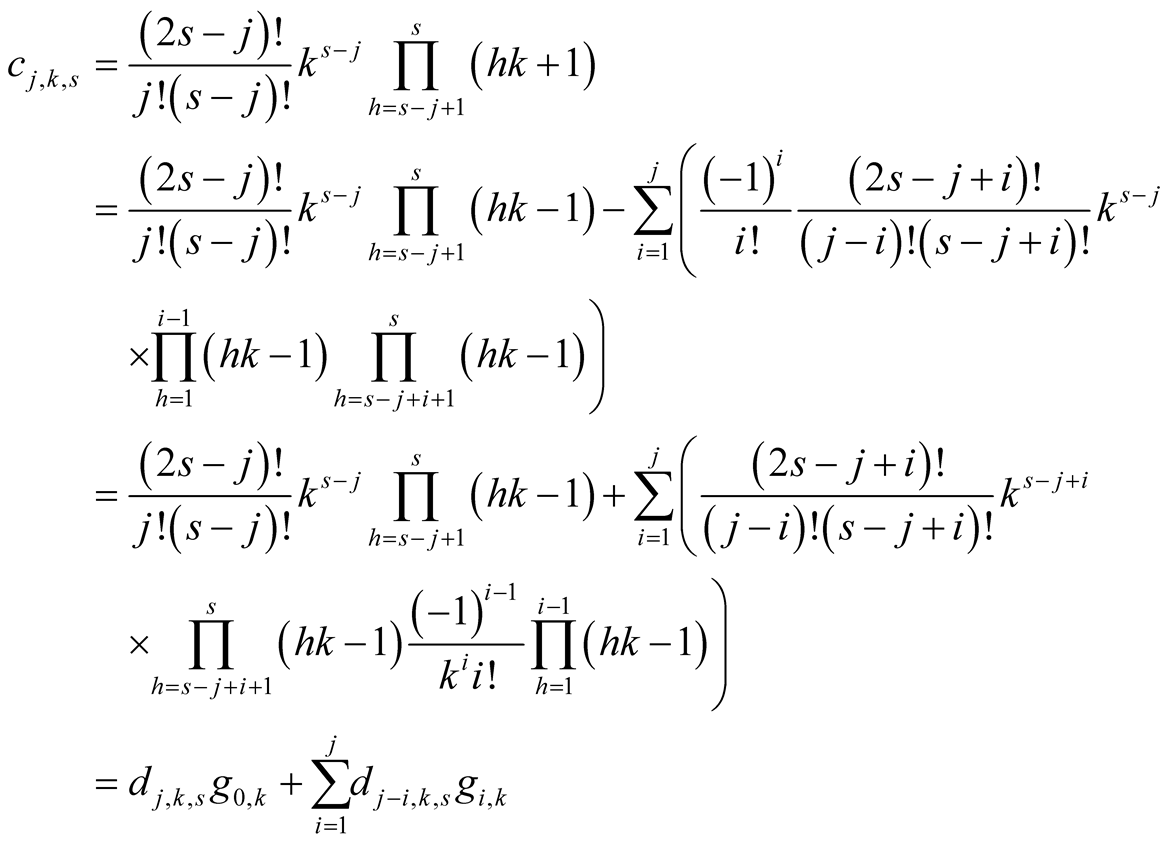 □
□
Lemma 13. For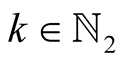 ,
, 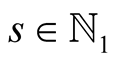 the numbers
the numbers 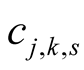 and
and 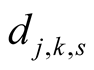 satisfy the system of equations
satisfy the system of equations
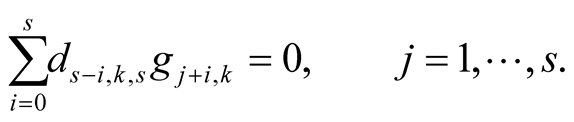
Proof. For 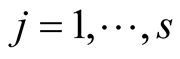 we obtain on the left-hand side
we obtain on the left-hand side
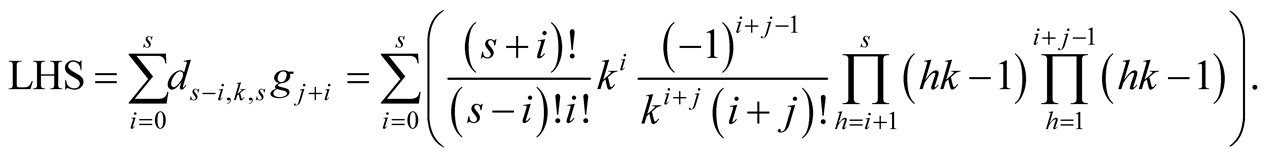
This expression, multiplied by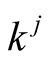 , is a polynomial of degree
, is a polynomial of degree 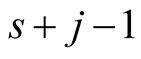 in variable
in variable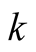 . Therefore it suffices to prove the equality for
. Therefore it suffices to prove the equality for 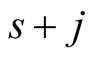 values
values 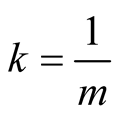 with
with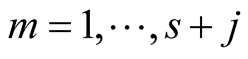 . For
. For  we have
we have 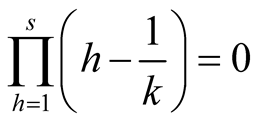 and hence the whole expression is equal to zero. For
and hence the whole expression is equal to zero. For 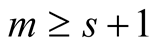 we obtain
we obtain
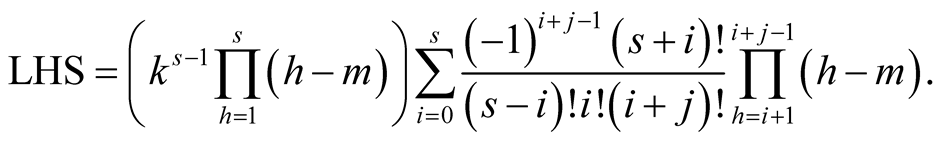
The second product is equal to zero for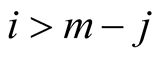 , therefore the summations ends for
, therefore the summations ends for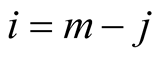 . Then Lemma 5 implies
. Then Lemma 5 implies
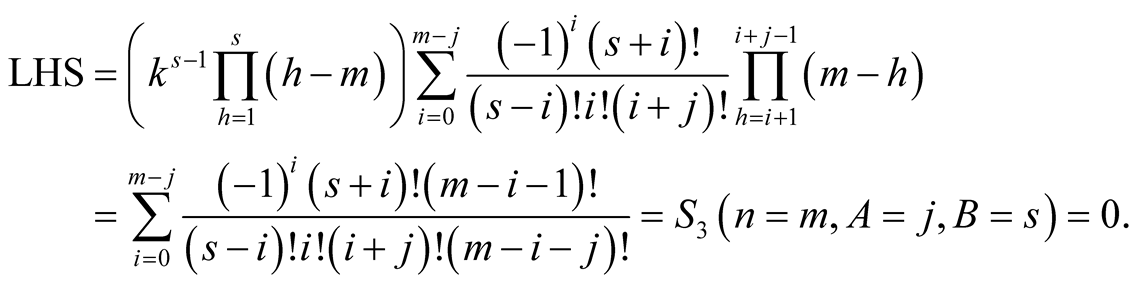 □
□
Lemma 14. Function 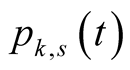 is the Padé approximation of the function
is the Padé approximation of the function 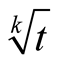 of order
of order  around
around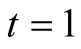 .
.
Proof. For 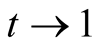 Lemma 10, Lemma 12 and Lemma 13 imply
Lemma 10, Lemma 12 and Lemma 13 imply
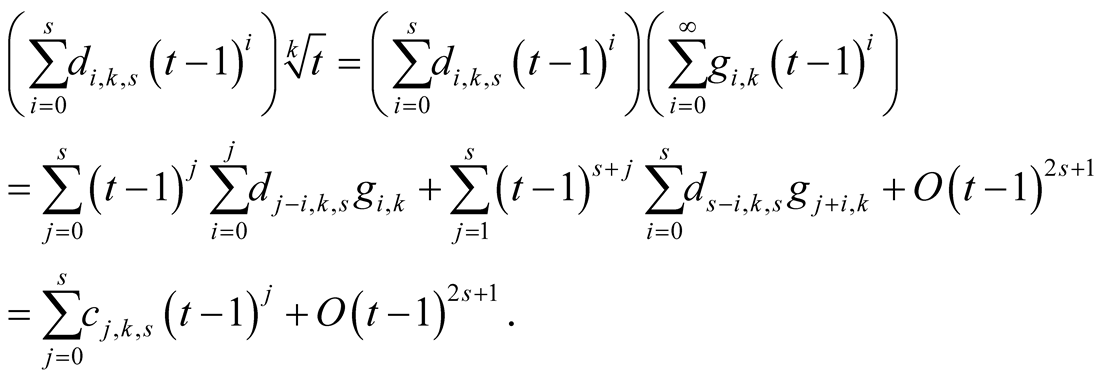
The result follows. □
Now we find the coefficients  and
and 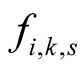 of the Padé approximation
of the Padé approximation
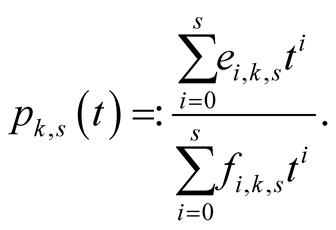
Lemma 15. For every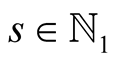 ,
, 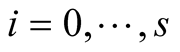 and
and 
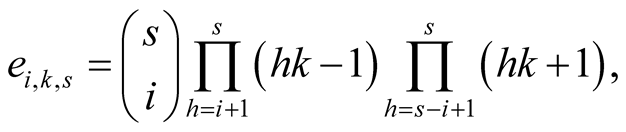 (6.20)
(6.20)
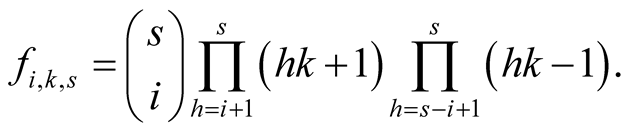 (6.21)
(6.21)
Proof. First we prove (6.21). From (6.19) we obtain
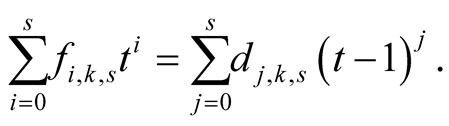
Binomial theorem then implies that
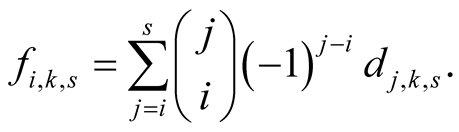
Thus equality (6.21) is equivalent to
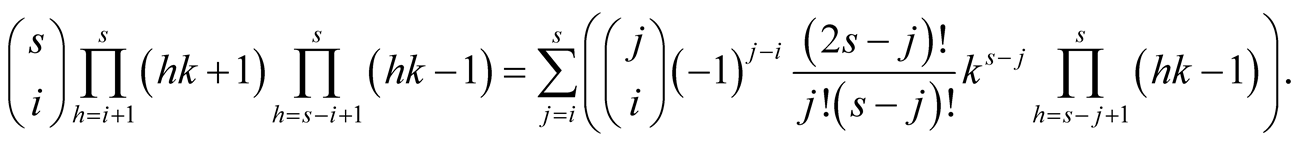 (6.22)
(6.22)
On both sides of (6.22) there are polynomials of degree 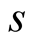 in variable
in variable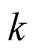 . Therefore it suffices to prove the equality for every
. Therefore it suffices to prove the equality for every 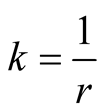 with
with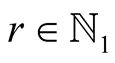 ,
,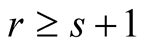 .
.
Lemma 7 implies
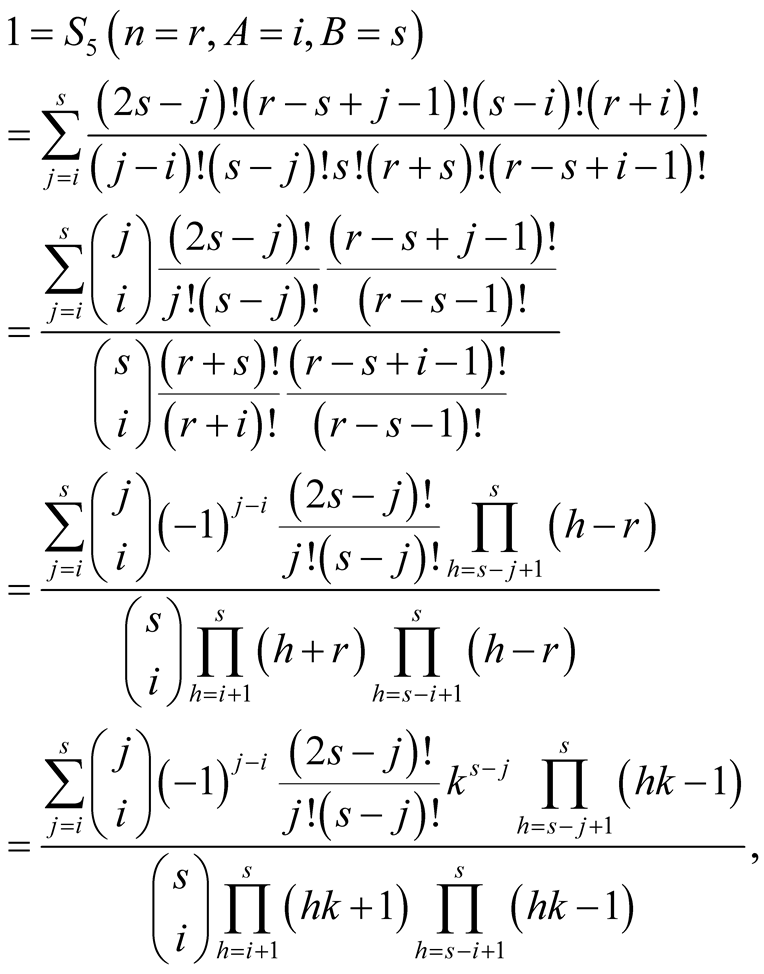
hence (6.22) and (6.21) follow.
Putting 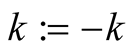 into (6.21) and applying binomial theorem in the same way we obtain (6.20). □
into (6.21) and applying binomial theorem in the same way we obtain (6.20). □
6.3. Bounds
By Lemma 14 the function 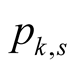 is Padé approximation, hence we know its properties in the neighbourhood of 1. Here we find global bounds for
is Padé approximation, hence we know its properties in the neighbourhood of 1. Here we find global bounds for 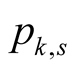 that are necessary for functionality of our algorithm.
that are necessary for functionality of our algorithm.
We need another two technical lemmas.
Lemma 16. For 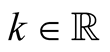 and
and 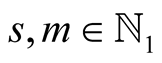
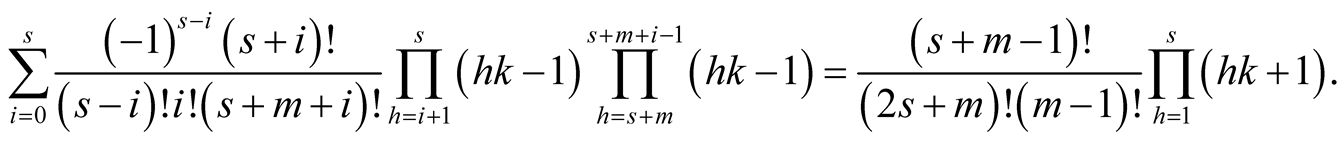
Proof. On both sides there are polynomials of degree 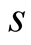 in variable
in variable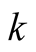 . Therefore it suffices to prove the equality for every
. Therefore it suffices to prove the equality for every 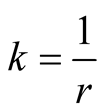 with
with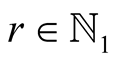 ,
,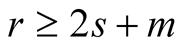 .
.
Lemma 9 implies

This implies the result. □
Lemma 17. For 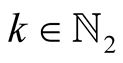 and
and 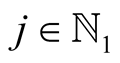 with
with 
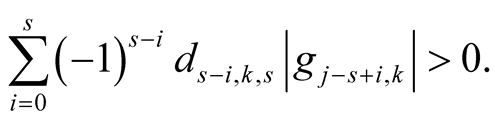
Proof. Put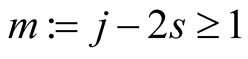 . Then
. Then
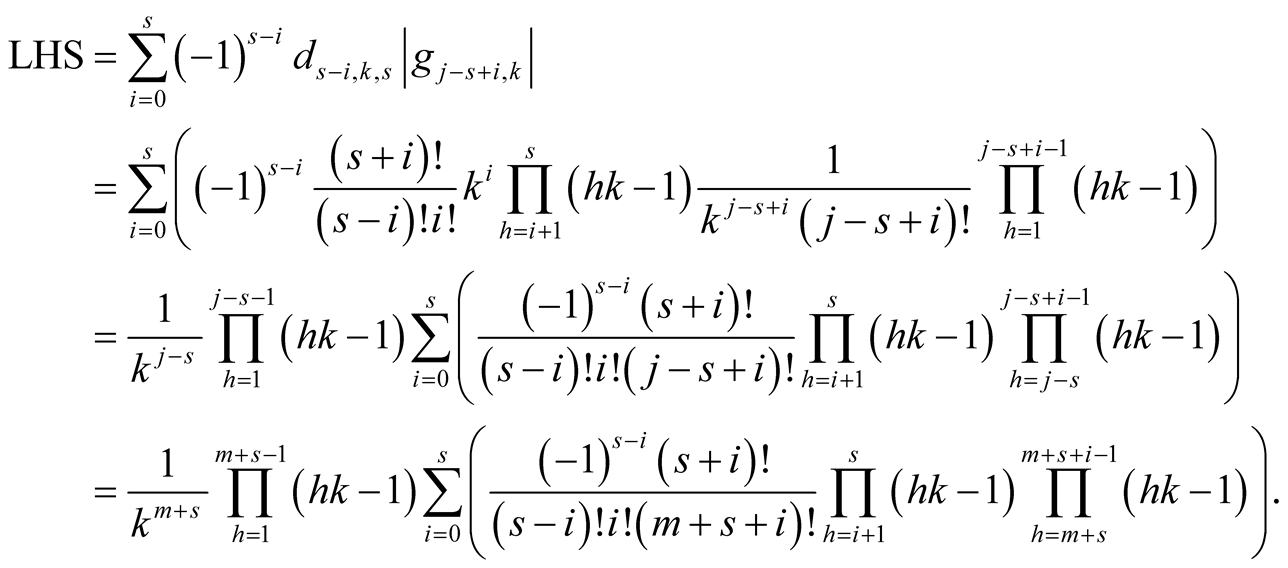
Lemma 16 implies
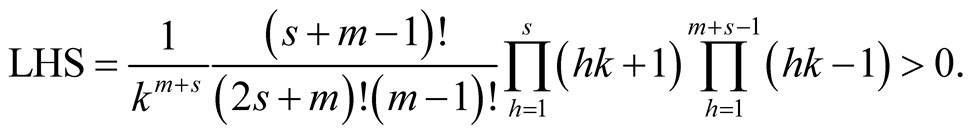 □
□
Now we find lower and upper bounds for the function .
.
Lemma 18. For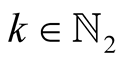 ,
, 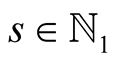 and
and 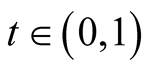 we have
we have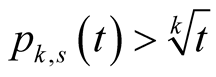 .
.
Proof. Put
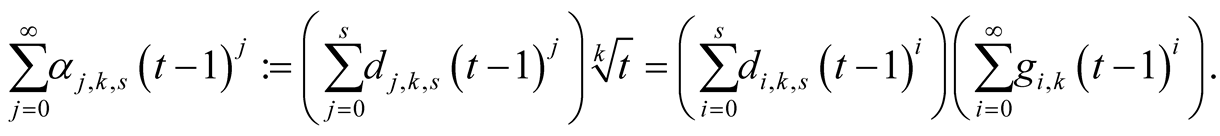 (6.23)
(6.23)
Lemma 12 and Lemma 13 imply
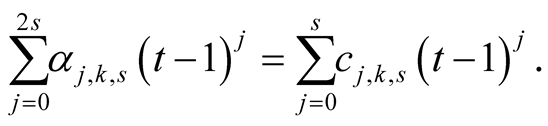 (6.24)
(6.24)
From (6.23) we obtain for 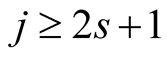
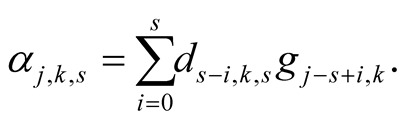
We have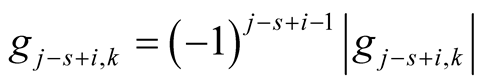 . Lemma 17 implies
. Lemma 17 implies
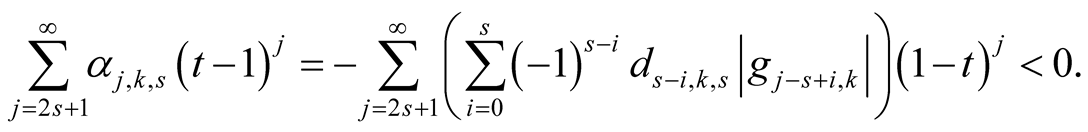 (6.25)
(6.25)
From (6.23), (6.24) and (6.25) we obtain

Lemma 15 implies that
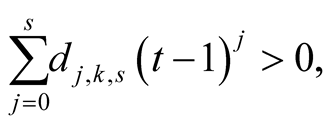
hence
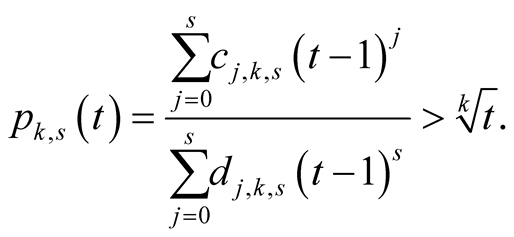 □
□
Lemma 19. For every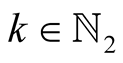 ,
, 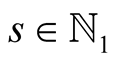 and
and 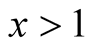 we have
we have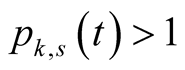 .
.
Proof. Directly from the definition of  and
and 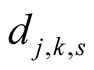 we obtain
we obtain
 (6.26)
(6.26)
The inequality is strict, since for 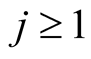 the main bracket in the numerator is greater than the main bracket in the denominator. □
the main bracket in the numerator is greater than the main bracket in the denominator. □
Now we prove that function 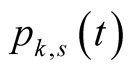 satisfies inequalities (3.2).
satisfies inequalities (3.2).
Lemma 20. For every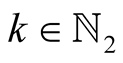 ,
, 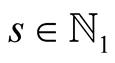 and
and 
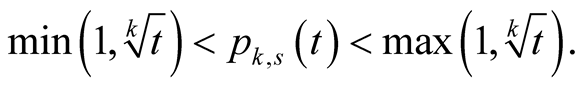
Proof. The proof splits into four cases.
1) For 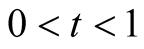 Lemma 18 implies that
Lemma 18 implies that .
.
2) Lemma 15 implies that 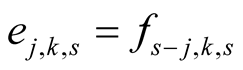 for every
for every . Hence
. Hence
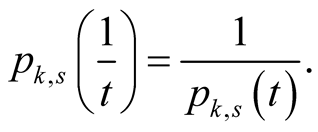 (6.27)
(6.27)
Using this and the first case we obtain that for 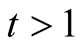 we have
we have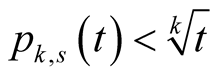 .
.
3) For 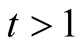 Lemma 19 implies that
Lemma 19 implies that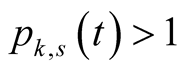 .
.
4) Using this and (6.27) we obtain for 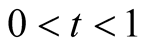 that
that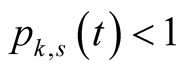 . □
. □
Acknowledgements
The author would like to thank to professor Andrzej Schinzel for recommendation of the paper [14] and also to author’s colleagues Kamil Brezina, Lukáš Novotný and Jan Štĕpnička for checking the results. Publication of this paper was supported by grant P201/12/2351 of the Czech Science Foundation, by grant 01798/2011/RRC of the Moravian-Silesian region and by grant SGS08/PrF/2014 of the University of Ostrava.
References
- Householder, A.S. (1970) The Numerical Treatment of a Single Nonlinear Equation. McGraw-Hill, New York.
- Hardy, G.H., Littlewood, J.E. and Pólya, G. (1952) Inequalities. Cambridge University Press, Cambridge.
- Borwein, J.M. and Borwein, P.B. (1987) Pi and the AGM. John Wiley & Sons, Hoboken.
- Gauss, C.F. (1866) Werke. Göttingen.
- Matkowski, J. (1999) Iterations of Mean-Type Mappings and Invariant Means. Annales Mathematicae Silesianae, 12, 211-226.
- Karatsuba, A. and Ofman, Yu. (1962) Umnozhenie mnogoznachnykh chisel na avtomatakh. Doklady Akademii nauk SSSR, 145, 293-294.
- Schönhage, A. and Strassen, V. (1971) Schnelle Multiplikation Großer Zahlen. Computing, 7, 281-292. http://dx.doi.org/10.1007/BF02242355
- Fürer, M. (2007) Faster Integer Multiplication. Proceedings of the 39th Annual ACM Symposium on Theory of Computing, San Diego, California, 11-13 June 2007, 55-67.
- Brent, R.P. (1975) Multiple-Precision Zero-Finding Methods and the Complexity of Elementary Function Evaluation. In: Traub, J.F., Ed., Analytic Computational Complexity, Academic Press, New York, 151-176.
- Knuth, D.E. (1998) The Art of Computer Programming. Volume 2: Seminumerical Algorithms. Addison-Wesley, Boston.
- Brezina, K. (2012) Smísené Pruměry. Master Thesis, University of Ostrava, Ostrava.
- Karatsuba, A. (1995) The Complexity of Computations. Proceedings of the Steklov Institute of Mathematics, 211, 169-183.
- Pan, V.Ya. (1961) Nekotorye skhemy dlya vychisleniya znacheni polinomov s veshchestvennymi koeffitsientami. Problemy Kibernetiki, 5, 17-29.
- Wilf, H. and Zeilberger, D. (1990) Rational Functions Certify Combinatorial Identities. Journal of the American Mathematical Society, 3, 147-158. http://dx.doi.org/10.1090/S0894-0347-1990-1007910-7
- Jarník, V. (1984) Diferenciální pocet 1. Academia, Praha.
NOTES

1In the last line we assume the hypothesis that all multiplication algorithms satisfy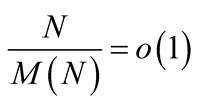 , see .
, see .

2Not always Horner’s method is optimal, see . In those cases Householder’s and our algorithms are faster.

