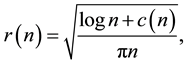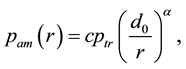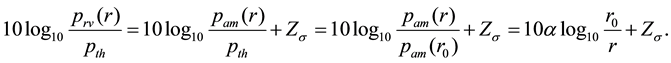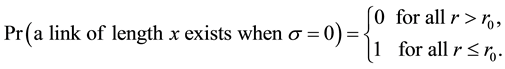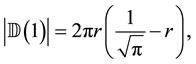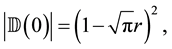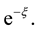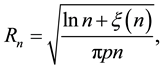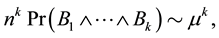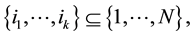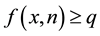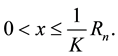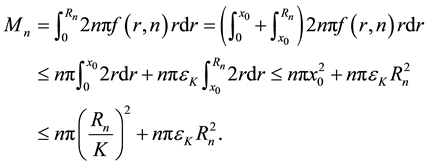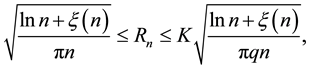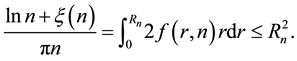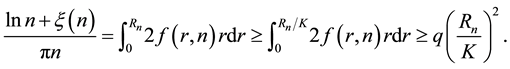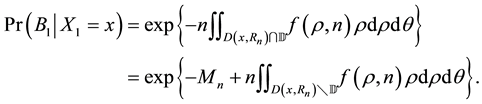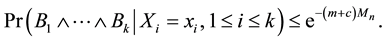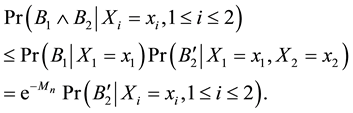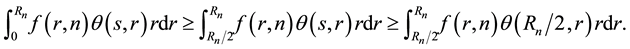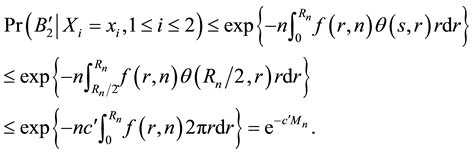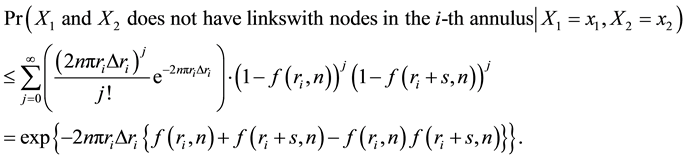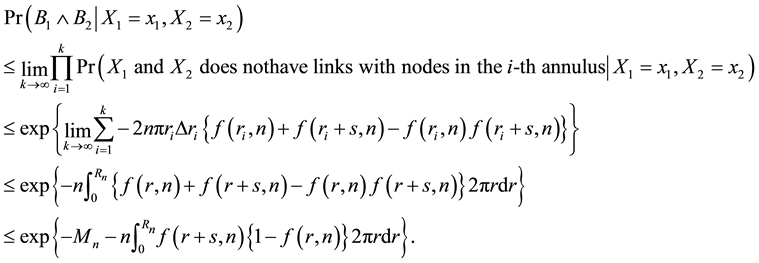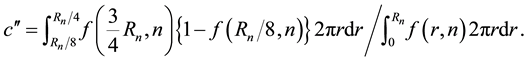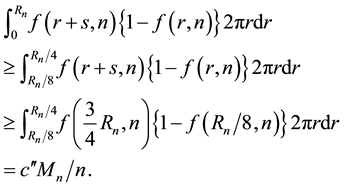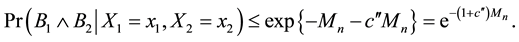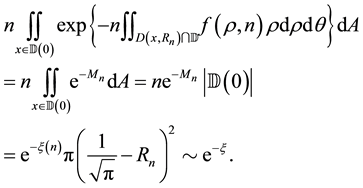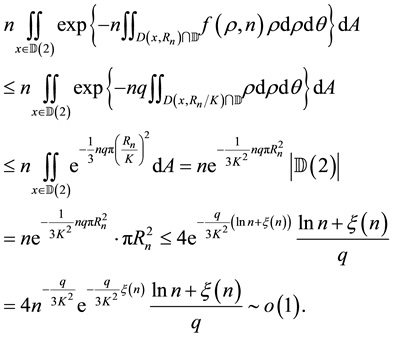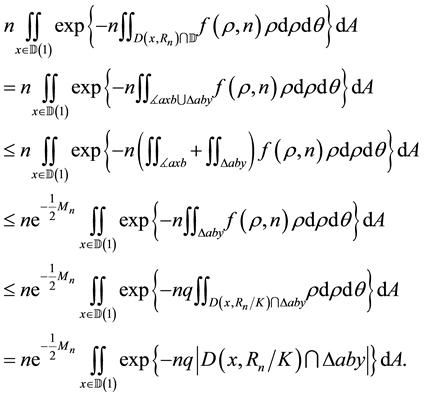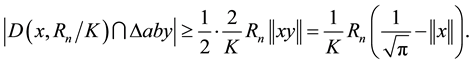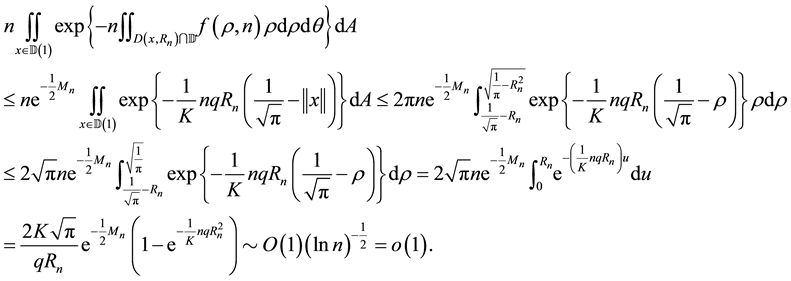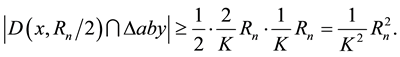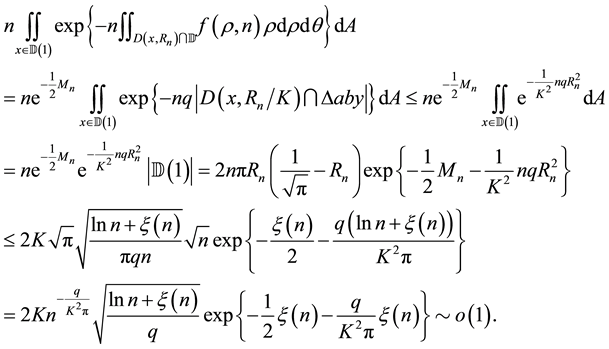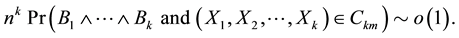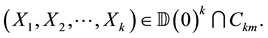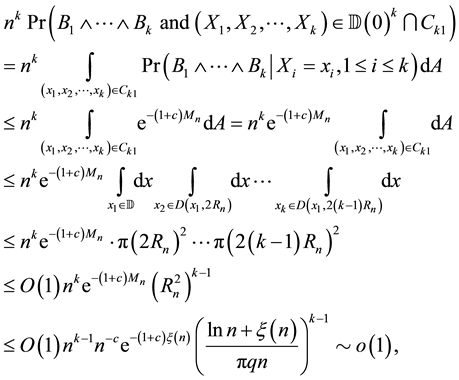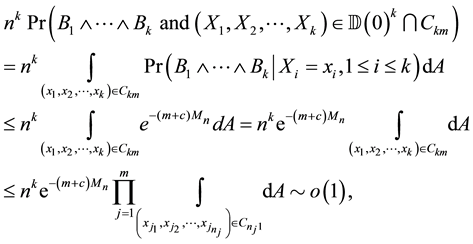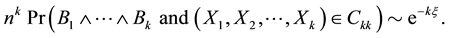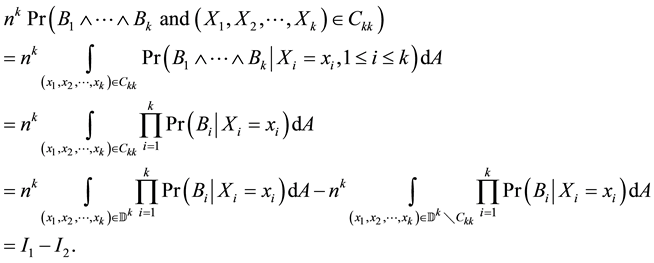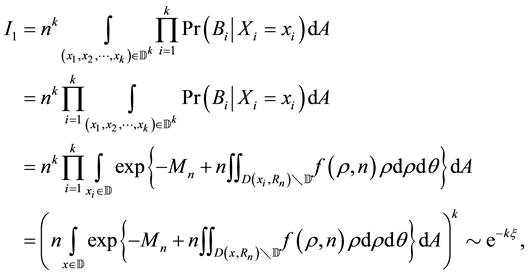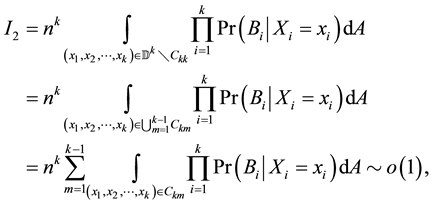Applied Mathematics
Vol.05 No.15(2014), Article ID:48599,15 pages
10.4236/am.2014.515219
Precise Asymptotic Distribution of the Number of Isolated Nodes in Wireless Networks with Lognormal Shadowing
Department of Mathematics, Sciences and Technology, Paine College, Augusta, USA
Email: lwang@paine.edu, ArgumedoA@paine.edu, WashingtonW@paine.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 June 2014; revised 5 July 2014; accepted 18 July 2014
ABSTRACT
In this paper, we study the connectivity of multihop wireless networks under the log-normal shadowing model by investigating the precise distribution of the number of isolated nodes. Under such a realistic shadowing model, all previous known works on the distribution of the number of isolated nodes were obtained only based on simulation studies or by ignoring the important boundary effect to avoid the challenging technical analysis, and thus cannot be applied to any practical wireless networks. It is extremely challenging to take the complicated boundary effect into consideration under such a realistic model because the transmission area of each node is an irregular region other than a circular area. Assume that the wireless nodes are represented by a Poisson point process with density n over a unit-area disk, and that the transmission power is properly chosen so that the expected node degree of the network equals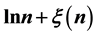 , where
, where 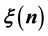 approaches to a constant
approaches to a constant 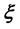 as
as . Under such a shadowing model with the boundary effect taken into consideration, we proved that the total number of isolated nodes is asymptotically Poisson with mean
. Under such a shadowing model with the boundary effect taken into consideration, we proved that the total number of isolated nodes is asymptotically Poisson with mean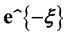 . The Brun’s sieve is utilized to derive the precise asymptotic distribution. Our results can be used as design guidelines for any practical multihop wireless network where both the shadowing and boundary effects must be taken into consideration.
. The Brun’s sieve is utilized to derive the precise asymptotic distribution. Our results can be used as design guidelines for any practical multihop wireless network where both the shadowing and boundary effects must be taken into consideration.
Keywords:
Connectivity, Asymptotic Distribution, Random Geometric Graph, Isolated Nodes, log-Normal Shadowing

1. Introduction
Connectivity is one of the most fundamental properties of multi-hop wireless networks. It is the premise for enabling a network with proper functions. The path-loss model (also known as the unit-disk communication model) of wireless networks assumes that the received signal strength at a receiving node from a transmitting node is only determined by a deterministic function of the Euclidean distance between the two nodes. Under such a simple communication model, two nodes are directly connected if and only if their Euclidean distance is no more than a given threshold, and network connectivity has been well studied in the literature (e.g., [1] -[7] ). However, in reality, the received signal strength often shows probabilistic variations induced by the shadowing effects that are unavoidably caused by different levels of clutter (e.g., ubiquitous background noises and obstructions such as buildings and trees) on the propagation path. In order to better capture physical reality, the variations of the received signal strength should be considered. It has been shown that a more accurate and realistic modeling of the physical layer is indeed important for better understanding of wireless multi-hop network characteristics [8] [9] . This generalized radio propagation model is referred to as the log-normal shadowing model which has been widely used in the literature [10] - [15] . The generalized shadowing model provides a good abstraction of large scale wireless multi-hop networks, and is a realistic model for many types of wireless multihop network applications such as sensor wireless networks for bush fire monitoring, ocean temperature monitoring, volcano monitoring, etc.
The study of multihop wireless networks with the log-normal shadowing model can date back to the early of 1980s [11] [12] . Under such a realistic model, researchers have investigated fundamental problems related to network connectivity such as the largest connected component in the network, the relation between having a connected network and having no isolated node, etc. [10] [13] - [15] . But most of the known results on network connectivity were obtained only based on simulation studies or ignoring the important boundary effect to avoid the challenging technical analysis under, and thus cannot be applied to any practical wireless networks. It is extremely challenging to take the complicated boundary effect into consideration under such a realistic shadowing model because the transmission area of each node is an irregular region other than a circular area. To the best of our knowledge, under such a realistic shadowing model, there are no theoretical results obtained by rigorous analytical studies in multihop wireless networks when the important boundary effect is taken into consideration.
In this paper, we assume that the wireless networking nodes are represented by a Poisson point process with density 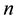 over a unit-area disk
over a unit-area disk 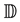 on the plane
on the plane , and that the transmission power is properly chosen so that the expected node degree of the network is equal to
, and that the transmission power is properly chosen so that the expected node degree of the network is equal to , where
, where 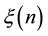 approaches to some constant
approaches to some constant 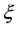 as
as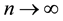 . We derive the precise asymptotic distribution of the number of isolated nodes in the network under the log-normal shadowing model, taking the complicated boundary effect into consideration. The Brun’s sieve is utilized to derive the precise asymptotic distribution.
. We derive the precise asymptotic distribution of the number of isolated nodes in the network under the log-normal shadowing model, taking the complicated boundary effect into consideration. The Brun’s sieve is utilized to derive the precise asymptotic distribution.
The vanishing of isolated nodes is not only a prerequisite but also a good indication of network connectivity. Under the path-loss model, it is well-known that the probability of having a connected network equals the probability of having no isolated nodes in the network as the node density 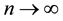 (see Penrose [16] ). With the log- normal shadowing model, such a result is predicted and has been verified by simulation studies (see Bettstetter et al. [10] ). Therefore, it is of importance to study the asymptotic distribution of the number of isolated nodes in the network under such a realistic shadowing model. The results obtained in this paper can be used as design guidelines for any practical multihop wireless network where both the shadowing and boundary effects must be taken into consideration.
(see Penrose [16] ). With the log- normal shadowing model, such a result is predicted and has been verified by simulation studies (see Bettstetter et al. [10] ). Therefore, it is of importance to study the asymptotic distribution of the number of isolated nodes in the network under such a realistic shadowing model. The results obtained in this paper can be used as design guidelines for any practical multihop wireless network where both the shadowing and boundary effects must be taken into consideration.
In what follows, 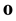 is the origin of the Euclidean plane
is the origin of the Euclidean plane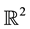 , and
, and  is the unit-area disk centered at
is the unit-area disk centered at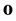
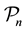
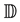

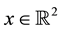

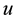
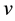
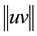
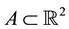
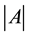
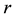
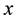
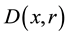
The remaining of this paper is organized as follows. In Section 2, we give a literature review for related work of our paper. The log-normal shadowing model is introduced and explained in Section 3. In Section 4, we give some definitions and geometric results that will be used to prove the main result of this paper. In Section 5, we derive the precise asymptotic distribution of the number of isolated nodes in the network under the log-normal shadowing model. Finally, we conclude our paper in Section 6.
2. Related Work
Under the unit-disk communication model, network connectivity has been extensively studied, and a huge number of existing research work are available in the literature [1] - [7] . Gupta et al. [3] showed that if each node uses the transmission radius
where 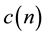
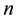
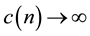
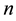
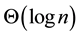
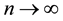
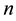

The log-normal shadowing model is a much more realistic radio propagation model and has been widely used by many researchers for network connectivity [10] [13] - [15] . Hekmat et al. investigated in [13] the largest connected component in wireless ad-hoc networks through simulations, where the 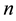
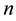
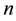
Most of the results in these known works were obtained only based on simulation studies or ignoring the important boundary effect to avoid the rigorous analysis by assuming the toroidal metric as done in the literature. To the best of our knowledge, there are no theoretical results on asymptotic distribution of the number of isolated nodes in the network obtained by rigorous analytical studies with the realistic log-normal shadowing model when the complicated boundary effect is taken into consideration.
3. The Log-Normal Shadowing Model
With the path-loss model, the received power levels decrease as the distance between the transmitter and the receiver increases. Attenuation of radio signals due to path-loss effect has been modelled by averaging the measured signal power over long times and distances around the transmitter. The averaged power at any given distance 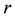
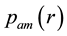
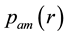
where 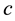
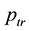
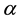

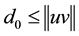

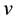

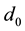
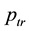
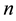
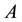
But the path-loss model could be inaccurate because in reality the received power levels may show significant variations around the area mean power value. Due to these variations, short links could disappear while long links could merge. The log-normal shadowing model allows for random power variations around the area mean power. With the log-normal shadowing model, the received mean power taken over all possible locations that are at distance 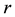
Assume that links are symmetric and the received power at node 
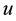
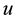
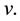

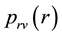
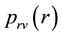
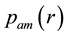
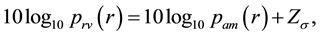
where 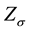


For any two nodes separated by the Euclidean distance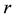
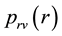


And we say that any two nodes are directly connected if and only if there exists a link between them.
Define 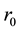

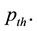
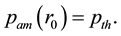
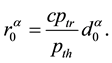
If both sides of Equation (1) minus 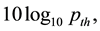
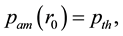
Then Equation (2) is equivalent to
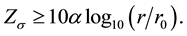
Thus for any two nodes separatedy the Euclidean distance 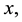
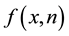

When 
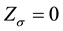
Thus, any two nodes are directly connected if and only if their Euclidean distance is at most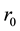

When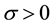
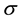
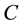
The following lemma demonstrates how the probability 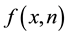
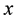
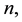
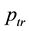
Lemma 1. When 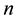
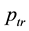
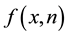


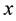
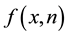
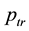
Proof. According to Equation (5), 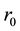
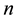

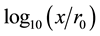
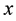
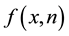

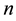

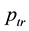
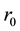
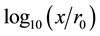

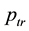
4. Preliminaries
In this section, we shall give some definitions that will be used to prove our main result of this paper. The results in this section are purely geometric, with no probabilistic content. Let 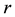
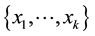
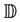
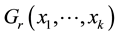

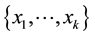
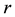
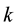
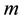
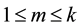

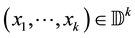
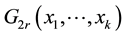
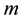
For the given maximum transmission radius r, the unit-area disk 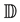
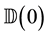
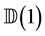
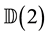
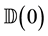

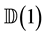
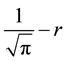

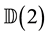
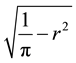

Then we have

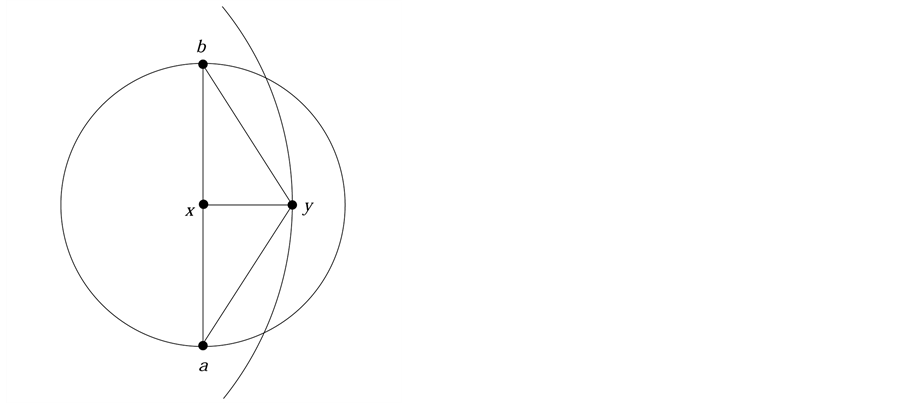
Figure 1. (a) Unit-disk communication model; (b) Log-normal shadowing model.
Figure 2. Partition of the unit-area disk
5. Precise Asymptotic Distribution of the Number of Isolated Nodes
In this section, we assume that all the nodes transmit at a uniform power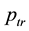
We use the same notations as in Section 3. Recall that 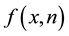
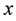
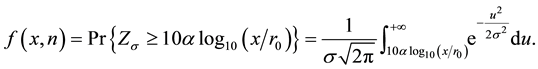
Let
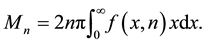
Refer to the discussions in [10] and [21] , 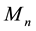
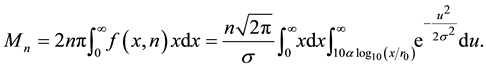
Based on our assumptions, 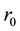
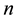
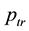

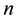
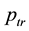
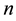
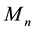
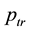
Let
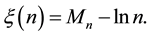
Then, when 

In this paper, we make the following two assumptions:
1) 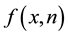


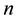
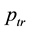

2) the transmission power 
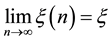
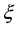
The main theorem of this paper is stated below:
Theorem 2. Under the two assumptions given above, the total number of the isolated nodes in the network is asymptotically Poisson with mean
Remarks. If the probability 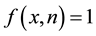
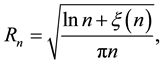
where 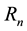
If the probability 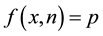
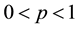
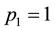
where 
Theorem 2 will be proved by using the Brun’s sieve in the form described, for example, in [23] , Chapter 8, which is an implication of the Bonferroni inequalities.
Theorem 3. (Brun’s sieve) Let 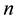

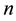
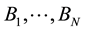
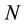
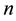
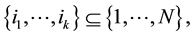
If there is a constant 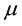

then 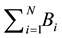
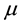

To apply Theorem 3, let 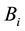
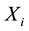
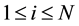
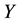
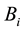
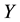
Therefore, in order to prove Theorem 2, it is sufficient to show that for any fixed positive integer 

The proof of this asymptotic equation will use the following lemmas.
Lemma 4. Assume the conditions of Theorem 2 hold. Then there exist a sufficiently large constant 
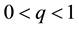
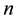
for all
Proof. We prove the lemma by contradiction and assume the contrary is true. Then for any arbitrarily large 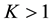
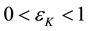


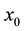
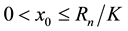
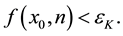
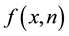

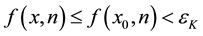

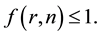
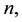
The above inequality holds for any arbitrarily large 
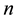
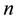
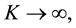
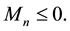
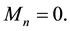
The following lemma shows that 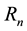
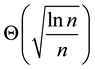
Lemma 5. Assume the conditions of Theorem 2 hold. Then we have 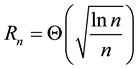
where 
Proof. Note that 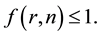
By Lemma 4, there exist a sufficiently large constant 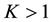
(both independent of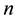
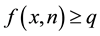
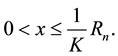
Thus, the lemma is proved.
Next we introduce a lemma that has only one event involved and has been proved in [18] (see Equation (10) and Equation (12) in [18] ).
Lemma 6. For any 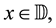
If 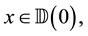
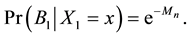
Lemma 7. For any 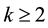
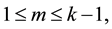
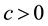
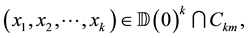
Proof. First we prove the lemma holds when 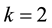
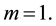
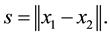
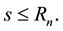
Case 1. 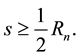
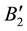
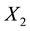
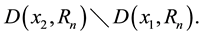
It remains to show that there is a constant 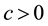
For any 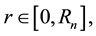
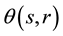

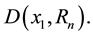
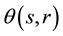
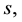
Let
Apply the same approach in deriving the probability for 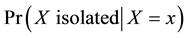
Case 2. 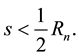
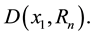

center 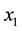
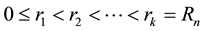
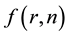
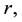
Note that the inequality still holds for annuli not fully contained in 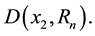
For any 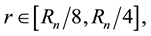
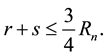
Then
Thus,
The lemma holds for the constant 


When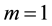
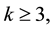
centers is at most
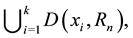
as the case for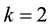
Next we assume 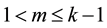

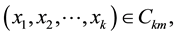
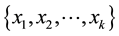
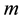
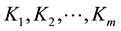

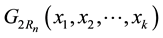
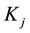
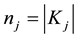
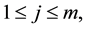
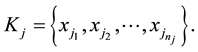
Since at least one 
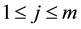
Thus, the lemma is proved.
Now we are ready to prove the asymptotic Equation (12). The proof of this asymptotic equation is divided into three lemmas. The case for 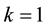
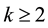


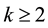
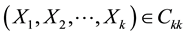
Lemma 8.
Proof.
We will prove

For the integral over 
For the integral over 
Next we calculate the integral over 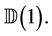

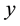
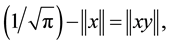
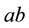

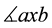
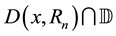
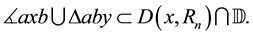
Therefore, by Equation (7) and Equation (17)
To complete the proof of the lemma, it is sufficient to prove that this integral over 
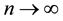
Case 1.
Thus,
The last equation holds since 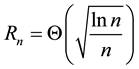
Case 2.
Thus,
Therefore, the lemma is proved.
Lemma 9. For any 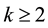
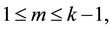
Proof. By Equations (15) and (16), it is straightforward to verify that the lemma holds when
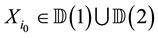
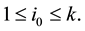
We first prove the case when 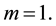
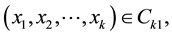
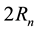

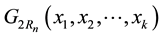



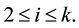
where the second last equation holds from Lemma 5.
Next we assume 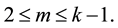
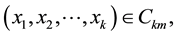
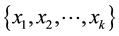
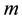
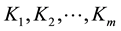
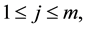
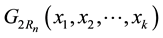
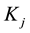

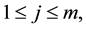
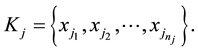
where the last equation holds by following the similar arguments as the case
This completes the proof of the lemma.
Lemma 10. For any 
Proof. For any 
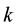
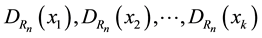

Next we calculate the two integrals 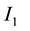
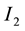
the last equation holds by following the same steps as we used in the proof of Lemma 8.
where the last equation holds from Lemma 9.
This completes the proof of the lemma.
6. Conclusion
In this paper, we assume that the wireless nodes are represented by a Poisson point process with density n over a unit-area disk, and that the transmission power is properly chosen so that the expected node degree of the network equals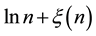

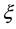


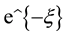
Acknowledgements
The work of
Cite this paper
LixinWang,AlbertoArgumedo,WilliamWashington, (2014) Precise Asymptotic Distribution of the Number of Isolated Nodes in Wireless Networks with Lognormal Shadowing. Applied Mathematics,05,2249-2263. doi: 10.4236/am.2014.515219
References
- 1. Bettstetter, C. (2004) On the Connectivity of Ad Hoc Networks. The Computer Journal, 47, 432-447.
http://dx.doi.org/10.1093/comjnl/47.4.432 - 2. Bettstetter, C. (2002) On the Minimum Node Degree and Connectivity of a Wireless Multihop Network. 3rd ACM International Symposium on Mobile Ad Hoc Networking and Computing, Lausanne, 80-91.
http://dx.doi.org/10.1145/513800.513811 - 3. Gupta, P. and Kumar, P. (1998) Critical Power for Asymptotic Connectivity in Wireless Networks. Stochastic Analysis, Control, Optimization and Applications, 547-566.
- 4. Philips, T.K., Panwar, S.S. and Tantawi, A.N. (1989) Connectivity Properties of a Packet Radio Network Model. IEEE Transactions on Information Theory, 35, 1044-1047.
http://dx.doi.org/10.1109/18.42219 - 5. Wan, P.-J. and Yi, C.-W. (2004) Asymptotic Critical Transmission Radius and Critical Neighbor Number for k-Connectivity in Wireless Ad Hoc Networks. MobiHoc 2006, Roppongi, 1-8.
- 6. Xue, F. and Kumar, P. (2004) The Number of Neighbors Needed for Connectivity of Wireless Networks. Wireless Networks, 10, 169-181.
http://dx.doi.org/10.1023/B:WINE.0000013081.09837.c0 - 7. Yi, C.-W., Wan, P.-J., Li, X.-Y. and Frieder, O. (2006) Asymptotic Distribution of the Number of Isolated Nodes in Wireless Ad Hoc Networks with Bernoulli Nodes. IEEE Transactions on Communications, 54.
- 8. Takai, M., Martin, J. and Bagrodia, R. (2001) Effects of Wireless Physical Layer Modeling in Mobile Ad Hoc Networks. ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc), Long Beach.
- 9. Zorzi, M. and Pupolin, S. (1995) Optimum Transmission Ranges in Multihop Packet Radio Networks in the Presence of Fading. IEEE Transactions on Communications, 43, 2201-2205.
http://dx.doi.org/10.1109/26.392962 - 10. Bettstetter, C. and Hartmann, C. (2005) Connectivity of Wireless Multihop Networks in a Shadow Fading Environment. Wireless Networks, 11, 571-579.
http://dx.doi.org/10.1007/s11276-005-3513-x - 11. Bernhardt, R.C. (1987) Macroscopic Diversity in Frequency Reuse Systems. IEEE Journal of Selected Areas in Communications SAC, 5, 862-878.
http://dx.doi.org/10.1109/JSAC.1987.1146594 - 12. Cox, D.C., Murray, R. and Norris, A. (1984) 800 MHz Attenuation Measured in and around Suburban Houses. AT & T Bell Laboratory Technical Journal, 63, 921-954.
http://dx.doi.org/10.1002/j.1538-7305.1984.tb00030.x - 13. Hekmat, R. and Mieghem, P.V. (2006) Connectivity in Wireless Ad-Hoc Networks with a Log-Normal Radio Model. Mobile Networks and Applications, 11, 351-360.
http://dx.doi.org/10.1007/s11036-006-5188-7 - 14. Mukherjee, S. and Avidor, D. (2005) On the Probability Distribution of the Minimal Number of Hops between Any Pair of Nodes in a Bounded Wireless Ad-Hoc Network Subject to Fading. International Workshop on Wireless Ad-Hoc Networks (IWWAN), London.
- 15. Stuedi, P., Chinellato, O. and Alonso, G. (2005) Connectivity in the Presence of Shadowing in 802.11 Ad Hoc Networks. IEEE Wireless Communications and Networking Conference, 2225-2230.
- 16. Penrose, M. (1997) The Longest Edge of the Random Minimal Spanning Tree. The Annals of Applied Probability, 7, 340-361. http://dx.doi.org/10.1214/aoap/1034625335
- 17. Penrose, M. (1999) A Strong Law for the Longest Edge of the Minimal Spanning Tree. The Annals of Applied Probability, 27, 246-260.
http://dx.doi.org/10.1214/aop/1022677261 - 18. Wang, L. and Baker, A.J. (2013) Critical Power for Vanishing of Isolated Nodes in Wireless Networks with Log-Normal Shadowing. IEEE MASS 2013, Hangzhou.
- 19. Bertoni, H. (2000) Radio Propagation for Modern Wireless Systems. Prentice Hall PTR, New Jersey.
- 20. Rappaport, T.S. (2001) Wireless Communications: Principles and Practice. 2nd Edition, Prentice Hall PTR, New Jersey.
- 21. Meester, R. and Roy, R. (1996) Continuum Percolation. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511895357 - 22. Yi, C.-W., Wan, P.-J., Lin, K.-W. and Huang, C.-H. (2006) Asymptotic Distribution of the Number of Isolated Nodes in Wireless Ad Hoc Networks with Unreliable Nodes and Links. IEEE GLOBECOM.
- 23. Alon, N. and Spencer, J.H. (2000) The Probabilistic Method. 2nd Edition, Wiley, New York.
http://dx.doi.org/10.1002/0471722154