Applied Mathematics
Vol.5 No.10(2014), Article
ID:46518,11
pages
DOI:10.4236/am.2014.510139
Application of Trial Equation Method for Solving the Getmanou Equation
Li Yang
Department of Mathematics, Northeast Petroleum University, Daqing, China
Email: liyang120918@163.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 March 2014; revised 21 April 2014; accepted 28 April 2014
ABSTRACT
Under the travelling wave transformation, some nonlinear partial differential equations such as the Getmanou equation are transformed to ordinary differential equation. Then using trial equation method and combing complete discrimination system for polynomial, the classifications of all single traveling wave solution to this equation are obtained.
Keywords:The Nonlinear Partial Differential Equation, Trial Equation Method, Complete Discrimination System for Polynomia, Traveling Wave Transform, the Getmanou Equation

1. Introduction
Many problems in natural and engineering sciences are modeled by partial differential equations (PDE). Looking for the solutions of the equation, especially the exact solutions, is very important. These exact solutions can describe many important phenomena in physics and other fields and also help physicists to understand the mechanisms of the complicated physical phenomena. Many mathematicians and physicists work in the field, and a variety of powerful methods have been employed to study nonlinear phenomena, such as the inverse scattering transform [1] , the Bäcklund transformation method [2] , the Darboux transformation [3] , the homogeneous balance method [4] , the tanh function method [5] , the exp-function method [6] , the G'/G-expansion method [7] , and so on.
Recently, Professor Liu proposed a powerful method named trial equation method [8] [9] for finding exact solutions to nonlinear differential equations. In this paper, I mainly use Liu’s trial equation method and the theory of complete discrimination system for the fouth-order polynomial [10] -[12] to solve exact solutions of the Getmanou equation which has already been solved based on discrimination system of the fifth-order polynomial by Fan [13] . But as we can see, the solving process is very simple and clear with the trial equation method combined with complete discrimination system for polynomial.
2. Application of Trial Equation Method
The Getmanou equation [12] reads as
 (1)
(1)
Or equivalently
 (2)
(2)
Taking the traveling wave transformation 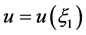 and
and , we can obtain the corresponding ODE
, we can obtain the corresponding ODE
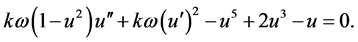 (3)
(3)
we take the trial equation as follows
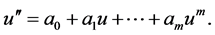 (4)
(4)
According to the trial equation method of rank homogeneous equation, balancing  with
with  gets
gets .
.
Equation (4) has the following specific form
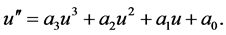 (5)
(5)
From Equation (5), we get
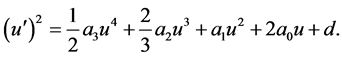 (6)
(6)
Substituting Equations (5) and (6) into Equation (3), we have
 (7)
(7)
where
 (8)
(8)
Let the coefficient  be zero, we will yield nonlinear algebraic equations. Solving the equations, we will determine the values of
be zero, we will yield nonlinear algebraic equations. Solving the equations, we will determine the values of . We get
. We get
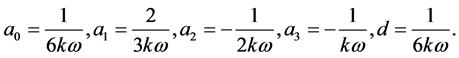 (9)
(9)
When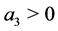 , we take transformations as follows
, we take transformations as follows
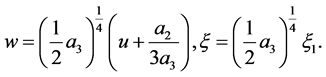 (10)
(10)
Then Equation (6) becomes
 (11)
(11)
where ![]() is a function of
is a function of  and
and
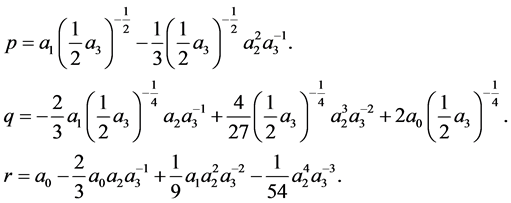 (12)
(12)
When , we take transformations as follows
, we take transformations as follows
 (13)
(13)
Then Equation (6) becomes
 (14)
(14)
where ![]() is a function of
is a function of  and
and
 (15)
(15)
We write the complete discrimination system for polynomial 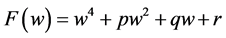 as follows
as follows
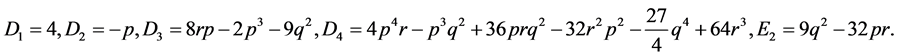 (16)
(16)
Then we consider the following ODE
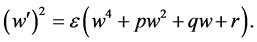 (17)
(17)
where . Rewrite Equation (17) by integral form as follows
. Rewrite Equation (17) by integral form as follows
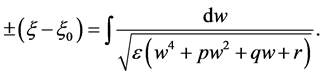 (18)
(18)
3. Classification of the Traveling Wave Solutions
According to the complete discrimination system for the fouth order polynomial, we give the corresponding single traveling wave solutions to Equation (1).
Case 1.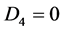 ,
,  ,
, . Then we have
. Then we have
 (19)
(19)
where  and
and ![]() are real numbers,
are real numbers, .
.
When , we have
, we have
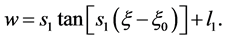 (20)
(20)
The corresponding solution is
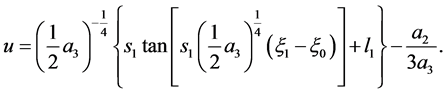 (21)
(21)
Case 2.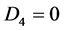 ,
,  ,
,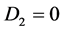 . Then we have
. Then we have
 (22)
(22)
When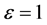 , we have
, we have
 (23)
(23)
The corresponding solution is
 (24)
(24)
Case 3.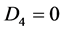 ,
, ,
, ,
, . Then we have
. Then we have
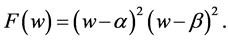 (25)
(25)
where ![]() and
and 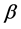 are real numbers,
are real numbers,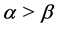 .
.
When 
(i) If 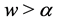 or
or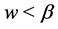 , we have
, we have
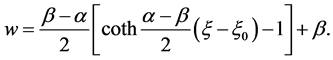 (26)
(26)
The corresponding solution is
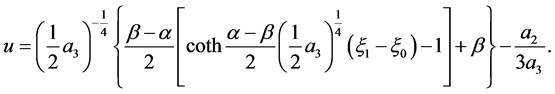 (27)
(27)
(ii) If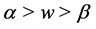 , we have
, we have
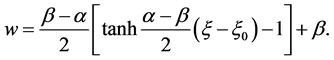 (28)
(28)
The corresponding solution is
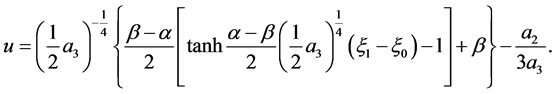 (29)
(29)
Case 4.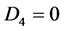 ,
, 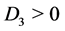 ,
,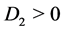 . Then we have
. Then we have
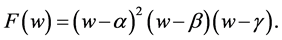 (30)
(30)
where![]() ,
, 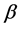 ,
, 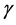 are real numbers, and
are real numbers, and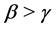 .
.
When 
(i) If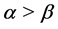 ,
, 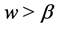 or if
or if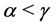 ,
,  , we have
, we have
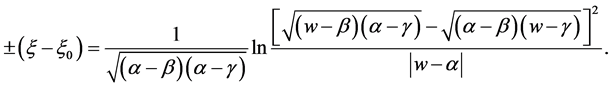 (31)
(31)
The corresponding solution is
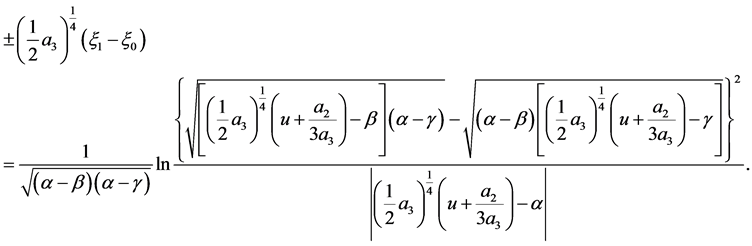 (32)
(32)
(ii) If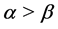 ,
, 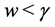 or if
or if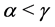 ,
,  , we have
, we have
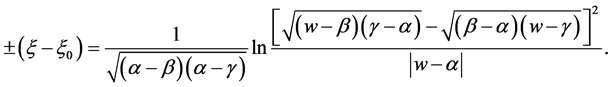 (33)
(33)
The corresponding solution is
 (34)
(34)
(iii) If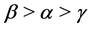 , we have
, we have
 (35)
(35)
The corresponding solution is
 (36)
(36)
When 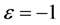
(i) If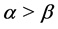 ,
, or if
or if ,
,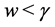 , we have the corresponding solution is
, we have the corresponding solution is
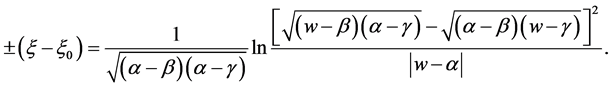 (37)
(37)
The corresponding solution is
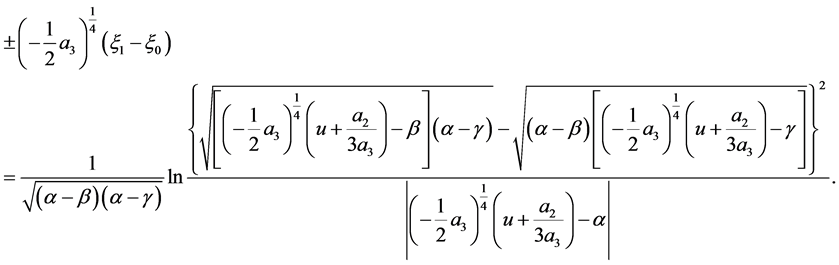 (38)
(38)
(ii) If ,
,  or if
or if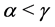 ,
, 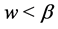 , we have
, we have
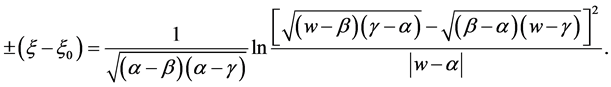 (39)
(39)
The corresponding solution is
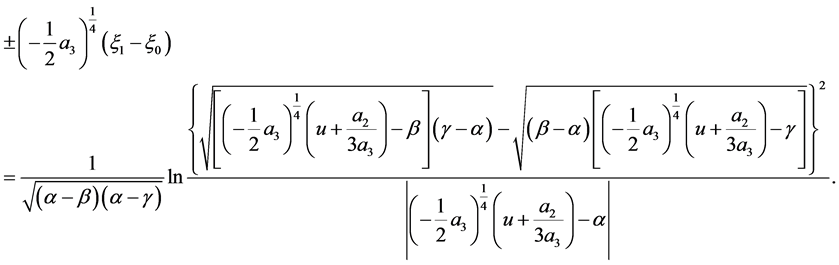 (40)
(40)
(iii) If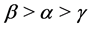 , we have
, we have
 (41)
(41)
The corresponding solution is
 (42)
(42)
Case 5. ,
,  ,
, 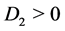 ,
, . Then we have
. Then we have
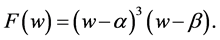 (43)
(43)
where ![]() and
and  are real numbers.
are real numbers.
When , if
, if ,
, 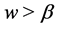 or if
or if ,
,  , we have
, we have
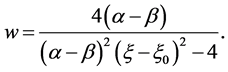 (44)
(44)
The corresponding solution is
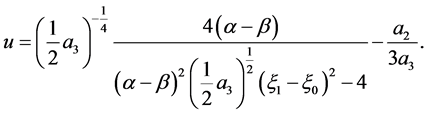 (45)
(45)
When , if
, if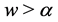 ,
,  or if
or if ,
, 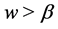 , we have
, we have
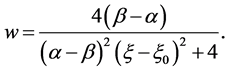 (46)
(46)
The corresponding solution is
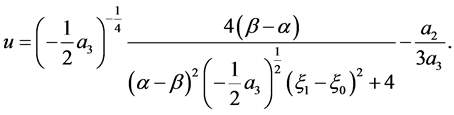 (47)
(47)
Case 6. ,
,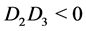 . Then we have
. Then we have
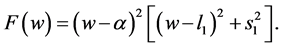 (48)
(48)
where![]() ,
, and
and ![]() are real numbers.
are real numbers.
When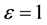 , we have
, we have
 (49)
(49)
The corresponding solution is
 (50)
(50)
where .
.
Case 7.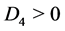 ,
, 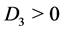 ,
,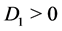 . Then we have
. Then we have
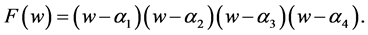 (51)
(51)
where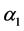 ,
, 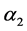 ,
, 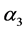 and
and 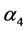 are real numbers, and
are real numbers, and .
.
When 
(i) If 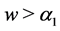 or
or , we have
, we have
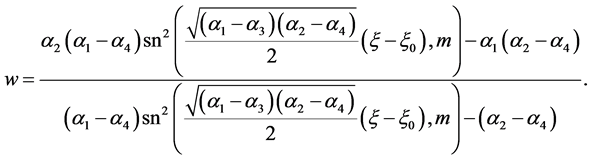 (52)
(52)
The corresponding solution is
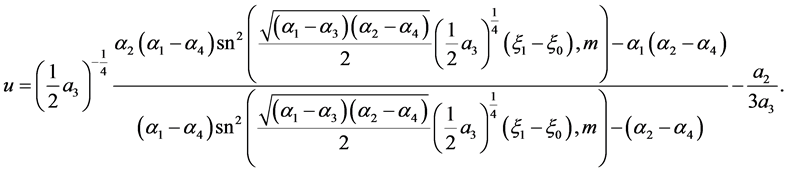 (53)
(53)
(ii) If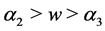 , we have
, we have
 (54)
(54)
The corresponding solution is
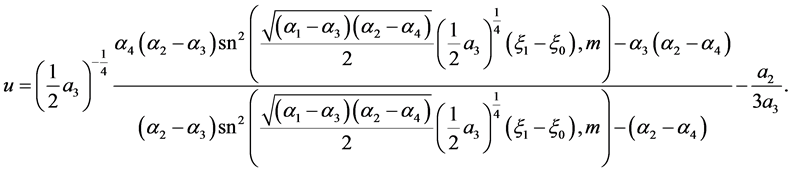 (55)
(55)
When 
(i) , we have
, we have
 (56)
(56)
The corresponding solution is
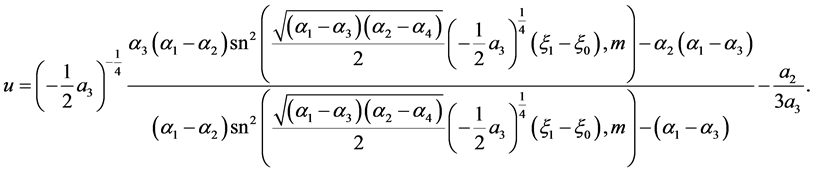 (57)
(57)
(ii) , we have
, we have
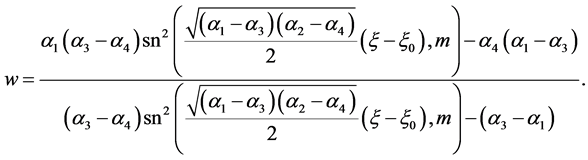 (58)
(58)
The corresponding solution is
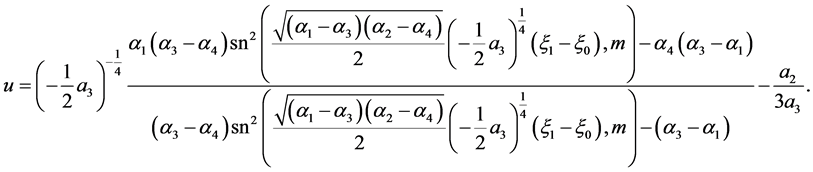 (59)
(59)
where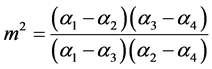 .
.
Case 8.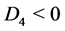 ,
,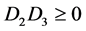 . Then we have
. Then we have
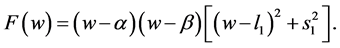 (60)
(60)
where![]() ,
,  ,
,  ,
, ![]() are real numbers, and
are real numbers, and ,
, .
.
When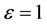 , we have
, we have
 (61)
(61)
The corresponding solution is
 (62)
(62)
When , we have
, we have
 (63)
(63)
The corresponding solution is
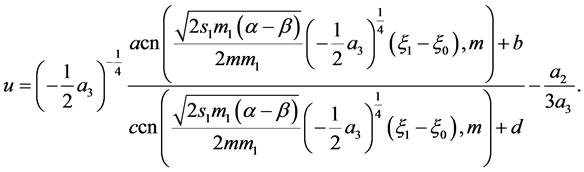 (64)
(64)
where
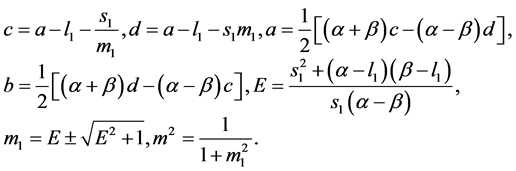 (65)
(65)
We choose  such that
such that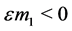 .
.
Case 9.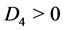 ,
,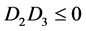 . Then we have
. Then we have
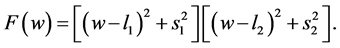 (66)
(66)
where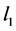 ,
, ![]() ,
, ![]() ,
,  are real numbers, and
are real numbers, and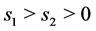 .
.
When , we have
, we have
 (67)
(67)
The corresponding solution is
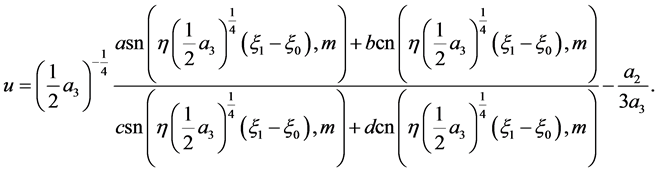 (68)
(68)
where
 (69)
(69)
In Equations (21) (24) (27) (29) (32) (34) (36) (38) (40) (42) (45) (47) (50) (53) (55) (57) (59) (62) (64) and (68), the integration constant 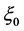 has been rewritten, but we still use it. The classifications of all single traveling wave solution to this equation are obtained.
has been rewritten, but we still use it. The classifications of all single traveling wave solution to this equation are obtained.
4. Conclusion
In this paper, the trial equation method combined with complete discrimination system for polynomial has been effectively used to solve the Getmanou equation. The obtained results emphasize that the method is completely useful. With the same method, some of other equations can be dealt with.
Acknowledgements
I would like to thank the referees for their valuable suggestions.
References
- Ablowitz, M.J. and Clarkson, P.A. (1992) Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge, 721-725.
- Satsuma J. and Kaup D.J. (1977) A Bäcklund Transformation for a Higher Order Korteweg-De Vries Equation. Journal of the Physical Society of Japan, 43, 692-697. http://dx.doi.org/10.1143/JPSJ.43.692
- Gu C., Hu, H. and Zhou, Z. (2006) Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry. Springer Berlin, Heidelberg.
- Wang M., Zhou, Y. and Li, Z. (1996) Application of a Homogeneous Balance Method to Exact Solutions of Nonlinear Equations in Mathematical Physics. Physics Letters A, 216, 67-75. http://dx.doi.org/10.1016/0375-9601(96)00283-6
- Fan E. (2000) Extended tanh-Function Method and Its Applications to Nonlinear Equations. Physics Letters A, 277, 212-218. http://dx.doi.org/10.1016/S0375-9601(00)00725-8
- He J.H. and Zhang, L.N. (2008) Generalized Solitary Solution and Compacton-Like Solution of the Jaulent —Miodek Equations Using the Exp-Function Method. Physics Letters A, 372, 1044-1047. http://dx.doi.org/10.1016/j.physleta.2007.08.059
- Wang M., Li, X. and Zhang, J. (2008) The (G'/G)-Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423. http://dx.doi.org/10.1016/j.physleta.2007.07.051
- Liu C.S. (2006) Trial Equation Method to Nonlinear Evolution Equations with Rank Inhomogenous: Mathematical Discussions and Its Applications. Communications in Theoretical Physics, 45, 219-223. http://dx.doi.org/10.1088/0253-6102/45/2/005
- Liu C.S. (2005) Trial Equation Method and Its Applications to Nonlinear Evolution Equations. Acta Physica Sinica, 54, 2505. (in Chinese)
- Liu C.S. (2007) Classification of All Single Travelling Wave Solutions to Calogero-Degasperis-Focas Equation. Communications in Theoretical Physics, 48, 601-604. http://dx.doi.org/10.1088/0253-6102/48/4/004
- Liu, C.S. (2006) Direct Integral Method, Complete Discrimination System for Polynomial and Applications to Classifications of All Single Traveling Wave Solutions to Nonlinear Differential Equations: A Survey. arXiv preprint nlin/ 0609058.
- Liu C.S. (2008) Solution of ODE
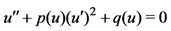 and Applications to Classifications of All Single Travelling Wave Solutions to Some Nonlinear Mathematical Physics Equations. Communications in Theoretical Physics, 49, 291- 296. http://dx.doi.org/10.1088/0253-6102/49/2/07
and Applications to Classifications of All Single Travelling Wave Solutions to Some Nonlinear Mathematical Physics Equations. Communications in Theoretical Physics, 49, 291- 296. http://dx.doi.org/10.1088/0253-6102/49/2/07 - Fan X.-F. (2010) Classification of All Single Traveling-Wave Solutions to Getmanou Equation. FIZIKA A, 19, 191- 196.

