Applied Mathematics
Vol.05 No.21(2014), Article ID:52119,8 pages
10.4236/am.2014.521315
ARIMA: An Applied Time Series Forecasting Model for the Bovespa Stock Index
Paulo Rotela Junior, Fernando Luiz Riêra Salomon, Edson de Oliveira Pamplona
Institute of Production Engineering and Management, Federal University of Itajuba, Itajuba, Brazil
Email: paulo.rotela@gmail.com, fer.salomon@hotmail.com, pamplona@unifei.edu.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 October 2014; revised 1 November 2014; accepted 15 November 2014
ABSTRACT
Due to the relative uncertainty involved with the variables which affect financial market behavior, forecasting future variations in a time series of the Brazilian stock market Index (Ibovespa) can be considered a difficult task. This article aims to evaluate the performance of the model ARIMA for time series forecasting of Ibovespa. The research method utilized was mathematical modeling and followed the Box-Jenkins method. In order to compare results with other smoothing models, the parameter of evaluation MAPE (Mean Absolute Percentage Error) was used. The results showed that the model utilized obtained lower MAPE values, thus indicating greater suitability. This therefore demonstrates that the ARIMA model can be used for time-series indices related to stock market index forecasting.
Keywords:
Forecasting, ARIMA, Time Series, MAPE, Ibovespa

1. Introduction
Economic crises in recent decades and the consequent financial losses demonstrate that markets, financial institutions and investors urgently needed to improve their models to measure and predict the risks to which they were exposed. Equity investments become a great alternative when compared to other applications, especially in long periods [1] .
Predicting the future behavior of a time series of data on the Bovespa Index (Index of shares of the São Paulo Stock Exchange) is not an easy task, given the uncertainties related to the variables that affect the behavior of financial markets and how they will impact prices practiced in the future. Studies applied to forecasting financial time series of assets, indices and investment portfolios are an important tool used for decision making in many areas, investment managers, asset pricing, and the areas responsible for risk management.
The genius of the work of Markowitz [2] in proving that the risk of a portfolio consisting of n assets is less than the weighted sum of the risks of each asset, given a different correlation of 1, laid the foundations of portfolio selection with a focus not only profitability, but the relationship between the risk taken and their return. This study, along with the work of Sharpe [3] and Fama [4] originated Modern Financial Theory, which combines the risk taken to the expected return in an efficient relationship.
This paper aims to evaluate the performance of the ARIMA model to predict the time series of the Bovespa Index, measured by MAPE (mean absolute error percentage) and compare it with other models. Historical data of monthly Bovespa quotations from January 1995 to January 2013 were used. The models were used to compare Single Exponential Smoothing and Double Exponential Smoothing.
This paper is organized as follows: In Section 2, a review of forecasting is presented. In Section 3, the research method is shown. In Section 4, analysis of historical data of the Bovespa Index, data transformation, the necessary adjustments and calculation of MAPE values are all examined based on the results found. Section 5 contains the conclusions of the study.
2. Forecasting
There are two main types of approaches to demand forecasting: qualitative methods and quantitative methods. The combination of qualitative and quantitative methods is approaching the ideal time to make a good forecast demand [5] .
The main qualitative methods are: Panel data approach, Delphi method, scenario planning, educated guess, executive committee consensus, sales force survey, Historical Analysis and Market Research [5] -[8] .
Quantitative methods are based on historical data (time series) and assume that past results are relevant for predicting the future [7] . The classical methods of time series are: Moving Average, Exponential Adjustment, Linear Trend, and Nonlinear Trend. These methods require that the series is stationary, i.e. the mean and covariance are constant between the periods. In this context, the auto regressive methods for stationary series, and AR (Auto Regressive) and ARMA (Auto Regressive Move Average) are the most suitable because they generate a more reliable prediction [9] .
Another critical effect on time series is the presence of seasonality, i.e. oscillations or disturbances in series occurring at regular intervals of less than one year. And, according to Bacci [8] , quantitative ARIMA models can describe two classes of processes: linear stationary processes and linear homogeneous non-stationary processes. The stationary linear processes use basically three types of models: auto regressive model of order p ; moving averages of order q
; moving averages of order q 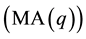 and auto regressive and moving average process of order p and q
and auto regressive and moving average process of order p and q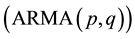 . Non-homogeneous stationary linear processes assume that the series are non-stationary in level and/or slope [10] . According to Pindyck and Rubinfeld [11] , the amount of times that the original series has to be differentiated to result in a stationary series is called order of homogeneity.
. Non-homogeneous stationary linear processes assume that the series are non-stationary in level and/or slope [10] . According to Pindyck and Rubinfeld [11] , the amount of times that the original series has to be differentiated to result in a stationary series is called order of homogeneity.
Some stationary random processes (forward constant average over time) can be modeled by means of a mixed autoregressive process and moving average ARMA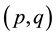 . Makridakis, Wheelwrigt and Hyndman [12] state that in this case, depending on the values of p and q, Yt will depend on the past p values of Y and past q values of
. Makridakis, Wheelwrigt and Hyndman [12] state that in this case, depending on the values of p and q, Yt will depend on the past p values of Y and past q values of  errors. This process is Equation (1):
errors. This process is Equation (1):
 . (1)
. (1)
For the process shown in (1), the stationary sum 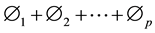 should be less than 1 [11] . According to Pindyck and Rubinfeld [11] and Fava [13] , non-stationary series can be transformed into stationary series where observations are differentiated one or more times.
should be less than 1 [11] . According to Pindyck and Rubinfeld [11] and Fava [13] , non-stationary series can be transformed into stationary series where observations are differentiated one or more times.
The first differentiation of the data is in Equation (2):
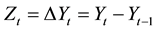 . (2)
. (2)
Being:
Yt = observation Y, in period t of the series Yt without differentiation;
Yt − 1 = observation Y, in period t − 1 of the series Yt without differentiation;
ΔYt = Zt = observation Z, in period t, belonging to series Zt with data from the series Yt differentiated for the first time.
The data series will be differentiated for the first time in the following manner: the value of the second datum is decreased from the first; the third will be decreased in the second, the fourth from the third, and so on. With this process, the differentiated series for the first time, Zt will have one less observation (n − 1 observations) than the original series Yt.
The second differentiation of data can be represented by Equation (3):
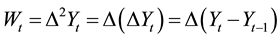 . (3)
. (3)
According to Bacci [8] , the series Yt differentiated a second time, or series Zt diffentiated once, will lead to the series Wt.
The differential data series Zt is obtained as follows: the value of the second observation decreased from the first observation forms the first observation, the value of the third diminished from the second provides the second and so on.
The twice differentiated series  will have n − 2 observations compared to the original series Yt. Thus, after one or more differentiations of Yt series to make it stationary, it produces a series stationary Wt, which can now be modeled as an ARMA process
will have n − 2 observations compared to the original series Yt. Thus, after one or more differentiations of Yt series to make it stationary, it produces a series stationary Wt, which can now be modeled as an ARMA process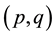 .
.
According to Pindyck and Rubinfeld [11] , the initial series Yt is an autoregressive process of order 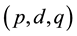 integrated moving average (MA), given by Equation (4):
integrated moving average (MA), given by Equation (4):
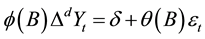 . (4)
. (4)
Being:
 ; with d = order of the stationary series Wt, that is, the number of times that the non-stationary series Yt was differentiated until becoming a stationary series Wt;
; with d = order of the stationary series Wt, that is, the number of times that the non-stationary series Yt was differentiated until becoming a stationary series Wt;
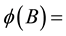 autoregressive operator;
autoregressive operator;
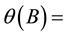 moving average operator;
moving average operator;

The construction of an ARIMA model is based on a cycle with the following stages [10] : Identification of a general class of models which will be analyzed; Specification of the model, based on autocorrelation analysis, partial autocorrelations and other criteria; Estimation of model parameters; Verification of the adjusted model, which is done by means of residual analysis to measure its suitability to carry out the forecast; If the model is not suitable, the cycle repeats from the identification of the model.
3. Materials and Methods
According to Bertrand and Fransoo [14] , this investigation can be classified as applied, having a descriptive empirical goal, since the researchers are interested in creating a model that adequately describes the causal relationships which may exist in reality, leading to the understanding of the current processes thus, fostering understanding of real processes. The approach to the problem was quantitative, and a mathematical modeling research method adopted. Figure 1 shows the Box-Jenkins method [15] :
Initially data collection was done using Economatica® software, using monthly closing prices of the Bovespa Index, for the period January 2000 to December 2012.
4. Results Analysis
The values obtained were plotted using Minitab® 16 Statistical Software for an initial evaluation of the data as shown in Figure 2.
It can be seen that the data is not stationary and the series presents variance from one period to another. The analysis used in this series demonstrated the need for a logarithmic transformation on the data which generate Figure 3. Figure 4 and Figure 5 show ACF (autocorrelation) and PACF (partial autocorrelation) transformed time series.
Tests for ACF (autocorrelation) and PACF (partial autocorrelation) indicated that the AR1 model ARIMA (0, 2, 1) model could be used to predict the behavior of the series, shown in Table 1 and Table 2.
A verification of the series’ residuals transformed by Log Bovespa Index and both tests were carried out, through which it was demonstrated that autocorrelation does not exist between series residuals, which enabled the utilization of both to forecast the behavior of the series, as shown in Figures 6-9.
Figure 1. Box-Jenkins Methodology. Source: Makridakis, Wheelwrigt and McGee [15] .
Figure 2. Plotting the Ibovespa time series.
Table 1. Coefficient statistics of the AR1 model.
Table 2. Chi-square statistics for the Box-Pierce modification (Lhung-Box).
Figure 3. Logarithmic plotting of the Ibovespa time series.
Figure 4. ACF of logarithmic Ibovespa.
Figure 5. PACF of logarithmic Ibovespa.
Figure 6. Residual plotting.
Figure 7. Graphical summary of the residues.
Figure 8. ACF of residuals.
Figure 9. PACF of residuals.
The next step was to realize tests to verify the accuracy of the models. Initially the model was used to forecast 10 months ahead in several periods of the series, trying to compare the MAPE between these periods, as shown in Figure 10 and Figure 11.
The use of this indicator (MAPE) to evaluate the models was used because this measures the absolute average, i.e., the sum of the percentage errors, in which the series data values undergo alterations throughout time, which influences the size of the error. Using the value of the error divided by the value of the observation, transforming the error as a percentage of this observation, diminishes the effects caused by variation of the values of the series, allowing one to compare the error between observations of distinct values.
A test of forecasting 10 months ahead in five distinct periods showed that, in all models, the error tends to increase after the second period, significantly impacting the average error. This fact could result from the choice of one model over another simply because of the errors from the second period are lower. This finding could be valid, if the prediction is used to making decisions in the midterm, in which the prediction of several periods ahead would determine actions to be taken and which could hardly be changed in the short term.
In the case of financial time series, significant changes in the forecasts made can trigger immediate decisions and corrections in a matter of minutes, or at worst a few days, repositioning strategies by hedging or even the rebalancing of the portfolio by the complete elimination of certain positions that would be affected or even entire investment strategies in a short space of time.
Figure 10. Forecast 10 points ahead, based on month 50.
Figure 11. Forecast 10 points ahead, based on the last month.
Thus, it was chosen to perform the forecast one-step-ahead, in the case of this study, one month ahead. In the various models analyzed, this prediction proved to be such as that found the lowest MAPE. Thus, it avoids using only a period of the series, analyze the ASM one-step-ahead composed of five periods, which evaluated the forecast of each of these periods, being the MAPE constructed from the absolute percent average of the sum of these errors.
Table 3 shows the comparison of MAPE obtained by using four AR1 models, Single Exponential Smoothing, Double Exponential Smoothing and ARIMA (0, 2, 1). It is observed that the MAPE of the AR1 model enables its use when compared to other options.
5. Conclusions
Through the results obtained, it is observed that the model is effective in its forecasts. The statistics of the AR1 model coefficients and Chi-square statistics for modified Box-Pierce (Ljung-Box) provide proof to this fact.
A MAPE (mean absolute error percentage) of 0.052% was obtained, a lower value than those found in predictions made with other models used for comparison.
This study sought to obtain short-term forecasts for the next month (one step ahead) in order to minimize pre- diction errors. The model can be considered adequate for predicting the Bovespa Index series, and can be used
Table 3. MAPE table (absolute average percent error).
as an aid to decision-making mechanism.
Acknowledgements
The authors would like to express their gratitude to the Brazilian agencies CNPq (National Counsel of Technological and Scientific Development), CAPES (Post-Graduate Federal Agency), and FAPEMIG (Foundation for the Promotion of Science of the State of Minas Gerais), which have been supporting the efforts for the development of this work in different ways and periods.
References
- Rotela, J.P., Pamplona, E.O. and Salomon, F.R. (2014) Otimização de Portfólios: Análise de Eficiência. RAE―Revista de Administração de Empresas, 54, 405-413. http://dx.doi.org/10.1590/S0034-759020140406
- Markowitz, H. (1952) Portfolio Selection. Journal of Finance, 7, 77-91.
- Sharpe, W.F. (1963) A Simplified Model for Portfolio Analysis. Management Science, 9, 277-293.
- Fama, E. (1970) Efficient Capital Markets: A Review of Theory and Empirical Work. Journal of Finance, 25, 383-417. http://dx.doi.org/10.2307/2325486
- Slack, M., Chambers, S. and Johnston, R. (2007) Operations Management. Prentice Hall/Financial Times, Upper Saddle River.
- Linstone, H.A. and Turoof, M. (1975) The Delphi Method: Techniques and Applications. Addison-Wesley, Boston.
- Gaither, N. and Frazier, G. (2001) Operations Management. South-Western, Ohio.
- Bacci, L.A. (2007) Combinação de métodos de séries temporais para a previsão da demanda de café no Brasil. Thesis, UNIFEI, Itajuba.
- Morettin, P.A and Toloi, C.M. (2006) Análise de Séries Temporais―2ª Edição Revista e Ampliada. 2nd Edition, Editora Edgar Blucher, São Paulo.
- Morettin, P.A. and Toloi, C.M. (1987) Previsão de séries temporais. 2nd Edition, Atual Editora, São Paulo.
- Pindyck, R.S. and Rubinfeld, D.L. (2008) Microeconomics. 7th Edition, Prentice Hall, Upper Saddle River.
- Makridakis, S., Wheelwrigt, S.C. and Hyndman, R.J. (1998) Forecasting: Methods and Applications. 3rd Edition, John Wiley & Sons, New York.
- Fava, V.L. (2000) Metodologia de Box-Jenkins para Modelos Univariados. In: Vasconcellos, M.A.S. and Alves, D., Eds., Manual de econometria: nível intermediário, Atlas, São Paulo, 205-232.
- Bertrand, J. and Fransoo, J. (2002) Operations Management Research Methodologies Using Quantitative Modeling. International Journal of Operations & Production Management, 22, 241-264. http://dx.doi.org/10.1108/01443570210414338
- Makridakis, S., Wheelwrigt, S.C. and Mcgee, V. (1983) Forecasting: Methods and Applications. 2nd Edition, John Wiley & Sons, New York.













