Applied Mathematics
Vol.05 No.03(2014), Article ID:42746,14 pages
10.4236/am.2014.53041
Solution of Nonlinear Stochastic Langevin’s Equation Using WHEP, Pickard and HPM Methods
Maha Hamed1, Magdy A. El-Twail2, Beih El-desouky1, Mohamed A. El-Beltagy3
1Department of Mathematics, Faculty of Science & Mansoura University, Mansoura, Egypt
2Department of Engineering Mathematics & Physics, Engineering Faculty, Cairo University, Giza, Egypt
3Department of Electrical & Computer Engineering, Engineering Faculty, Effat University, Jeddah, KSA
Email: maha_hamed8@yahoo.com, mebeltagy@effatuniversity.edu.sa
Copyright © 2014 Maha Hamed et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Maha Hamed et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
Received October 22, 2013; revised November 22, 2013; accepted November 30, 2013
This paper introduces analytical and numerical solutions of the nonlinear Langevin’s equation under square nonlinearity with stochastic non-homogeneity. The solution is obtained by using the Wiener-Hermite expansion with perturbation (WHEP) technique, and the results are compared with those of Picard iterations and the homotopy perturbation method (HPM). The WHEP technique is used to obtain up to fourth order approximation for different number of corrections. The mean and variance of the solution are obtained and compared among the different methods, and some parametric studies are done by using Matlab.
Keywords:
Nonlinear Stochastic D.E; Langevin’s Equation; WHEP Technique; Picard Approximation; HPM Technique
1. Introduction
Stochastic differential equations based on the white noise process provide a powerful tool for dynamically modeling complex and uncertain aspects. Developing efficient numerical methods for simulating SPDEs is a very important while challenging research topic. The study of random solutions of partial differential equations was developing continuously since Kampe de Feriet in 1955 [1] and Bharucha-Reid in 1965 [2]. It was 1973 when Lo Dato V. had discussed the mathematical problems associated with Navier-Stokes equation [3], a general solution for the heat conducting problem with random source, initial and boundary conditions that was introduced by B. A. Georges [4]. The Langevin’s equation [5] with square nonlinear losses and stochastic non-homogeneity is solved by using different techniques, mainly the WHEP technique [6-11], the Picard approximation [8-10] and HPM [9-11].
It is appropriate to assume that the nonlinear term in SPDE affecting the phenomena under study is small enough; then its intensity is controlled by means of a frank small parameter, saying ε [12]. In (WHE) approach, there is no randomness directly involved in the computations.
The application of WHE aims to find a truncated series of the solution process of the differential equation. The truncated series composes of two major parts: the first is the Gaussian part which consists of the first two terms, while the rest of the series constitutes the non-Gaussian part. In nonlinear cases, there exist difficulties in solving the resultant set of the deterministic set of integro-differential obtained after the direct application of WHE. The WHEP technique was introduced in [6] using perturbation method to solve perturbed nonlinear equation.
The WHE was developed by Norbert Wiener [13]. Wiener constructed an orthonormal random base for expanding homogeneous chaos depending on white noise and used it to study problems in statistical mechanics. Cameron and Martin [14] developed a more explicit and intuitive formulation for Wiener-Hermite expansion, and this technique is now known as Wiener-Chaos expansion (WCE). Their development was based on an explicit discretization of the white noise process through its Fourier expansion, which was missed in Wiener’s original formalism. Since Cameron and Martin’s work, WHE has become a useful tool in stochastic analysis involving white noise (Brownian motion) [14]. Also, another formulation was suggested and applied by Meecham and his co-workers [15,16]. They have developed a theory of turbulence involving a truncated WHE of the velocity field. This technique was also used by M. El-Tawil and his co-workers [6-10].
The main goal of this paper is to apply the WHEP technique in solving the nonlinear stochastic Langevin’s equation and compare the solution with those of Picard’s and HPM techniques. In Section 2, the problem will be introduced; in Section 3, the application of WHEP technique is considered; the Picard approximation technique is applied in Section 4; Section 5 describes the application of HPM method; Section 6 represents the results for every method; and Section 7 shows comparisons between the different techniques.
2. Problem Formulation
In this paper, the nonlinear stochastic Langevin’s equation with external stochastic excitation in the form of white noise is considered. It formulates general relation between the velocity 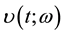 of a unit mass particle and the non homogeneity random forces
of a unit mass particle and the non homogeneity random forces  of a fluid medium with phenomenological coefficient
of a fluid medium with phenomenological coefficient 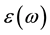 such that [8,17]:
such that [8,17]:
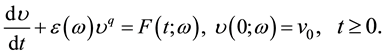 (1)
(1)
The variable  is a random output of a triple probability space
is a random output of a triple probability space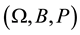 , where
, where 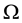 is a sample space, B is a
is a sample space, B is a 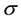 -algebra associated with
-algebra associated with 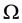 and P is a probability measure. For simplicity, ω will be dropped later on.
and P is a probability measure. For simplicity, ω will be dropped later on.
The following assumptions are taken for simplicity:
・ Constant phenomenological coefficient;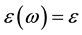 .
.
・ deterministic initial condition;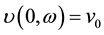 .
.
・ Nonlinearity of second order;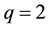 .
.
・ Medium forces in terms of white noise 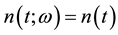 enveloped by a deterministic function
enveloped by a deterministic function 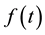 and scaled by scalar amplitude
and scaled by scalar amplitude 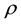 i.e.
i.e.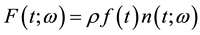 .
.
Under the above hypothesis; the model becomes
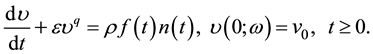 (2)
(2)
Theorem: The solution of Equation (2), if exists, is a power series in 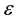 when using Picard approximation technique i.e.
when using Picard approximation technique i.e.
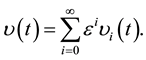
The theorem can be proved using the mathematical induction with the Picard iterative technique as in [7].
The deterministic solution of Equation (2) at 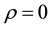 [8], is:
[8], is:

which can be expanded as follows,

The solution is a series of successive addition and subtractions of the ascendant orders of the quantity 
3. WHEP Technique
Due to the completeness of the Wiener-Hermite set [15], any arbitrary stochastic process 

where 


functional 


To obtain approximate solutions of these deterministic kernels, one can use perturbation technique in the case of having a perturbed system depending on a small parameter

If 

where NC refers to the number of corrections, m is the order, the statistical properties of the solution can be calculated as [7]:

Applying the WHEP algorithm [18] to get the deterministic set of differential equations. The envelop function 



For NC = 1: we have the following

For NC = 2: We have the above equations in addition to:

For NC = 3: We have the above equations in addition to:

4. Picard Approximation
It is based on generating recursive convergent approximations for the solution until reaching certain level of accuracy defined according to the nature of the problem or to the measure in the scope of the analysis [19,20].
In the case of nonlinear Langevin’s equation, Picard algorithm converges to the exact instant of the time at which the solution explodes. In this case there is a relation between the number of approximations and the values of parameters. The more number of approximations, the closer we are to the exact solution.
First, an arbitrary initial approximation should be suggested

which is substituted in Equation (2). First let us discuss the convergence of the model taking 




We shall choice two arbitrary initial approximations in Picard approximations to simulate the model of Langevin’s equation, the two cases of initial approximations are:
5. Homotopy Perturbation Method (HPM)
The HPM is proved to be an effective, simple, and convenient to solve nonlinear PDE problems [22,23]. In HPM, a parameter, 


where 

with the boundary conditions:

In which A is a nonlinear differential operator which can be decomposed into a linear operator R and a nonlinear operator N, B is a boundary operator and 



Now, setting

The rate of convergence of HPM depends greatly on the initial approximation 
HPM is a simple technique which enables the extension of the applicability of the perturbation methods from small value applications to general ones. Applying HPM technique on Equation (2) with,




The homotopy function takes the following form :

Equivalently:

Using Equation (17) in Equation (24) and equating the similar powers of p in both sides of the equation, one can get the following:





We have many choices in guessing the initial approximation together with its initial conditions which greatly affects the consequent approximations. We shall consider the choice of

which satisfies the initial condition. The statistical measures of the different orders can be obtained as:
1st order:

2nd order:

3rd order:

4th order:

6. Results
6.1. Results of WHEP Technique
Figures 1-8 show the mean and the variance of fourth order for first, second and third corrections. As shown in Figure 1 for case of 


Figure 1. Fourth order mean of first, second and third corrections. Comparison between the different corrections for ε = 0.5 of pure white noise.
Figure 2. Fourth order variance of first, second and third corrections. Comparison between the different corrections for ε = 0.5 of pure white noise.
Figure 3. Fourth order mean of first, second and third corrections. Comparison between the different corrections for ε = 0.01 of pure white noise.
Figure 4. Fourth order variance of first, second and third corrections. Comparison between the different corrections for ε = 0.01 of pure white noise.
Figure 5. Fourth order mean of first, second and third corrections. Comparison between the different corrections for ε = 0.5 of decaying white noise.
Figure 6. Fourth order variance of first, second and third corrections. Comparison between the different corrections for ε = 0.5 of decaying white noise.
Figure 7. Fourth order mean of first, second and third corrections. Comparison between the different corrections for ε = 0.01 of decaying white noise.
Figure 8. Fourth order variance of first, second and third corrections. Comparison between the different corrections for ε = 0.01 of decaying white noise.
For small value of nonlinearity strength


There is no obvious difference in mean and variance for case of 


Figures 6 and 8 for

Decreasing the nonlinearity strength in Figures 6 and 8 make the variance increasing with time until fixed to certain time after which it begin to make the explosion.
To know the effect of increasing order in the accurate of the solution, fixed the third correction as case of test as follows.
Figure 9 shows the mean in different models which give us knowledge about decreasing 




Figure 9. Third correction mean of first, second, third and fourth orders. Comparison between the different orders for ε = 0.5, ε = 0.01. Case of pure and decaying white noise.
said before.
Figures 10 shows the coincident of all orders such as that in mean but in this case of the variance, we find the first order deviate from the others at increasing time and the interval of that depend on the parameter’s value, all plots of variance has the same trajectory of increasing variance to reach its peak then decreasing to certain time after which it make the deviation.
6.2. Results of Picard Approximation
Figures 11-14 prove that Picard approximation gives good result for


6.3. Results of HPM Method
Figures 5 and 6 are semi-similar to Figures 19 and 20 at which we can see the simulations of the orders in HPM are look like the simulations of the corrections in WHEP technique and the fourth order here is similar to our guess of fourth correction which diverge to positive infinity.
Figures 7 and 8 are semi-similar to Figures 21 and 22 which prove that increasing order of solution will give the accurate location at which the solution explodes and more convergence to the exact solution of this model.
Figure 10. Third correction variance of first, second, third and fourth orders. Comparison between the different orders for ε = 0.5, ε = 0.01. Case of pure and decaying white noise.
Figure 11. Mean of last iteration (n) for ε = 0.5; 0.01 of first case of initial approximation.
Figure 12. Variance of last iteration (n) for ε = 0.5; 0.01 of first case of initial approximation.
Figure 13. Mean of last iteration (n) for ε = 0.5; 0.01 of second case of initial approximation.
Figure 14. Variance of last iteration (n) for ε = 0.5; 0.01 of second case of initial approximation.
Figure 15. Comparison between Picard mean using the first and second cases of initial approximations for ε = 0.5.
Figure 16. Comparison between Picard variance using the first and second cases of initial approximations for ε = 0.5.
Figure 17. Comparison between Picard mean using the first and second cases of initial approximations for ε = 0.01.
The changing of ε makes a difference in the results, in Figure 23 increasing ε than 1 doesn’t make any prob- lem in the solution but decreasing this value gives good results, and also changing in ρ doesn’t make any change in the mean, but in variance it makes change in delaying the explosion and gives good solution especially for
Figure 18. Comparison between Picard variance using the first and second cases of initial approximations for ε = 0.01.
Figure 19. Comparison of the first, second, third and fourth orders mean for ε = 0.5 and λ = 2.
Figure 20. Comparison of the first, second, third and fourth orders variance for ε = 0.5 and λ = 2.
Figure 21. Comparison of the first, second, third and fourth orders mean for ε = 0.01 and λ = 2.
Figure 22. Comparison of the first, second, third and fourth orders variance for ε = 0.01 and λ = 2.
decreasing this parameter.
6.4. Comparison between Different Methods
The comparison between all methods depends greatly on decreasing the nonlinearity strength
7. Conclusion
Picard is reaching the solution in a numerical way to deduce the mathematical formulas which deplete too much effort despite of the convergence between the two cases of initial approximations: the first case of initial appro- ximation was more convergent to WHEP technique and HPM methods than the second one. The WHEP technique seems to be efficient because of its corrections in spite of being analytically lengthy. The HPM is easier in computation but for higher order to calculate the variance, and it is complicated but not more than the WHEP which needs huge analytical calculations and formulations. HPM expectedly depends highly on the initial guess. WHEP and HPM are convergent to each other than any other two compared methods, and every order in HPM
Figure 23. The fourth order variance for different ε and λ = 2.
Figure 24. Comparison between Picard, WHEP and HPM fourth order mean for first case of Picard.
Figure 25. Comparison between Picard, WHEP and HPM fourth order variance for first case of Picard.
has the same trajectory of the opposite correction in WHEP, which means the first order in HPM looks like the first correction in WHEP and so until the fourth one.
References
- K. De Feriet, “Random Solutions of Partial Differential Equations,” Proceedings of the 3rd Berkeley Symposium on Mathematical Statistics and Probability, Vol. III, 1956, pp. 199-208.
- R. Bharucha, “A Survey on the Theory of Random Functions,” The Institute of Mathematical Sciences, Matscience Report 31, 1965.
- V. Lo Dato, “Stochastic Processes in Heat and Mass Transport,” Probabilistic Methods in Applied Mathematics, Vol. 3(A), 1973, pp. 183-212.
- B. A. Georges, “Random Generalized Solutions to the Heat Equations,” Journal of Mathematical Analysis and Applications, Vol. 60, No. 1, 1977, pp. 93-102. http://dx.doi.org/10.1016/0022-247X(77)90051-8
- W. T. Coffey and Y. P Kalmykov, “The Langevin Equation, with Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering,” 3rd Edition, World Scientific Publishing Company, Singapore City, 2012.
- M. A. El-Tawil, “The Application of the WHEP Technique on Partial Differential Equations,” International Journal of Differential Equations and Applications, Vol. 7, No. 3, 2003, pp. 325-337.
- M. A. El-Beltagy and M. A. El-Tawil, “Toward a Solution of a Class of Non-Linear Stochastic perturbed PDEs Using Automated WHEP Algorithm,” Applied Mathematical Modelling, 2013, in Press. http://dx.doi.org/10.1016/j.apm.2013.01.038
- M. El Tawil and W. Shawky “Wiener Functional, Integrals, and Stochastic Differential Equations Solutions Using Euler- Maruyama, Picard and WHEP Computer Simulation Stud,” BSc Thesis, Engineering faculty, Cairo University, Cairo, 2011.
- M. A. El-Tawil and A. Fareed, “Solution of Stochastic Cubic and Quintic Nonlinear Diffusion Equation Using WHEP, Pickard and HPM Methods,” Open Journal of Discrete Mathematics, Vol. 1, No. 1, 2011, pp. 6-21. http://dx.doi.org/10.4236/ojdm.2011.11002
- M. El-Tawil and N. El-Molla, “The Approximate Solution of a Nonlinear Diffusion Equation Using Some Techniques, a Comparison Study,” Applied Mathematics and Computing, Vol. 29, No. 1-2, 2009, pp. 281-299.
- A. S. El-Johani, “Comparisons between WHEP and Homotopy Perturbation Techniques in Solving Stochastic Cubic Oscillatory Problems,” AIP Conference Proceedings, Vol. 1148, 2010, pp. 743-752. http://dx.doi.org/10.1063/1.3225426
- J. C. Cortes, J. V. Romero, M. D. Rosello and R. J. Villanueva, “Applying the Wiener-Hermite Random Technique to Study the Evolution of Excess Weight Population in the Region of Valencia (Spain),” American Journal of Computational Mathe- matics, Vol. 2, No. 4, 2012, pp. 274-281. http://dx.doi.org/10.4236/ajcm.2012.24037
- N. Wiener, “Nonlinear Problems in Random Theory,” MIT Press, John Wiley, Cambridge, 1958.
- R. H. Cameron and W. T. Martin, “The Orthogonal Development of Non-Linear Functionals in Series of Fourier-Hermite Functionals,” Annals of Mathematics, Vol. 48, No. 2, 1947, pp. 385-392. http://dx.doi.org/10.2307/1969178
- T. Imamura, W. Meecham and A. Siegel, “Symbolic Calculus of the Wiener Process and Wiener-Hermite Functionals,” Jour- nal of Mathematical Physics, Vol. 6, No. 5, 1965, pp. 695-706. http://dx.doi.org/10.1063/1.1704327
- W. C. Meecham and D. T. Jeng, “Use of the Wiener-Hermite Expansion for Nearly Normal Turbulence,” Journal of Fluid Mechanics, Vol. 32, No. 2, 1968, pp. 225-235. http://dx.doi.org/10.1017/S0022112068000698
- R. Riganti and N. Bellomo, “Nonlinear Stochastic Systems in Physics and Mechanics,” World Scientific Publishing Co., Singapore City, 1987.
- M. El-Beltagy and A. Al-Johani, “Higher-Order WHEP Solutions of Quadratic Nonlinear Stochastic Oscillatory Equation,” Engineering, Vol. 5, No. 5A, 2013, pp. 57-69.
- E. A. Ibijola and B. J. Adegboyegun, “A Comparison of Adomian’s Decomposition Method and Picard Iterations Method in Solving Nonlinear Differential Equations,” Nigeria Global Journal of Science Frontier Research Mathematics and Decision Sciences, Vol. 12, No. 7, 2012.
- I. K. Youssef, “Picard Iteration Algorithm Combined with Gauss-Seidel Technique for Initial Value Problems,” Applied Mathematics and Computation, Vol. 190, No. 1, 2007, pp. 345-355. http://dx.doi.org/10.1016/j.amc.2007.01.058
- R. Riganti and N. Bellomo, “Nonlinear Stochastic Systems in Physics and Mechanics,” World Scientific Publishing Co., Singapore City, 1987.
- J. H. He, “Application of Homotopy Perturbation Method to Nonlinear Wave Equations,” Chaos Solitons Fractals, Vol. 26, No. 3, 2005, pp. 295-300. http://dx.doi.org/10.1016/j.chaos.2005.03.006
- J. H. He, “Homotopy Perturbation Method for Solving Boundary Value Problems,” Physics Letters A, Vol. 350, No. 1-2, 2006, pp. 87-88.




























