Applied Mathematics
Vol.4 No.10C(2013), Article ID:38401,8 pages DOI:10.4236/am.2013.410A3009
A Spectral Integral Equation Solution of the Gross-Pitaevskii Equation*
Physics Department, University of Connecticut, Storrs, Connecticut, USA
Email: george.rawitscher@uconn.edu
Copyright © 2013 George Rawitscher. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 8, 2013; revised September 8, 2013; accepted September 15, 2013
Keywords: Iterative Solution of the Gross-Pitaevskii Equation; Spectral Solution of an Integral Equation; Bose-Einstein Condensates
ABSTRACT
The Gross-Pitaevskii equation (GPE), that describes the wave function of a number of coherent Bose particles contained in a trap, contains the cube of the normalized wave function, times a factor proportional to the number of coherent atoms. The square of the wave function, times the above mentioned factor, is defined as the Hartree potential. A method implemented here for the numerical solution of the GPE consists in obtaining the Hartree potential iteratively, starting with the Thomas Fermi approximation to this potential. The energy eigenvalues and the corresponding wave functions for each successive potential are obtained by a spectral method described previously. After approximately 35 iterations a stability of eight significant figures for the energy eigenvalues is obtained. This method has the advantage of being physically intuitive, and could be extended to the calculation of a shell-model potential in nuclear physics, once the Pauli exclusion principle is allowed for.
1. Introduction
The phenomenon of Bose-Einstein condensation of an assembly of atoms, predicted in 1924 [1-3], was finally observed experimentally in 1995 [4,5] for atoms confined in a trap at very low temperatures. An approximate non-linear equation that describes the Bose-Einstein Condensate (BEC) wave function was established in 1961 by E. P. E. Gross [6,7], and independently by L. P. Pitaevskii [8]. This is a Schrödinger-like equation, now called the Gross-Pitaevskii equation (GPE), describes the wave function of 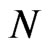 Bose particles interacting coherently and confined in an atomic trap. In this equation only the short range part of the interaction between the atoms is included in terms of the scattering length of two colliding atoms. Numerical solutions of this non-linear GPE began to be obtained in the middle 60’ies, both for the time independent form [9], as well as for the time dependent form [10]. An extensive review of the early work is given in [11], and both experimental as well as theoretical work continues actively today. On the theoretical side various diverse methods for the solution of the GPE have been developed. Amongst them, some based on mathematical theorems [12,13], others based on spectral expansions [14], others using extensive numerical methods [15], and others that also include the interaction of the BEC atoms with the surrounding non-condensed atomic medium [16-20].
Bose particles interacting coherently and confined in an atomic trap. In this equation only the short range part of the interaction between the atoms is included in terms of the scattering length of two colliding atoms. Numerical solutions of this non-linear GPE began to be obtained in the middle 60’ies, both for the time independent form [9], as well as for the time dependent form [10]. An extensive review of the early work is given in [11], and both experimental as well as theoretical work continues actively today. On the theoretical side various diverse methods for the solution of the GPE have been developed. Amongst them, some based on mathematical theorems [12,13], others based on spectral expansions [14], others using extensive numerical methods [15], and others that also include the interaction of the BEC atoms with the surrounding non-condensed atomic medium [16-20].
One aspect emphasized in the present study is the description of the coherent interaction of the atoms in the BEC in terms of a related Hartree potential, . This potential arises naturally in the GPE, due to the presence of the third power of the wave function
. This potential arises naturally in the GPE, due to the presence of the third power of the wave function 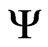 in that equation, by rewriting the term
in that equation, by rewriting the term 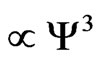 as
as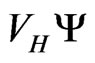 . This potential contains the square of the wave function, hence is nonlinear, and is proportional to the number of coherent atoms times the scattering length of the interacting atoms. Such a term was introduced previously [21], and in the context of nuclear physics where it is called the Hartree-Fock potential since it incorporates the effect of the Pauli exclusion imposed on the fermions [22-24].
. This potential contains the square of the wave function, hence is nonlinear, and is proportional to the number of coherent atoms times the scattering length of the interacting atoms. Such a term was introduced previously [21], and in the context of nuclear physics where it is called the Hartree-Fock potential since it incorporates the effect of the Pauli exclusion imposed on the fermions [22-24].
If 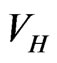 were known, then the GPE could be written as an ordinary linear
were known, then the GPE could be written as an ordinary linear 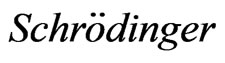 equation, that could be solved by conventional means for the ground or excited states of
equation, that could be solved by conventional means for the ground or excited states of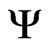 . Since
. Since 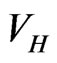 is not known, it can nevertheless be obtained iteratively, by starting from a good approximation to
is not known, it can nevertheless be obtained iteratively, by starting from a good approximation to 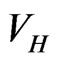 solving for the corresponding wave function that in turn defines a better approximation to
solving for the corresponding wave function that in turn defines a better approximation to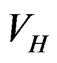 , and so on. To demonstrate the viability of this scheme, and to exhibit values of
, and so on. To demonstrate the viability of this scheme, and to exhibit values of  both for the ground and several excited states of the BEC, is the purpose of the present paper. A very related study by Esry [25] is to be noted. That paper also emphasizes the Hartree potential, and also uses it for a different iterative procedure. However, that study is more general, in that it includes correlations between pairs of particles, as well as exchange contributions, and further, the potential
both for the ground and several excited states of the BEC, is the purpose of the present paper. A very related study by Esry [25] is to be noted. That paper also emphasizes the Hartree potential, and also uses it for a different iterative procedure. However, that study is more general, in that it includes correlations between pairs of particles, as well as exchange contributions, and further, the potential 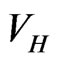 is not displayed. Furthermore, the numerical method of the present study is different, in that it uses a spectral Chebyshev expansion for the solution of the integral equation associated with the differential GPE.
is not displayed. Furthermore, the numerical method of the present study is different, in that it uses a spectral Chebyshev expansion for the solution of the integral equation associated with the differential GPE.
One advantage of the present method is that 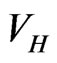 has intuitive significance, excited states can also be obtained easily, and the method can be generalized to the case that the interaction between two of the atoms has a finite range, in contrast to the zero-range assumption of the GPE. Further, the binding energies and wave functions for each successive value of
has intuitive significance, excited states can also be obtained easily, and the method can be generalized to the case that the interaction between two of the atoms has a finite range, in contrast to the zero-range assumption of the GPE. Further, the binding energies and wave functions for each successive value of  are obtained by a spectral integral equation method (S-IEM) that is not a variational method. Spectral methods [26-28] are becoming increasingly significant in modern numerical approaches for their accuracy and computational economy. In the S-IEM the full radial domain is divided into partitions, and in each partition the wave function is expanded in a series of Chebyshev polynomials, whose coefficients are calculated by solving linear equations [29,30]. The SIEM has been applied to the solution of several physics problems [31-40], and a pedagogical description is available in [41,42].
are obtained by a spectral integral equation method (S-IEM) that is not a variational method. Spectral methods [26-28] are becoming increasingly significant in modern numerical approaches for their accuracy and computational economy. In the S-IEM the full radial domain is divided into partitions, and in each partition the wave function is expanded in a series of Chebyshev polynomials, whose coefficients are calculated by solving linear equations [29,30]. The SIEM has been applied to the solution of several physics problems [31-40], and a pedagogical description is available in [41,42].
A future envisaged application of this method is in the calculation of a shell model potential in nuclear physics. In this case several (but not many) nucleons occupy a given “shell”, but the confining potential will turn out to be different for each shell. Hence the shell potential becomes non-local, and it is hoped that the present method may facilitate the formulation of this non-locality. Similarly, the optical model potential describing nucleon-nucleus scattering is also non-local, (but for more reasons) and efforts to determine its nature are in progress [43- 45].
The present investigation is limited to a spherically symmetric confining well, and only the partial wave corresponding to an angular momentum 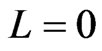 is included. The confining well is assumed to be harmonic, but other forms can also be considered. The organization of this paper is as follows: In Section 2 the formalism of the GPE is reviewed, a physically justified set of input parameters is proposed, and the Thomas-Fermi approximation to
is included. The confining well is assumed to be harmonic, but other forms can also be considered. The organization of this paper is as follows: In Section 2 the formalism of the GPE is reviewed, a physically justified set of input parameters is proposed, and the Thomas-Fermi approximation to 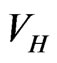 is implemented. Section 3 contains results for
is implemented. Section 3 contains results for 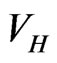 and the corresponding excitation energies, and Section 4 contains the summary and conclusions.
and the corresponding excitation energies, and Section 4 contains the summary and conclusions.
2. Formalism
The three-dimensional form of the GPE can be written [11]
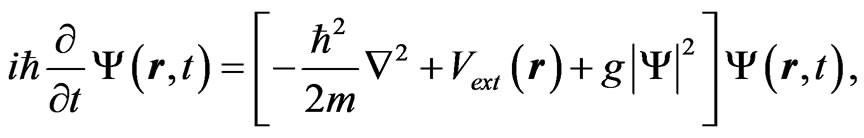 (1)
(1)
where 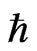 is Planck’s constant divided by
is Planck’s constant divided by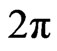 ,
, 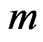 is the mass of the Boson,
is the mass of the Boson, 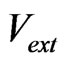 is the confining trap potential, usually written as a sum of three harmonic potentials
is the confining trap potential, usually written as a sum of three harmonic potentials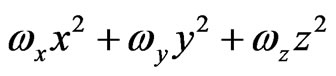 , and
, and  is a constant proportional to the number
is a constant proportional to the number 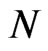 of particles in the trap times the scattering length
of particles in the trap times the scattering length 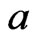 of two of the Bosons. This constant can be written as [9]
of two of the Bosons. This constant can be written as [9]
 (2)
(2)
with
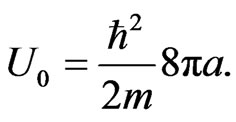 (3)
(3)
A stationary solution 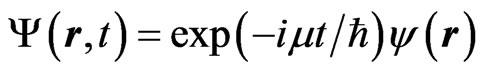 obeys [9]
obeys [9]
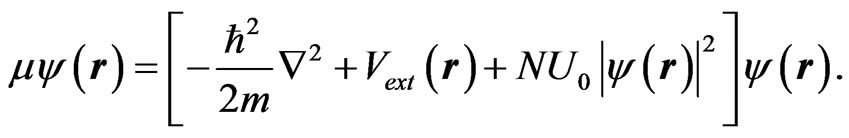 (4)
(4)
If one now assumes that 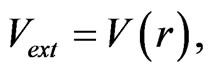 i.e., that the trap potential is spherically symmetric, makes a partial wave expansion of
i.e., that the trap potential is spherically symmetric, makes a partial wave expansion of , and retains only the angular momentum
, and retains only the angular momentum 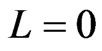 part of the expansion,
part of the expansion,
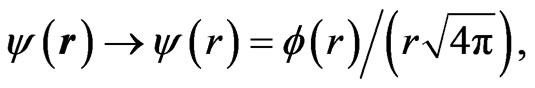 (5)
(5)
then  satisfies the radial Equation [9]
satisfies the radial Equation [9]
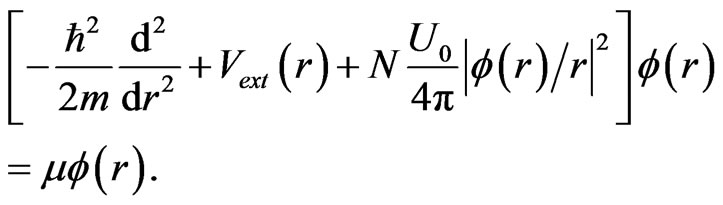 (6)
(6)
Here 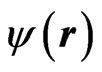 describes the wave function of one of the particles, and since the probability of finding this particle is unity, i.e.,
describes the wave function of one of the particles, and since the probability of finding this particle is unity, i.e., 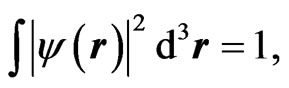 one finds, in view of Equation (5),
one finds, in view of Equation (5),
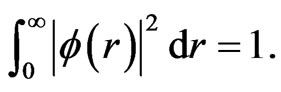 (7)
(7)
The first, second, etc., iterations of 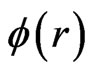 are denoted as
are denoted as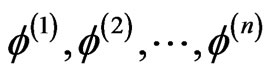 , the corresponding Hartree potentials are denoted as
, the corresponding Hartree potentials are denoted as
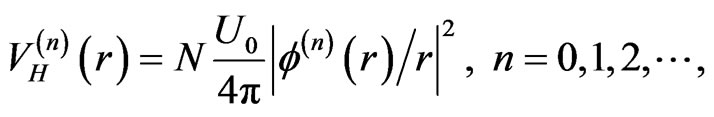 (8)
(8)
and the iterative equations are
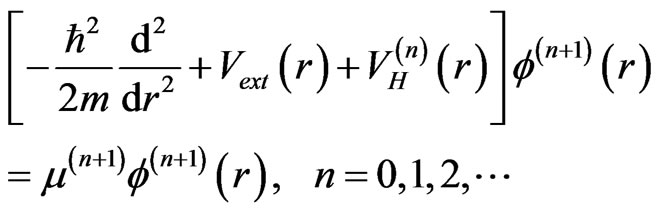 (9)
(9)
The functions  all go to zero at the origin of
all go to zero at the origin of , decay to zero as gaussians as
, decay to zero as gaussians as  if
if  is assumed to be harmonic, and obey the normalization condition (7) for each iteration. For each fixed value of
is assumed to be harmonic, and obey the normalization condition (7) for each iteration. For each fixed value of , the eigenfunctions
, the eigenfunctions  and eigenvalues
and eigenvalues 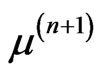 of Equation (9) are determined iteratively by a Hartree procedure described previously, both for bound states [39] as well as for Sturmian eigenvalues [40]. The feature that the function
of Equation (9) are determined iteratively by a Hartree procedure described previously, both for bound states [39] as well as for Sturmian eigenvalues [40]. The feature that the function 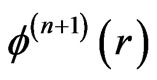 and the eigenvalue
and the eigenvalue 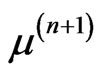 are determined simultaneously in each new iteration is what makes the present approach different from other iterative approaches. In summary, two nested iterations are performed: 1) One that finds the solutions of Equation (9) for each value of
are determined simultaneously in each new iteration is what makes the present approach different from other iterative approaches. In summary, two nested iterations are performed: 1) One that finds the solutions of Equation (9) for each value of , and 2) The iterative progression from
, and 2) The iterative progression from 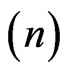 to
to 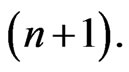 The latter proceeds non-monotonically, as seen in the numerical example given further on, and the first has been used successfully in several applications [41,42]. This double iteration procedure is different from the procedures cited above [9,10,12,13,20,46, 47]. Another difference from previous calculations is that the differential Equation (9) is transformed into a Lippmann-Schwinger integral equation, that is solved with the use of Green’s functions in configuration space [29, 39]. These functions require wave-numbers, rather than energies as input parameters. The calculations are done by means of a semi-spectral Chebyshev expansion method that gives a reliable accuracy [31-38].
The latter proceeds non-monotonically, as seen in the numerical example given further on, and the first has been used successfully in several applications [41,42]. This double iteration procedure is different from the procedures cited above [9,10,12,13,20,46, 47]. Another difference from previous calculations is that the differential Equation (9) is transformed into a Lippmann-Schwinger integral equation, that is solved with the use of Green’s functions in configuration space [29, 39]. These functions require wave-numbers, rather than energies as input parameters. The calculations are done by means of a semi-spectral Chebyshev expansion method that gives a reliable accuracy [31-38].
2.1. Numerical Inputs
In order to solve Equations (8) and (9), two steps are required. First a set of physically reasonable values for the potentials have to be established, and subsequently a transformation of variables is made so as to render the equations more transparent, and all quantities become expressed in terms of new distance and energy units.
The atoms in the trap are assumed to have a mass  and the scattering length
and the scattering length 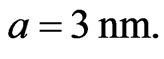 The confining trap potential is assumed to be harmonic
The confining trap potential is assumed to be harmonic
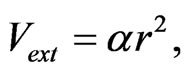 (10)
(10)
and the value of the coefficient 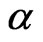 is obtained by requiring that at a distance of
is obtained by requiring that at a distance of  from the center of the trap the value of
from the center of the trap the value of 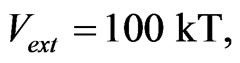 with
with 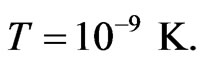 This yields
This yields 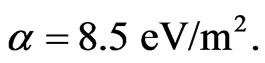 Next, both sides of Equation (6) are multiplied by
Next, both sides of Equation (6) are multiplied by , a new unit of distance
, a new unit of distance 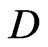 is chosen
is chosen
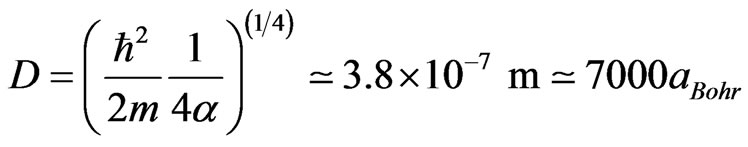 (11)
(11)
and by further multiplying by 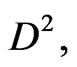 Equation (9) is transformed into dimensionless units
Equation (9) is transformed into dimensionless units
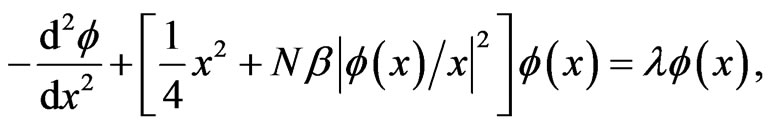 (12)
(12)
and the normalization Equation (7) is changed to
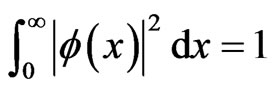 . (13)
. (13)
Here
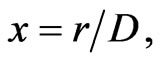 (14)
(14)
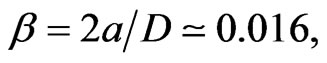
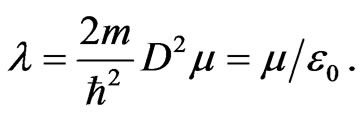 (15)
(15)
The energy unit 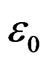 is thus
is thus
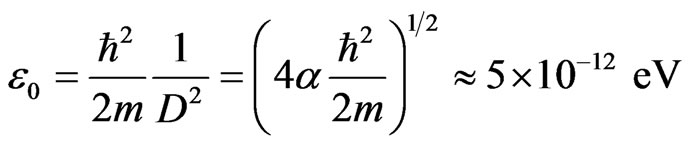 . (16)
. (16)
In order to solve Equation (12) numerically, a constant 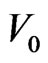 is subtracted from both sides
is subtracted from both sides

with the result
 (17)
(17)
where
 (18)
(18)
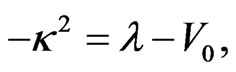 (19)
(19)
and where the dimensionless Hartree potential is given by
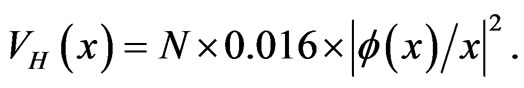 (20)
(20)
The effect of 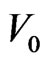 is to move the bottom of the harmonic well to a negative energy, but
is to move the bottom of the harmonic well to a negative energy, but 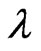 still measures the eigenvalue energy above the bottom of the well. To this, thus moved harmonic potential, is added the Hartree potential
still measures the eigenvalue energy above the bottom of the well. To this, thus moved harmonic potential, is added the Hartree potential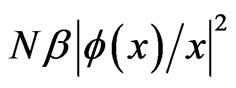 , which is positive (repulsive) if the scattering length
, which is positive (repulsive) if the scattering length 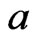 is positive. The advantage of having subtracted
is positive. The advantage of having subtracted 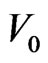 is that the wave number
is that the wave number  required as input to the Green’s function
required as input to the Green’s function 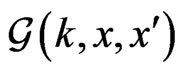 becomes purely imaginary,
becomes purely imaginary, 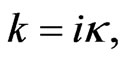 and thus the asymptotic value of
and thus the asymptotic value of  decreases exponentially. However, since the potential
decreases exponentially. However, since the potential 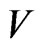 continues to grow positively as
continues to grow positively as 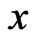 increases, the asymptotic form of
increases, the asymptotic form of 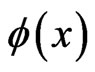 should decrease to zero like a Gaussian function. This behavior is indeed found to be the case in the numerical evaluations.
should decrease to zero like a Gaussian function. This behavior is indeed found to be the case in the numerical evaluations.
2.2. The Thomas-Fermi Approximation
This approximation to 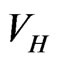 is obtained by dropping the kinetic energy term from the GPE (4) or (6). As already noted previously [48,49], this approximation, denoted as
is obtained by dropping the kinetic energy term from the GPE (4) or (6). As already noted previously [48,49], this approximation, denoted as 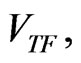 gets better the larger the number
gets better the larger the number 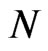 of coherent atoms in the trap. However, since the function
of coherent atoms in the trap. However, since the function 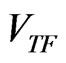 drops abruptly to zero at the outer edge of
drops abruptly to zero at the outer edge of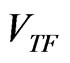 , it is difficult to incorporate this function into the numerical calculations [15,25]. This difficulty is overcome in the present investigation, by fitting to
, it is difficult to incorporate this function into the numerical calculations [15,25]. This difficulty is overcome in the present investigation, by fitting to 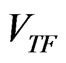 a smooth extension that decreases to zero exponentially, and subsequently using this fit for the start of the iterations for
a smooth extension that decreases to zero exponentially, and subsequently using this fit for the start of the iterations for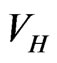 . The derivation of
. The derivation of 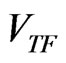 will be repeated here for completeness.
will be repeated here for completeness.
By discarding the second order derivative in Equation (12), one obtains
 (21)
(21)
where the maximum value of 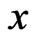 is
is 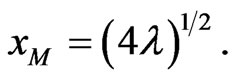 The value of
The value of  is not known until one takes into account the normalization condition (13). The integrals can be done analytically for the case that the confining potential is harmonic, with the result
is not known until one takes into account the normalization condition (13). The integrals can be done analytically for the case that the confining potential is harmonic, with the result
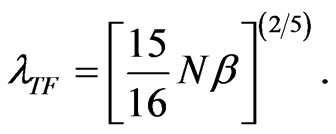 (22)
(22)
The corresponding value of  is
is
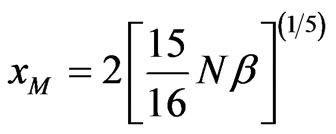 . (23)
. (23)
A numerical example for the case that 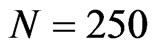 is illustrated in Figure 1.
is illustrated in Figure 1.
3. Results
As described in Section 2 the calculation consists of two nested iterations. For each Hartree potential 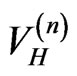 the corresponding eigenvalue
the corresponding eigenvalue 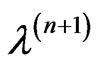 and eigenfunction
and eigenfunction  is calculated by a hybrid iterative method, implemented by means of a spectral Chebyshev expansion described in [39]. The resulting Hartree potential
is calculated by a hybrid iterative method, implemented by means of a spectral Chebyshev expansion described in [39]. The resulting Hartree potential
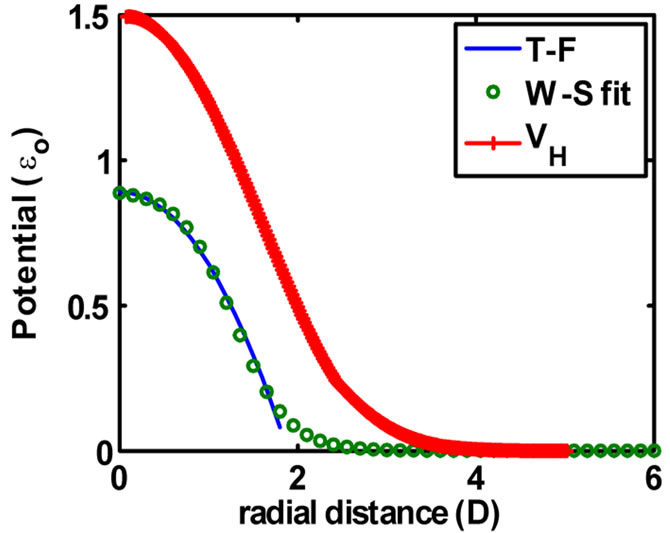
Figure 1. The Thomas Fermi aproximation to 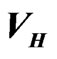 for N = 250 and
for N = 250 and 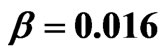 is represented by the solid line. The Woods-Saxon fit to this potential is represented by open circles, while the final non linear Hartree potential for the ground state is represented by the thick line. These potentialds are given in units of
is represented by the solid line. The Woods-Saxon fit to this potential is represented by open circles, while the final non linear Hartree potential for the ground state is represented by the thick line. These potentialds are given in units of 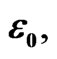 Equation (16).
Equation (16).
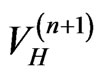 , given by
, given by 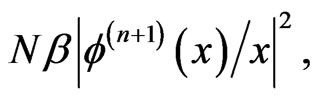 is thus obtainedand so forth. Two different methods are used in order to initiate the procedure.
is thus obtainedand so forth. Two different methods are used in order to initiate the procedure.
The first starts from the eigenfunction of the harmonic potential, in the absence of 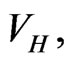 the resulting function
the resulting function
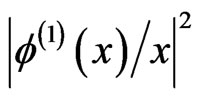 is fitted with a Woods-Saxon form, and after multiplication by
is fitted with a Woods-Saxon form, and after multiplication by 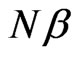 the value of
the value of 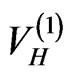 is obtained, and the process is repeated for subsequent iterations. Results with this method for the values
is obtained, and the process is repeated for subsequent iterations. Results with this method for the values
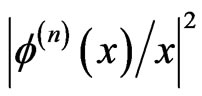 are illustrated in Figure 2 for the ground state solutions. The convergence is oscillatory, and the gap between successive values of
are illustrated in Figure 2 for the ground state solutions. The convergence is oscillatory, and the gap between successive values of 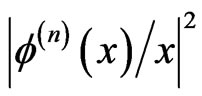 gradually decreases. The corresponding values of the ground state excitation energy are illustrated in Figure 3 by the points labelled as “H”, which also shows the oscillatory nature of the convergence. The first point, close to 1.4, corresponds to the excitation energy for the pure harmonic oscillator, which is smaller than the final excitation energy, close to 2.0. That increase is due to the repulsive nature of the Hartree potential.
gradually decreases. The corresponding values of the ground state excitation energy are illustrated in Figure 3 by the points labelled as “H”, which also shows the oscillatory nature of the convergence. The first point, close to 1.4, corresponds to the excitation energy for the pure harmonic oscillator, which is smaller than the final excitation energy, close to 2.0. That increase is due to the repulsive nature of the Hartree potential.
The second method starts the iteration with a smoothed fit to the Thomas Fermi potential, as shown by the open circles in Figure 1. The corresponding excitation energies are displayed by the open circles in Figure
Figure 2. Iterative values of 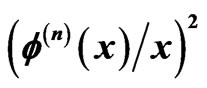 as a function of the dimensionless radial distance
as a function of the dimensionless radial distance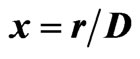 , for the ground BEC state. The iteration number
, for the ground BEC state. The iteration number 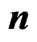 is shown in the legend. The iterations start with the ground-state solution
is shown in the legend. The iterations start with the ground-state solution 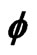 of the harmonic potential
of the harmonic potential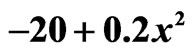 , that, in view of Equation (20) with
, that, in view of Equation (20) with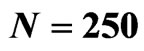 , provides the first value to
, provides the first value to  and hence of
and hence of  defined in Equation (20). The functions
defined in Equation (20). The functions  for
for  are fitted by hand with a combination of Wood-Saxon functions in order to obtain an approximation to the next Hartree potential. For each iteration the normalization of
are fitted by hand with a combination of Wood-Saxon functions in order to obtain an approximation to the next Hartree potential. For each iteration the normalization of 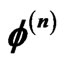 is given by
is given by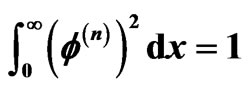 .
.
3. It is clear that the Thomas Fermi form for the Hartree potential provides a much better starting approximation for the iterations than the harmonic oscillator eigenfunction.
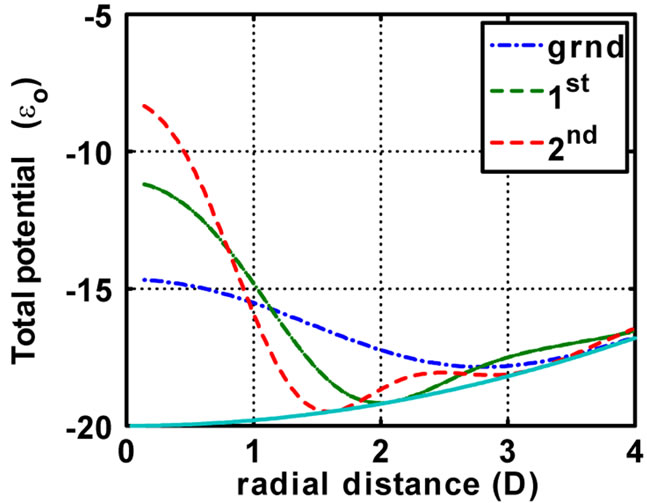
Not only the ground state of the GPE can be obtained with this iterative method starting from the fitted Thomas Fermi (TF) approximation to the Hartree potential, but with the same TF potential the higher excited states can also be obtained iteratively. The results for the ground, first and second excited states are displayed in Figure 4.
The excitation energies for the GPE lie above the values for the pure Harmonic potential well, confirming that the corresponding Hartree potentials are repulsive. It is interesting to note that for a larger value of the number 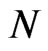 of coherent particles, the excitation energies are slightly lower. According to Equation (15) these energies are given in units of
of coherent particles, the excitation energies are slightly lower. According to Equation (15) these energies are given in units of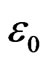 , Equation (16)
, Equation (16)

Figure 3. The ground state energies above the bottom of the attractive trap well, as a function of the number 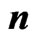 of iterations. The iterations labeled “H” were started with the eigenfunction of the Harmonic well, while the ones labelled “TF” where started with a fit to the Thomas-Fermi approximation to the Hartree potential. The conditions are the same as in Figure 2, and the energies are given in terms of
of iterations. The iterations labeled “H” were started with the eigenfunction of the Harmonic well, while the ones labelled “TF” where started with a fit to the Thomas-Fermi approximation to the Hartree potential. The conditions are the same as in Figure 2, and the energies are given in terms of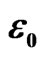 .
.
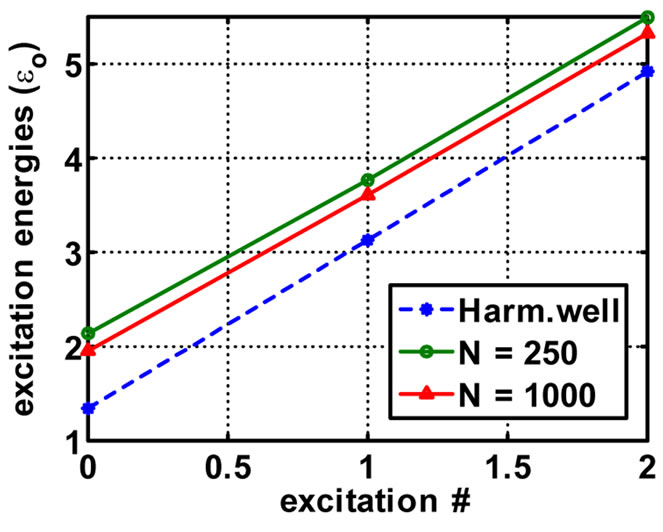
Figure 4. The final energies, in units of  of the ground, first and second excited states. The lowest set of points correspond to the harmonic well alone, and the other points are for the GP cases with N = 250 and 1000, respectively. The ground, first and second excited states are located on the x-axis at the points 0, 1, and 2, respectively.
of the ground, first and second excited states. The lowest set of points correspond to the harmonic well alone, and the other points are for the GP cases with N = 250 and 1000, respectively. The ground, first and second excited states are located on the x-axis at the points 0, 1, and 2, respectively.
The Hartree potentials, when added to the harmonic trap potential, are displayed in Figures 5 and 6 for the values of 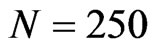 and
and , respectively. The properties of the Hartree potentials can be inferred from these graphs: as
, respectively. The properties of the Hartree potentials can be inferred from these graphs: as 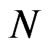 increases, these potentials increase proportionally, but the functions
increases, these potentials increase proportionally, but the functions 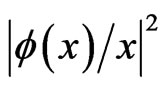 do not change significantly.
do not change significantly.
Computational Details
The calculations are done with MATLAB on a desk PC using an Intel TM2 Quad, with a CPU Q 9950, a frequency of 2.83 GHz, and a RAM of 8 GB. For the case of 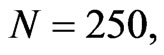 forty iterations take between 6 and 7 seconds. Table 1 of energy values for the ground and first excited states (in units of
forty iterations take between 6 and 7 seconds. Table 1 of energy values for the ground and first excited states (in units of 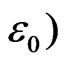 indicates the rate of convergence.
indicates the rate of convergence.
4. Summary and Conclusions
A method is presented of solving for the  partial wave function of the the Gross Pitaevskii nonlinear differential equation. A Hartree potential
partial wave function of the the Gross Pitaevskii nonlinear differential equation. A Hartree potential 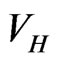 is used as a key vehicle for performing the iterations that converge for a low number of
is used as a key vehicle for performing the iterations that converge for a low number of 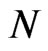 of atoms in the trap. This potential is defined as the wave-function squared times a factor proportional to the number
of atoms in the trap. This potential is defined as the wave-function squared times a factor proportional to the number 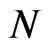 of coherent atoms
of coherent atoms
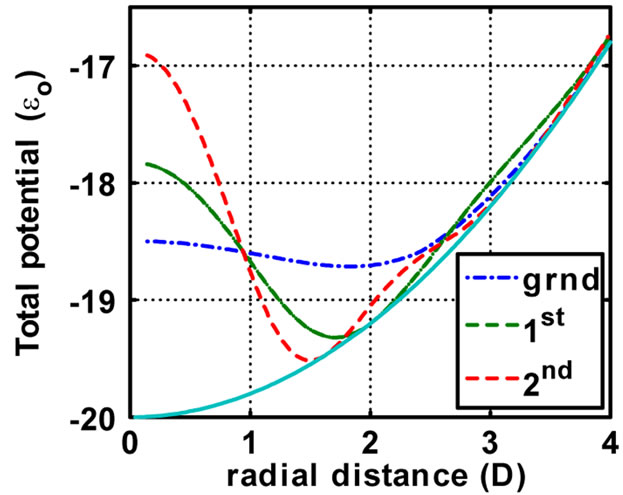
Figure 5. The sum of Harmonic and converged Hartree potentials for the ground, first and second BEC excited states, for N = 250, in units of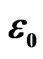 .
.
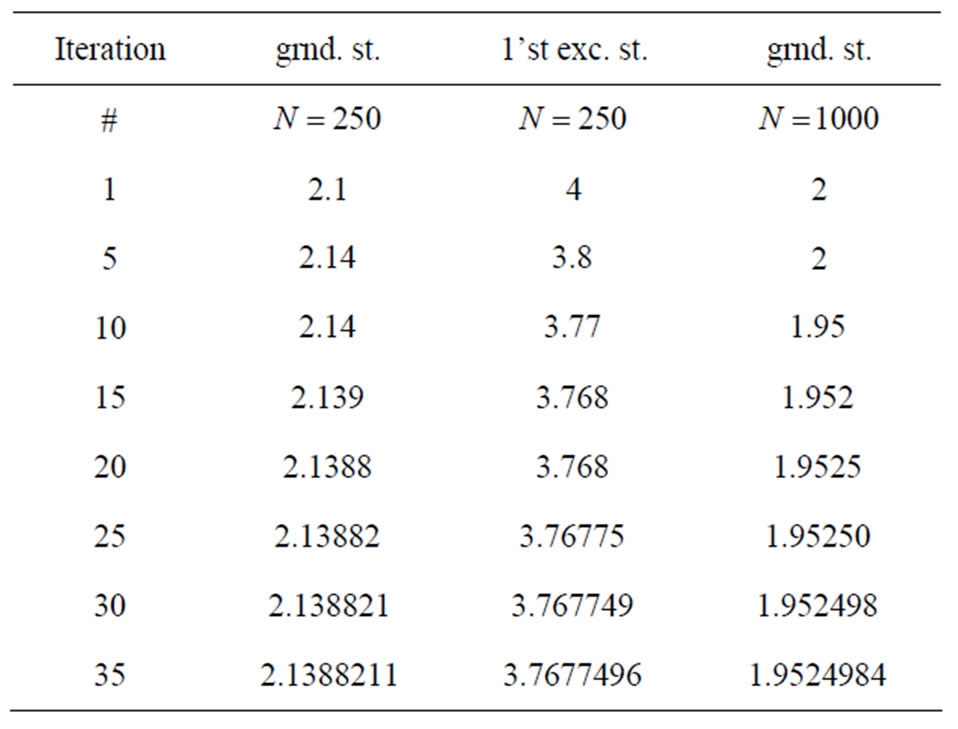
Table 1. Convergence of the excitation energies given in units described in the text.
and the (positive) scattering length. The parameters of the equation are determined from physical considerations. The Hartree potentials and binding energies are obtained for the ground, first and second excited states for  and
and 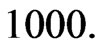 It is found that the start of the iterative process based on the Thomas-Fermi approximation to
It is found that the start of the iterative process based on the Thomas-Fermi approximation to  is more efficient than when the iterations are started from the eigenfunction of the harmonic well, as is shown in Figure 3. The iterations that lead from one
is more efficient than when the iterations are started from the eigenfunction of the harmonic well, as is shown in Figure 3. The iterations that lead from one  to the next, as described in Equation (9), converge rather slowly. After each 5 iterations the stability of the excitation energy increases approximately by one significant figure, but the computational complexity is not excessive. The knowledge of
to the next, as described in Equation (9), converge rather slowly. After each 5 iterations the stability of the excitation energy increases approximately by one significant figure, but the computational complexity is not excessive. The knowledge of 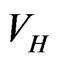 is suggestive for future applications, such as for refining a mean-field potential for nucleons in a nucleus, once the Pauli exclusion principle for the nucleons is taken into account. This approach may lead to different nuclear mean field potentials for different shells.
is suggestive for future applications, such as for refining a mean-field potential for nucleons in a nucleus, once the Pauli exclusion principle for the nucleons is taken into account. This approach may lead to different nuclear mean field potentials for different shells.
REFERENCES
- S. N. Bose, “Plancks Gesetz und Lichtquantenhypothese,” Zeitschrift für Physik, Vol. 26, No. 1, 1924, pp. 178-181. http://dx.doi.org/10.1007/BF01327326
- A. Einstein, “Quantentheorie des einatomigen idealen Gases,” Sitzungsberichte der Preußischen Akademie der Wissenschaften, 1924, p. 261.
- A. Einstein, “Quantentheorie des einatomigen idealen Gases. 2. Abhandlung,” Sitzungsberichte der Preußischen Akademie der Wissenschaften, 1925, p. 3.
- M. H. Anderson, J. R. Ensher, M. R. Matthews, C. E. Wieman and E. A. Cornell, “Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor,” Science, Vol. 269, No. 5221, 1995, pp. 198-201. http://dx.doi.org/10.1126/science.269.5221.198
- K. B. Davis, M. O. Mewes, M. R. Andrews, N. J. van Druten, D. S. Durfee, D. M. Kurn and W. Ketterle, “BoseEinstein Condensation in a Gas of Sodium Atoms,” Physical Review Letters, Vol. 75, No. 22, 1995, pp. 3969- 3973. http://dx.doi.org/10.1103/PhysRevLett.75.3969
- E. P. Gross, “Structure of a Quantized Vertex in Boson Systems,” Nuovo Cimento, Vol. 20, No. 3, 1961, pp. 454- 477. http://dx.doi.org/10.1007/BF02731494
- E. P. Gross, “Hydrodynamics of a Superfluid Condensate,” Jurnal of Mathematical Physics, Vol. 4, No. 2, 1963, pp. 195-207. http://dx.doi.org/10.1063/1.1703944
- L. P. Pitaevskii, “Dyamics of Collapse of a Confined Bose Gas,” Physics Letters A, Vol. 221, No. 1-2, 1996, pp. 14-18. http://dx.doi.org/10.1016/0375-9601(96)00538-5
- M. Edwards and K. Burnett, “Numerical Solution of the Nonlinear Schrodinger Equation for Small Samples of Trapped Neutral Atoms,” Physical Review A, Vol. 51, No. 2, 1995, pp. 1382-1386. http://dx.doi.org/10.1103/PhysRevA.51.1382
- P. A. Ruprecht, M. J. Holland, K. Burnett and M. Edwards, “Time-Dependent Solution of the Nonlinear Schrodinger Equation for Bose-Condensed Trapped Neutral Atoms,” Physical Review A, Vol. 51, No. 6, 1995, pp. 4704-4711. http://dx.doi.org/10.1103/PhysRevA.51.4704
- F. Dalfovo, S. Giorgini, L. P. Pitaevskii and S. Stingari, “Theory of Bose-Einstein Condensation in Trapped Gases,” Reviews of Modern Physics, Vol. 71, No. 3, 1999, pp. 463-512. http://dx.doi.org/10.1103/RevModPhys.71.463
- Y.-S. Choi, I. Koltracht, P. J. McKenna and N. Savytska, “Global Monotone Convergence of Newton Iteration for a Nonlinear Eigen-Problem,” Linear Algebra and Its Applications, Vol. 357, No. 1-3, 2002, pp. 217-228. http://dx.doi.org/10.1016/S0024-3795(02)00383-X
- Y.-S. Choi, J. Javanainen, I. Koltracht, M. Koštrun, P. J. McKenna and N. Savytska, “A Fast Algorithm for the Solution of the Time-Dependent Gross-Pitaevskii Equation,” Journal of Computational Physics, Vol. 190, No. 1, 2003, pp. 1-21. http://dx.doi.org/10.1016/S0021-9991(03)00235-3
- C. M. Dion and E. Cancès, “Spectral Method for the Time-Dependent Gross-Pitaevskii Equation with a Harmonic Trap,” Physical Review E, Vol. 67, No. 4, 2003, Article ID: 046706. http://dx.doi.org/10.1103/PhysRevE.67.046706
- B. I. Schneider and D. L. Feder, “Numerical Approach to the Ground and Excited States of a Bose-Einstein Condensed Gas Confined in a Completely Anisotropic Trap,” Physical Review A, Vol. 59, No. 3, 1999, pp. 2232-2242. http://dx.doi.org/10.1103/PhysRevA.59.2232
- T. Bergeman, D. L. Feder, N. L. Balazs and B. I. Schneider, “Bose Condensates in a Harmonic Trap near the Critical Temperature,” Physical Review A, Vol. 61, No. 6, 2000, Article ID: 063605. http://dx.doi.org/10.1103/PhysRevA.61.063605
- A. Gammal, T. Frederico, L. Thomio and P. Chomaz, “Atomic Bose-Einstein Condensation with Three-Body Interactions and Collective Excitations,” Journal of Physics B, Vol. 33, No. 19, 2000, p. 4053. http://dx.doi.org/10.1088/0953-4075/33/19/316
- Ž. Marojević, E. Göklü and C. Lämmerzahl, “Energy Eigenfunctions of the 1D Gross-Pitaevskii Equation,” Computer Physics Communications, Vol. 184, No. 8, 2013, pp. 1920-1930. http://dx.doi.org/10.1016/j.cpc.2013.03.023
- M. Caliari and S. Rainer, “GSGPEs: A MATLAB Code for Computing the Ground State of Systems of Gross-Pitaevskii Equations,” Computer Physics Communications, Vol. 184, No. 3, 2013, pp. 812-823. http://dx.doi.org/10.1016/j.cpc.2012.10.007
- W. Bao, D. Jaksch and P. A. Markowich, “Numerical Solution of the Gross-Pitaevskii Equation for Bose-Einstein Condensation,” Journal of Computational Physics, Vol. 187, No. 1, 2003, pp. 318-342. http://dx.doi.org/10.1016/S0021-9991(03)00102-5
- J. C. Gunn and J. M. F. Gunn, “An Exactly Soluble Hartree Problem in an External Potential,” European Journal of Physics, Vol. 9, No. 1, 1988, p. 51. http://dx.doi.org/10.1088/0143-0807/9/1/009
- J. W. Negele, “Structure of Finite Nuclei in the LocalDensity Approximation,” Physical Review, Vol. 1, No. 4, 1970, pp. 1260-1321. http://dx.doi.org/10.1103/PhysRevC.1.1260
- J. W. Negele and D. Vautherin, “Density-Matrix Expansion for an Effective Nuclear Hamiltonian,” Physical Review C, Vol. 5, No. 5, 1971, pp. 1472-1493. http://dx.doi.org/10.1103/PhysRevC.5.1472
- D. Vautherin and D. M. Brink, “Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei,” Physical Review C, Vol. 5, No. 3, 1972, pp. 626-647. http://dx.doi.org/10.1103/PhysRevC.5.626
- B. D. Esry, “Hartree-Fock Theory for Bose-Einstein Condensates and the Inclusion of Correlation Effects,” Physical Review A, Vol. 55, No. 2, 1997, pp. 1147-1159. http://dx.doi.org/10.1103/PhysRevA.55.1147
- A. Deloff, “Semi-Spectral Chebyshev Method in Quantum Mechanics,” Annals of Physics, Vol. 322, No. 6, 2007, pp. 1373-1419. http://dx.doi.org/10.1016/j.aop.2006.07.004
- L. N. Trefethen, “Spectral Methods in MATLAB,” Society for Industrial and Applied Mathematics, Philadelphia, 2000. http://dx.doi.org/10.1137/1.9780898719598
- J. P. Boyd, “Chebyshev and Fourier Spectral Methods,” 2nd Revised Edition, Dover Publications, Mineola, 2001.
- R. A. Gonzales, J. Eisert, I. Koltracht, M. Neumann and G. Rawitscher, “Integral Equation Method for the Continuous Spectrum Radial Schroedinger Equation,” Journal of Computational Physics, Vol. 134, No. 1, 1997, pp. 134-149. http://dx.doi.org/10.1006/jcph.1997.5679
- R. A. Gonzales, S.-Y. Kang, I. Koltracht and G. Rawitscher, “Integral Equation Method for Coupled Schrödinger Equations,” Journal of Computational Physics, Vol. 153, No. 1, 1999, pp. 160-202. http://dx.doi.org/10.1006/jcph.1999.6272
- G. H. Rawitscher, B. D. Esry, E. Tiesinga, J. P. Burke Jr. and I. Koltracht, “Comparison of Numerical Methods for the Calculation of Cold Atom Collisions,” Journal of Chemical Physics, Vol. 111, No. 23, 1999, pp. 10418- 104226. http://dx.doi.org/10.1063/1.480431
- G. H. Rawitscher, C. Merow, M. Nguyen and I. Simbotin, “Resonances and Quantum Scattering for the Morse Potential as a Barrier,” American Journal of Physics, Vol. 70, No. 9, 2002, pp. 935-944. http://dx.doi.org/10.1119/1.1485714
- G. H. Rawitscher, S. Y. Kang and I. Koltracht, “A Novel Method for the Solution of the Schrödinger Equation in the Presence of Exchange Terms,” Journal of Chemical Physics, Vol. 118, No. 20, 2003, pp. 9149-9157. http://dx.doi.org/10.1063/1.1567254
- G. Rawitscher and W. Gloeckle, “Integrals of the TwoBody T Matrix in Configuration Space,” Physical Review, Vol. A 77, No. 1, 2008, Article ID: 012707. http://dx.doi.org/10.1103/PhysRevA.77.012707
- G. Rawitscher, “Calculation of the Two-Body Scattering K-Matrix in Configuration Space by an Adaptive Spectral Method,” Journal of Physics A: Mathematical and Theoretical, Vol. 42, No. 1, 2009, Article ID: pp. 015201. http://dx.doi.org/10.1088/1751-8113/42/1/015201
- G. Rawitscher and J. Liss, “The Vibrating Inhomogeneous String,” American Journal of Physics, Vol. 79, No. 4, 2011, pp. 417-427. http://dx.doi.org/10.1119/1.3534837
- G. H. Rawitscher, “Solution of the Schroedinger Equation Containing a Perey-Buck Nonlocality,” Nuclear Physics A, Vol. 886, 2012, pp. 1-16. http://dx.doi.org/10.1016/j.nuclphysa.2012.05.001
- G. Rawitscher, “Iterative Evaluation of the Effect of Long-Range Potentials on the Solution of the Schrödinger Equation,” Physical Review A, Vol. 87, No. 3, 2013, Article ID: 032708. http://dx.doi.org/10.1103/PhysRevA.87.032708
- G. Rawitscher and I. Koltracht, “An Economical Method to Calculate Eigenvalues of the Schrödinger Equation,” European Journal of Physics, Vol. 27, No. 5, 2006, p. 1179. http://dx.doi.org/10.1088/0143-0807/27/5/017
- G. Rawitscher, “Iterative Solution of Integral Equations on a Basis of Positive Energy Sturmian Functions,” Physical Review E, Vol. 85, No. 2, 2012, Article ID: 026701. http://dx.doi.org/10.1103/PhysRevE.85.026701
- G. Rawitscher and I. Koltracht, “Description of an Efficient Numerical Spectral Method for Solving the Schroedinger Equation,” Computing in Science and Engineering, Vol. 7, 2005, p. 58.
- G. Rawitscher, “Applications of a Numerical Spectral Expansion Method to Problems in Physics: A Retrospective,” In: T. Hempfling, Ed., Operator Theory, Advances and Applications, Vol. 203, Birkäuser Verlag, Basel, 2009, pp. 409-426.
- S. G. Cooper and R. S. Mackintosh, “Energy Dependent Potentials Determined by Inversion: The p+α Potential Up to 65 MeV,” Physical Review C, Vol. 54, No. 6, 1996, pp. 3133-3152. http://dx.doi.org/10.1103/PhysRevC.54.3133
- K. Amos, L. Canton, G. Pisent, J. P. Svenne and D. van der Knijff, “An Algebraic Solution of the Multichannel Problem Applied to Low Energy Nucleon—Nucleus Scattering,” Nuclear Physics A, Vol. 728, No. 1-2, 2003, pp. 65-95. http://dx.doi.org/10.1016/j.nuclphysa.2003.08.019
- M. I. Jaghoub and G. H. Rawitscher, “Evidence of Nonlocality Due to a Gradient Term in the Optical Model,” Nuclear Physics A, Vol. 877, 2012, pp. 59-69. http://dx.doi.org/10.1016/j.nuclphysa.2011.12.004
- S. K. Adhikari, “Numerical Study of the Spherically Symmetric Gross-Pitaevskii Equation in Two Space Dimensions,” Physical Review E, Vol. 62, No. 2, 2000, pp. 2937-2944. http://dx.doi.org/10.1103/PhysRevE.62.2937
- S. K. Adhikari, “Stability and Collapse of a Coupled Bose-Einstein Condensate,” Physics Letters A, Vol. 281, No. 4, 2001, pp. 265-271. http://dx.doi.org/10.1016/S0375-9601(01)00132-3
- F. Dalfovo and S. Stringari, “Bosons in Anisotropic Traps: Ground State and Vortices,” Physical Review A, Vol. 53, No. 4, 1996, pp. 2477-2485. http://dx.doi.org/10.1103/PhysRevA.53.2477
- G. Baym and C. J. Pethick, “Ground-State Properties of Magnetically Trapped Bose-Condensed Rubidium Gas,” Physical Review Letters, Vol. 76, No. 1, 1996, pp. 6-9. http://dx.doi.org/10.1103/PhysRevLett.76.6
NOTES
*PACS numbers: 02.70.-c; 03.75.Gg; 67.85.-d.