Applied Mathematics
Vol.4 No.10(2013), Article ID:37486,10 pages DOI:10.4236/am.2013.410192
Matrix Measure with Application in Quantized Synchronization Analysis of Complex Networks with Delayed Time via the General Intermittent Control*
Department of Mathematics, Heze University, Heze, China
Email: qunli-zhang@126.com
Copyright © 2013 Qunli Zhang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 19, 2013; revised August 19, 2013; accepted August 26, 2013
Keywords: Matrix Measure; The General Intermittent Control; Exponential Stability; Quantized Synchronization; Complex Networks
ABSTRACT
This paper concerned with the quantized synchronization analysis problem. The scope of state vectors of dynamic systems, based on the matrix measure, is estimated. By using the general intermittent control, some simple yet generic criteria are derived ensuring the exponential stability of dynamic systems. Then, both the general intermittent networked controller and the quantized parameters can be designed, which guarantee that the nodes of the complex network are synchronized. Finally, simulation examples are given to illustrate the effectiveness and feasibility of the proposed method.
1. Introduction
Since its origins in the work of Fujisaka and Yamada [1- 3], Afraimovich, Verichev, and Rabinovich [4], and Pecora and Carrol [5], the study of synchronization of chaotic systems [6-19] is of great practical significance and has received great interest in recent years. In the above literatures, the approach applied to stability analysis is basically the Lyapunov’s method. As we all know, the construction of a proper Lyapunov function usually becomes very skillful, and the Lyapunov’s method does not specifically describe the convergence rate near the equilibrium point of the system. Hence, there is little compatibility among all of the stability criteria obtained so far.
The concept named the matrix measur [20-25] has been applied to the investigation of the existence, uniqueness or stability analysis of the equilibrium. Intermittent control [26-29] has been used for a variety of purposes in engineering fields such as manufacturing, transportation, air-quality control and communication. A wide variety of synchronization or stabilization using the periodically intermittent control method has been studied (see [27- 32]). Compared with continuous control methods [7-14], intermittent control is more efficient when the system output is measured intermittently rather than continuously. All of intermittent control and impulsive control are belong to switch control. But the intermittent control is different from the impulsive control, because impulsive control is activated only at some isolated moments, namely it is of zero duation, while intermittent control has a nonzero control width.
But it should be mentioned that the influence caused by quantization has not been considered in their results. It is well known that in modern networked systems, quantization is an indispensable step that aims at saving limited bandwidth and energy consumption [33]. Quantization cannot be avoided in the digital control setting, and it is indeed a natural way to be inserted into the control design complexity constraints of the controller and communication constraints of the channels which connect the controller and the plant [34]. The important application of quantization in real world can be found in humanmachine interaction, for instance, see [35-37]. Therefore, it is essential and important to investigate the exponential quantized synchronization problem of networks with mixed delays by periodically intermittent control.
Our interest focuses on the class of commonly intermittent controller with time duration, where the control is activated in certain nonzero time intervals, and is off in other time intervals. A special case of such a control law is of the form
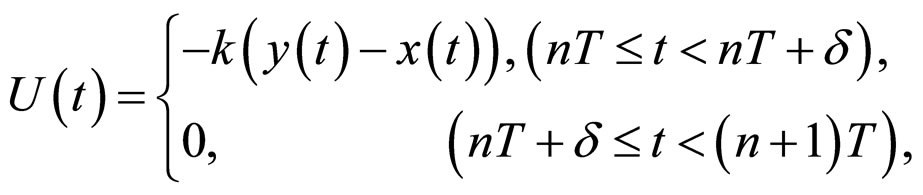
where 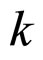 denotes the control strength,
denotes the control strength,  denotes the switching width, and T denotes the control period. The general intermittent controller
denotes the switching width, and T denotes the control period. The general intermittent controller
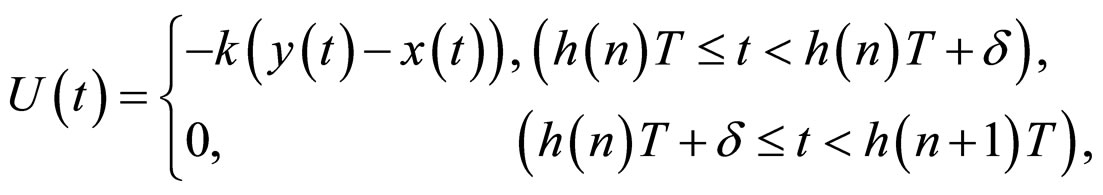
where 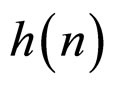 is a strictly monotone increasing function on
is a strictly monotone increasing function on![]() , has been studied (see [38]).
, has been studied (see [38]).
Moreover, a logarithmic quantizer 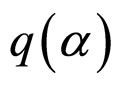 has quantization levels give by
has quantization levels give by
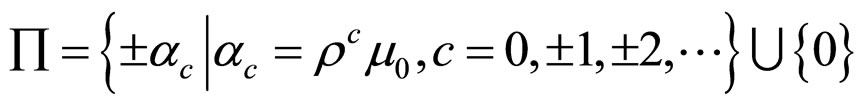 where the quantization densitie is
where the quantization densitie is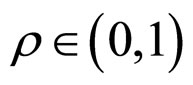 , and the scaling parameter is
, and the scaling parameter is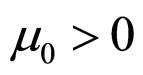 . Then, the quantizer
. Then, the quantizer 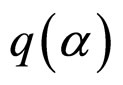 is defined as follow
is defined as follow
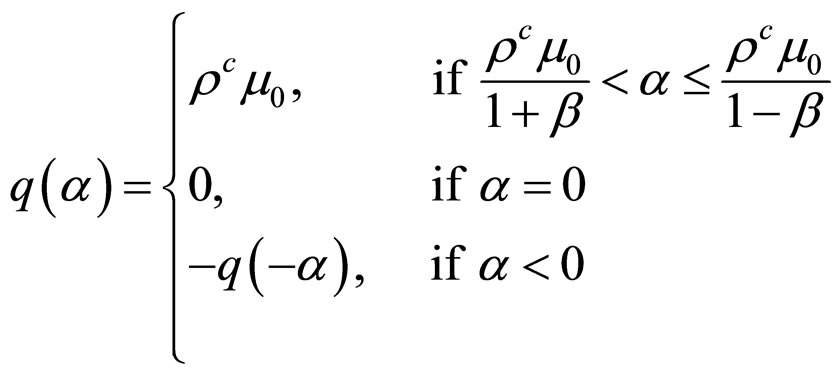 (1)
(1)
where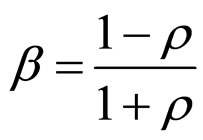 . Based on (1), it is obvious that
. Based on (1), it is obvious that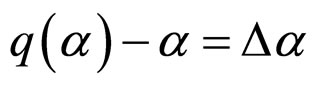 and the quantization synchronization error
and the quantization synchronization error  (see [39-43]).
(see [39-43]).
In this paper, based on matrix measure and Gronwall inequality, the general intermittent controller
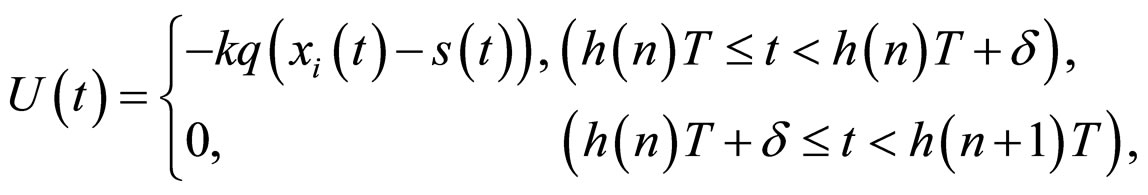
where  is a strictly monotone increasing function on
is a strictly monotone increasing function on![]() ,
,
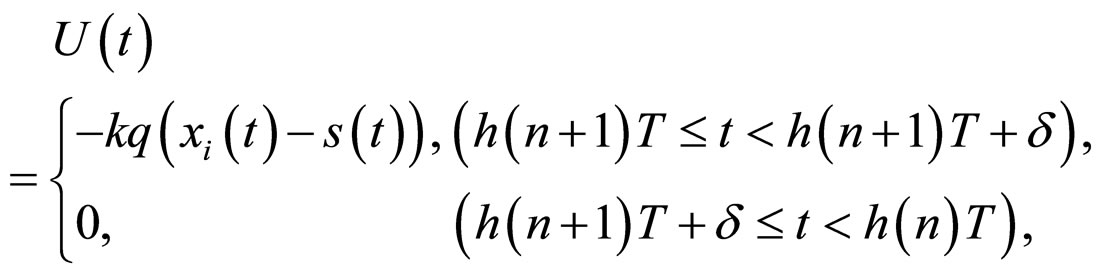
where  is a strictly monotone decreasing function on
is a strictly monotone decreasing function on![]() , is designed. Then the sufficient yet generic criteria for synchronization of complex networks with and without delayed item are obtained.
, is designed. Then the sufficient yet generic criteria for synchronization of complex networks with and without delayed item are obtained.
This paper is organized as follows. In Section 2, some necessary background materials are presented. In Section 3, the state vectors scope estimated via matrix measure are formulated. Section 4 deals with the quantized synchronization. The theoretical results are applied to complex networks, and numerical simulations of delayed neural network systems are shown in this section. Finally, some concluding remarks are given in Section 5.
2. Preliminaries
Let  be a Banach space endowed with the l2-norm
be a Banach space endowed with the l2-norm
 , i.e.
, i.e.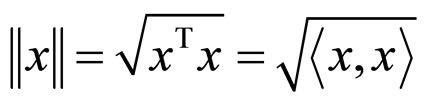 , where
, where  is inner product, and
is inner product, and  be a open subset of
be a open subset of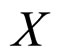 . We consider the following system:
. We consider the following system:
 (2)
(2)
where 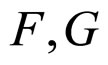 are nonlinear operators defined on
are nonlinear operators defined on , and
, and 
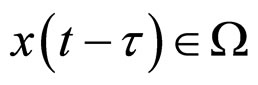 , and
, and ![]() is a time-delayed positive constant, and
is a time-delayed positive constant, and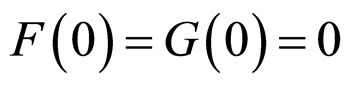 .
.
Definition 1 [12,26,28,44] System (2) is called to be exponentially stable on a neighborhood  of the equilibrium point, if there exist constants
of the equilibrium point, if there exist constants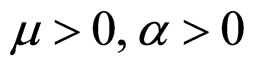 , such that
, such that
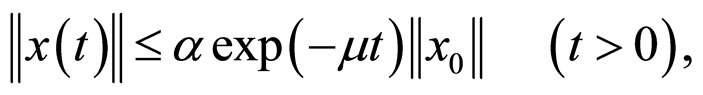
where 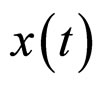 is any solution of (2) initiated from
is any solution of (2) initiated from 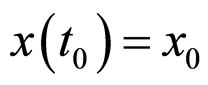 .
.
Definition 2 [20-25] Suppose that 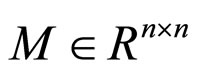 is a matrix. Let
is a matrix. Let 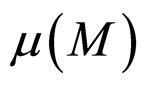 be the matrix measure of
be the matrix measure of 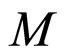 defined as
defined as
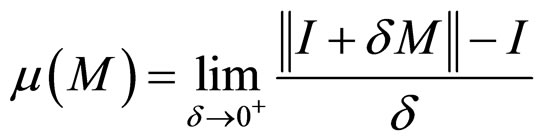 where
where 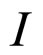 is the identity matrix.
is the identity matrix.
Lemma [20-25] The matrix measure 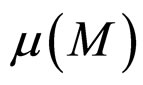 is well defined for the l2-norm
is well defined for the l2-norm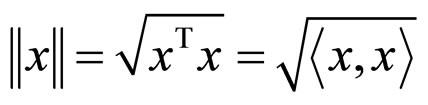 , the induced matrix measure is given by
, the induced matrix measure is given by
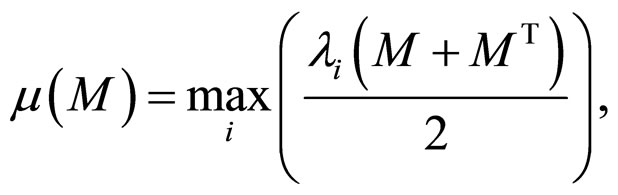
where  denotes all eigenvalues of the matrix
denotes all eigenvalues of the matrix .
.
3. Estimating the Scope of the State Vectors
We consider the following system:
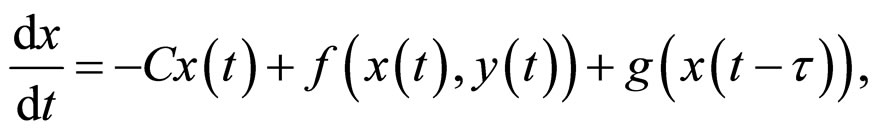 (3)
(3)
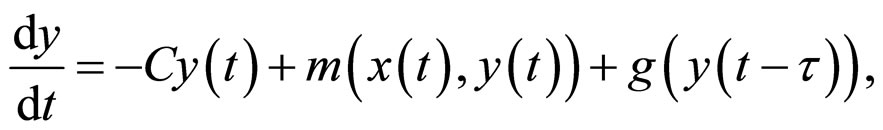 (4)
(4)
where 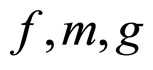 are nonlinear operators defined on
are nonlinear operators defined on , and
, and 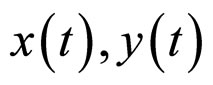
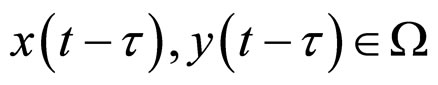 , and
, and ![]() is a timedelayed positive constant, and
is a timedelayed positive constant, and 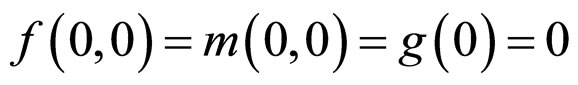 .
.
Theorem 1 For any 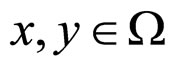 in the system (3), (4), if the operator
in the system (3), (4), if the operator 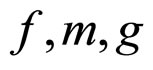 satisfies
satisfies
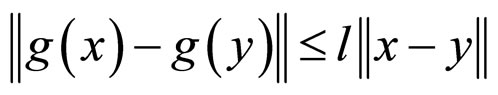 , (5)
, (5)
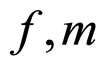 is bound, where
is bound, where 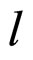 is a positive constant. The solutions
is a positive constant. The solutions 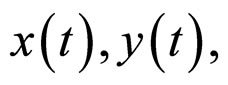 initiated from
initiated from 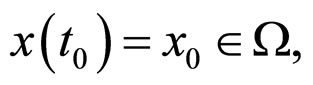
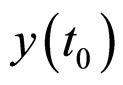
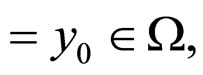 of the system (3) and (4) satisfy
of the system (3) and (4) satisfy
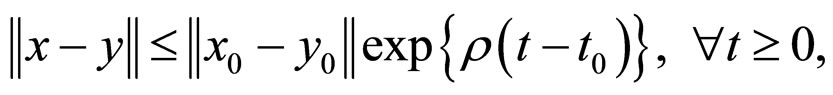
where 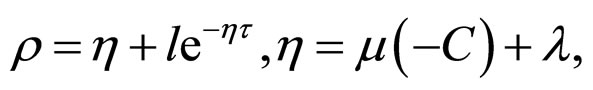
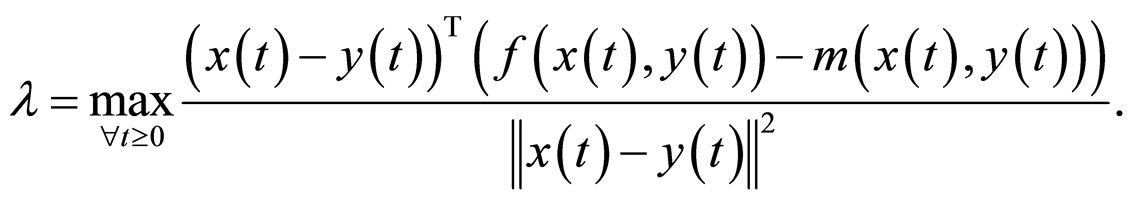
Proof Under the initial conditions 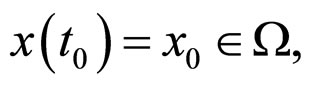
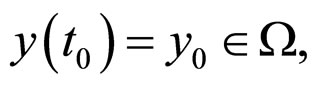 we have
we have
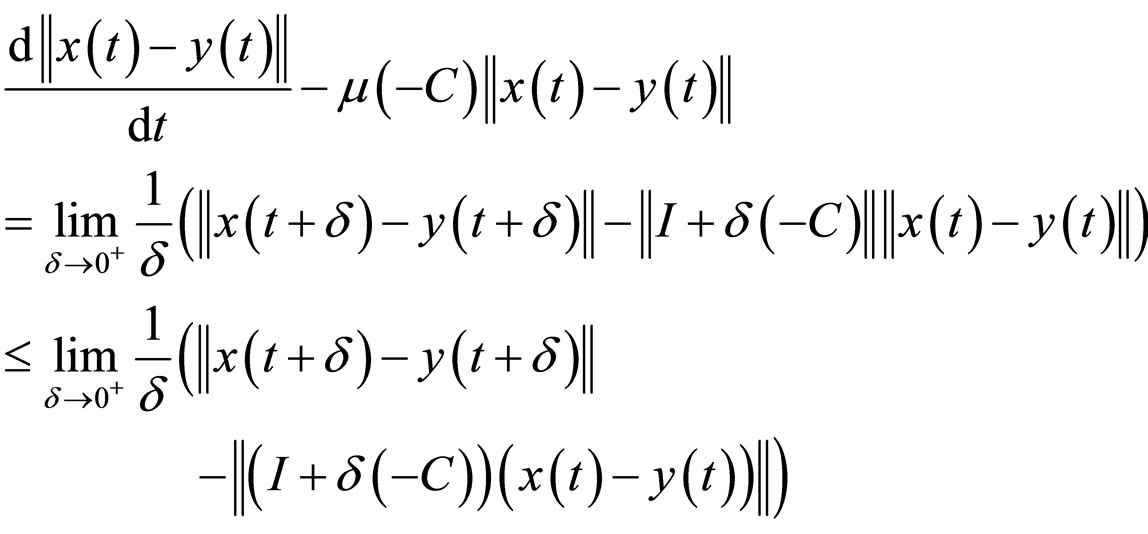
for any .
.
Let 
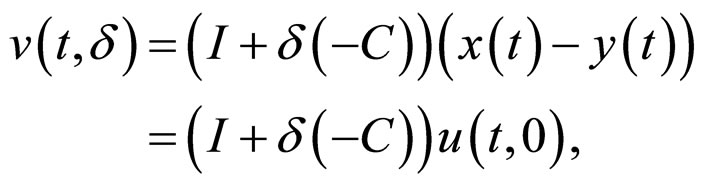
then
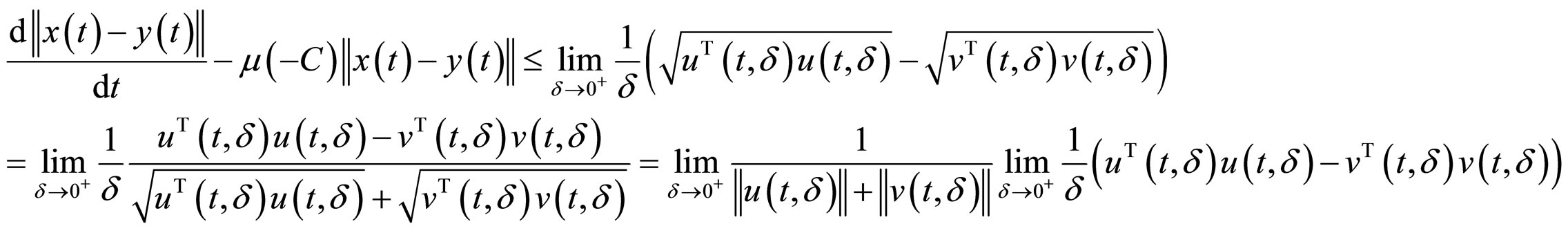

Using Cauchy-Bunyakovsky Inequality and condition (5), we obtain

So
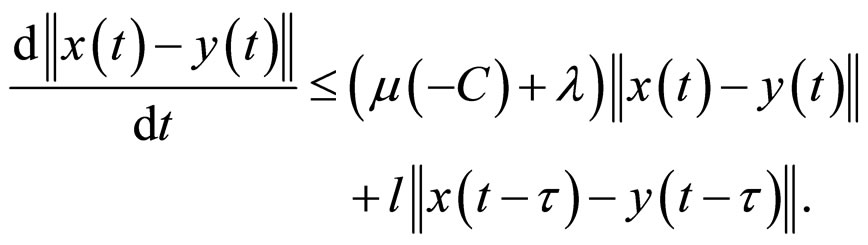
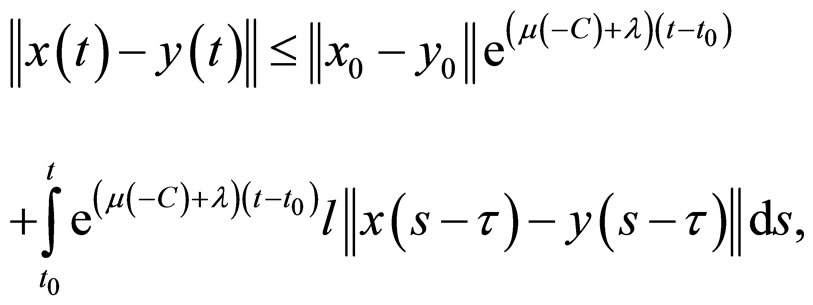
Namely
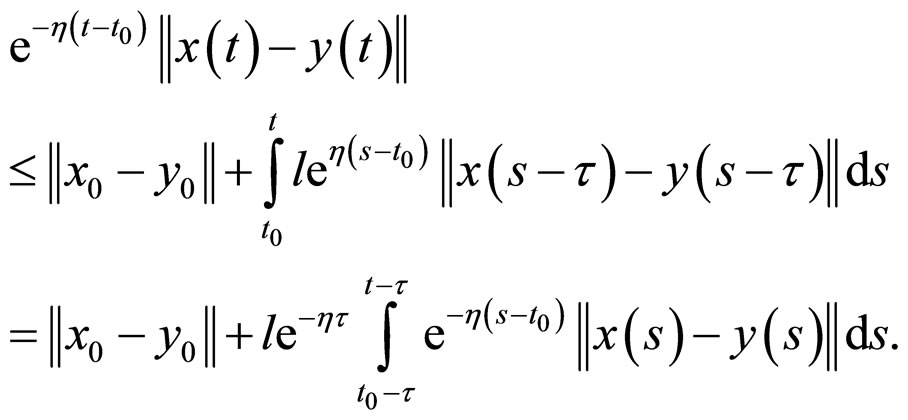
Using the Gronwall inequality [45,46], we have
![]() that is
that is

4. Synchronization via the General Intermittent Control and Examples
Consider a delayed complex dynamical network consisting of 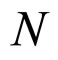 linearly coupled nonidentical nodes described by
linearly coupled nonidentical nodes described by
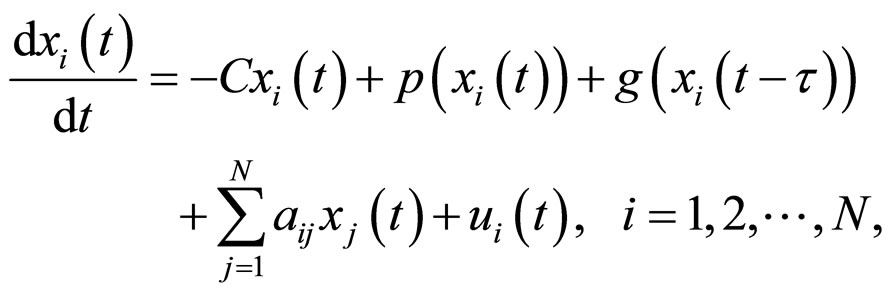 (6)
(6)
where 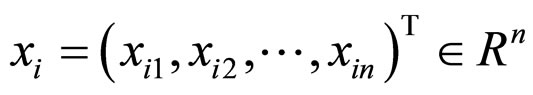 is the state vector of the ith node,
is the state vector of the ith node, 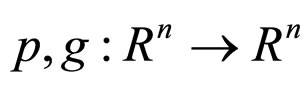 are nonlinear vector functions,
are nonlinear vector functions, 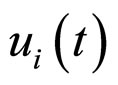 is the control input of the ith node, and
is the control input of the ith node, and ![]() is the coupling figuration matrix representing the coupling strength and the topological structure of the complex networks, in which
is the coupling figuration matrix representing the coupling strength and the topological structure of the complex networks, in which  if there is connection from node i to node
if there is connection from node i to node 
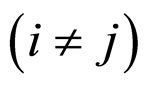 , and is zero, otherwise, and the constraint
, and is zero, otherwise, and the constraint
 , is set.
, is set.
A complex network is said to achieve asymptotical synchronization if
 , (7)
, (7)
where 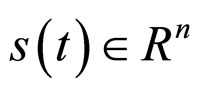 is a solution of a real target node, satisfying
is a solution of a real target node, satisfying
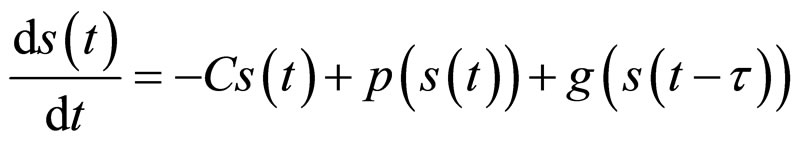 .
.
For our synchronization scheme, let us define error vector and control input 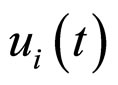 as follows, respectively:
as follows, respectively:
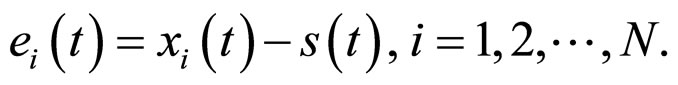 When
When 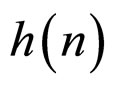 is a strictly monotone increasing function on n with
is a strictly monotone increasing function on n with ![]()
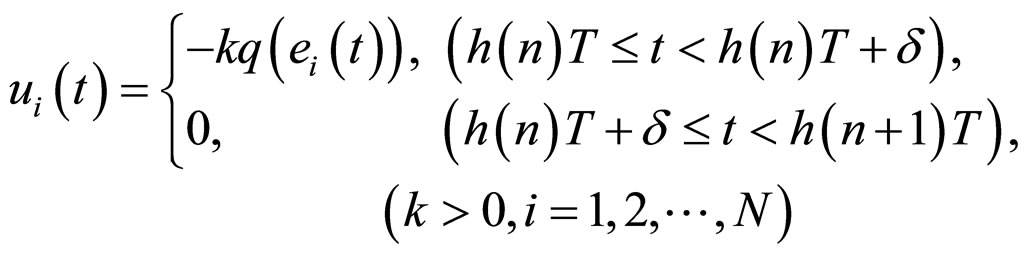 (8)
(8)
When  is a strictly monotone decreasing function on n with
is a strictly monotone decreasing function on n with 
![]()
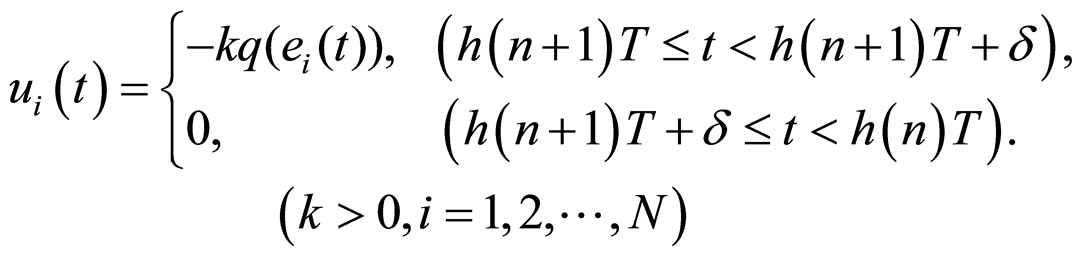 (9)
(9)
In this work, the goal is to design suitable function  and parameters
and parameters![]() ,
, ![]() and
and 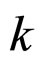 satisfying the condition (7). The error system follows from the expression (6), (8) and (9)
satisfying the condition (7). The error system follows from the expression (6), (8) and (9)
 (10)
(10)
When  is a strictly monotone increasing function on
is a strictly monotone increasing function on ![]() with
with 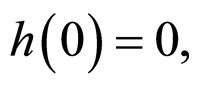
![]() we obtain the following result:
we obtain the following result:
Theorem 2 Suppose that the operator ![]() in the network (6) satisfies condition (5), and
in the network (6) satisfies condition (5), and 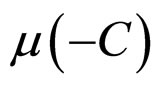 is defined as Definition 2,
is defined as Definition 2,
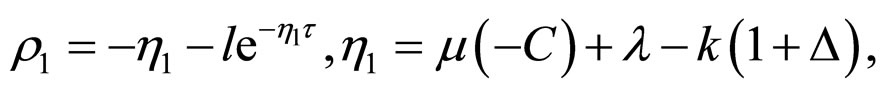
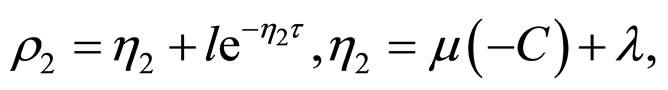 where the constant
where the constant

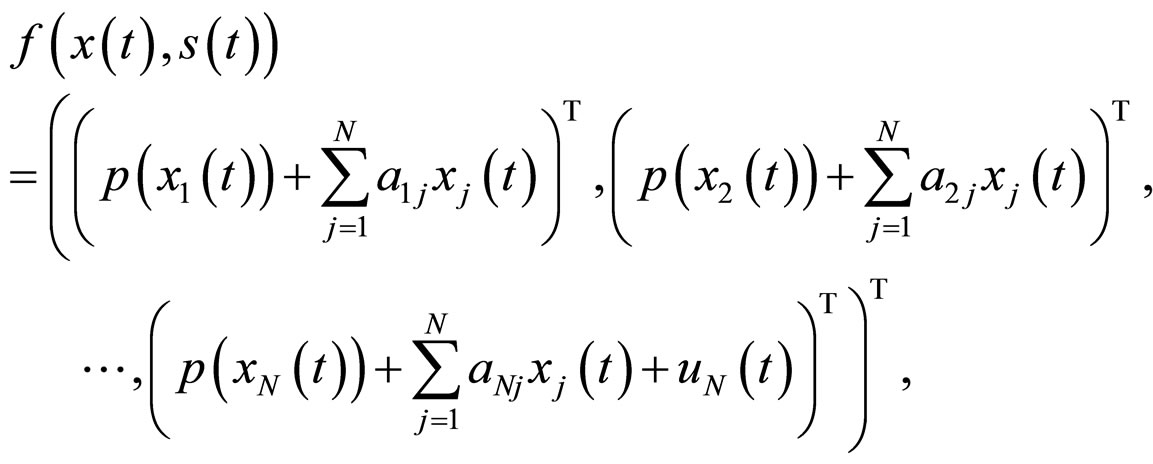
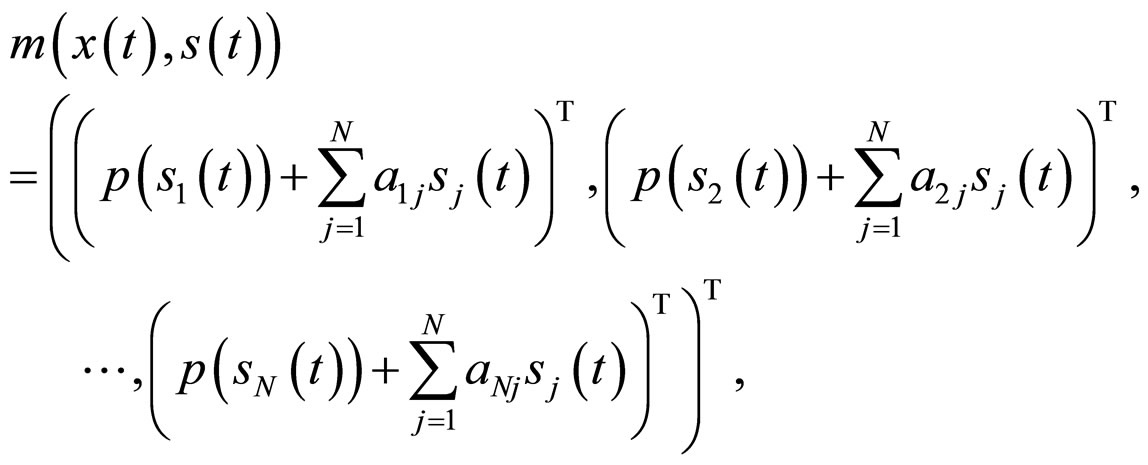
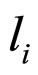

 satisfies
satisfies 
Then the synchronization of network (6) is achieved if the parameters![]() ,
, ![]() ,
, 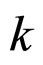 ,
, ![]() and
and ![]() satisfy
satisfy
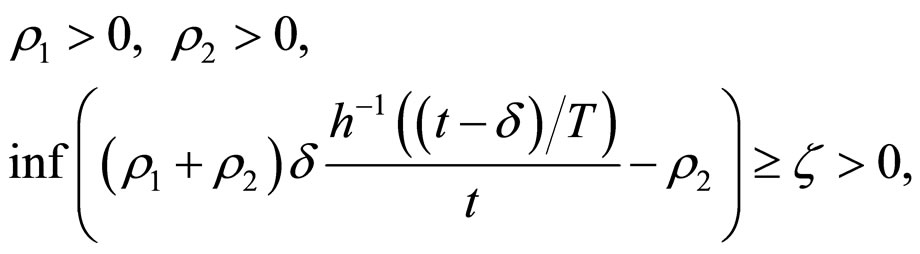 (11)
(11)
where 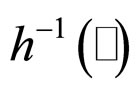 is the inverse function of the function
is the inverse function of the function 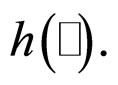
Proof From Theorem 1, the following conclusion is valid:
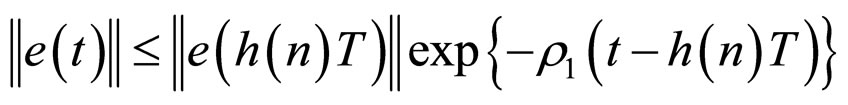 (12)
(12)
for any ;
;
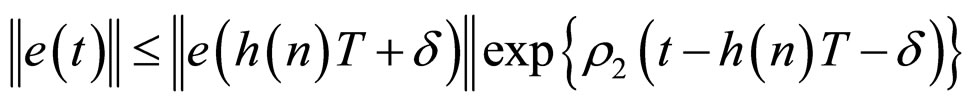 (13)
(13)
for any .
.
In the following, we use mathematical induction to prove, for any nonnegative integer![]() ,
,
 (14)
(14)
1) For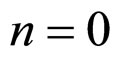 , from (12) and (13), we can see that
, from (12) and (13), we can see that
a) For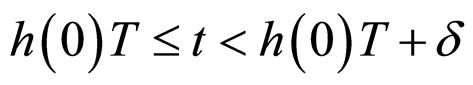 ,
,
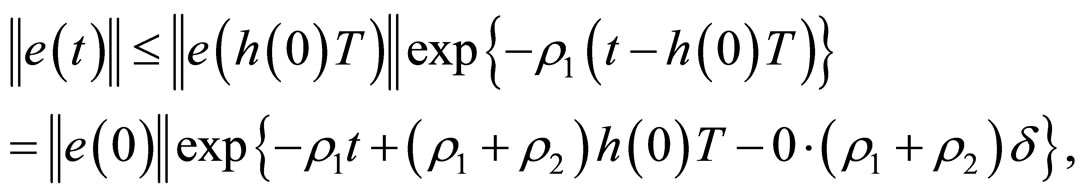
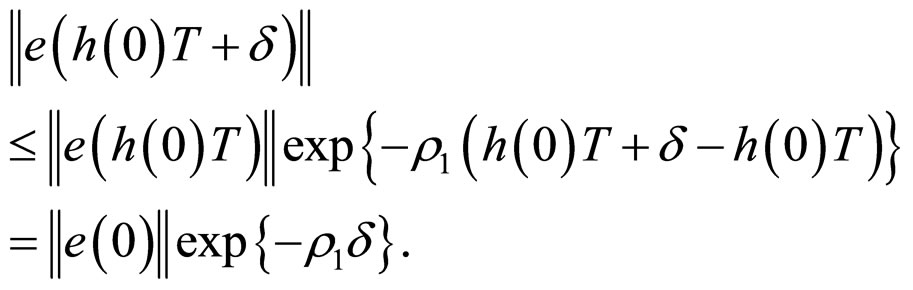
b) For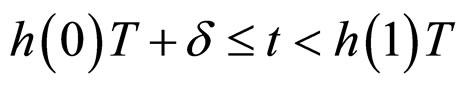 ,
,
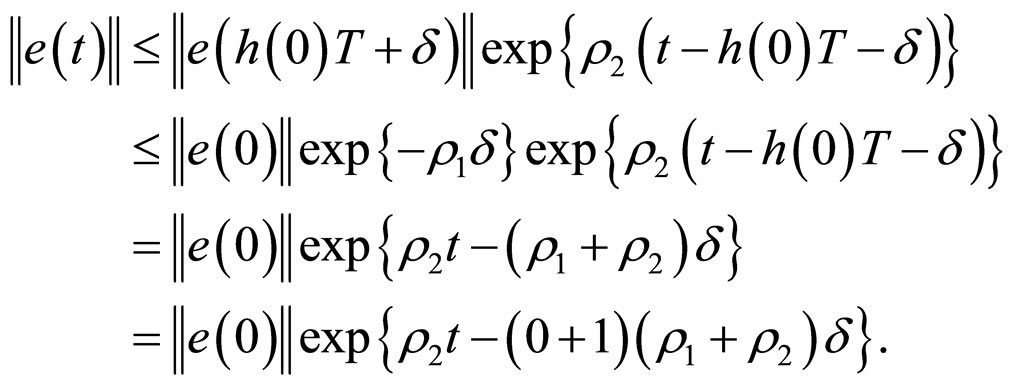
So (14) is true for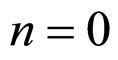 .
.
2) Assume that (14) is true for all , that is
, that is
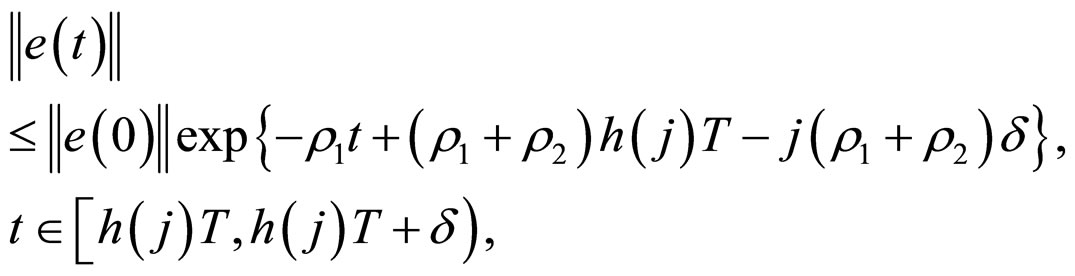
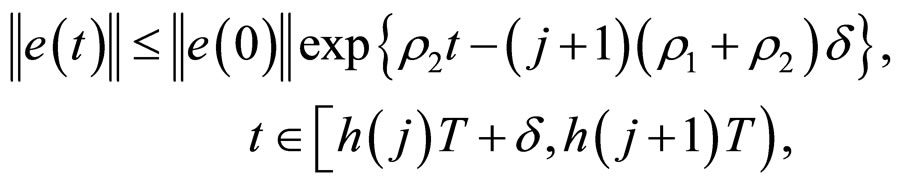
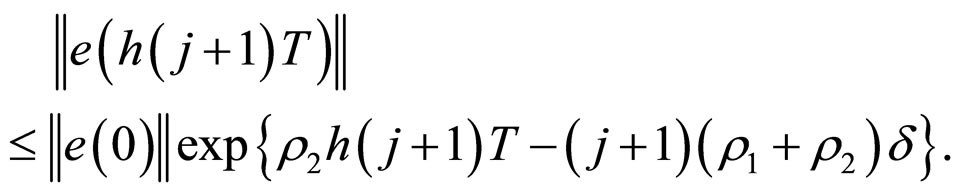
We will prove (14) is also true when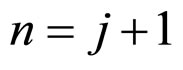 . From (12) and (13), it is easy to see that
. From (12) and (13), it is easy to see that
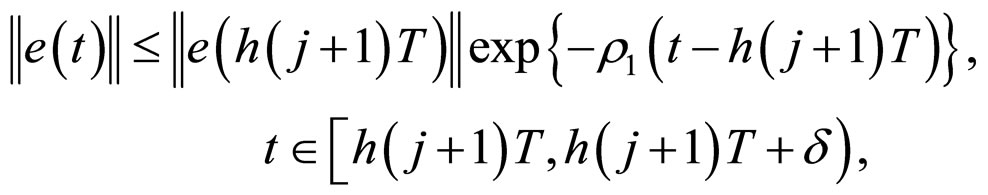
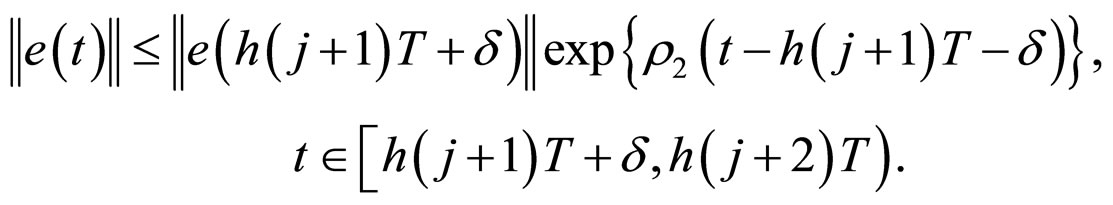
Then, for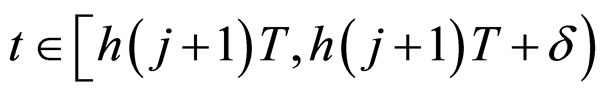 , we have
, we have

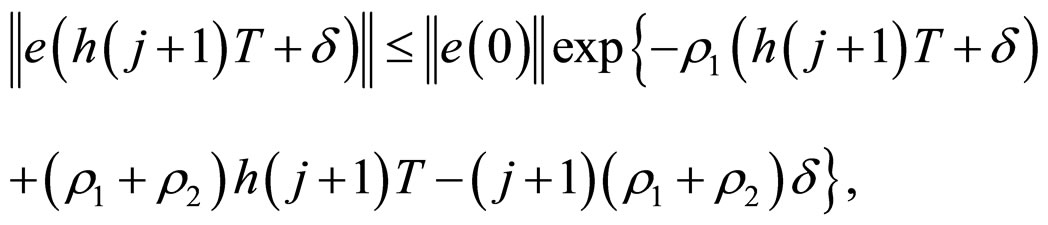
and also, for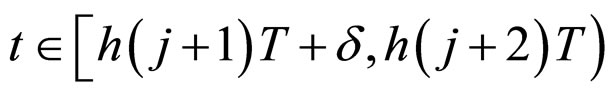 , it follows from above results that
, it follows from above results that
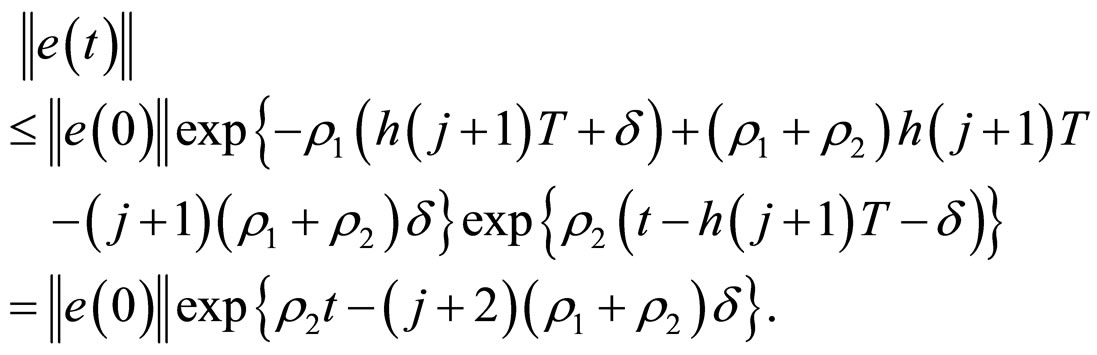
From above discussion, we can see that the (14) is always correct for any nonnegative integer![]() .
.
When 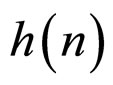 is a strictly monotone increasing function on
is a strictly monotone increasing function on ![]() and
and , it is easy to obtain
, it is easy to obtain 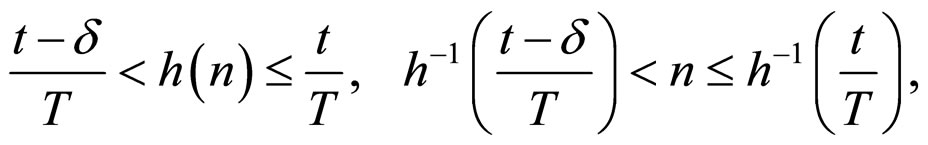
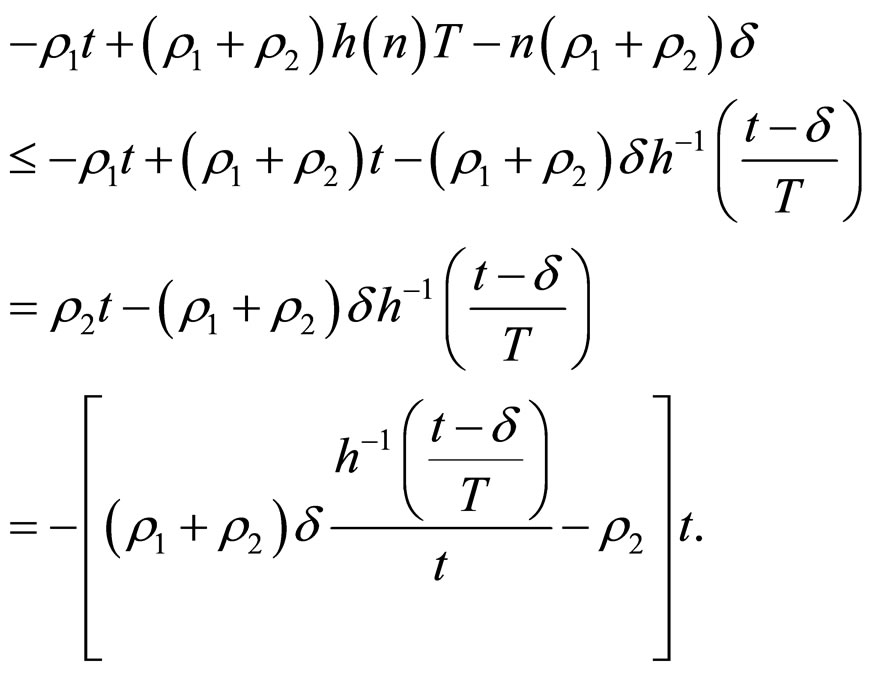
When  is a strictly monotone increasing function on
is a strictly monotone increasing function on ![]() and
and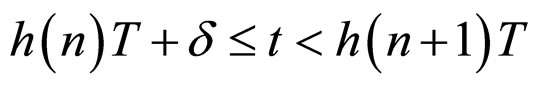 , it follows that
, it follows that
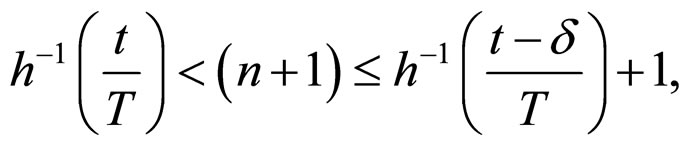
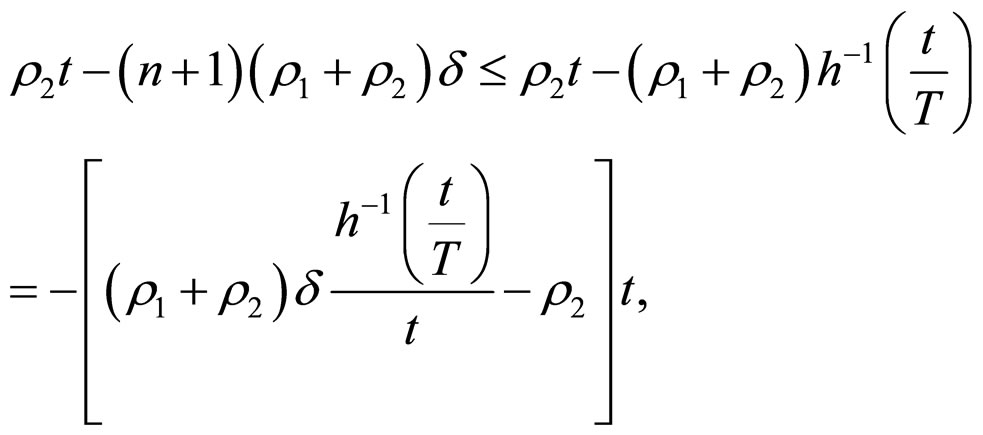
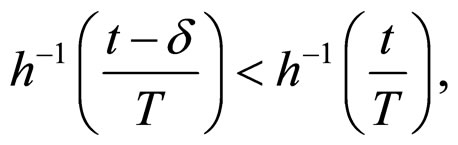
then
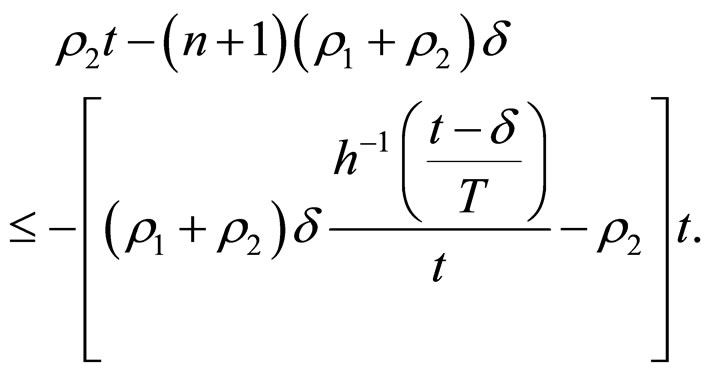
Therefore
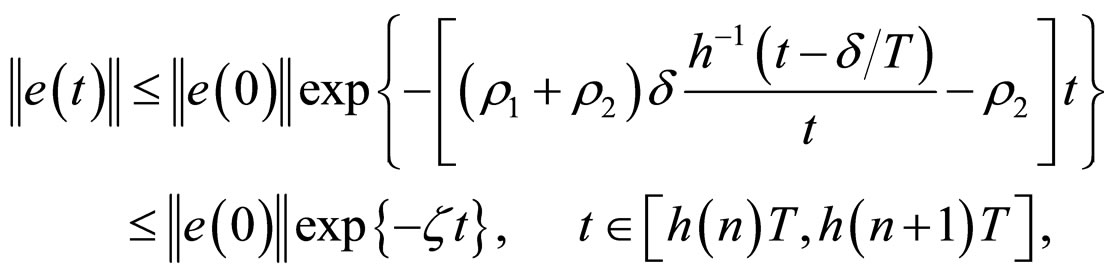
when 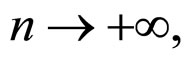

 is obtained under the condition (11). So the synchronization of the network (6) is achieved.
is obtained under the condition (11). So the synchronization of the network (6) is achieved.
When 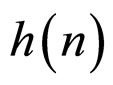 is a strictly monotone decreasing function on
is a strictly monotone decreasing function on ![]() with
with![]() , we obtain the following result:
, we obtain the following result:
Theorem 3 Suppose that the operator ![]() in the network (6) satisfies condition (5), and
in the network (6) satisfies condition (5), and 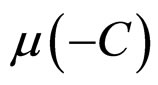 is defined as Definition 2,
is defined as Definition 2, 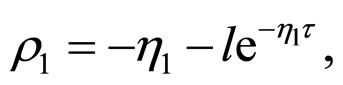
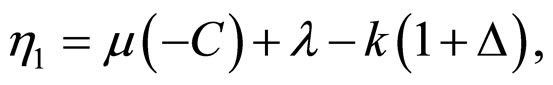
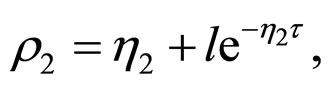
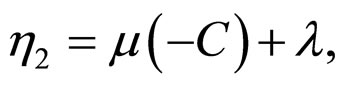
where the constant
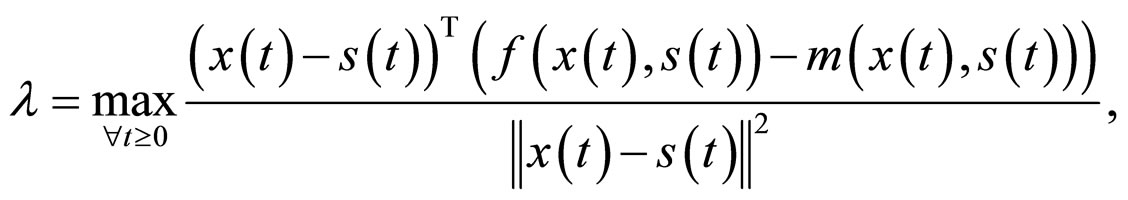
![]() are the same as Theorem 2. So the synchronization of networks (6) is achieved if the parameters
are the same as Theorem 2. So the synchronization of networks (6) is achieved if the parameters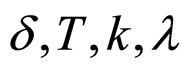 , and
, and ![]() satisfy
satisfy
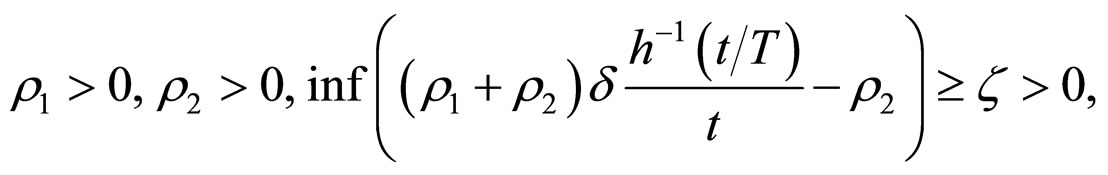 (15)
(15)
where 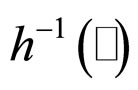 is the inverse function of the function
is the inverse function of the function 
Proof From Theorem 1, the following conclusion is valid:
 (16)
(16)
for any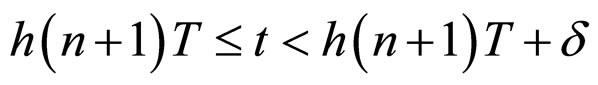 ;
;
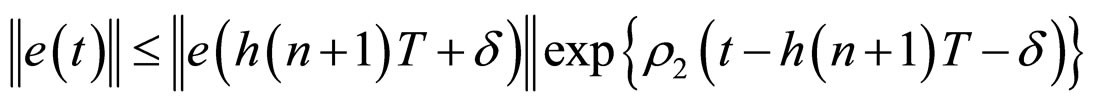 (17)
(17)
for any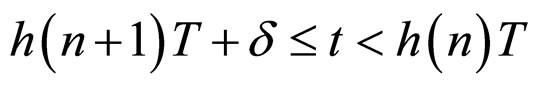 .
.
From (16) and (17), imitating Theorem 2,we can prove
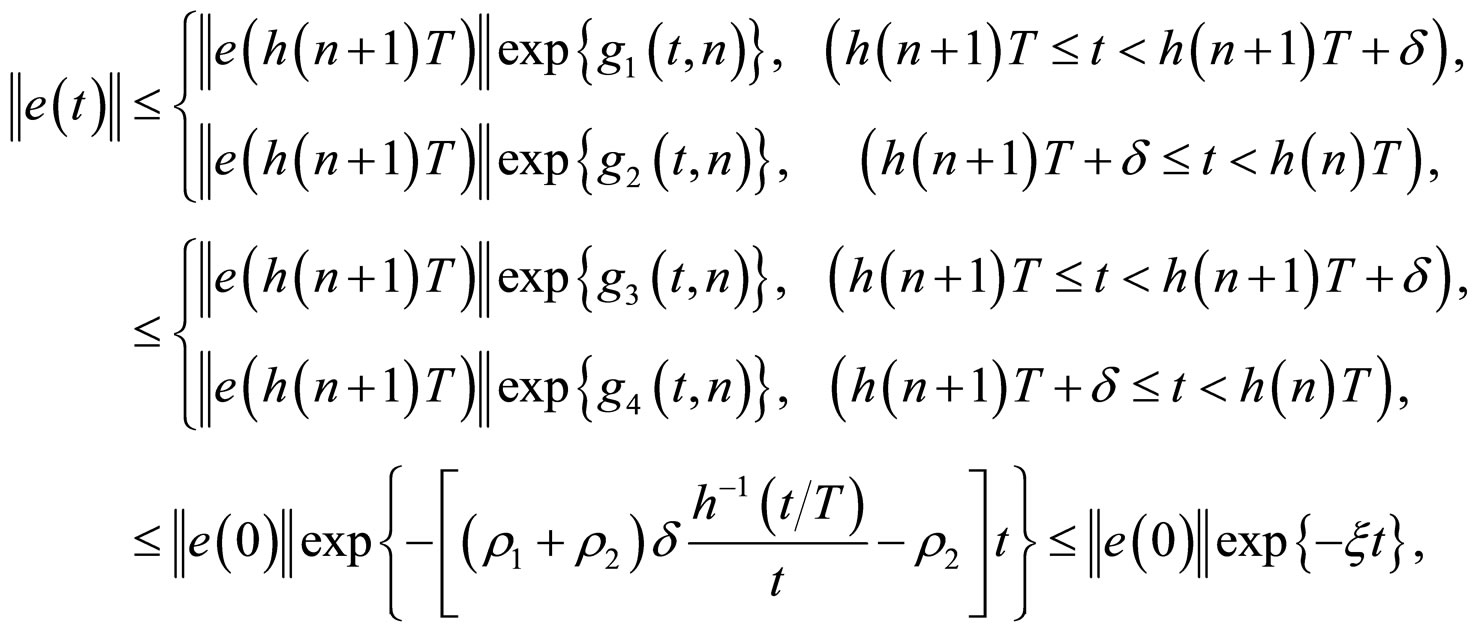
where
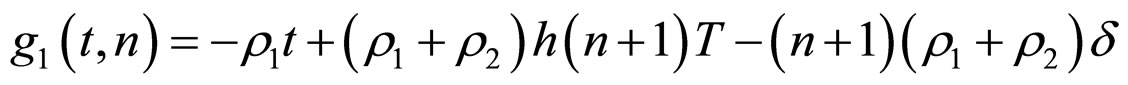 ,
,
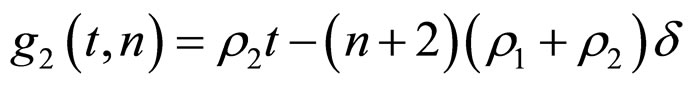 ,
,
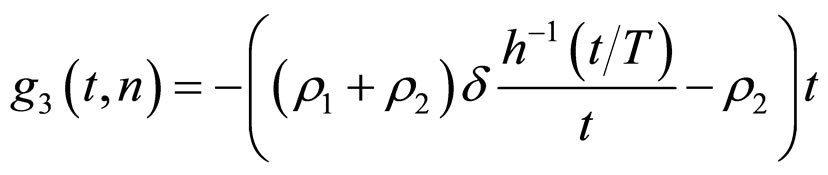 ,
,
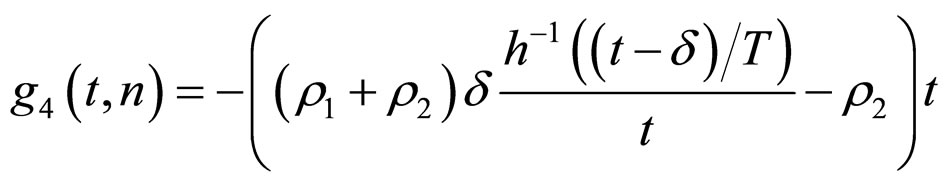 .
.
when 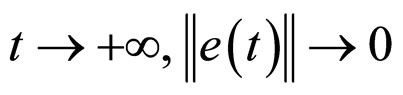 is obtained under the condition (15). So the synchronization of network (6) is achieved.
is obtained under the condition (15). So the synchronization of network (6) is achieved.
Corollary 1 Supposing that 

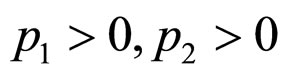 , and the rest of restricted conditions are invariable. Then the synchronization of the network (6) is achieved if the parameters
, and the rest of restricted conditions are invariable. Then the synchronization of the network (6) is achieved if the parameters![]() ,
, ![]() and
and 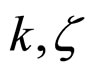 satisfy
satisfy
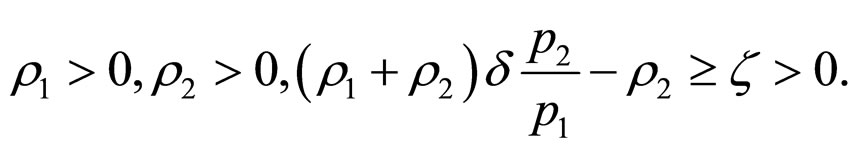
Corollary 2 when we add normally distributed white noise randn (size(t)), the result similar to Theorem 2 and Theorem 3 is obtained if the condition (11) or (12) , respectively, is satisfied.
In the simulations of following examples, we always choose 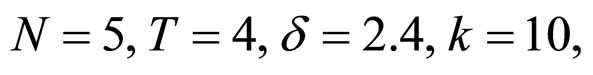 the matrix
the matrix
 .
.
Let the initial condition be

Example 1 Consider a delayed system [47]:
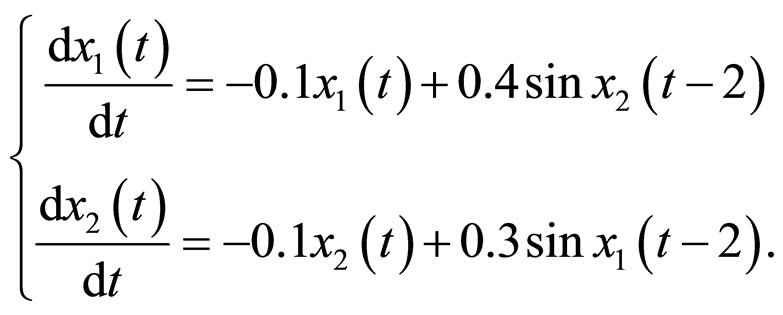 (18)
(18)
The function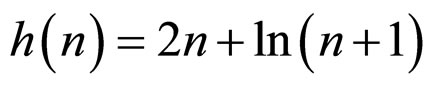 ,
, 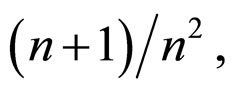
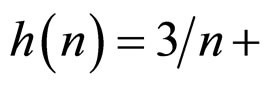 which are the strictly monotone increasing or decreasing function on
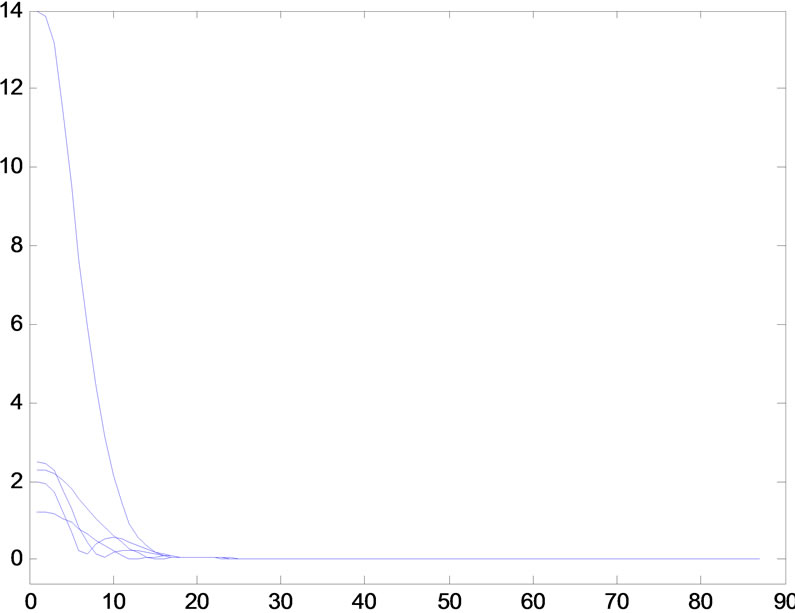
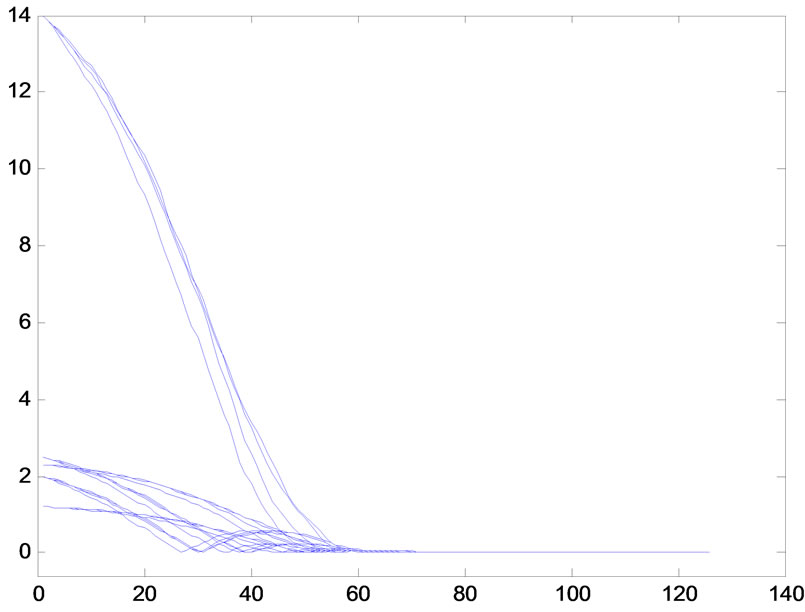
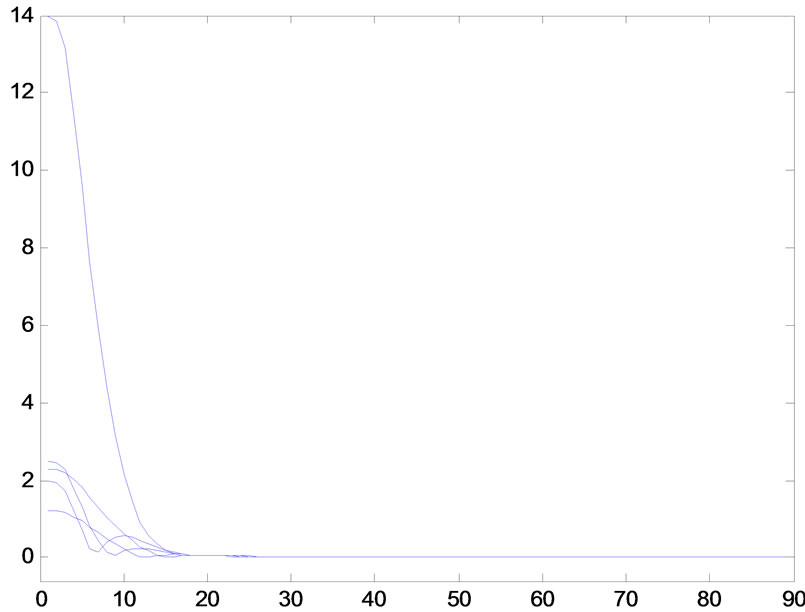
which are the strictly monotone increasing or decreasing function on![]() , respectively, then they can be clearly seen that the synchronization of network (6), which is composed of system (18), is realized in Figures 1-4 (Excited by parameter white-noise), respectively.
, respectively, then they can be clearly seen that the synchronization of network (6), which is composed of system (18), is realized in Figures 1-4 (Excited by parameter white-noise), respectively.
 (a)
(a) (b)
(b)
Figure 1. Synchronization error when h(n) = 2n + 1n(n + 1). (a) The error xi1 − s1, (i = 1, 2, 3, 4, 5); (b) The error xi2 − s2, (i = 1, 2, 3, 4, 5).
 (a)
(a) (b)
(b)
Figure 2. Synchronization error when h(n) = 2n + 1n(n + 1), white noise 0.5 (xi − s) randn (size(t)), (i = 1, 2, 3, 4, 5). (a) The error xi1 − s1, (i = 1, 2, 3, 4, 5); (b) The error xi2 − s2, (i = 1, 2, 3, 4, 5).
 (a)
(a)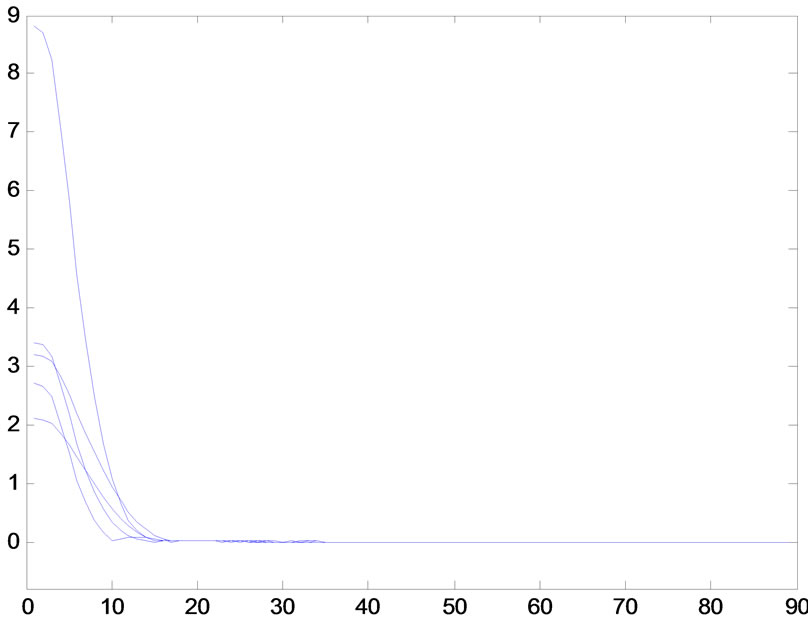 (b)
(b)
Figure 3. Synchronization error when h(n) = 3/n + (n + 1)/n2. (a) The error xi1 − s1, (i = 1, 2, 3, 4, 5); (b) The error xi2 − s2, (i = 1, 2, 3, 4, 5).
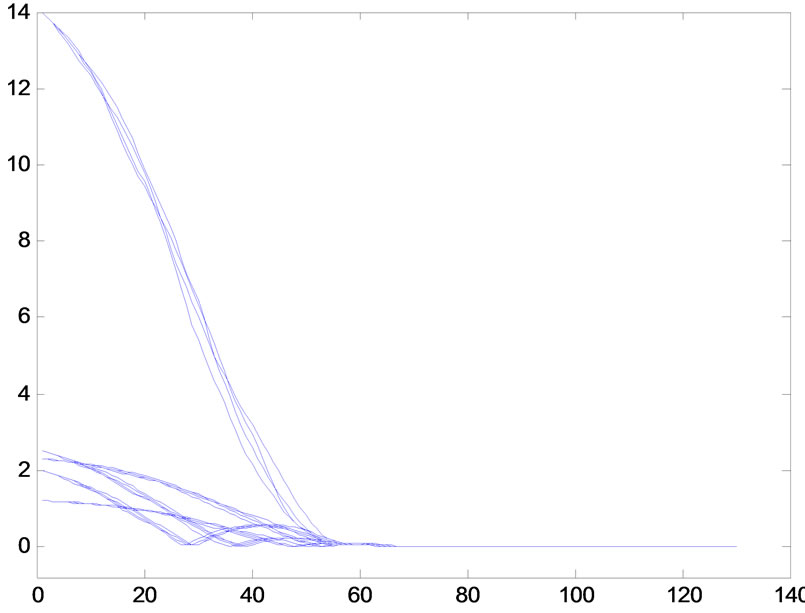 (a)
(a)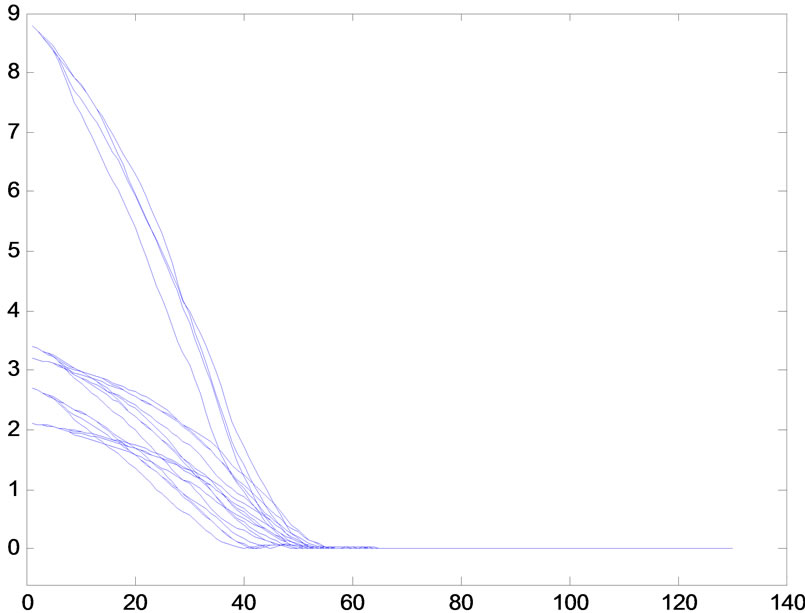 (b)
(b)
Figure 4. Synchronization error when h(n) = 3/n + (n + 1)/n2, white noise 0.5 (xi − s) randn (size(t)), (i = 1, 2, 3, 4, 5). (a) The error xi1 − s1, (i = 1, 2, 3, 4, 5); (b) The error xi2 − s2, (i = 1, 2, 3, 4, 5).
5. Conclusion
Approaches for quantized synchronization of complex networks with delayed time via general intermittent which uses the nonlinear operator named the matrix measure have been presented in this paper. Strong properties of global and exponential synchronization have been achieved in a finite number of steps. Numerical simulations have verified the effectiveness of the method.
REFERENCES
- H. Fujisaka and T. Yamada, “Stability Theory of Synchronized Motion in a Coupled-Oscillator System,” Progress of Theoretical Physics, Vol. 69, No. 1, 1983, pp. 32-47. http://dx.doi.org/10.1143/PTP.69.32
- H. Fujisaka and T. Yamada, “A New Intermittency in Coupled Dynamical Systems,” Progress of Theoretical Physics, Vol. 74, No. 4, 1985, pp. 918-921. http://dx.doi.org/10.1143/PTP.74.918
- H. Fujisaka and T. Yamada, “Stability Theory of Synchronized Motion in Coupled-Oscillator Systems IV,” Progress of Theoretical Physics, Vol. 75, No. 5, 1986, pp. 1087-1104. http://dx.doi.org/10.1143/PTP.75.1087
- V. S. Afraimovich, N. N. Verichev and M. I. Rabinovich, “Stochastic Synchronization of Oscillations in Dissipative Systems,” Radiophysics and Quantum Electronics, Vol. 29, No. 9, 1986, pp. 747-751.
- L. M. Pecora and T. L. Carroll, “Synchronization in Chaotic Systems,” Physical Review Letters, Vol. 64, No. 8, 1990, pp. 821-824. http://dx.doi.org/10.1103/PhysRevLett.64.821
- W. H. Deng, J. H. Lu and C.-P. Li, “Stability of N-Dimensional Linear Systems with Multiple Delays and Application to Synchronization,” Journal of Systems Science and Complexity, Vol. 19, No. 2, 2006, pp. 149-156.
- E. M. Elabbasy, H. N. Agiza and M. M. El-Dessoky, “Global Synchronization Criterion and Adaptive Synchronization for New Chaotic System,” Chaos, Solitons and Fractals, Vol. 23, No. 4, 2005, pp. 1299-1309.
- Q. L. Zhang, J. Zhou and G. Zhang, “Stability Concerning Partial Variables for a Class of Time-Varying Systems and Its Applications in Chaos Synchronization,” Proceedings of the 24th Chinese Control Conference, South China University of Technology Press, Guangzhou, 2005, pp. 135-139.
- Q. L. Zhang and G. J. Jia, “Chaos Synchronization of Morse Oscillator via Backstepping Design,” Annals of Differential Equations, Vol. 22, No. 3, 2006, pp. 456-460.
- Q. L. Zhang, “Synchronization of Multi-Chaotic Systems via Ring Impulsive Control,” Control Theory & Applications, Vol. 27, No. 2, 2010, pp. 226-232.
- Z. Tang and J. W. Feng, “Adaptive Cluster Synchronization for Nondelayed and Delayed Coupling Complex Networks with Nonidentical Nodes,” Abstract and Applied Analysis, Vol. 2013, 2013, Article ID: 946243.
- B. Li and Q. K. Song, “Synchronization of Chaotic Delayed Fuzzy Neural Networks under Impulsive and Stochastic Perturbations,” Abstract and Applied Analysis, Vol. 2013, 2013, Article ID: 543549.
- M. Han, Y. Liu and J. Q. Lu, “Impulsive Control for the Synchronization of Chaotic Systems with Time Delay,” Abstract and Applied Analysis, Vol. 2013, 2013, Article ID: 647561.
- S. J. Dan, S. X. Yang and W. Feng, “Lag Synchronization of Coupled Delayed Chaotic Neural Networks by Periodically Intermittent Control,” Abstract and Applied Analysis, Vol. 2013, 2013, Article ID: 501461.
- C.-M. Lin, M.-H. Lin and R.-G. Yeh, “Synchronization of Unified Chaotic System via Adaptive Wavelet Cerebellar Model Articulation Controller,” Neural Computing and Applications, 2012, pp. 1-9. http://dx.doi.org/10.1007/s00521-012-1021-3
- J. D. Cao and L. L. Li, “Cluster Synchronization in an Array of Hybrid Coupled Neural Networks with Delay,” Neural Networks, Vol. 22, No. 4, 2009, pp. 335-342.
- L. L. Li and J. D. Cao, “Cluster Synchronization in an Array of Coupled Stochastic Delayed Neural Networks via Pinning Control,” Neurocomputing, Vol. 74, No. 5, 2011, pp. 846-856. http://dx.doi.org/10.1016/j.neucom.2010.11.006
- H. Reza and P. Mass, “Delay-Range-Dependent Exponential H∞ Synchronization of a Class of Delayed Neural Networks,” Chaos, Solitons and Fractals, Vol. 41, No. 3, 2009, pp. 1125-1135. http://dx.doi.org/10.1016/j.chaos.2008.04.051
- J. D. Cao, D. W. C. Ho and Y. Q. Yang, “Projective Synchronization of a Class of Delayed Chaotic Systems via Impulsive Control,” Physics Letters A, Vol. 373, No. 35, 2009, pp. 3128-3133. http://dx.doi.org/10.1016/j.physleta.2009.06.056
- Z. Zahreddine, “Matrix Measure and Application to Stability of Matrices and Interval Dynamical Systems,” International Journal of Mathematics and Mathematical Sciences, Vol. 2003, No. 2, 2003, pp. 75-85. http://dx.doi.org/10.1155/S0161171203202295
- J. T. Sun, Y. P. Zhang, Y. Q. Liu and F. Q. Deng, “Exponential Stability of Interval Dynamical System with Multidelay,” Applied Mathematics and Mechanics, Vol. 23, No. 1, 2002, pp. 87-91.
- G. D. Zong, Y. Q. Wu and S. Y. Xu, “Stability Criteria for Switched Linear Systems with Time-Delay,” Control Theory & Applications, Vol. 25, No. 5, 2008, pp. 295- 305.
- Y. H. Yuan, Q. L. Zhang and B. Chen, “Robust Fuzzy Control Based on Matrix Measure for Nonlinear Descriptor Systems with Time-Delay,” Control and Decision, Vol. 22, No. 2, 2007, pp. 174-178.
- L. M. Ding, J. B. Quan, Y. Zhang and Z. X. Li, “The Fixed Point Theorem and Asymptotic Stability of a Delay-Differential System,” Journal of Air Force Radar Academy, Vol. 23, No. 3, 2009, pp. 203-204.
- Y. X. Guo, “Matrix Measure and Uniform Ultimate Boundedness with Respect to Partial Variables for FDEs,” Journal of Wuhan University of Science and Engineering, Vol. 21, No. 4, 2008, pp. 15-19.
- J. J. Huang, C. D. Li and Q. Han, “Stabilization of Delayed Chaotic Neural Networks by Periodically Intermittent Control,” Circuits, Systems & Signal Processing, Vol. 28, No. 4, 2009, pp. 567-579. http://dx.doi.org/10.1007/s00034-009-9098-3
- J. Yu, H. J. Jiang and Z. D. Teng, “Synchronization of Nonlinear Systems with Delay via Periodically Intermittent Control,” Journal of Xinjiang University (Natural Science Edition), Vol. 28, No. 3, 2010, pp. 310-315.
- Z. Y. Dong, Y. J. Wang, M. H. Bai and Z. Q. Zuo, “Exponential Synchronization of Uncertain Master-Slave Lur’e Systems via Intermittent Control,” Journal of Dynamics and Control, Vol. 7, No. 4, 2009, pp. 328-333.
- W. G. Xia and J. D. Cao, “Pinning Synchronization of Delayed Dynamical Networks via Periodically Intermittent Control,” Chaos, Vol. 19, No. 1, 2009, Article ID: 013120. http://dx.doi.org/10.1063/1.3071933
- P. Smolen, D. Baxter and J. Byrne, “Mathematical Modeling of Gene Networks Review,” Neuron, Vol. 26, No. 3, 2000, pp. 567-580. http://dx.doi.org/10.1016/S0896-6273(00)81194-0
- Y. Wang, J. Hao and Z. Zuo, “A New Method for Exponential Synchronization of Chaotic Delayed Systems via Intermittent Control,” Physics Letters A, Vol. 374, No. 19-20, 2010, pp. 2024-2029. http://dx.doi.org/10.1016/j.physleta.2010.02.069
- T. Huang, C. Li, W. Yu and G. Chen, “Synchronization of Delayed Chaotic Systems with Parameter Mismatches by Using Intermittent Linear State Feedback,” Nonlinearity, Vol. 22, No. 3, 2009, pp. 569-584. http://dx.doi.org/10.1088/0951-7715/22/3/004
- H. Zhang, H. C. Yan, F. W. Yang and Q. J. Chen, “Quantized Control Design for Impulsive Fuzzy Networked Systems,” IEEE Transactions on Fuzzy Systems, Vol. 19, No. 6, 2011, pp. 1153-1162. http://dx.doi.org/10.1109/TFUZZ.2011.2162525
- F. Fagnani and S. Zampieri, “Quantized Stabilization of Linear Systems: Complexity versus Performance,” IEEE Transactions on Automatic Control, Vol. 49, No. 9, 2004, pp. 1534-1548. http://dx.doi.org/10.1109/TAC.2004.834111
- S. Sqartini, B. Schuller and A. Hussain, “Cognitive and Emotionan Infromation Processing for Human-Machine Interaction,” Cognitive Computation, Vol. 4, No. 4, 2012, pp. 383-387. http://dx.doi.org/10.1007/s12559-012-9180-1
- J. B. Kim, J. S. Park and Y. H. Oh, “Speaker-Characterized Emotion Recognition Using Online and Iterative Speaker Adaptation,” Cognitive Computation, Vol. 4, No. 4, 2012, pp. 398-408. http://dx.doi.org/10.1007/s12559-012-9132-9
- L. I. Per lovsky and D. S. Levine, “The Drive for Creativity and the Escape from Creativity: Neurocognitive Mechanisms,” Cognitive Computation, Vol. 4, No. 3, 2012, pp. 292-305.
- Q. L. Zhang, “The Generalized Dahlquist Constant with Applications in Synchronization Analysis of Typical Neural Networks via General Intermittent Control,” Advances in Artificial Neural Systems, Vol. 2011, 2011, Article ID: 249136. http://dx.doi.org/10.1155/2011/249136
- G. T. Hui, B. N. Huang, Y. C. Wang and X. P. Meng, “Quantized Control Design for Coupled Dynamic Networks with Communication Constraints,” Cognitive Computation, Vol. 5, No. 2, 2013, pp. 200-206.
- L. A. Montestruque and P. J. Antsaklis, “Static and Dynamic Quantization in Model-Based Networked Control Systems,” International Journal of Control, Vol. 80, No. 1, 2007, pp. 87-101. http://dx.doi.org/10.1080/00207170600931663
- Q. Ye, H. B. Zhu and B. T. Cui, “Synchronization Analysis of Delayed Hybrid Dynamical Networks with Quantized Impulsive Effects,” Control Theory & Applications, Vol. 30, No. 1, 2013, pp. 61-68.
- W. Liu, Z. M. Wang and M. K. Ni, “Quantized Feedback Stabilization of Model-Based Networked Control Systems,” Control and Decision, Vol. 28, No. 2, 2013, pp. 285-288.
- R. Q. Lu, F. Wu and A. K. Xue, “A Reset Quantized-State Controller for Linear Systems,” Control Theory & Applications, Vol. 29, No. 4, 2012, pp. 507-512.
- X. X. Liao, “Theory and Application of Stability for Dynamical Systems,” National Defence Industry Press, Beijing, 2000, pp. 15-40.
- B. Shi, D. C. Zhang and M. J. Gai, “Theory and Applications of Differential Equations,” National Defense Industry Press, Beijing, 2005, pp. 18-23.
- J. C. Kuang, “Applied Inequalities,” Shandong Science and Technology Press, Jinan, 2004, pp. 564-570.
- C. Liu, C. D. Li and S. K. Duan, “Stabilization of Oscillating Neural Networks with Time-Delay by Intermittent Control,” International Journal of Control, Automation and Systems, Vol. 9, No. 6, 2011, pp. 1074-1079. http://dx.doi.org/10.1007/s12555-011-0607-3
NOTES
*This work is supported by the National Natural Science Foundation of China (11071141), the Natural Science Foundation of Shandong Province of China (ZR2011AL018, ZR2011AQ008) and a Project of Shandong Province Higher Educational Science and Technology Program (J11LA06), the Research Rund Project of Heze University under Grant: XY10KZ01.

