Applied Mathematics
Vol.5 No.1(2014), Article ID:41617,11 pages DOI:10.4236/am.2014.51009
A Method to Predict Amino Acids at Proximity of Beta-Sheet Axes from Protein Sequences
1Analyse Algébrique, Institut de Mathématique de Jussieu, Université Pierre et Marie Curie, Paris, France
2Centre d’Informatique Pour la Biologie, Institut Pasteur, Paris, France
3Département de Virologie, Institut Pasteur, Paris, France
Email: aguillou@math.jussieu.fr, bernard.caudron@pasteur.fr, jjestin@pasteur.fr
Received June 21, 2013; revised July 21, 2013; accepted July 28, 2013
ABSTRACT
A general and elementary protein folding step was described in a previous article. Energy conservation during this folding step yielded an equation with remarkable solutions over the field of rational numbers. Sets of sequences optimized for folding were derived. In this work, a geometrical analysis of protein beta-sheet backbone structures allows the definition of positions of topological interest. They correspond to amino acids’ alpha carbons located on a unique axis crossing all beta-sheet’s strands or at proximity of this axis defined here. These positions of topological interest are shown to be highly correlated with the absence of sequences optimized for folding. Applications in protein structure prediction for the quality assessment of structural models are envisioned.
Keywords:Polypeptide Chain; Protein Structure; Topology; Beta-Strand; Folding; Amino Acid; Structure Prediction
1. Introduction
Protein structure prediction from sequences remains a major challenge even though the problem is several decades old [1,2]. Protein structure prediction was recently achieved using ab initio methods for small proteins, using templates with sequence or fold similarity or using sets of correlated mutations [3-9]. One-dimensional protein sequences can generally be predicted from gene sequences on genomic scales [10,11]. Secondary structures can also be efficiently predicted computationally from protein sequences [12-17]. However, three-dimensional protein structures have generally been solved experimentally and computationally by time-consuming and costly approaches such as X-ray diffraction on protein crystals or nuclear magnetic resonance on concentrated protein solutions. Independently, studies on protein folding allowed major conceptual advances on the understanding of general protein properties linked to their conversion of one dimensional sequences into three-dimensional structures [18-21]. Molten globules and pre-molten globules have been characterized [22,23]. A rugged funnel-like energy landscape was described for protein folding [24]. Small model systems allowed protein folding simulations to be carried out [25,26]. Protein engineering and folding kinetics were combined to define folding pathways at the level of single amino acid residues [27]. Consideration of an elementary folding step allowed edge strands in beta-sheets to be predicted from protein sequences [28]. A link was also established here between protein sequences and three-dimensional structure information: the focus is in this work on amino acids at proximity of the axis crossing the beta-sheet’s strands.
Methods
The program pdb2 [28] was written in Perl v5.8.9. It can be used on the Mobyle platform at Institut Pasteur [29] and makes use of files from the Protein Data Bank (PDB) [30]. Protein lengths were in the range of 50 to 250 amino acids. Sequences optimized for folding (SOF) as shown in Figure 1 were computed as described earlier [28]. Small proteins and designed proteins were not included in this study. Proteins were chosen because of their distinct folds as described in the structural classification of proteins (SCOP) [32].
The gap is characterized by an integer value, which is the integer part of the middle of the gap’s ends corresponding to the set of amino acid positions for which no SOF were found (Figures 1 and 2). Independently, positions of topological interest (TIPs) were determined from the protein domain structures’ backbone either by visual analysis of the structure using the Pymol software or by automatic annotation using pdb22 (see below). For each protein consisting of L amino acids, the number of TIPs T and the number of gaps G were noted in the Annex Table A1. A coincidence was defined as an amino acid position where a TIP coincides with a gap within a small error range e depending on the protein length L. For proteins of length L between 51 and 100, the gap position was defined plus or minus two amino acids (e = 2), thereby corresponding to 5 amino acid positions. Similarly, for proteins of length 101 - 150, 151 - 200 and 201 - 250, the error e was defined as 3, 4 and 5 respectively (Figure 2). For example, the structure with PDB reference (1c3g) with 170 amino acids numbered from 180/1 to 349/170 in the structure and sequence files respectively allows the definition of 10 TIPs corresponding to amino acid alpha carbons on the three following axes at positions numbered (266/87; 291/112; 316/137), (188/9; 228/49; 253/74), (206/27; 212/33; 247/68; 238/59). The model applied to the corresponding sequence allows the definition of two gaps between amino acids 28 and 31 (noted 29 and coinciding with TIP 27) and between amino acids 89 and 90 (noted 89 coinciding with TIP 87). Given that the differences between TIP and gap numbers is 2 in both cases and as an error of 4 is allowed for proteins of 170 amino acids, the number C of coincidences is two for the two gaps (Annex Table A1). The www interface for the identification of gaps is available for any protein sequence at the following address: http://mobyle.pasteur.fr/cgi-bin/portal.py#forms::pdb2; it accepts PDB file names as entries (4 characters).
The program pdb22 is available at the address: http://mobyle.pasteur.fr/cgi-bin/portal.py#forms::pdb22; it is also a program written in perl and uses the same entry files as pdb2. The pdb22 output file (.xls) provides for each protein within the list its PDB name, the amino acid number and name in three-letter code, the start and the end of beta-strands indicated as amino acid numbers, the name of the sheet noted on the lines corresponding to amino acids found at the intersection of a beta-strand with the sheet axis and the distance D, which is calculated

Figure 1. Set of sequences with optimal folding properties. SOFs (red) were calculated as in [28] for the central protein domain of Clostridium symbiosum pyruvate phosphate dikinase (PDB reference 2fm4) [31]. A gap defined by the absence of SOF is found between amino acids 114 and 115 and is characterized by the integer part of the gap’s middle (114).
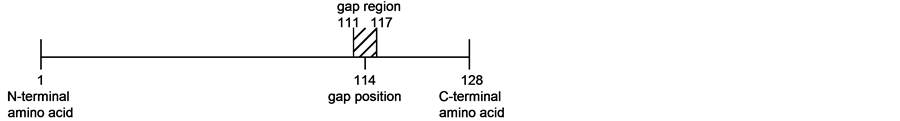
Figure 2. Representation of a gap position and of a gap region in a protein sequence. For the protein domain of PDB reference 2fm4 which is 128 amino acids long [31], the small error e of plus or minus 3 amino acids around the gap position is applied to proteins of lengths 101 and 150 for the prediction of topologically interesting positions (TIPs).
in Angströms and averaged per beta-strand for each sheet consisting of n strands using the following equation:
 (1)
(1)
where mindist(i) is the minimal distance between an alpha carbon of strand i and the sheet axis. The distance d is estimated for each pair of amino acids defining an axis characterized by the atomic coordinates of one amino acid’s alpha carbon in the first strand and another one in the sequence’s last strand. The sheet axis is defined as the axis for which the distance d is minimal. For a sheet, the minimum of all distances d is noted D.
The probability q for having C coincidences occurring at random, that is the probability for G gaps to coincide with T TIPs within the error range e was calculated according to Equation (2) deriving from the exclusion-inclusion principle (cf. Annex for the equation’s proof).
 (2)
(2)
with

The corresponding probabilities q are reported for each protein structure defined by its PDB reference in the Annex Table A1. It appears that for 14 of the proteins, the probability q is higher than 0.5.
In order to compute the p-value of the test, the probability of failing at most 14 times within 46 experiments (one experiment for each protein structure associated to a PDB reference) when the probability of failure is taken as 0.5 was computed using the binomial law as in Equation (3):
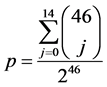 (3)
(3)
The severity of this statistical test is highlighted for example by the data obtained for the protein of 193 amino acids referenced 3pn3 in the PDB, for which the correct identification of one coincidence for the gap was not considered as successful because of the large number of TIPs defined which is associated to a probability (q > 0.5; Annex Table A1). The numerical value of p @ 0.0057 indicates the statistical significance, which is far below the commonly accepted standard threshold of 0.05.
Independently, a program (pdb7) was written to make use of lists of PDB files as entries and to provide within the output sequence file the gaps and TIPs calculated using pdb2 and pdb22 respectively. For each beta-sheet, the axis was defined as the line minimizing the distance for all strands from one alpha carbon per beta-strand to the line defined by two alpha carbons taken in the first and last strands in the protein sequence as described above. Analysis of the pdb7 output files yielded the results for the 248 correlations evaluated between gaps and TIPs (Table 1).
3. Results
An elementary step of protein folding was described as a folding unit or chemical group folding onto a folding entity to yield a larger folding entity [28]. Criteria that are sufficient to define protein subsequences with optimal folding properties were derived [28].
A gap was defined as one or several amino acid(s) position(s) for which no sequence with optimal folding properties (SOF) is found. A quarter of the proteins analyzed yielded graphs of SOF which did not contain any gap. As an example, a single gap was noted between amino acids 114 and 115 for the central domain of C. symbiosum pyruvate phosphate dikinase (Figure 1). The gap’s position was defined as the integer part of the middle of the gap (Figures 1 and 2).
Topologically interesting positions (TIPs) can be determined from protein domain structures’ atomic coordinates. Beta-sheets are typically curved planes in three dimensions because of the twist found within beta-strands [33]. Still, there generally exists at least one axis crossing most, if not all, beta-strands of the sheet (Figure 3): we define here a sheet axis as a straight line crossing the sheet’s beta-strands, and which is generally perpendicular to the beta-strands (cf. Methods). The axis was chosen to cross the first and last strands at amino acids’ alpha carbons. For the other strands, one amino acid per strand is further chosen for its proximity to the axis. The axis minimizing the distance to their alpha carbon is represented as a circle including the set of amino acids which are on the axis or closest to the axis in the pyruvate phosphate dikinase domain sheet structure (Figure 3). The intersection of this axis with each beta-strand yields one alpha carbon at an amino acid position defined as a topologically interesting position or TIP.
An error e for the gaps’ positions prediction was allowed and chosen to increase slightly as a function of in
aDistance is the difference between a gap position and a topologically interesting position (TIP) within a beta-strand sequence; brelative occurrence assuming a random assignment of gaps and TIPs within seven amino acids long beta-strands; coccurrences in a non-redundant set of proteins with at least one seven amino acids long beta-strand deriving from the PDB.
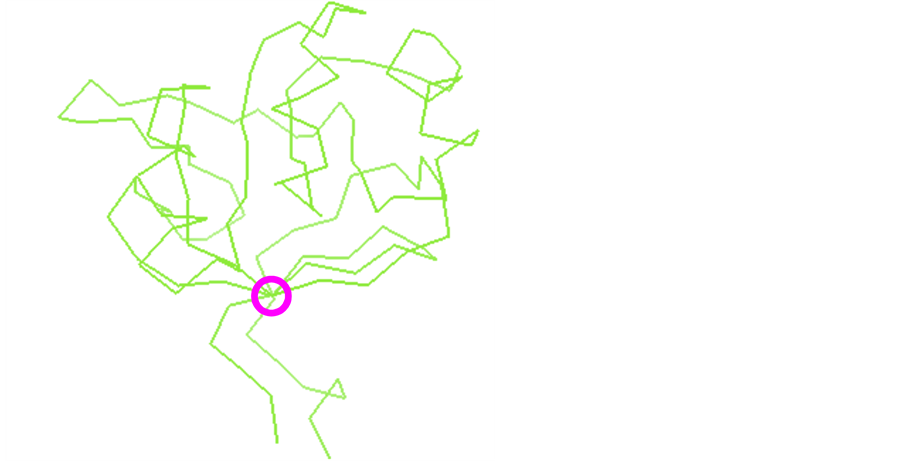
Figure 3. Positions of topological interest and a beta-sheet axis. Topologically interesting positions (TIPs) shown for a protein domain (PDB reference 2fm4) whose backbone is represented by links between adjacent alpha carbons from amino acids [31]. TIPs are found on a beta-sheet axis within the circle shown in pink; they are numbered 8, 21, 114, 123. Amino acid 114 in the sequence file is numbered 497 in the structure file.
creasing proteins’ length as described in the methods section (Figure 2). The statistical evidence that TIPs and gaps are strongly correlated derives from a binomial test on the analysis of domain structures (Annex Table A1). The p-value (<0.0057) calculated (cf. Methods) shows the correlation. Given that gaps can be straightforwardly calculated for any protein sequence, the correlation between gaps and topologically interesting amino acid positions (TIPs) provides information on the three-dimensional protein structure.
To obtain an independent proof of this conclusion, another program (pdb7) was then written for automatic annotation of gaps and TIPs on protein sequences: the hypothesis that the observed distribution of distances between gaps and TIPs (Table 1) follows the calculated distribution assuming a random assignment is excluded given the statistical p-value (0.0032).
4. Discussion
An elementary protein folding step was described [28]. Application of classical mechanics and of the total energy conservation law to an elementary folding step yielded a quadratic equation with remarkable solutions over the field of rational numbers [28].
While numerical applications of equations from classical mechanics are commonly done over the field of real numbers, the following pieces of evidence indicate that discreteness provides a useful basis which is adapted in particular for the understanding of why the genetic code is the way it is. The genetic code is remarkable because of its quasi-universality within living organisms on earth and because it is about four billion years old [34]. The role of selection pressures in the definition of amino acid assignments to codons was largely discussed in the context of the coevolution of the genetic code with essential proteins [35,36]. A side-chain volume conservation was further found to be statistically significant for amino acids involved in precursor-product relationships within biosynthetic pathways and put in the context of side-chains’ packing in protein beta-sheets [37]. From the experimental side, the genetic code was engineered in multiple studies for applications in protein engineering [38-40]. From the theoretical side, discrete symmetries associated to degeneracy in the genetic code were identified by Rumer [41,42]. The discrete nature of the most frequent mutations provided a rationale accounting for those symmetries [43]. Independently, kinetic energy conservation in polypeptide chains during molecular evolution was found to be consistent with the grouping of codons in the genetic code; the formalism consisting of energy conservation laws with solutions over the field of rational numbers was thereby validated for amino acids by the genetic code’s codon arrangement [44]. The field of rational numbers was also taken into consideration for another extension of classical mechanics [45].
This mathematical and physical formalism provides information on beta-sheet structures from protein sequences as shown recently for the prediction of edge strands [28] and above for the prediction of amino acids at proximity of beta-sheet axes (Figure 3). Protein beta-strands and their arrangement in beta-sheets were extensively described [46-49]. Numerous studies have been undertaken to identify rules linking the beta-strands’ sequences and three-dimensional structural properties of the corresponding beta-sheets [33,50-61]. The notion of random quasi-spherical proteins was recently introduced [62]. Several computational approaches allow the prediction of beta-sheet topology with accuracies around 80% for sheets of more than four beta-strands [63-67]. The parallel or anti-parallel character was also predicted by computational methods [68-70].
In this work, the absence of sequences optimized for folding was linked to topological information on protein beta-sheets. It should be of interest to extend this analysis to other secondary structure elements such as protein helices while considering the impact of protein families and classes [71,72].
5. Conclusion
There is a need for practical methods describing complex chemical processes [73]. Predicting the sequence-specific folding of a polypeptide chain into a three-dimensional structure remains a challenge. An axis characterizing the topology of beta-sheets was defined in this work. The fast computational method described here combining the identification of amino acids at proximity of beta-sheet axes (using pdb22) and the identification of gaps (using pdb7) derives three-dimensional structure information on beta-sheets from protein sequences at scales of topological interest for structural domains of less than 250 amino acids. Both the formalism based on energy conservation during an elementary protein folding step [28] and the definition of beta-sheet axes should therefore improve protein structure prediction strategies by implementation as quality assessment methods for structural models [74-76]: it provides new criteria for the selection of the most accurate protein structural models out of thousands of them. A quantitative evaluation of this method’s efficiency may be achieved within the next challenge for the critical assessment of techniques for protein structure prediction such as CASP11 [77,78].
Acknowledgements
The authors thank B. Néron for interfacing pdb2 and pdb22, Y. Benoist and A. Kempf for discussions.
REFERENCES
- C. B. Anfinsen, “Some Observations on the Basic Principles of Design in Protein Molecules,” Comparative Biochemistry and Physiology, Vol. 4, No. 2-4, 1962, pp. 229-240. http://dx.doi.org/10.1016/0010-406X(62)90007-5
- C. Clementi, “Coarse-Grained Models of Protein Folding: Toy Models or Predictive Tools?” Current Opinion in Structural Biology, Vol. 18, No. 1, 2008, pp. 10-15. http://dx.doi.org/10.1016/j.sbi.2007.10.005
- L. A. Kelley and M. J. E. Sternberg, “Protein Structure Prediction on the Web: A Case Study Using the Phyre Server,” Nature Protocols, Vol. 4, No. 3, 2009, pp. 363-371. http://dx.doi.org/10.1038/nprot.2009.2
- S. Y. Lee and J. Skolnick, “Tasser-wt: A Protein Structure Prediction Algorithm with Accurate Predicted Contact Restraints for Difficult Protein Targets,” Biophysical Journal, Vol. 99, No. 9, 2010, pp. 3066-3075. http://dx.doi.org/10.1016/j.bpj.2010.09.007
- R. Norel, D. Petrey and B. Honig, “Pudge: A Flexible, Interactive Server for Protein Structure Prediction,” Nucleic Acids Research, Vol. 38, Suppl. 2, 2010, pp. W550-554. http://dx.doi.org/10.1093/nar/gkq475
- A. Leaver-Fay, M. Tyka, S. M. Lewis, et al., “ROSETTA3: An Object-Oriented Software Suite for the Simulation and Design of Macromolecules,” Methods in Enzymology, Vol. 487, 2011, pp. 545-574. http://dx.doi.org/10.1016/B978-0-12-381270-4.00019-6
- J. Thompson and D. Baker, “Incorporation of Evolutionary Information into Rosetta Comparative Modeling,” Proteins, Vol. 79, No. 8, 2011, pp. 2380-2388. http://dx.doi.org/10.1002/prot.23046
- J. I. Sulkowska, F. Morcos, M. Weigt, et al., “Genomics-Aided Structure Prediction,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 109, No. 26, 2012, pp. 10340-10345. http://dx.doi.org/10.1073/pnas.1207864109
- D. S. Marks, T. A. Hopf and C. Sander, “Protein Structure Prediction from Sequence Variation,” Nature Biotechnology, Vol. 30, No. 11, 2012, pp. 1072-1080. http://dx.doi.org/10.1038/nbt.2419
- I. Iliopoulos, S. Tsoka, M. A. Andrade, et al., “Evaluation of Annotation Strategies Using an Entire Genome Sequence,” Bioinformatics, Vol. 19, No. 6, 2003, pp. 717-726. http://dx.doi.org/10.1093/bioinformatics/btg077
- A. S. Juncker, L. J. Jensen, A. Pierleoni, et al., “Sequence-Based Feature Prediction and Annotation of Proteins,” Genome Biology, Vol. 10, 2009, p. 206. http://dx.doi.org/10.1186/gb-2009-10-2-206
- B. Rost and C. Sander, “Prediction of Protein Secondary Structure at Better than 70% Accuracy,” Journal of Molecular Biology, Vol. 232, No. 2, 1993, pp. 584-599. http://dx.doi.org/10.1006/jmbi.1993.1413
- D. Bordo and P. Argos, “The Role of Side-Chain Hydrogen Bonds in the Formation and Stabilization of Secondary Structure in Soluble Proteins,” Journal of Molecular Biology Vol. 243, No. 3, 1994, pp. 504-519. http://dx.doi.org/10.1006/jmbi.1994.1676
- J. Selbig, T. Mevissen and T. Lengauer, “Decision Free-Based Formation of Consensus Protein Secondary Structure Prediction,” Bioinformatics, Vol. 15, No. 12, 1999, pp. 1039-1046. http://dx.doi.org/10.1093/bioinformatics/15.12.1039
- D. T. Jones, “Protein Secondary Structure Prediction Based on Position-Specific Scoring Matrices,” Journal of Molecular Biology, Vol. 292, No. 2, 1999, pp. 195-202. http://dx.doi.org/10.1006/jmbi.1999.3091
- J. Martin, J. F. Gibrat and F. Rodolphe, “Analysis of an Optimal Hidden Markov Model for Secondary Structure Prediction,” BMC Structural Biology, Vol. 6, 2006, p. 25. http://dx.doi.org/10.1186/1472-6807-6-25
- C. A. Floudas, “Computational Methods in Protein Structure Prediction,” Biotechnology and Bioengineering, Vol. 97, No. 2, 2007, pp. 207-213. http://dx.doi.org/10.1002/bit.21411
- L. Mirny and E. Shakhnovich, “Protein Folding Theory: From Lattice to All-Atom Models,” Annual Review of Biophysics and Biomolecular Structure, Vol. 30, 2001, pp. 361-396. http://dx.doi.org/10.1146/annurev.biophys.30.1.361
- G. D. Rose, P. J. Fleming, J. R. Banavar and A. Maritan, “A Backbone-Based Theory of Protein Folding,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 103, No. 45, 2006, pp. 16623-16633. http://dx.doi.org/10.1073/pnas.0606843103
- K. A. Dill, S. B. Ozkan, M. S. Shell and T. R. Weikl, “The Protein Folding Problem,” Annual Review of Biophysics, Vol. 37, No. 1, 2008, pp. 289-316. http://dx.doi.org/10.1146/annurev.biophys.37.092707.153558
- D. Thirumalai, E. P. O’Brien, G. Morrison and C. Hyeon, “Theoretical Perspectives on Protein Folding,” Annual Review of Biophysics, Vol. 39, No. 1, 2010, pp. 159-183. http://dx.doi.org/10.1146/annurev-biophys-051309-103835
- O. B. Ptitsyn, “Molten Globule and Protein Folding,” Advances in Protein Chemistry, Vol. 47, 1995, pp. 83-229. http://dx.doi.org/10.1016/S0065-3233(08)60546-X
- A. F. Chaffotte, J. I. Guijarro, Y. Guillou, et al., “The ‘Pre-Molten Globule’, a New Intermediate in Protein Folding,” Journal of Protein Chemistry, Vol. 16, No. 5, 1997, pp. 433-439. http://dx.doi.org/10.1023/A:1026397008011
- J. N. Onuchic, Z. Luthey-Schulten and P. G. Wolynes, “Theory of Protein Folding: The Energy Landscape Perspective,” Annual Review of Physical Chemistry, Vol. 48, 1997, pp. 545-600. http://dx.doi.org/10.1146/annurev.physchem.48.1.545
- R. D. Schaeffer, A. Fersht and V. Daggett, “Combining Experiment and Simulation in Protein Folding: Closing the Gap for Small Model Systems,” Current Opinion in Structural Biology, Vol. 18, No. 1, 2008, pp. 4-9. http://dx.doi.org/10.1016/j.sbi.2007.11.007
- J. A. Hegler, J. Latzer, A. Shehu, et al., “Restriction versus Guidance in Protein Structure Prediction,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 106, No. 36, 2009, pp. 15302-15307. http://dx.doi.org/10.1073/pnas.0907002106
- A. Matouschek, J. T. Kellis Jr., L. Serrano and A. R. Fersht, “Mapping the Transition State and Pathway of Protein Folding by Protein Engineering,” Nature, Vol. 340, 1989, pp. 122-126. http://dx.doi.org/10.1038/340122a0
- A. Guilloux, B. Caudron and J. L. Jestin, “A Method to Predict Edge Strands in Beta-Sheets from Protein Sequences,” Computational and Structural Biotechnology Journal, Vol. 7, 2013, Article ID: e201305001. http://dx.doi.org/10.5936/csbj.201305001
- H. Ménager, V. Gopalan, B. Néron, S. Larroudé, J. Maupetit, A. Saladin, P. Tufféry, Y. Huyen and B. Caudron, “Bioinformatics Applications Discovery and Composition with the Mobyle Suite and MobyleNet,” Lecture Notes in Computer Science, Vol. 6799, 2012, pp. 11-22. http://dx.doi.org/10.1007/978-3-642-27392-6_2
- F. C. Bernstein, T. F. Koetzle, G. J. Williams, et al., “The Protein Data Bank. A Computer-Based Archival File for Macromolecular Structures,” European Journal of Biochemistry, Vol. 80, No. 2, 1977, pp. 319-324. http://dx.doi.org/10.1111/j.1432-1033.1977.tb11885.x
- Y. Lin, J. D. Lusin, D. Ye, et al., “Examination of the Structure, Stability, and Catalytic Potential in the Engineered Phosphoryl Carrier Domain of Pyruvate Phosphate Dikinase,” Biochemistry, Vol. 45, No. 6, 2006, pp. 1702-1711. http://dx.doi.org/10.1021/bi051816l
- L. Lo Conte, B. Ailey, T. J. Hubbard, et al., “SCOP: A Structural Classification of Proteins Database,” Nucleic Acids Research, Vol. 28, No. 1, 2000, pp. 257-259. http://dx.doi.org/10.1093/nar/28.1.257
- B. K. Ho and P. M. Curmi, “Twist and Shear in Beta-Sheets and Beta-Ribbons,” Journal of Molecular Biology, Vol. 317, No. 2, 2002, pp. 291-308. http://dx.doi.org/10.1006/jmbi.2001.5385
- M. Eigen, B. F. Lindemann, M. Tietze, et al., “How Old Is the Genetic Code? Statistical Geometry of tRNA Provides an Answer,” Science, Vol. 244, No. 4905, 1989, pp. 673-679. http://dx.doi.org/10.1126/science.2497522
- M. A. Jimenez-Montano, “Protein Evolution Drives the Evolution of the Genetic Code and Vice Versa,” Biosystems, Vol. 54, No. 1, 1999, pp. 47-64. http://dx.doi.org/10.1016/S0303-2647(99)00058-1
- M. Di Giulio, “The Origin of the Genetic Code: Theories and Their Relationships, a Review,” Biosystems, Vol. 80, No. 2, 2005, pp. 175-184. http://dx.doi.org/10.1016/j.biosystems.2004.11.005
- M. Di Giulio, “The β-Sheets of Proteins, the Biosynthetic Relationships between Amino Acids, and the Origin of the Genetic Code,” Origins of Life and Evolution of the Biosphere, Vol. 26, No. 6, 1996, pp. 589-609. http://dx.doi.org/10.1007/BF01808222
- L. Wang and P. G. Schultz, “Expanding the Genetic Code,” Angewandte Chemie International Edition, Vol. 44, No. 1, 2004, pp. 34-66. http://dx.doi.org/10.1002/anie.200460627
- N. Budisa, “Engineering the Genetic Code,” Wiley-VCH, Weinheim, 2006.
- K. Wang, W. H. Schmied and J. W. Chin, “Reprogramming the Genetic Code: From Triplet to Quadruplet Codes,” Angewandte Chemie International Edition, Vol. 51, No. 10, 2012, pp. 2288-2297. http://dx.doi.org/10.1002/anie.201105016
- Y. B. Rumer, “About the Codon’s Systematization in the Genetic Code,” The Proceedings of the USSR Academy of Sciences, Vol. 167, 1966, pp. 1393-1394.
- V. I. Shcherbak, “Rumer’s Rule and Transformation in the Context of the Co-Operative Symmetry of the Genetic Code,” Journal of Theoretical Biology, Vol. 139, No. 2, 1989, pp. 271-276. http://dx.doi.org/10.1016/S0022-5193(89)80104-3
- J. L. Jestin, “A Rationale for the Symmetries by Base Substitutions of Degeneracy in the Genetic Code,” Biosystems, Vol. 99, No. 1, 2010, pp. 1-5. http://dx.doi.org/10.1016/j.biosystems.2009.07.009
- A. Guilloux and J. L. Jestin, “The Genetic Code and Its Optimization for Kinetic Energy Conservation in Polypeptide Chains,” Biosystems, Vol. 109, No. 2, 2012, pp. 141-144. http://dx.doi.org/10.1016/j.biosystems.2012.03.001
- J. X. Madarasz and G. Szekely, “Special Relativity over the Field of Rational Numbers,” International Journal of Theoretical Physics, Vol. 52, No. 5, 2013, pp. 1706-1718. http://dx.doi.org/10.1007/s10773-013-1492-8
- L. Pauling and R. B. Corey, “Configurations of Polypeptide Chains with Favored Orientations around Single Bonds: Two New Pleated Sheets,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 37, No. 11, 1951, pp. 729-740. http://dx.doi.org/10.1073/pnas.37.11.729
- F. R. Salemme, “Structural Properties of Protein β-Sheets,” Progress in Biophysics and Molecular Biology, Vol. 42, 1983, pp. 95-133. http://dx.doi.org/10.1016/0079-6107(83)90005-6
- C. Chothia, “Conformation of Twisted β-Pleated Sheets in Proteins,” Journal of Molecular Biology, Vol. 75, No. 2, 1973, pp. 295-302. http://dx.doi.org/10.1016/0022-2836(73)90022-3
- E. Koh, T. Kim and H. S. Cho, “Mean Curvature as a Major Determinant of β-Sheet Propensity,” Bioinformatics, Vol. 22, No. 3, 2006, pp. 297-302. http://dx.doi.org/10.1093/bioinformatics/bti775
- M. J. Sternberg and J. M. Thornton, “On the Conformation of Proteins: An Analysis of β-Pleated Sheets,” Journal of Molecular Biology, Vol. 110, No. 2, 1977, pp. 285-296. http://dx.doi.org/10.1016/S0022-2836(77)80073-9
- M. J. Sternberg and J. M. Thornton, “On the Conformation of Proteins: Towards the Prediction of Strand Arrangements in β-Pleated Sheets,” Journal of Molecular Biology, Vol. 113, No. 2, 1977, pp. 401-418. http://dx.doi.org/10.1016/0022-2836(77)90149-8
- M. J. Sternberg and J. M. Thornton, “On the Conformation of Proteins: Hydrophobic Ordering of Strands in β-Pleated Sheets,” Journal of Molecular Biology, Vol. 115, No. 1, 1977, pp. 1-17. http://dx.doi.org/10.1016/0022-2836(77)90242-X
- G. Von Heijne and C. Blomberg, “Some Global β-Sheet Characteristics,” Biopolymers, Vol. 17, No. 8, 1978, pp. 2033-2037. http://dx.doi.org/10.1002/bip.1978.360170817
- M. A. Wouters and P. M. Curmi, “An Analysis of Side Chain Interactions and Pair Correlations within Antiparallel β-Sheets: the Differences between Backbone Hydrogen-Bonded and Non-Hydrogen-Bonded Residue Pairs,” Proteins, Vol. 22, No. 2, 1995, pp. 119-131. http://dx.doi.org/10.1002/prot.340220205
- I. Ruczinski, C. Kooperberg, R. Bonneau and D. Baker, “Distributions of Beta Sheets in Proteins with Application to Structure Prediction,” Proteins: Structure, Function, and Bioinformatics, Vol. 48, No. 1, 2002, pp. 85-97. http://dx.doi.org/10.1002/prot.10123
- J. S. Richardson and D. C. Richardson, “Natural β-Sheet Proteins Use Negative Design to Avoid Edge-to-Edge Aggregation,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 99, No. 5, 2002, pp. 2754-2759. http://dx.doi.org/10.1073/pnas.052706099
- A. E. Kister, A. S. Fokas, T. S. Papatheodorou and I. M. Gelfand, “Strict Rules Determine Arrangements of Strands in Sandwich Proteins,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 103, No. 11, 2006, pp. 4107-4110. http://dx.doi.org/10.1073/pnas.0510747103
- T. S. Papatheodorou and A. S. Fokas, “Systematic Construction and Prediction of the Arrangement of the Strands of Sandwich Proteins,” Journal of the Royal Society Interface, Vol. 6, No. 30, 2009, pp. 63-73. http://dx.doi.org/10.1098/rsif.2008.0192
- N. Koga, R. Tatsumi-Koga, G. Liu, R. Xiao, T. B. Acton, G. T. Montelione and D. Baker, “Principles for Designing Ideal Protein Structures,” Nature, Vol. 491, No. 7423, 2012, pp. 222-227. http://dx.doi.org/10.1038/nature11600
- C. M. Santiveri, J. Santoro, M. Rico and M. A. Jimenez, “Factors Involved in the Stability of Isolated Beta-Sheets: Turn Sequence, β-Sheet Twisting, and Hydrophobic Surface Burial,” Protein Science, Vol. 13, No. 4, 2004, pp. 1134-1147. http://dx.doi.org/10.1110/ps.03520704
- B. Caudron and J. L. Jestin, “Sequence Criteria for the Anti-Parallel Character of Protein β-Strands,” Journal of Theoretical Biology, Vol. 315, 2012, pp. 146-149. http://dx.doi.org/10.1016/j.jtbi.2012.09.011
- M. Brylinski, M. Gao and J. Skolnick, “Why not Consider a Spherical Protein? Implications of Backbone Hydrogen Bonding for Protein Structure and Function,” Physical Chemistry Chemical Physics, Vol. 13, No. 38, 2011, pp. 17044-17055. http://dx.doi.org/10.1039/c1cp21140d
- J. Cheng and P. Baldi, “Three-Stage Prediction of Protein β-Sheets by Neural Networks, Alignments and Graph Algorithms,” Bioinformatics, Vol. 21, Suppl. 1, 2005, pp. i75-i84. http://dx.doi.org/10.1093/bioinformatics/bti1004
- R. Rajgaria, Y. Wei and C. A. Floudas, “Contact Prediction for β and alpha-β Proteins Using Integer Linear Optimization and Its Impact on the First Principles 3D Structure Prediction Method ASTRO-FOLD,” Proteins, Vol. 78, No. 8, 2010, pp. 1825- 1846. http://dx.doi.org/10.1002/prot.22696
- Z. Aydin, Y. Altunbasak and H. Erdogan, “Bayesian Models and Algorithms for Protein β-Sheet Prediction,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, Vol. 8, No. 2, 2011, pp. 395-409. http://dx.doi.org/10.1109/TCBB.2008.140
- A. Subramani and C. A. Floudas, “β-Sheet Topology Prediction with High Precision and Recall for β and mixed α/β Proteins,” PLoS ONE, Vol. 7, No. 3, 2012, Article ID: e32461. http://dx.doi.org/10.1371/journal.pone.0032461
- N. S. Burkoff, C. Varnai and D. L. Wild, “Predicting Protein β-Sheet Contacts Using a Maximum Entropy-Based Correlated Mutation Measure,” Bioinformatics, Vol. 29, No. 5, 2013, pp. 580-587. http://dx.doi.org/10.1093/bioinformatics/btt005
- R. E. Steward and J. M. Thornton, “Prediction of Strand Pairing in Antiparallel and Parallel β-Sheets Using Information Theory,” Proteins, Vol. 48, No. 2, 2002, pp. 178-191. http://dx.doi.org/10.1002/prot.10152
- O. Zimmermann, L. Wang and U. H. Hansmann, “BETTY: Prediction of β-Strand Type from Sequence,” In In Silico Biology, Vol. 7, No. 4-5, 2007, pp. 535-542.
- N. Zhang, G. Duan, S. Gao, J. S. Ruan and T. Zhang, “Prediction of the Parallel/Antiparallel Orientation of β-Strands Using Amino Acid Pairing Preferences and Support Vector Machines,” Journal of Theoretical Biology, Vol. 263, No. 3, 2010, pp. 360-368. http://dx.doi.org/10.1016/j.jtbi.2009.12.019
- A. V. Efimov, “Standard Structures in Proteins,” Progress in Biophysics and Molecular Biology, Vol. 60, No. 3, 1993, pp. 201-239. http://dx.doi.org/10.1016/0079-6107(93)90015-C
- C. A. Orengo and J. M. Thornton, “Protein Families and Their Evolution—A Structural Perspective,” Annual Review of Biochemistry, Vol. 74, 2005, pp. 867-900. http://dx.doi.org/10.1146/annurev.biochem.74.082803.133029
- W. Thiel, “Theoretical Chemistry—Quo Vadis?” Angewandte Chemie International Edition, Vol. 50, No. 40, 2011, pp. 9216- 9217. http://dx.doi.org/10.1002/anie.201105305
- S. C. Lovell, I. W. Davis, W. B. Arendall III, P. I. W. de Bakker, J. M. Word, M. G. Prisant, J. S. Richardson and D. C. Richardson, “Structure Validation by Cα Geometry: φ, ψ and Cβ Deviation,” Proteins, Vol. 50, No. 3, 2003, pp. 437-450. http://dx.doi.org/10.1002/prot.10286
- B. Wallner and A. Elofsson, “Identification of Correct Regions in Protein Models Using Structural, Alignment, and Consensus Information,” Protein Science, Vol. 15, No. 4, 2006, pp. 900-913. http://dx.doi.org/10.1110/ps.051799606
- P. Benkert, M. Biasini and T. Schwede, “Toward the Estimation of the Absolute Quality of Individual Protein Structure Models,” Bioinformatics, Vol. 27, No. 3, 2011, pp. 343-350. http://dx.doi.org/10.1093/bioinformatics/btq662
- D. Fischer, L. Rychlewski, R. L. Dunbrack Jr., A. R. Ortiz and A. Elofsson, “CAFASP3: The Third Critical Assessment of Fully Automated Structure Prediction Methods,” Proteins, Vol. 53, No. S6, 2003, pp. 503-516. http://dx.doi.org/10.1002/prot.10538
- D. Cozzetto, A. Kryshtafovych, K. Fidelis, J. Moult, B. Rost and A. Tramontano, “Evaluation of Template-Based Models in CASP8 with Standard Measures,” Proteins, Vol. 77, No. S9, 2009, pp. 18-28. http://dx.doi.org/10.1002/prot.22561
Abbreviations
PDB is the Protein Data Bank; SCOP is the structural classification of proteins; SOF is a sequence optimized for folding; a gap consists of one or several contiguous amino acids position(s) for which no SOF were found; G is the number of gaps; TIPs are Topologically Interesting Positions; T is the number of TIPs; e is the error tolerated around a gap and is defined as plus or minus a number of amino acids; C is the number of coincidences between TIPs and gaps; L is the number of amino acids of a protein or its length; D is the sum for all strands of a beta-sheet of the distances from the sheet axis to the closest amino acid alpha carbon in each strand; q is a probability as defined in Equation (2); p is the statistical p-value as defined in Equation (3).
Annex: Proof of the Inclusion-Exclusion Formula
We give here a proof of the formula for the probability of having at least C coincidences between the G gaps and T TIPs in a protein of length L, up to an acceptable error of e:

The last fraction in the sum is the probability for the T TIPs to avoid j choosen gaps. With the additional binomial coefficient , we may moreover choose the j gaps we want to avoid.
, we may moreover choose the j gaps we want to avoid.
But some events appear several times in these terms. Fix an integer k between G – C + 1 and G. A distribution of TIPs avoiding exactly k gaps gets counted 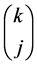 times in the term:
times in the term:
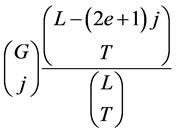
for every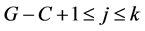 : those are the possibilities to choose j among the k gaps the distribution avoids. To get an exact formula for the probability of avoiding at least G – C + 1 gaps, there is a need to compensate this via an inclusion-exclusion method. To prove that in the sum above one counts exactly one time a configuration of TIPs avoiding exactly k gaps, it remains to prove the formula:
: those are the possibilities to choose j among the k gaps the distribution avoids. To get an exact formula for the probability of avoiding at least G – C + 1 gaps, there is a need to compensate this via an inclusion-exclusion method. To prove that in the sum above one counts exactly one time a configuration of TIPs avoiding exactly k gaps, it remains to prove the formula:

For the sake of readability, let us note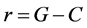 . Then one may transform it:
. Then one may transform it:

Hence the sum we are interested in is rewritten:
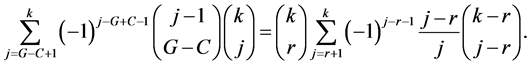
And it remains to prove:

We may use an analytic proof. Define the polynomial in two variables:
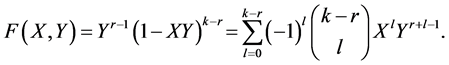
Now let  and eventually:
and eventually:
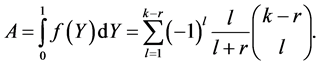
Putting  one sees that
one sees that  It thus remains a simple equality to check, namely
It thus remains a simple equality to check, namely 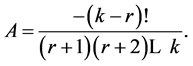 Using the factorized form of
Using the factorized form of  we get
we get  Then one computes the integral via integration by parts:
Then one computes the integral via integration by parts:
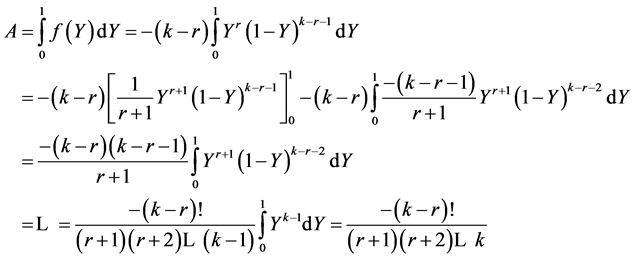
Annex
aIn Annex Table A1, TIPs can also include secondary positions of topological interest defined by the intersection of the polypeptide chain with the axis involving the Nand C-termini for protein domain structures with few beta-strands to ensure that T ≥ G and allow thereby for predictions to be tested.


