Applied Mathematics
Vol.4 No.7(2013), Article ID:34313,5 pages DOI:10.4236/am.2013.47141
How an Effective “Cosmological Constant” May Affect a Minimum Scale Factor, to Avoid a Cosmological Singularity (Breakdown of the First Singularity Theorem)
Physics Department, Chongqing University, Chongqing, China
Email: abeckwith@uh.edu
Copyright © 2013 Andrew Walcott Beckwith. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 29, 2013; revised May 29, 2013; accepted June 7, 2013
Keywords: Raychaudhuri Equation; Fundamental Singularity Theorem; Bianchi I Universe; Effective Cosmological Parameter
ABSTRACT
We once again reference Theorem 6.1.2 of the book by Ellis, Maartens, and MacCallum in order to argue that if there is a non zero initial scale factor, that there is a partial breakdown of the Fundamental Singularity theorem which is due to the Raychaudhuri equation. Afterwards, we review a construction of what could happen if we put in what Ellis, Maartens, and MacCallum call the measured effective cosmological constant and substitute  in the Friedman equation. i.e. there are two ways to look at the problem, i.e. after
in the Friedman equation. i.e. there are two ways to look at the problem, i.e. after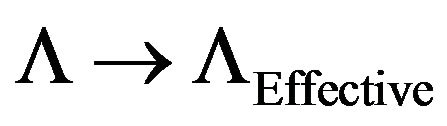 , set
, set 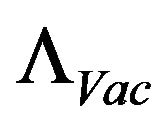 as equal to zero, and have the left over
as equal to zero, and have the left over  as scaled to background cosmological temperature, as was postulated by Park (2002) or else have
as scaled to background cosmological temperature, as was postulated by Park (2002) or else have 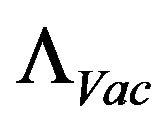 as proportional to
as proportional to 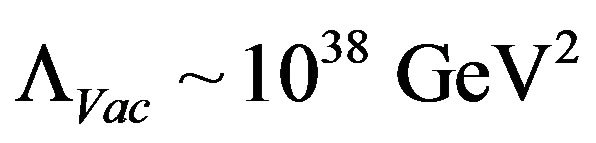 which then would imply using what we call a 5-dimensional contribution to
which then would imply using what we call a 5-dimensional contribution to  as proportional to
as proportional to . We find that both these models do not work for generating an initial singularity.
. We find that both these models do not work for generating an initial singularity.  removal as a non zero cosmological constant is most easily dealt with by a Bianchi I universe version of the generalized Friedman equation. The Bianchi I universe case almost allows for use of Theorem 6.1.2. But this Bianchi 1 Universe model almost in fidelity with Theorem 6.1.2 requires a constant non zero shear for initial fluid flow at the start of inflation which we think is highly unlikely.
removal as a non zero cosmological constant is most easily dealt with by a Bianchi I universe version of the generalized Friedman equation. The Bianchi I universe case almost allows for use of Theorem 6.1.2. But this Bianchi 1 Universe model almost in fidelity with Theorem 6.1.2 requires a constant non zero shear for initial fluid flow at the start of inflation which we think is highly unlikely.
1. Introduction
The present document is to determine what may contribute to a nonzero initial radius, i.e. not just an initial nonzero energy value, as Kauffman’s paper [1] would imply, and how different models of contributing vacuum energy, initially may affect divergence from the first singularity theorem. The choices of what can be used for an effective cosmological constant will affect if we have a four dimensional universe in terms of effective contributions to vacuum energy, or if we have a five dimensional universe. The second choice will probably necessitate a tie in with Kaluza Klein geometries, leaving open possible string theory cosmology. In order to be self contained, this paper will give partial re productions of Beckwith’s [2], but the 2nd half of this document will be completely different, i.e. when considering an effective cosmological constant. With four different cases, the last case is unphysical, even if it has, via rescaling zero effective cosmological constant, due to an effective “fluid mass”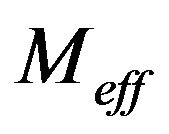 .
.
2. Looking at the First Singularity Theorem and How It Could Fail
Again, we restate at what is given by Ellis, Maartens, and MacCallum [3] as to how to state the fundamental singularity theorem.
Theorem 6.1.2 (Irrotational Geodestic singularities) If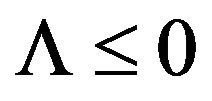 ,
,  , and
, and 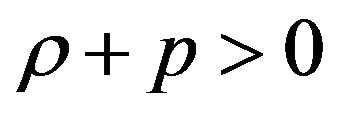 in a fluid flow for which
in a fluid flow for which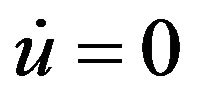 ,
, 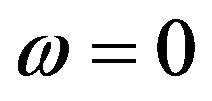 and
and  at some time
at some time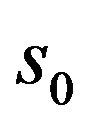 , then a spacetime singularity, where either
, then a spacetime singularity, where either 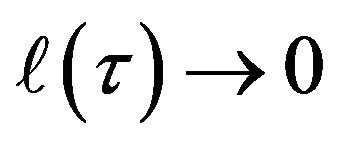 or
or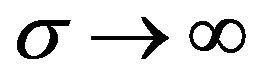 , occurs at a finite proper time
, occurs at a finite proper time 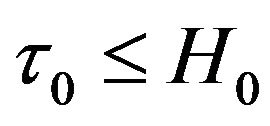 before
before .
.
As was brought up by Beckwith [2], if there is a non zero initial energy for the universe, a supposition which is counter to ADM theory as seen in Kolb and Turner [4] (1991), then the supposition by Kauffman [1] is supportable with evidence, i.e. then if there is a non zero initial energy, is this in any way counter to Theorem 6.1 above? We will review this question, keeping in mind that. 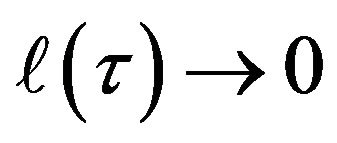 is in reference to a scale factor, as written by Ellis, Maartens, and MacCallum [3], vanishing.
is in reference to a scale factor, as written by Ellis, Maartens, and MacCallum [3], vanishing.
3. Looking at How to Form 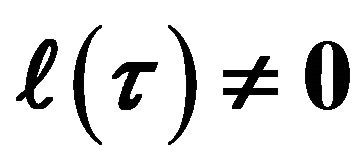 for All Scale Factors
for All Scale Factors
What was done by Beckwith [2] involved locking in the value of Planck’s constant initially. Doing that locking in of an initial Planck’s constant would be commensurate with some power of the mass within the Hubble parameter, namely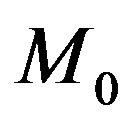 ,
,
 (1)
(1)
We would argue that a given amount of mass, 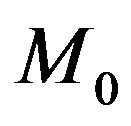 would be fixed in by initial conditions, at the start of the universe and that if energy, is equal to mass
would be fixed in by initial conditions, at the start of the universe and that if energy, is equal to mass 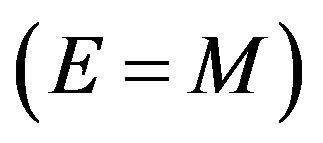 that in fact locking in a value of initial energy, according to the dimensional argument of
that in fact locking in a value of initial energy, according to the dimensional argument of 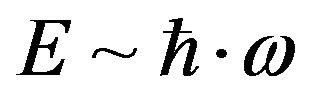 that having a fixed initial energy of
that having a fixed initial energy of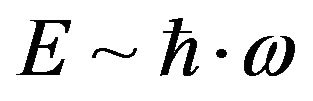 , with Planck’s constant fixed would be commensurate with, for very high frequencies,
, with Planck’s constant fixed would be commensurate with, for very high frequencies,  of having a non zero initial energy, thereby confirming in part Kauffmann [1], as discussed in Appendix A, for conditions for a non zero lower bound to the cosmological initial radius. If so then we always have
of having a non zero initial energy, thereby confirming in part Kauffmann [1], as discussed in Appendix A, for conditions for a non zero lower bound to the cosmological initial radius. If so then we always have . We will then next examine the consequences of
. We will then next examine the consequences of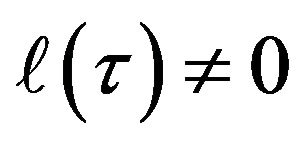 . i.e. what if
. i.e. what if 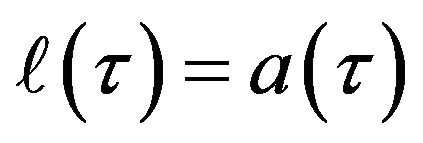 for a FLRW cosmology?
for a FLRW cosmology?
4. 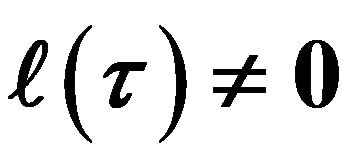 and What to Look for in Terms of the Raychaudhuri-Elders Equation for
and What to Look for in Terms of the Raychaudhuri-Elders Equation for 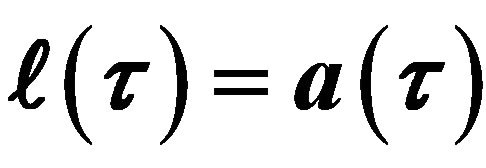 at the Start of Cosmological Expansion in FLRW Cosmology
at the Start of Cosmological Expansion in FLRW Cosmology
We will start off with 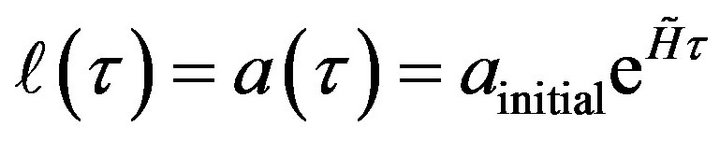 with
with 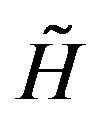 an initial huge Hubble parameter
an initial huge Hubble parameter
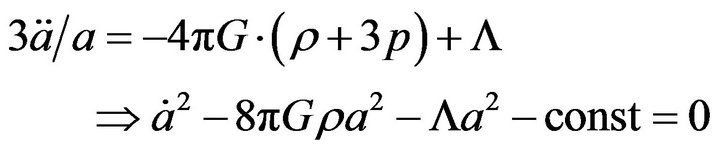 (2)
(2)
Equation (2) above becomes, with 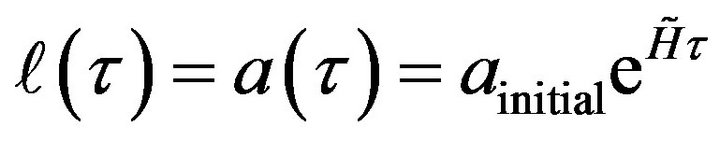 introduced will lead to
introduced will lead to
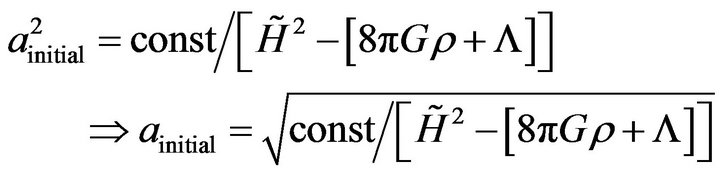 (3)
(3)
5. Analyzing Equation (3) for Different Candidate Values of , with
, with  for Three Cases
for Three Cases
The equation to look at if we have 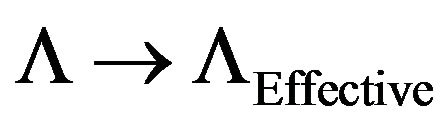 put into Equation (3) is to go to, instead to looking at
put into Equation (3) is to go to, instead to looking at
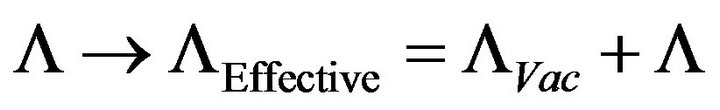 (4)
(4)
Case 1 set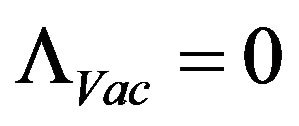 , and
, and  [5] such that in the present era with T about 2.7 today
[5] such that in the present era with T about 2.7 today
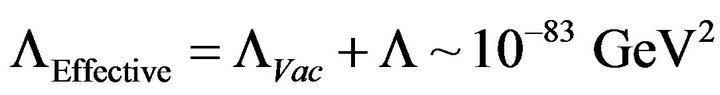 (today) (5)
(today) (5)
This would change to , if the temperature T were about 
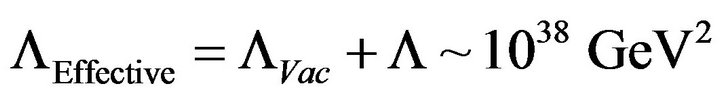 (Plank era) (6)
(Plank era) (6)
The upshot, is that if we have Case 1, we will not have a singularity if we use Theorem 6.1 Case 2 set , and such that
, and such that  in the present era with T about 2.7 today The upshot, is that if we have Case 2, we will not have a singularity if we use Theorem 6.1 [3] unless the expression
in the present era with T about 2.7 today The upshot, is that if we have Case 2, we will not have a singularity if we use Theorem 6.1 [3] unless the expression  is less than or equal to zero. In reality this does not happen, and we have
is less than or equal to zero. In reality this does not happen, and we have
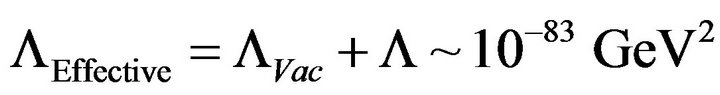 (always) (7)
(always) (7)
Case 3, set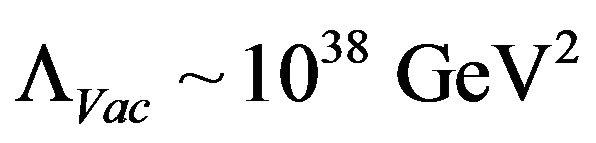 , and set
, and set 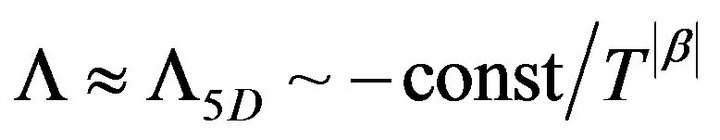 for all eras. Such that
for all eras. Such that
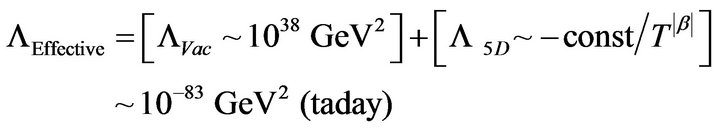 (8)
(8)
Also, we have that
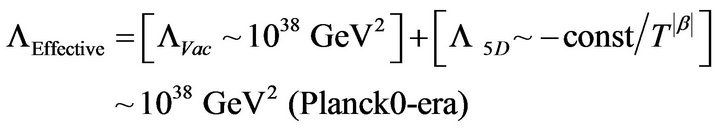 (9)
(9)
The only way to have any fidelity as to this Theorem 6.1 would be to eliminate the cosmological constant entirely. There is, one model where we can, in a sense “remove” a cosmological constant, as given by Ellis, Maartens, and MacCallum [3], and that is the Bianchi I universe model, as given on page 459 [3].
6. Bianchi I Universe in the Case of 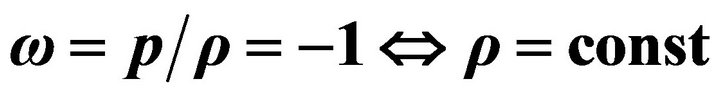
In this case, we have pressure as the negative quantity of density, and this will be enough to justify writing [3]
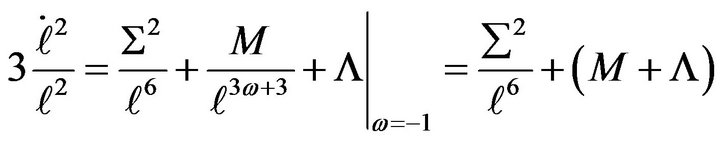 (10)
(10)
If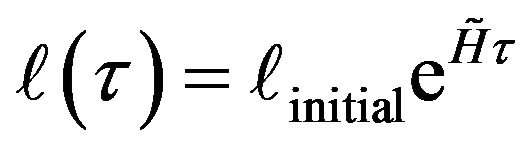 , we can re write Equation (10) as, if the sheer term in fluid flow, namely
, we can re write Equation (10) as, if the sheer term in fluid flow, namely 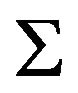 is a non zero constant term (i.e. at the onset of inflation, this is dubious) [3].
is a non zero constant term (i.e. at the onset of inflation, this is dubious) [3].
 (11)
(11)
In this situation, we are speaking of a cosmological constant and we will collect 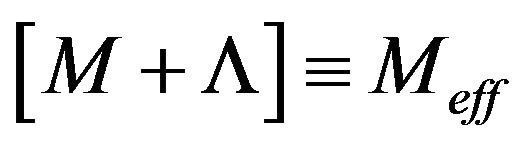 such that
such that
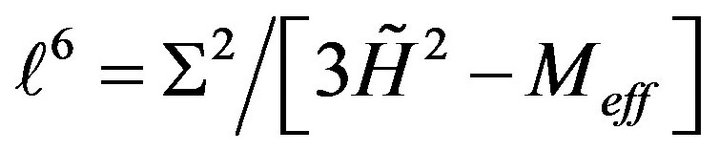 (12)
(12)
If we speak of a fluid approximation, this will lead to for Planck times looking at 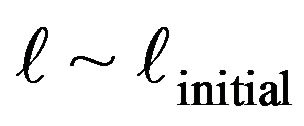 so we solve
so we solve
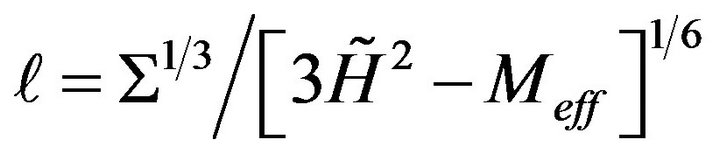 (13)
(13)
The above equation no longer has an effective cosmological constant, i.e. if matter is the same as energy, in early inflation, Equation (13) is a requirement that we have, effectively, for a finite but very large 
 (14)
(14)
7. Use of Thermal History of Hubble Parameter Equation Represented by Equation (14)
Ellis, Maartens, and MacCallum [3] treatment of the thermal history will then be, if 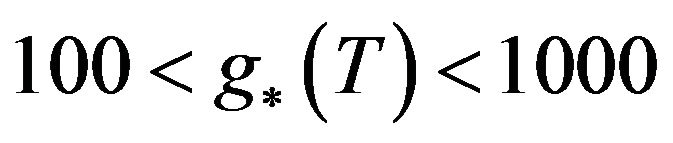
 (15)
(15)
Then we have for Equation (14), if the value of Equation (15) is very large due to Plank temperature values initially
 (16)
(16)
This assumes that there is an effective mass which is equal to adding both the Mass and a cosmological constant together. In a fluid model of the early universe. This is of course highly unphysical. But it would lead to Equation (13) having a non zero but almost infinitesimally small Equation (13) value. The vanishing of a cosmological constant inside an effective (fluid) mass, as given above by 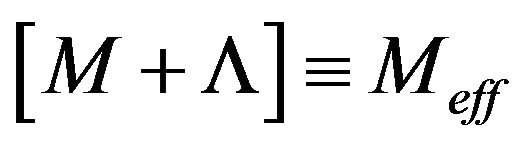 means that if we treat Equation (15) above as ALMOST infinite in value, that we ALMOST can satisfy Theorem 6.1 as written above. The fact that
means that if we treat Equation (15) above as ALMOST infinite in value, that we ALMOST can satisfy Theorem 6.1 as written above. The fact that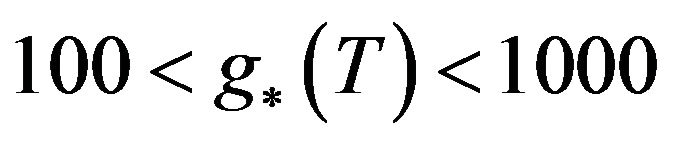 , i.e. we do not have infinite degrees of freedom, means that we get out of having Equation (15) become infinite, but it comes very close.
, i.e. we do not have infinite degrees of freedom, means that we get out of having Equation (15) become infinite, but it comes very close.
8. Use of Thermal History of Hubble Parameter Equation Represented by Equation (3) and an Effective Cosmological Parameter
Case 1 if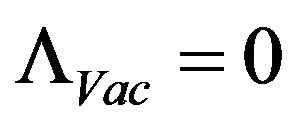 . But the cosmological parameter has a temperature dependence. Is the following true when the temperatures get enormous [2,5]?
. But the cosmological parameter has a temperature dependence. Is the following true when the temperatures get enormous [2,5]?
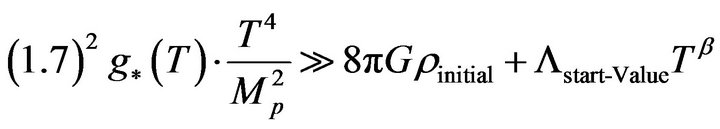 (17)
(17)
Not necessarily, It could break down.
Case 2 set , and such that
, and such that  (cosmological constant). Then we have
(cosmological constant). Then we have
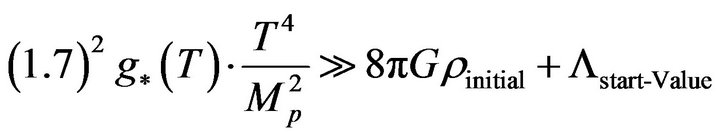 (18)
(18)
Yes, but we have problems because the cosmological parameter, while still very small is not zero or negative. So Theorem 6.1.2 above will not hold. But it can come close if the initial value of the cosmological constant is almost zero.
Case 3 when we can no longer use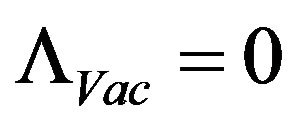 . Is the following true? When the Temperature is Planck temp?
. Is the following true? When the Temperature is Planck temp?
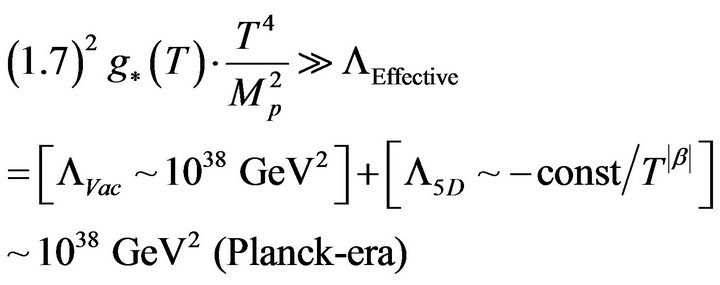 (19)
(19)
Almost certainly not true. Our section eight is far from optimal in terms of fidelity to Theorem 6.1.
We are close to Theorem 6.1.2 [3] on our Section seven. But this requires a demonstration of the constant value of the following term, in Section 7, namely in the Bianchi universe model, that the sheer term in fluid flow, namely  is a non zero constant term (i.e. at the onset of inflation, this is dubious). If it,
is a non zero constant term (i.e. at the onset of inflation, this is dubious). If it,  , is not zero, then even close to Planck time, it is not likely we can make the assertion mentioned above in Section 7.
, is not zero, then even close to Planck time, it is not likely we can make the assertion mentioned above in Section 7.
9. Conclusion: Non Singular Solutions to Cosmological Evolution Require New Thinking. No Initial Singularity
For Section 7 above we have almost an initial singularity, if we replace a cosmological constant with
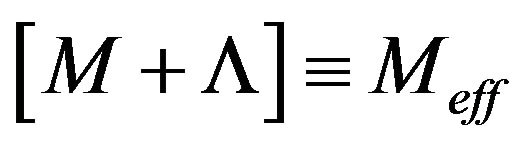 , And we also are assuming then, a thermal expression for the Hubble parameter given by EllisMaartens and Mac Callum [3] as a
, And we also are assuming then, a thermal expression for the Hubble parameter given by EllisMaartens and Mac Callum [3] as a 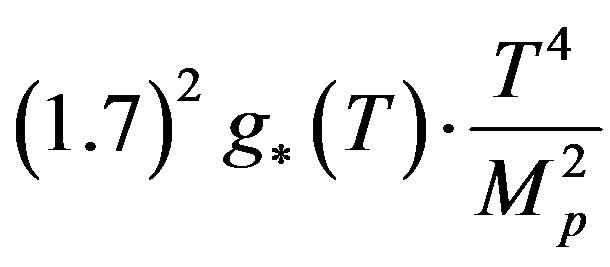
term which is almost infinite in initial value. Our conclusion is that we almost satisfy Theorem 6.1 if we assume an initially almost perfect fluid model to get results near fidelity with the initial singularity theorem (Theorem 6.1). This is dubious in that it is unlikely that , as a shear term is not zero, but constant over time, even initially.
, as a shear term is not zero, but constant over time, even initially.
The situation when we look at effective cosmological “constants” is even worse. i.e. Case 1 to Case 3 in Section eight no where come even close to what we would want for satisfying the initial singularity theorem (Theorem 6.1).
We as a result of these results will in future work examine applying Penrose’s CCC cosmology [6] to get about problems we run into due to the singularity theorem cosmology as represented by Theorem 6.1 above.
10. Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 110752. Also thanks to my father for his lifetime commitment to making me engaged in science before his death in September 29, 2012, in Eagle, Idaho.
REFERENCES
- S. Kauffmann, “ A Self Gravitational Upper Bound on Localized Energy Including That of Virtual Particles and Quantum Fields, Which Yield a Passable Dark Energy Density Estimate.” http://arxiv.org/abs/1212.0426
- A. Beckwith, “How Massive Gravitons (and Gravitinos) May Affect and Modify the Fundamental Singularity Theorem (Irrotational Geodestic Singularities from the Raychaudhuri Equation).” http://vixra.org/abs/1304.0147
- G. Ellis, R. Maartens and M. A. H. MacCallum, “Relativistic Cosmology,” Cambridge University Press, Cambridge, 2012. doi:10.1017/CBO9781139014403
- E. Kolb and M. Turner, “The Early Universe,” Westview Press, 1994.
- D. K. Park, H. Kim and S. Tamarayan, “Nonvanishing Cosmological Constant of Flat Universe in Brane World Scenarios,” Physics Letters, Vol. B535, 2002, pp. 5-10. doi:10.1016/S0370-2693(02)01729-X
- R. Penrose, “Cycles of Time,” The Bodley Head, London, 2010.
Appendix A: Indirect Support for a Massive Graviton
We follow the recent work of Kauffmann [1], which sets an upper bound to concentrations of energy, in terms of how he formulated the following equation put in below as Equation (A1). Equation (A1) specifies an inter-relationship between an initial radius R for an expanding universe, and a “gravitationally based energy” expression we will call  which lead to a lower bound to the radius of the universe at the start of the Universe’s initial expansion, with manipulations. The term
which lead to a lower bound to the radius of the universe at the start of the Universe’s initial expansion, with manipulations. The term 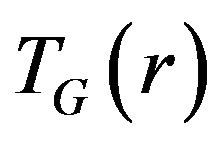 is defined via Equation (A2) afterwards. We start off with Kauffmann’s [1]
is defined via Equation (A2) afterwards. We start off with Kauffmann’s [1]
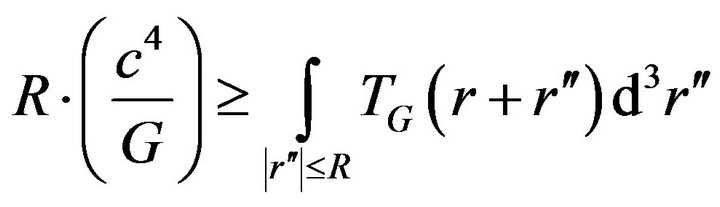 (A1)
(A1)
Kauffmann calls  a “Planck force” which is relevant due to the fact we will employ Equation (A1) at the initial instant of the universe, in the Planckian regime of space-time. Also, we make full use of setting for small r, the following:
a “Planck force” which is relevant due to the fact we will employ Equation (A1) at the initial instant of the universe, in the Planckian regime of space-time. Also, we make full use of setting for small r, the following:
 (A2)
(A2)
i.e. what we are doing is to make the expression in the integrand proportional to information leaked by a past universe into our present universe, with Ng style quantum infinite statistics use of
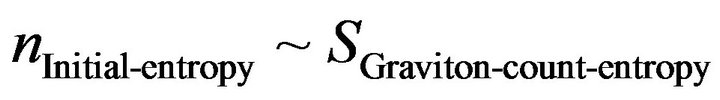 (A3)
(A3)
Then Equation (A1) will lead to
 (A4)
(A4)
Here,  , and
, and
 , and
, and
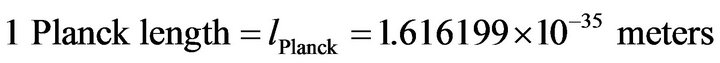
where we set  with
with , and
, and
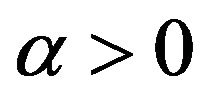 . Typically
. Typically  is about
is about 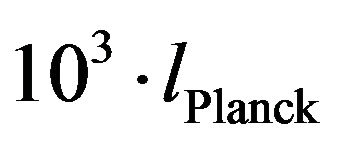 at the outset, when the universe is the most compact. The value of const is chosen based on common assumptions about contributions from all sources of early universe entropy, and will be more rigorously defined in a later paper.
at the outset, when the universe is the most compact. The value of const is chosen based on common assumptions about contributions from all sources of early universe entropy, and will be more rigorously defined in a later paper.

