Applied Mathematics
Vol.4 No.1A(2013), Article ID:27500,7 pages DOI:10.4236/am.2013.41A035
Derivative-Based Midpoint Quadrature Rule
Department of Mathematics, University of Central Arkansas, Conway, USA
Email: clarenceb@uca.edu
Received October 12, 2012; revised November 12, 2012; accepted November 19, 2012
Keywords: Numerical Integration; Numerical Quadrature; Midpoint Rule; Open Newton-Cotes Integration; Derivative-Based Quadrature
ABSTRACT
A new family of numerical integration formula is presented, which uses the function evaluation at the midpoint of the interval and odd derivatives at the endpoints. Because the weights for the odd derivatives sum to zero, the derivative calculations cancel out for the interior points in the composite form, so that these derivatives must only be calculated at the endpoints of the overall interval of integration. When using N subintervals, the basic rule which uses the midpoint function evaluation and the first derivative at the endpoints achieves fourth order accuracy for the cost of N/2 function evaluations and 2 derivative evaluations, whereas the three point open Newton-Cotes method uses 3N/4 function evaluations to achieve the same order of accuracy. These derivative-based midpoint quadrature methods are shown to be more computationally efficient than both the open and closed Newton-Cotes quadrature rules of the same order. This family of derivative-based midpoint quadrature rules are derived using the concept of precision, along with the error term. A theorem concerning the order of accuracy of quadrature rule using the concept of precision is provided to justify its use to determine the leading order error term.
1. Introduction
Open Newton-Cotes quadrature formula rely on a weighted averaged of function evaluations of the form
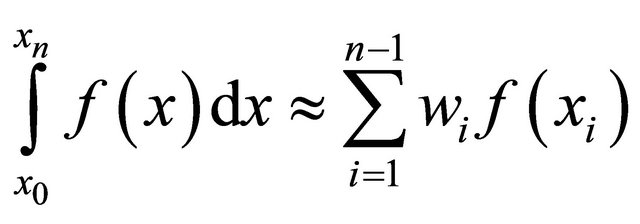 (1)
(1)
where there are n + 1 distinct uniformly distributed integration points at  within the interval [a, b], where
within the interval [a, b], where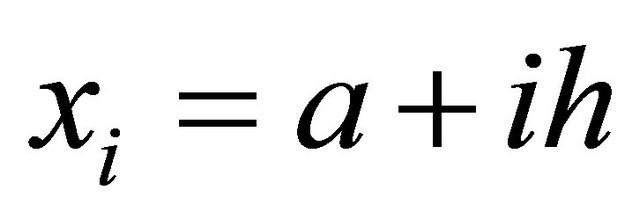 , and n − 1 weights wi. A common approach to finding the weights wi is based on the precision of a quadrature formula, which is the largest positive integer P such that the quadrature formula exactly integrated the monomials xk for
, and n − 1 weights wi. A common approach to finding the weights wi is based on the precision of a quadrature formula, which is the largest positive integer P such that the quadrature formula exactly integrated the monomials xk for 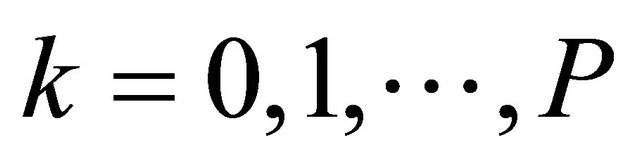 but not
but not![]() . Using the method of undetermined coefficients, this approach generates a system of P + 1 linear equations for the weights wi. Since the monomials
. Using the method of undetermined coefficients, this approach generates a system of P + 1 linear equations for the weights wi. Since the monomials 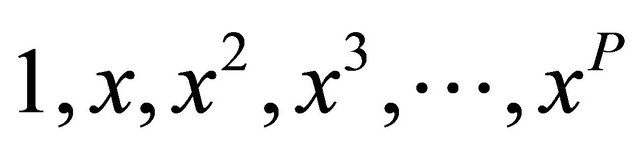 are linearly independent, the linear system obtained via this approach has a unique solution.
are linearly independent, the linear system obtained via this approach has a unique solution.
The midpoint rule is
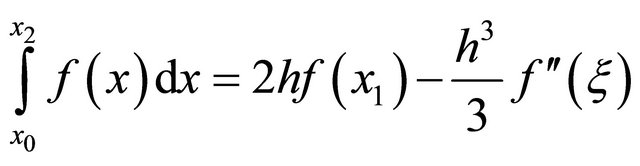 (2)
(2)
for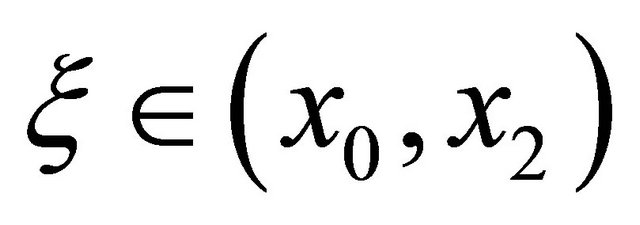 . In the composite form, the formula for the midpoint rule is
. In the composite form, the formula for the midpoint rule is
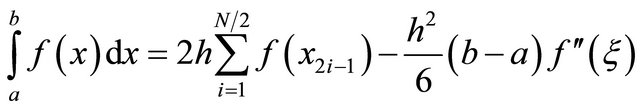 (3)
(3)
for . This quadrature rule uses N/2 function evaluations and is second order accurate.
. This quadrature rule uses N/2 function evaluations and is second order accurate.
The two-point open Newton-Cotes rule is
 (4)
(4)
for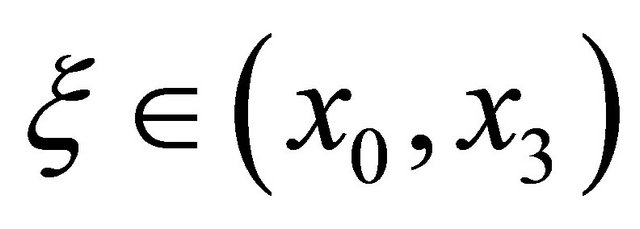 . In the composite form, the formula for n = 1 open Newton-Cotes quadrature rule is
. In the composite form, the formula for n = 1 open Newton-Cotes quadrature rule is
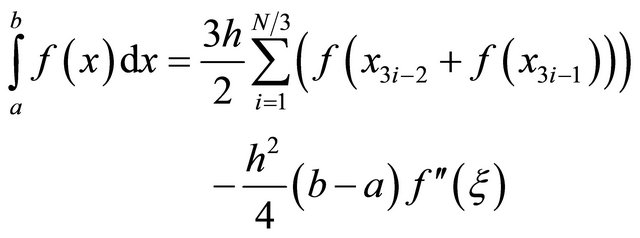 (5)
(5)
for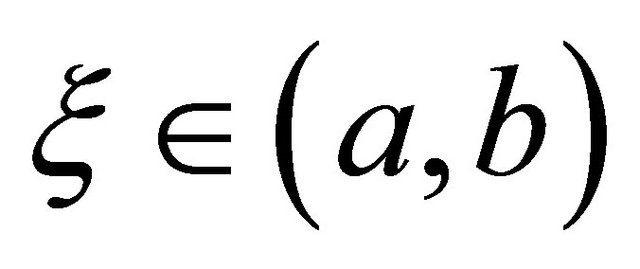 . This quadrature rule uses 2N/3 function evaluations and is also second order accurate.
. This quadrature rule uses 2N/3 function evaluations and is also second order accurate.
The three-point open Newton-Cotes or Milne’s rule is
 (6)
(6)
for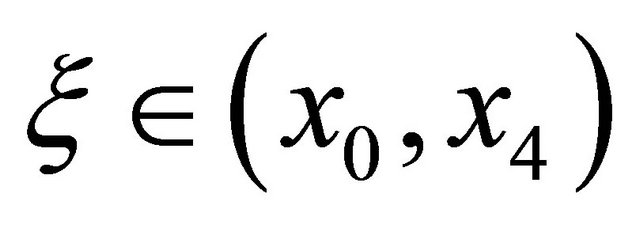 . In the composite form, the formula for n = 2 open Newton-Cotes quadrature rule is
. In the composite form, the formula for n = 2 open Newton-Cotes quadrature rule is
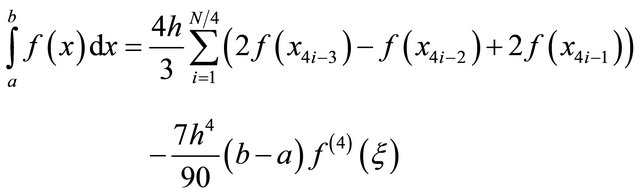 (7)
(7)
for . This quadrature rule uses 3N/4 function evaluations. This rule is fourth order accurate.
. This quadrature rule uses 3N/4 function evaluations. This rule is fourth order accurate.
These stencils can be generated quickly via mathematical software programs. From these results, in their basic forms, one can observe that the order of accuracy when the number of evaluation points n is odd is n + 2; whereas, the order of accuracy when the number of evaluation points is even is only n + 1. For their related composite quadrature formula for integrals over general intervals, the order of accuracy is reduced by one.
The precision of a numerical integration scheme is directly related to the number of parameters that can be manipulated within the numerical quadrature formula. For some cases, the precision is one higher than this number as the case for the midpoint rule and Simpson’s rule, due to advantageous cancellations within these formula. For closed Newton-Cotes quadrature, the number of parameters is one more than the number of intervals, since the endpoints are included; whereas for open Newton-Cotes quadrature, the number of parameters is one less than the number of intervals, since only the interior points are included. For Gauss-Legendre integration, both the locations and the weights need to be specified, for the generic interval [−1, 1], so there are twice as many parameters as evaluation locations for this type of quadrature. In each of these methods, by increasing the number of parameters, the precision and the order of accuracy of these methods increases.
Work by Dehghan et al., and related publications have focused on increasing the order of accuracy of standard numerical integration formula by two orders of accuracy by including the location of boundaries of the interval as two additional parameters, and rescaling the original integral to fit the optimal boundary locations. Using the concept of precision, they set up a system of nonlinear equations, which are solved approximately using a computer algebra system. Their system is nonlinear since the location of the endpoints along with the weights are parameters within the system. They have applied this technique to Gauss-Legendre quadrature [1], Gauss-Lobatto quadrature [2], Gauss-Chebyshev integration [3], closed Newton-Cotes integration [4], Gauss-Radau integration [5], Chebyshev-Newton-Cotes quadrature [6], semi-open Newton-Cotes [7] and open Newton-Cotes [8].
Burg [9] took a different approach by including first and higher order derivatives at the evaluation locations within the closed Newton-Cotes quadrature framework, in order to increase the number of parameters and hence the precision and order of accuracy of the resulting formula. He was able to establish theoretical error bounds for several of the derivative-based closed Newton-Cotes quadrature formula and showed that the resulting quadrature rules were more computationally efficient than similar order closed Newton-Cotes quadrature formula.
In this paper, the use of derivatives at the endpoints is investigated within the context of the midpoint rule, which is the one-point open Newton-Cotes quadrature rule or equivalently the one-point Gauss-Legendre quadrature rule. Because of the odd nature of the midpoint rule, the use of odd derivatives produces highly advantageous results, creating quadrature rules that are much more efficient than existing open or closed NewtonCotes quadrature rules. These new schemes are presented in the next section. In Section 3, a comparison of the computational costs of these methods is presented, where the minimum number of subintervals to achieve an error of 10−12 is calculated along with the number of function and derivative evaluations. Finally, in Section 4, numerical results are presented that demonstrate that the predicted order of accuracy is actually observed. A theorem concerning the leading order error term in a quadrature rule is proved in the appendix, along with an associated conjecture concerning the overall error in a quadrature rule.
2. Derivative-Based Midpoint Rule
A new class of quadrature formula based on derivatives can be obtained from the midpoint method by looking for quadrature form
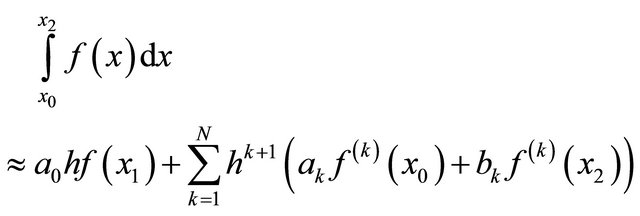 (8)
(8)
where N is the number of derivatives to include in the quadrature formula and h is the uniform spacing between each location xi. By using the concept of precision, a system of 2N + 1 linear equations can be derived for the coefficients ak and bk.
For instance, for N = 1 which only uses the first derivative, the quadrature formula as the form
 (9)
(9)
which creates the following system involving three parameters a0, a1 and b1
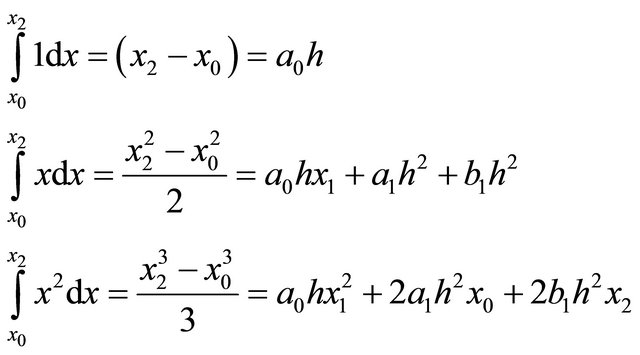 (10)
(10)
Solving for the undetermined coefficients a0, a1 and b1 and using the relationships that x1 = x0 + h and x2 = x0 + 2h, the numerical integration scheme for the first derivative-based midpoint rule
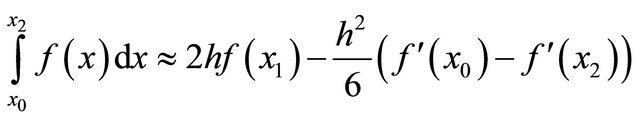 (11)
(11)
As was the case with the midpoint rule, the precision for this quadrature rule is one higher than expected, since it exactly integrates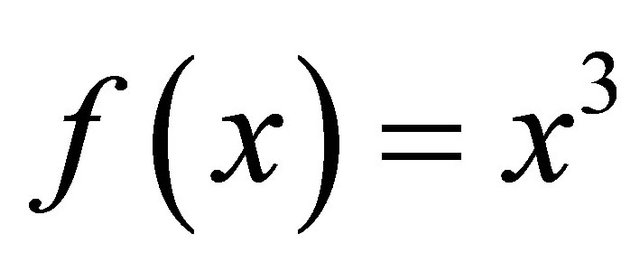 .
.
The error term for this quadrature rule and the other quadrature rules presented in this paper have been obtained by using a theorem and conjecture based on the concept of precision. Proved in the appendix, this theorem states that the error between the exact integral and the quadrature rule is related to the difference between the integral of the monomials and the numerical quadrature of the monomials. For the first derivative midpoint based quadrature rule shown above, since the precision is three, this rule exactly integrates the monomials 1, x, x2 and x3, but not x4. The leading order error term for this rule is based on the difference between the integral of x4 and the quadrature rule approximation of x4. The conjecture simplifies the infinite Taylor series into a single term, similar to the Taylor remainder term for the truncated Taylor series. Using this observation, the first derivativebased midpoint rule with error term is
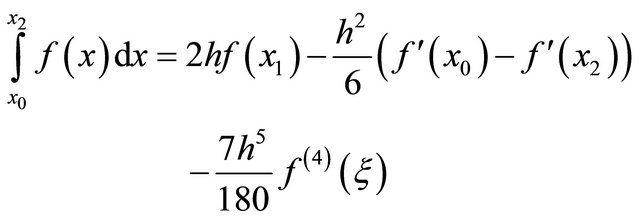 (12)
(12)
for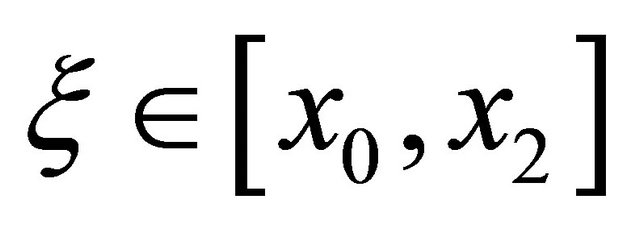 . Thus, this quadrature rule is fifth order accurate. Because the coefficients a1 and b1 sum to zero, these derivatives cancel out through the interior when used in the composite form, so the composite form of the quadrature rule is
. Thus, this quadrature rule is fifth order accurate. Because the coefficients a1 and b1 sum to zero, these derivatives cancel out through the interior when used in the composite form, so the composite form of the quadrature rule is
 (13)
(13)
for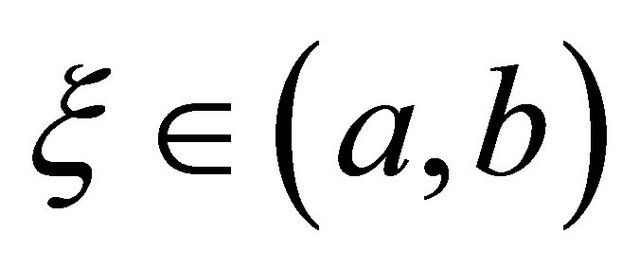 . This fourth-order quadrature rule uses N/2 function evaluations and two derivative evaluations.
. This fourth-order quadrature rule uses N/2 function evaluations and two derivative evaluations.
For the N = 2 case which uses the first and second derivatives, the quadrature formula has the form
 (14)
(14)
Using the concept of precision, this formula generates five equations with the five unknowns a0, a1, a2, b1 and b2, by exactly integrating the monomials  through x4. Solving this system, the optimal quadrature rule is
through x4. Solving this system, the optimal quadrature rule is
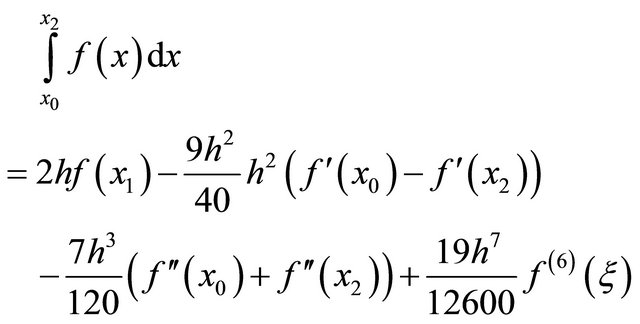 (15)
(15)
for some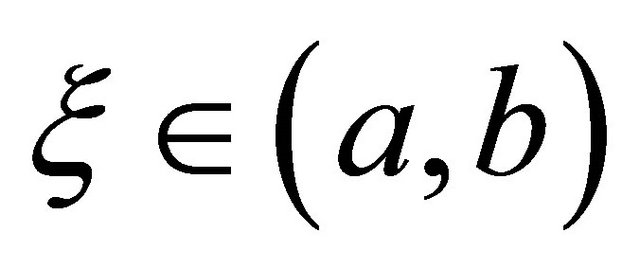 . Unfortunately, the signs of coefficients for the second derivatives are the same, so the same beneficial canceling does not occur here.
. Unfortunately, the signs of coefficients for the second derivatives are the same, so the same beneficial canceling does not occur here.
The N = 3 case, dealing only with the first and third derivatives, does have the nice cancellation. This quadrature rule can be stated as
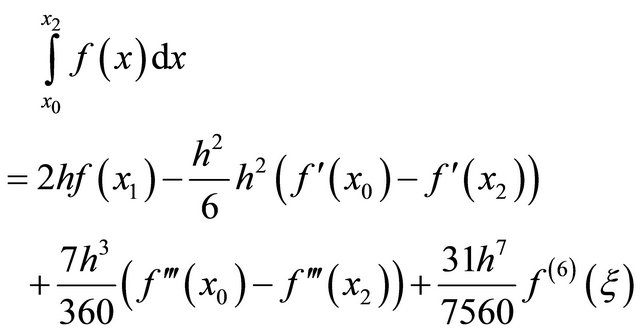 (16)
(16)
Because of this cancellation, the composite formula involving the first and third derivatives can be written as
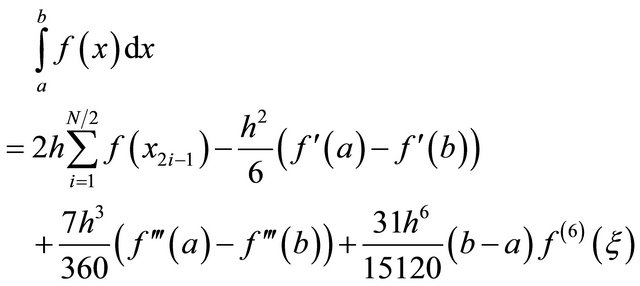 (17)
(17)
for . This sixth-order quadrature rule uses N/2 function evaluations, two first derivative evaluations and two third derivative evaluations.
. This sixth-order quadrature rule uses N/2 function evaluations, two first derivative evaluations and two third derivative evaluations.
This pattern continues for all cases dealing with odd derivatives result in quadrature rules where the derivatives cancel out at the interior points and must only be evaluated at the endpoints of the overall interval. By using the first, third and fifth derivatives, an eighth-order quadrature rule can be defined, which uses N/2 function evaluations and two first, third and fifth derivatives. This quadrature rule has the form
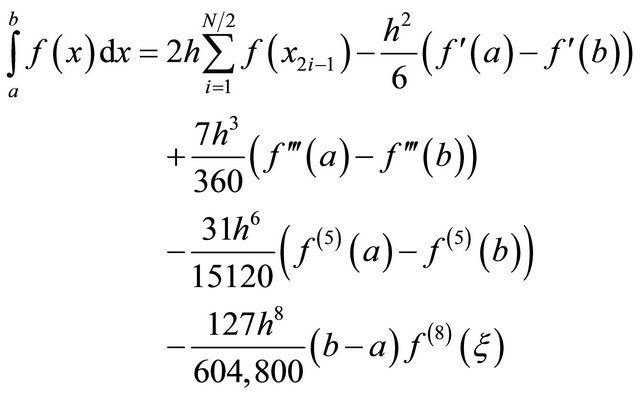 (18)
(18)
for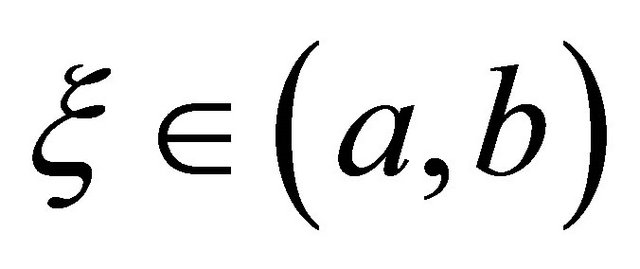 . This pattern continues for higher derivatives, assuming that only the odd derivatives are used in the quadrature formula.
. This pattern continues for higher derivatives, assuming that only the odd derivatives are used in the quadrature formula.
As a last comment, the pattern for generating higher order accuracy derivative-based quadrature rules of the open Newton-Cotes type involves the use of a central difference approximation to the derivative in the error term, using a one order lower derivative. As a result, the weights for the lower order derivatives do not change as the quadrature formula is expanded. Because of this relationship, the weights for the next derivative terms involve the coefficients for the leading order error term in the lower order quadrature rule, as can be clearly seen in the preceding cases.
3. Computational Efficiency in Composite Form
To compare the computational efficiency of the various open and closed Newton-Cotes formula along with the derivative-based midpoint quadrature formula, the number of calculations required by each quadrature formula to guarantee a level of accuracy of 10−12 is calculated for the following integrals:
 (19)
(19)
In Table 1, the number of function and derivative evaluations for the various quadrature formula presented herein is listed for the first integral. The best second order accurate method is the midpoint method. Assuming that the derivative evaluations are roughly the same amount of computational complexity as the function evaluations, the best fourth order accurate method is the first derivative-based midpoint method, using 829 function and derivative evaluations. The best sixth order accurate method is the derivative-based midpoint method using the first and third derivatives, which requires only 93 function and derivative evaluations. The eighth order accurate derivative based method requires only 37 function and derivative evaluations to guarantee an accuracy of less than 10−12.
In Table 2, the numerical function and derivative evaluations for the various quadrature formula presented herein is listed for the second integral. As was the case with the first integral, the derivative-based midpoints obtain the desired level of accuracy using fewer function and derivative evaluations than either the closed or open Newton-Cotes methods. The computational cost for each of these methods is shown in Table 3, confirms that these methods will always be the most efficient, due to the size of the constant coefficient. As seen in these results, the derivative-based methods are computationally superior to either the closed or open Newton-Cotes methods of the same order of accuracy.
Table 1. Computational Cost for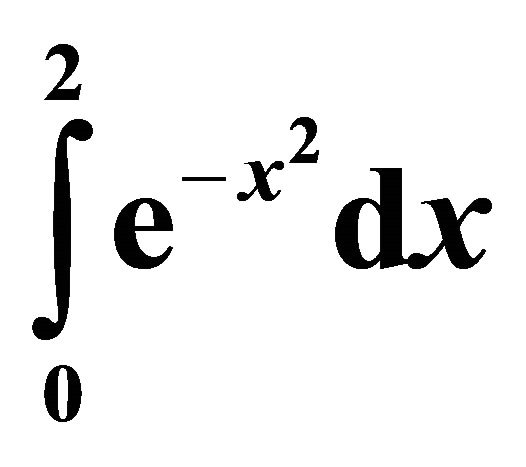 .
.

Table 2. Computational Cost for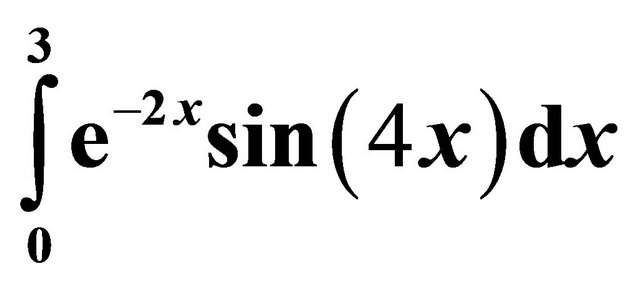 .
.
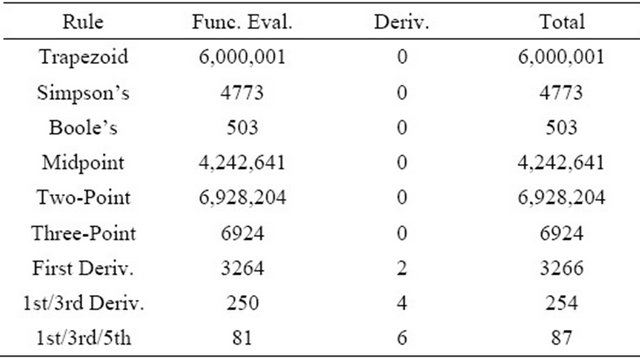
Table 3. Computational Cost for Closed and Open NewtonCotes and Derivative-Based Quadrature Formula.

4. Numerical Results
To demonstrate the accuracy of the new numerical integration formula based on the inclusion of the derivativethe values of 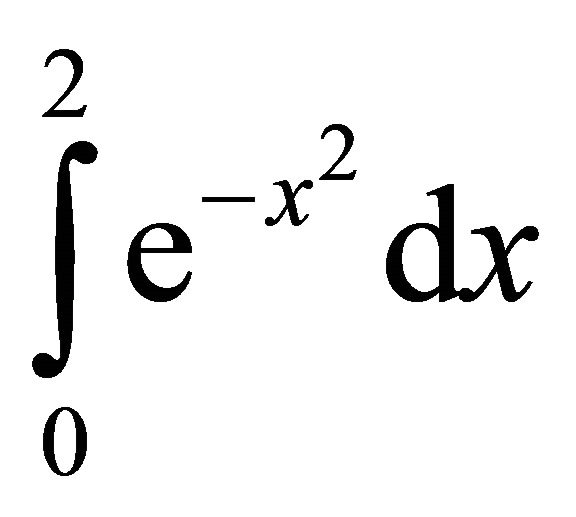 and
and 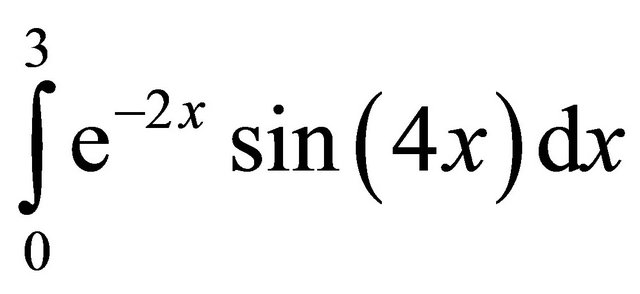 are estimated using the midpoint rule and the first three derivative-based midpoint quadrature rules, dealing with the first derivative, the first and third derivatives and the first, third and fifth derivatives.
are estimated using the midpoint rule and the first three derivative-based midpoint quadrature rules, dealing with the first derivative, the first and third derivatives and the first, third and fifth derivatives.
The calculation of the order of accuracy is obtained using the following approach. Let 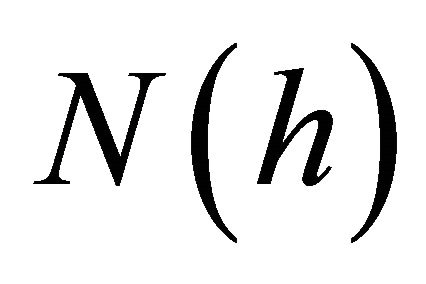 represent the numerical results using step size
represent the numerical results using step size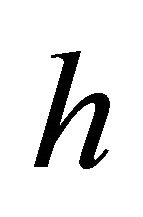 . The following formula is used to calculate the observed order of accuracy
. The following formula is used to calculate the observed order of accuracy![]() , involving numerical results
, involving numerical results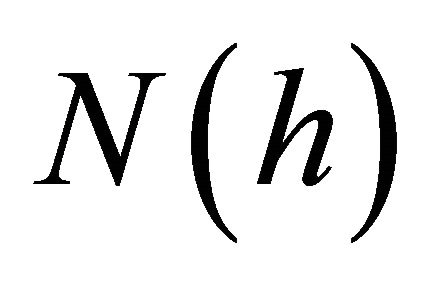 ,
, 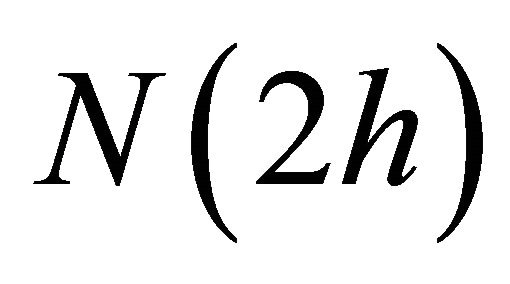 and
and 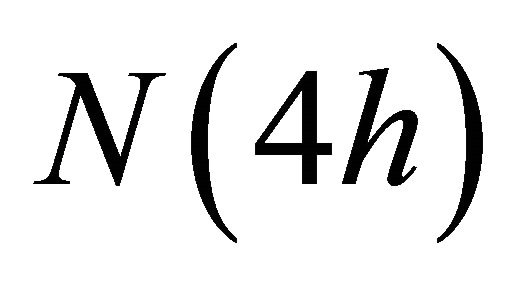 or
or
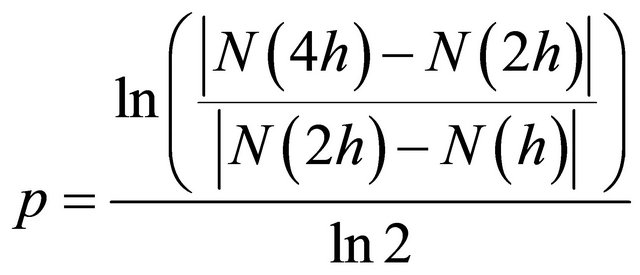 (20)
(20)
The programming language REXX [10,11] was used to generate these numerical results, using 50 significant digits for the calculations.
In Tables 4-7, the results for the numerical approximation to 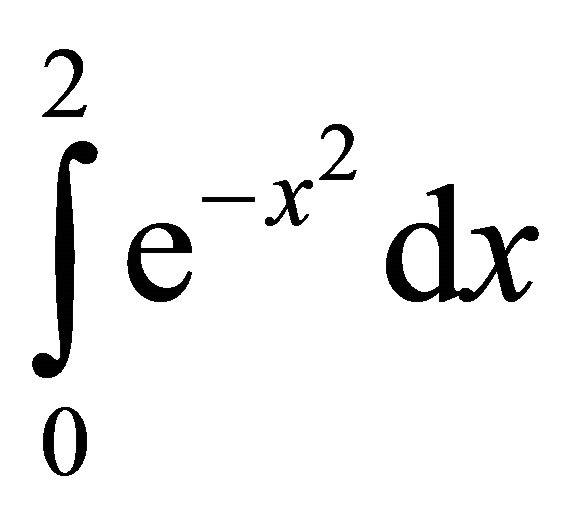 are shown; and in Tables 8-11, the results for the numerical approximation to
are shown; and in Tables 8-11, the results for the numerical approximation to
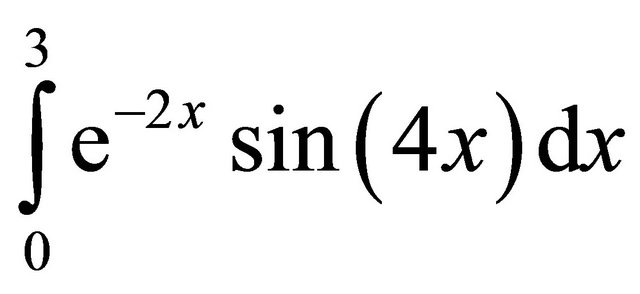 are shown. For both integrals, the observed order of accuracy of the derivative-based midpoint quadrature formula is converging to the appropriate theoretical order of accuracy. The first derivative-based midpoint rule is clearly fourth order accurate; the first and third derivative rule is demonstrating sixth order accuracy; and the quadrature rule using first, third and fifth derivatives shows eighth order accurate results. For these methods, the derivatives are only evaluated at the overall endpoints of the interval of integration, rather than at the interior points. Thus, these methods are only slightly more computationally expensive than the midpoint rule, even though their accuracies are significantly higher.
are shown. For both integrals, the observed order of accuracy of the derivative-based midpoint quadrature formula is converging to the appropriate theoretical order of accuracy. The first derivative-based midpoint rule is clearly fourth order accurate; the first and third derivative rule is demonstrating sixth order accuracy; and the quadrature rule using first, third and fifth derivatives shows eighth order accurate results. For these methods, the derivatives are only evaluated at the overall endpoints of the interval of integration, rather than at the interior points. Thus, these methods are only slightly more computationally expensive than the midpoint rule, even though their accuracies are significantly higher.
Table 4. Midpoint Rule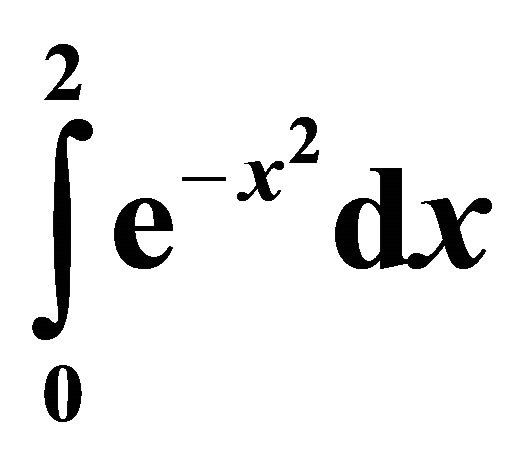 .
.
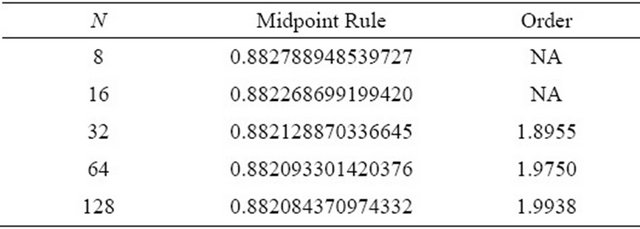
Table 5. First Derivative Rule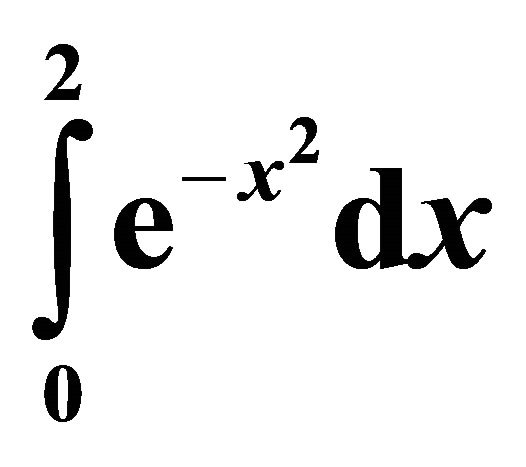 .
.
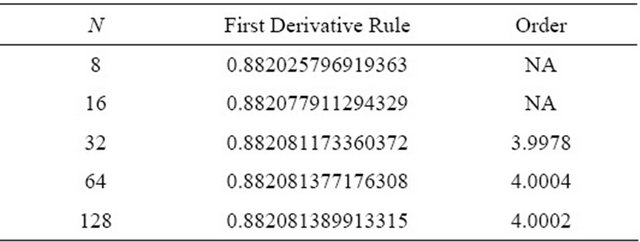
Table 6. 1st/3rd Deriv. Rule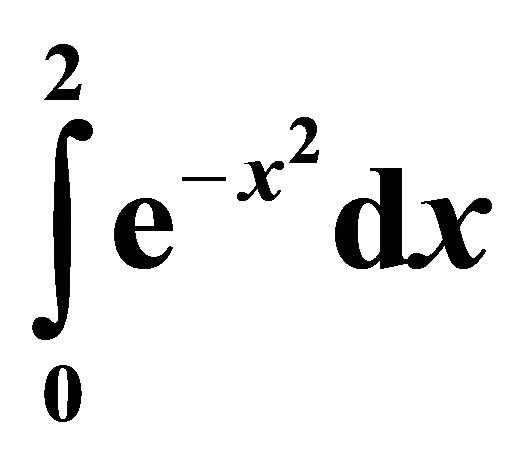 .
.
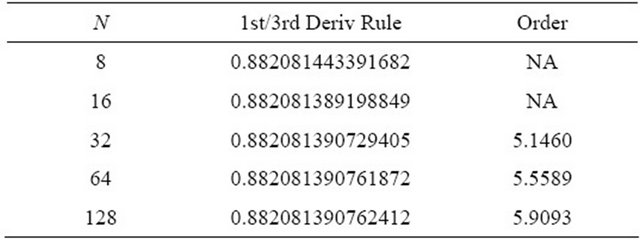
Table 7. 1st/3rd/5th Deriv. Rule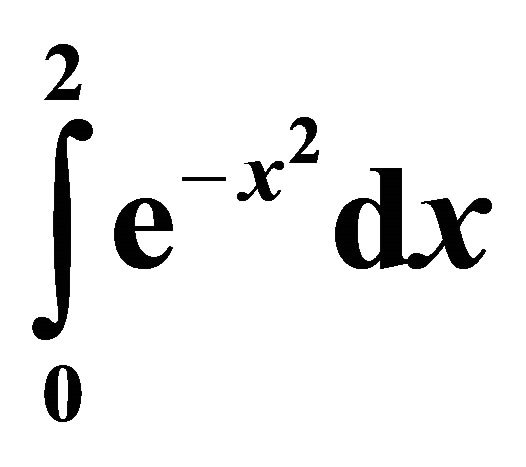 .
.

Table 8. Midpoint Rule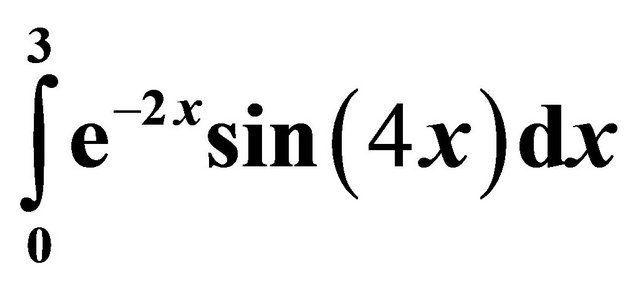 .
.
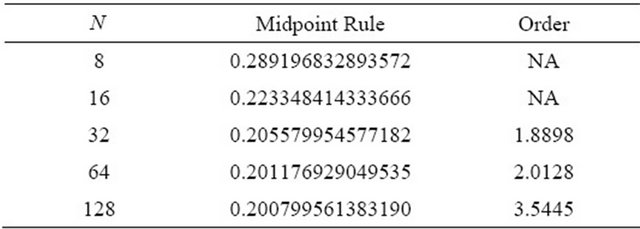
Table 9. First Deriv. Rule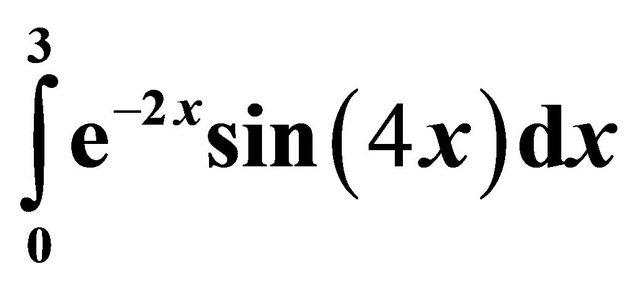 .
.
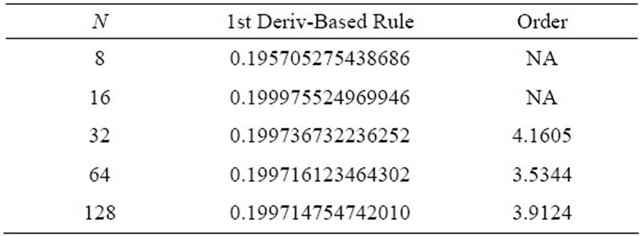
Table 10. 1st/3rd Deriv. Rule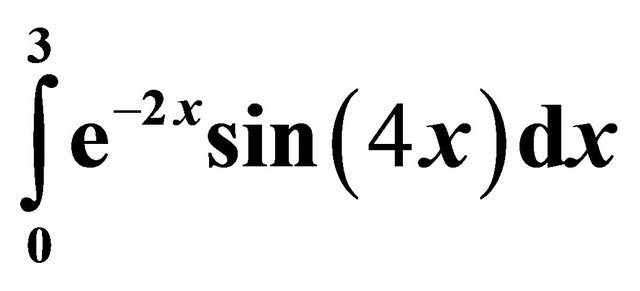 .
.
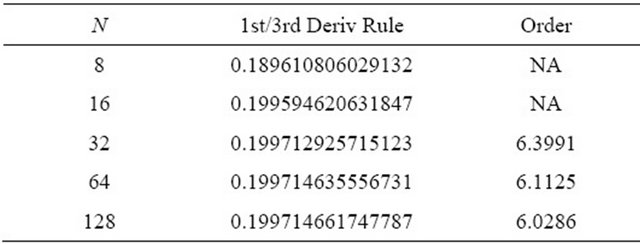
Table 11. 1st/3rd/5th Deriv. Rule .
.
5. Conclusions
New derivative-based midpoint quadrature rules were presented, along with their error terms. When using only odd derivatives, the coefficients for the odd derivatives sum to zero; thus, when using these quadrature rules in a composite formula, all of the derivatives at interior points cancel out. As a result, higher order accurate quadrature rules can be generated by only evaluating the odd derivatives at two locations, which are the endpoints of the interval of integration. These new derivative-based quadrature rules are much more computationally efficient than the open and closed Newton-Cotes formula of the same order of accuracy. Additionally, these derivative-based midpoint quadrature rules build upon each other, so that the only change needed to increase the order of accuracy is to determine the coefficients (or weights) for the next odd derivative, without changing the weights for the lower odd derivatives.
The computational cost for each of these methods was analyzed and compared to both the open and the closed Newton-Cotes formula for two different integrals
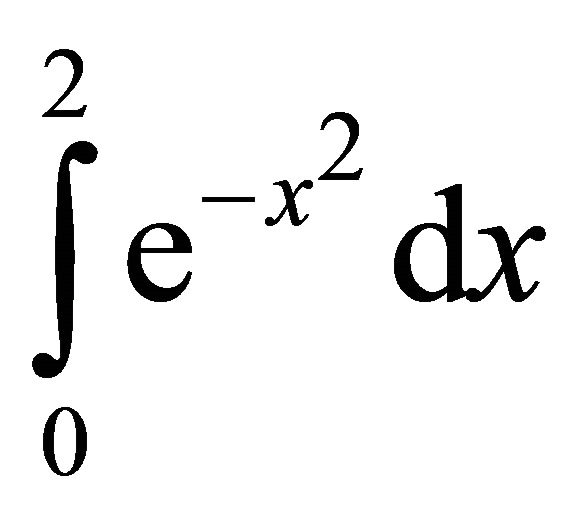 and
and . The new derivativebased midpoint quadrature formula were superior computationally to the same order open or closed NewtonCotes formula, primarily because of the computational efficiency of the midpoint rule, which only evaluates the function at half of the nodes, and the increase in the order of accuracy by evaluating the derivative at only two locations.
. The new derivativebased midpoint quadrature formula were superior computationally to the same order open or closed NewtonCotes formula, primarily because of the computational efficiency of the midpoint rule, which only evaluates the function at half of the nodes, and the increase in the order of accuracy by evaluating the derivative at only two locations.
These quadrature rules were obtained by using the concept of precision. If a quadrature rule has precision P, then it exactly integrates the monomials 1, x, through xP but not![]() . Using this concept, a system of P + 1 linear equations in the coefficients of the quadrature formula can be generated. Furthermore, as is shown in the appendix, the concept of precision can be used to generate the leading order error term for the quadrature formula.
. Using this concept, a system of P + 1 linear equations in the coefficients of the quadrature formula can be generated. Furthermore, as is shown in the appendix, the concept of precision can be used to generate the leading order error term for the quadrature formula.
REFERENCES
- E. Babolian, M. Masjed-Jamei and M. R. Eslahchi, “On Numerical Improvement of Gauss-Legendre Quadrature Rules,” Applied Mathematics and Computation, Vol. 160, No. 3, 2005, pp. 779-789. doi:10.1016/j.amc.2003.11.031
- M. R. Eslahchi, M. Masjed-Jamei and E. Babolian, “On Numerical Improvement of Gauss-Lobatto Quadrature Rules,” Applied Mathematics and Computation, Vol. 164, No. 3, 2005, pp. 707-717. doi:10.1016/j.amc.2004.04.113
- M. R. Esclahchi, M. Dehghan and M. Masjed-Jamei, “On Numerical Improvement of the First Kind Gauss-Chebyshev Quadrature Rules,” Applied Mathematics and Computation, Vol. 165, No. 1, 2005, pp. 5-21. doi:10.1016/j.amc.2004.06.102
- M. Dehghan, M. Masjed-Jamei and M. R. Eslahchi, “On Numerical Improvement of Closed Newton-Cotes Quadrature Rules,” Applied Mathematics and Computation, Vol. 165, No. 2, 2005, pp. 251-260. doi:10.1016/j.amc.2004.07.009
- M. Masjed-Jamei, M. R. Eslahchi and M. Dehghan, “On Numerical Improvement of Gauss-Radau Quadrature Rules,” Applied Mathematics and Computation, Vol. 168, No. 1, 2005, pp. 51-64. doi:10.1016/j.amc.2004.08.046
- M. R. Esclahchi, M. Dehghan and M. Masjed-Jamei, “The First Kind Chebyshev-Newton-Cotes Quadrature Rules (Closed Type) and Its Numerical Improvement,” Applied Mathematics and Computation, Vol. 168, No. 1, 2005, pp. 479-495. doi:10.1016/j.amc.2004.09.048
- M. Dehghan, M. Masjed-Jamei and M. R. Eslahchi, “The Semi-Open Newton-Cotes Quadrature Rule and Its Numerical Improvement,” Applied Mathematics and Computation, Vol. 171, No. 2, 2005, pp. 1129-1140. doi:10.1016/j.amc.2005.01.137
- M. Dehghan, M. Masjed-Jamei and M. R. Eslahchi, “On Numerical Improvement of Open Newton-Cotes Quadrature Rules,” Applied Mathematics and Computation, Vol. 175, No. 1, 2006, pp. 618-627. doi:10.1016/j.amc.2005.07.030
- C. O. E. Burg, “Derivative-Based Closed Newton-Cotes Numerical Quadrature,” Applied Mathematics and Computation, Vol. 218, No. 13, 2012, pp. 7052-7065 doi:10.1016/j.amc.2011.12.060
- The REXX Language Association. http://www.rexxla.org
- http://www.rexxinfo.org
Appendix
In this appendix, a theorem concerning the leading order error term in a quadrature rule is proved. Based on its association with the Taylor Remainder Theorem, a conjecture concerning the overall error term in a quadrature rule is made. A definition for a general quadrature rule of precision P is given below, followed by the theorem, its proof and the conjecture.
Definition: A numerical quadrature rule 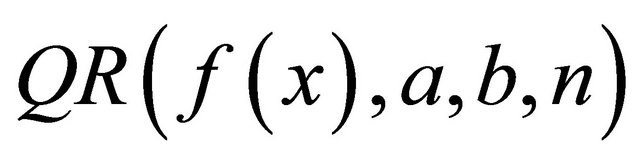 approximates the integral
approximates the integral
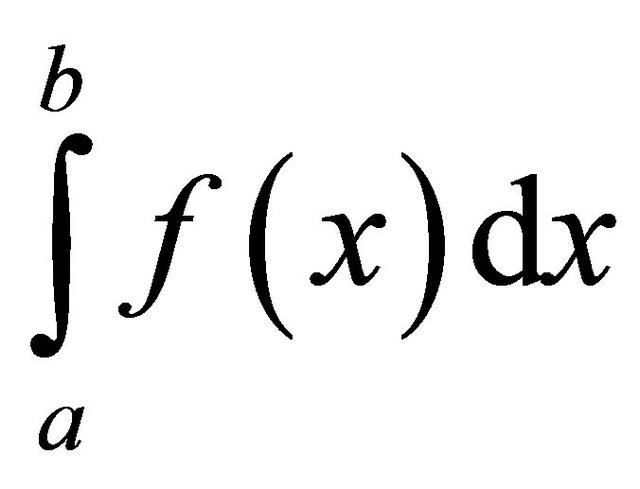
using n uniformly spaced subintervals xi = a + ih where 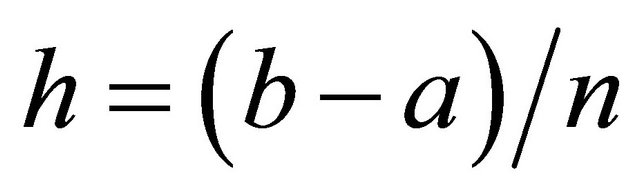 to precision P if it exactly integrates the monomials 1, x, x2 through xP but not
to precision P if it exactly integrates the monomials 1, x, x2 through xP but not![]() .
.
Theorem: Let  be infinitely differentiable on [a, b] and its Taylor series centered at x = a converges for all
be infinitely differentiable on [a, b] and its Taylor series centered at x = a converges for all . Let
. Let 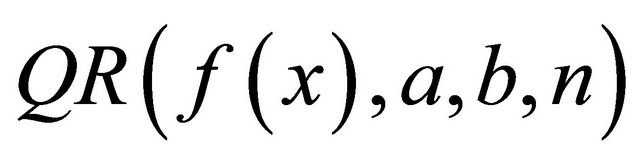 be a quadrature rule of precision P. Then, the error between
be a quadrature rule of precision P. Then, the error between
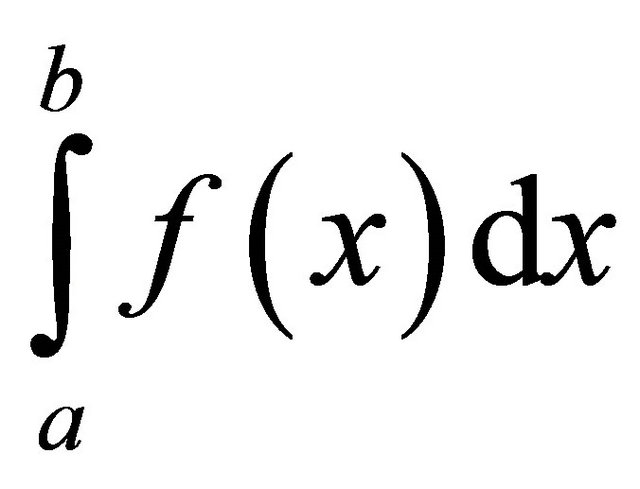 and approximation obtained by the quadrature rule is
and approximation obtained by the quadrature rule is
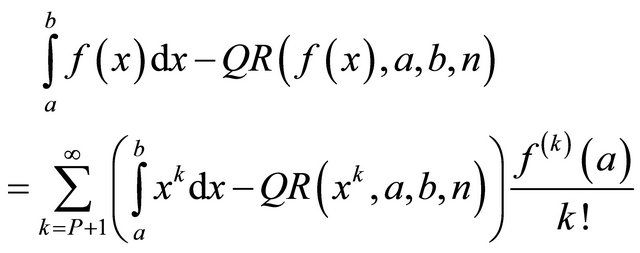 (21)
(21)
Proof: This proof relies heavily on the Taylor series of  centered at
centered at![]() , which is
, which is
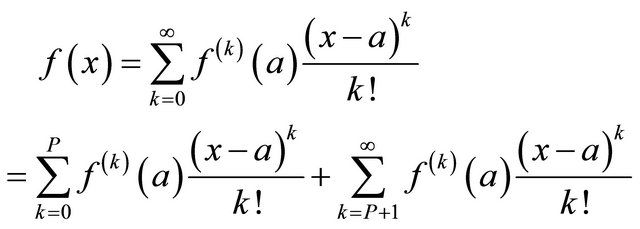 (22)
(22)
Since the quadrature rule 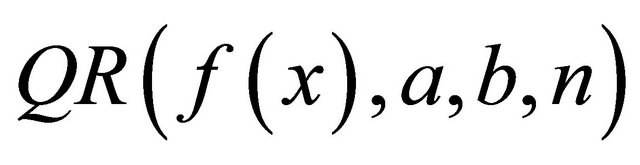 exactly integrates the monomials from x0 through xP, we know that
exactly integrates the monomials from x0 through xP, we know that
 (23)
(23)
for all . By simple algebraic manipulations of lower order terms, it is obvious that
. By simple algebraic manipulations of lower order terms, it is obvious that
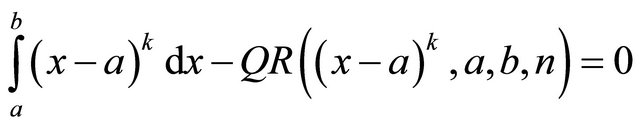 (24)
(24)
as well, for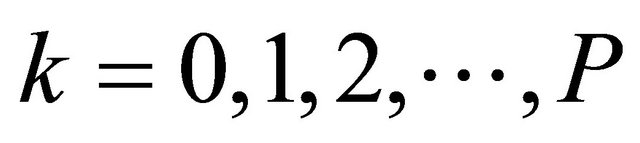 . Multiplying each equation by
. Multiplying each equation by 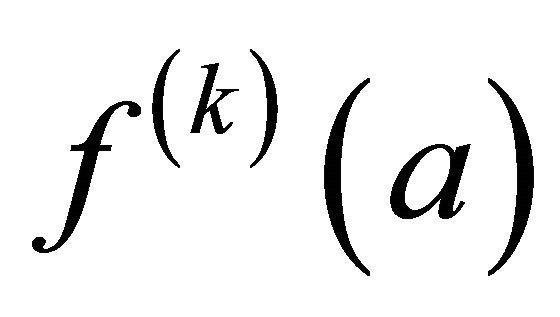 and dividing by
and dividing by , the quadrature rule exactly integrates each of the first P + 1 terms in the Taylor series of
, the quadrature rule exactly integrates each of the first P + 1 terms in the Taylor series of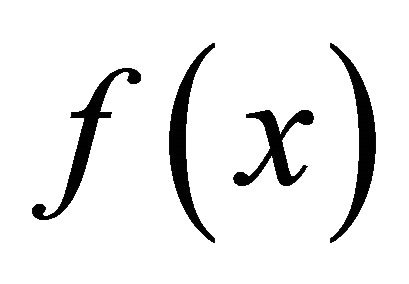 , or
, or
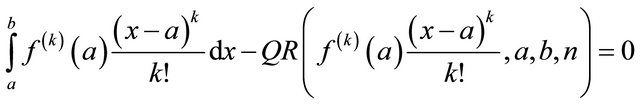 (25)
(25)
for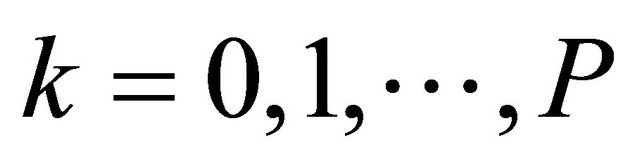 . Thus,
. Thus,
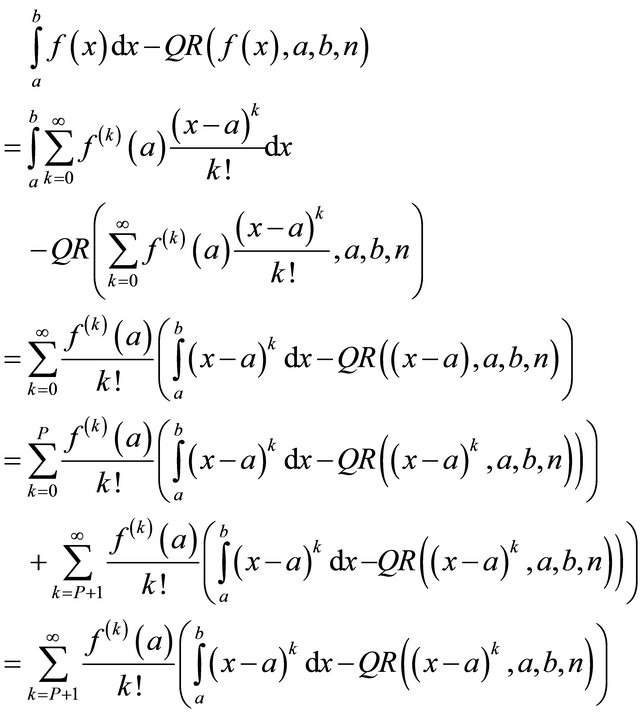 (26)
(26)
Note: the infinite summation can be interchanged with the definite integral, since the Taylor series converges for all values of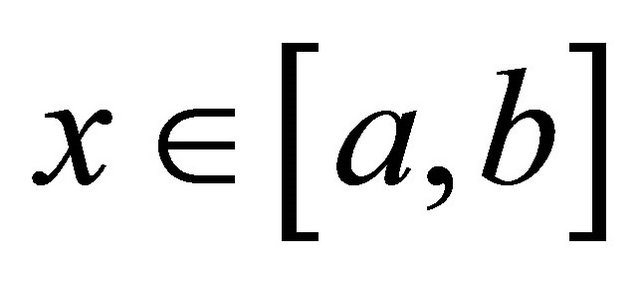 .
.
Thus, the error term in the numerical quadrature rule approximation to the exact integral is an infinite Taylor series where the coefficients are determined from the monomials ![]() and higher. Because of this relationship to the Taylor series, the following conjecture is reasonable, since it follows the pattern observed in the infinite Taylor series and the Taylor polynomial with its remainder term. The error term obtained from this conjecture agrees with the error terms for all quadrature formula that the author has studied.
and higher. Because of this relationship to the Taylor series, the following conjecture is reasonable, since it follows the pattern observed in the infinite Taylor series and the Taylor polynomial with its remainder term. The error term obtained from this conjecture agrees with the error terms for all quadrature formula that the author has studied.
Conjecture: Let 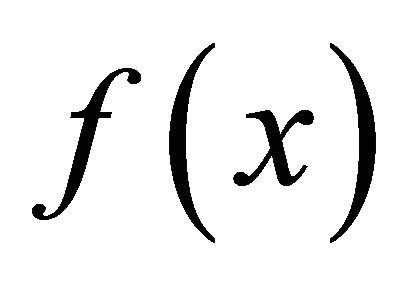 have
have  continuous derivatives on [a, b]. Let
continuous derivatives on [a, b]. Let 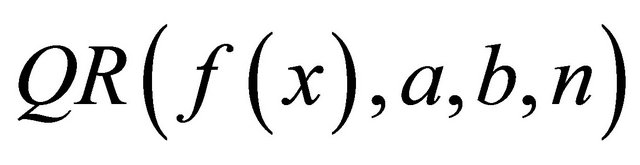 be a quadrature rule of precision P. Then, the error between
be a quadrature rule of precision P. Then, the error between 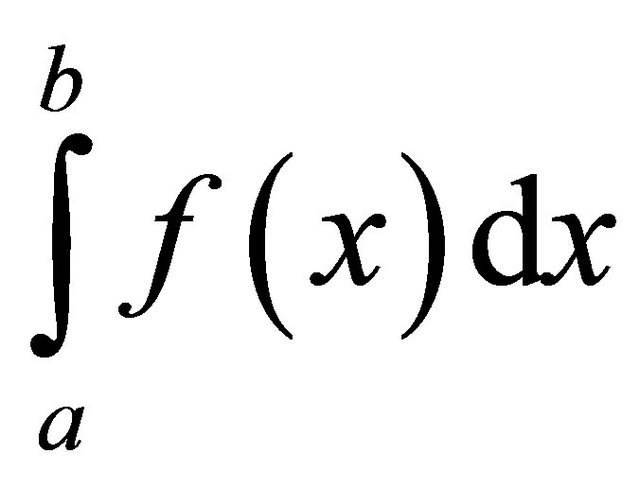 and approximation obtained by the quadrature rule is
and approximation obtained by the quadrature rule is
 (27)
(27)
for some .
.

