Applied Mathematics
Vol. 3 No. 12A (2012) , Article ID: 26010 , 8 pages DOI:10.4236/am.2012.312A285
Estimate of an Hypoelliptic Heat-Kernel outside the Cut-Locus in Semi-Group Theory
Laboratoire de Mathematiques, Université de Franche-Comté, Besançon, France
Email: remi.leandre@univ-fcomte.fr
Received July 2, 2012; revised August 2, 2012; accepted August 9, 2012
Keywords: Subriemannian Geometry; Heat-Kernels
ABSTRACT
We give a proof in semi-group theory based on the Malliavin Calculus of Bismut type in semi-group theory and Wentzel-Freidlin estimates in semi-group of our result giving an expansion of an hypoelliptic heat-kernel outside the cut-locus where Bismut’s non-degeneray condition plays a preominent role.
1. Introduction
Let us consider some vector fields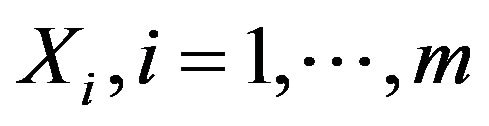 on
on 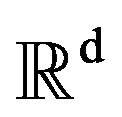 with bounded derivatives at each order. We consider the generator
with bounded derivatives at each order. We consider the generator
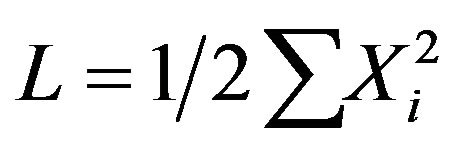 (1)
(1)
It generates a Markov semi-group Pt acting on bounded continuous f functions on . The natural question is to know if the semi-group has an heat-kernel:
. The natural question is to know if the semi-group has an heat-kernel:
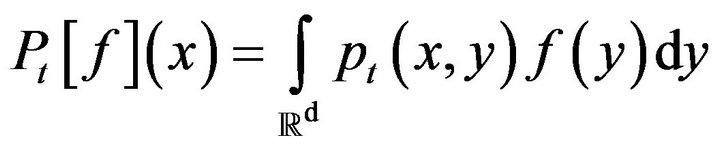 (2)
(2)
Let us suppose that the strong Hoermander hypothesis is checked: in such a case Hoermander ([1]) proved the existence of a smooth heat kernel. Malliavin [2] proved again this theorem by using a probabilistic representation of it. A lot of tools of stochastic analysis were translated recently by Léandre in semi-group theory. We refer to the review papers [3]. In particular [4] proved again the existence of the heat kernel by using the Malliavin Calculus of Bismut type in semi-group theory.
Let us recall what is strong Hoermander hypothesis.
Let
 (3)
(3)
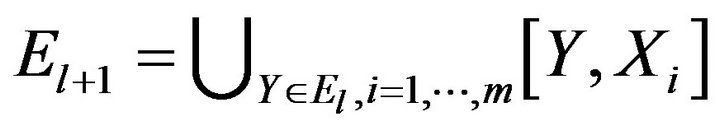 (4)
(4)
Strong Hoermander hypothesis in ![]() is the following: there exits an l such that
is the following: there exits an l such that
 (5)
(5)
Under Hoermander hypothesis in x,  exists and is smooth in y.
exists and is smooth in y.
Let h be a path from [0,1] into  with finite energy
with finite energy
 (6)
(6)
The Hilbert space of  such that (6) is satisfied is denoted by
such that (6) is satisfied is denoted by .
.
We consider the horizontal curve 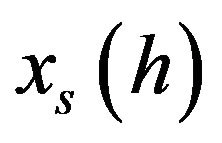 starting from
starting from![]() :
:
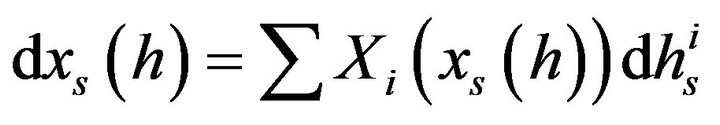 (7)
(7)
We consider the control distance 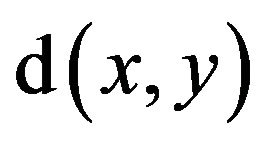
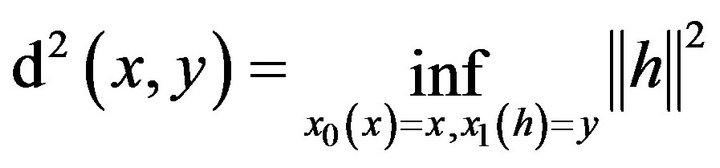 (8)
(8)
By standard result of semi-riemannian geometry ([5], [6]), if the Hoermander hypothesis is checked in all![]() ,
,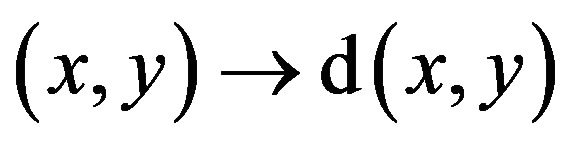 is finite continuous.
is finite continuous.
Bismut in his seminal book [7] has introduced the notion of cut-locus associated to the sub-riemannian distance . We will recall in the first part what is the cut-locus in sub-riemannian geometry.
. We will recall in the first part what is the cut-locus in sub-riemannian geometry.
Bismut in his seminal book [3] pointed out the relationship between the Malliavin Calculus, Wentzel-Freidlin estimates and short time asymptotics of heat-kernels. This relationship was fully performed by Léandre in [8,9]. In particular, by using probabilistic technics we proved:
Theorem 1. (Léandre [9]). If ![]() and
and ![]() are not in the cut-locus of the sub-riemannian distance, we have when
are not in the cut-locus of the sub-riemannian distance, we have when 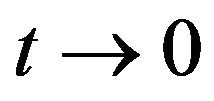
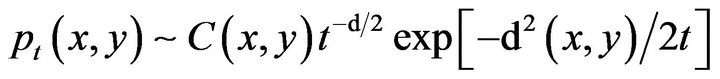 (9)
(9)
where .
.
In the proof we used a mixture between large deviation estimates, the Malliavin Calculus and the Bismutian procedure. Several authors laters ([10,11]) have presented other probabilistic proofs of (9). See [12] in a special case. We refer to [13] for an analytic proof of this result.
Remark. The complement of the cut-locus is an opensubset of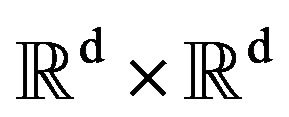 : estimate (9) is uniform on any compact set of the complement of the cut-locus.
: estimate (9) is uniform on any compact set of the complement of the cut-locus.
For readers interested by short time asymptotics of heat-kernels by using probabilistic methods, we refer to the review papers [14-16] and to the book of Baudoin [17]. We refer to the books of Davies [18] and of Varopoulos-Coulhon-Saloff-Coste [19] for analytical methods and to the review of Jerison-Sanchez [20] and Kupka [6].
The object of this paper is to translate in semi-group theory the proof of Theorem 1 of Takanobu-Watanabe [11], by using the tools of stochastic analysis for estimate of heat kernels we have translated in semi-group theory in [21,22] and [23] for Varadhan type estimates.
2. The Cut Locus Associated to a Sub-Riemannian Distance
The material of this part is taken on [7]. But we refer to [11] for a nice introduction to it.
We consider the map  starting from
starting from![]() . This map is a Frechet smooth function from
. This map is a Frechet smooth function from  into
into . We consider
. We consider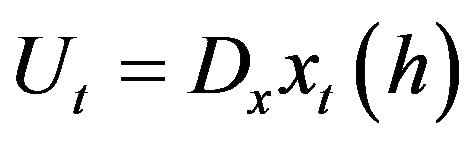 . It satisfied the linear equation starting from
. It satisfied the linear equation starting from :
:
 (10)
(10)
We get
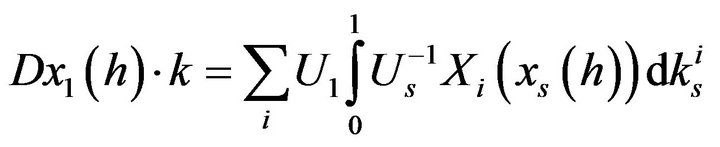 (11)
(11)
The Gram matrix associate to the map 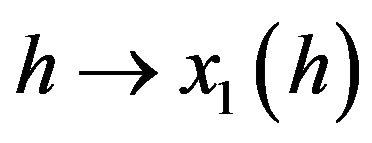 is
is
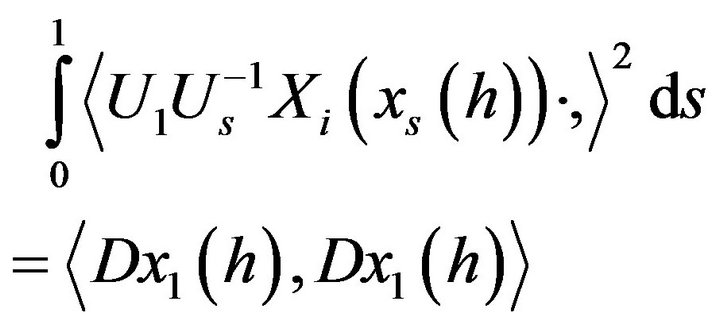 (12)
(12)
Bismut introduced the question to know if 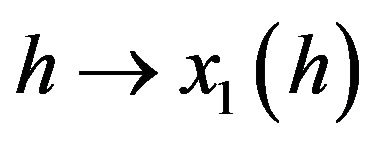 is a submersion. It is fullfilled if and only if the Gram matrix
is a submersion. It is fullfilled if and only if the Gram matrix 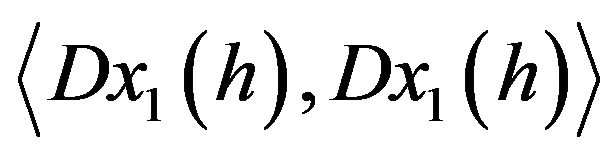 is invertible.
is invertible.
By standard result on Carnot-Caratheodory distance
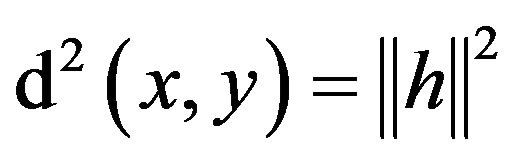 for some
for some 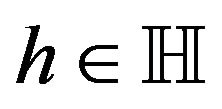 such that
such that
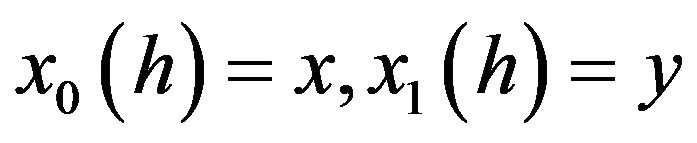 .
.
Let be ![]() the set of h such that
the set of h such that
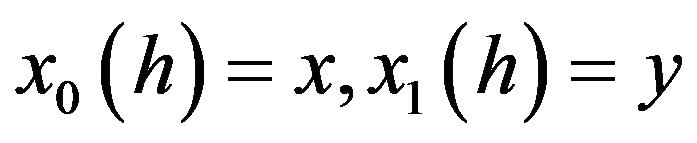 . The main remark of Bismut [7] is the following: if
. The main remark of Bismut [7] is the following: if 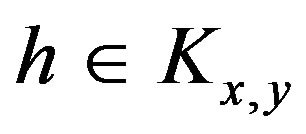 and
and 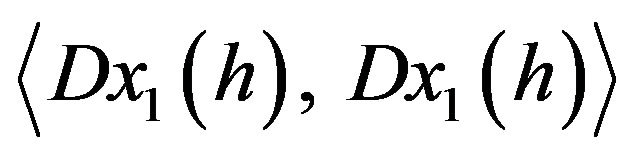 is invertible, then
is invertible, then ![]() is in a neighborhood of h a submanifold of
is in a neighborhood of h a submanifold of  by using the implicit function theorem.
by using the implicit function theorem.
We recall the following definition:
Definition 2. (Bismut [7]) We say that  are not in the cut-locus of the cut-locus of the sub-riemannian distance
are not in the cut-locus of the cut-locus of the sub-riemannian distance  if the following 3 conditions are checked:
if the following 3 conditions are checked:
1)  for only one element of
for only one element of![]() .
.
2) The Gram matrix 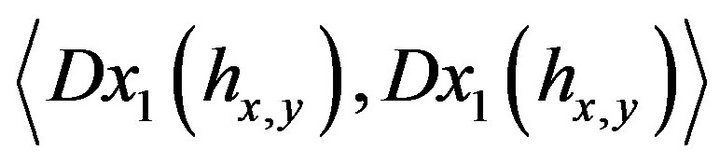 is invertible.
is invertible.
3)  is a non-degenerated minimum of the energy function
is a non-degenerated minimum of the energy function  on
on![]() .
.
Condition 3) has a meaning because ![]() is a manifold on a neighborhood of
is a manifold on a neighborhood of .
.
As traditional in sub-riemannian geometry, we consider the Hamiltonian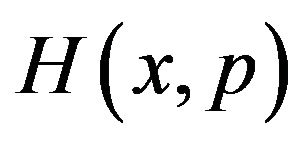 . It is the function from
. It is the function from 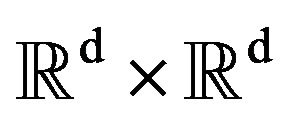 into
into 
 (13)
(13)
When there is an Hamiltonian, people introduced classically the Hamilton-Jacobi equation associated. In sub-riemannian geometry, this was introduced by Gaveau [24]. A bicharacteristic is the solution of the ordinary differential equation on 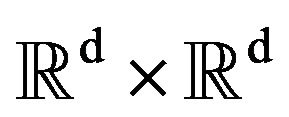 starting from
starting from :
:
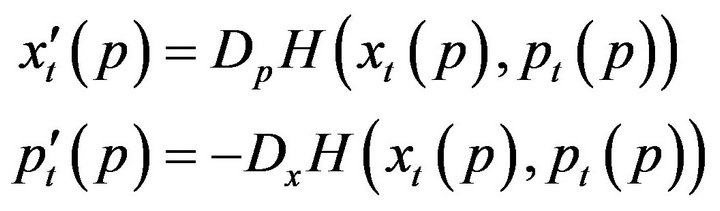 (14)
(14)
We put
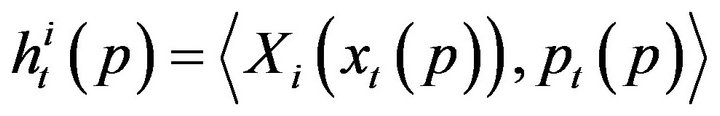 (15)
(15)
We recall some classical result on sub-riemannian geometry (See [11], p. 204):
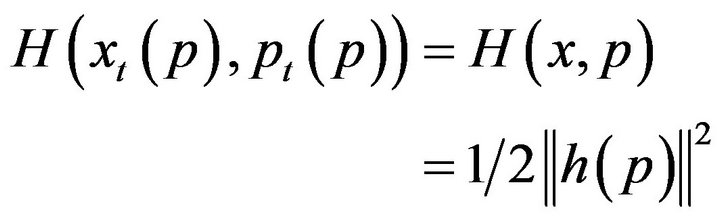 (16)
(16)
 (17)
(17)
 (18)
(18)
Let us recall one of the main result of [7]. If 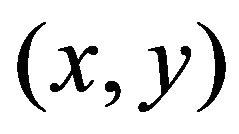 does not belong to the cut locus of
does not belong to the cut locus of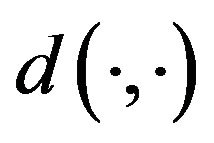 , then
, then
 for a convenient bicharectiristic.
for a convenient bicharectiristic.
By using result of [11] pp. 206-207, we can compute the Hessian of the energy in 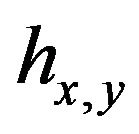 in
in![]() . It is equal to
. It is equal to
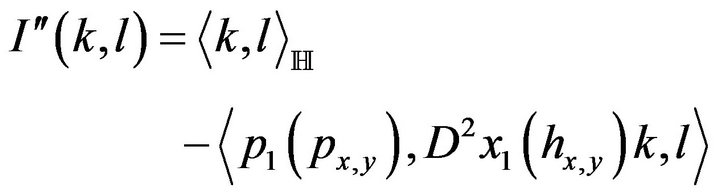 (19)
(19)
We can compute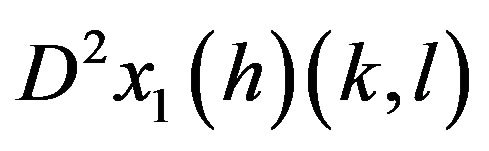 . It is given by
. It is given by
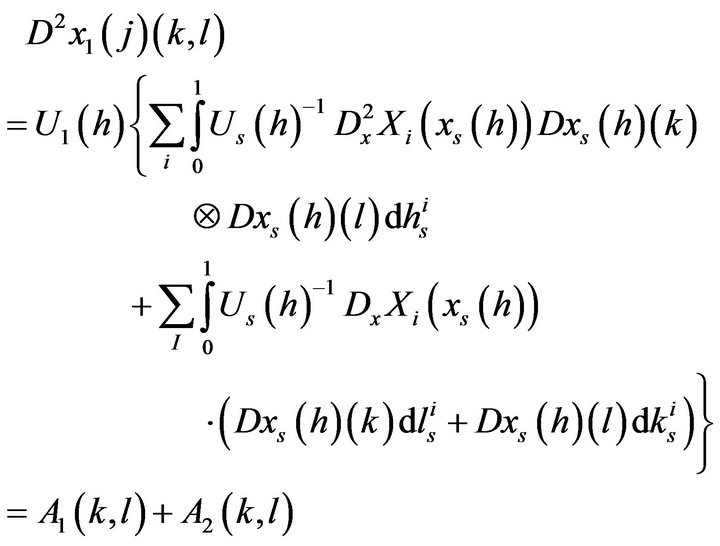 (20)
(20)
3. Scheme of the Proof of Theorem 1
We translate in semi-group the proof of [9] in the way presented in [12].
See [22] for similar considerations for logarithmic estimates of the heat-kernel.
We consider 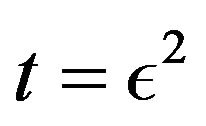 classically and introduce the operator
classically and introduce the operator
 (21)
(21)
Classically
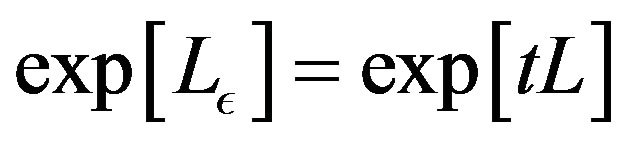 (22)
(22)
We consider the unique curve of minimum enegy 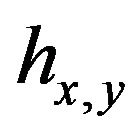 sucht
sucht 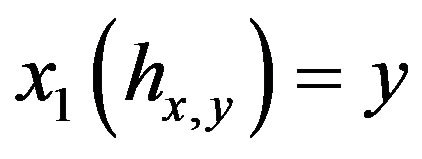 and we introduce the operator
and we introduce the operator
 (23)
(23)
This generates a time inhomogeneous semi-group. According the Girsanov formula in semi-group theory of Léandre [4], we introduce the vector field on :
:
 (24)
(24)
and the generator written in Itô form
 (25)
(25)
According [21], p. 207, we have:
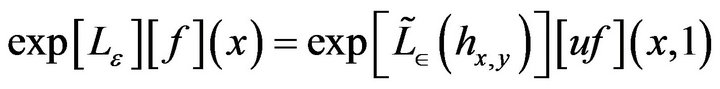 (26)
(26)
We consider the generator
 (27)
(27)
It differs from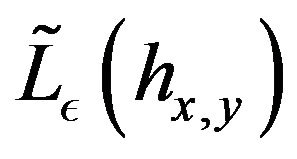 by
by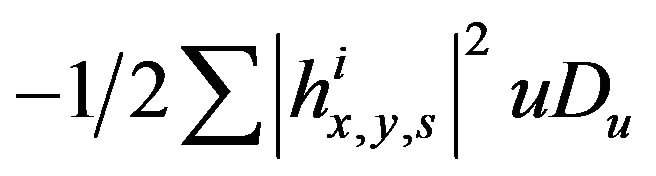 . This last vector field commute with
. This last vector field commute with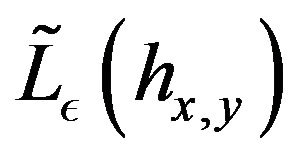 . We deduce that
. We deduce that
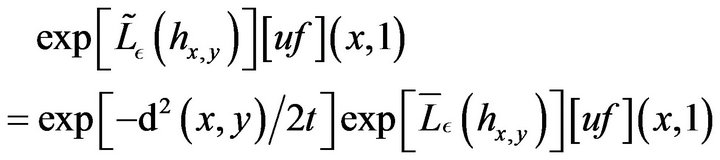 (28)
(28)
We consider the vector fields
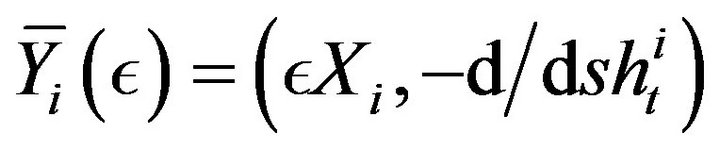 (29)
(29)
and the generator
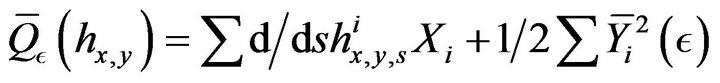 (30)
(30)
We have clearly that
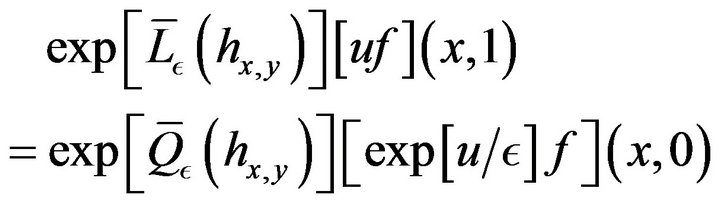 (31)
(31)
Let us consider the flow 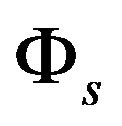 associated to the ordinary differential Equation (7)
associated to the ordinary differential Equation (7)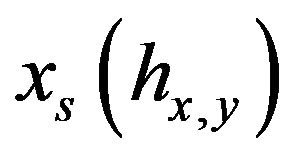 . Let us introduce the vector fields
. Let us introduce the vector fields
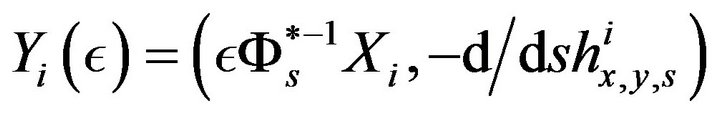 (32)
(32)
and the time-dependent generator
 (33)
(33)
We have the main formula
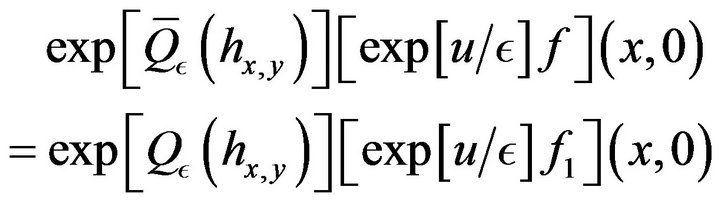 (34)
(34)
where 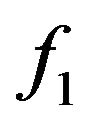 is the map which to z associate
is the map which to z associate . Since
. Since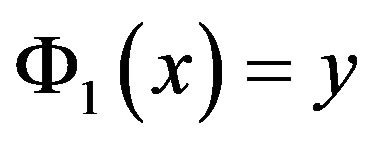 , we have only to estimate the density in
, we have only to estimate the density in ![]() of the measure which to
of the measure which to 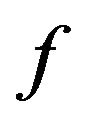 associates
associates
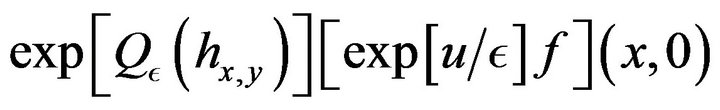 (35)
(35)
We can suppose without any restriction that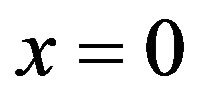 .
.
We perform the dilation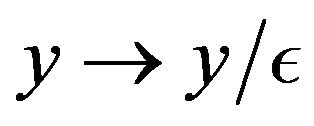 .
.
This means that we have to consider the vector fields
 (36)
(36)
and the generator
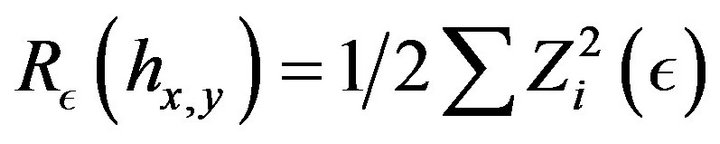 (37)
(37)
We consider the density  ot the measure which to the test function f associates
ot the measure which to the test function f associates
 (38)
(38)
The main result of [21] is the following: for some 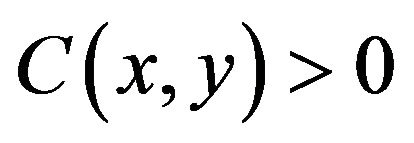
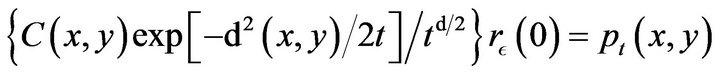 (39)
(39)
The main difference with [21] is in treatment of the term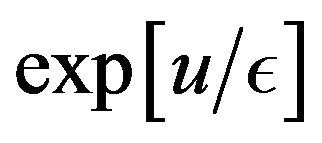 . We refer to [9,10,12] for the treatment of that expression by using stochastic analysis.
. We refer to [9,10,12] for the treatment of that expression by using stochastic analysis.
In Part 2, 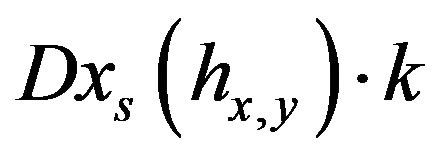 and
and 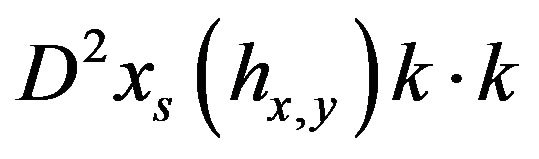 satisfy a system of stochastic differential equations in cascade with associated vector fields
satisfy a system of stochastic differential equations in cascade with associated vector fields . We denote
. We denote  the generic element of
the generic element of . We consider the vector fields
. We consider the vector fields
 (40)
(40)
and the generator
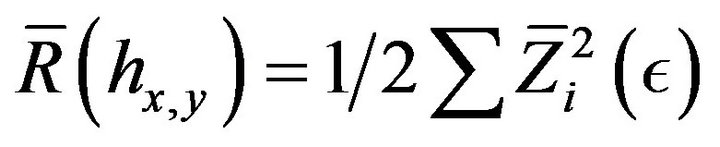 (41)
(41)
From (14), (15), (18), the density  is equal to the density
is equal to the density 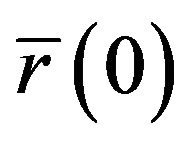 in 0 of the measure which to f associates
in 0 of the measure which to f associates
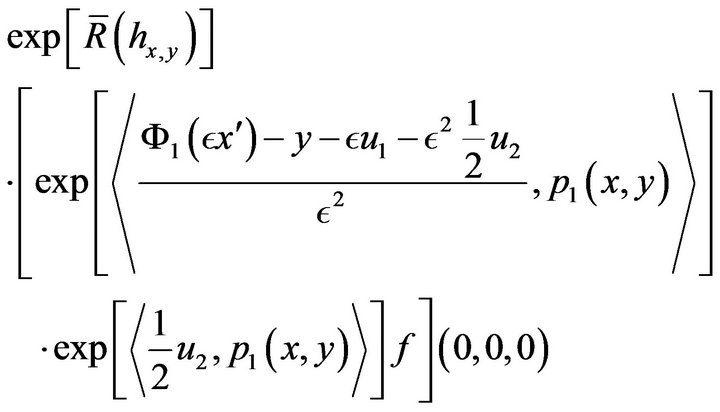 (42)
(42)
where 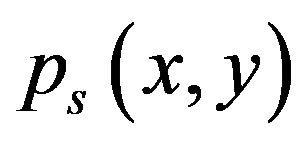 is associated to
is associated to  by the procedure of the Part 2. Theorem 1 will follow from Theorem 6.
by the procedure of the Part 2. Theorem 1 will follow from Theorem 6.
We consider 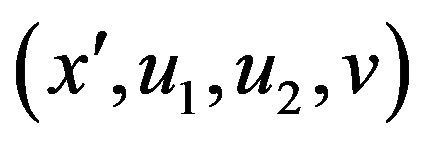 the generic element of
the generic element of 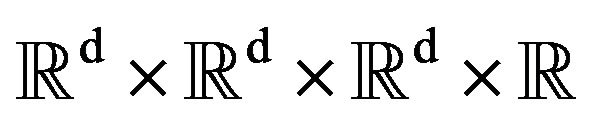 and
and
 (43)
(43)
and the generator
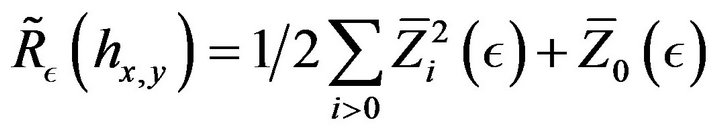 (44)
(44)
The following lemma is proved in the appendix and was originally proved by stochastic analysis in [12].
Lemma 3. For any positive![]() , there exists a
, there exists a  such that
such that
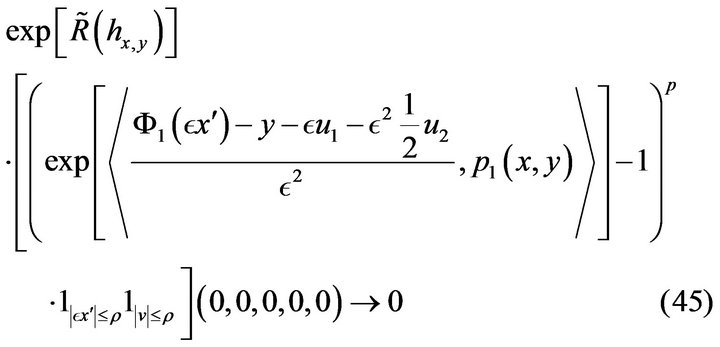
when 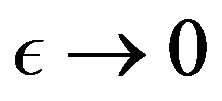
The next lemma is due to Bismut [7] and is proved without using stochastic analysis in the appendix:
Lemma 4. Let 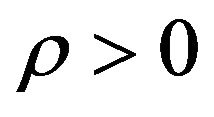 be very small. There exists a
be very small. There exists a  such that
such that
 (46)
(46)
The remaining part of the scheme of the proof is to apply the Malliavin Calculus of Bismut type depending of a parameter of [21], Part 3 to the the semi-group
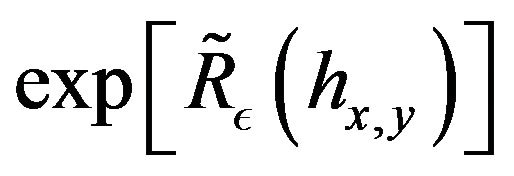 . We will apply an improvement of Theorem 1 of [21]. We consider
. We will apply an improvement of Theorem 1 of [21]. We consider

where  is the set on invertible matrices on
is the set on invertible matrices on 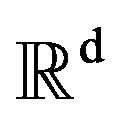 and
and 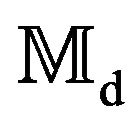 the set of symmetric matrices on
the set of symmetric matrices on 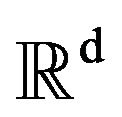 (
( is called the Malliavin matrix). We consider if
is called the Malliavin matrix). We consider if 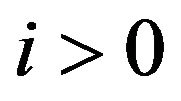 the vector fields on
the vector fields on 
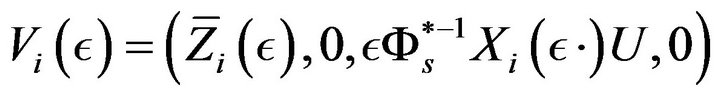 (47)
(47)
and
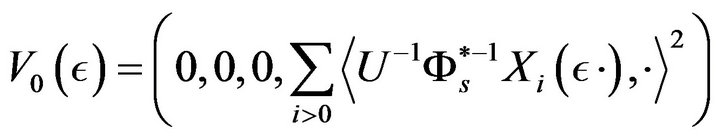 (48)
(48)
Let be the generator
 (49)
(49)
It generates a time inhomogeneous semi-group. We have Lemma 5. For all positive![]() , the uniform Malliavin condition is checked:
, the uniform Malliavin condition is checked:
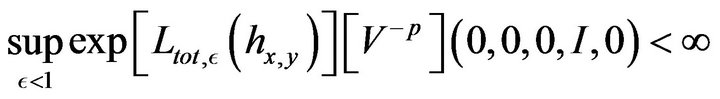 (50)
(50)
Theorem 1 is a consequence of the next theorem, (which is an extension of Theorem 1 of [21]) and of (39):
Theorem 6. When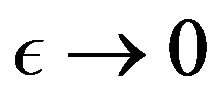 ,
, 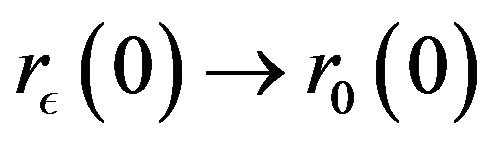 where
where 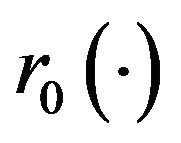 is the density of the measure which to f associates
is the density of the measure which to f associates
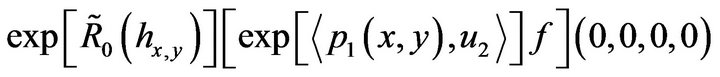 (51)
(51)
First of all, we recall the Wentzel-Freidlin estimates translated in semi-group theory by Léandre [22,23,25]:
Theorem 7. (Wentzel-Freidlin) Let ![]() some time dependent vector fields with bounded derivatives at each order on
some time dependent vector fields with bounded derivatives at each order on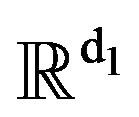 ,
, . We consider the control distance
. We consider the control distance  as in (8) and the diffusion semi-group
as in (8) and the diffusion semi-group
 . We suppose that the control distance is continuous. Then for any open subset
. We suppose that the control distance is continuous. Then for any open subset 
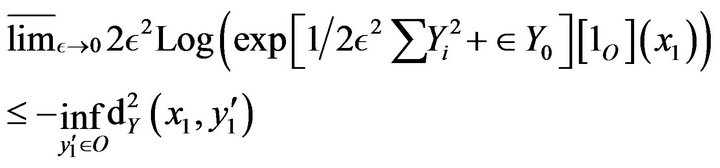 (52)
(52)
Proof of Theorem 6. Let 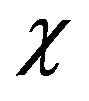 be a smooth function from
be a smooth function from  into
into 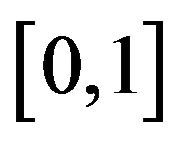 equals to 1 and 0 and equals to 0 if
equals to 1 and 0 and equals to 0 if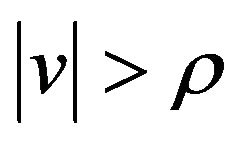 . By Wentzel-Freidlin estimates, we can find an
. By Wentzel-Freidlin estimates, we can find an  such that if
such that if .
.
 (53)
(53)
By the integration by part of the Malliavin Calculus and the Technical Lemma 5, we have if α is a multi-index
 (54)
(54)
Therefore we have only to estimate the density in 0 of the measure which to f associate
 (55)
(55)
By using Lemma 3, Lemma 4, Lemma 5 the density of this measure tends to 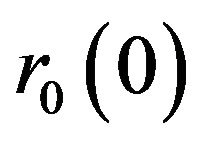 by using the Malliavin Calculus of Bismut type which depends of a parameter of [21]. □
by using the Malliavin Calculus of Bismut type which depends of a parameter of [21]. □
4. Proof of the Technical Lemmas
Proof of Lemma 3. Let us first show that
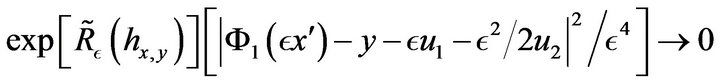
(56)
(We will omitt to write later the obvious initial condition which appear in various semi-group later). We introduce a polynomial F of degre less or equal to 2 in  and in
and in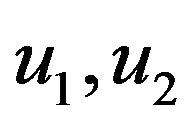 . Let us compute the Taylor expansion of
. Let us compute the Taylor expansion of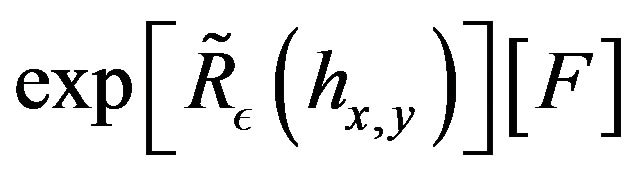 . We use Lemma 1 of [21].
. We use Lemma 1 of [21].
If the degree of 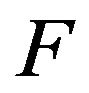 in
in  is 2, the two first terms of the Taylor expansion are 0 and the term of order 2 is
is 2, the two first terms of the Taylor expansion are 0 and the term of order 2 is
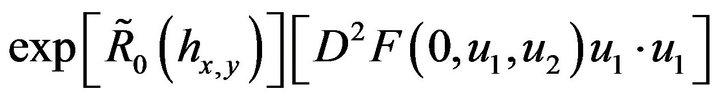 (57)
(57)
where we take partial derivatives in the first component. If the polynomial  is of degree 1 in
is of degree 1 in , the term of order 1 is
, the term of order 1 is
 (58)
(58)
and the term of order two is
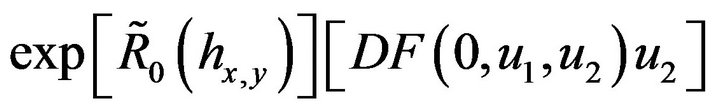 (59)
(59)
Lemma 3 will arise from the translation in semi-group theory of Lemma 3.4 of [12].
For all ![]() there exists a
there exists a  such that
such that
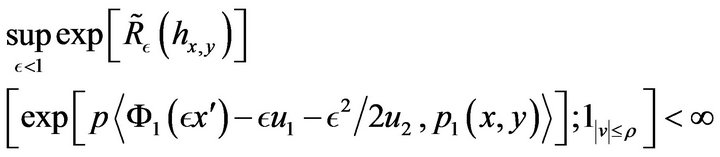
(60)
The proof follows slightly the line of Lemma 3.4 of [12]. We don’t write the convenient enlarged semigroups when we enlarge the space. We follow the notation of [12],  being replaced by
being replaced by 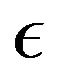 and
and 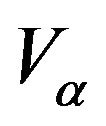 being replaced by
being replaced by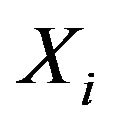 .
.
We introduce the new coordinate
 (61)
(61)
We use the Itô formula in semi-group theory of [25]. This leads to introduce extra coordinates in the vector fields:
1)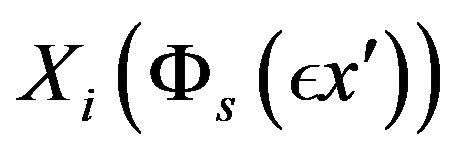 .
.
2) 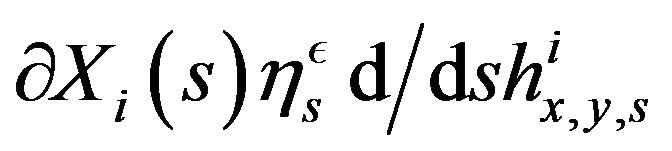
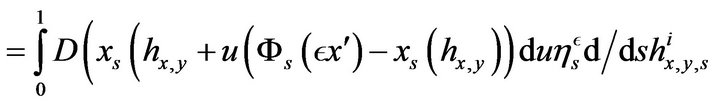
We introduce the new variable 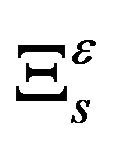 which is associated to the extra component vector fields 3)
which is associated to the extra component vector fields 3)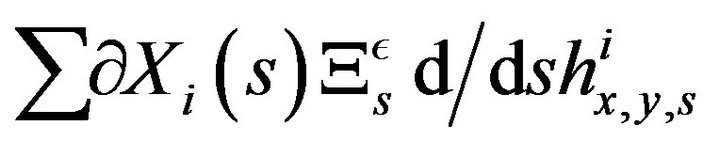 .
.
We use another time the Itô formula in semi-group theory of [25] (11). This leads to introduce the vector field associated to another variable .
.
4) 
We introduce an extra variable 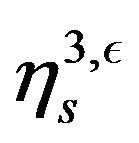 associated to another component in the drift which is
associated to another component in the drift which is .
.
We get for another enlarged semi-group
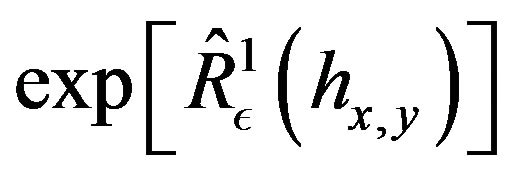 an extension of formula 3.44 of [12], but with
an extension of formula 3.44 of [12], but with 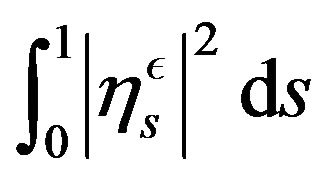 instead of
instead of .
.
Lemma 8. For all , there exists
, there exists  such that
such that
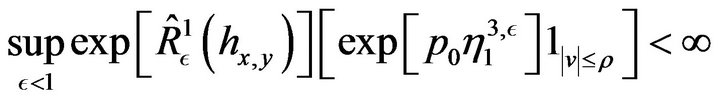 (62)
(62)
We postpone later the proof of this lemma which is an analog of the quasi-continuity lemma of [25].
Next we consider another enlarged semi-group to look the couple  and
and 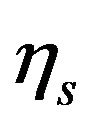 together. We use the Itô formula in semi-group theory of [25] (11), [22,23]. We introduce 1)
together. We use the Itô formula in semi-group theory of [25] (11), [22,23]. We introduce 1) 
 .
.
By introducing a cascade of vector fields, we can translate in semi-group theory (3.45) of [12]. We introduce a variable 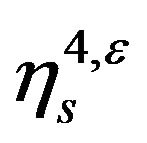 associate to the new component in the drift
associate to the new component in the drift 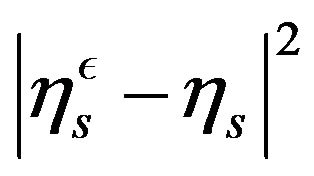 and we can state an analog of Lemma 8 for a convenient enlarged semi-group
and we can state an analog of Lemma 8 for a convenient enlarged semi-group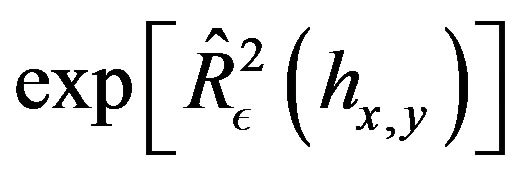 .
.
For every![]() , there exists a small
, there exists a small  such that
such that
 (63)
(63)
which is the analog of (3.46) in [12] where we have replaced 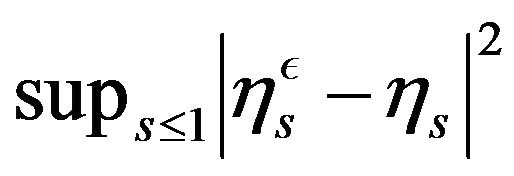 by
by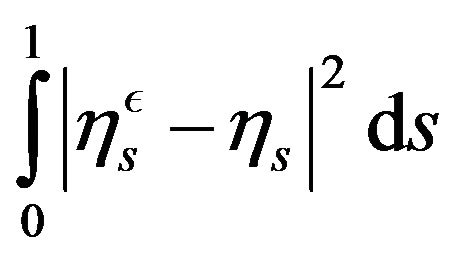 .
.
Let be 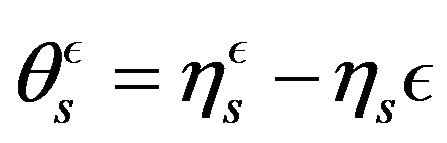 and
and  associated to the extracomponent vector fields:
associated to the extracomponent vector fields:
1)  for the diffusion part.
for the diffusion part.
2) 
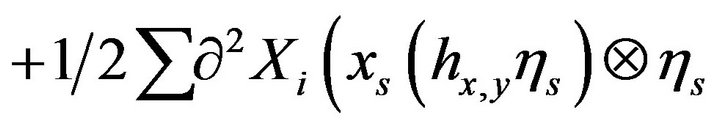 for the drift part.
for the drift part.
We use another time the Itô formula in semi-group theory of [25] (11) for a convenient enlarged semi-group established to study together 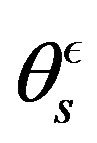 and
and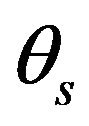 . This allow to study
. This allow to study  and we conclude exactly as in pages 29, 30 of [12] with a small improvement of Lemma 8 to study (3.46), (3.47) of [12]. □
and we conclude exactly as in pages 29, 30 of [12] with a small improvement of Lemma 8 to study (3.46), (3.47) of [12]. □
Proof of Lemma 4. We assemble the semi-group
 and the semi-group
and the semi-group 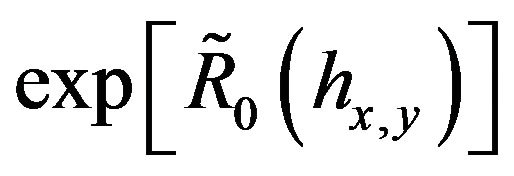 together in a total semi-group
together in a total semi-group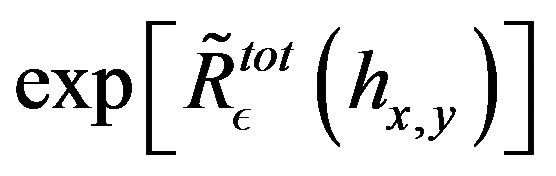 . We have some variables
. We have some variables 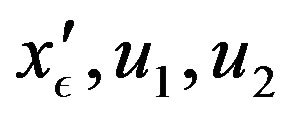 and
and![]() . We have
. We have
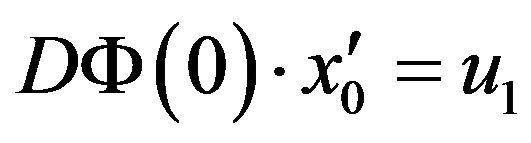 (64)
(64)
Let 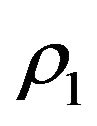 be small and
be small and  be very small. We use the exponential inequality in semi-group theory of Lemma 8. For a small
be very small. We use the exponential inequality in semi-group theory of Lemma 8. For a small  and a small
and a small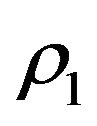 , we have (we omitt to write the obvious initial values in the considered semigroups)
, we have (we omitt to write the obvious initial values in the considered semigroups)
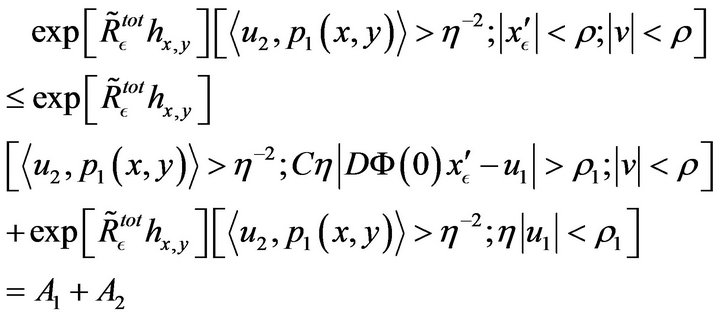
(65)
We choose a small 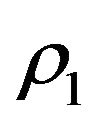 and a very small
and a very small . The exponential inequalities of the proof of Lemma 8 show
. The exponential inequalities of the proof of Lemma 8 show
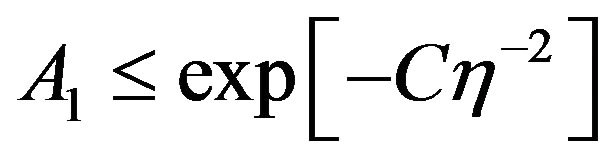 (66)
(66)
It remains to estimate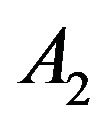 . We scale the vector fields
. We scale the vector fields 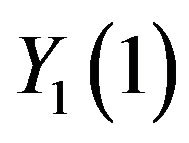 by
by  and
and 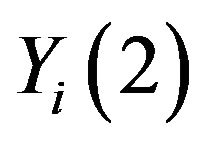 by
by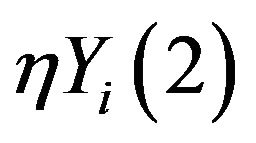 . We get a generator
. We get a generator  and a new Markov semi-group
and a new Markov semi-group
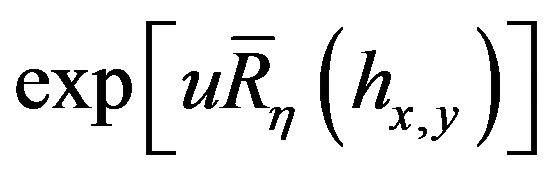 . By a scaling argument, we recognize in
. By a scaling argument, we recognize in
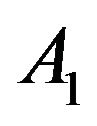

By a simple improvement of the large deviation estimates of Theorem 7, we get
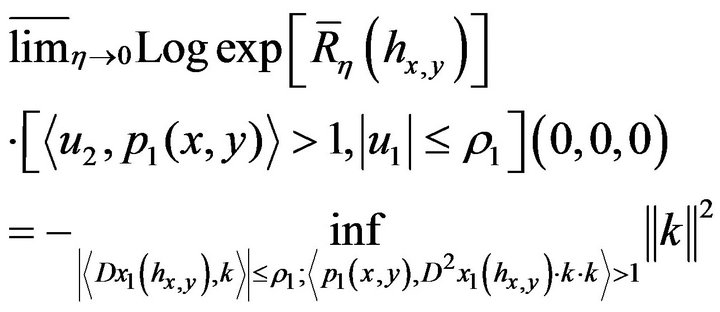 (68)
(68)
We chose a small 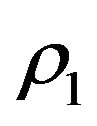 and we use (20) and the fact
and we use (20) and the fact  don’t belong to the cut-locus in part 2. We deduce that if
don’t belong to the cut-locus in part 2. We deduce that if  is very small, that there exists a
is very small, that there exists a 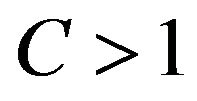 such that
such that

Remark. This result is traditionnally hold by using the theory of Fredholm determinant.
Proof of Lemma 5. We assemble together the semigroup 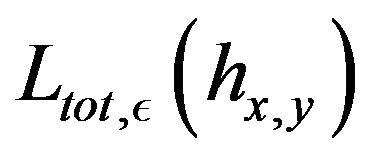 and
and  in a global generator
in a global generator  We get therefore a total semi-group
We get therefore a total semi-group . We get the Malliavin matrix
. We get the Malliavin matrix 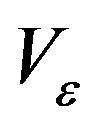 and
and
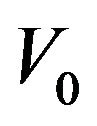 . But
. But  is nothing else that
is nothing else that
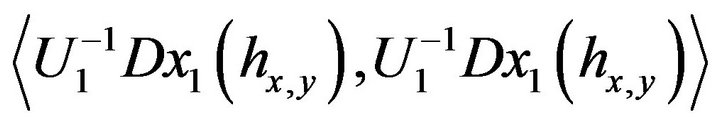 which is invertible because
which is invertible because  don’t belong to the cut-locus of the subriemannian geometry.
don’t belong to the cut-locus of the subriemannian geometry.
Moreover, by omitting to write the obvious starting conditions, we get for a small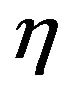 :
:
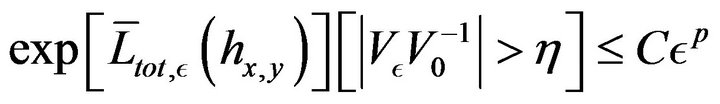 (70)
(70)
for all p. Therefore for a small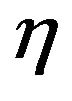 :
:
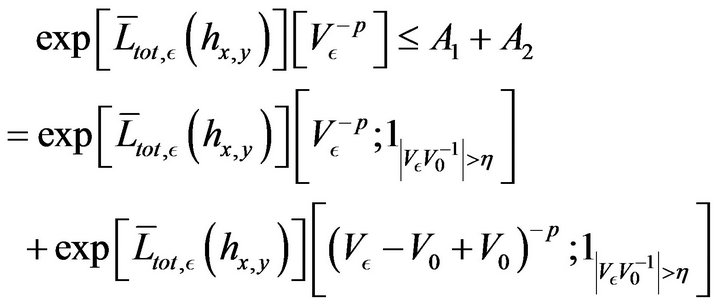 (71)
(71)
Since  is constant invertible,
is constant invertible, 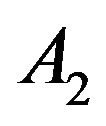 is bounded independent of
is bounded independent of ![]() if
if  is small enough. By the results of [22,23], there exist
is small enough. By the results of [22,23], there exist 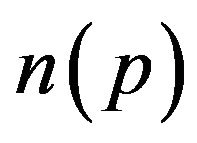 such that:
such that:
 (72)
(72)
By Hoelder inequality, we deduce that 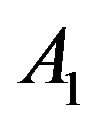 is bounded independent of
is bounded independent of![]() . □
. □
Proof of Lemma 8. This follows clearly the line of the quasi-continuity lemma for Wentzel-Freidlin estimates in semi-group theory of [25]. We sketch the proof.
We recall the elementary Kolmogorov lemma of the theory of stochastic processes ([26,27]).
Let 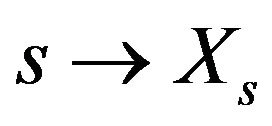 be a family of random variables parametrized by
be a family of random variables parametrized by 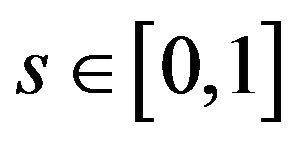 with values in
with values in  equals to 0 or 1 in
equals to 0 or 1 in  such that
such that
 (73)
(73)
for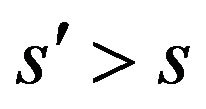 . There exists a continuous version of
. There exists a continuous version of 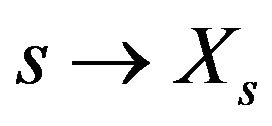 and the
and the 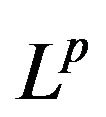 norm of
norm of  can be estimated only in terms of the data (73).
can be estimated only in terms of the data (73).
Let us recall that  is a time dependent generator. For
is a time dependent generator. For 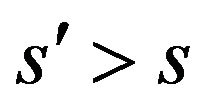 there is a time inhomogeneous semigroup
there is a time inhomogeneous semigroup . By the Burkholder-DaviesGundy inequality in semi-group theory of [16] (19), we have
. By the Burkholder-DaviesGundy inequality in semi-group theory of [16] (19), we have
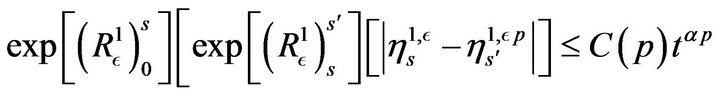 (74)
(74)
There we can define a continuous stochastic process with probability measure  associated to
associated to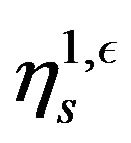 .
.
We use the Paul Levy martingale exponential in semigroup theory of [25] (33), (46). We get
 (75)
(75)
By the Kolmogorov lemma, we get
 (76)
(76)
By standard computations, we deduce that
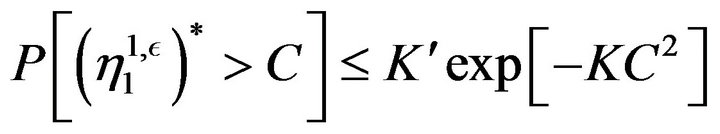 (77)
(77)
But 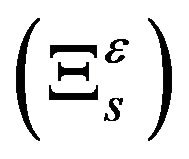 is bounded, and by the same type of argument we deduce that
is bounded, and by the same type of argument we deduce that
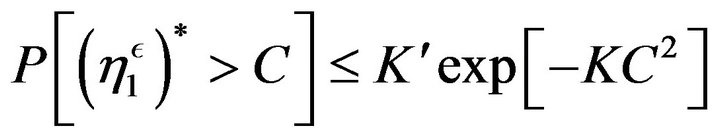 (78)
(78)
But
 (79)
(79)
such that
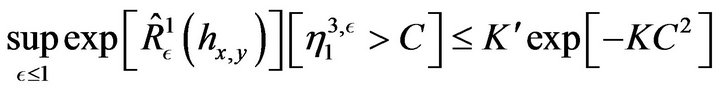 (80)
(80)
5. Conclusion
We have translated in semi-group theory some classical result of stochastic analysis for subelliptic heat-kernels where Bismutian non degeneracy condition [7] plays a preominent role.
REFERENCES
- L. Hoermander, “Hypoelliptic Second Order Differential Equations,” Acta Mathematica, Vol. 119, No. 1, 1967, pp. 147-171. doi:10.1007/BF02392081
- P. Malliavin, “Stochastic Calculus of Variations and Hypoelliptic Operators,” In: K. Itô, Ed., Stochastic Analysis, Kinokuniya, Tokyo, 1978, pp. 195-263.
- R. Léandre, “Malliavin Calculus of Bismut Type in SemiGroup Theory,” Far East Journal of Mathematical Sciences, Vol. 30, 2008, pp. 1-26.
- R. Léandre, “Malliavin Calculus of Bismut Type without Probability,” In: V. S. Sunder and A. M. Boutet de Monvel, Eds., Festchrift in Honour of K. Sinha, Proceedings of Indian Academy Sciences—Mathematical Sciences, Vol. 116, 2006, pp. 507-518.
- M. Gromov, “Carnot-Caratheodory Spaces Seen from within,” In: A. Bellaiche, Ed., Sub-Riemannian Geometry, Birkhauser, Boston, 1996, pp. 79-323. doi:10.1007/978-3-0348-9210-0_2
- I. Kupka, “Géométrie Sous-Riemannienne,” In Séminaire Bourbaki, Astérisque, Vol. 241, 1997, pp. 351-380.
- J. M. Bismut, “Large Deviations and the Malliavin Calculus,” Birkhauser, Boston, 1984.
- R. Léandre, “Estimation en Temps Petit de la Densité d’Une Diffusion Hypoelliptique,” C. R. A. S. Série I, Vol. 301, 1985, pp. 801-804.
- R. Léandre, “Intégration dans la Fibre Associée a une Diffusion Dégénérée,” Probability Theory and Related Fields, Vol. 76, No. 3, 1987, pp. 341-358. doi:10.1007/BF01297490
- G. Ben Arous, “Méthode de Laplace et de la Phase Stationnaire sur l’Espace de Wiener,” Stochastic, Vol. 25, No. 3, 1988, pp. 125-153. doi:10.1080/17442508808833536
- S. Takanobu and S. Watanabe, “Asymptotic Expansion Formulas of Schilder Type for a Class of Conditional Wiener Functional Integration,” In: K. D. Elworthy and N. Ikeda, Eds., Asymptotic Problems in Probability Theory: Wiener Functionals and Asymptotics, Longman, New York, 1992, pp. 194-241.
- S. Watanabe, “Analysis of Wiener Functionals (Malliavin Calculus) and Its Applications to Heat Kernels,” Annals of Probability, Vol. 15, No. 1, 1987, pp. 1-39. doi:10.1214/aop/1176992255
- T. J. S. Taylor, “Off Diagonal Asymptotics of Hypoelliptic Diffusion Equations and Singular Riemannian Geometry,” Pacific Journal of Mathematics, Vol. 136, No. 2, 1989, pp. 379-394. doi:10.2140/pjm.1989.136.379
- S. Kusuoka, “More Recent Theory of Malliavin Calculus,” Sugaku Expositions, Vol. 5, 1992, pp. 155-173.
- R. Léandre, “Appliquations Quantitatives et Qualitatives du Calcul de Malliavin,” In: M. Métivier and S. Watanabe, Eds., Stochastic Analysis, L. N. M., Vol. 1322, Springer, Berlin, 1988, pp. 109-134.
- S. Watanabe, “Stochastic Analysis and Its Applications,” Sugaku, Vol. 5, 1992, pp. 51-72.
- F. Baudoin, “An Introduction to the Geometry of Stochastic Flows,” Imperial College Press, London, 2000.
- E. B. Davies, “Heat Kernels and Spectral Theory,” Cambridge University Press, Cambridge, 1992.
- N. Varopoulos, L. Saloff-Coste and T. Coulhon, “Analysis and Geometry on Groups,” Cambridge University Press, Cambridge, 1992.
- D. Jerison and A. Sanchez-Calle, “Subelliptic Differential Operators,” In: C. Berenstein, Ed., Complex Analysis III, L. N. M., Vol. 1277, Springer, Berlin, 1987, pp. 46-77. doi:10.1007/BFb0078245
- R. Léandre, “Varadhan Estimates without Probability: Lower Bounds,” In: D. Baleanu, et al., Eds., Mathematical Methods in Engineerings,” Springer, Berlin, 2007, pp. 205-217.
- R. Léandre, “Varadhan Estimates in Semi-Group Theory: Upper Bound,” In: M. Garcia-Planas, et al., Eds., Applied Computing Conference, WSEAS Press, Athens, 2008, pp. 77-81.
- R. Léandre, “Large Deviations Estimates in Semi-Group Theory,” In: T. E. Simos, et al., Eds., Numerical Analysis and Applied Mathematics, A. I. P. Proceedings, American Institute Physics, Melville, 2008, pp. 351-355.
- B. Gaveau, “Principe de Moindre Action, Propagation de la Chaleur et Estimées Sous-Elliptique sur Certains Groupes Nilpotents,” Acta Mathematica, Vol. 107, 1977, pp. 43-101.
- R. Léandre, “Wentzel-Freidlin Estimates in Semi-Group Theory,” In: Y. C. Soh, Ed., Control, Automation Robotics and Vision, 2008, pp. 2233-2235.
- P. A. Meyer, “Flot d’Une Équation Différentielle Stochastique,” In: P. A. Meyer, et al., Eds., Séminaire de Probabilités XV, L. N. M., Vol. 850, Springer, Berlin, 1981, pp.100-117.
- P. Protter, “Stochastic Integration and Differential Equations,” Springer, Berlin, 1995.

