Applied Mathematics
Vol. 3 No. 3 (2012) , Article ID: 18099 , 5 pages DOI:10.4236/am.2012.33039
Application of the Hybrid Differential Transform Method to the Nonlinear Equations
Department of Mathematics, Faculty of Arts and Sciences, Ondokuz Mayis University, Samsun, Turkey
Email: *incicilingir@gmail.com
Received January 2, 2012; revised February 13, 2012; accepted February 22, 2012
Keywords: Hybrid Differential Transform/Finite Difference Method; Nonlinear Initial Value Problems; Numerical Solution
ABSTRACT
In this paper, a hybrid method is introduced briefly to predict the behavior of the non-linear partial differential equations. The method is hybrid in the sense that different numerical methods, differential transform and finite differences, are used in different subdomains. Our aim of this approach is to combine the flexibility of differential transform and the efficiency of finite differences. An explicit hybrid method for the transient response of inhomogeneous nonlinear partial differential equations is presented; applying finite difference scheme on the fixed grid size is used to approximate the space discretisation, whereas the differential transform method is used for time operator. Comparison of the efficiency of the different approaches is a very important aspect of this study. In our test cases, the hybrid approach is faster than the corresponding highly optimized finite difference method in two dimensional computations. We compared our hybrid approach’s results with the exact and/or numerical solutions of PDE which obtained from Adomian Decomposition Method. Results show that the hybrid approach may be an important tool to reduce the execution time and memory requirements for large scale computations and get remarkable results in predicting the solutions of nonlinear initial value problems.
1. Introduction
Many problems in mathematical physics, theoretical physics, chemical physics and theoretical biology are modeled by the so-called initial value and boundary value problems in the second-order nonlinear partial differential equations. Nonlinear equations also cover the cases of the following types: surface waves incompressible fluids, hydro magnetic waves in cold plasma, acoustic waves in inharmonic crystal, etc. However, these equations are difficult to be solved analytically and sometimes it is impossible then application must be made with relevant numerical methods such as shooting method, finite difference etc. In recent years, differential transform method has been used to solve this type of equation [1-11].
The differential transform method is a numerical method based on Taylor expansion. This method constructs an analytical solution in the form of a polynomial which is widely equivalent explicit form of solution. The main advantage of this method is to solve both linear and nonlinear equations without linearization. Using differential transform method, we can avoid from complexity of expansions of derivatives and compute derivatives as symbolically.
When solving initial value problems, the truncation error produced by the finite difference method is greater than that produced by the differential transform method. Hence, in this work we develop a hybrid method which combines the differential transform and the finite difference method. Using this hybrid method, numerical solution can be obtained from a simple iterative procedure. The hybrid method has an advantage to solve nonlinear equations is examined without using linearization. In the literature, there are other hybrid methods. For example, the method used by Beilina’s [12] study includes both the finite difference and finite element methods.
2. Differential Transform Method
We introduce the main features of the differential transformation method [1,5,6,11] according to the differential transform of the nth derivative of a function in one variable defined as follows:
 (1)
(1)
In Equation (1), 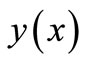 is the original function,
is the original function,  is the transformed function and the differential inverse transform of
is the transformed function and the differential inverse transform of 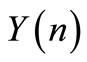 is defined as follows:
is defined as follows:
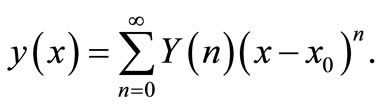 (2)
(2)
In real applications, function is expressed by a finite series and Equation (2) can be written as
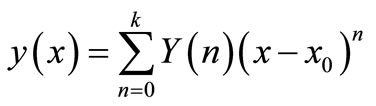 (3)
(3)
From Equation (1), we obtain
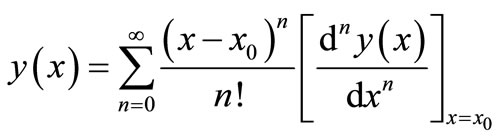 (4)
(4)
Actually Equation (4) implies that the concept of differential transform is derived from Taylor series expansion. Although DTM is not able to evaluate the derivatives symbolically, relative derivatives can be calculated by an iterative way which is described by the transformed equations of the original function. In this study Equation (4) also implies
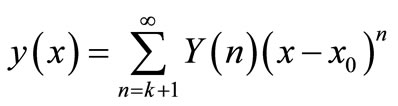 (5)
(5)
is negligibly small. In fact k is decided by the convergence of natural frequency.
After taking differential transformation with respect to time variable, we apply finite difference method to PDE with respect to x variable and their derivatives. The region 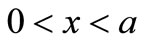 is divided into several equal intervals and each interval has a width h. Take second order accurate central difference approximation with respect to the first and second order derivatives, equations are rewritten and computed iteratively. The solutions are compared with the other published numerical solutions of these equations.
is divided into several equal intervals and each interval has a width h. Take second order accurate central difference approximation with respect to the first and second order derivatives, equations are rewritten and computed iteratively. The solutions are compared with the other published numerical solutions of these equations.
3. Illustration of Hybrid Method
To show the effectiveness of the proposed hybrid differential transform method and to give an understandable overview of the methodology three different models of nonlinear differential equations with different initial and boundary conditions will be discussed in the following section. Then our results are compared with published work of Wazwaz [13] in which Adomian decomposition method was used to solve the same equations.
Example 1:
The function u satisfies the nonlinear equation
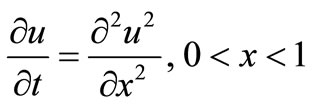 (6)
(6)
The initial condition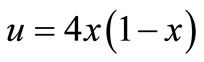 ,
, 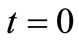
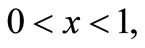 and the boundary conditions
and the boundary conditions 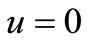 at
at 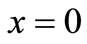 and 1,
and 1,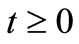 .
.
If the equation is expanded and taken the differential transform of variables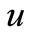 ,
,  ,
,  ,
, 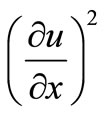 with respect to time,
with respect to time,
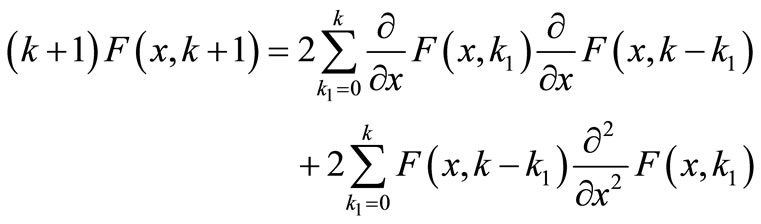 (7)
(7)
where 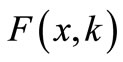 is differential transformation of
is differential transformation of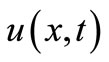 . Then the central finite difference method is applied to the Equation (7), we get
. Then the central finite difference method is applied to the Equation (7), we get
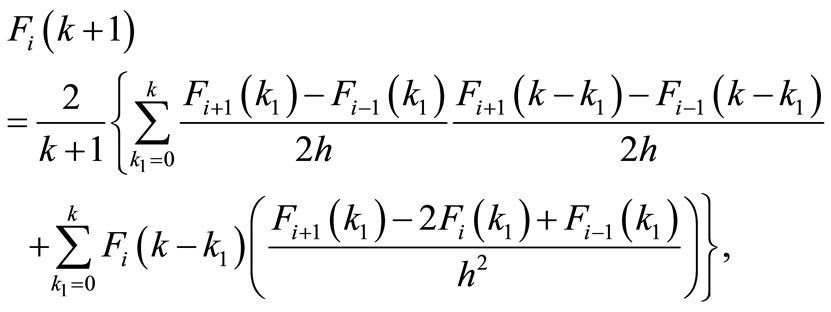 (8)
(8)
where 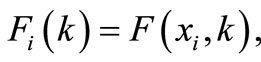
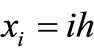 . The initial and boundary conditions are
. The initial and boundary conditions are
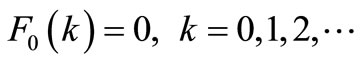 (9)
(9)
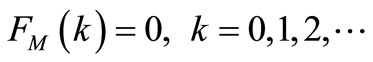 (10)
(10)
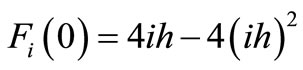 (11)
(11)
The process of programming consists of three major steps. First, 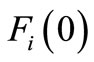 are determined from the initial conditions as well as the boundary conditions. Secondly, for
are determined from the initial conditions as well as the boundary conditions. Secondly, for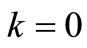 ,
, 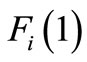 can be calculated using the iteration formula of Equation (8) together with the initial and boundary conditions (9)-(11) and
can be calculated using the iteration formula of Equation (8) together with the initial and boundary conditions (9)-(11) and 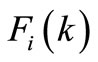 for
for  can be achieved sequentially following the same iteration process. Finally, the solutions of
can be achieved sequentially following the same iteration process. Finally, the solutions of 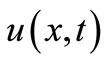 at time
at time 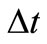 can be approximated by the partial sum of Equation (2). These solutions are adopted as the initial values in the next time interval. We get some solution series which are evaluated up to
can be approximated by the partial sum of Equation (2). These solutions are adopted as the initial values in the next time interval. We get some solution series which are evaluated up to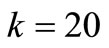 . Comparison of numerical solution of nonlinear PDE with the Maple 11 solution is shown in Table 1. According to the table, the simulation results are very compatible with the Maple solutions.
. Comparison of numerical solution of nonlinear PDE with the Maple 11 solution is shown in Table 1. According to the table, the simulation results are very compatible with the Maple solutions.
Example 2:
Let us consider the following inhomogeneous initial value problem
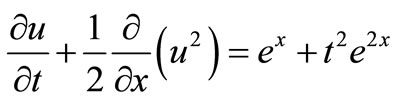 (12)
(12)
 (13)
(13)
Substituting the differential transformation 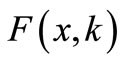 of
of 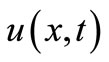 into Equation (12) gives,
into Equation (12) gives,
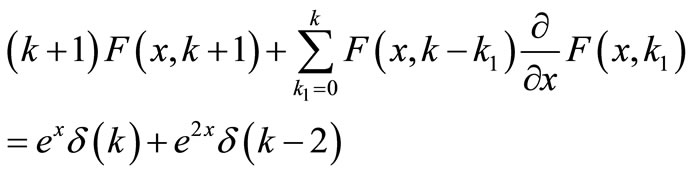 (14)
(14)
After discretizating with central difference formula the PDE becomes,
 (15)
(15)
and initial condition is
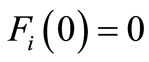 (16)
(16)
where  is Kronecker Delta Function and
is Kronecker Delta Function and 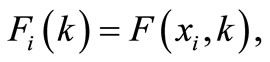
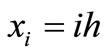 .
.
Using second order finite difference method boundary values were obtained as follows,
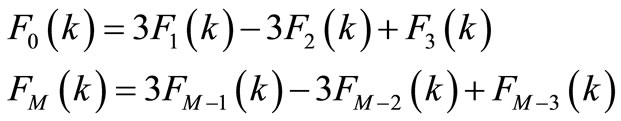
Evaluating the recurrence relation in Equation (15) and transformed initial condition (16) and computed boundary values,  for
for  are easily obtained and use the inverse transformation rule in DTM. Then we had the numerical solution and compared with other published work of Wazwaz [13]. As shown in Table 2, our simulation results exactly coincide with the ADM solutions.
are easily obtained and use the inverse transformation rule in DTM. Then we had the numerical solution and compared with other published work of Wazwaz [13]. As shown in Table 2, our simulation results exactly coincide with the ADM solutions.
Example 3:
We will consider the following nonlinear inhomogeneous advection problem
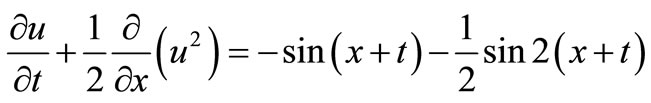 (17)
(17)
with initial condition
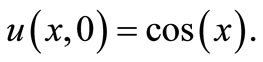 (18)
(18)
Using differential transform method to time variable
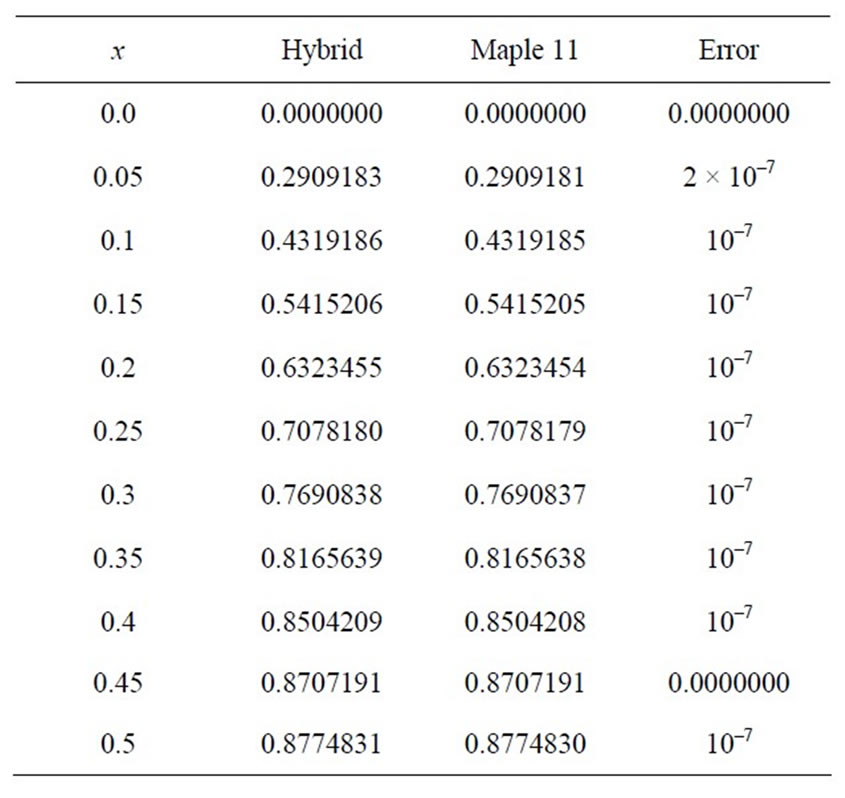
Table 1. Comparison of numerical results with the Maple 11 solution at t = 0.01.
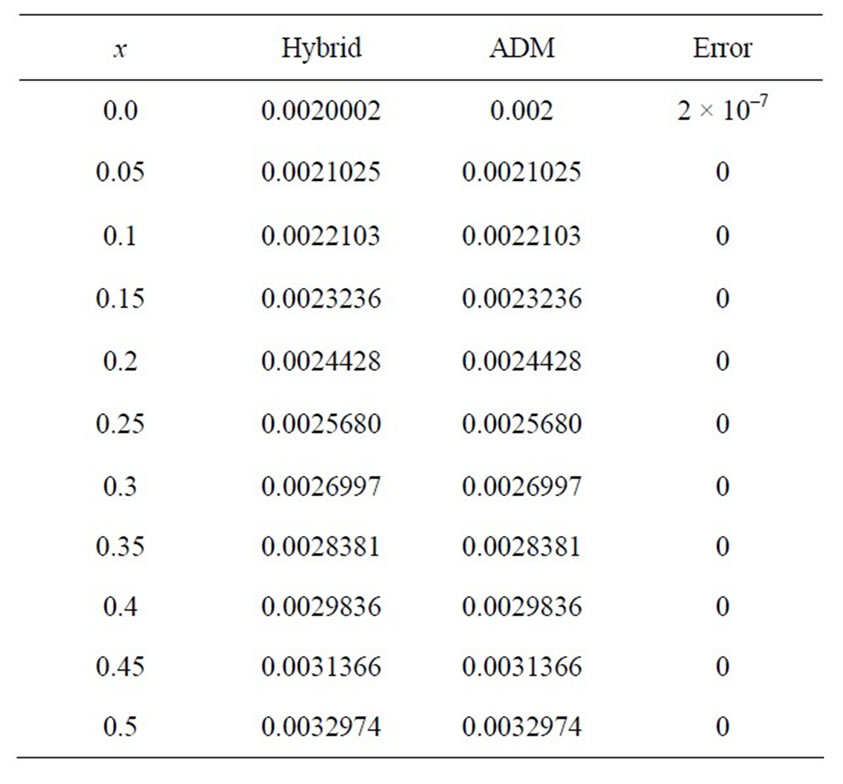
Table 2. Comparison of numerical results with ADM solutions at t = 0.002 for h = 0.1, ∆t = 0.0001.
for linear and nonlinear terms of equation, (17) gives
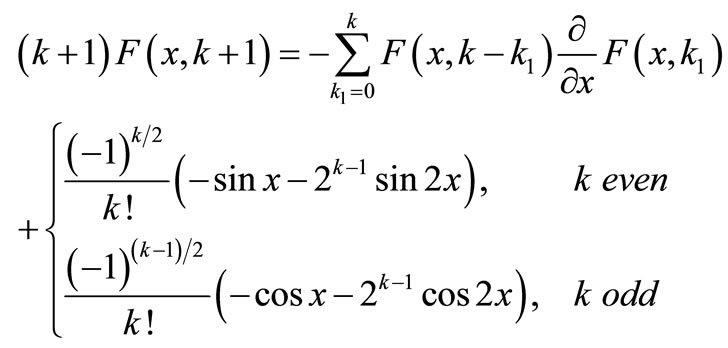 (19)
(19)
where  is the differential transform of
is the differential transform of . After using central finite difference method for derivatives according to x variable
. After using central finite difference method for derivatives according to x variable
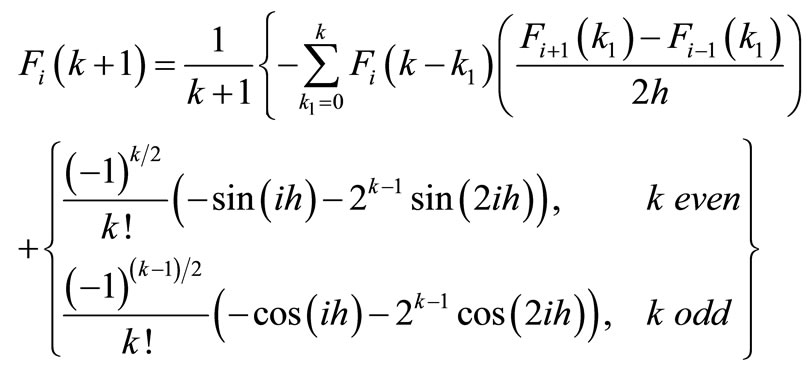 (20)
(20)
and initial condition is
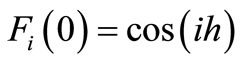 (21)
(21)
Equation (19) is an iterating process and using this process we get numerical solutions as in Table 3 for 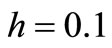 and
and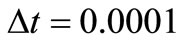 . We compare the solutions of Hybrid Differential Transform with the solutions of Adomian Decomposition Method (Wazwaz [13]). As shown in Table 3, the error between the simulation and ADM results is quite small.
. We compare the solutions of Hybrid Differential Transform with the solutions of Adomian Decomposition Method (Wazwaz [13]). As shown in Table 3, the error between the simulation and ADM results is quite small.
Tables 1-3 show the exact values, the approximation solutions obtained from the hybrid differential transform method and the absolute errors that results from comparing the approximate solutions and the Maple 11 or ADM solutions. The Hybrid Method results agree with the published work of Wazwaz [13], who considered the same equations, for nonlinear initial value problems to six decimal places after rounding.
4. Conclusions
The hybrid method is employed to predict nonlinear partial equations. Some simulation results are illustrated and discussed to compare with other published work. Three
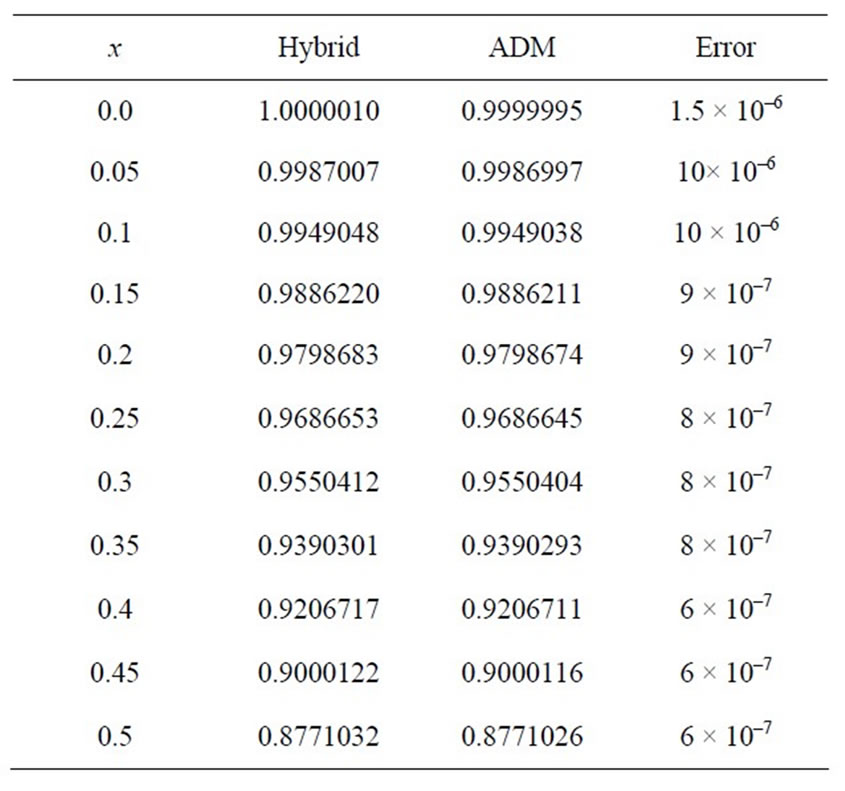
Table 3. Comparison of numerical results with ADM solution at t = 0.001.
advantages that are briefly explained in this study of this method are as follows:
1) The hybrid method provides an iterative procedure to calculate the numerical solutions; therefore, it is not necessary to carry out complicated symbolic computation.
2) From the nonlinear partial differential equations considered, it has been shown that the proposed method can obtain very accurate numerical approximation.
3) The last and most important advantage is that we do not use linearization in solution procedure. Moreover we can avoid some complex operation therefore; the Hybrid Method provides an iterative procedure to calculate the numerical solutions without using linearization.
It may be concluded that this method is very powerful and efficient in obtaining numerical solutions for these types of partial differential equations with initial conditions.
REFERENCES
- I. H. A.-H. Hassan, “Differential Transform Technique for Solving Higher Order Initial Value Problems,” Applied Mathematics and Computation, Vol. 154, No. 2, 2004, pp. 299-311. doi:10.1016/S0096-3003(03)00708-2
- A. Arikoglu and I. Ozkol, “Solution of Difference Equations by Using Differential Transform Method,” Applied Mathematics and Computation, Vol. 174, No. 2, 2006, pp. 1216-1228. doi:10.1016/j.amc.2005.06.013
- F. Ayaz, “Solution of the System of Differential Equations by Differential Transform Method,” Applied Mathematics and Computation, Vol. 147, No. 2, 2004, pp. 547-567. doi:10.1016/S0096-3003(02)00794-4
- C. W. Bert and H. Zeng, “Analysis of Axial Vibration of Compound Bars by Differential Transform Method,” Journal of Sound and Vibration, Vol. 275, No. 3-5, 2004, pp. 641-647. doi:10.1016/j.jsv.2003.06.019
- C. K. Chen and S. S. Chen, “Application of the Differential Transform Method to a Non-Linear Conservative System,” Applied Mathematics and Computation, Vol. 154, No. 2, 2004, pp. 431-441. doi:10.1016/S0096-3003(03)00723-9
- C. L. Chen and Y. C. Liu, “Solutions of Two-BoundaryValue Problems Using the Differential Transform Method,” Journal of Optimization Theory and Application, Vol. 99, No. 1, 1998, pp. 23-35. doi:10.1023/A:1021791909142
- H. P. Chu and C. L. Chen, “Hybrid Differential Transform and Finite Difference Method to Solve the Nonlinear Heat Conduction Problem,” Communication in Nonlinear Science and Numerical Simulation, Vol. 13, No. 8, 2008, pp. 1605-1614. doi:10.1016/j.cnsns.2007.03.002
- B. L. Kuo, “Applications of the Differential Transform Method to the Solutions of the Free Convection Problem,” Applied Mathematics and Computation, Vol. 165, No. 1, 2005, pp. 63-79. doi:10.1016/j.amc.2004.04.090
- O. U. Richardson, “The Emission of Electricity from Hot Bodies,” Longman, Green and Co., London, 1921.
- Y. L. Yeh, C. C. Wang and M. J. Jang, “Using Finite Difference and Differential Transformation Method to Analyze of Large Deflections of Orthotropic Rectangular Plate Problem,” Applied Mathematics and Computation, Vol. 190, No. 2, 2007, pp. 1146-1156. doi:10.1016/j.amc.2007.01.099
- J. K. Zhou, “Differential Transformation and Its Applications for Electrical Circuits,” Huazhong University Press, Wuhan, 1986.
- L. Beilina, “Adaptive Hybrid Finite Element/Difference Method for Maxwell’s Equations: A Priori Error Estimate and Efficiency,” Applied and Computational Mathematics, Vol. 9, No. 2, 2010, pp. 176-197.
- A. M. Wazwaz, “Partial Differential Equations Methods and Applications,” Taylor & Francis, London, 2002.
NOTES
*Corresponding author.

