Received 19 May 2015; accepted 23 June 2015; published 26 June 2015

ABSTRACT

The present value model of asset prices a la Campbell and Shiller predicts the price-rent ratio in the housing market to be stationary. The observed movements in the actual price-rent ratio, often exhibiting large and long swings in the ratio, may put into question the validity of the standard present value model. In this paper, we allow for two sources of possibly unwieldy deviations in the price-rent ratio in the standard present value model, and examine the relative importance of the standard model and the two extra features using the Italian house market data. The results strongly support the validity of the standard present value model, in which the up- and down- swings in the price-rent ratio are mostly explained by the movement in the expected risk premium, whereas the bubble and regime-switching expectation does not make sizable contributions to the price-rent ratio. Our results suggest that the standard present value model is a reliable vehicle in explaining the price-rent ratio.

Keywords:

Italian Price-Rent Ratio, Bubble Regimes, Regime-Switching Expectation

1. Introduction

The present value model proposed by Campbell and Shiller [1] [2] has gained popularity and been frequently used in asset pricing literature. This model ties the asset’s fundamental value to the discounted sum of its future payoffs or dividends. Adapted to the housing market, the present value model provides two key implications: 1) house prices and rents should be of the same order of integration and 2) if the two variables are both nonstationary in level but stationary in first differences, they should be cointegrated so that their ratio (i.e., the price-to- rent ratio) is stationary. Resorting to these features, quite a few papers have applied the present value model to stock market (e.g., Campbell and Ammer [3] ) or housing market (e.g., Campbell et al. [4] and Kishor and Morely [5] ).

The actual movements in the price-rent ratio, however, often stand in contrast to the prediction of the present value model. Of the plots in Figure 1 of the Italian housing market data since 1979, Q1 provides an illustration: in contrast to the three apparent episodes of boom-bust in the real house price, the movements of real rents series have been relatively subdued over the whole period. As a result, the price-rent ratio follows the price movement very closely, and exhibits intermittent boom-bust around the sample average. To the extent that future rents are the intrinsic income flow and therefore expected to move more or less hand with house price, large and long swings in their ratio may put into question the applicability of the present value model in the first place.

Such large and sustained deviations in the price-rent ratio from the historical average motivate us to examine whether the present value model in its standard form can still be used for empirical studies. We introduce two possible sources of erratic movements in the price-rent ratio into the otherwise standard present value model. We first allow for a repeatedly gestating and collapsing bubble as an additional driver of the Italian price-rent ratio. In particular, we specify the bubble component as temporarily expanding and collapsing across the two regimes. Once the presence of two distinctive regimes is allowed, there emerges another issue in applying the present value model. In fact, an implicit yet crucial assumption made in the vast majority of the literature is that the fundamental processes underlying the housing market are stable over time. If the two distinctive regimes are

recognized, however, the public will naturally revise their expectations of future fundamentals depending on the information they have about the current regime. In this vein, we specify that the means of the fundamental processes are regime-dependent and evaluate the conditional expectation of the public explicitly taking the presence of two regimes into account. The modified model turns out to be a Markov-Switching present value model.

When we apply the result modified model to the housing market of Italy, the results strongly support the standard present value model as a valid vehicle to examine the price-rent ratio. The boom-bust behavior of the Italian price-rent ratio is mostly explained by the movement in the expected risk premium, whereas the bubble and regime-switching expectation does not make any sizable contributions to the price-rent ratio. Our results suggest that the standard present value model is a reliable vehicle in explaining the price-rent ratio, even if it exhibits long swings, as long as it is mean-reverting within a reasonable period of time.

2. The Model

Our point of departure is the standard Campbell-Shiller model for the price-rent ratio

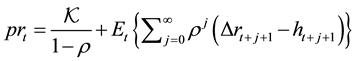(1)

where 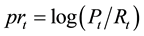is the log price-rent ratio, 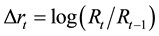is the real rent growth, and

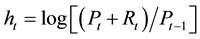is the log gross real return from housing, with 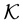the linearization constant. The dis-

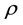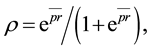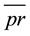count factor is determined as where is the sample average of the log price-rent ratio.

We now introduce two modifications into Equation (1): first, the log gross real return, , is broken down into the real interest rate, 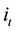(corresponding to the risk-free rate of return), and the excess rate of return, 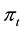, (reflecting the risk premium for investing in housing).² Then we add a rational bubble component 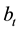satisfying

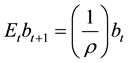, so that the actual price-rent ratio is represented as

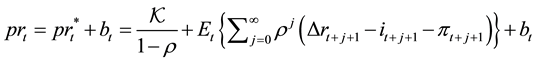(1')

where corresponds to the intrinsic log price-rent ratio determined as a weighted average of the expected future housing market fundamentals, i.e., rent growth, real interest rate, and excess returns.

Following Van Binsbergen and Koijen [8] , we treat the expected rent growth, , expected real interest rate, , and the expected housing premium, , as unobserved components following AR(2) processes³:

(2a)

(2b)

(2c)

where the shocks to the expectations, , are a Gaussian i.i.d. process with a general covariance

matrix. Note that the intercepts, , are time varying so that the means of expected fundamentals may change over time. More details of the intercepts are discussed in the next subsection.

The realized series of rent growth and real interest rate are equal to their respective expectations plus idiosyncratic innovations:⁴

(3)

where the unexpected innovations, , follow a Gaussian i.i.d. distribution with a diagonal covariance matrix,. We assume that and are mutually uncorrelated at any leads or lags.

As discussed in the introduction, we assume the bubble component switches between the exploding regime and non-exploding regime. The regime-dependence of is governed by a hidden state variable. In the non-exploding regime with, the bubble is assumed to follow a stationary AR process with a drift and a Gaussian i.i.d. disturbance:

(4a)

where. Equation (4a) allows for the bubble to die out slowly. When the bubble has switched from a non-exploding regime to an exploding one (i.e., is followed by), it evolves as

(4b)

When the bubble continues to remain in the exploding regime (i.e., is followed by), we put

(4c)

Finally, the hidden state variable follows a first order Markov process with transition probabilities

(5)

independently of at any lead and lag.

We now turn to the time-varying intercepts of the expected future fundamentals. Our assumption is that individuals observe the current regime and form their expectations in a regime-specific way. More specifically, the intercepts are specified to differ across the two regimes as follows:

(6)

Since the Markov chain for in Equation (5) is time-invariant, we can solve for the intrinsic price-rent ratio taking regime-dependent expectations into account. Cast in the companion form, the laws of motion in (2a)-(2c) are

(2')

where

, , ,

, , ,

and

The law of iterated expectation then allows us to re-write as

. (7)

In evaluating the conditional expectations in Equation (7), it is in order to deal with the regime-dependent intercepts for. Concentrating on the occurrences of, we can show that

(8)

where, , , and the factor loading for

is given by. It is then straightforward to establish similar results for

and in Equation (7) In sum, we have

(9)

where, , and is the regime-dependent intercept of.5

From the perspective of an econometrician, it is more realistic to assume that neither the realizations of nor the transition probabilities are in his/her information set. That being the case, the practical version of the present value model to be estimated can be cast into a state space form subject to Markov switching, the measurement block comprises Equations ((3), (1'), (10)) and the transition block has Equations ((2'), (4a)-(4c)). Note that the Markov-Switching nature of the model manifests itself in the intercept of the intrinsic log price-rent, as well as in the evolution of the bubble component.

3. Application: What Drives the Italian Price-Rent Ratio?

The modified present value model is applied to examining the price-rent ratio in Italy. We first estimated the model via the approximate likelihood method in Kim and Nelson [9] . The dataset we use comprises the quarterly series of real house price, real rent, price to rent ratio, nominal interest rate, and the core CPI inflation of Italy, all spanning 1979: Q1 to 2013: Q4. The real house price, real rents, and price-rent ratio are obtained from the OECD statistical warehouse as seasonally adjusted series. Since the price-rent ratio only is available as an index with 2010 as the base year, we rescale the original series to match the price to rent ratio for Italy in 2013 available from Global Property Guide.6 We then get the rent series by dividing the real house price index with the re-scaled price-rent ratio. Nominal interest rate is the short-term government bond yield rate obtained from the OECD Main Economic Indicators database.7 Core CPI is obtained from the same source and transformed into year-on-year inflation rates, which are then subtracted from the nominal interest rate to yield the real interest rate series.

Once the state-space model is estimated, the relative importance of the three fundamental expectation factors and the bubble in driving housing prices can be evaluated by their factor loadings to the price-rent ratio. Since our model involves the fundamental and bubble components, we proceed in two steps. We first measure the importance of the three expectation factors for the intrinsic price-rent ratio using Equation (9). Our aim here is to identify the main driving factor of the housing market in the absence of bubbles. We will then move on to evaluating how much the bubble component has driven the housing market.

Using the estimated parameters and Equation (9), we plot in Figure 2 the factor loadings (in solid line) of the expected market fundamentals on to the intrinsic price-rent ratio (in dotted line). Evidently, the movements

in the fundamental price-rent ratio are mostly explained by the expected housing premium,. In particular, the three episodes of boom-bust in the intrinsic price-rent ratio are almost entirely driven by the fluctuations in the expected housing premium, even if the shifts in the expectations are allowed. The dominance of the expected premium is reminiscent of the previous studies on asset price movements: Cambell and Ammer [3] find for the US stock market that approximately 70% of the variance of excess stock returns is attributable to the “news” about future risk premiums for holding stocks, whereas approximately 15% of the stock return variance is attributable to “news” about future dividends. Also, Campbell et al. [4] find that changes in expected future housing premiums are the main source of variation in rent-price ratios in the US housing market at the national, regional, and metropolitan levels.

The results in Figure 2 are tempting for us to conclude that the standard present value is reliable in explaining the price-rent ratio and that the expected housing premium is the dominant force in the Italian housing price movements. We note, however, these results only have bearings for the intrinsic part of the price-rent ratio, not the actual price-rent ratio ridden with a speculative bubble. Given that our estimation results do not yet rule out the presence of bubble in the actual price-rent ratio, the contribution of the bubble component should be evaluated in comparison with those of the fundamentals.

Figure 3 examines the importance of the bubble component. In the top panel, the actual price-rent ratio and its estimated intrinsic counterpart are plotted, along with the filtered probabilities of expanding-bubble regime. We note that the two price-rent ratios are moving in tandem, although the estimated probabilities of exploding bubble regime captures the boom-bust movements in the ratio. These results suggest that the historical movements in the Italian housing price have largely been free of speculative bubbles and that the up- and down swings

in the ratio are driven by the expected housing risk premium. The insignificance of bubble in the Italian price- rent ratio is further supported in the bottom panel. Here, the % of bubble in the actual price-rent ratio is plotted along with the probabilities of exploding bubble. Clearly, the % of bubble has been around 0, except for its sudden decrease around the late 1970s.

4. Conclusions

To the extent that future rents are the intrinsic income flow that determines the fundamental value of housing units, house prices and rents are expected to move more or less hand. In contrast to this intuition, the actual movements in the price-rent ratio often exhibit too large and long swings to be justified by the standard present- value model.

We extend the standard present value model by allowing for two alternative sources of the unwieldy deviations in the price-rent ratio, i.e., the presence of periodically collapsing bubble and the changes in agents’ expectations depending on the realized bubble regimes. We then examine the relative importance of the standard and the two extra features in explaining the actual price-rent ratio in Italy. The results strongly support the standard present value model as a vehicle to examine the price-rent ratio. The boom-bust behavior of the Italian price-rent ratio is mostly explained by the movement in the expected risk premium, whereas the bubble and regime-switching expectation do not make any sizable contributions to the price-rent ratio. Our results suggest that the standard present value model can be used in explaining the price-rent ratio, even if it exhibits long swings, as long as it is mean-reverting within a reasonable period of time.

Acknowledgements

This work was supported by Hankuk University of Foreign Studies Research Fund. This is gratefully acknowledged by the authors.

References

NOTES

^*Corresponding author.

¹Real house price and rents series are obtained from the OECD database available at the link: http://www.oecd.org/eco/outlook/focusonhouseprices.htm.

²Balke and Wohar [6] [7] and Kishor and Morely [5] adopt a similar decomposition.

³As in Van Binsbergen and Koijen [8] , we also used the AR(1) specification in an earlier version of the paper. The AR(2) specification turned out to better fit the data with more realistic dynamics.

⁴By considering the observations of the rent growth and real interest rate only, we are treating housing risk premium as residuals given data on price-rent ratio.

⁵More details of deriving Equation (9) are available from authors upon request.

⁶The Italian annual rental yields, the inverse of the price-rent ratio, was 3.7% as of as of June 2013. Refer to the link: http://www.globalpropertyguide.com/Europe/italy.

⁷Refer to the link: http://stats.oecd.org/mei/.

⁸For the ease of visual inspection, all plotted series are demeaned.