Journal of Biophysical Chemistry
Vol.4 No.2(2013), Article ID:31790,11 pages DOI:10.4236/jbpc.2013.42013
Theoretical investigation of the dispersion interaction in argon dimer and trimer
![]()
1Chemistry Department, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia; *Corresponding Author: walid_m76@yahoo.com, aquasti@kau.edu.sa
2Chemistry Department, Faculty of Science, Cairo University, Giza, Egypt
Copyright © 2013 Abdullah H. Quasti, Walid I. Hassan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 9 December 2012; revised 11 January 2013; accepted 21 January 2013
Keywords: Vdw Clusters; Dispersion Interaction; Argon Dimer and Trimer; Ab Initio Computation; Density Functional Theory
ABSTRACT
The ultimate aim of the present work is to establish an acceptable level of computation for the van der waals (vdw) complexes that is able to pick up appreciable amount of dispersion interaction energy, reproduce the equilibrium separation within the acceptable limits and at the same time cost and time effective. In order to reach this aim vdw clusters where pure isotropic dispersion interaction occur, namely, Ar dimer and trime were investigated. Computations using different basis sets and at different levels of theory have been carried out. Three basis sets, namely, the 6-31++G**, the 6-311++G** and the aug-cc-pvdz basis set, were found superior to all other basis sets used. The high performance and relative small CPU time of the 6-31++G** basis set make it a good candidate for use with large vdw clusters, especially those of interest in biology. Three compound methods were applied in the present work, namely G1, G2 and G2 Moller-Plesset (MP2) and the complete basis set method, CBS-Q. These methods failed to detect the attraction dispersion interaction in the dimer. The predicted repulsive interaction seems dominant in all these methods. Some of the recently developed Density Functional Theory (DFT) methods that were parameterized to account for the dispersion interaction were also evaluated in the present work. Results come to the conclusion that, in contrast to the claims made, state-of-theart Density Functional Theory methods are incapable of accounting for dispersion effects in a quantitative way, although these methods predict correctly the inter-atomic separations and are thus considered a real improvement over the conventional methods. BS-SE has been computed, analyzed and discussed.
1. INTRODUCTION
The interest in cluster research has grown enormously during the last decade, due to its intermediate position; clusters represent the bridge to the understanding of the transition from the gas-phase to the condensed phase. Dispersion attraction interactions are important determinant of the properties of these clusters.
Dispersion interactions are either isotropic as in the case of rare-gases or anisotropic in nature as in the case of HF, CO. methane etc. In the former case, empirical fitting of experimental data has successfully yielded both interaction energies and geometries, whereas in the case of anisotropic interaction, a quantitative description is currently beyond experimental limits.
Theoretical efforts concentrate on rare gas interactions due to the ability to compare results with experiments and thus be able to evaluate the level of theoretical model employed.
The appropriate theoretical model can thus be extended to molecules. The literature contains several theoretical calculations along these lines [1-10]. However, the question of what is the appropriate method to be used to evaluate vdw interactions, still exists. This is due to three main reasons concerning the size and flexibility of the basis set, electron-correlation and basis set superposition error. In addition, extension to relatively large molecular system is governed by basis set limitations due to computational demands. The Ar dimer is one of the most interesting vdw molecules and is the subject of several experimental [11-15] and theoretical investigations [2- 4,16,17]. Stoicheff et al. [11] did ultraviolet laser spectroscopy of Ar2 and analyzed transitions to the ground electronic state. They obtained what is probably the most straight forward experimental determination of the potential energy surface. The dissociation energy De = 99.2 cm−1 with an estimated error of 1% at equilibrium bond length of 3.761A.
Theoretically Ar2 has been investigated both by constructing empirical potentials [1-10] and by ab inito methods [14,15]. Aziz [18] presented a highly accurate potential of Ar [2], which is much more accurate than the previous HFD-B2 potential and is able to predict many properties with high accuracy. Aziz’s potential predicted a well-depth of 99.7 cm−1. On the other hand, the MP4 calculation of Chalasinski et al. underestimates the welldepth by 25% mainly due to the lack of higher-than fpolarization functions. Very few ab initio computation recovered over 90% of the well-depth. One of the best such computation is due to Woon [17] using augmented correlation consistent basis sets, a well-depth of 94.4 cm−1 was obtained using the CCSDCT and a aug-cc-pv6z. He was able to obtain, what is possibly, the best theoretically computed well-depth for Ar2 of 452.4 μEh at a separation of 3.766 A.
The studies of the rare-gase vdw molecules stated earlier aims to establish methods that can be extended for systems of real interest. In this sense, the use of the aug-cc-pv6z and similar basis sets seems meaningless. The present project aims to investigate the vdw interaction between aromatic species and Ar, in an effort to rationalize some experimental observation of ion-beam scattering in Ar matrices. To establish a reliable and computationally feasible theoretical model, the Ar dimer and trimer were investigated first. Results then can be extended to Ar-aromatic and aromatic-aromatic systems. The ultimate aim of the present work is, thus, to establish an acceptable level of computation for the vdw complexes that is able to pick up appreciable amount of dispersion interaction energy, reproduce the equilibrium separation within the acceptable limits and at the same time cost and time effective. In order to reach this aim the following objectives are set and executed:
1) Investigate closely the PES of interactions among some vdw clusters where pure isotropic dispersion interaction occurs, namely, Ar dimer and trimer. Fitting the computational results to a Lennard-Jones type potential will shed light on the different forces in the vdw clusters under investigation.
2) The effect of basis set size, polarization and diffuse functions on the stabilization energy and equilibrium separation of the studied clusters will be investigated.
3) To calculate the correlation energy at different levels of theory and determine the appropriate level that is both accurate enough and cost effective.
4) To examine closely the performance of some of the popular computational methods such as the compound, complete basis set and DFT methods.
5) To reach a conclusion as to the appropriate level required to localize such weak interactions within the framework of a cost effective theoretical model.
2. METHOD OF CALCULATIONS
Ab initio calculations were performed using the Gaussian 09 program [19]. All standard Gaussian basis sets have been used and examined and compared to the augcc-pvxz sets. The complete basis set methods G1, G2 and CBS-Q were also tested. Some possible Density Functional Theory methods have been applied. Electron correlation correction was handled by the perturbation method of Moller-Plesset up to the fourth-order (MP- 4SDTQ). Post MP4 corrections for residual correlation effects were treated with the theory of quadratic configuration interaction QCISD(T). BSSE was estimated by the function counterpoise method Proposed by Boys and Bernadi [20].
3. RESULTS AND DISCUSSION
Table 1 presents the interaction energies and equilibrium separation for the Ar dimer computed using the standard Gaussian Basis sets. The information about the intermolecular potentials lies out in the 8th, 9th, 10th and significant figures, so a small effect can have disproportional effect of the computational results. Table 1 clearly conforms that Restricted Hartree Fock (RHF) is useless for computations of the intermolecular interaction of the vdw type. Note that RHF predicts bond lengths that are far too large and the predicted Re values tend to increase as the orbital basis is improved. To understand the reason for this behaviour let us consider two argon atoms infinitely separated. Their electron clouds are essentially non-overlapping and being essentially spherical charge distributions, there is no interaction due to static electrical dipoles, quadrupoles or higher multipole moments.
At smaller separations, the charge cloud begins to overlap and the Pauli exclusion principle implies that the orbitals have to distort to maintain orthogonality. The more the orbitals distort, the higher the energy, thus a repulsive interaction. The Hartree-Fock theory actually provided a good description of the repulsive wall of the potential energy curve.
Small basis RHF computations, Table 1, shows very weak attraction due to basis set superposition error (BSSE), as indicated by a small counterpoise correction to the RHF energy (last column of Table 1). The RHF-predicted Re values become infinite in the complete basis set limit.
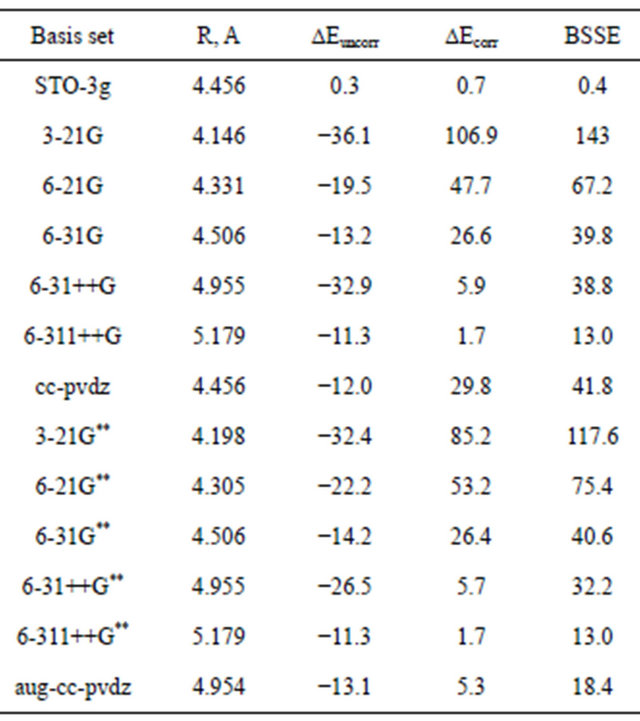
Table 1. Dispersion interaction energy (μHartree) for Ar2 computed using different basis sets at the HF-level.
Table 2 presents calculations using the same set of standard Gaussian basis sets and the correlation energy is accounted for at the MP4 level. In all cases studied, the well-position is shifted to, shorter interatomic separation with a corresponding dramatic increase in the well-depth. These results clearly indicate that dispersion energy is an electron correlation effect associated with correlated fluctuation dipoles.
Table 3 presents details of the computations carried out using the three basis sets 6-3l++G**, 6-311++G** and Aug-cc-pvdz at different levels of Moller-plesset perturbbation calculation. Careful inspection of Table 3 reveals the following:
1) The aug-cc-pvdz basis at the MP4 level seems to be superior to the Gaussian triple-zeta basis sets.
2) The superiority of the aug-cc-pvdz basis set comes on the expense of time. This basis set is much more time consuming than the Gaussian basis sets. A typical relative CPU time is given in Table 3, where the Dz basis set consumes about double the time consumed by any other Gaussian basis set.
3) The 6-31++G** basis set seems to be the faster. At the HF-SCF level this Gaussian basis set is superior to all other basis sets in terms of well-depth. At the MP4 level, it picks up as much as 96% of the total interaction energy computed by the Dz basis set.
Both the diffuse and the polarization functions play an important role in determining well depth where, the correlation interaction seems to dominate the well-position.
As stated before, electron-correlation in the case of vdw molecules result mainly from fluctuation of the in-
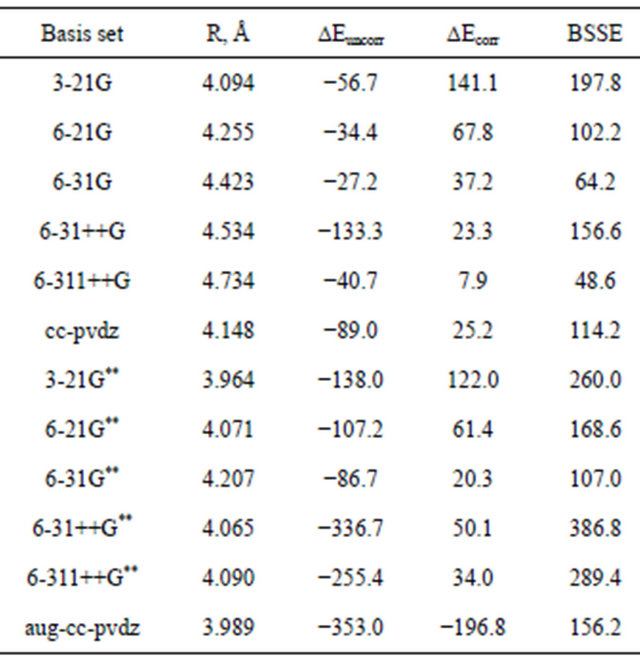
Table 2. Dispersion interaction energy (μHartree) for Ar2 computed using different basis sets at the MP4-level.
teraction dipoles. These fluctuations are either attractive or repulsive and thus, the true wave function has slightly higher amplitude at one point (attractive) and lower at another point (repulsive). This enhanced amplitude is expressed by a double excitation in the configuration interaction wave function in which an s orbital of one atom is replaced by a p orbital on the same atom. In MollerPlesset perturbation theory this double excitation makes an important contribution to the first order wave function, thus to the second-order energy E(MP2). Table 4 shows the correlation energy at different levels of MP computation for Ar2. It is worth noting that the correlation energy picked up at the MP2 level represents 99.9% of the total correlation that can be picked up at the MP4.
Of course, one needs to compute all the higher-order MP perturbation corrections to get as much as possible of the correlation energy. However, as it is obvious that the second order contribution turns out to dominates, and since one cannot afford to do everything right, then for vdw systems one would recommend a large-basis E(MP2) computation rather than a small-basis E(MP4) computation.
3.1. Basis Set Superposition Error (BSSE)
In supermolecule picture the interaction energy is defined as
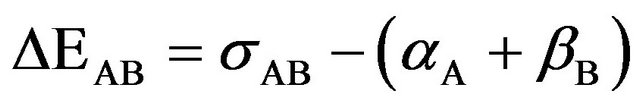 (1)
(1)
where σAB is the supermolecule basis set, αA and βB are the corresponding basis sets for the fragments A and B respectively. It has been argued that Equation (1) overestimates intermolecular attraction for weakly bonded systems. Since basis sets used in practice are of finite size, at the
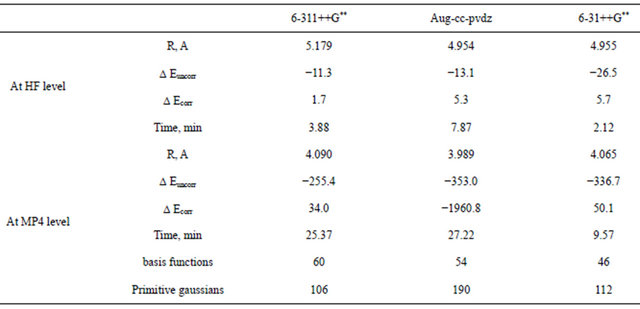
Table 3. Comparison of the computational results of Ar2 obtained using the augmented double-zeta and the Gaussian-triple-zeta basis sets.

Table 4. Correlation energy (μHartree) picked up at different levels of MP computation for Ar2.
equilibrium configuration of AB, the basis set functions centred on A assist in lowering the energy of B and vice versa, an effect termed BSSE by Liu and Mclean [21]. The BSSE correction can be estimated by a counterpoise correction technique.
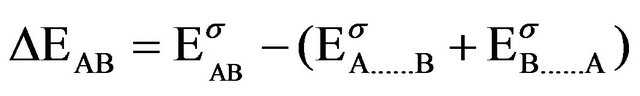 (2)
(2)
where EA……B is the energy of the system when B is Ghost atom and EB……A is the energy of the system when A is Ghost atom. Even though, Schwente and Truhlar raised serious doubt over the usefulness of this procedure. For all Gaussian basis sets used the cp correction decrease dramatically as the size of the basis set increase as shown in Figure 1. The cp correction to the E(MP2) contribution is much larger for a given basis set. This is a somewhat can traversal issue. Some would argue that one should require that the ghost atom orbitals be orthogonal to the orbitals that would be occupied if the ghost atom were a true since the occupied orbitals is not available to the virtual orbitals of the dimers. Others would argue it is better to just forget about the cp correction to E(MP2) altogether.
Results of the present work are consistent with those of Liedl [22] and indicate clearly that for Ar2, the E(MP2) potentials seem to coverage better with systematically increasing basis sets when one simply used uncorrected energies. The basis sets used in the present work show interaction potential curves Figure 2 which are repulsive except in very small regions around the equilibrium separation which exhibit essentially BSSE. So, the RHF cp correction is negligible.
3.2. Compound Computational Methods
The aim of the present study is to achieve the highest possible accuracy and maintain the same level of theory for the Ar-Benzene and the Benzene-Benzene complexes. A Varity of compound theoretical models have been developed in an attempt to achieve high accuracy by combining the results of several different calculations as an approximation to a single very high level computation which is much too expensive to be practical. Two welldocumented methods, the Gaussian-1 [23] and Gaussian- 2 [24] methods (G1 and G2 for short) will be considered in the present work. These two methods are tested and are known to be reliable for molecules, however they are
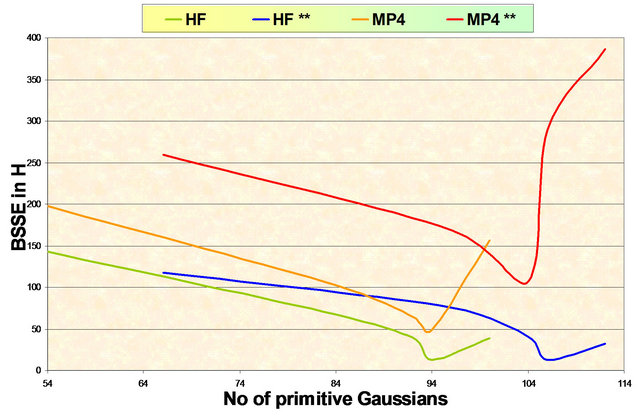
Figure 1. Variation of the BSSE with the number of primitive gaussians in the basis set at different levels of theory.
not yet tested for van der waal complexes.
The G1-procedure involves the following steps:
1) Initial geometry optimization at HF-6-31G (d) level. Verify the minimum energy structure by frequency calculation where the zero-point energy is calculated.
2) Define the geometry by MP2 (full) optimization.
3) Compute a base level energy Ebase at the MP4/6-3 11G (d, p)
4) Correct the base energy by including diffuse function at the MP4/6-311G+ (d, p) level.
5) Correct the base energy with higher polarization function on heavy atoms at the MP4/6-311G (2d, p) level.
6) Correct the base energy for residual correlation effects beyond the fourth order computing the QCISD (T)/ 6-311G (d, p) energy.
7) Correct the energy from step 6 for remaining basis set deficiencies by empirically estimating the remaining correlation energy between spin-paired electrons with the formula:
 (3)
(3)
where nα is the number of alpha electrons and nβ is the number of beta electrons in the molecule. This term is known as the higher level correlation.
Therefore, the total G1 energy may be written as:
 (4)
(4)
the quantity G1 is an approximation to an energy calculated directly at QSISD(T)/6-311+G(2df,p). replacing this one very large calculation with four smaller ones is much faster.
The G2 theory adds some additional corrections to G1 final result. The major term is a correction at the MP2 level, details of the G1 and G2 methods are given in the original publications [23,24].
Table 5 presents the results of G1, G2 and the modified G2MP2 method [25] for the Ar atom and for the dimer. Generally, the three computed methods failed to detect the attraction dispersion interaction in the dimer. The predicted repulsive interaction seems dominant in
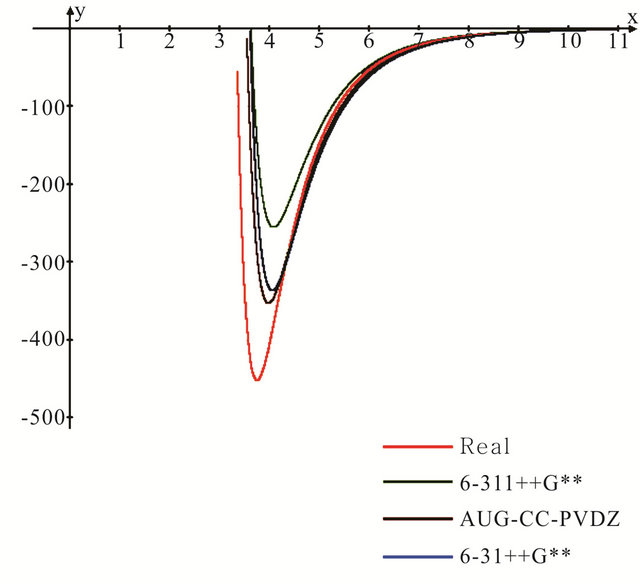
Figure 2. Lennard-Jones potential energy curves for the argon dimer computed using the selected three basis sets as compared to the experimental potential.
the three compound methods. The error introduced by the approximation made in the successive steps seems to be greater than the dispersion interaction in the dimer. One may thus conclude that irrespective of the success reported of the G1, G2 and G2MP2 methods for compounds where real chemical bonds exist, these methods are not suitable and can't be used in the case of the week vdw complexes.
3.3. Complete Basis Set Models
The complete basis set (CBS) [26] methods aims to overcome the main source of error in ab intio calculations that result from basis set truncation. A CBS calculation typically include a HF-calculation at a very large basis set, an MP2 calculation with a medium size basis set (this is also the level where the CBS extrapolation is performed) and one or more, higher-level with a medium-to modest basis set. The most sophisticated of these methods is the CBS-Q [24] implemented in the Gaussian 09 program this method is well tested for molecules where real chemical bonds exist. In the present work, calculations using, CBS-Q model is carried out on the Ar2 vdw molecule in order to correctly estimate dispersion energies. Table 6 presents results of computations using the CBS-Q model as compared to a full computation at the QCISD(T)/6-3l++G** it is obvious that the CBS-Q method predicted a very repulsive potential for the Ar2. This is true even if one changed the initial starting basis set 6-3l++G** or the Aug-cc-pvdz basis sets. The predict equilibrium separation Re is 4.178 A in good agreement with our previous computational results. One may conclude at this point that the dispersion, interaction

Table 5. Energy quantities (a.u.) computed using G1, G2 and G2-MP2 methods for Ar and Ar2 dimer.

Table 6. Comparison between energy quantities computed using complete basis set (CBS-Q) and QCISD(T) methods for Ar and Ar2 dimer with 6-31++G** basis set.
which is responsible for the formation of the dimer is mainly a correlation phenomena and is much smaller than the energy introduced by the approximations introduced by extrapolation A full QCISD(T)/6-311++G** calculation, which is the reference for the G1, G2 and the CBS-Q models, yields an Ar-Ar equilibrium separation of 4.088 A, 28% longer than the experimental value. The stabilization dispersion interaction energy predicted by the QCISD(T)/6-3 11++G** calculation is 259 μ Eh which is about 57% of the experimental value. At the MP4 level, the HF/6-3 11++G** calculation predicted almost the same equilibrium separation and is able to pick up only 56.5% of the stabilization energy. It is interesting to extent this comparison to the aug-cc-pvdz calculation, where the QCISD(T) is again superior to the MP4 calculation by 5% nearer to equilibrium separation .
3.4. Density Functional Calculations
The wide popularity of the DFT methods and its significant success in describing the electronic structure of molecules allows us to extend the present investigation of the Ar dimer to include results of calculations using different DFT approaches. Table 7 summarizes the results of such computations using a number of DFT methods. These methods fall into three main groups, namely the local exchange and correlation functional (LDA) exemplified by the Xα, VWN and Slater methods; the gradient corrected functional (GGA) exemplified by the BP86, LYP and B-LYP methods; and the hybrid methods such as the B3LYP and B3PW91.
Inspection of the data in Table 7 reveals that all DFT methods are unable to predict reliable asymptotic behaveiour of the interaction energy between the two close-shell argon atoms. Therefore, the region of the van der waals minimum is described by all these methods in a rather erratic manner. LDA strongly over binds, some GGA functional lead to repulsive interaction potential. In general, the predicted minima are characterized by a very large well-depth. This may be simply explained on the basis of the fact that, dispersion van der waals forces are due to long-range electron correlation effects that are notoriously absent from local and semi-local density functional leading to an incorrect description of the asymptotic behaviour of the potential energy of interaction between non-polar systems. There is, therefore, a growing need for exchange-correlation (XC) functional going beyond the LDA and the GGA as these don’t account for longrang correlations occurring in weakly bounded compound as the Vdw molecules. Recently, few articles appear in the literature along these lines [27,28], yet the proposed functionals are still not fully tested.
Inspection of data given in Table 7 and that in figure reveals that the B3LYP combined DFT method which is known to perform well in describing molecules and their vibrations, yields very bad repulsive picture for the argon dimer. The aug-cc-pvdz basis set gave the extreme repulsive potential.
The other combined methods that use Beck’s exchange functional shows the same trend e.g. BVWN, BVWN5, BLYP, BPL, BP86 and B3P86. Perez-Jorda et al. [29] have used HF-exchange and standard DFT correlation functional, in their investigation of some rare-gas vdw dimers, their results were in general, acceptable and
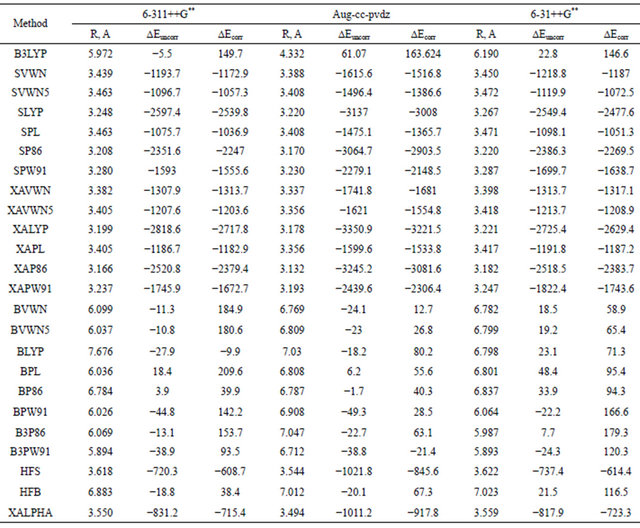
Table 7. Dispersion interaction energies (μEH) computed using different basis sets for Ar2 at the DFT level.
much better than those obtained by the DFT exchange functionals. This point ought to be examined carefully, since the failure of most DFT calculations on vdw complexes was attributed to correlation functional and not to the exchange one.
The failure of conventional DFT methods in predicting the dispersion interaction lead to the development of DFT methods specially designed to account for this type of weak long rang interaction [30-32]. In the present work, few of these methods were used and evaluated for the pure anisotropic vdw interaction in the Argon dimer. Table 8 summaries the results of computations using different long rang DFT methods.Inspection of results in Table 8 indicates clearly that these modified DFT methods cannot account quantitatively for the well-depth in the model pure anisotropic vdw complexes. However, these methods show considerable improvement over the conventional methods in predicting the equilibrium separation. In all schemes an empirical correction consisting of a C6r−6 term is introduced that is damped at short range. The coefficient C6 is calculated either from average molecular or atomic polarizabilities. This term accounts qualitatively for the attraction nature, however, the results of the present work come to the conclusion that, in contrast to the claims made, state-of-the-art DFT methods are incapable of accounting for dispersion effects in a quantitative way.
3.5. The Potential Energy Curve
One way of examining the full interaction behaviour between the two argon atoms is to fit data to a Morse or similar potential energy function. In the present work, we fit computational results to a Lennard-Jones [6-12] function of the form,
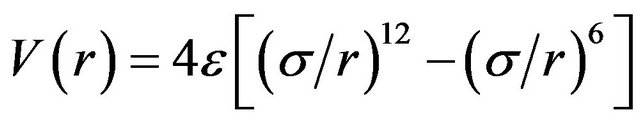 (5)
(5)
where ε is the well-depth and σ is the collision diameter (the separation for which the energy is zero). LennardJones equation may also be expressed in terms of the separation at which the energy passes through a minimum rm.
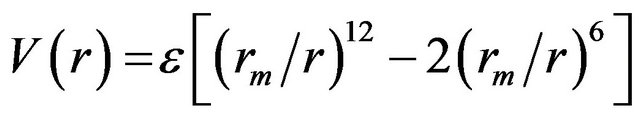 (6)
(6)
where rm = 21/6 σ
Results of the Lennard-Jones fitting are given in Table 9. Inspection of the data given in this table is very instructive and can be summarized as:
1) The quality of the basis set has no straight forward influence on the collision parameter σ, which oscillates between 3.59 and 4.2 A. Thus the small 3-21G** basis set predicted a σ value of 3.649 A which is very close to 3.627 A that predicted by the much extended basis set 6-311++G**.
2) Also, rm obtained from empirical potential of the
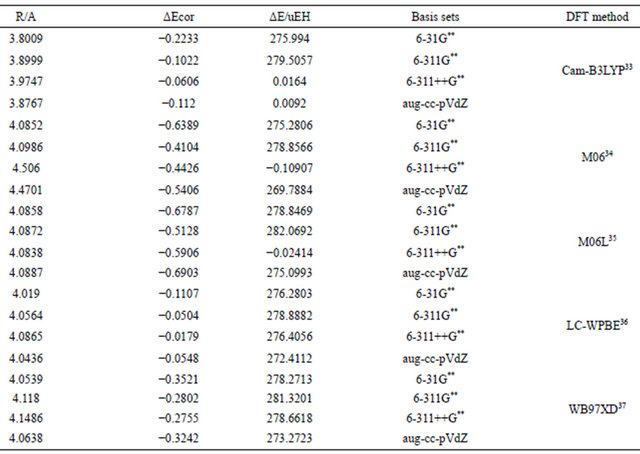
Table 8. Dispersion interaction energies (μEH) computed using different basis sets for Ar2 using DFT-D methods.
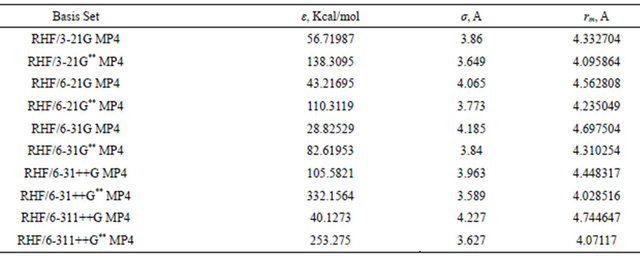
Table 9. Lennad-Jones parameters computed for argon dimer using different basis sets.
computation data is always greater than the equilibrium value. This difference can be reduced by reducing the step size.
3) The well-depth, however seems, much more dependent on the quality of the basis set and is very close to values obtained by optimization. The number of primitive Gaussians is not the determining factor, it is the type of these Gaussians which is of importance in determining the extent of dispersion interaction. Thus, for example the 3-21G basis predicts a well-depth which is slight deeper than that predicted by the 6-21G basis set.
4) The inclusion of polarization function has a pronounced effect on the depth of the well. Thus, going from the 6-21G to the 6-21G** basis set results in an increase in the well-depth of 61%. The same is also true for the two basis sets, 6-31G and 6-31G** where more than 65% increase in Є is observed.
5) Diffuse functions seem to play a crucial role in determining the well-depth. A 73% increase in Є is observed on going from 6-31G to the 6-31++G basis set.
6) It is Worth nothing at this point that, the 6-31++G** basis set seems to be superior and yields the best potential parameters
Figure 2 presents the Lennard-Jones potential curves computed for the Ar dimer using the 6-31++G**, 6- 311++G** and aug-cc-pvdz basis sets. The experimental potential is also shown in the same figure for reference. It is evident that the three theoretical models are able to predict the repulsive side of the well satisfactorily, however, they behave in a different manner in describing the long rang attractive side. Both the aug and 6-31++G** basis sets reproduce the experimental behaviour in the long rang attractive side in an excellent manner.
3.6. The Argon Trimer
In the previous section, we have established that an acceptable level of computation for the vdw complexes that is able to pick up appreciable amount of dispersion interaction energy, reproduce the equilibrium separation within the acceptable limits and in the same time cost and time effective can be achieved using the aug-cc-pvdz, 6-311++G** or the 6-31++G** basis sets at the MP2 level of theory. In the present section, we will farther examine this model as applied to the Ar-trimer. This vdw complex may exist in a linear or a triangular structure. Table 10 and 11 present the results of our computation on these two structures using different basis sets at HF and MPz levels of theory. Careful inspection of the data given in Tables 10 and 11 reveals the following:
1) Computations indicate the isosceles triangular previous experimental [28,29] and theoretical [31] studies.
2) The stabilization dispersion energy computed by the

Table 10. Total energy (Hartree), dispersion energy and equilibrium separation in the linear argon trimer at the HF and MP2 levels.
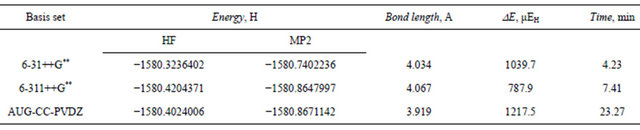
Table 11. Total energy (Hartree), dispersion energy and equilibrium separation in the Ar3 isosceles triangular structure at the HF and MP2 levels.
aug-cc-pvdz basis set at the MP2 level is 1217 μEh indicating the tight vdw binding in the trimer. The 6- 31++G** basis set was able to pick up 85.4% of this stabilization dispersion energy, whereas the larger 6-311++ G** basis set was able to pick up only 64.7%. These results elaborate upon our previous conclusion that the triple zeta Gaussian basis set 6-31++G** is capable of describing the forces that govern the formation and stabilization of the Ar vdw clusters satisfactorily and on a modest CPU time.
The interatomic separation predicted for the Ar3 clusters is slightly longer than that for the dimer. The traingular structure shows slightly longer (0.014A) re value as calculated by the 6-31++G** basis set. This value is 5% longer than the value reported by Gonzales et al. [31]. The aug-cc-pvdz basis set predicted the shortest equilibrium separation (3.92A) which is in much better agreement with the reported value.
REFERENCES
- Aziz, R.A. and Slaman, M.J. (1986) The Argon and krypton interatomic potentials revisited. Molecular Physics, 58, 679.
- Aziz, R.A. and Chen, H.H. (1977) An accurate intermolecular potential for argon. Journal of Chemical Physics, 67, 5179. doi:10.1063/1.434827
- Aziz, R.A. (1979) Molecular physics: An international journal at the interface between chemistry and physics. Molecular Physics, 38, 177. doi:10.1080/00268977900101591
- Van den Biesen, J.J., Hermans, R.M. and Van den Meijdenberg, C.J.N. (1982) Experimental total collision cross sections in the glory region for noble gas systems. Physica A, 115, 396-439.
- Koide, A., Meath, W.J. and Allnatt, A.R. (1980) Molecular physics: An international journal at the interface between chemistry and physics. Molecular Physics, 39, 895- 911. doi:10.1080/00268978000100771
- Douketis, C., Scoles, G., Marchetti, S., Zen, M. and Thakkar, A.J. (1982) Intermolecular forces via hybrid hartreefock-SCF plus damped dispersion (HFD) energy calculations. An improved spherical model. Journal of Chemical Physics, 76, 3057. doi:10.1063/1.443345
- Buck, U., Dondi, M.J., Valbusa, U., Klein, M.L. and Scoles, G. (1973) Determination of the interatomic potential of krypton. Physical Review A, 8, 2409-2416. doi:10.1103/PhysRevA.8.2409
- Goubert, L., Desoppere, E., Wieme, W., Polak, R., Paidarova, I. and Billing, G.D. (1995) Semiclassical study of Ar2*(3. SIGMA.u+) excimers in a pure Ar afterglow by means of a diatomics-in-molecules potential energy surface for the Ar3* system. Journal of Chemical Physics, 99, 15479. doi:10.1021/j100042a023
- Weiss, S. (1997) Dimer and trimer formation in dense gaseous argon: A MD study. Journal of Chemical Physics, 101, 3367-3370. doi:10.1021/jp970057g
- Lawrence, L.L. (1997) Rotational dependence of turning point surfaces and vibrational frequencies for Lennard-Jones argon clusters. Molecular Physics, 91, 1097. doi:10.1080/00268979709482797
- Herman, P.R., Madej, A.A. and Stoicheff, B.P. (1987) Rovibronic spectra of Ar2 and coupling of rotation and electronic motion. Chemical Physics Letters, 134, 209-213. doi:10.1016/0009-2614(87)87123-3
- Liu, K., Elrod, M.J., Loser, J.G., Cruzan, J.D., Pugliano, N., Brown, M.G., Rzepiela, J. and Saykally, R.J. (1994) FarIR vibration-rotation-tunnelling spectroscopy of the water trimer. Faraday Discussion, 97, 35-41.
- Pribble, R.N. and Zwier, T.S. (1994) Probing Hydrogen Bonding in benzene-(water)N clusters using resonant iondip IR spectroscopy. Faraday Discussion, 97, 229-241.
- Howard, R.E., Plank, T.L., Trussell, S.R. and Saadevadi, B. (1987) Chemical Physics Letters, 142, 33-36. doi:10.1016/0009-2614(87)87245-7
- Kalus, R. (1998) Formation of argon dimers in ternary monomer collisions—A classical trajectory study. Journal of Chemical Physics, 109, 8289.
- Kamiya, M., Tsuneda, T. and Hirao, K. (2002) A density functional study of van der waals interactions. Journal of Chemical Physics, 117, 6010. doi:10.1063/1.1501132
- Woon, D.E. (1993) Accurate modeling of intermolecular forces: A systematic møller-plesset study of the argon dimer using correlation consistent basis sets. Journal of Chemical Physics Letters, 204, 29-35. doi:10.1016/0009-2614(93)85601-J
- Aziz, R.A. (1993) A highly accurate interatomic potential for argon. Journal of Chemical Physics, 99, 4518. doi:10.1063/1.466051
- Gaussian, Revision, B., Hasegawa, Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li, X., Knox, J.E., Hratchian, H.P., Cross, J.B., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R.E., Yazyev, O., Austin, A.J., Cammi, R., Pomelli, C., Ochterski, J.W., Ayala, P.Y., Morokuma, K., Voth, G.A., Salvador, P., Dannenberg, J.J., Zakrzewski, V.G., Dapprich, S., Daniels, A.D., Strain, M.C., Farkas, O., Malick, D.K., Rabuck, A.D., Raghavachari, K., Foresman, J.B., Ortiz, J.V., Cui, Q., Baboul, A.G., Clifford, S., Cioslowski, J., Stefanov, B.B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I., Martin, R.L., Fox, D.J., Keith, T., Al-Laham, M.A., Peng, C.Y., Nanayakkara, A., Challacombe, M., Gill, P.M.W., Johnson, B., Chen, W., Wong, M.W., Gonzalez, C. and Pople, J.A. (2009) Gaussian, Inc., Pittsburgh.
- Boys, S.F. and Bernardi, F. (1970) The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Modern Physics, 19, 553-566.
- Liu, B. and Mclean, A.D. (1973) Accurate calculation of the attractive interaction of two ground state helium atoms. Journal of Chemical Physics, 59, 4557. doi:10.1063/1.1680654
- Liedl, K.R., Sekusak, S. and Mayer, E. (1997) Has the dimer of carbonic acid a lower energy than its constituents water and carbon dioxide? Journal of American Chemical Society, 119, 3782. doi:10.1021/ja961802q
- J.A. Pople, Head-Gordon, M., Fox, D.F., Raghavachari, K. and Curtiss, L.A. (1989) Gaussian-1 theory: A general procedure for prediction of molecular energies. Journal of Chemical Physics, 90, 5622. doi:10.1063/1.456415
- Curtiss, L.A., Raghavachari, K., Trucks, G.W. and Pople, J.A. (1991) Gaussian-2 theory for molecular energies of firstand second-row compounds. Journal of Chemical Physics, 94, 7221. doi:10.1063/1.460205
- Curtiss, L.A., Raghavachari, K. and Pople, J.A. (1993) Gaussian-2 theory using reduced møller-plesset orders. Journal of Chemical Physics, 98, 1293. doi:10.1063/1.464297
- Ochtreski, J.W., Petersson, G.A. and Montgomery, J.A. (1996) A complete basis set model chemistry. V. Extensions to six or more heavy atoms. Journal of Chemical Physics, 104, 2598. doi:10.1063/1.470985
- Kamiya, M., Tsuneda, T. and Hirao, K. (2002) A density functional study of van der waals interactions. Journal of Chemical Physics, 117, 6010. doi:10.1063/1.1501132
- Wu, Q. and Yang, W. (2002) Empirical correction to density functional theory for van der waals interactions. Journal of Chemical Physics, 116, 515. doi:10.1063/1.1424928
- Perez-Jorda, J.M., Fabian, E.S. and Perez-Jimenez, A.J. (1999) Density-functional study of van der waals forces on rare-gas diatomics: Hartree-fock exchange. Journal of Chemical Physics, 110, 1916.
- Grimme, S. (2011) Density functional theory with London dispersion corrections. Advanced Reviews, 1, 211- 228.
- Grimme, S., Antony, J., Schwabe, T. and Mück-Lichtenfeld, C. (2007) Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of (Bio)organic molecules. Organic & Biomolecular Chemistry, 5, 741-758. doi:10.1039/b615319b
- Gräfenstein, J. and Cremer, D. (2009) An efficient algorithm for the density-functional theory treatment of dispersion interactions. Journal of Chemical Physics, 130, 124105. doi:10.1063/1.3079822

