Psychology
Vol.05 No.18(2014), Article ID:51702,11 pages
10.4236/psych.2014.518207
Predicting Academic Achievement of High-School Students Using Machine Learning
Hudson F. Golino1, Cristiano Mauro Assis Gomes2, Diego Andrade2
1Núcleo de Pós-Graduação, Pesquisa e Extensão, Faculdade Independente do Nordeste, Vitória da Conquista, Brazil
2Department of Psychology, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil
Email: hfgolino@gmail.com, cristianogomes@ufmg.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 September 2014; revised 23 October 2014; accepted 12 November 2014
ABSTRACT
The present paper presents a relatively new non-linear method to predict academic achievement of high school students, integrating the fields of psychometrics and machine learning. A sample composed by 135 high-school students (10th grade, 50.34% boys), aged between 14 and 19 years old (M = 15.44, DP = 1.09), answered to three psychological instruments: the Inductive Reasoning Developmental Test (TDRI), the Metacognitive Control Test (TCM) and the Brazilian Learning Approaches Scale (BLAS-Deep Approach). The first two tests have a self-appraisal scale attached, so we have five independent variables. The students’ responses to each test/scale were analyzed using the Rasch model. A subset of the original sample was created in order to separate the students in two balanced classes, high achievement (n = 41) and low achievement (n = 47), using grades from nine school subjects. In order to predict the class membership a machine learning non-linear model named Random Forest was used. The subset with the two classes was randomly split into two sets (training and testing) for cross validation. The result of the Random Forest showed a general accuracy of 75%, a specificity of 73.69% and a sensitivity of 68% in the training set. In the testing set, the general accuracy was 68.18%, with a specificity of 63.63% and with a sensitivity of 72.72%. The most important variable in the prediction was the TDRI. Finally, implications of the present study to the field of educational psychology were discussed.
Keywords:
Machine Learning, Assessment, Prediction, Intelligence, Learning Approaches, Metacognition

1. Introduction
Machine learning is a relatively new science field composed by a broad class of computational and statistical methods to make predictions, inferences, and to discover new relations in data (Flach, 2012; Hastie, Tibshirani, & Friedman, 2009) . There are two main areas within the machine learning field. The unsupervised learning focuses in the discovery and detection of new relationships, patterns and trends in data. The supervised learning area, by the other side, focuses in the prediction of an outcome using a given set of predictors. If the outcome is categorical, then the task to be accomplished is named classification, if it is numeric then the task is called regression.
There are several types of algorithms to perform classification and regression (Hastie et al., 2009) . Among these algorithms, the tree based models are supervised learning techniques of special interest to the psychology and to the education research field. It can be used to discover which variable, or combination of variables, better predicts a given outcome, e.g. high or low academic achievement. It can identify the cutoff points for each variable that maximally predict the outcome, and can also be applied to study the non-linear interaction effects of the independent variables and its relation to the quality of the prediction (Golino & Gomes, 2014) . Within psychology, there are a growing number of applications of the tree-based models in different areas, from ADHA diagnosis (Eloyan et al., 2012; Skogli et al., 2013) to perceived stress (Scott, Jackson, & Bergeman, 2011) , suicidal behavior (Baca-Garcia et al., 2007; Kuroki & Tilley, 2012) , adaptive depression assessment (Gibbons et al., 2013) , emotions (Tian et al., 2014; van der Wal & Kowalczyk, 2013) and education (Blanch & Aluja, 2013; Cortez & Silva, 2008; Golino & Gomes, 2014; Hardman, Paucar-Caceres, & Fielding, 2013) .
The main benefit of using the tree-based models in psychology is that they do not make any assumption regarding normality, linearity of the relation between variables, homoscedasticity, collinearity or independency (Geurts, Irrthum, & Wehenkel, 2009) . The tree-based models also do not demand a high sample-to-predictor ratio and are more suitable to interaction effects (especially non-linearity) than the classical techniques, such as linear and logistic regression, ANOVA, MANOVA, structural equation modelling and so on. Finally, the tree- based models, especially the ensemble techniques, can lead to high prediction accuracy, since they are known as the state-of-the-art methods in terms of prediction accuracy (Flach, 2012; Geurts et al., 2009) . The current paper focuses on the methodological aspects of the classification tree (Breiman, Friedman, Olshen, & Stone, 1984) and its most famous ensemble technique, Random Forest (Breiman, 2001a) . To illustrate the use of tree-based models in educational psychology, the Random Forest algorithm will be used to predict levels of academic achievement of high school students (low vs. high). Finally, we will discuss the limits and possibilities of this new predictive method to the field of educational psychology.
Recursive Partitioning and Ensemble Techniques
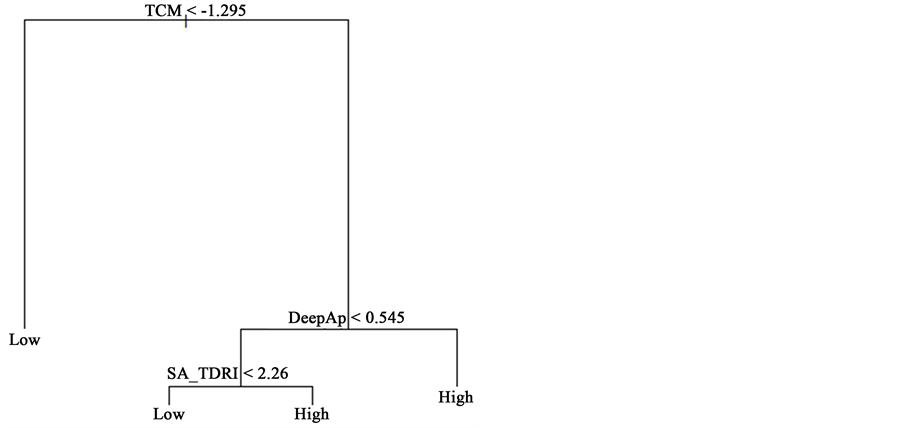
A classification tree partitions the feature space into several distinct mutually exclusive regions (non-overlap- ping). Each region is fitted with a specific model that designates one of the classes to that particular space. The class is assigned to the region of the feature space by identifying the majority class in that region. In order to arrive in a solution that best separates the entire feature space into more pure nodes (regions), recursive binary partition is used. A node is considered pure when 100% of the cases are of the same class, for example, low academic achievement. A node with 90% of low achievement and 10% of high achievement students is more “pure” then a node with 50% of each. Recursive binary partitions work as follows. The feature space is split into two regions using a specific cutoff from the variable of the feature space (predictor) that leads to the most purity configuration. Then, each region of the tree is modeled accordingly to the majority class. One or two original nodes are also split into more nodes, using some of the given predictors that provide the best fit possible. This splitting process continues until the feature space achieves the most purity configuration possible, with Rm regions or nodes classified with a distinct Ck class. If more than one predictor is given, then the selection of each variable used to split the nodes will be given by the variable that splits the feature space into the most purity configuration. In a classification tree, the first split indicates the most important variable, or feature, in the prediction. Let’s take a look in Figure 1 to see how a classification tree looks like.
Figure 1 shows the classification tree presented by Golino and Gomes (2014) with three predictors of the academic achievement (high and low) of medicine students: The Metacognitive Control Test (TCM), Deep Learning Approach (DeepAp) and the Self-Appraisal of the Inductive Reasoning Developmental Test (SA_ TDRI). The most important variable in the prediction was TCM, since it was the predictor located at the first
Figure 1. A classification tree from Golino and Gomes (2014) .
split of the classification tree. The first split indicates the variable that separates the feature space into two purest nodes. In the case shown in Figure 1, 52.50% of the sample used to grow the tree had a TCM score smaller than −1.295, and were classified as having a low academic achievement. The remaining 47.5% had a TCM score greater than −1.295, and were classified in the low or in the high achievement class accordingly their scores on the DeepAp and on the SA_TDRI. Those with a TCM score greater than −1.295 and a DeepAp score greater than .545 were classified as belonging to the high achievement class. The same occurred to those with a TCM score greater than −1.295, a DeepAp score lower than .545 and a SA_TDRI score greater than 2.26. Finally, the participants with a TCM score greater than −1.295, a DeepAp score lower than .545 but with a SA_TDRI score smaller than 2.26 were classified as belonging to the low achievement group. This classification tree presented a total accuracy of 72.50%, with a sensitivity of 57.89% and a specificity of 85.71% (Golino & Gomes, 2014) .
Geurts, Irrthum and Wehenkel (2009) argue that learning trees are among the most popular algorithms of machine learning due to its interpretability, flexibility and ease of use. Interpretability referrers to its easiness of understanding. It means that the model constructed to map the feature space (predictors) into the output space (dependent variable) is easy to understand, since it is a roadmap of if-then rules. The description of Figure 1 above shows exactly that. James, Witten, Hastie and Tibshirani (2013) points that the tree models are easier to explain to people than linear regression, since it mirrors more the human decision-making then other predictive models. Flexibility means that the tree techniques are applicable to a wide range of problems, handles different kind of variables (including nominal, ordinal, interval and ratio scales), are non-parametric techniques and does not make any assumption regarding normality, linearity or independency (Geurts et al., 2009) . Furthermore, it is sensible to the impact of additional variables to the model, being especially relevant to the study of incremental validity. It also assesses which variable or combination of them, better predicts a given outcome, as well as calculates which cutoff values are maximally predictive of it. Finally, the ease of use means that the tree based techniques are computationally simple, yet powerful.
In spite of the qualities of the learning trees, it suffers from two related limitations. The first one is known as the overfitting issue. Since the feature space is linked to the output space by recursive binary partitions, the tree models can learn too much from data, modeling it in such a way that may turn out a sample dependent model. Being sample dependent, in the sense that the partitioning is too suitable to the data set in hand, it will tend to behave poorly in new data sets. Golino and Gomes (2014) showed that in spite of having a total accuracy of 72.50% in the training sample, the tree presented in Figure 1 behaved poorly in a testing set, with a total accuracy of 64.86%. The difference between the two data sets is due to the overfit of the tree to the training set.
The second issue is exactly a consequence of the overfitting, and is known as the variance issue. The predictive error in a training set, a set of features and outputs used to grown a classification tree for the first time, may be very different from the predictive error in a new test set. In the presence of overfitting, the errors will present a large variance from the training set to the test set used, as shown by the results of Golino and Gomes (2014) . Additionally, the classification tree does not have the same predictive accuracy as other classical machine learning approaches (James et al., 2013) . In order to prevent overfitting, the variance issue and also to increase the prediction accuracy of the classification trees, a strategy named ensemble trees can be used.
The ensemble trees are simply the junction of several models to perform the classification task based on the prediction made by every single tree. The most famous ensemble tree algorithm is the Random Forest (Breiman, 2001a) , that is used to increase the prediction accuracy, decrease the variance between data sets and to avoid overfitting.
The procedure takes a random subsample of the original data set (with replacement) and of the feature space to grow the trees. The number of the selected features (variables) is smaller than the number of total elements of the feature space. Each tree assigns a single class to the each region of the feature space for every observation. Then, each class of each region of every tree grown is recorded and the majority vote is taken (Hastie et al., 2009; James et al., 2013) . The majority vote is simply the most commonly occurring class over all trees. As the Random Forest does not use the entire observations (only a subsample of it, usually 2/3), the remaining observations (known as out-of-bag, or OOB) is used to verify the accuracy of the prediction. The out-of-bag error can be computed as a “valid estimate of the test error for the bagged model, since the response for each observation is predicted using only the trees that were not fit using that observation” (James et al., 2013: p. 323) .
As pointed by Breiman (2001a) , the number of selected variables is held constant during the entire procedure for growing the forest, and usually is set to square-root of the total number of variables. Since the Random Forest subsamples the original sample and the predictors, it is considered an improvement over other ensemble trees, as the bootstrap aggregating technique (Breiman, 2001b) , or simply bagging. Bagging is similar to Random Forest, except for the fact that does not subsample the predictors. Thus, bagging creates correlated trees (Hastie et al., 2009) , which may affect the quality of the prediction. The Random Forest algorithm decorrelates the trees grown, and as a consequence it also decorrelates the errors made by each tree, yielding a more accurate prediction.
Why decorrelating the trees is so important? Following the example created by James et al. (2013) , imagine that we have a very strong predictor in our feature space, together with other moderately strong predictors. In the bagging procedure, the strong predictor will be in the top split of most of the trees, since it is the variable that better separates the classes available in our data. By consequence, the bagged trees will be very similar to each other, making the predictions and the errors highly correlated. This may not lead to a decrease in the variance if compared to a single tree. The Random Forest procedure, on the other hand, forces each split to consider only a subset of the features, opening chances for the other variables to do their job. The strong predictor will be left out of the bag in a number of situations, making the trees very different from each other. Therefore, the resulting trees will present less variance in the classification error and in the OOB error, leading to a more reliable prediction. In sum, the Random Forest is an ensemble of trees that improves the prediction accuracy, decreases variance and avoids overfitting by using only a subsample of the observations and a subsample of predictors. It has two main tuning parameters. The first is the size of the subsample of features used in each split (mtry), which is mandatory to be smaller than the total number of features, and is usually set as the square root of the total number of predictors. The second tuning parameter is the number of trees to grow (ntree).
The present paper investigates the prediction of academic achievement of high-school students (high achieve- ment vs. low achievement) using two psychological tests and one educational scale: the Inductive Reasoning Developmental Test (TDRI), the Metacognitive Control Test (TCM) and the Brazilian Learning Approaches Scale (BLAS-Deep approach). The first two tests have a self-appraisal scale attached, so we have five independent variables. In the next section will be presented the participants, instruments used and the data analysis procedures.
2. Method
2.1. Participants
The sample is composed by 135 high-school students (10th grade, 50.34% boys), aged between 14 and 19 years old (M = 15.44, DP = 1.09), from a public high-school from [omitted as required by the review process]. The sample was selected by convenience, and represents approximately 90% of the students of the 10th grade. The students received a letter inviting them to be part of the study. Those who agreed in participating signed a inform consent, and confirmed they would be present in the schedule days to answer all the instruments.
2.2. Measures and Procedures
2.2.1. The Inductive Reasoning Developmental Test (TDRI) and Its Self-Appraisal Scale (SA_TDRI)
The Inductive Reasoning Developmental Test (TDRI) was developed by Gomes and Golino (2009) and by Golino and Gomes (2012) to assess developmental stages of reasoning based on Common’s Hierarchical Complexity Model (Commons, 2008; Commons & Pekker, 2008; Commons & Richards, 1984) and on Fischer’s Dynamic Skill Theory (Fischer, 1980; Fischer & Yan, 2002) . This is a pencil-and-paper test composed by 56 items, with a time limit of 100 minutes. Each item presents five letters or set of letters (see Figure 2), being four with the same rule and one with a different rule. The task is to identify which letter or set of letters have the different rule.
Golino and Gomes (2012) evaluated the structural validity of the TDRI using responses from 1459 Brazilian people (52.5% women) aged between 5 to 86 years (M = 15.75, SD = 12.21). The results showed a good fit to the Rasch model (INFIT mean = .96; SD = .17) with a high separation reliability for items (1.00) and a moderately high for people (.82). The item’s difficulty distribution formed a seven cluster structure with gaps between them, presenting statistically significant differences in the 95% C.I. level (t-test). The CFA showed an adequate data fit for a model with seven first-order factors and one general factor [χ2 (61) = 8832.594, p = .000, CFI = .96, RMSEA = .059]. The latent class analysis showed that the best model is the one with seven latent classes (AIC: 263.380; BIC: 303.887; Loglik: −111.690). The TDRI test has a self-appraisal scale attached to each one of the 56 items. In this scale, the participants are asked to appraise their achievement on the TDRI items, by reporting if he/she passed or failed the item. The scoring procedure of the TDRI self-appraisal scale works as follows. The participant receive a score of 1 in two situations: 1) if the participant passed the ith item and reported that he/she passed the item, and 2) if the participant failed the ith item and reported that he/she failed the item. On the other hand, the participant receives a score of 0 if his appraisal does not match his performance on the ith item: 1) he/ she passed the item, but reported that failed it, and 2) he/she failed the item, but reported that passed it.
2.2.2. The Metacognitive Control Test (TCM) and Its Self-Appraisal Scale (SA_TCM)
The Metacognitive Control Test (TCM) was developed by Golino and Gomes (2013) to assess the ability of people to control intuitive answers to logical-mathematical tasks. The test is based on Shane Frederick’s Cognitive Reflection Test (Frederick, 2005) , and is composed by 15 items. The structural validity of the test was assessed by Golino and Gomes (2013) using responses from 908 Brazilian people (54.8% women) aged between 9 to 86 years (M = 27.70, SD = 11.90). The results showed a good fit to the Rasch model (INFIT mean = 1.00; SD = .13) with a high separation reliability for items (.99) and a moderately high for people (.81). The TCM also has a self-appraisal scale attached to each one of its 15 items. The TCM self-appraisal scale is scored exactly as the TDRI self-appraisal scale: an incorrect appraisal receives a score of 0, and a correct appraisal receives a score of 1.
2.2.3. The Brazilian Learning Approaches Scale (EABAP)
The Brazilian Learning Approaches Scale (EABAP) is a self-report questionnaire composed by 17 items, developed by Gomes and colleagues (Gomes, 2010; Gomes, Golino, Pinheiro, Miranda, & Soares, 2011) . Nine items were elaborated to measure deep learning approaches, and eight items measure surface learning approaches. Each item has a statement that refers to a student’s behavior while learning. The student considers how much of the behavior described is present in his life, using a Likert-like scale ranging from (1) not at all, to (5) entirely present. BLAS presents reliability, factorial structure validity, predictive validity and incremental validity as good marker of learning approaches. These psychometrical proprieties are described respectively in Gomes et al. (2011), Gomes (2010) , and Gomes and Golino (2012) . In the present study only the deep learning approach items (DeepAp) were used. We will analyze only the nine deep approach items using the partial credit Rasch model.
Figure 2. Example of TDRI’s item 1 (from the first developmental stage assessed).
2.3. Data Analysis
2.3.1. Estimating the Students’ Ability in Each Test/Scale
The student’s ability estimates on the inductive reasoning developmental test, on the metacognitive control test, on the Brazilian learning approaches scale, and on the self-appraisal scales were computed using the original data set of each test/scale, through the software Winsteps (Linacre, 2012) . This procedure was followed in order to achieve reliable estimates, since only 135 students answered the tests. The mixture of the original data set from each test to the high-school students’ answers did not significantly change the reliability or fit to the models used. A summary of the separation reliability and fit of the items, the separation reliability of the sample (after adding the data from the high-school students) and the statistical model used is provided in Table 1.
2.3.2. Defining the Achievement Classes (High vs. Low)
The final grade in the following nine school subjects was provided by the school at the end of the academic year: arts, philosophy, physics, history, informatics, math, chemistry, sociology and Brazilian Portuguese. The final grades ranged from 0 to 10, and the students were considered approved in the academic year in each school subject only if he/she had a grade equal to or above seven. Students with grades lower than seven in a particular school subject are submitted to an additional assessment. Finally, those with an average grade of seven or more are considered able to proceed to the next school grade (11th grade). Otherwise, the students need to re-do the current grade (10th grade). From the total sample, only 65.18% (n = 88) were considered able to proceed to the next school year and 34.81% (n = 47) were requested to re-do the 10th grade. These two groups could be used to compose the high and the low achievement classes. However, since the tree-based models require balanced classes (i.e., classes with approximately the same number of cases) we needed to subset the high achievement class (those who proceeded to the next school grade) in order to obtain a subsample closer to the low achievement class size (those who would need to re-do the 10th grade). Therefore, we computed the mean final grade over all nine grades for every student, and verified the mean of each group of students. Those who passed to the next school grade had a mean final grade of 7.69 (SD = .48), while those who would need to re-do the 10th grade had a mean final grade of 6.06 (SD = 1.20). We select every student with a mean final grade equals to or higher than 7.69 (n = 41) and called them the “high achievement” group. The 47 students that would need to re- do the 10th grade formed the “low achievement” group. Finally, we had 88 students divided in two balanced classes.
2.3.3. Machine Learning Procedures
The sample was randomly split in two sets with equal sizes, training and testing, for cross-validation. The training set is used to grow the trees, to verify the quality of the prediction in an exploratory fashion, and to adjust the tuning parameters. Each model created using the training set is applied in the testing set to verify how it performs on a new data set.
Since the single trees usually lead to overiftting and to high variance between datasets, we used only the Random Forest algorithm through the random Forest package (Liaw & Wiener, 2012) of the R software (R Development Core Team, 2011). As pointed in the introduction, the Random Forest has two main tuning parameters: the number of trees (ntree) and the number of variables used (mtry). We set mtry as two, because is the
Table 1. Item reliability, item fit, person reliability, person fit and model used by instrument.
integer closest to the square root of the total number of predictors (5), and ntree as 10,000. In order to verify the quality of the prediction both in the training (modeling phase) and in the testing set (cross-validation phase), the total accuracy, the sensitivity and specificity were used. Total accuracy is the proportion of observations correctly classified:
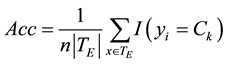
where 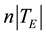 is the number of observations in the testing set. In spite of being an important indicator of the
is the number of observations in the testing set. In spite of being an important indicator of the
general prediction’s quality, the total accuracy is not an informative measure of the errors in each class. For example, a general accuracy of 80% can represent an error-free prediction for the C1 class, and an error of 40% for the C2 class. In the educational scenario, it is preferable to have lower error in the prediction of the low achievement class, since students at risk of academic failure compose this class. So, the sensitivity will be preferred over general accuracy and specificity. The sensitivity is the rate of observations correctly classified in a target class, e.g. C1 = low achievement, over the number of observations that belong to that class:
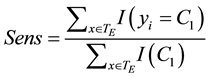
Specificity, on the other hand, is the rate of correctly classified observations of the non-target class, e.g. C2 = high achievement, over the number of observations that belong to that class:
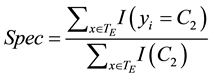
Finally, the model construct in the training set will be applied in the testing set for cross-validation. Since the Random Forest is a black box technique―i.e. there is only a prediction based on majority vote and no “typical tree” to look at the partitions―to determine which variable is important in the prediction one importance measure will be used: the mean decrease of accuracy. It indicates how much in average the accuracy decreases on the out-of-bag samples when a given variable is excluded from the model (James et al., 2013) .
2.3.4. Descriptive Analysis Procedures
After estimating the student’s ability in each test or scale the Shapiro-Wilk test of normality will be conducted in order to discover which variables presented a normal distribution. To verify if there is any statistically significant difference between the students’ groups (high achievement vs. low achievement) the two-sample T test will be conducted in the normally distributed variables and the Wilcoxon Sum-Rank test in the non-normal variables, both at the .05 significance level. In order to estimate the effect sizes of the differences, the R’s compute.es package (Del Re, 2013) is used. This package computes the effect sizes, along with their variances, confidence intervals, p-values and the common language effect size (CLES) indicator using the p-values of the significance testing. McGraw and Wong (1992) developed the CLES indicator as a more intuitive tool than the other effect size indicators. It converts an effect into a probability that a score taken at random from one distribution will be greater than a score taken at random from another distribution (McGraw & Wong, 1992) . In other words, it expresses how much (in %) the score from one population is greater than the score of the other population if both are randomly selected (Del Re, 2013) .
3. Results
3.1. Descriptive
The Brazilian Learning Approaches Scale (Deep Learning) presented a normal distribution (W = .99, p-value = .64), while all the other four variables presented a p-value smaller than .001. There was a statistically significant difference at the 99% level between the high and the low achievement groups in the median Rasch score of the Inductive Reasoning Developmental ( High = 2.14, σ2 = 5.80,
High = 2.14, σ2 = 5.80, 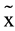 Low = −1.47, σ2Low = 15.52, W = 1359, p < .01), in the median Rasch score of the Metacognitive Control Test (
Low = −1.47, σ2Low = 15.52, W = 1359, p < .01), in the median Rasch score of the Metacognitive Control Test ( High = −1.03, σ2 = 7.29,
High = −1.03, σ2 = 7.29,  Low = −3.40, σ2Low = 4.37, W = 928, p < .01), in the median Rasch score of the TDRI’s self-appraisal scale (
Low = −3.40, σ2Low = 4.37, W = 928, p < .01), in the median Rasch score of the TDRI’s self-appraisal scale (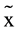 High = 2.03, σ2 = 3.01,
High = 2.03, σ2 = 3.01, 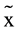 Low = 1.16, σ2Low = 4.66, W = 1152, p < .001), in the median Rasch score of the TCM’s self-appraisal scale (
Low = 1.16, σ2Low = 4.66, W = 1152, p < .001), in the median Rasch score of the TCM’s self-appraisal scale (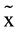 High = 1.07, σ2 = 4.18,
High = 1.07, σ2 = 4.18, 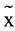 Low = −1.08, σ2Low = 2.45, W = 954, p < .01) and in the mean Rasch score of the Brazilian learning approaches scale-deep approach (
Low = −1.08, σ2Low = 2.45, W = 954, p < .01) and in the mean Rasch score of the Brazilian learning approaches scale-deep approach (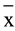 High = 1.13, σ2 = .80,
High = 1.13, σ2 = .80, 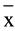
According to Cohen (1988) , the effect size is considered small when it is between .20 and .49, moderate between .50 and .79 and large when values are over .80. Only the difference in the Rasch score of the inductive reasoning developmental test presented a large effect size (d = .88, p < .05).
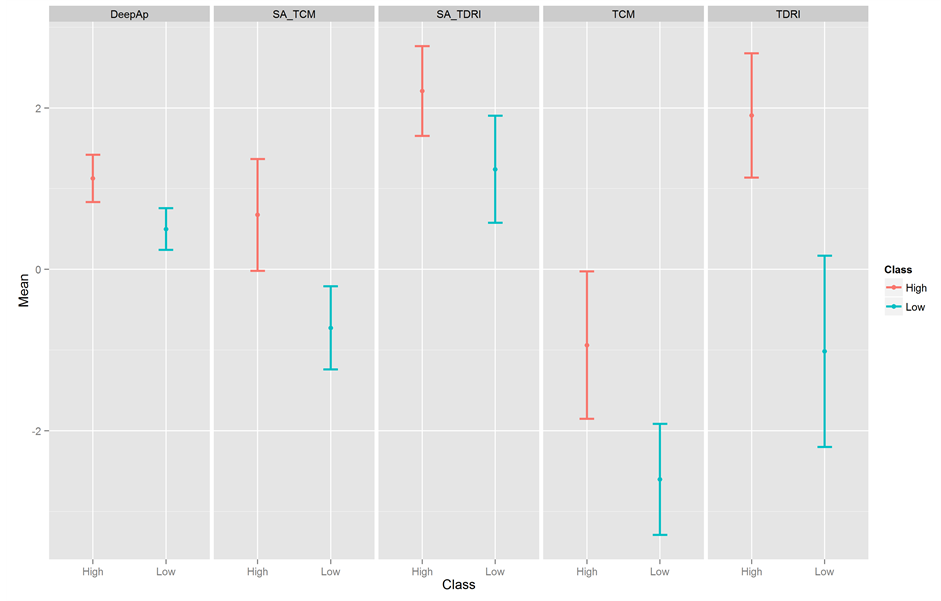
As pointed before, the common language effect size indicates how often a score sampled from one distribution is greater than the score sampled from the other distribution if both are randomly selected (McGraw & Wong, 1992) . Then, considering the common language effect size, the probability that a TDRI score taken at random from the high achievement group is greater than a TDRI score taken at random of the low achievement group is 73.41%. It means that out of 100 TDRI scores from the high achievement group, 73.41 will be greater than the TDRI scores of the low achievement group. The Rasch scores of the other tests have moderate effect sizes. Their common language effect size varied from 64.92% to 70.10%, meaning that the probability of a score taken at random at the high achievement group be greater than a score taken at random in the low achievement group is at least 64.92% and at most 70.10%. Figure 3 shows the mean score for each test and its 95% confidence interval by both classes (low and high).
3.2. Machine Learning Results
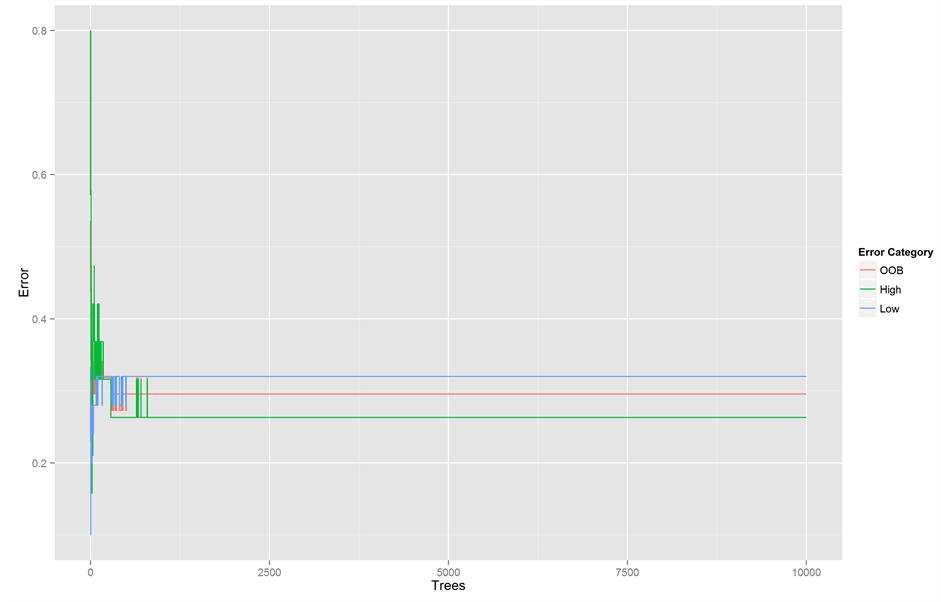
The result of the Random Forest model with 10,000 trees showed an out-of-bag error rate of .29, a total accuracy of 75.00%, a sensitivity of 68.00% and a specificity of 73.69%. The mean decrease accuracy showed the inductive reasoning developmental stage (TDRI) as the most important variable in the prediction, since when it is left out of the prediction the accuracy decreases 66.22% in average. The second most important variable is the deep learning approach, which is associated with a mean decrease accuracy of 28.45% when is not included in the predictive model. In third place is the metacognitive control test (19.68%); in the fourth position is the TDRI self-appraisal scale (19.50%), followed by the TCM self-appraisal scale (5.78%). Figure 4 shows the high achievement prediction error (green line), the out-of-bag error (red line) and the low achievement prediction error (black line) per tree. The errors become more stable with approximately more than 1700 trees.
The predictive model constructed in the training set was applied in the testing set for cross-validation. It presented a total accuracy of 68.18%, a sensitivity of 72.72% and a specificity of 63.63%. There was a difference of 6.82% in the total accuracy, of 2.28% in the sensitivity, and of 10.06% in the specificity.
4. Discussion
The present paper briefly introduced the concept of recursive partitioning used in the tree-based models of machine learning. The tree-based models are very useful to study the role of psychological and educational constructs in the prediction of academic achievement. Unlike the most classical approaches, such as linear and logistic regression, as well as the structural equation modeling, the tree-based models do not make assumptions about the normality of data, the linearity of the relation between the variables, neither requires homoscedasticity, collinearity or independence (Geurts, Irrthum, & Wehenkel, 2009) . A high predictor-to-sample ratio can be used
Table 2. Tests, effect sizes and common language effect size (CLES).
Figure 3. Score means and its 95% confidence intervals for each test, by class (high vs. low academic achievement).
Figure 4. Random Forest’s out-of-bag error (red), high achievement prediction error (green) and low achievement predic- tion error (blue).
without harm to the quality of the prediction, and missingness is well handled by the prediction algorithms. The tree-based models are also more suitable to non-linear interaction effects than the classical techniques. When several trees are ensemble to perform a prediction it generally leads to a high accuracy (Flach, 2012; Geurts et al., 2009) , decreasing the chance of overfitting and diminishing the variance between datasets. The focus of the current paper was the application of this relatively new predictive method in the educational psychology field.
Psychology is taking advantage of the tree-based models in a broad set of applications (Baca-Garcia et al., 2007; Eloyan et al., 2012; Gibbons et al., 2013; Kuroki & Tilley, 2012; Scott, Jackson, & Bergeman, 2011; Skogli et al., 2013; Tian et al., 2014; van der Wal & Kowalczyk, 2013) . Within education, Blanch and Aluja (2013) , Cortes and Silva (2008) and Golino and Gomes (2014) applied the tree-based models to predict the academic achievement of students from the secondary and tertiary levels using a set of psychological and socio-demographic variables as predictors. The discussion of their methods and results are beyond the scope of the current paper, since we focused on the methodological aspects of machine learning, and how it can be applied in the educational psychology field.
In the present paper we showed the Rasch scores of the tests and scales used significantly differentiated the high achievement from the low achievement 10th grade students. Inductive reasoning presented a large effect size, while the deep learning approach, metacognitive control and self-appraisals presented moderate effect sizes. The random forest prediction lead to a total accuracy of 75%, a sensitivity of 68% and a specificity of 73.69% in the training set. The testing set result was a little bit worse, with a total accuracy of 68.18%, a sensitivity of 72.72% and a specificity of 63.63%. The most important variable in the prediction was the inductive reasoning that was associated with a mean decrease accuracy of 66.22% when left out of the prediction bag. The deep learning approach was the second most important variable (mean decrease accuracy of 28.45%), followed by metacognitive control (19.68%), TDRI self-appraisal (19.50%) and TCM self-appraisal (5.78%). This result reinforces previous findings that showed incremental validity of the learning approaches in the explanation of academic performance beyond intelligence, using traditional techniques (Chamorro-Premuzic & Furnham; 2008; Furnham Monsen, & Ahmetoglu, 2009; Gomes & Golino, 2012 ). It also reinforces the incremental validity of metacognition, over intelligence, in the explanation of academic achievement (van der Stel & Veenman, 2008; Veenman & Beishuizen, 2004).
5. Conclusion
The application of machine learning models in the prediction of academic achievement/performance, especially the tree-based models, represents an innovative complement to the traditional techniques such as linear and logistic regression, as well as structural equation modelling (Blanch & Aluja, 2013) . More than the advantages pointed earlier, the tree-based models can help us to understand the non-linear interactions between psycho- educational variables in the prediction of academic outcomes. These machine learning models not only represent an advance in terms of prediction accuracy, but also represent an advance in terms of inference. Future studies could benefit from employing a larger and broader sample, involving students from different schools. It would also be interesting to investigate, in the future, the impact of varying the tuning parameters of the random forest model in the accuracy, sensitivity, specificity and variability of the prediction.
Acknowledgements
The current research was financially supported by a grant provided by the Fundação de Amparo à Pesquisa de Minas Gerais (FAPEMIG) to the authors. The authors also receive grants provided by the Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP) and by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) of the Brazil’s Ministry of Science, Technology and Innovation.
References
- Baca-Garcia , E., Perez-Rodriguez, M., Saiz-Gonzalez, D., Basurte-Villamor, I., Saiz-Ruiz, J., Leiva-Murillo, J. M., & de Leon, J. (2007). Variables Associated with Familial Suicide Attempts in a Sample of Suicide Attempters. Progress in Neuro-Psychopharmacology & Biological Psychiatry, 31, 1312-1316. http://dx.doi.org/10.1016/j.pnpbp.2007.05.019
- Blanch, A., & Aluja, A. (2013). A Regression Tree of the Aptitudes, Personality, and Academic Performance Relationship. Personality and Individual Differences, 54, 703-708. http://dx.doi.org/10.1016/j.paid.2012.11.032
- Breiman , L. (2001a). Random Forests. Machine Learning, 1, 5-32. http://dx.doi.org/10.1023/A:1010933404324
- Breiman, L. (2001b). Bagging Predictors. Machine Learning, 24, 123-140. http://dx.doi.org/10.1007/BF00058655
- Breiman, L., Friedman, J., Olshen, R., & Stone, C. (1984). Classification and Regression Trees. New York: Chapman & Hall.
- Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.), Hillsdale, NJ: Lawrence Erlbaum Associates.
- Commons, M. L., & Richards, F. A. (1984). Applying the General Stage Model. In M. L. Commons, F. A. Richards, & C. Armon (Eds.), Beyond Formal Operations. Late Adolescent and Adult Cognitive Development: Late Adolescent and Adult Cognitive Development (Vol. 1, pp. 141-157). New York: Praeger.
- Commons, M. L. (2008). Introduction to the Model of Hierarchical Complexity and Its Relationship to Postformal Action. World Futures, 64, 305-320. http://dx.doi.org/10.1080/02604020802301105
- Commons, M. L., & Pekker, A. (2008). Presenting the Formal Theory of Hierarchical Complexity. World Futures, 64, 375- 382. http://dx.doi.org/10.1080/02604020802301204
- Cortez, P., & Silva, A. M. G. (2008). Using Data Mining to Predict Secondary School Student Performance. In A. Brito, & J. Teixeira (Eds.), Proceedings of 5th Annual Future Business Technology Conference, Porto, 5-12.
- Del Re, A. C. (2013). compute.es: Compute Effect Sizes. R Package Version 0.2-2. http://cran.r-project.org/web/packages/compute.es
- Eloyan, A., Muschelli, J., Nebel, M., Liu, H., Han, F., Zhao, T., Caffo, B. et al. (2012). Automated Diagnoses of Attention Deficit Hyperactive Disorder Using Magnetic Resonance Imaging. Frontiers in Systems Neuroscience, 6, 61. http://dx.doi.org/10.3389/fnsys.2012.00061
- Fischer, K. W. (1980). A Theory of Cognitive Development: The Control and Construction of Hierarchies of Skills. Psychological Review, 87, 477-531. http://dx.doi.org/10.1037/0033-295X.87.6.477
- Fischer, K. W., & Yan, Z. (2002). The Development of Dynamic Skill Theory. In R. Lickliter, & D. Lewkowicz (Eds.), Conceptions of Development: Lessons from the Laboratory. Hove: Psychology Press.
- Flach, P. (2012). Machine Learning: The Art and Science of Algorithms That Make Sense of Data. Cambridge: Cambridge University Press. http://dx.doi.org/10.1017/CBO9780511973000
- Frederick, S. (2005). Cognitive Reflection and Decision Making. Journal of Economic Perspectives, 19, 25-42. http://dx.doi.org/10.1257/089533005775196732
- Geurts, P., Irrthum, A., & Wehenkel, L. (2009). Supervised Learning with Decision Tree-Based Methods in Computational and Systems Biology. Molecular BioSystems, 5, 1593-1605. http://dx.doi.org/10.1039/b907946g
- Gibbons, R. D., Hooker, G., Finkelman, M. D., Weiss, D. J., Pilkonis, P. A., Frank, E., Moore, T., & Kupfer, D. J. (2013). The Computerized Adaptive Diagnostic Test for Major Depressive Disorder (CAD-MDD): A Screening Tool for Depression. Journal of Clinical Psychiatry, 74, 669-674. http://dx.doi.org/10.4088/JCP.12m08338
- Golino, H. F., & Gomes, C. M. A. (2012). The Structural Validity of the Inductive Reasoning Developmental Test for the Measurement of Developmental Stages. In K. Stålne (Chair), Adult Development: Past, Present and New Agendas of Research, Symposium Conducted at the Meeting of the European Society for Research on Adult Development, Coimbra, 7-8 July 2012.
- Golino, H. F., & Gomes, C. M. A. (2013). Controlando pensamentos intuitivos: O que o pão de queijo e o café podem dizer sobre a forma como pensamos. In C. M. A. Gomes (Chair), Neuroeconomia e Neuromarketing, Symposium conducted at the VII Simpósio de Neurociências da Universidade Federal de Minas Gerais, Belo Horizonte.
- Golino, H. F., & Gomes, C. M. A. (2014). Four Machine Learning Methods to Predict Academic Achievement of College Students: A Comparison Study. Revista E-PSI, 4, 68-101.
- Gomes, C. M. A., & Golino, H. F. (2009). Estudo exploratório sobre o Teste de Desenvolvimento do Raciocinio Indutivo (TDRI). In D. Colinvaux (Ed.), Anais do VII Congresso Brasileiro de Psicologia do Desenvolvimento: Desenvolvimento e Direitos Humananos (pp. 77-79). Rio de Janeiro: UERJ. http://www.abpd.psc.br/files/congressosAnteriores/AnaisVIICBPD.pdf
- Gomes, C. M. A. (2010). Perfis de estudantes e a relação entre abordagens de aprendizagem e rendimento Escolar. Psico, 41, 503-509.
- Gomes, C. M. A., & Golino, H. F. (2012). Validade incremental da Escala de Abordagens de Aprendizagem. Psicologia: Reflexão e Crítica, 25, 623-633. http://dx.doi.org/10.1590/S0102-79722012000400001
- Gomes, C. M. A., Golino, H. F., Pinheiro, C. A. R., Miranda, G. R., & Soares, J. M. T. (2011). Validação da Escala de Abordagens de Aprendizagem (EABAP) em uma amostra brasileira. Psicologia: Reflexão e Crítica, 24, 19-27. http://dx.doi.org/10.1590/S0102-79722011000100004
- Hardman , J., Paucar-Caceres, A., & Fielding, A. (2013). Predicting Students’ Progression in Higher Education by Using the Random Forest Algorithm. Systems Research and Behavioral Science, 30, 194-203. http://dx.doi.org/10.1002/sres.2130
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference and Prediction (2nd ed.). New York: Springer. http://dx.doi.org/10.1007/978-0-387-84858-7
- James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning with Applications in R. New York: Springer. http://dx.doi.org/10.1007/978-1-4614-7138-7
- Kuroki, Y., & Tilley, J. L. (2012). Recursive Partitioning Analysis of Lifetime Suicidal Behaviors in Asian Americans. Asian American Journal of Psychology, 3, 17-28. http://dx.doi.org/10.1037/a0026586
- Liaw, A., & Wiener, M. (2012). Random Forest: Breiman and Cutler’s Random Forests for Classification and Regression. R Package Version 4.6-7. http://cran.r-project.org/web/packages/randomForest/
- Linacre, J. M. (2012). Winsteps® Rasch Measurement Computer Program. Beaverton, OR: Winsteps.com.
- McGraw, K. O., & Wong, S. P. (1992). A Common Language Effect Size Statistic. Psychological Bulletin, 111, 361-365. http://dx.doi.org/10.1037/0033-2909.111.2.361
- Scott, S. B., Jackson, B. R., & Bergeman, C. S. (2011). What Contributes to Perceived Stress in Later Life? A Recursive Partitioning Approach. Psychology and Aging, 26, 830-843. http://dx.doi.org/10.1037/a0023180
- Skogli, E., Teicher, M. H., Andersen, P., Hovik, K., & Øie, M. (2013). ADHD in Girls and Boys―Gender Differences in Co-Existing Symptoms and Executive Function Measures. BMC Psychiatry, 13, 298. http://dx.doi.org/10.1186/1471-244X-13-298
- Tian, F., Gao, P., Li, L., Zhang, W., Liang, H., Qian, Y., & Zhao, R. (2014). Recognizing and Regulating e-Learners’ Emotions Based on Interactive Chinese Texts in e-Learning Systems. Knowledge-Based Systems, 55, 148-164. http://dx.doi.org/10.1016/j.knosys.2013.10.019
- van der Wal, C., & Kowalczyk, W. (2013). Detecting Changing Emotions in Human Speech by Machine and Humans. Applied Intelligence, 39, 675-691. http://dx.doi.org/10.1007/s10489-013-0449-1