Journal of Environmental Protection
Vol.07 No.06(2016), Article ID:66407,11 pages
10.4236/jep.2016.76077
Quantitative Evaluation and Uncertainty Assessment on Geostatistical Simulation of Soil Salinity Using Electromagnetic Induction Technique
Haijiang Wang, Shaotin Ren, Zhexia Hao, Li Meng, Wei Wei, Cui Jing*
The Key Laboratory of Oasis Ecological Agriculture, Xinjiang Production and Construction Group/College of Agriculture, Shihezi University, Shihezi, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 March 2016; accepted 9 May 2016; published 12 May 2016
ABSTRACT
Diagnosis of soil salinity and characterizing its spatial variability both vertically and horizontally are needed to establish control measures in irrigated agriculture. In this regard, it is essential that salinity development in varying soil depths be known temporally and spatially. Apparent soil electrical conductivity, measured by electromagnetic induction instruments, has been widely used as an auxiliary variable to estimate spatial distribution of field soil salinity. The main objectives of this paper were adopted a mobile electromagnetic induction (EMI) system to perform field electromagnetic (EM) survey in different soil layers, to evaluate the uncertainty through Inverse Distance Weighted (IDW) and Ordinary Kriging (OK) methods, and to determine which algorithm is more reliable for the local and spatial uncertainty assessment. Results showed that EM38 data from apparent soil electrical conductivity are highly correlated with salinity, more accurate for estimating salinity from multiple linear regression models, which the correlation coefficient of 0 - 20, 20 - 40, 40 - 60 and 60 - 80 cm were 0.9090, 0.9228, 0.896 and 0.9085 respectively. The comparison showed that the prediction accuracy of two methods also displays good performance for soil salinity, the estimation precision of IDW method (with E = 0.8873, 0.9075, 0.8483 and 0.901, RPD = 9.64, 8.01, 8.17 and 11.23 in 0 - 20, 20 - 40. 40 - 60 and 60 - 80 cm soil layers, respectively) was superior to that of OK (with E = 0.8857, 0.872, 0.8744 and 0.8822, RPD = 9.44, 7.83, 8.52 and 10.88, respectively), but differences of two methods in predictions are not significant. The obtained salinity map was helpful to display the spatial patterns of soil salinity and monitor and evaluate the management of salinity.
Keywords:
Soil Salinity, Spatial Distribution, Electromagnetic Induction, IDW, OK

1. Introduction
Soil salinity is not only the most serious environmental issue, but also the most frequently cited soil and agricultural utilization problem for farmers in the arid or semi-arid regions, especially the newly-reclaimed desertification lands in China [1] . Salinization of irrigated lands is a common phenomenon wherever irrigation is practiced under arid or semi-arid conditions. Salinization is accelerated when the field is underlain with a shallow, semi-confined aquifer exerting upward hydraulic pressure, thereby impeding drainage of the overlying soil layers [2] - [4] .
To prevent further soil degradation, soil salinity monitoring is essential so that proper and timely decisions regarding soil management can be made. For this purpose, precision agriculture can be used. The EM38 ground conductivity meter (Geonics Ltd, Canada) is considered one of the best tools for the appraisal of soil salinity in a geospatial context [5] [6] . The EM38 offer the potential to measure numerous soils attributes without the need for destructive sampling.
Over the last 30 years the application of electromagnetic (EM) induction instruments for natural resource management has increased. For example, the root-zone sensing EM38 has been used to map soil management zones [7] and discern the spatial distribution of average soil moisture [8] [9] , soil salinity [10] - [12] , clay content [13] [14] , and canon exchange capacity [15] . This is because the EM38 measures the apparent soil electrical conductivity, which is a function of these soil properties. As a consequence, related soil management issues such deep drainage risk [16] and depth to a water table [17] have also been mapped using digital soil mapping methods.
Geostatistical methods find wide applications, for example in geology, meteorology, hydrology and ecology, such as kriging, have been introduced into soil science to provide estimation at unsampled locations [18] - [21] . With the application of geostatistical methods, Huang et al. [22] mapped spatial patterns of soil salinity on the field scale from aboveground electromagnetic induction (EM) readings by substantially reducing the number of soil samples. Barbiéro et al. [23] studied the salt distribution in middle Senegal valley to understand its variability, and to describe its structure and spatial arrangement using a portable EM38. Tripathi et al. [24] delineated the spatial distribution of ECato assess cause and management of soil salinization in an irrigated cotton-growing field using a mobile electromagnetic sensing system. In a more rigorous analysis, Triantafilis et al. [25] compared several geostatistical models in order to determine an optimal approach for accurately predicting soil salinity from EM38 field survey data within the Namoi valley in Australia. Similarly, Yang and Yao [26] applied several geostatistical approaches and studied the spatial similarity of EM38 data of various sample quantities to determine the optimal prediction method.
In this paper, we describe an approach to determine optimal operation modes for the establishment of multiple linear regression models to estimate salinity from apparent soil electrical conductivity measured by EM38. It also provides a basis for the selection of optimized operation modes of EM38 infield survey. Secondly, we applied IDW and OK methods to determine the spatial variability and patterns of soil salinity over the study area, comparing and validating the accuracy of the spatial estimation of soil salinity based on a series of realization. Finally, determining which method is more reliable for the study scale and spatial uncertainty assessment, illustrating trend maps of soil salinity distribution for study area.
2. Materials and Methods
2.1. Study Area
This study was conducted on Beiwucha Farm located in the Manasi River Basin, the north of Tianshan Mountains, Xinjiang Uygur autonomous region, in northwestern China (Figure 1). It was reclaimed in 2011 and cultivated cotton in 2012-2014. The research field covers 0.385 km2 (550 × 70 m) with a 0.2% - 0.4% slope northwest to southeast; the area is 380 m above sea level and experience an arid climate with mean annual temperature, precipitation, evaporation and frost-free period of 7.6˚C, 148.5 mm, 1972 mm and 187 d over a 20-year
Figure 1. Distribution map of in situ soil cores and EM survey.
period, respectively.
The farmland for the present study was reclaimed in 2011 and cotton was planted in 2011-2014. Soil salinity is known as a most significant problem in this farm and large areas of salt-affected land was observed due to a very saline shallow water table (average mineralization of 35.0 g∙L−1and water table of 0.5 to 2.5 m).
2.2. EM Survey and Soil Sampling
Initially, observation soil sites were arranged on a grid in the study plot, with an average interval of 10 m from northeast to southeast (X) and 10 m from southeast to northwest (Y) (Figure 1), and a total of 250 soil sites were selected. At each site, an electromagnetic induction (type EM38) was placed on the ground surface and measurements in both the vertical (EMv) and horizontal (EMh) modes of operation were made. Later 70 sites which covered a wide range of soil salinity were randomly chosen from the total 250 soil sites for soil sampling. We were focused on 0 - 80 cm arable layer for cotton root growth regions because of using drip irrigation under mulch in study area; soil samples were obtained by hand augering at 0 - 20, 20 - 40. 40 - 60 and 60 - 80 cm soil layers intervals to a depth of 0.8 m for the laboratory analyses of electrical conductivity (EC). In all, EM measurements (EMh and EMv) of 250 sites and soil samples of 70 in situ cores (280 soil samples) were collected. Soil sampling and EM gauging was carried out from March 25th to April 5th 2013 when soil moisture conditions were relatively uniform across the plot.
2.3. Laboratory Analysis
All soil samples were air-dried, crushed, and passed through a 2-mm sieve. The 1:5 soils: water suspensions were prepared by weighing 12 g of soil into a pop-top tube, adding 60 ml of deionized water, and shaking for 30 min on an end-over-end shaker. After being left for 30 min, the EC1:5 of the supernatant were measured with a conductivity meter directly (Miller et al. 2006). In addition, 200 soil samples of 50 profiles that varied greatly in soil salinity were chosen and prepared for analysis of total dissolved salts (TDS).The TDS of soil samples was determined by summing up the dominant cations (Ca2+, Mg2+, Na+, K+) and anions (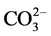 ,
, 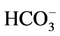 , Cl−,
, Cl−,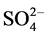 ) of 1:5 soil water extracts. A comparison between EC1:5 and the TDS showed a strong positive linear relationship, and the equation of the fitted line relating the TDS (g∙kg−1) to EC1:5 (dS∙m−1) values were given by:
) of 1:5 soil water extracts. A comparison between EC1:5 and the TDS showed a strong positive linear relationship, and the equation of the fitted line relating the TDS (g∙kg−1) to EC1:5 (dS∙m−1) values were given by:
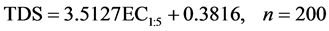 (1)
(1)
The TDS values of the rest 80 soil samples (20 profiles) whose TDS values were not measured were estimated from EC1:5 on the basis of this relationship (r2 = 0.9517). The TDS value was used as a surrogate for the widely used ECe to determine soil salinity in our study.
2.4. Spatial Estimation Methods
2.4.1. Inverse Distance Weighted (IDW)
IDW is arguably the most commonly used method in GIS among the moving window average type approaches [27] [28] . It is a local and exact method that predicts an unknown spatial value at a target location using the observed values at the nearest sample locations in straight-line distance and assigns a weight that is inversely proportional to the straight-line distance from the respective sample location.
2.4.2. Ordinary Kriging (OK)
Kriging is a spatial interpolation method that builds on the geostatistical principle of regionalized variables [29] . It predicts an unknown value of a target location using a linear combination of observed values at the nearby sample locations whose weights are determined by a stochastic model of the spatial dependence quantified by the semivariogram. Among the many variants of kriging, we will adopt ordinary kriging [30] , which is the most widely used form of spatial interpolation method among the family of kriging methods [28] [31] . It is also a suitable candidate for making a direct comparison with IDW, as both methods use the same set of sample locations and assume that the sum of the weights between the sample locations to be 1. This means that the composition of the weights assigned by each method determines the level of accuracy of the prediction.
2.5. Evaluation Criteria
We used cross-validation to validate the accuracy of interpolation algorithms and examine the difference between the measured values and the predicted values using mean absolute errors (MAE) or relative MAE (MAE %) (Equation (2)), root-mean-square error (RMSE) or relative RMSE (RMSE %) (Equation (3)), ratio of prediction to deviation (RPD) (Equation (4)) and model efficiency factor (E) (Equation (5)). The RPD indicates strength of statistical correlation between measured and predicted values. MAE, RMSE and E values indicate degree of agreement between measured and predicted values. Detailed descriptions and definitions of these model performance parameters are given by [32] [33] .
 (2)
(2)
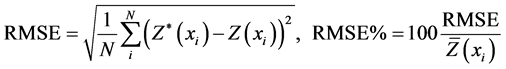 (3)
(3)
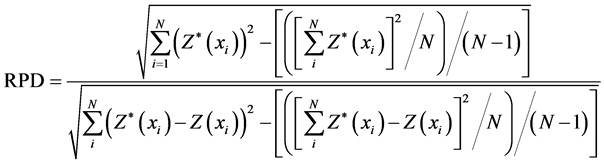 (4)
(4)
 (5)
(5)
where  is the observed (measured) value of Z at locations
is the observed (measured) value of Z at locations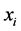 ,
, 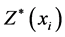 is the predicted value at the same locations,
is the predicted value at the same locations, 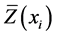 ,
, 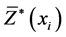 is the average measured and predicted value, respectively. N is the number of values in the dataset.
is the average measured and predicted value, respectively. N is the number of values in the dataset.
Conventional statistical analyses were conducted using the software package SPSS 17.0 for Windows (SPSS Inc., Mat Lab, USA). Geostatistical analyses and mapping were performed by using Arc GIS 10.0 software package (Environmental Systems Research Institute, Redlands, CA).
3. Results and Discussion
3.1. Calibration of EM Measurements
Fifty sites out of the 70 in situ sampling sites were selected for the spatial simulation of soil salinity, and the rest 20 sites were used for validation of IDW, OK algorithms. In the calibration procedure, the TDS data was selected as the dependent variable and apparent soil electrical conductivity (EMh and EMv) made by the EM38 as the independent variable. The linear regression model was then fitted the data from the selected 50 sampling sites. This yielded of predictive equations across the whole soil profile (Table 1). Readers are referred [34] - [36] for similar approaches with variations.
Both EMh and EMv measurements showed significant linearity with the TDS at each soil layer. Multiple linear regression using EMh and EMv as independent variables gained higher regression coefficients than those fitted by linear regression (Table 1), the correlation coefficient of 0 - 20, 20 - 40, 40 - 60 and 60 - 80 cm were 0.9090, 0.9228, 0.896 and 0.9085 respectively. The multiple linear predictive equations were then used to reconstruct the salinity profiles at the 180 soil sites where EM measurements were made.
3.2. Descriptive Statistics
Summary statistics and normal test of soil salinity from multiple linear regression datasets was performed in different soil layers, and the results, present in Table 2, indicated that the average soil salinity value was comparatively high with regard to the generally accepted limit for most agricultural crops. The minimum and maximum of soil salinity were 9.56 g/kg in 20 - 40 cm soil layer and 40.06 g/kg in 0 - 20 cm soil layer, respectively, the means were greater than 24.0 g/kg in different soil layers. As it resulted also from the parameters of one- sample Kolmogorov-Smirnov (K-S) normality test (p < 0.05, two-tailed), skewness and kurtosis, the data of all variables did follow normal distributions.
3.3. Semivariogram Analysis
The experimental semivariogram γ(h) measuring the spatial autocorrelation between data pairs as a function of the displacement between the pairs was calculated and the scatter plot of γ(h) vs. h (lag distance) was gained. Then different theoretical semivariance models were used to fit the calculated values, and the model with the best fitting value and the smallest nugget value was selected [37] . The fitted parameters of the semivariograms and cross-semivariograms at both orientations were summarized in Table 3. These semivariogram parameters include the nugget value C0, partial sill (C), sill (C0 + C), range value a and nugget-sill-ratio (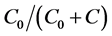 ). Validation information used to determine the goodness of fit includes determination coefficient (r2), residual sum of squares (RSS) and significance level of F test.
). Validation information used to determine the goodness of fit includes determination coefficient (r2), residual sum of squares (RSS) and significance level of F test.
More often than not, positive nuggets were observed during surveys of most soil properties [38] . In this study, namely nugget-to-sill 
3.4. Spatial Distribution of Soil Salinity
Ordinary kriging and IDW methods were applied to estimate the soil salinity of EM38 data at unsampled locations
Table 1. Regression relationships between apparent soil electrical conductivity and salinity (n = 50).
Table 2. Summary statistics of soil salinity.
Table 3. Fitted parameters of experimental semivariogram of TDS, where C0 is nugget, C is partial sill, C0 + C is sill, 
using semivariogram models in Table 3. Considering the whole application, including trend analysis, semivariogram calculation and interpolation was applied to generate the spatial distribution map. Raster maps (2 m × 2 m) of soil salinity across the study area were presented in Figure 2.
A jack-knifing procedure of cross-validation was employed to statistically evaluate the performance of the spatial prediction of TDS data. The results showed that root mean square error (RMSE) of ordinary kriging for 0 - 20, 20 - 40, 40 - 60 and 60 - 80 cm prediction was 0.8852, 0.9 077, 0.8926 and 0.9143, respectively, while it was 0.9177, 0.9524, 0.9376 and 0.9408 for IDW, respectively, which indicates high prediction precision and reliability of IDW method to the interpolation plots of soil salinity (Figure 2).
Figure 2 shows the local and regional variation information of soil salinity at each of layers in 0 - 0.8 m soil solum. Soil salinity exhibited strip and block patterns, and similar spatial patterns can be observed from maps of all soil layers. As was plainly illustrated that, for both OK and IDW, the grids of TDS < 15.0 g/kg almost no position, the grids of 15.0 < TDS < 20.0 g/kg generally concentrated in the east-central positions, the grids of 20.0 < TDS < 25.0 g/kg mostly occurred in east-central and south-east portions of the study domain, the grids of 25.0 < TDS < 30.0 g/kg considered as the predominant soil salinization type, spread throughout the whole study plot, the grids of TDS > 30 g/kg were mainly situated in the northwest and southwest sporadically. It was also apparent that the northwest and southeast region of the study area were most salinized compared with other regions, especially at soil layers of 0 - 20 and 60 - 80 cm. This phenomenon can be explained by many reasons. For one thing, this highly salinized position is situated in low-lying area, more influences from the shallow water table and high groundwater mineralization to 60 - 80 cm layer. For another, intense evaporation and scarce precipitation in the study area have induced soluble salt to transport upward to 0 - 20 cm layer.
3.5. Spatial Estimation and Its Performance
With the 20 observation soil sites (80 soil samples) randomly selected as external dataset to estimate the prediction yields of IDW and OK methods. Figure 3 shows good performance of TDS by both methods, comparing to coefficient of determination (R2), R2 between predictions and observations ranges from 0.6074 to 0.5918 for IDW method and from 0.6219 to 0.5088 for OK method. This result reveals that IDW prediction value has better performance than OK in different soil layers, except 40 - 60 cm.
Based on the statistical parameters as discussed, both IDW and OK model are validated using the model efficiency factor E and RPD of predicted values. The E and RPD between reference measurements, i.e. accurate or good prediction if RPD and E values are higher than 2.5 and 0.80 respectively by Farifteh et al. (2007), suggest an accurate to good prediction. It is observed from Table 4 that IDW method (with E = 0.8873, 0.9075, 0.8483 and 0.901, RPD = 9.64, 8.01, 8.17 and 10.83 in 0 - 20, 20 - 40, 40 - 60 and 60 - 80 cm soil layer, respectively) predicts an accurate TDS slightly better than OK methods. In addition to MAE% and RMSE%, it is considered that IDW performs slightly better, differences between IDW and OK methods in predictions are significant for both variables based on the analysis of covariance (ANOVA) test (P < 0.05).
4. Conclusions
With the application of soil sampling and site-specific measure of electromagnetic induction instruments (EM38), relationships between soil salinity and electromagnetic induction measurement were calibrated. By using GIS and geostatistical technique, spatial distribution of soil salinity at the field scale was mapped and quantitatively evaluated based on the field survey of mobile EMI system.
Owing to the high-efficient and non-invasive nature of EM measurements, they were selected as the covariate of soil salinity. In our study, sampling sites for measurement of salinity using conventional lab techniques and via electromagnetic induction instruments were selected. Analysis results indicated that apparent soil electrical conductivity measured by EM38 was strongly correlated with soil salinity, the multiple linear combinations of
Figure 2. Spatial distribution plots of soil salinity at various soil layers (A by IDW, B by OK method).
Figure 3. Plots of the measured versus predicted values and the fitted regression line and equation at various soil layers (A by IDW, B by OK method).
Table 4. Performance of predicted values using IDW and OK methods.
EM measurements (EMh and EMv) were established in terms of their response to salinity at different soil layers, the correlation coefficient of 0 - 20, 20 - 40, 40 - 60 and 60 - 80 cm were 0.9091, 0.9228, 0.896 and 0.9085 respectively. Descriptive statistics showed, the average soil salinity value was comparatively high (the maximum value was 40.06 g/kg) and the data of all variables did follow normal distributions from K-S normality test.
Ordinary kriging and IDW methods were applied to estimate the soil salinity of EM38 data at unsampled locations using semivariogram and with the 20 observation soil sites (80 soil samples) randomly selected as external dataset to estimate the prediction yields. The comparison showed that the prediction accuracy of two methods also shows good performance for soil salinity, IDW (with E = 0.8873, 0.9075, 0.8483 and 0.901, RPD = 9.64, 8.01, 8.17 and 11.23 in 0 - 20, 20 - 40, 40 - 60 and 60 - 80 cm soil layers, respectively) was superior to that of OK method (with E = 0.8857, 0.872, 0.8744 and 0.8822, RPD = 9.44, 7.83, 8.52 and 10.88, respectively), indicating IDW method was more suitable for the spatial estimation of the present soil property, distribution type and data arrangement in our research scale. In this study, soil profile to depth of 0 - 20 and 60 - 80 cm is our interest for the reason that more soil salinity at these layers, because the soil sampling and EM survey was performed in springtime, just the intense evaporation and scarce precipitation in the study area have induced soluble salt to transport upward to surface layer, and shallow water table.
Considering the soil conditions of high initial salinity, arid climate and the bad conditions of groundwater in Xinjiang region, the EM instruments were reliable profile salinity screening tools for salinized soil in our study area. Our results show that the decisive factor for soil salinization is capillary rise from the saline shallow water table and matrix matrices. Due to the particular soil and climate conditions, high salt-stress tolerance crops such as cotton and wheat are probably the pioneer crops that can be grown successfully. Installation of irrigation and drainage facilities may in some cases be a necessity because natural salinity levels are such that significant yield losses can be expected.
Acknowledgements
The authors are grateful for the financial support of the Key Projects in the Bingtuan Science & Technology of Xinjiang, China (2014AB002) and Projects of International Cooperation and Exchanges of China (2015DFA11660). We would also like to thank the reviewers for their time spent in improving the paper.
Cite this paper
Haijiang Wang,Shaotin Ren,Zhexia Hao,Li Meng,Wei Wei,Cui Jing, (2016) Quantitative Evaluation and Uncertainty Assessment on Geostatistical Simulation of Soil Salinity Using Electromagnetic Induction Technique. Journal of Environmental Protection,07,844-854. doi: 10.4236/jep.2016.76077
References
- 1. Zhou, D., Xu, J.C., Wang, L., Lin, Z.L. and Liu, L.M. (2015) Identifying and Managing Risk Factors for Salt-Affected Soils: A Case Study in a Semi-Arid Region in China. Environmental Monitoring and Assessment, 187, 421. http://dx.doi.org/10.1007/s10661-015-4639-7
- 2. Bouarfa, S. and Kuper, M. (2012) Groundwater in Irrigation Systems: From Menace to Mainstay. Irrigation and Drainage, 61, 1-13. http://dx.doi.org/10.1002/ird.1651
- 3. Purkey, D.R. and Wallender, W.W. (2001) Drainage Reduction under Land Retirement over a Shallow Water Table. Journal of Irrigation and Drainage Engineering, 127, 1-7. http://dx.doi.org/10.1061/(ASCE)0733-9437(2001)127:1(1)
- 4. Wichelns, D. and Qadir, M. (2015) Achieving Sustainable Irrigation Requires Effective Management of Salts, Soil Salinity, and Shallow Groundwater. Agricultural Water Management, 157, 31-38. http://dx.doi.org/10.1016/j.agwat.2014.08.016
- 5. Alonso, M.F., Corwin, D.L., Oster, J.D., Maas, J. and Kaffka, S.R. (2013) Modeling a Sustainable Salt Tolerant Grass- Livestock Production System under Saline Conditions in the Western San Joaquin Valley of California. Sustainability- Basel, 5, 3839-3857. http://dx.doi.org/10.3390/su5093839
- 6. Berkal, I., Walter, C., Michot, D. and Djili, K. (2014) Seasonal Monitoring of Soil Salinity by Electromagnetic Conductivity in Irrigated Sandy Soils from a Saharan Oasis. Soil Research, 52, 769-780. http://dx.doi.org/10.1071/SR13305
- 7. Triantafilis, J., Kerridge, B. and Buchanan, S.M. (2009) Digital Soil-Class Mapping from Proximal and Remotely Sensed Data at the Field Level. Agronomy Journal, 101, 841-853. http://dx.doi.org/10.2134/agronj2008.0112
- 8. Urdanoz, V. and Aragues, R. (2012) Comparison of Geonics EM38 and Dualem 1S Electromagnetic Induction Sensors for the Measurement of Salinity and Other Soil Properties. Soil Use and Management, 28, 108-112. http://dx.doi.org/10.1111/j.1475-2743.2011.00386.x
- 9. Emadi, M., Shahriari, A.R., Sadegh-Zadeh, F., JaliliSeh-Bardan, B. and Dindarlou, A. (2016) Geostatistics-Based Spatial Distribution of Soil Moisture and Temperature Regime Classes in Mazandaran Province, Northern Iran. Archives of Agronomy and Soil Science, 62, 502-522. http://dx.doi.org/10.1080/03650340.2015.1065607
- 10. Neely, H.L., Morgan, C.L.S., Hallmark, C.T., McInnes, K.J. and Molling, C.C. (2016) Apparent Electrical Conductivity Response to Spatially Variable Vertisol Properties. Geoderma, 263, 168-175.
- 11. Qadir, M., Quillerou, E., Nangia, V., Murtaza, G., Singh, M., Thomas, R.J., et al. (2014) Economics of Salt-Induced Land Degradation and Restoration. Natural Resources Forum, 38, 282-295. http://dx.doi.org/10.1111/1477-8947.12054
- 12. Sun, Y.R., Cheng, Q., Lin, J.H., Schellberg, J. and Lammers, P.S. (2013) Investigating Soil Physical Properties and Yield Response in a Grassland Field Using a Dual-Sensor Penetrometer and EM38. Journal of Plant Nutrition and Soil Science, 176, 209-216. http://dx.doi.org/10.1002/jpln.201200104
- 13. Triantafilis, J., Huckel, A.I. and Odeh, I.O.A. (2001) Comparison of Statistical Prediction Methods for Estimating Field-Scale Clay Content Using Different Combinations of Ancillary Variables. Soil Science, 166, 415-427. http://dx.doi.org/10.1097/00010694-200106000-00007
- 14. Doolittle, J.A., Indorante, S.J., Potter, D.K., Hefner, S.G. and McCauley, W.M. (2002) Comparing Three Geophysical Tools for Locating Sand Blows in Alluvial Soils of Southeast Missonr. Journal of Soil and Water Conservation, 57, 175-182.
- 15. Triantafilis, J., Lau, K.L. and Buchanan, S.M. (2009) Field Level Digital Soil Mapping of Canon Exchange Capacity Using Electromagnetic Induction and a Hierarchical Spatial Regression Model in the Lower Namoi Valley. Australian Journal of Soil Research, 47, 651-663. http://dx.doi.org/10.1071/SR08240
- 16. Li, H.Y., Shi, Z., Webster, R. and Triantafilis, J. (2013) Mapping the Three-Dimensional Variation of Soil Salinity in a Rice-Paddy Soil. Geoderma, 195, 31-41. http://dx.doi.org/10.1016/j.geoderma.2012.11.005
- 17. Buchanan, S.M. and Triantafilis, J. (2009) Mapping Water Table Depth Using Geophysical and Environmental Variables. Ground Water, 47, 80-96. http://dx.doi.org/10.1111/j.1745-6584.2008.00490.x
- 18. Li, H.Y., Webster, R. and Shi, Z. (2015) Mapping Soil Salinity in the Yangtze Delta: REML and Universal Kriging (E-BLUP) Revisited. Geoderma, 237, 71-77. http://dx.doi.org/10.1016/j.geoderma.2014.08.008
- 19. Li, X.M., Yang, J.S., Liu, M.X., Liu, G.M. and Yu, M. (2012) Spatio-Temporal Changes of Soil Salinity in Arid Areas of South Xinjiang Using Electromagnetic Induction. Journal of Integrative Agriculture, 11, 1365-1376.
- 20. Bhat, S., Motz, L.H., Pathak, C. and Kuebler, L. (2015) Geostatistics-Based Groundwater-Level Monitoring Network Design and Its Application to the Upper Floridan Aquifer, USA. Environmental Monitoring and Assessment, 187, 4183. http://dx.doi.org/10.1007/s10661-014-4183-x
- 21. Silva, A.F., Barbosa, A.P., Zimback, C.R.L., Landim, P.M.B. and Soares, A. (2015) Estimation of Croplands Using Indicator Kriging and Fuzzy Classification. Computers and Electronics in Agriculture, 111, 1-11.
- 22. Huang, J., Subasinghe, R., Malik, R.S. and Triantafilis, J. (2015) Salinity Hazard and Risk Mapping of Point Source Salinisation Using Proximally Sensed Electromagnetic Instruments. Computers and Electronics in Agriculture, 113, 213-224.
- 23. Barbiéro, L., Cunnac, S., Mané, L., Laperrousaz, C., Hammecker, C. and Maeght, J.L. (2001) Salt Distribution in the Senegal Middle Valley: Analysis of a Saline Structure on Planned Irrigation Schemes from N’Galenka Creek. Agricultural Water Management, 46, 201-213. http://dx.doi.org/10.1016/S0378-3774(00)00088-3
- 24. Tripathi, R., Nayak, A.K., Shahid, M., Raja, R., Panda, B.B., Mohanty, S., et al. (2015) Characterizing Spatial Variability of Soil Properties in Salt Affected Coastal India Using Geostatistics and Kriging. Arabian Journal of Geosciences, 8, 10693-10703. http://dx.doi.org/10.1007/s12517-015-2003-4
- 25. Triantafilis, J., Odeh, I.O.A. and Mcbratney, A.B. (2001) Five Geostatistical Models to Predict Soil Salinity from Electromagnetic Induction Data across Irrigated Cotton. Soil Science Society of America Journal, 65, 869-878. http://dx.doi.org/10.2136/sssaj2001.653869x
- 26. Yang, J.S. and Yao, R.J. (2007) Comparison of Interpolation Approaches Based on Spatial Variability of Apparent Soil Electrical Conductivity with an Electromagnetic Induction. Transactions of CSAE, 23, 50-57.
- 27. Burrough, P.A. and McDonnell, R. (1998) Principles of Geographic Information Systems. Oxford University Press, New York.
- 28. Lloyd, C.D. (2010) Spatial Data Analysis. Oxford University Press, New York.
- 29. Matheron, G. (1963) Principles of Geostatistics. Economic Geology, 58, 1246-1266. http://dx.doi.org/10.2113/gsecongeo.58.8.1246
- 30. Journel, A.G. and Huijbregts, C.J. (1978) Mining Geostatistics. Academic Press, London.
- 31. Del Monego, M., Ribeiro, P.J. and Ramos, P. (2015) Comparing the Performance of Geostatistical Models with Additional Information from Covariates for Sewage Plume Characterization. Environmental Science and Pollution Research, 22, 5850-5863. http://dx.doi.org/10.1007/s11356-014-3709-7
- 32. Robinson, T.P. and Metternicht, G. (2006) Testing the Performance of Spatial Interpolation Techniques for Mapping Soil Properties. Computers and Electronics in Agriculture, 50, 97-108. http://dx.doi.org/10.1016/j.compag.2005.07.003
- 33. Farifteh, J., Van der Meer, F., Atzberger, C., Carranza, E.J.M. (2007) Quantitative Analysis of Salt-Affected Soil Reflectance Spectra: A Comparison of Two Adaptive Methods (PLSR and ANN). Remote Sensing of Environment, 110, 59-78. http://dx.doi.org/10.1016/j.rse.2007.02.005
- 34. Triantafilis, J., Laslett, G.M. and Mcbratney, A.B. (2000) Calibrating an Electromagnetic Induction Instrument to Measure Salinity in Soil under Irrigated Cotton. Soil Science Society of America Journal, 64, 1009-1017. http://dx.doi.org/10.2136/sssaj2000.6431009x
- 35. Sudduth, K.A., Kitchen, N.R., Wiebold, W.J., Batchelor, W.D., Bollero, G.A., Bullock, D.G., Clay, D.E., Palm, H.L., Pierce, F.J., Schuler, R.T. and Thelen, K.D. (2005) Relating Apparent Electrical Conductivity to Soil Properties across the North-Central USA. Computers and Electronics in Agriculture, 46, 263-283. http://dx.doi.org/10.1016/j.compag.2004.11.010
- 36. Herrero, J., Netthisinghe, A., Hudnall, W.H. and Pérez-Covet, O. (2011) Electromagnetic Induction as a Basis for Soil Salinity Monitoring within a Mediterranean Irrigation District. Journal of Hydrology, 405, 427-438. http://dx.doi.org/10.1016/j.jhydrol.2011.05.041
- 37. Goovaerts, P. (1997) Geostatistics for Natural Resources Evaluation. Oxford University Press, New York.
- 38. McBratney, A.B. and Webster, R. (1981) Spatial Dependence and Classification of the Soil along a Transect in Northeast Scotland. Geoderma, 26, 63-82. http://dx.doi.org/10.1016/0016-7061(81)90076-8
- 39. Cambardella, C.A., Moorman, T.B., Novak, J.M., Parkin, T.B., Turco, R.F. and Konopka, A.E. (1994) Field-Scale Variability of Soil Properties in Central Iowa Soils. Soil Science Society of America Journal, 58, 1501-1511. http://dx.doi.org/10.2136/sssaj1994.03615995005800050033x
NOTES
*Corresponding author.






