Journal of Environmental Protection
Vol.05 No.08(2014), Article ID:46826,5 pages
10.4236/jep.2014.58075
The Numerical Investigation on Oil Slick Behavior behind the Oil Boom
Kai Gong, Pavel Tkalich, Haihua Xu
Tropical Marine Science Institute, National University of Singapore, Singapore City, Singapore
Email: tmsgk@nus.edu.sg
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2014; revised 2 May 2014; accepted 24 May 2014
ABSTRACT
The dynamics of contained oil spills is investigated based on multiphase CFD (Computational Fluid Mechanics) model. The oil slick shape behind the oil boom under water current is studied. The velocity field in the oil slick is compared with the velocity field in pure water flow. The thickness of the oil slick is studied quantitatively. It is found that there is a fixed linear relationship between the oil slick relative thickness and the Froude number for different oil, different current velocity, different boom draft and different volume of oil.
Keywords:
Oil Spill, Oil Boom, Oil Slick, CFD, VOF (Volume of Fluid), Multiphase Flow

1. Introduction
Marine oil spills can cause serious damage to natural resources and to those whose livelihoods depend on these resources. Therefore, it is important to improve techniques and equipment that facilitate spill cleanup [1] . The common response to an oil spill on water is to contain the oil with booms and recover it with skimming devices. However, in some situations, the booms fail to hold the oil and the oil will escape underneath the boom due to hydrodynamic forces. Poor recovery of oil using booms requires significantly higher cleanup costs. Therefore a better understanding of the dynamics of oil slicks is required [2] .
Besides wind and wave effects, there are three failure mechanisms for the oil boom in the current [3] : drainage failure, entrainment failure and critical accumulation failure. In drainage failure, the boom draft is insufficient to contain the oil slick and some oil goes underneath the barrier. Cross and Hoult described the oil slick profile theoretically [4] [5] . In entrainment failure, oil droplets are broken off from the oil and are swept underneath the boom if the buoyancy forces are insufficiently large [6] . Leibovich [6] and Milgram et al. [7] ascribe the entrainment to breaking of Kelvin-Helmholtz water-oil interfacial waves at sufficiently large relative velocity. Many experimental results can be found in the literatures [6] -[9] . For highly viscous oils of kinematic viscosities exceeding 3000 cSt, Delvigne [3] showed a third failure mechanism: critical accumulation (oil creep) for relative velocities exceeding about 0.15 m/s, independently of the boom draft. Johnston [10] indicated that this mode of failure is due to an insufficient circulation within the oil and suggested to use Bingham-plastic model instead of Newtonian model to improve the understanding of this mode of failure.
Although oil boom is widely used, it is far from being fully investigated. For understanding the boom failure mechanism, it is important to investigate the oil slick behavior behind the boom and the details of the flow field near the boom. For the limit of the measurement approach, it is hard to know the details of the flow field in the oil slick. CFD has its advantages to obtain the process of the oil slick propagation and the details of the flow field in the oil slick. Tkalich et al. [11] -[13] developed a multiphase oil spill model to simulate consequences of oil spill in the marine environment. Goodman et al. [14] [15] investigated the boom failure mechanisms using CFD approach. They only qualitatively studied the boom failure but did not give the quantitative details of the oil slick profiles and the velocity field. In this paper, an open source CFD software package, OpenFOAM v2.2.2, has been used to simulate the oil water flow around a boom. The details of the flow field in the oil slick are studied and the thickness of oil slick is investigated quantitatively.
2. Governing Equation
For the purpose of investigating the oil slick behavior behind the boom under a water current, a CFD software, OpenFOAM, is employed to carry out the numerical simulation. In this software, the Reynolds averaged Navier- Stokes equations (RANS equations) are solved numerically and 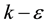 turbulence modelling is adopted. The volume of fluid (VOF) method is used to track the interface between the oil and water. The incompressible RANS momentum equation solved in the software can be written as:
turbulence modelling is adopted. The volume of fluid (VOF) method is used to track the interface between the oil and water. The incompressible RANS momentum equation solved in the software can be written as:
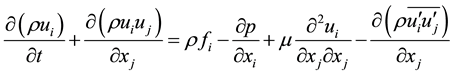 (1)
(1)
where 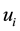 is the fluid velocity vector,
is the fluid velocity vector, 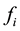 is the external force vector,
is the external force vector, 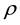 is the fluid density, p is the pressure,
is the fluid density, p is the pressure, 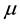 is the dynamic viscosity,
is the dynamic viscosity, 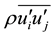 is the Reynolds stress and can be approximated by using Boussinesq’s isotropic eddy viscosity hypothesis as follows:
is the Reynolds stress and can be approximated by using Boussinesq’s isotropic eddy viscosity hypothesis as follows:
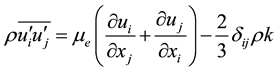 (2)
(2)
where 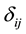 is the Kronecker delta, k is the turbulent kinetic energy,
is the Kronecker delta, k is the turbulent kinetic energy, 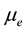 is an effective viscosity, the sum of the turbulent eddy viscosity
is an effective viscosity, the sum of the turbulent eddy viscosity 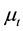 and molecular dynamic viscosity
and molecular dynamic viscosity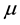 :
:
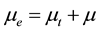 (3)
(3)
The turbulent eddy viscosity 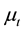 is calculated using the standard
is calculated using the standard 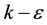 model [16] as follows:
model [16] as follows:
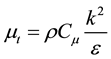 (4)
(4)
where 




where



3. Numerical Simulations
The numerical simulation scenarios are chosen as the similar geometry with the real situation of the Singapore sea area. The computational domain is 30 m long and 5 m deep (see Figure 1). The oil boom is placed near the surface and in the middle of the computational domain in length direction. The boom draft D is chosen as 0.5 m or 1 m. The current velocity U range is chosen of 0.1 - 0.5 m/s at interval of 0.1 m/s.
There are four type of oil (listed in Table 1) used in the simulation which include from light to heavy oil and from low to high viscosity oil. The initial oil volume Q is chosen as 1.2 m3 or 3.6 m3 per unit boom length.
A summary of cases are listed in Table 2. For every case label, there are five different current velocities from 0.1 m/s to 0.5 m/s. Therefore, a total of 80 cases of oil slick are carried out in this study.
For the numerical simulation of all the case, the same meshes are adopted with just slight difference between different boom drafts. The total number of cells is about 53,000. The minimum cell size is 0.025 m. The finest cells are placed near the boom and the water surface. Figure 2 shows the meshes used in the simulation.
4. Analysis of the Numerical Results
4.1. Flow Field near the Boom
First at all, a case without oil has been carried out to compare with the case with oil. Figure 3 shows the flow
Table 1. Four type of oil used in simulation.
Table 2. Summary of the simulation cases.
Figure 1. Schematic drawing of the computational domain.
Figure 2. Schematic drawing of the computational domain.
Figure 3. Comparison of the flow field near the boom with (at right) and without (at left) oil.
field near the boom of these two cases. It shows that the current velocity distribution is almost same at the section far from the boom in the case without oil (left). But for the case with oil (right), the velocity distribution is changed in the oil slick. This phenomenon means that it is not enough to estimate the boom efficiency only based on the velocity field of the case without oil. It is necessary to carry out the numerical simulation of the case with oil based on multiphase model.
Figure 4 shows the comparison of the oil slick behavior of low and high viscosity oil when the flow becomes steady. For the low viscosity oil (top figure), the oil slick is longer. For the high viscosity, a head wave is formed on the upstream edge of the slick. The streamline shows that there is only one main vortex in the oil slick for the low viscosity oil and two vortices in the oil slick for the high viscosity oil.
4.2. Oil Slick Behaviors behind the Boom
Figure 5 shows the relationship between the densimetric Froude number and the relative thickness of the oil slick. Where the densimetric Froude number is defined as follows:

And the relative thickness is defined as the ratio of the oil slick thickness h and the oil characteristic length
Figure 4. The streamline of the flow field and the behavior of the oil slick behind the boom (Top: case b; bottom: case f; current velocity U = 0.5 m/s).
Figure 5. The relative thickness of oil slick versus the densimetric Froude number.


This formula shows that the oil slick thickness is an function of initial oil volume Q, the current velocity U, the density of oil 

5. Conclusion
A series of numerical simulation cases are carried out based on OpenFOAM multiphase solver in order to study the oil slick behavior behind the oil boom. The flow field near the boom is studied. The relationship of the relative thickness of oil slick with the Froude number is analyzed. It is found that there is a linear relationship between the relative oil slick thickness and the Froude number. This means that we can estimate the relative oil slick thickness using Froude number by the fixed linear relationship regardless of boom draft, initial oil volume and oil type.
References
- Amini, A., Bollaert, E., Boillat, J.-L. and Schleiss, A.J. (2008) Dynamics of Low-Viscosity Oils Retained by Rigid and Flexible Barriers. Ocean Engineering, 35, 1479-1491. http://dx.doi.org/10.1016/j.oceaneng.2008.06.010
- Chebbi, R. (2009) Profile of Oil Spill Confined with Floating Boom. Chemical Engineering Science, 64, 467-473. http://dx.doi.org/10.1016/j.ces.2008.10.001
- Delvigne, G.A.L. (1989) Barrier Failure by Critical Accumulation of Viscous Oil. Oil Spill Conference, San Antonio, 13-16 February 1989, 143-148.
- Cross, R.H. and Hoult, D.P. (1971) Collection of Oil Slicks. Journal of the Waterways, Harbors, and Coastal Engineering Division, Proceedings of the American Society of Civil Engineers, 97, 313-322.
- Cross, R.H. and Hoult, D.P. (1972) Oil Booms in Tidal Currents. Journal of the Waterways, Harbors, and Coastal Engineering Division, Proceedings of the American Society of Civil Engineers, 98, 25-34.
- Leibovich, S. (1976) Oil Slick Instability and the Entrainment Failure of Oil Containment Booms. Journal of Fluids Engineering, 98, 98-103. http://dx.doi.org/10.1115/1.3448229
- Milgram, J.H. and Van Houten, R.J. (1978) Mechanics of a Restrained Layer of Floating Oil above a Water Current. Journal of Hydronautics, 12, 93-108. http://dx.doi.org/10.2514/3.63119
- Lee, C.M. and Kang, K.H. (1997) Prediction of Oil Boom Performance in Currents and Waves. Spill Science & Technology Bulletin, 4, 257-266. http://dx.doi.org/10.1016/S1353-2561(98)00022-X
- Violeau, D., Buvat, C., Abed-Meraim, K. and De Nanteuil, E. (2007) Numerical Modeling of Boom and Oil Spill with SPH. Coastal Engineering, 54, 895-913. http://dx.doi.org/10.1016/j.coastaleng.2007.06.001
- Johnston, A.J., Fitzmaurice, M.R. and Watt, R.G.M. (1993) Oil Spill Containment: Viscous Oils. Oil Spill Conference, Tampa, 10 August 1993, 89-94.
- Tkalich, P. and Chan, E.S. (2001) A High Resolution Oil Spill Model. Proceedings of International Conference on Port and Maritime R&D and Technology, Singapore, 29-31 October 2001, 647-652.
- Tkalich, P. (2002) Oil Spill Modelling with a CFD Approach. Proceedings of 6th International Marine Environmental Modelling Semina, Trondheim, 2-4 September 2002, 255-274.
- Tkalich, P., Huda, M.D.K. and Gin, K.Y.H. (2003) A Multiphase Oil Spill Model. Journal of Hydraulic Research, 41, 115-125. http://dx.doi.org/10.1080/00221680309499955
- Goodman, R.H., Brown, H.M., An, C.-F. and Rowe, R.D. (1996) Dynamic Modelling of Oil Boom Failure Using Computational Fluid Mechanics. Spill Science & Technology Bulletin, 3, 213-216. http://dx.doi.org/10.1016/S1353-2561(97)00015-7
- Brown, H.M., Goodman, R.H., An, C.-F. and Bittner, J. (1997) Boom Failure Mechanisms: Comparison of Channel Experiments with Computer Modelling Results. Spill Science & Technology Bulletin, 3, 217-220.
- Launder, B.E. and Spalding, D.B. (1974) The Numerical Computation of Turbulent Flows. Computer Methods in Applied Mechanics and Engineering, 3, 269-289. http://dx.doi.org/10.1016/0045-7825(74)90029-2












