Communications and Network
Vol.6 No.2(2014), Article ID:46372,13 pages
DOI:10.4236/cn.2014.62015
Community Detection in Dynamic Social Networks
Nathan Aston, Wei Hu*
Department of Computer Science, Houghton College, Houghton, USA
Email: *wei.hu@houghton.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2014; revised 30 April 2014; accepted 7 May 2014
ABSTRACT
There are many community detection algorithms for discovering communities in networks, but very few deal with networks that change structure. The SCAN (Structural Clustering Algorithm for Networks) algorithm is one of these algorithms that detect communities in static networks. To make SCAN more effective for the dynamic social networks that are continually changing their structure, we propose the algorithm DSCAN (Dynamic SCAN) which improves SCAN to allow it to update a local structure in less time than it would to run SCAN on the entire network. We also improve SCAN by removing the need for parameter tuning. DSCAN, tested on real world dynamic networks, performs faster and comparably to SCAN from one timestamp to another, relative to the size of the change. We also devised an approach to genetic algorithms for detecting communities in dynamic social networks, which performs well in speed and modularity.
Keywords:Community Detection, Dynamic Social Networks, Density, Genetic Algorithms

1. Introduction
Social networks, such as Facebook and Twitter, have been rapidly growing in recent years. Such a network can be represented as a graph, where a node represents a user and an edge represents their affiliation with others. Figure 1 illustrates this idea. These affiliations can represent friendships or likes, as in Facebook, or followings, as in Twitter. Nodes with similar affiliations tend to group into densely knit communities to form network structures. Moreover, research has discovered three characteristics of social network structure. First, the small world phenomenon can be described as any two nodes that are related to each other through only a small number of other nodes. Second, the power law is the distribution of node degree following the pattern of a power func-
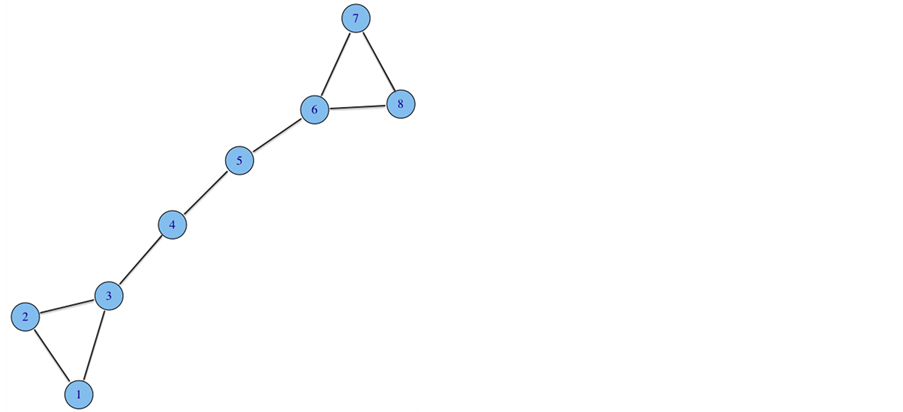
Figure 1. Illustrates a graph with nodes connected to other nodes by edges.
tion. The third is the observed community structures within a network [1] . The fast growth of social networking sites in the past decade has caused a need to analyze its community structures.
A community in a network is a group of nodes that are densely connected inside and sparsely outside. Community detection can reveal information about the users in each community, such as common interests, relationships, or views. Similarities between individuals within a community can be used in advertisements, where one user’s likes can be applicable for the other users within the same community; behavioral trends between individuals of a common community; or even similarities between genes in a genetic sequence.
There is no fixed order or form to network structures, as they arise randomly in different shapes and sizes [1] , leading to difficulties in detecting communities accurately. There are many community detection algorithms in use today, ranging from label propagation [1] to density analysis [2] . Many of these algorithms are designed to discover communities in static networks and do not scale well. Networks today include millions of nodes and billions of edges and are continually changing their structure. Community detection in dynamic networks involves the process of incorporating the community model of a previous timestamp, or snapshot of a network structure, into the detection of the next to improve the efficiency of detecting the new community structure.
Additionally, another aspect about community structure is that many community detection algorithms discover the best possible community membership for each node in the network, but some nodes are too distant from all other nodes and should be considered outliers. Also, there are those nodes that bridge two or more communities, which may or may not be members of the communities they bridge. These bridging nodes are called hubs.
2. Related Work
A general density-based clustering algorithm DBSCAN, Density Based Spatial Clustering of Applications with Noise, was proposed by Ester et al. [3] . DBSCAN forms communities from individual nodes labeled core points. These core points must satisfy a user-defined number of neighbors within a given radius. A node with a neighborhood that is too small is labeled a noise point, unless it falls within the neighborhood of a core point, which then it is labeled a border point. Core points connect to other nearby core points to form the center of a community. Ester et al. [3] devise the means to group these types of densely connected communities.
The SCAN algorithm (Structural Clustering Algorithm for Networks) [2] , derived from DBSCAN, is capable of discovering communities, hubs, and outliers in a network. A community is grown from a group of centralized nodes which all satisfy a given neighborhood size. To define the neighborhood of a node, a user-defined threshold, ε, is introduced. Instead of looking at a node’s immediate neighbors, SCAN uses the ε neighborhood of a node and groups it with those who share a common set of neighbors [2] . A structural similarity measure is used to calculate the similarity between two nodes. Its time complexity is O(n) due to the one time pass through of the set of nodes in the network.
An incremental updating process was described in the DENGRAPH-IO algorithm [4] . This algorithm uses its own variation of DBSCAN, called DENGRAPH, to update the current community structure of a network from a previously detected structure and its changes over time. The changes in nodes and edges are eventually reflected in the edges alone. Incrementally, each edge change, whether added or removed, is incorporated into the previous structure of the network, and an update to the community structure is performed in relation to the edge change. This algorithm defines six possible outcomes that an edge change in the network would cause to a community structure. An added feature to DENGRAPH, compared to SCAN, is that it can discover overlapping communities, by allowing each node to inherit multiple community labels instead of one. Also, to define a density-based neighborhood of a node, DENGRAPH uses the distance between two nodes, while SCAN uses neighborhood similarity.
Similar to community detection by node density is the idea of edge density. This density measures the ratio of the number of inter community edges to the number of intra community edges [1] . Darts et al. introduce the study of edge density in community detection and provided insight into its implementations with other community detection approaches [5] . They introduced the density measure of actual number of edges divided by the possible number of edges, where a community absorbs nodes that allow a specified edge density threshold to remain satisfied.
A common benchmark algorithm used in many comparisons is the Label Propagation Algorithm (LPA) [6] . This algorithm starts out with each node having a unique label, or community membership. It progresses through multiple iterations, which consist of each node acquiring the label from each of its neighbors and taking on the label of the majority; in the case of a tie, a label is randomly selected. Iterations are performed until a convergence is discovered or a designated number of iterations is reached.
LPA is a simple and effective algorithm that can only find disjoint communities, with no overlap. So a variation of the LPA algorithm was proposed that helped to incorporate community overlap. SLPA (Speaker—Listener Label Propagation Algorithm) [7] incorporates LPA with the allowance of each node to hold more than one label to discover overlapping communities.
Genetic algorithm (GA) is a technique that imitates the process of gene inheritance, mutation, selection, and crossover to optimize the solution to a problem. For the use of GA with community detection, the genes represent all individual nodes and their corresponding community. To find a gene that satisfies a good community structure of a network, the gene must maximize a given fitness function, such as modularity. In finding this maximized gene, a population is used consisting of multiple genes, each representing a different community structure. A user-defined number of iterations is performed over the population which mutates each gene into a cross between two or more genes that produce the highest values due to the fitness function. At the end of the iterations, the gene with the highest value from the fitness function is used as the final community structure. More on the use of genetic algorithms in networks can be read at [8] .
3. Density Based Community Detection
Ester et al. [3] , in their formulation of the DBSCAN algorithm, proposed definitions on how to relate nodes to one another in a density-based structure. Density-based community detection is defined where each node in a community share a greater number of connections with each other than with those outside. Let G = {V, E} be the network graph, where V is the set of nodes and E is the set of edges. Also let N(v), where v∈ V, be the set of neighbors of node v, including v, and let E(v) be the set of all edges incident to v. There are several definitions that must be covered to describe the structure of communities in a density-based network. Figure 2 illustrates these points.
3.1. Epsilon-Neighborhood of Nodes
The use of a node’s neighbor is insufficient to define a densely connected community, because a densely connected community must have a high similarity with neighbors in its own community. So to handle these more closely related neighbors, the idea of an ε-neighborhood was formulated.
In DBSCAN, Ester et al. [3] uses a distance function to relate the closeness between two nodes. Their ε-neighborhood incorporated all neighbors that meet a user-defined threshold ε. Given any two nodes u and v:
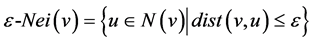
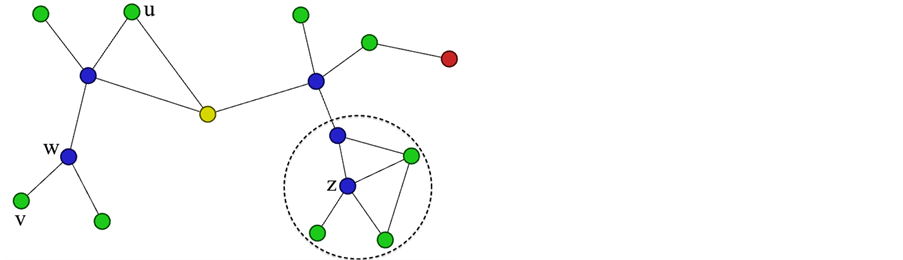
Figure 2. Shows the definitions of density structure. Node z is shown with its ε-neighborhood, v is directly reachable from w, u is structurally reachable from w, and u and v are structurally connected. The single yellow node is a hub node between the two communities and the red node is an outlier.
SCAN takes a different approach when relating nodes closeness. They define a similarity function that finds a ratio between the number of neighbors they both share in common to the number of neighbors that they each have:

The more neighbors they both have in common, the greater their similarity will be; in the range of (0, 1). So Xu et al. uses a slightly modified version of the ε-neighborhood definition:
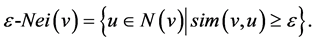
3.2. Core Nodes
A node that is considered a core node is one that contains an ε-neighborhood that has a size that satisfies a user-defined threshold of m nodes: |ε-Nei(v)| ≥ m. According to Xu et al., a m of 2 is recommended for analysis.
3.3. Direct Structure Reachability
A node u is directly reachable from node v, if v is a core node and u is in the epsilon-neighborhood of v:
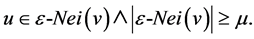
3.4. Structure Reachability
A node u is structurally reachable from node v if there is a chain of nodes that
are all directly reachable from the previous until u is reached. This is only capable
if the chain of nodes are core nodes, seen by the definition of directly reachable: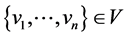 ;
;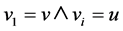 ;
;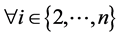 : Directly Reachable (vi-1,
vi).
: Directly Reachable (vi-1,
vi).
3.5. Structural Connectivity
Two nodes (v, u) are structurally connected if there exists a node x from which
v and u are structurally reachable. The two nodes, in this case, can be border nodes,
and the node that connects them is a core: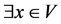 ; Structure Reachable(x,
v) ⋀ Structure Reachable(x, u).
; Structure Reachable(x,
v) ⋀ Structure Reachable(x, u).
3.6. Hubs and Outliers
By SCAN, a node v is a hub node if it does not belong to any community, but it does
have more than two neighbors belonging to different communities: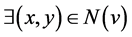 ; x ≠ y ⋀ Community(x)
≠ Community(y).
; x ≠ y ⋀ Community(x)
≠ Community(y).
A node v is an outlier if it does not belong to any community, and it does not contain
more than one neigh- boring node that belongs to different communities:
~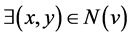 ; x ≠ y ⋀ Community(x) ≠ Community(y).
; x ≠ y ⋀ Community(x) ≠ Community(y).
4. Community Structure Reformation Due to Network Changes
In this section, we will introduce the process of updating a dynamic network and the six scenarios that may arise.
4.1. Updating Similarity Value Between Nodes
A change in the structure of a network, such as an edge being added or removed,
would affect the similarities between the two nodes that are incident to this edge.
Instead of checking the similarity of all edges in the network, only those edges
that are related to these two nodes need to be updated. Edge similarities to recalculate
due to an edge change of nodes v and u are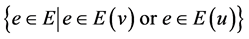 .
.
4.2. Effects of a Network Change
Falkowski [4] introduces six possible outcomes that a change in a network would produce. Each of these six scenarios is split into two groups by how that changes the community structure. There is the idea of a positive change, where a change will create a new community, a community will receive a new member, or two communities merge. Then there is a negative change, which could remove a community, remove a member from a community, or split a community into two [4] . These two groups with three scenarios within are the fundamental ideas for updating a dynamic network.
Within a positive change, a creation of a community, an addition to a community or a merge of two communities may occur. A creation of a new community would result when nodes become cores and have no ε-neighbors that were cores previously; these new core nodes would establish a new community with its ε-neighborhood. An addition to a community will occur when a node, which previously had not belonged to a community, obtains a similarity with a core that is greater than ε, thus it now belongs to the community of this core. Then a merging of two communities will happen when a core of one community obtains a similarity with a core of another community that is greater than ε, and then the communities of these cores will become one.
In a negative change, a split of a community, removal from a community, or removal of a community may occur. A split will occur when a node, that was once a core, now is no longer a core, and it creates a gap between the other cores of the community. This gap will create a division between two or more chains of cores causing each chain of cores to form separate communities. A removal from a community occurs when a node no longer has a strong connection, or high enough similarity, to a core of its community and is no longer labeled as a member of that community. A removal of a community happens when all cores of a community are reduced from their core status and the community is removed.
To determine whether a change will produce a positive or negative change to a network is not an easy task. Any change in a network will involve an addition or removal of an edge. Then by these two principles, [4] relates the two groups of scenarios with edge changes as: a new edge produces a positive scenario, and the removal of an edge produces a negative scenario. This idea may work for the distance-based approach for Falkowski, but according to our trials on a similarity based approach; this is not always the case. The next section illustrates our algorithm, which handles the edge changes of a network.
5. DSCAN: Improvements to SCAN
Our study is based on the algorithm SCAN [2] and applies improvements to its density based detection. Our modifications to SCAN allow it to form communities without the user-defined threshold of epsilon and can update a dynamic network of timestamps. We propose the algorithm DSCAN (Dynamic SCAN), which can handle these dynamic networks.
SCAN’s threshold of ε, in the range of (0, 1), defines the minimum similarity between two adjacent nodes that must exist for the two nodes to be ε neighbors. This ε-neighborhood is what defines the community structure. Having to rely on user specifications for ε can decrease performance if an incorrect ε is used, and performing multiple runs with different epsilons is costly. In our research with testing various networks, we have discovered that possible good epsilons for any network fall in the range of (0.4, 0.8). An ε too low will produce few large communities, while a larger ε will result many small communities. For our study, to calculate the ε-neighborhood of a node, we perform a check ε the range (0.4, 0.8) and take an average of those results. This approach produces comparable results and alleviates the need to run multiple times to check all ε values. Xu et al. found a good value of μ to be 2, which is the value that we have also used.
Algorithm 1 illustrates the dynamic updating of a network with DSCAN. Given a sequence of timestamps of a network, perform SCAN on the first timestamp. Then for all consecutive timestamps, obtain the difference in edges between the two timestamps. The network is updated from the nodes of each edge change of the networks, illustrated in Method 1. This update on the network handles a node that either becomes a core or was a core and now no longer is. When a change in the network is detected and needs to be updated, an existing cluster id or a new cluster id is propagated through all structurally connected nodes to form a new community. Method 2 explains the propagation of an id through this new community. One final change to the network is when a node no longer belongs to the cluster. Method 3 shows how to handle these nodes and make them either a hub or an outlier.
|
Method 3: makeHubOrOutlier |
|
Input: Vertex v |
|
ids = ids of neighbors of v if ||ids|| > 1: make v a hub else: make v an outlier |
6. Genetic Algorithms Applied to Dynamic Networks
In addition to SCAN, we also researched the topic of genetic algorithms and their use with dynamic networks. Genetic algorithm (GA) is a technique that imitates the process of gene inheritance, mutation, selection, and crossover to optimize the solution to a problem. For the use of GA with community detection, the genes represent all individual nodes and their corresponding community. To find a gene that satisfies a good community structure of a network, the gene must maximize a given fitness function, such as modularity. In finding this maximized gene, a population is used consisting of multiple genes, each representing a different community structure. A user-defined number of iterations is performed over the population which mutates each gene into a cross between two or more genes that produce the highest values due to the fitness function. At the end of the iterations, the gene with the highest fitness function value it used as the final community structure. More on the use of genetic algorithms in networks can be read at [8] .
Genetic algorithms start with a random structure for each gene of the population, and from there slowly selects the best genes to mutate into fitter ones. For the use of genetic algorithms in dynamic networks, if only a small change to the network has occurred, then the previous community structure will produce a good value for the fitness function. The idea leads to needing fewer iterations over the population to find a good structure than is needed when starting with the beginning random population.
To make use of this idea of fewer iterations, we introduce a user-defined number of iterations, not for the total number of population mutations, but the number of consecutive iterations where no better gene is found. This parameter allows for a better termination of genetic algorithms, when there is a clear time in the iterations that no more genes could be discovered rather than terminating in the middle of a sequence of better genes being discovered.
We propose the algorithm GAD (Genetic Algorithm Dynamic) for the use of genetic algorithms with dynamic networks. GAD uses the previously found “best” gene of the previous timestamp as a gene in the population of the next. This results in the next timestamp starting with a gene in the population with a relatively good fitness. If this gene happens to still be the best gene for the current timestamp, then the genetic algorithm will not mutate the population an unnecessary amount of times.
7. Dynamic Network Datasets
In our measuring the performance of our algorithms, we experiment on three real world networks of varying size.
arXiv HEP-TH Physics Network. This high energy physics citation network contains up to 27,770 nodes and 352,807 edges. Each node corresponds to a particular paper in a database, and each edge represents a citation from one paper to another. The network’s data includes a period from January 1993 to April 2003 and the timestamp for each citation on when it was added to the database [9] . This information made it possible to create timestamps for the network’s change over time. We converted this information into 844 timestamps by what consecutive days the graph had changed.
MIT Social Evolution Call-SMS Network. This is a considerably smaller graph composed of up to 80 nodes and 273 edges. This network illustrates the mobile phone usage between undergraduate students in a dormitory. Mobile phone usage involves calls or SMS texts between students in the same dormitory. This growing network depicts the relationships and connections that establish from October 2008 until May 2009 [10] . Our timestamps for this network are by days that show new communication between two individuals.
MIT Friends and Family Network. This dataset was created to study the decision process of individuals in response to social interaction. We focused on the SMS network of this dataset, depicting the communication between individuals, similar to the Call-SMS network. The network consists of up to 80 nodes and 150 edges. We created timestamps in the same way as the Call-SMS network, by days that show a change in communication.
8. Results
We have proposed two algorithms to handle community detection in dynamic social networks, DSCAN and GAD. Both algorithms detect communities faster than their original static community detection counterparts with little to no decrease in overall modularity, which we used as our measure for evaluating the quality of the community detection of our algorithms. GAD shows a considerable increase in both speed and modularity over GA.
8.1. DSCAN on Dynamic Social Networks
Our algorithm DSCAN performs community detection on dynamic networks faster than SCAN, with little to no performance decrease. Our implementation of averaging over the range of 0.4 to 0.8 for a good epsilon value produces results very similar to the best epsilon value chosen from the same range on SCAN.
DSCAN is capable of updating a network in a more efficient manner than SCAN can on the whole network. This is done by recalculating the new community structure only in the areas of the network that showed a change in structure. In Figure 3, the runtime of the arXiv network is displayed between SCAN detecting the community structure on each timestamp versus DSCAN updating the network for each timestamp. It is clear that DSCAN can perform the update faster than SCAN does the whole network on most timestamps. The timestamps where DSCAN displays a longer runtime is related to the number of changes that occurred in that timestamp, as shown in Figure 4. A large number of changes causes DSCAN to update the whole network and not be restricted to a certain area. This demonstrates that DSCAN is best performed on smaller changes to increase runtime. On average, using a machine with a 2.7 GHz quad-core AMD processor with 32GB of memory, SCAN calculated all timestamps in 74 minutes and DSCAN ran in only 55 minutes. The other two networks were too small to see a significant increase in speed between the two algorithms.
Modularity is the most used measure in evaluating the quality of communities found by community detection algorithms. Modularity [11] is simply defined as:
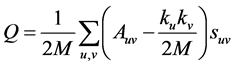
where A is the adjacency matrix of the network, ki is the degree of node i, and sij is 1 if nodes i and j have the same community membership, and 0 otherwise. Modularity is the standard for calculating the goodness of the community structure of a network, butmodularity performs best when all nodes are grouped into their idealcommunities. With SCAN, and DSCAN, not all nodes are members of a community. Hubs and outliers do not belong to any community, which decreases the modularity. With this idea, it is difficult to compare SCAN and DSCAN with other algorithms that do not incorporate the idea of hubs and outliers. Figure 5 shows the modularity of the communities for each timestamp of the arXiv network with SCAN, DSCAN, and the non-hub and outlier algorithm Infomap. From Figure 6, the number of hubs and outliers increases over time, decreasing the modularity shown in Figure 5. Figure 7 also gives some more information on the impact that the hubs and out-
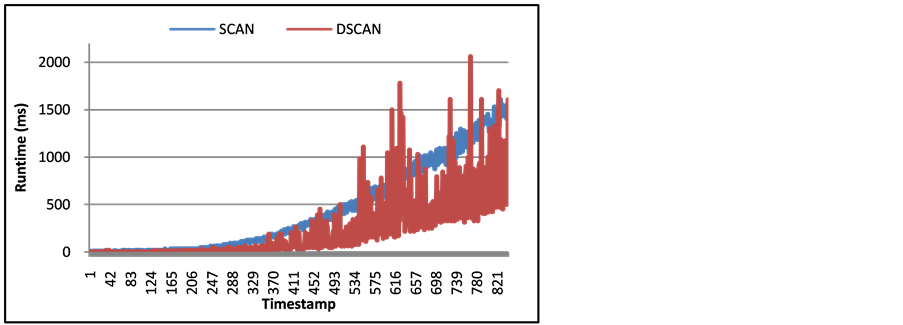
Figure 3. Runtime (ms) of SCAN and SCAND on arXiv Network for each timestamp.
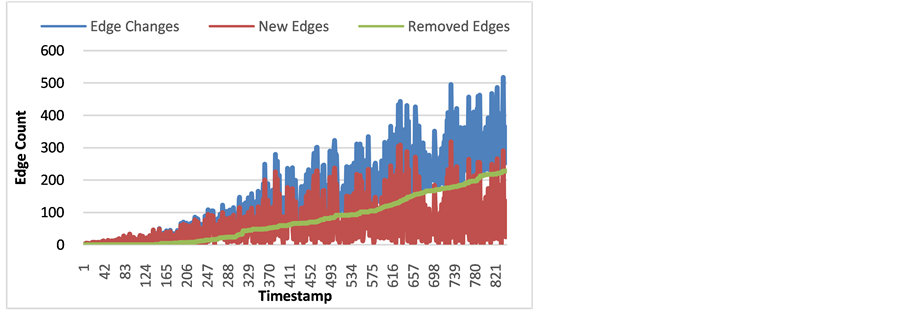
Figure 4. Number of New Edges (red), Removed Edges (green), and Edge changes in total (blue) of arVix Network for each timestamp.
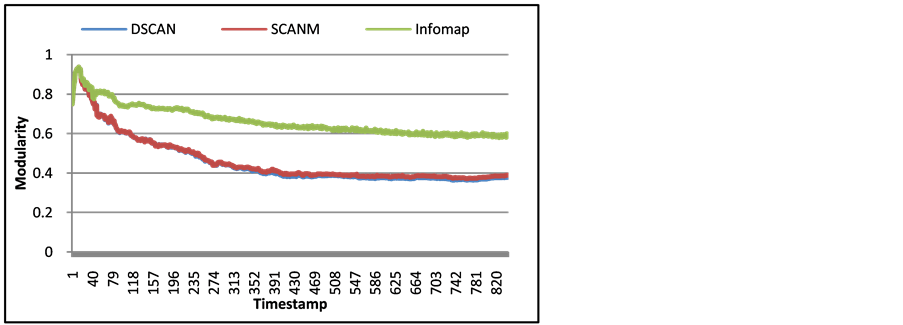
Figure 5. Modularity of arXiv Network for each timestamp with DSCAN, SCAN with multiple epsilon averaging (SCANM), and Infomap.
liers have on the arXiv network’s modularity. Since modularity is based upon the edges of a network, the more edges with nodes not in the same community, the lower modularity becomes. Figure 6 shows the average degree of hubs and outliers for each timestamp of arXiv. With this information, the number of edges that affect the value of modularity is the average degrees from Figure 7 times the number of hubs and outliers from Figure 6.
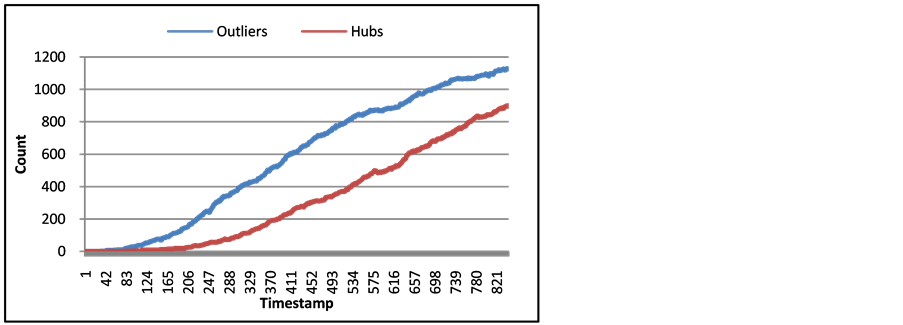
Figure 6. Number of outliers and hubs of arXiv Network for each timestamp.

Figure 7. Average Degree of outliers, hubs, and hub communities of arXiv Network for each timestamp.
This number is approaching 3000 edges near the final timestamps of arXiv.Comparing SCAN and DSCAN by themselves with modularity will still be an effective measure.
Our implementation of SCAN using an average of epsilon values performs almost exactly as the best epsilon value would from normal SCAN. Figure 8 and Figure 9 of the modularity on the SMS and Call-SMS networks respectively, show that SCAN with multiple epsilons performs nearly the same as SCAN with using the epsilon with the highest modularity. There are very insignificant fluctuations between the timestamps on both networks, which is acceptable compared to having to run SCAN multiple times to check which epsilon value is the best to use. Figure 5, Figure 8, and Figure 9 also show that DSCAN performs similarly to SCAN as well. The modularity of each timestamp is almost the same between SCAN, SCAN with multiple epsilon, and DSCAN.
We have shown that DSCAN performs community detection on dynamic networks almost similarly to what SCAN would produce by doing the entire network. This dynamic updating a community structure is an important concept when dealing with networks that grow to a large size.
8.2. GAD on Dynamic Social Networks
GAD produces a more stable runtime of genetic algorithms through each timestamp, while reducing the number of iterations needed to find a good final community membership. To run a comparison between GAD and normal genetic algorithms (GA), we ran GAD as normal over all timestamps and ran GA on each timestamp individually. Figure 10 and Figure 11 show the modularity of communities in the final timestamp compared between GA and GAD on the Call-SMS and SMS networks. As is seen from the figures, GAD produced stable results in

Figure 8. Modularity of SMS for each timestamp with DSCAN, SCAN using the best epsilon, and SCAN with multiple epsilon averaging (SCANM).
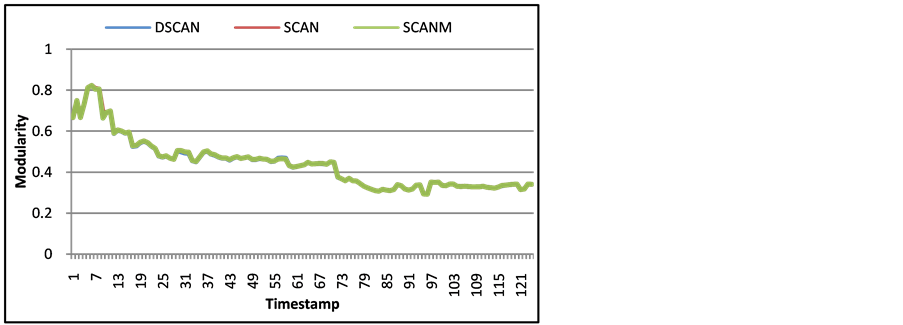
Figure 9. Modularity of Call-SMS for each timestamp with DSCAN, SCAN using the best epsilon, and SCAN with multiple epsilon averaging (SCANM).
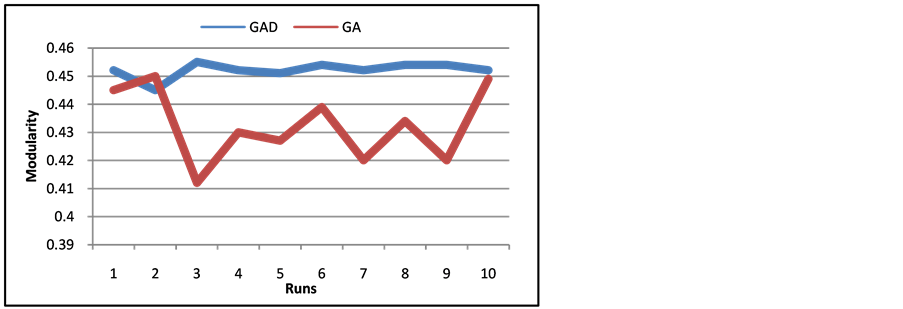
Figure 10. Modularity of SMS Network of ten runs of GA and GAD.
terms of modularity for every run. GA does not always produce a good community structure each time it runs, unless the number of iterations was increased more, increasing the runtime.
Figure 12 and Figure 13 show the runtime of GAD over all timestamps and the sum of GA runtimes of each timestamp on the Call-SMS and SMS networks. GAD decreases the iteration count of the Call-SMS network by

Figure 11. Modularity of Call-SMS Network of ten runs of GA and GAD.
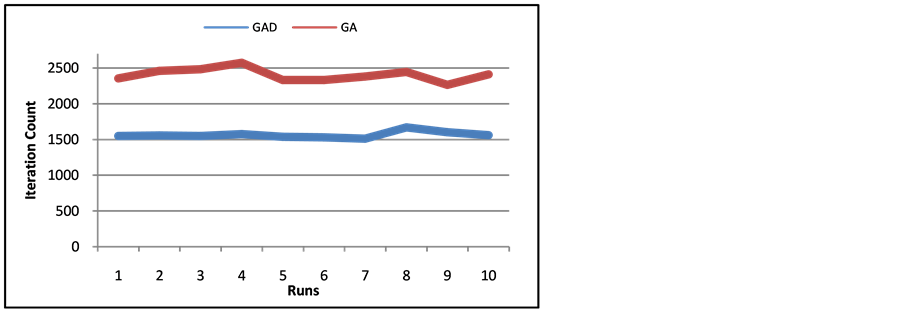
Figure 12. Number of Iterations of SMS Network of ten runs of GA and GAD.
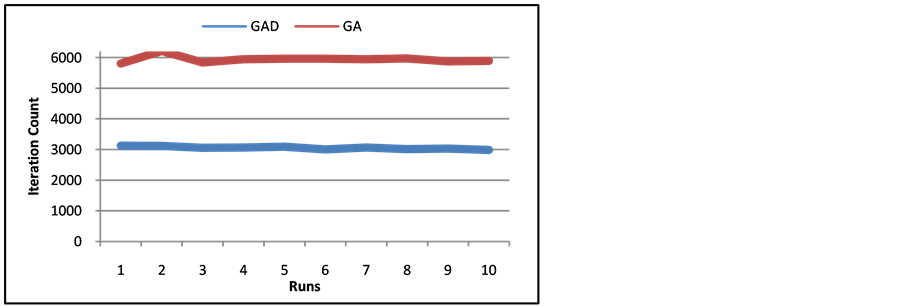
Figure 13. Number of Iterations of Call-SMS Network of ten runs of GA and GAD.
about 50% and the SMS network by about 35%. With the performance stability and the iteration decrease, it is clear that the techniques of GAD improve genetic algorithms tremendously for dynamic networks.
9. Conclusions
We have shown that DSCAN and GAD are faster in runtime and comparable, if not better, in modularity to their static community detection counterparts. This speed increase and low loss in modularity is ideal when large dynamic social networks are involved, which are constantly changing their structure. But as we have shown with our experiments on the arXiv network, the number of changes from one timestamp to another is a deciding factor in the runtime of a DSCAN. With this, it is feasible to run DSCAN after only a few changes have occurred in the network, keeping the community structure up to date more often.
Techniques like those shown in DSCAN and GAD,may possibly be used in other community detection algorithms for converting them to dynamic community detection algorithms. With the rapid increase in the size of social networks, it is costly and even infeasible to use static community detection techniques to analyze these networks. Community detection needs to start swaying to the side of dynamic network community detection to keep up with modern networks. This is an important area of future work in the field of community detection.
Acknowledgements
We thank Houghton College for its financial support. We also want to thank Dr. Xu for his SCAN algorithm code.
References
- Fortunato, S. (2010) Community Detection in Graphs. Physics Reports, 486, 75-174. http://dx.doi.org/10.1016/j.physrep.2009.11.002
- Xu, X., Yuruk, N., Feng, Z. and Schweiger, T. (2007) SCAN: A Structural Clustering Algorithm for Networks. KDD’07. ACM, 824-833. http://dx.doi.org/10.1145/1281192.1281280
- Ester, M., Kriegel, H.-P., Sander, J. and Xu, X. (1996) A Density-Based Algorithm for Discovering Communities in Large Spatial Databases with Noise. Proceedings of 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96).
- Falkowski, T. (2009) Community Analysis in Dynamic Social Networks. PhD. Otto-von-Guericke-University, Magdeburg.
- Ronhovde, R.K., Peter, R. and Nussinov, Z. (2013) An Edge Density Definition of Overlapping and Weighted Graph Communities. arXiv preprint arXiv:1301.3120.
- Raghavan, U.N., Albert, R. and Kumara, S. (2007) Near Linear Time Algorithm to Detect Community Structures in Large-Scale Networks. Physical Review E, 76, 036106. http://dx.doi.org/10.1103/PhysRevE.76.036106
- Xie, J., Szymanski, B.K. and Liu, X. (2011) SLPA: Uncovering Overlapping Communities in Social Networks via a Speaker-Listener Interaction Dynamic Process. Proc. ICDM Workshop, 344-349.
- Pizzuti, C. (2008) GA-Net: A Genetic Algorithm for Community Detection in Social Networks. PPSN, Volume 5199 of Lecture Notes in Computer Science, pages 1081-1090. Springer.
- Leskovec, J., Kleinberg, J. and Faloutsos, C. (2005) Graphs over Time: Densification Laws, Shrinking Diameters and Possible Explanations. ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD).
- Dong, W., Lepri, B. and Pentland, A.S. (2011) Modeling the Co-Evolution of Behaviors and Social Relationships Using Mobile Phone Data, Media, 134-143,
NOTES

*Corresponding author.


