Advances in Pure Mathematics
Vol.06 No.10(2016), Article ID:70894,18 pages
10.4236/apm.2016.610059
Locally Defined Operators and Locally Lipschitz Composition Operators in the Space 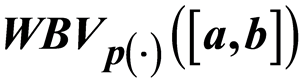
José Atilio Guerrero1, Odalis Mejía2, Nelson Merentes2
1Departamento de Matemática y Fsica, Universidad Nacional Experimental del Táchira, San Cristóbal, Venezuela
2Departamento de Matemática, Universidad Central de Venezuela, Caracas, Venezuela
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 14, 2016; Accepted: September 24, 2016; Published: September 27, 2016
ABSTRACT
We give a neccesary and sufficient condition on a function 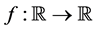 such that the composition operator (Nemytskij Operator) H defined by
such that the composition operator (Nemytskij Operator) H defined by 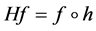 acts in the space
acts in the space 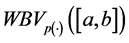 and satisfies a local Lipschitz condition. And, we prove that every locally defined operator mapping the space of continuous and bounded Wiener
and satisfies a local Lipschitz condition. And, we prove that every locally defined operator mapping the space of continuous and bounded Wiener 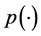 -variation with variable exponent functions into itself is a Nemytskij com- position operator.
-variation with variable exponent functions into itself is a Nemytskij com- position operator.
Keywords:
Generalized Variation, 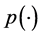 -Variation in Wiener’s Sense, Variable Exponent, Convergence, Helly’s Theorem, Local Operator
-Variation in Wiener’s Sense, Variable Exponent, Convergence, Helly’s Theorem, Local Operator

1. Introduction
This paper lies in the field of variable exponent function spaces, exactly we will deal with the space 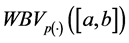 of bounded
of bounded 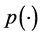 -variation in Wiener’s sense with vari- able exponent (see [1] , [2] ).
-variation in Wiener’s sense with vari- able exponent (see [1] , [2] ).
Variable exponent Lebesgue spaces appeared in the literature in 1931 in the paper by Orlicz [3] . He was interested in the study of function spaces that contain all measurable functions 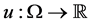 such that
such that

for some 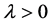 and
and 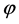 satisfying some natural assumptions, where
satisfying some natural assumptions, where 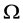 is an open set in
is an open set in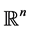 . This space is denotated by
. This space is denotated by 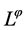 and it is now called Orlicz space. However, we point out that in [3] the case
and it is now called Orlicz space. However, we point out that in [3] the case 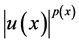 corresponding to variable exponents is not included. In the 1950’s, these problems were systematically studied by Nakano [4] , who developed the theory of modular function spaces. Nakano explicitly mentioned variable exponent Lebesgue spaces as an example of more general spaces he considered, see Nakano [4] p. 284. In 1991, Kováčik and Rákosník [5] established several basic properties of spaces
corresponding to variable exponents is not included. In the 1950’s, these problems were systematically studied by Nakano [4] , who developed the theory of modular function spaces. Nakano explicitly mentioned variable exponent Lebesgue spaces as an example of more general spaces he considered, see Nakano [4] p. 284. In 1991, Kováčik and Rákosník [5] established several basic properties of spaces  and
and 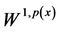 with variable exponents. Their results were extended by Fan and Zhao [6] in the framework of Sobolev spaces
with variable exponents. Their results were extended by Fan and Zhao [6] in the framework of Sobolev spaces
With the emergence of nonlinear problems in applied sciences, standard Lebesgue and Sobolev spaces demostrated their limitations in applications. The class of nonlinear problems with variable exponents growth is a new research field and it reflects a new kind of physical phenomena.
It is well known that the class of nonlinear operator equations of various types has many useful applications in describing numerous problems of the real world. A number of equations which include a given operators have arisen in many branches of science such as the theory of optimal control, economics, biological, mathematical physics and engineering. Among nonlinear operators, there is a distinguished class called composi- tion operators. Next we define such operators.
Definition 1.1. Given a function

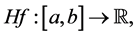

More generally, given 

This operator is also called superposition operator or susbtitution operator or Nemytskij operator. The operator in the form (1.1) is usually called the (autonomous) composition operator and the one defined by (1.2) is called non-autonomos.
A rich source of related questions are the excellent books by J. Appell and P. P. Zabrejko [7] and J. Appell, J. Banas, N. Merentes [8] .
E. P. Sobolevskij in 1984 [9] proved that the autonomous composition operator associate to 







In this paper, we obtained two main results. The organization of this paper is as follows. Section 2, we gather some notions and preliminary facts, and necessary back- ground about the class of functions of bounded 




2. Preliminaries
Throughout this paper, we use the following notation: Let a function 

meter of the image 




In 2013 R. Castillo, N. Merentes and H. Rafeiro [1] introduced the notion of bounded variation space in the Wiener sense with variable exponent on 
Definition 2.1 (See [1] ). Given a function



is called Wiener variation with variable exponent (or 






In case that





Definition 2.2. (Norm in


where 

Theorem 2.3 (See [1] ). Every sequence in 
In 2015, O. Mejía, N. Merentes and J. L. Sánchez [2] showed the following properties of elements of 
Lemma 2.4 (General properties of the 

(P1) minimality: if
(P2) monotonicity: if 




(P3) semi-additivity: if
(P4) change of a variable: if 

strictly) monotone function, then
(P5) regularity:
The following structural theorem is taken from [2] , this gives us a characterization of the members of
Theorem 2.5 (see [2] ). The map 







Given



Proposition 2.6. Suppose that 



Proof. Let 






Afterwards, we choose 






Then for these y, we have
Lemma 2.7. Let
Proof. Let 


Thus
Proposition 2.8. Let 


that is, the Luxemburg norm is lower semi-continuous on
Proof. Let 






By the pointwise convergence of 


for all 


therefore
hence
that is,
Passing the limit as 


semicontinuous, i.e.,
if 


Lemma 2.9 (Invariance Principle). Let 



Proof. The function 
is an affine homeomorphism with inverse the function 
such that: 


defines a 1-1 correspondence between all partitions 




3. Locally Lipschitz Composition Operators
In this section, we expose one of the main results of this paper. We demonstrate that a result of the Sobolevskij type is also valid in the space 

Theorem 3.1. Let 



Proof. First let us assume that 






The finiteness of 


Fix 






By the classical mean value theorem we find 


Now, by definition of I we have
Making a simple calculation
Since 

Again by the mean value theorem we find 





and
By definition of J we have
Again a simple calculation shows that
Since 

Summing up both partial sums and observing that 


which proves the assertion.
Conversely, suppose that H satisfies a Lipschitz condition. By assumption, the constant

is finite for each
This shows that h is locally Lipschitz, and so the derivative 





Given



creasing sequence of positive real numbers converging to 0; without loss of generality,
we may assume that 



Since the composition operator H associate to h acts in the space


Now, we show that the sequences 

in Wiener’s sense for all 






Then, 

obtain the estimates
Since the partition 
holds for every 


2.7, the definition of the function 

hence

which shows that the sequence 
Theorem 2.3 ensures the existence of a pointwise convergent subsequence of


verges pointwise on 

Now setting


we note that

for almost all







It remains to prove that 




where 
whenever the sequence 








4. Locally Defined Operators
In this section, we present our second main result, which is related to the notion of locally defined operator. We prove that every locally defined operator mapping the space of continuous and bounded 
Definition 4.1. Let 









holds true.
Remark 4.1. For some pairs 







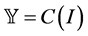





Definition 4.2. (See [13] ) An operator 
1) left-hand defined, if and only if for every 

2) right-hand defined, if and only if for every 

From now on, let

Theorem 4.3. (See [13] ) The operator 
The locally defined operators have been the subject of intensive research and many applications of then can be found in the literature (See, for instance [22] , [23] and the references therein).
Theorem 4.4. Let




Proof. We begin by showing that for every 


implies that
To this end choose arbitrary 


belongs to

and
Since






Hence




Since, for all
the condition (4.2) implies that
according to Definition 4.2, we get
Therefore, by the continuity of 


Suppose now that 





The sequence of functions
for all


and
for all
so

Similar reasoning shows, that

From (4.4) and (4.5), we obtain that 

Let us observe that

and for all

and for every 


Put
From (4.7), (4.8) and (4.9) the function 

and

To show that 





Take an arbitrary




therefore, by (4.10) and (4.12)
in the case when
in the case when


By the lower semicontinuity of 
and the convergence of series 

Thus there exist a function 

According to the first part of the proof, we have
Hence, by continuity of 



When 
To define the function



Of course


Since, by (4.13), for all functions f,
according to what has already been proved, we have

To prove the uniqueness of h, assume that 
for all 





which proves the uniqueness of h.
5. Conclusion
In this paper, we get two important results. In Theorem 3.1, we show that the result of the Sobolevkij type is valid for the space of functions of bounded 




Acknowledgements
This research has been partially supported by the Central Bank of Venezuela. We want to give thanks to the library staff of B.C.V for compiling the references. Also, we are grateful with the referees and editors for their comments and suggestions on this work.
Cite this paper
Guerrero, J.A., Mejía, O. and Merentes, N. (2016) Locally Defined Operators and Locally Lipschitz Composition Operators in the Space
References
- 1. Castillo, R., Merentes, N. and Rafeiro, H. (2014) Bounded Variation Spaces with p-Variable. Mediterranean Journal of Mathematics, 11, 1069-1079.
http://dx.doi.org/10.1007/s00009-013-0342-5 - 2. Mejía, O., Merentes, N. and Sánchez, J.L. (2015) The Space of Bounded -Variation in Wiener’s Sense with Variable Exponent. Journal Advances in Pure Mathematics, 5, 703-716.
http://dx.doi.org/10.4236/apm.2015.511064 - 3. Orlicz, W. (1931) über konjugierte exponentenfolgen. Studia Mathematica, 3, 200-211.
- 4. Nakano, H. (1950) Modulared Semi-Ordered Linear Spaces. Maruzen Co., Ltd., Tokyo.
- 5. Kovácik, O. and Rákosník, J. (1991) On Spaces and . Czechoslovak Mathematical Journal, 41, 592-618.
- 6. Fan, X., Zhao, Y. and Zhao, D. (2001) Compact Imbedding Theorems with Symmetry of Strauss-Lions Type for the Space . Journal of Mathematical Analysis and Applications, 255, 333-348.
http://dx.doi.org/10.1006/jmaa.2000.7266 - 7. Appell, J. and Zabreiko, P.P. (1990) Nonlinear Superposition Operators. Cambridge University Press, Cambridge.
- 8. Appell, J., Banas, J. and Merentes, N. (2014) Bounded Variation and Around. De Gruyter, Berlin, Boston.
- 9. Sovolevskij, E.P. (1984) The Superposition Operator in Hölder Spaces. (Russian). VINITI No. 3765-84, Voronezh.
- 10. Appell, J., Merentes, N. and Sánchez, J.L. (2011) Locally Lipschitz Composition Operator in Spaces of Functions Of bounded Variation. Annali di Matematica, 190, 33-43.
http://dx.doi.org/10.1007/s10231-010-0135-4 - 11. Merentes, N., Rivas, S. and Sánchez, J.L. (2012) Locally Lipschitz Composition Operator in Spaces of . Nonlinear Analysis Series A: Theory, Methods & Applications, 75, 1751-1757.
- 12. Mejía, O., Merentes, N. and Rzepka, B. (2014) Locally Lipschitz Composition Operator in Space of the Functions of Bounded -Variation. Journal of Function Spaces, 2014, 1-8.
- 13. Lichawski, K., Matkowski, J. and Mis, J. (1989) Locally Defined Operators in the Space of Differentiable Functions. Bulletin of the Polish Academy of Sciences—Mathematics, 37, 315-325.
- 14. Matkowski, J. and Wróbel, M. (2008) Locally Defined Operators in the Space of Whitney Differentiable Functions. Nonlinear Analysis: Theory, Methods & Applications, 68, 2933-2942.
- 15. Matkowski, J. and Wróbel, M. (2009) Representation Theorem for Locally Defined Operators in the Space of Whitney Differentiable Functions. Manuscripta Mathematica, 129, 437-448.
http://dx.doi.org/10.1007/s00229-009-0283-2 - 16. Wróbel, M. (2010) Locally Defined Operators and a Partial Solution of a Conjecture. Nonlinear Analysis: Theory, Methods & Applications, 72, 495-506.
- 17. Wróbel, M. (2011) Locally Defined Operators in the Hölder’s Spaces. Nonlinear Analysis: Theory, Methods & Applications, 74, 317-323.
- 18. Matkowski, J. and Wróbel, M. (2010) The Bounded Local Operators in the Banach Space of Höolder Functions. Vol. 15 of Scientific Issues, Mathematics, Jan Dlugosz University in Czestochowa.
- 19. Wrobel, M. (2010) Representation Theorem for Local Operators in the Space of Continuous and Monotone Functions. Journal of Mathematical Analysis and Applications, 372, 45-54.
http://dx.doi.org/10.1016/j.jmaa.2010.06.013 - 20. Wrobel, M. (2013) Locally Defined Operators in the Space of Functions of Bounded φ-Variation. Real Analysis Exchange, 38, 79-94.
- 21. Aziz, W., Guerrero, J.A., Maldonado, K. and Merentes, N. (2015) Locally Defined Operators in the Space of Functions of Bounded Riesz-Variation. Journal of Mathematics, 2015, 1-4.
http://dx.doi.org/10.1155/2015/925091 - 22. Azbelev, N.V. and Simonov, P.M. (2003) Stability of Differential Equation with Aftereffect. Taylor & Francis, New York.
- 23. Matkowski, J. (2010) Local Operators and a Characterization of the Volterra Operator. Annals of Functional Analysis, 1, 36-40.
http://dx.doi.org/10.15352/afa/1399900990










































































