Advances in Pure Mathematics
Vol.4 No.5(2014), Article ID:45966,6 pages DOI:10.4236/apm.2014.45029
Epimorphisms between Finite 4-Valued Modal Algebras
Aldo V. Figallo1, Elda Pick2, Susana Saad3
1Instituto de Ciencias Básicas, Universidad Nacional de San Juan, San Juan, Argentina
2Facultad de Ingeniería, Universidad Nacional de San Juan, San Juan, Argentina
3Instituto de Ciencias Básicas, Facultad de Filosofía, Universidad Nacional de San Juan, San Juan, Argentina
Email: avfigallo@gmail.com, epick@unsj.edu.ar, ssaad@unsj.edu.ar
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 19 December 2013; revised 19 January 2014; accepted 26 January 2014
Abstract
In this paper, we determine conditions for the existence of an epimorphism between two finite 4-valued modal algebras and state a method to obtain it. Furthermore, we obtain formulas which generalize those indicated by R. Sikorski for finite Boolean algebras [1] , and by M. Abad and A. V. Figallo for finite 3-valued  ukasiewicz algebras [2] .
ukasiewicz algebras [2] .
Keywords:Four Valued Modal Algebras, Tetravalent Modal Algebras, De Morgan Algebra, Epimorphisms, Automorphisms

1. Introduction
Tetravalent modal algebras were first considered by A. Monteiro and studied mainly by I. Loureiro, A. V. Figallo, A. Ziliani and P. Landini (see [3] -[10] ). Later, in 2000, J. M. Font and M. Rius [11] showed their interest in the logics originated by the lattice aspects of these algebras. Following A. V. Figallo’s terminology, we call them four-valued modal algebras (or 4-valued modal algebras). In addition, the interesting 2013 work by M. Coniglio and M. Figallo (see [12] ) has given, in our opinion, a new impulse to the profound study and development of the tetravalent modal algebras. For further information the reader interested in this subject is referred to the bibliography recommended below.
Let us now recall that An algebra 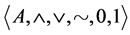 of type
of type 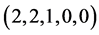 is a De Morgan algebra [13] if
is a De Morgan algebra [13] if 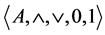 is a bounded distributive lattice with least element 0, greatest element 1, and
is a bounded distributive lattice with least element 0, greatest element 1, and 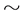 satifies the equations
satifies the equations  and
and  .
.
It is known that a finite De Morgan algebra  is determined by its determinant system
is determined by its determinant system , where
, where 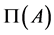 is the ordered set of all prime elements of
is the ordered set of all prime elements of  and
and 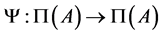 is an antitone involution of
is an antitone involution of
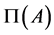 . Thus,
. Thus, 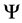 has the following properties:
has the following properties:
(i)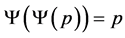 , for each
, for each (ii) if
(ii) if 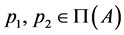 and
and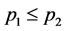 , then
, then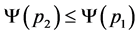 .
.
Moreover, the operation  is given in the following way:
is given in the following way:
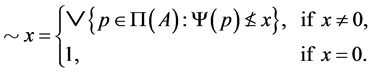
In 1978 A. Monteiro defined the 4-valued modal algebras (or 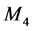 -algebras) as algebras
-algebras) as algebras 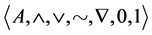 of type
of type , where
, where 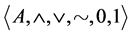 is a De Morgan algebra and the properties
is a De Morgan algebra and the properties
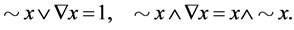
are verified.
We assume the reader to be familiar with the theory of  -algebras as it is given in [3] [4] . In particular, in [4] is the demonstration of the following properties, which are used in this paper:
-algebras as it is given in [3] [4] . In particular, in [4] is the demonstration of the following properties, which are used in this paper:

If the operator 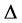 is defined by the formula
is defined by the formula , then it is easy to see that
, then it is easy to see that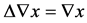 .
.
In what follows, we only consider finite 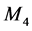 -algebras.
-algebras.
From [13] me have that the determinant system 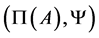 of an
of an 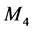 -algebra
-algebra 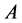 has connected components of the three following types:
has connected components of the three following types:



The ordered set 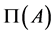 has the following diagram:
has the following diagram:

We will denote by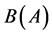 ,
, 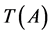 , and
, and 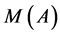 the ordered sets
the ordered sets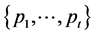 ,
, 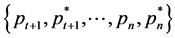 ,
, 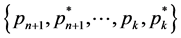 , respectively.
, respectively.
Frequently we will write 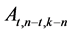 instead of
instead of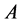 .
.
On the other hand, the operator 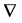 is given by the formula
is given by the formula
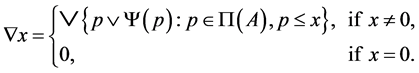
Then,

2. M4-Epimorphisms and M4-Functions
We will denote the sets 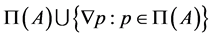 and
and 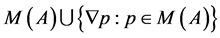 by
by  and
and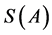 , respectively.
, respectively.
The lemma given below will be used in the proof of Lemma 2.5 Lemma 2.1 If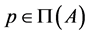 , then either
, then either  or
or 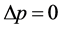
Proof. If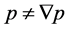 , then
, then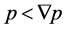 , so
, so 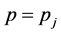 with
with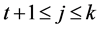 . Then,
. Then,
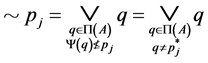 ,
,
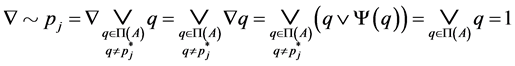 .
.
Thus, 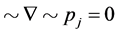 , that is
, that is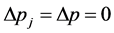 . In what follows, we will denote with
. In what follows, we will denote with 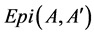 the set of all
the set of all  -epimorphisms from the
-epimorphisms from the  -algebra
-algebra 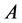 into the
into the  -algebra
-algebra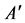 .
.
Definition 2.1 A mapping 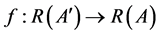 is called an
is called an  -function if and only if the following conditions are satisfied:
-function if and only if the following conditions are satisfied:
(M1)  is one to one(M2)
is one to one(M2) 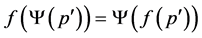 for all
for all 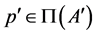 and
and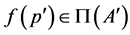 (M3)
(M3) 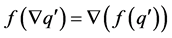 for all
for all .
.
We will denote by  the set of all
the set of all 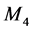 -functions from
-functions from 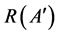 into
into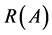 .
.
Lemma 2.2 If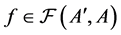 ,
, 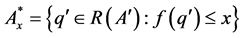 and
and , then:
, then:
(i)  is an isotone map,
is an isotone map,
(ii)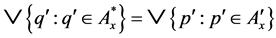 .
.
Proof.
(i) If  and
and , then
, then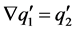 . Thus,
. Thus,  , and by (M1) we obtain
, and by (M1) we obtain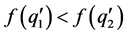 .
.
(ii) Let ,
, 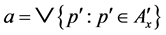 ,
, 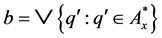 ,
, . It is easy to see that
. It is easy to see that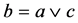 . We shall show that
. We shall show that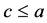 . Indeed, if
. Indeed, if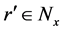 , then there exists
, then there exists 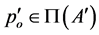 such that
such that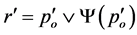 . Hence,
. Hence,  and
and . Since
. Since , we obtain
, we obtain 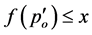 and
and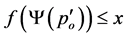 , with
, with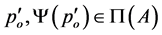 , that is
, that is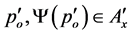 . Hence,
. Hence,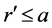 ; thus,
; thus,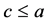 . Finally,
. Finally,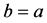 .
.
Definition 2.2 Let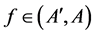 .
. 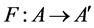 is an
is an 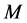 -function associated with
-function associated with  if and only if
if and only if 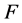 is defined by:
is defined by:
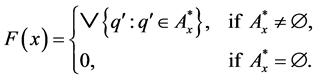
We denote by  the set of all
the set of all 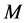 -functions.
-functions.
The following lemma is used to prove that every  -function is an epimorphism.
-function is an epimorphism.
Lemma 2.3
(I) If 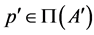 and
and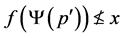 , then
, then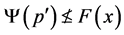 .
.
(II) If , then
, then 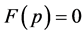 or
or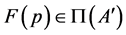 .
.
(III)If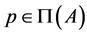 , then
, then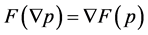 .
.
Proof.
(I) Assume that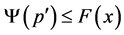 . Since
. Since  and
and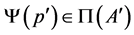 , it follows that there exists
, it follows that there exists , such that
, such that . From this we obtain
. From this we obtain ; as a consequence,
; as a consequence,  , which contradicts the hypothesis.
, which contradicts the hypothesis.
(II) Suppose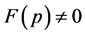 . There are two possibilities for
. There are two possibilities for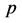 :
:
(a)  is minimal in
is minimal in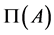 . As
. As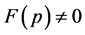 ,
,  , then there exists
, then there exists 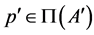 such that
such that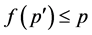 . Since
. Since 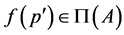 and
and 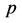 is minimal, then
is minimal, then 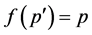 must hold, and from (M1),
must hold, and from (M1),  results. Thus,
results. Thus, 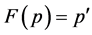 with
with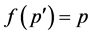 .
.
(b) 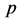 is maximal and not minimal in
is maximal and not minimal in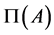 . Then,
. Then, 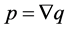 with
with  and
and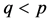 . From
. From  there exists
there exists 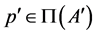 such that
such that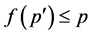 . If
. If  we get
we get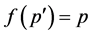 , and then
, and then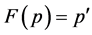 . If
. If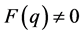 , as in (a), there exists a unique
, as in (a), there exists a unique 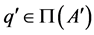 such that
such that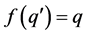 . Moreover, (i)
. Moreover, (i)  because if
because if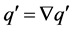 , then
, then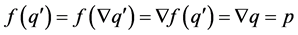 , which is not possible. Consequently, (ii)
, which is not possible. Consequently, (ii)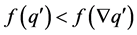 .
.
From (i) it follows that  is Type II or Type III; in the latter case
is Type II or Type III; in the latter case 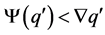 and therefore
and therefore
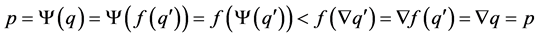 , which is not possible. Then,
, which is not possible. Then, 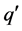 is Type II, so that
is Type II, so that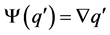 , then
, then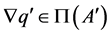 , and thus (iii)
, and thus (iii) . From (ii) and (iii) it results
. From (ii) and (iii) it results . Therefore,
. Therefore, 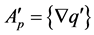 , so
, so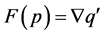 .
.
(III) Let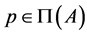 .
.
(a) If , then from (II)
, then from (II) , with
, with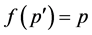 . Thus,
. Thus, ; then,
; then,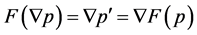 .
.
(b) If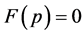 , then
, then . There are two cases:
. There are two cases:
(b1)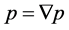 . Then,
. Then,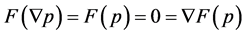 .
.
(b2)  and
and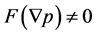 , then:
, then:
(b21) if , then
, then 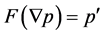 with
with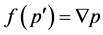 , and
, and ; therefore, by (M1)
; therefore, by (M1)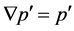 . Moreover, it is clear that
. Moreover, it is clear that 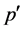 is a minimal prime, because if
is a minimal prime, because if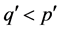 , then
, then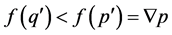 , which is not possible. Then,
, which is not possible. Then, 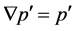 is minimal, and as a consequence,
is minimal, and as a consequence,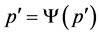 . Thus,
. Thus,  , which is a contradiction. Then,
, which is a contradiction. Then, 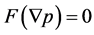 holds; therefore,
holds; therefore, 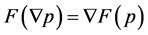
(b22) if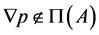 , then
, then 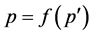 is Type III; therefore,
is Type III; therefore, 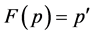 and
and 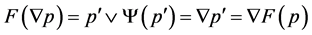 .
.
Lemma 2.4 If , then
, then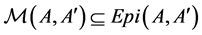 .
.
Proof. Let 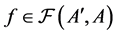 and
and 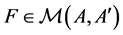 be the
be the 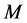 -function associated by
-function associated by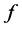 .
.
(a) It is obvious that 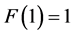 and
and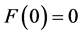 .
.
(b) . Actually, it is easy to see that
. Actually, it is easy to see that ; moreover,
; moreover,  if and only if
if and only if . Since
. Since ,
,  or
or  must hold; hence,
must hold; hence,  or
or , that is
, that is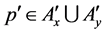 ; then
; then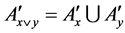 . Finally,
. Finally,
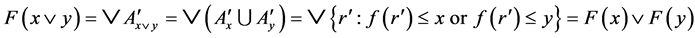 .
.
(c)  for all
for all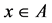 . Indeed,
. Indeed,
(c1)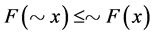 .
.
It is sufficient to show that, if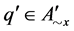 , then
, then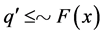 .
.
If , then
, then 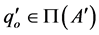 and
and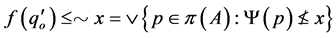 . Hence, there exists
. Hence, there exists 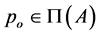 such that
such that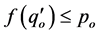 , and
, and . Then,
. Then, 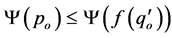 holds. Taking into account that
holds. Taking into account that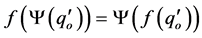 , by Lemma 2.3(I), we have that
, by Lemma 2.3(I), we have that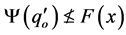 ; then
; then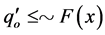 .
.
(c2)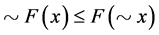 .
.
Let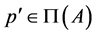 . The proof is a consequence of the fact that the following conditions are pairwise equivalent:
. The proof is a consequence of the fact that the following conditions are pairwise equivalent:
(1)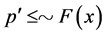 (2)
(2)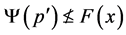 (3)
(3) 
(4) (5)
(5) (6)
(6) 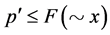
(d)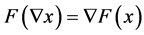 , for all
, for all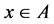 , which is inmediate consequence of (III),
, which is inmediate consequence of (III), 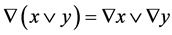 and (b).
and (b).
(e) 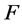 is clearly onto.
is clearly onto.
Lemmas 2.5 and 2.6 are necessary to show that all 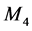 -epimorphisms are an
-epimorphisms are an 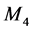 -function M.
-function M.
Lemma 2.5 If 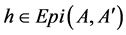 and
and , then there exists a unique
, then there exists a unique 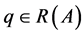 such that
such that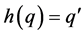 .
.
Proof.
(1) (a) If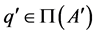 , then there is
, then there is  such that
such that 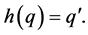 Indeed, let
Indeed, let ; since
; since 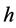 is onto, there exists
is onto, there exists  such that
such that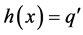 ; therefore
; therefore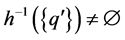 , and then,
, and then,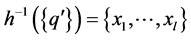 . If
. If , then,
, then,  and
and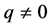 . If
. If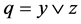 , then
, then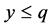 ,
, 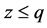 and
and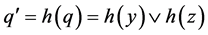 ; since
; since
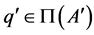 ,
, 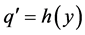 or
or 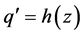 must hold. If
must hold. If , then
, then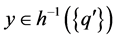 ; therefore
; therefore 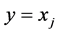 for some
for some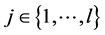 ; hence,
; hence,  and so
and so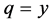 . Then
. Then 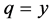 or
or . Thus,
. Thus, .
.
(b) If 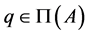 and
and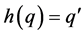 , then
, then  is unique. Indeed, if
is unique. Indeed, if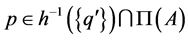 , then
, then 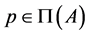 and
and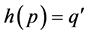 . Accordlingly,
. Accordlingly, 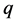 is the smallest
is the smallest 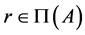 such that
such that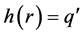 ,
, . If
. If , then
, then ; by Lemma 2.1,
; by Lemma 2.1, 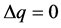 must hold. Furthermore,
must hold. Furthermore,  , and then
, and then 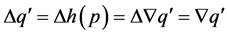 . On the other hand,
. On the other hand, 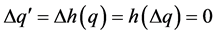 , which is a contradiction.
, which is a contradiction.
(2) If , then there is
, then there is 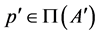 such that
such that ; by 1. there is a unique
; by 1. there is a unique  such that
such that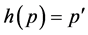 . Let
. Let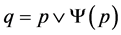 ; it is easy to prove that
; it is easy to prove that 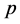 and
and 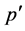 are of the same type. So
are of the same type. So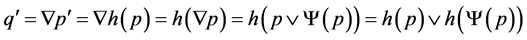 .
.
In addition, the following holds: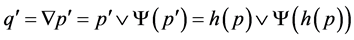 , giving the result that follows:
, giving the result that follows:
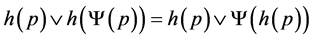 (i)
(i)
Moreover, ;
; ; then
; then
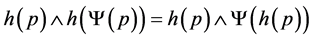 (ii)
(ii)
From (i) and (ii), it follows that . It is evident that
. It is evident that  is unique and
is unique and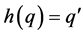 .
.
Definition 2.3 Let . The function
. The function 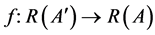 is induced by
is induced by 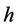 if
if 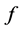 is defined by
is defined by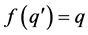 , if and only if
, if and only if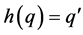 .
.
Lemma 2.6 Every function induced by an 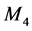 -epimorphism is an
-epimorphism is an 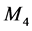 -function.
-function.
Proof. 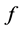 be the function induced by the
be the function induced by the 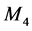 -epimorphism
-epimorphism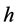 .
.
(M1) It is easy to prove that  is one to one.
is one to one.
(M3) Let , with
, with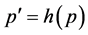 . Therefore,
. Therefore,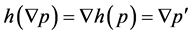 ; consequently,
; consequently,  , i.e.
, i.e.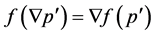 .
.
As a consequence of (M1) and (M3), 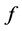 is an order-preserving function.
is an order-preserving function.
(M2) Let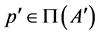 ,
, 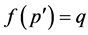 with
with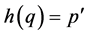 .
.
(1) If 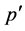 is Type I, then
is Type I, then , and
, and
(a) if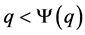 , since
, since 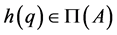 and
and 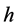 is one to one on the set of all prime
is one to one on the set of all prime  that
that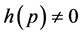 ,
, 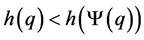 must hold; then
must hold; then , which is a contradiction.
, which is a contradiction.
(b) if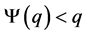 , then
, then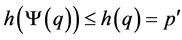 . If
. If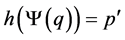 , then
, then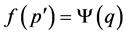 ; since f es one to one must be
; since f es one to one must be , which is a contradiction. So
, which is a contradiction. So 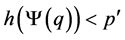 and consequently
and consequently 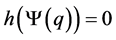 and then
and then , which is not possible.
, which is not possible.
This shows that in this case 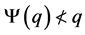 and
and ; as a result
; as a result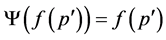 , so that either
, so that either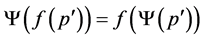 , or
, or 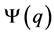 and
and 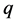 are not comparable, which is not possible since
are not comparable, which is not possible since 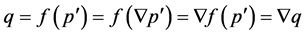 .
.
(2) If 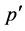 is Type II, then either
is Type II, then either  or
or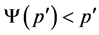 . In the first case
. In the first case  and therefore
and therefore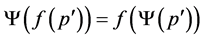 . A similar argument is valid if
. A similar argument is valid if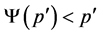 .
.
(3) If  is Type III, then
is Type III, then 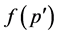 is Type III, and it is not comparable with
is Type III, and it is not comparable with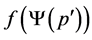 ; consequently,
; consequently,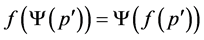 .
.
Lemma 2.7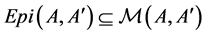 .
.
Proof. If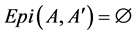 , the proof is obvious. Let
, the proof is obvious. Let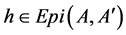 ,
,  the function induced by
the function induced by , and
, and 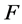 the
the 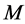 -function associated to
-function associated to . It is clear that
. It is clear that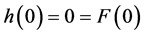 . Let
. Let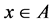 ,
, . Then,
. Then, 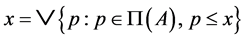 and consequently,
and consequently,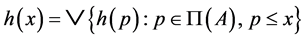 . For each
. For each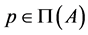 ,
,  , let
, let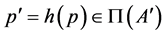 . Then
. Then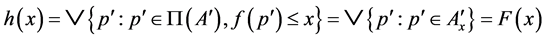 . Thus,
. Thus,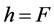 ; as a consequence,
; as a consequence, . Teorema 2.1
. Teorema 2.1 .
.
Proof. It follows from Lemmas 2.4 and 2.7. Teorema 2.2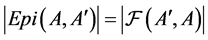 .
.
Remarks 2.1 Let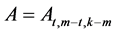 ,
,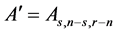 . Then(i)
. Then(i)  if only if
if only if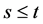 ,
,  , and
, and .
.
(ii) The following holds

where 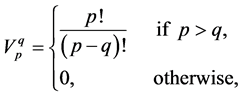
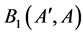 is the set of all injective functions
is the set of all injective functions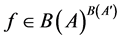 ,
, 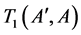 is the set of all injective functions
is the set of all injective functions
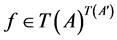 such that
such that 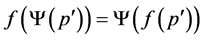 for each
for each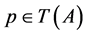 ,
, 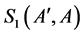 is the set of all injective functions
is the set of all injective functions 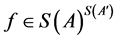 such that
such that 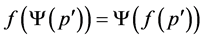 for all
for all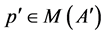 , and
, and 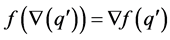 for all
for all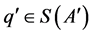 .
.
Teorema 2.3 If ,
, 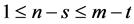 , and
, and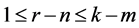 , then
, then

Proof. If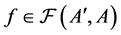 ,
, 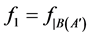 ,
, 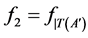 and
and , then the map
, then the map 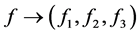 is a bijective correspondence between
is a bijective correspondence between  and
and . From this, Theorem 2.1 and Remarks 2.1 this theorem follows.
. From this, Theorem 2.1 and Remarks 2.1 this theorem follows.
An immediate consequence of theorem 2.3 is
Teorema 2.4 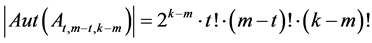
,
References
- Sikorski, R. (1949) On the Inducing of Homomorphisms by Mappings. Fundamenta Mathematicae, 36, 7-22.
- Abad, M. and Figallo, A.V. (1992) On the Lukasiewicz homomorphisms. Instituto de Ciencias Básicas, UNSJ, 1-12.
- Loureiro, I. (1982) Axiomatisation et proprietes des algèbres modales tetravalentes. C.R. Acad. Sc. Paris, t. 295, Serie I, 555-557.
- Loureiro, I. (1984) Finite Tetravalent Modal Algebras. Revista de la Unión Matemática Argentina, 31, 187-191.
- Loureiro, I. (1983) Prime Spectrum of a Tetravalent Modal Algebras. Notre Dame Journal of Formal Logic, 24, 389- 394. http://dx.doi.org/10.1305/ndjfl/1093870382
- Figallo, A.V. (1990) Notes on Generalized N-Lattices. Revista de la Unión Matemática Argentina, 35, 61-65.
- Figallo, A.V. (1992) On the Congruence in Four-Valued Modal Algebras. Portugaliae Mathematica, 49, 249-261.
- Figallo, A.V. and Ziliani, A. (1991) Symmetric Tetra-Valued Modal Algebras. Notas de la Sociedad Matemática de Chile, 10, 133-141.
- Ziliani, A. (1995) On Axioms and Properties of Monadic Four-Valued Algebras. Actas del Tercer Congreso Dr. A.R.R. Monteiro, Instituto de Matemática, U. N. del Sur, Argentina, 69-78.
- Figallo A.V. and Landini, P. (1995) On Generalized I-Algebras and Modal 4-Valued Algebras. Reports on Mathematical Logic, 29, 3-18.
- Font, J.M. and Rius, M. (2000) An Abstract Algebraic Logic Approach to Tetravalent Modal Logics. Journal of Symbolic Logic, 65, 481-518. http://dx.doi.org/10.2307/2586552
- Coniglio, M.E. and Figallo, M. (2013) Hilbert-Style Presentations of Two Logics Associated to Tetravalent Modal Algebras. Studia Logica, 102, 525-539. http://dx.doi.org/10.1007/s11225-013-9489-0
- Monteiro, A. (1960) Matrices de Morgan Caracteristiques Pour le Calcul Propositionnel Classique. Anais da Academia Brasileira de Ciências, 52, 1-7.
AMS 2000 Subject Classification
Primary 08A35, 06D30. Secondary 03G25.

