ABSTRACT

This paper deals with spaces such that their compactification is a resolvable space. A characterization of space such that its one point compactification (resp. Wallman compactification) is a resolvable space is given.

1. Introduction

In 1943, Hewitt [1] has introduced the notion of resolvable space as follows: A topological space is said to be resolvable if it has two disjoint dense subsets. Hence a topological space X is resolvable if and only if X is written as a union of two disjoint dense subsets. Hewitt in [1] has also called a topological space X maximally irresolvable if each dense subset of X is open. Nowadays, maximally irresolvable spaces are called submaximal spaces.

Recently, Belaid et al. [2], were interested in spaces such that their compactifications are submaximal. They proved that if X is a topological space and 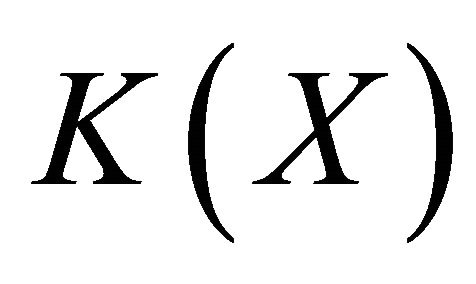is a compactification of X, then the following statements are equivalent:

1) 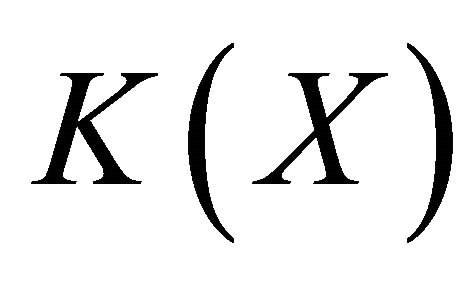is submaximal.

2) For each dense subset D of X, the following properties hold:

a) D is co-finite in K(X);

b) for each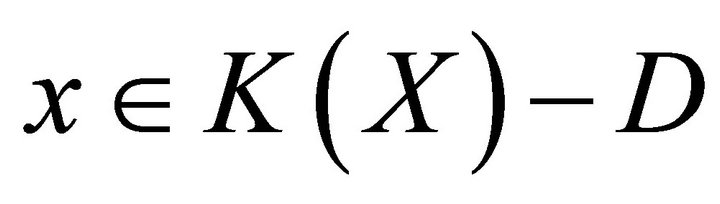, is closed.

It is clear that a compactification of resolvable spaces is resolvable. Hence the following question is natural:

“Characterize spaces X such that a compactification of X is a resolvable space?”

The first section is devoted to a brief study of spaces X such that their compactification is a resolvable space. The particular case of the one-point compactification is given.

The purpose of the second section is to give an intrinsic topological characterization of spaces X such that the Wallman compactification 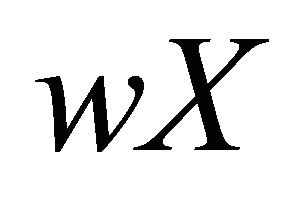of X is a resolvable space.

2. Resolvable Space and Compactifications

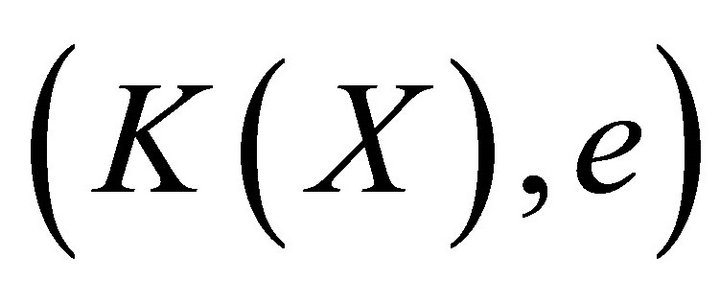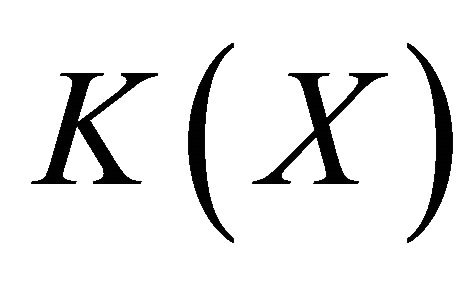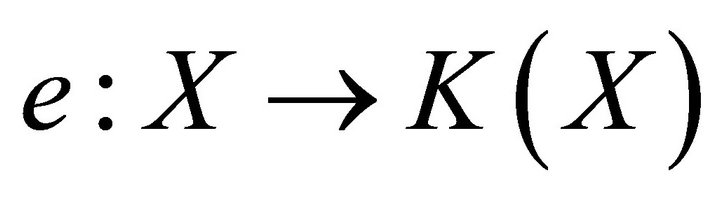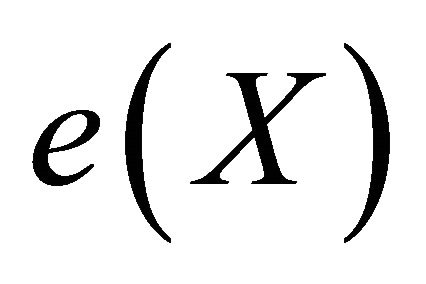First, recall that a compactification of a topological space X is a couple, where is a compact space and is a continuous embedding (e is a continuous one-to-one map and induces a homeomorphism from X onto) such that is a dense subspace of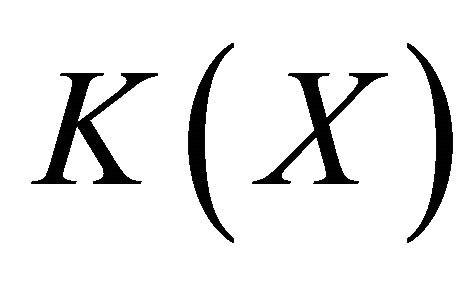. When a compactification

of 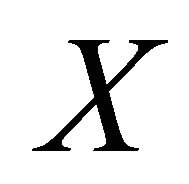is given, 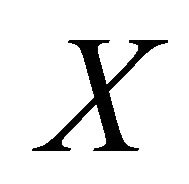will be identified with 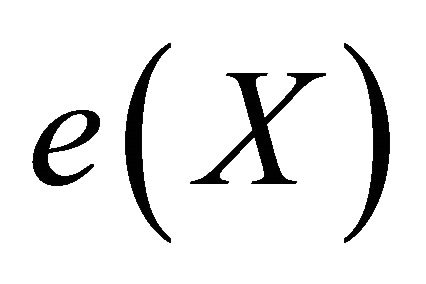and assumed to be dense in.

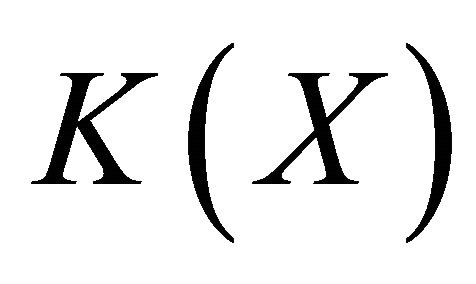Let us give some basic facts about space such that its compactification is a resolvable space.

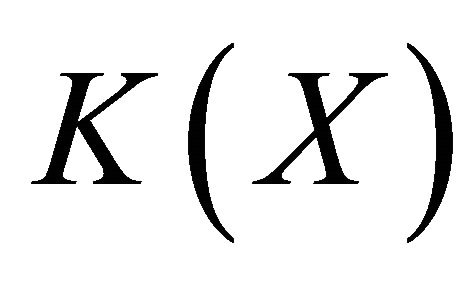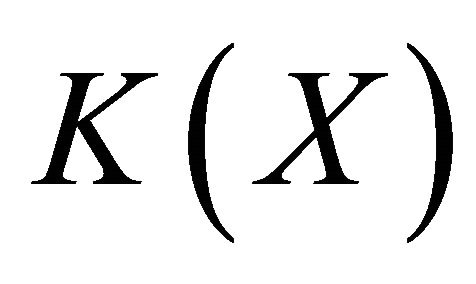Lemma 2.1 Let X be a topological space, be a compactification of X and be a subset of. If X is an open set of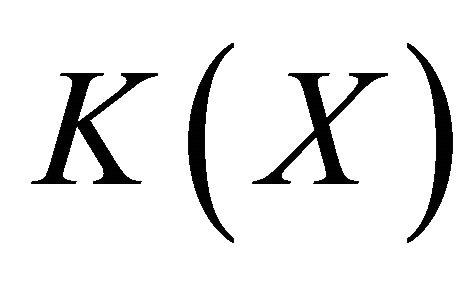, then the following statements are equivalent:

1) A is a dense subset of;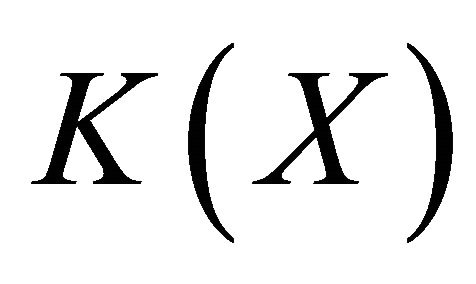

2) 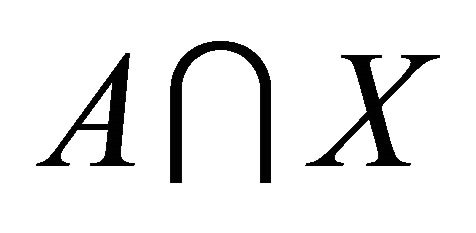is a dense subset of.

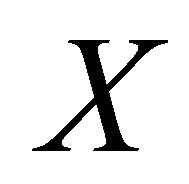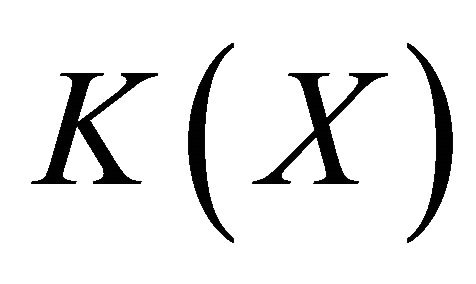Proof. 1) 2) Let be an open set of. Since is an open set of, is an open set of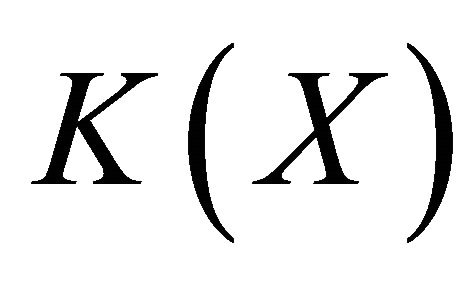. Hence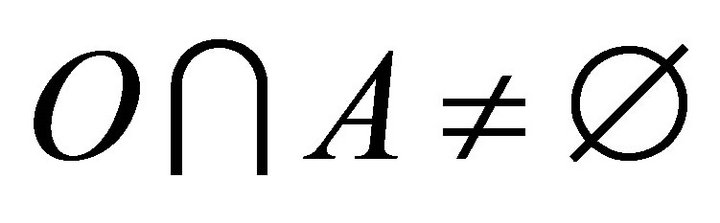. Thus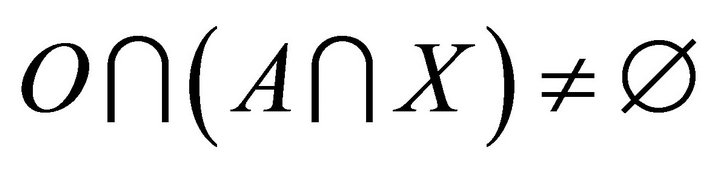; so that 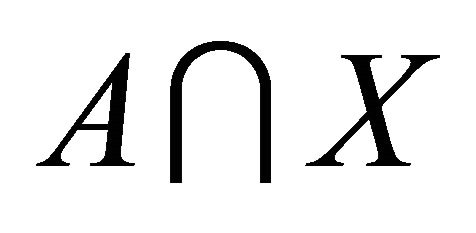is a dense set of.

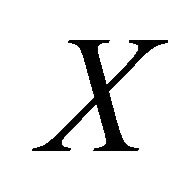2) 1) Let be an open set of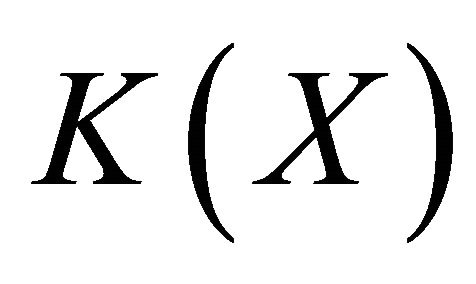. Since 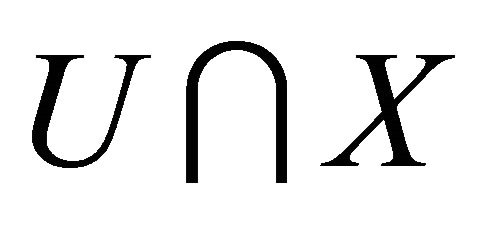is a non-empty open set of,

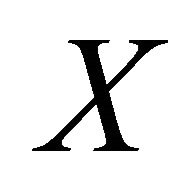. Then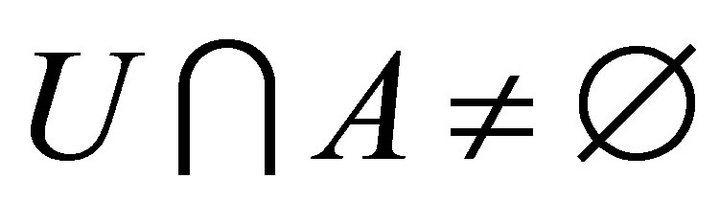. Therefore is a dense set of.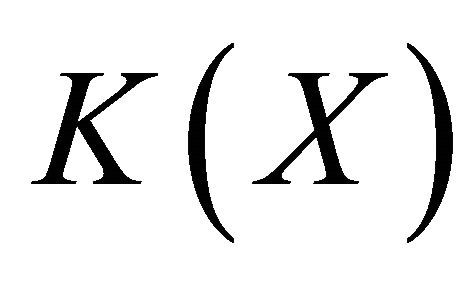

An immediate consequence of Lemma 1.1 is the following.

Proposition 2.2 Let X be a topological space and 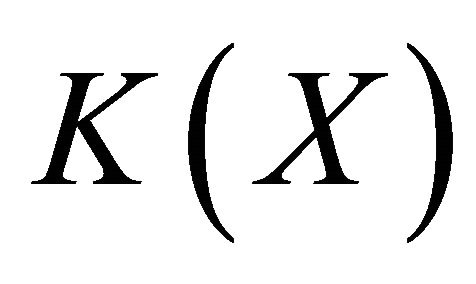be a compactification of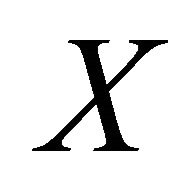. If X is an open set of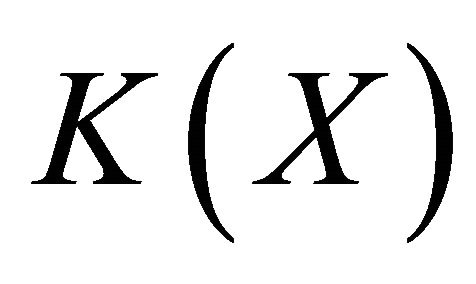, then the following statements are equivalent:

1) 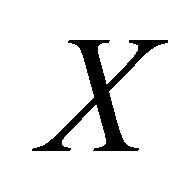is resolvable;

2) is resolvable.

Let us recall the construction of the one-point compactification: For any non-compact space X the one-point compactification of is obtained by adding one extra point (called a point at infinity) and defining the open sets of 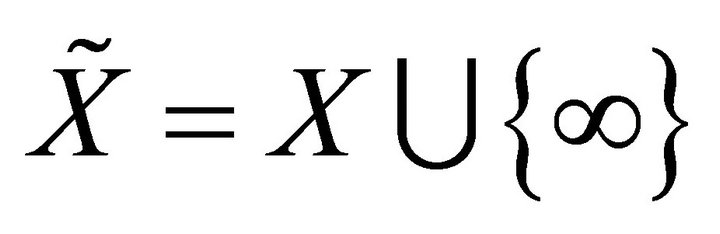to be the open sets of X together with the sets of the form, where is an open set of X such that 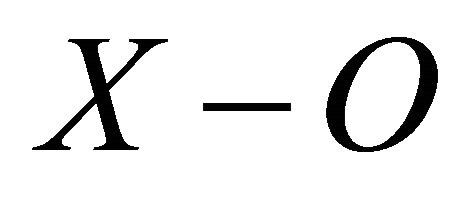is a closed compact set of X. The one point compactification 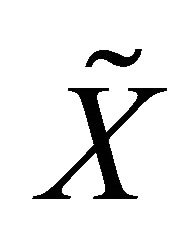of X is also called the Alexandroff compactification of X [3].

The following result characterizes space such that its one point compactification is a resolvable space. Its proof follows immediately from Proposition 2.2; thus it is omitted.

Proposition 2.3 Let X be a non-compact topological space. Then the following statements are equivalent:

1) The one-point compactification 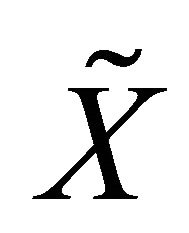of is resolvable;

2) is resolvable.

3. Resolvable Space and Wallman Compactification

First, recall that the Wallman compactification of 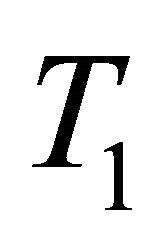- space was introduced, in 1938, by Wallman [4] as follows:

Let 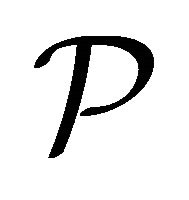be a class of subsets of a topological space 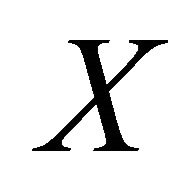which is closed under finite intersections and finite unions.

A 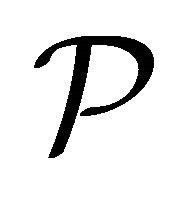-filter on 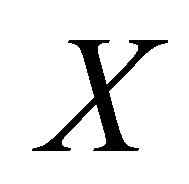is a collection 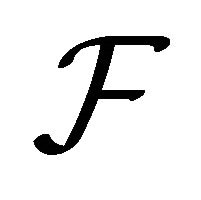of nonempty elements of 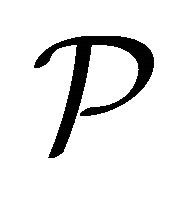with the properties:

1) is closed under finite intersections;

2) 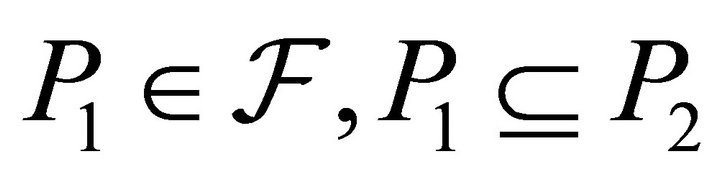implies.

A 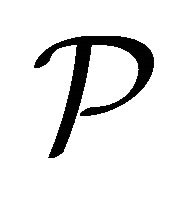-ultrafilter is a maximal 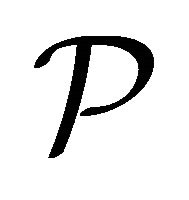-filter. When 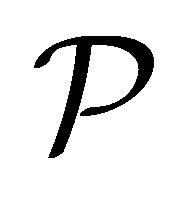is the class of closed sets of X, then the -filters are called closed filters.

The points of the Wallman compactification 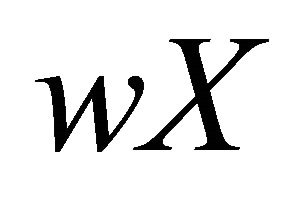of a space 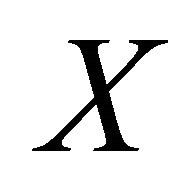are the closed ultrafilters on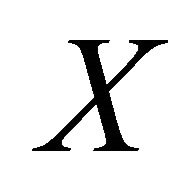. For each closed set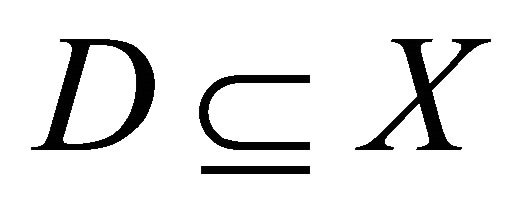, define to be the set

. Thus

is a base for the closed sets of a topology on.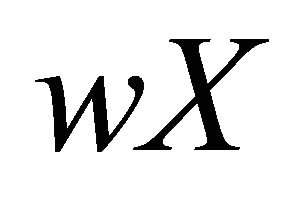

Let 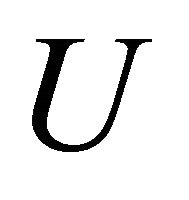be an open set of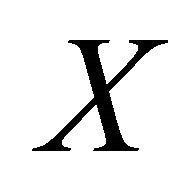, we define

, it is easily seen that the class is a base for open sets of the topology of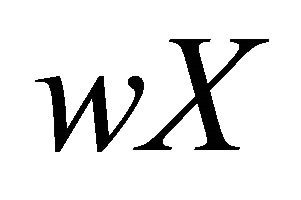. The following properties of 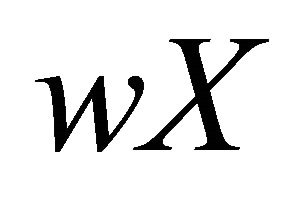are frequently useful:

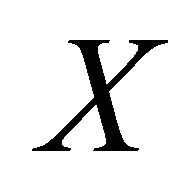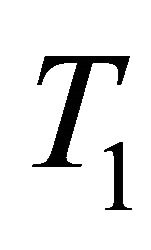Proposition 3.1 Let be a -space and the Wallman compactification of. Then the following statements hold:

1) is a -space;

2) For 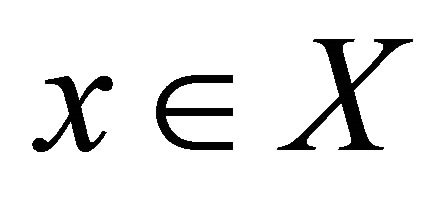and

. Then is an embedding of X into 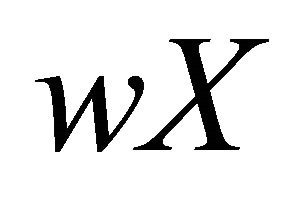(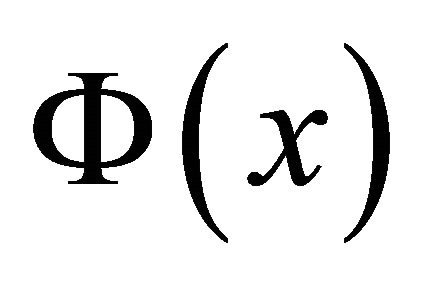will be identified to).

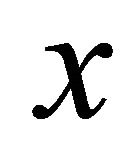3) If 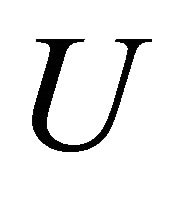is an open set of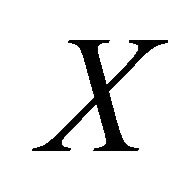, then

.

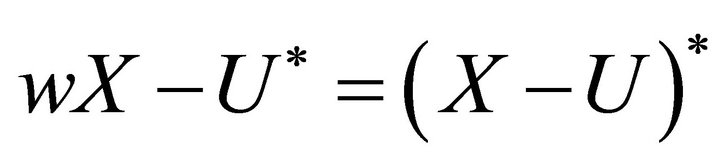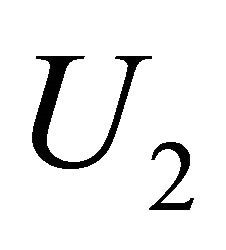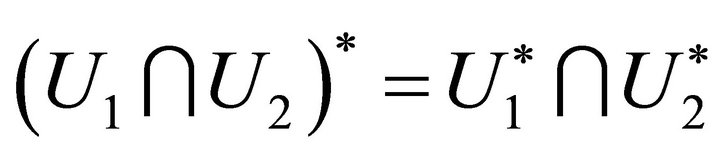4) If and are two open sets of, then and.

Recall that Kovar in [5] has characterized space with finite Wallman compactification remainder as following:

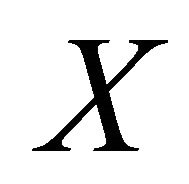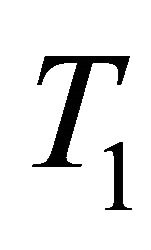Proposition 3.2 Let be a -space. Then the following statements are equivalent:

1);

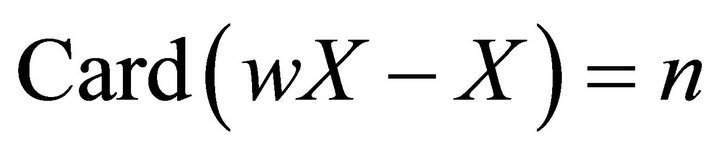2) There exists a collection of 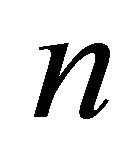pairwise disjoint non-compact closed sets of X and every family of noncompact pairwise disjoint closed sets of X contain at most 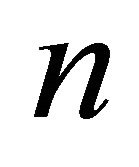elements.

The following proposition follows immediately from Proposition 3.2 and Proposition 3.1-1).

Proposition 3.3 Let X be a 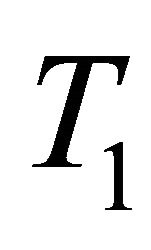-space and 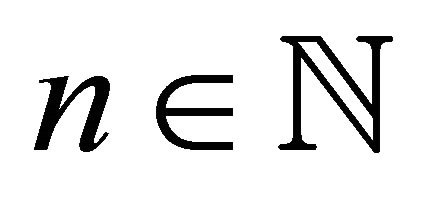such that every family of non-compact pairwise disjoint closed sets of X contains at most 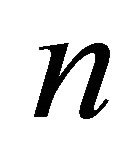elements. Then X is resolvable if and only if 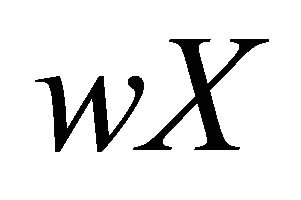is resolvable.

The following lemma has been given in [2] as Remark 4.5 and Remark 4.9.

Lemma 3.4 Let X be a -space. Then the following properties hold:

1) If is a closed non-compact subset of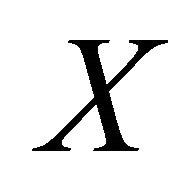, then there exists 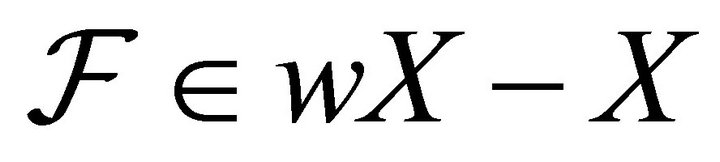such that.

2)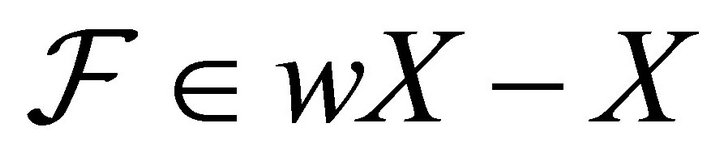. Then for each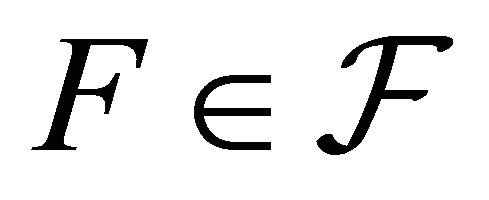, is a non-compact closed set of.

The following result is an immediate consequence of Lemma 3.4.

Corollary 3.5 Let X be a 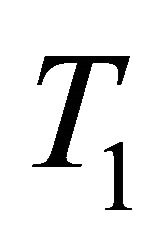-space, 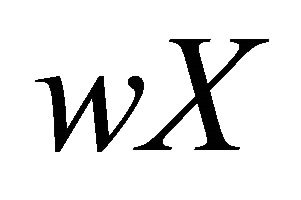be the Wallman compactification of X and 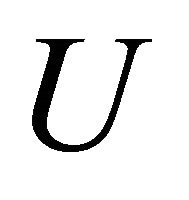be an open set of X. Then the following statements are equivalent:

1);

2) There exists a non compact closed set of 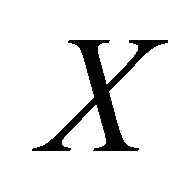such that.

Now, we are in a position to give a characterization of spaces such that their Wallman compactification is resolvable.

Theorem 3.6 Let X be a 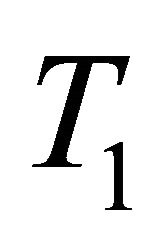-space. Then the following statements are equivalent:

1) The Wallman compactification of X is resolvable;

2) There exist two disjoint subsets 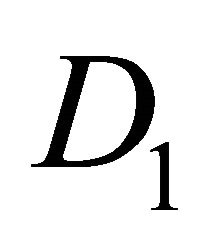and of X such that:

a).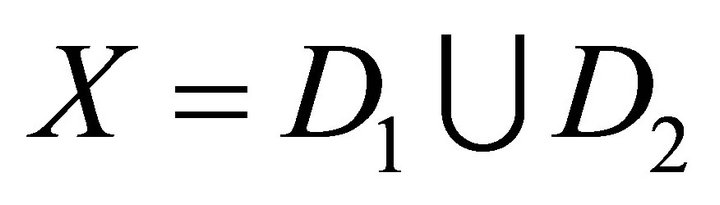

b) For 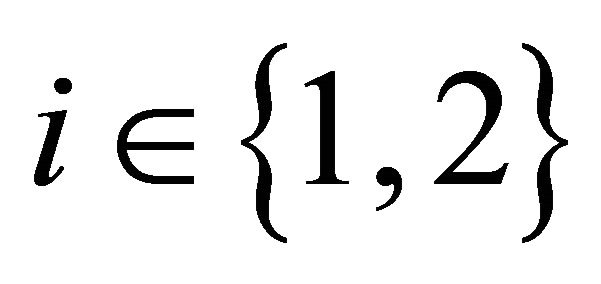and for each non empty open set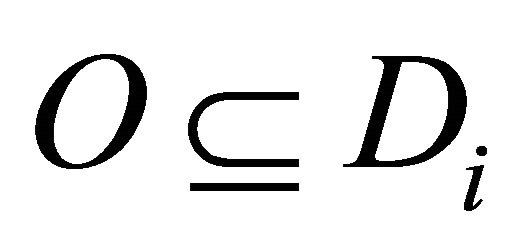, there exists a non compact closed set of 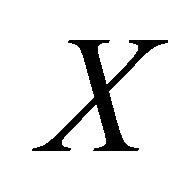such that.

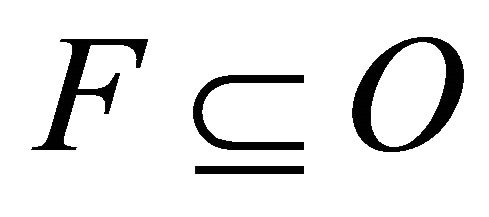Proof. 1) 2) Since 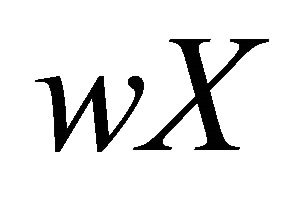is a resolvable space, there exist two disjoint dense sets A₁ and A₂ of 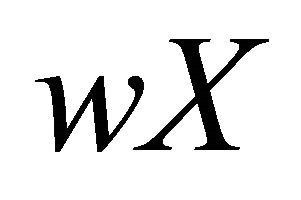such that 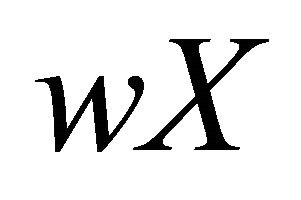is the union of A₁ and A₂. Set 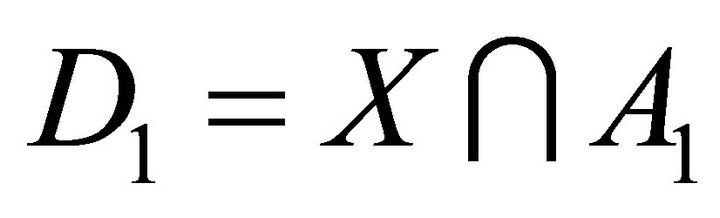and.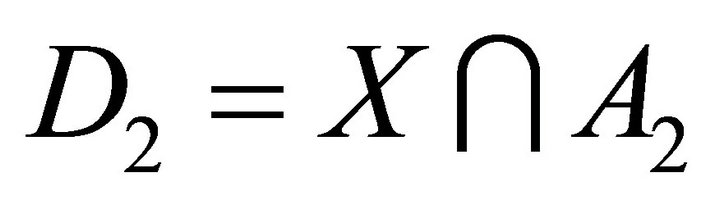

Let 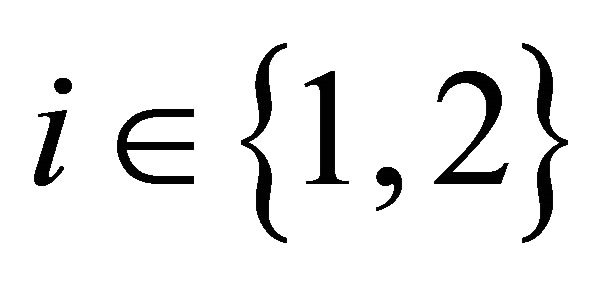and be a non empty open set of such that. Set such that. Since 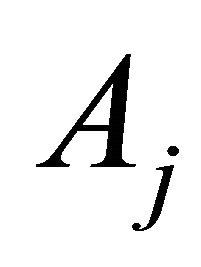is a dense subset of,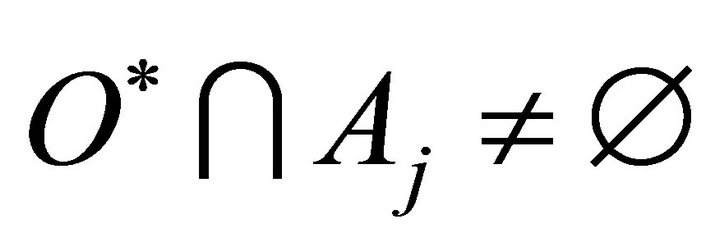. Now,

implies that

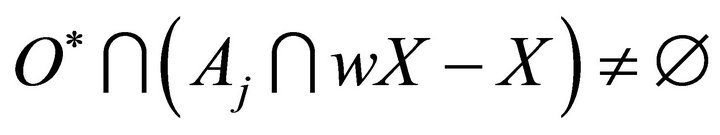. It follows that there exists

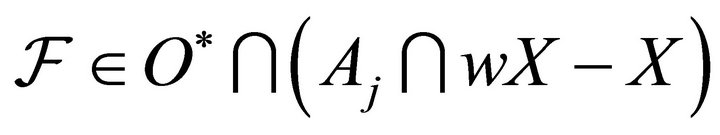, and thus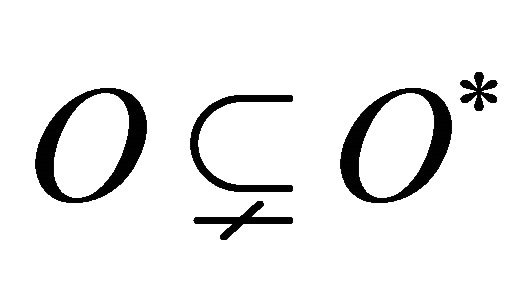. According to Corollary C4 there exists a non compact closed set of such that 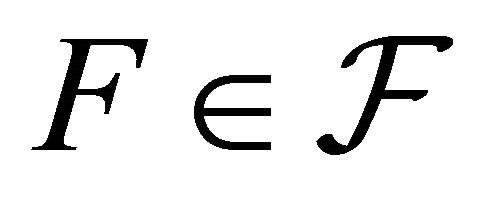and.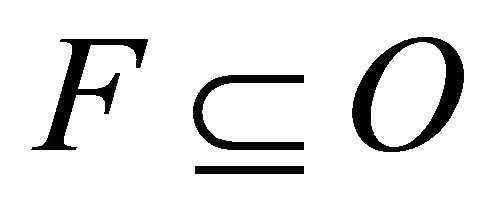

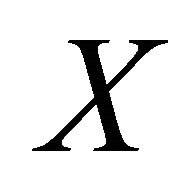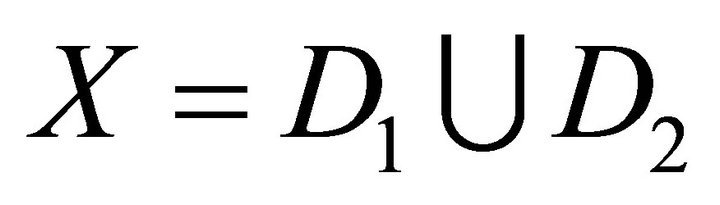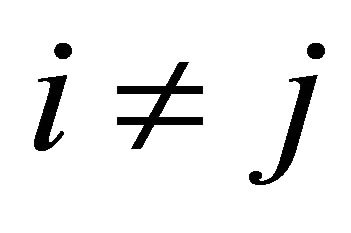2) 1) Let be two disjoint subsets of satisfying the condition b) and such that. Let in 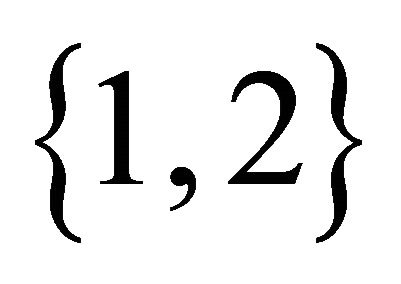and we define

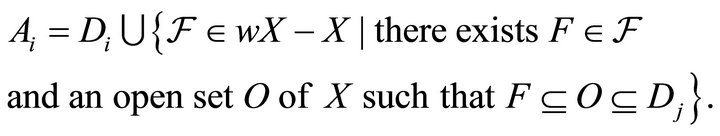
It is immediate that.

Now, let 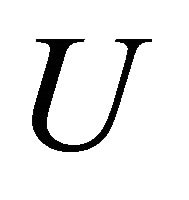be a open set of. We consider two cases:

Case 1:. Then. So

.

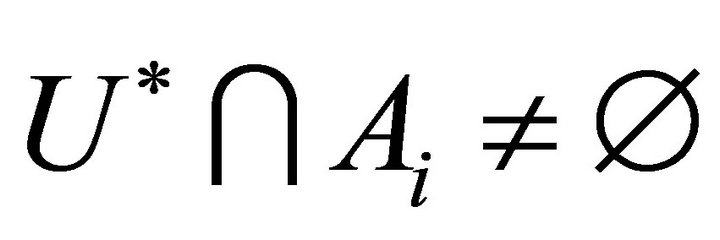Case 2: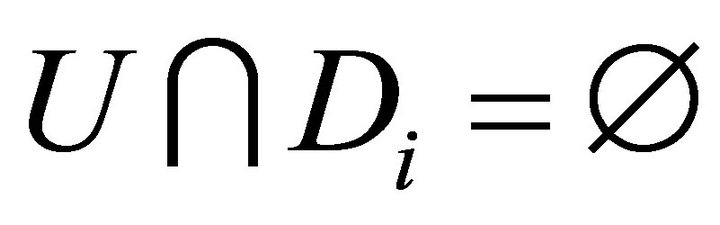. Then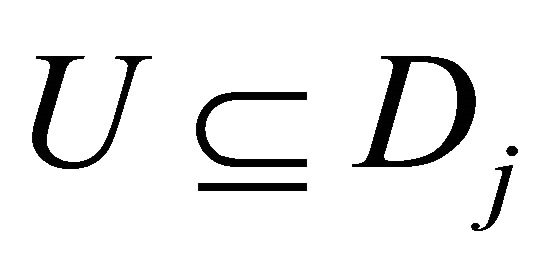. By condition b), there exists a non compact closed F of X such tha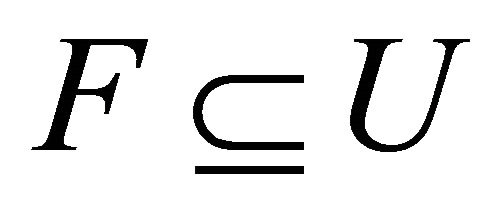t. Let 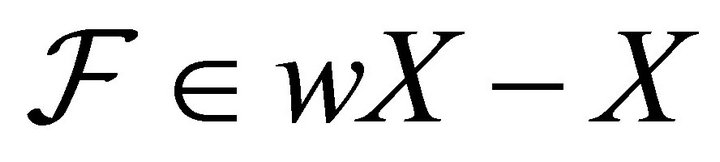such that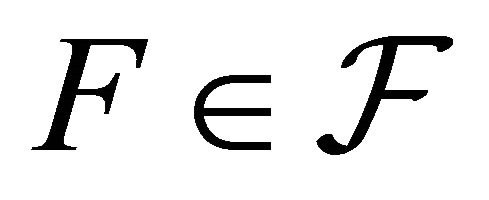. Hence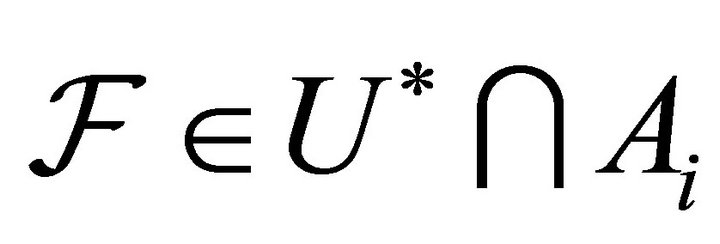. Thus.

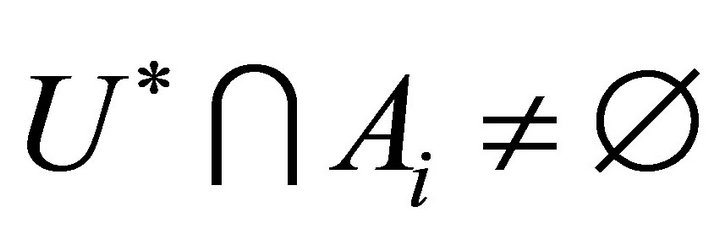Therefore 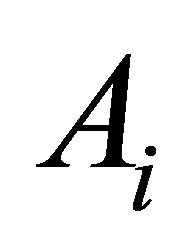is a dense set of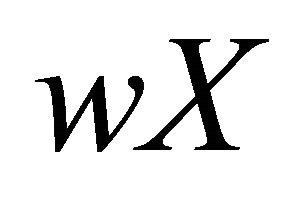; so that 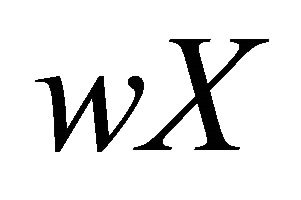is a resolvable space.

Example 3.7 Let be the set of all rational numbers equipped with the natural topology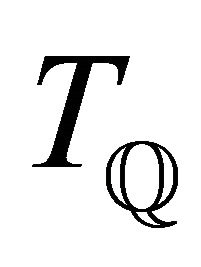. Let

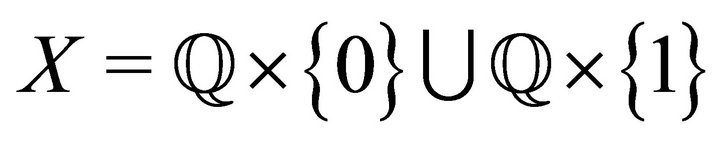equipped with the topology

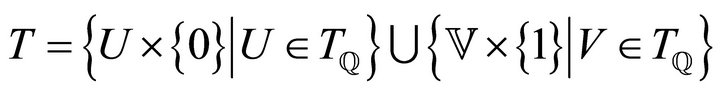. It is immediate that the topological space 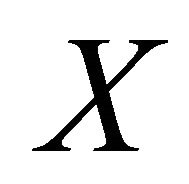satisfies the condition 2) of the Theorem 2.6. Then 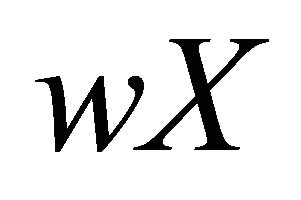is a resolvable space.

The previous result incites us to ask the following question.

Question 3.8 Let X be a space. We denote by 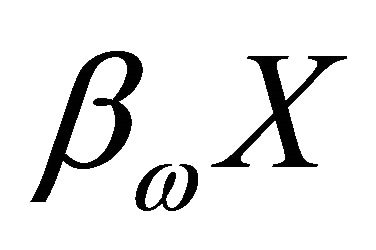(resp.) the -compactifcation of X introduced by Herrlich in [6] (resp. the Stone Cech compactification). When is 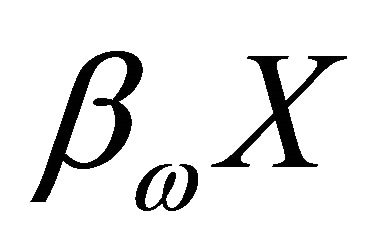(resp.) a resolvable space?

4. Acknowledgements

This paper has been supported by deanship of scientific research of University of Dammam under the reference 2011085.

REFERENCES