Advances in Pure Mathematics
Vol.3 No.1A(2013), Article ID:27567,5 pages DOI:10.4236/apm.2013.31A029
Semi-Commutative Differential Operators Associated with the Dirac Opetator and Darboux Transformation
Doshisha University, Kyoto, Japan
Email: *momiya@mail.doshisha.ac.jp
Received November 20, 2012; revised December 21, 2012; accepted December 29, 2012
Keywords: KdV Polynomials; mKdV (−) Polynomials; Schrödinger Operator; Dirac Operator
ABSTRACT
In the present paper, the semi-commutative differential oparators associated with the 1-dimensional Dirac operator are constructed. Using this results, the hierarchy of the mKdV (−) polynomials are expressed in terms of the KdV polynomials. These formulas give a new interpretation of the classical Darboux transformation and the Miura transformation. Moreover, the recursion operator associated with the hierarchy of the mKdV (−) polynomials is constructed by the algebraic method.
1. Introduction
The main purpose of the present paper1 is to construct the semi-commutative differential operators associated with the 1-dimensional Dirac operator
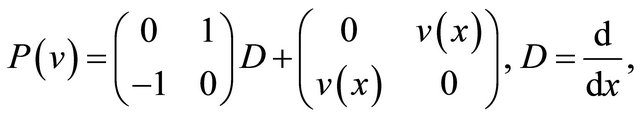 (1)
(1)
where the potential  is the infinitely differentiable function. Define the 1st order ordinary differential operartors by
is the infinitely differentiable function. Define the 1st order ordinary differential operartors by
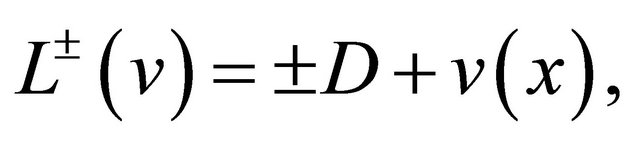 (2)
(2)
then, the oprtator 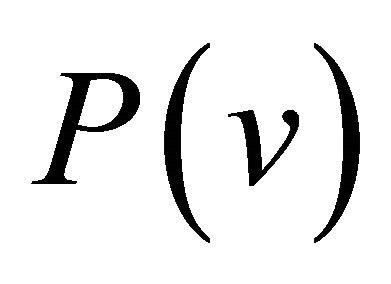 is expressed as
is expressed as
 (3)
(3)
Note that the variable x can be regarded as both real or complex throughout the paper.
The differential operators A, B are said to be semicommutative, if the commutator  is the multiplicative operator. As for the 1-dimensional Schrödinger operator
is the multiplicative operator. As for the 1-dimensional Schrödinger operator
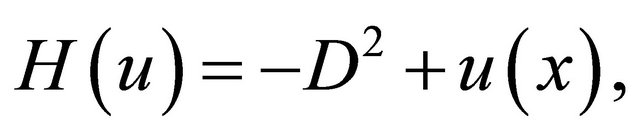 (4)
(4)
the identities
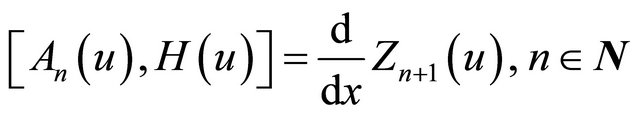 (5)
(5)
are well known for the differential operator 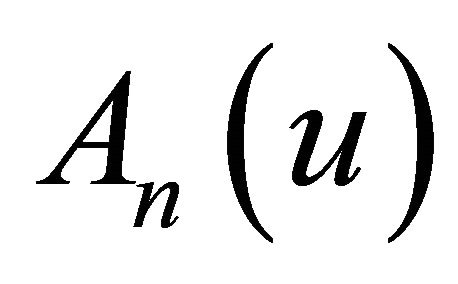 of the order
of the order  difined by
difined by
 (6)
(6)
where 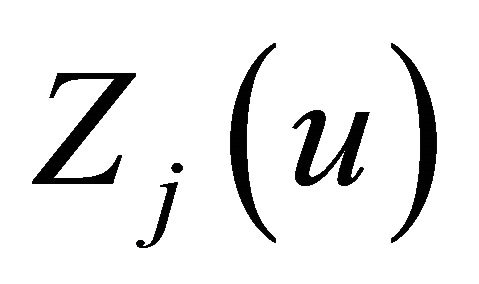 are the KdV polynomials which will be explained precisely in Section 2.
are the KdV polynomials which will be explained precisely in Section 2.
On the other hand, in [1], R. M. Miura discovered the following interesting fact; if  solves the mKdV (−) equation
solves the mKdV (−) equation
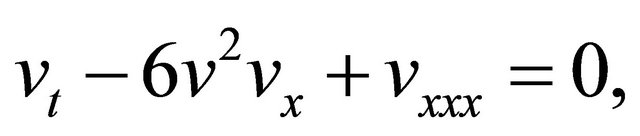
then both functions 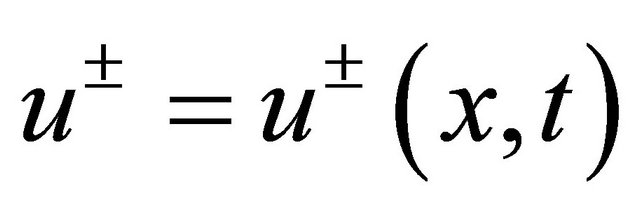 defined by
defined by
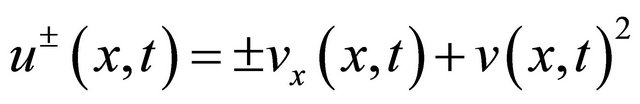 (7)
(7)
solve the KdV equation
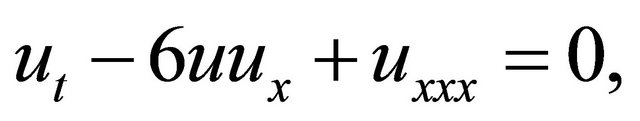 (8)
(8)
where the subscript denotes the partial differentiation. The transformation defined by (7) is the Miura transformation which plays the crucial role in the soliton theory. By (7), we have immediately the relation
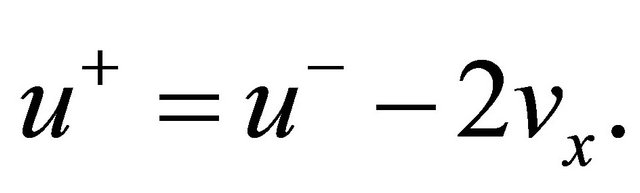 (9)
(9)
The transformation  defined by (9) is nothing but the Darboux transformation. Using the KdV polynomial, the relation (9) can be expressed as
defined by (9) is nothing but the Darboux transformation. Using the KdV polynomial, the relation (9) can be expressed as
 (10)
(10)
Considering the above facts, we investigate the problem to express the differential polynomials 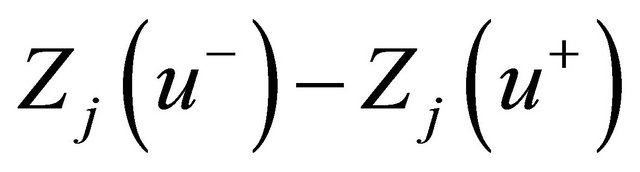 in terms of the function
in terms of the function  for the stationary case, i.e., when the function v is independent of the time variable t, i.e., in what follows
for the stationary case, i.e., when the function v is independent of the time variable t, i.e., in what follows 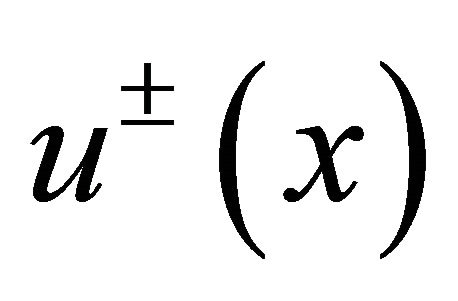 are defined by
are defined by

As a result, we obtain the new formulation of the stationary mKdV (−) hierarchy.
In our previous works [2,3], it is clarified that the semi-commutative operators and Darboux transformation are deeply related to the spectral theory of the differential operator 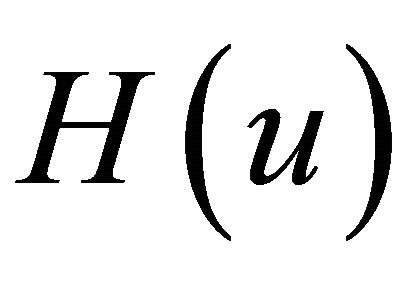 when the potential
when the potential 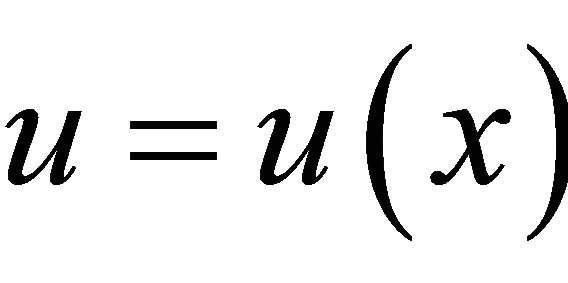 is algebrogeometric. The aim of our work is to extend these results concerned with the 1-dimensional Schrödinger operator
is algebrogeometric. The aim of our work is to extend these results concerned with the 1-dimensional Schrödinger operator 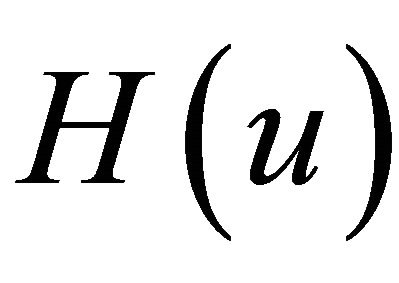 to the 1-dimensional Dirac operator
to the 1-dimensional Dirac operator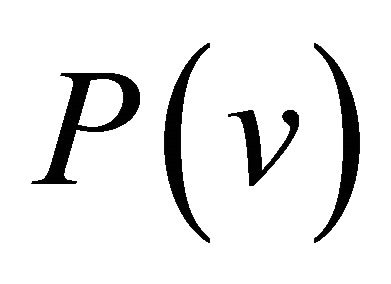 . The present work can be regarded as the first step of it. By applying the results of the present paper, we can obtain the various transformation formulas concerned with the algebro-geometric elliptic potential. These results will be reported in the forthcoming paper.
. The present work can be regarded as the first step of it. By applying the results of the present paper, we can obtain the various transformation formulas concerned with the algebro-geometric elliptic potential. These results will be reported in the forthcoming paper.
The contents of the present paper are as follows. In Section 2, we explain the fundamental materials which are necessary for the present work. In Section 3, calculation of the commutator of the Dirac operator and the differential operator constructed from the semi-commutative operator of the KdV hierarchy is carried out, and the main theorem of the present paper is stated. Section 4 is devoted to the proof of the main theorem. In Section 5, we construct the recursion operator associated with the mKdV hierarchy.
2. Preliminaries
The KdV polynomials 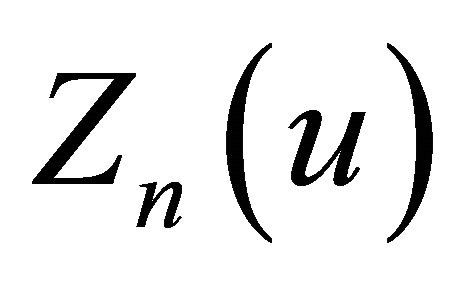 are differential polynomials defined by the recurrence relation
are differential polynomials defined by the recurrence relation
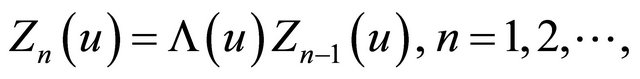 (11)
(11)
with the condition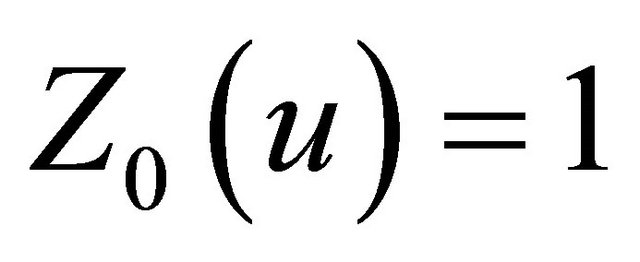 , where
, where 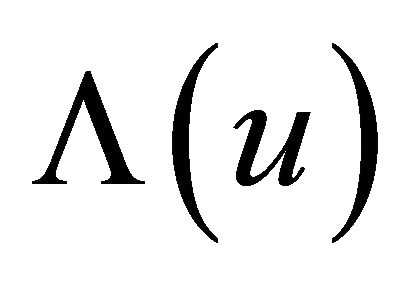 is the formal pseudo-differential operator defined by
is the formal pseudo-differential operator defined by
 (12)
(12)
Then  turn out to be the differential polynomials in
turn out to be the differential polynomials in . For examples, we have
. For examples, we have

If 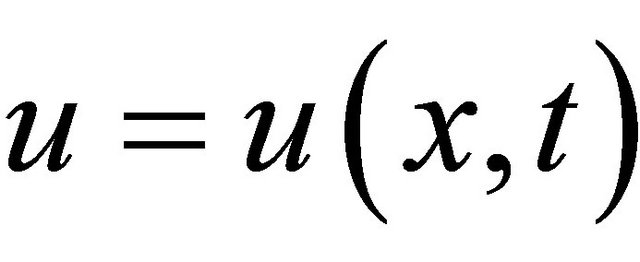 depends also on the time variable t, then the evolution equation
depends also on the time variable t, then the evolution equation

is nothing but the KdV equation. Hence, we call them the KdV polynomials. See [3] for more details of the KdV polynomials.
In what follows, we will often use the higher order derivatives of the differential polynomials . So, for the brevity, we will use the following notations of derivatives of the KdV polynomials defined by
. So, for the brevity, we will use the following notations of derivatives of the KdV polynomials defined by
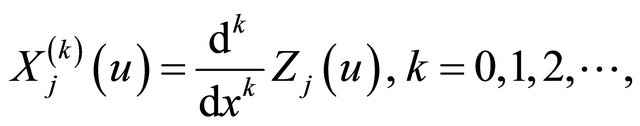
where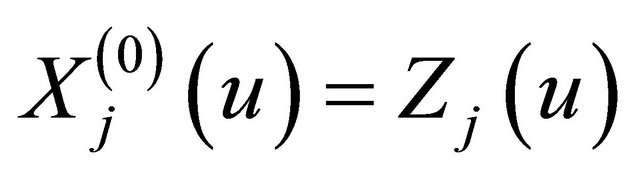 . Thus we have
. Thus we have
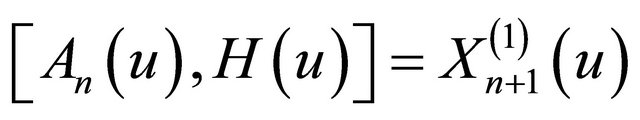
From now on, we restrict ourselves to the stationary problem, i.e., the function 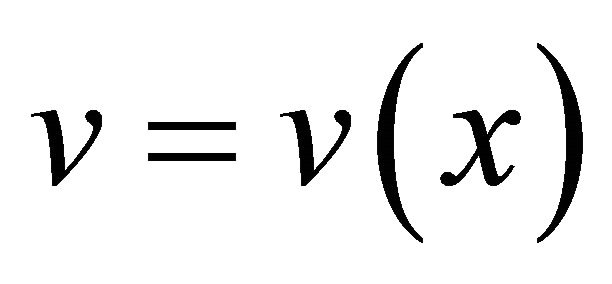 under consideration depends only on the space variable x.
under consideration depends only on the space variable x.
One immediately verifies the identities
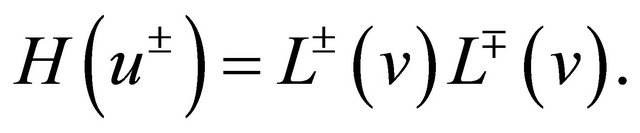 (13)
(13)
Define the multi-component operator 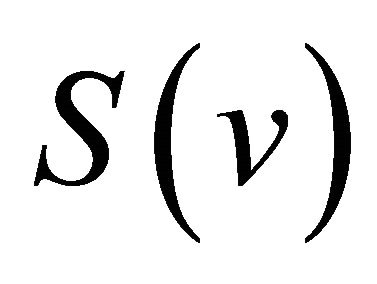 by
by
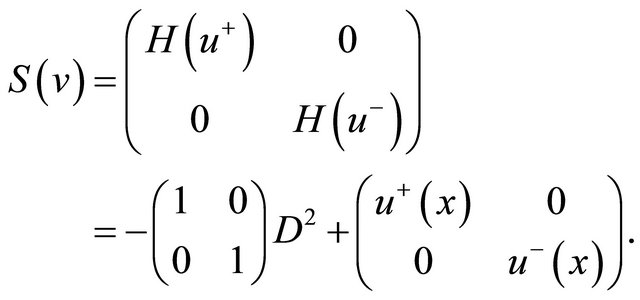 (14)
(14)
By (13), one can show immediately the operator identity
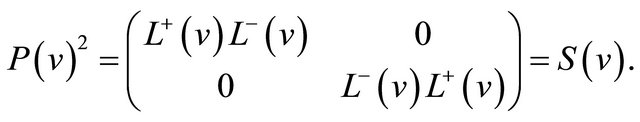 (15)
(15)
On the other hand, define the multi-component differential operator  by
by
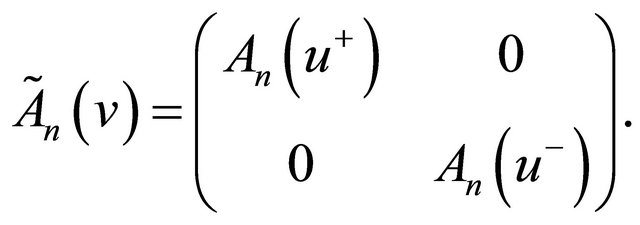 (16)
(16)
Then, by (5), (14), and (16), we have immediately
 (17)
(17)
Therefore the operator 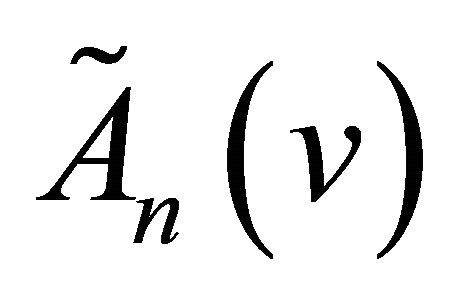 are semi-commutative with the operator
are semi-commutative with the operator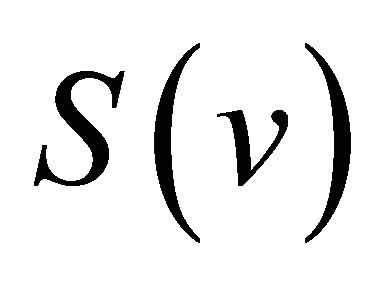 .
.
3. Calculation of 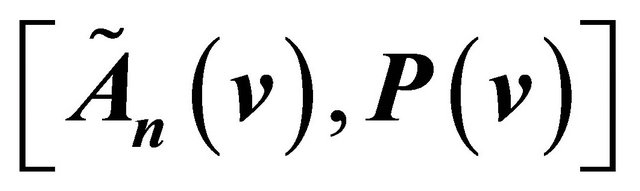
Define the scalar differential operators 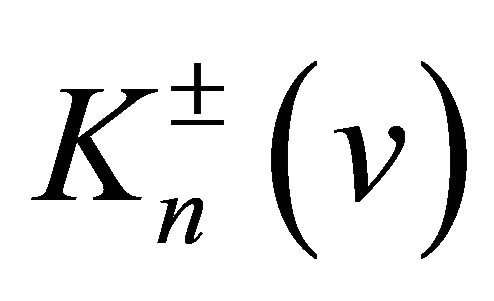 by
by
 (18)
(18)
respectively. By direct calculation, we have immediately
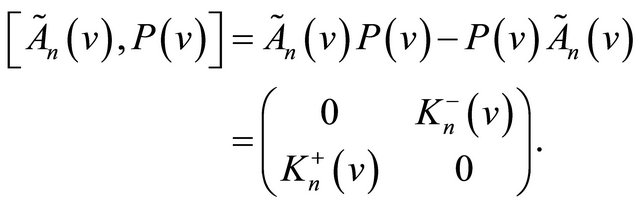 (19)
(19)
By the definition (6) of the operator , we have immediately
, we have immediately
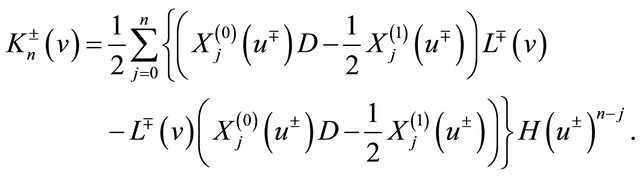 (20)
(20)
By (15), we have
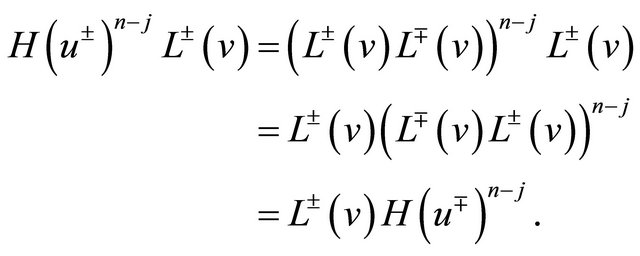
Furthermore, by the definition (2) of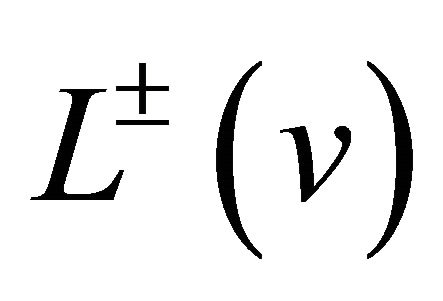 , one verifies
, one verifies
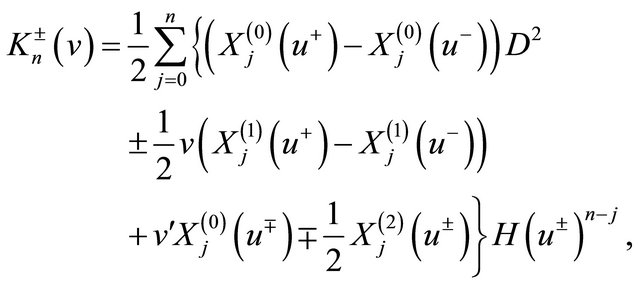 (21)
(21)
where we used the identity
 (22)
(22)
where
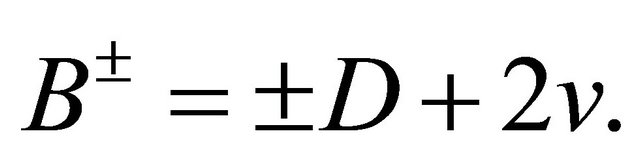
The identity (22) is derived in [4], and is called the fundamental identity of the Darboux transformation in it, By the fundamental identity (22), we have immediately
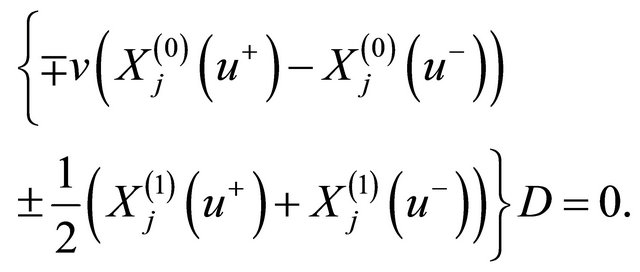
Put
 (23)
(23)
then we can express the identity (21) in terms of 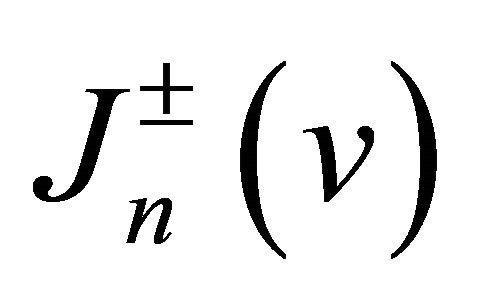 as
as
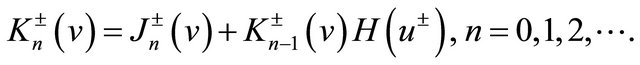 (24)
(24)
For , one verifies easily
, one verifies easily
 ,
,
 .
.
Thus, for 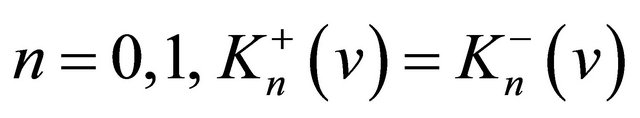 hold, and they are not differential operators, but are the multipricative operator. Thus, the operator
hold, and they are not differential operators, but are the multipricative operator. Thus, the operator  and the Dirac operator
and the Dirac operator 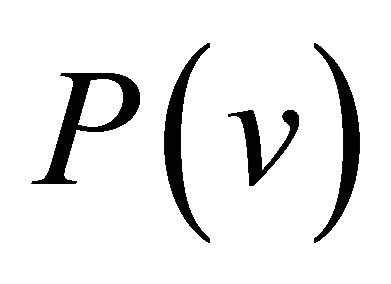 turns out to be semi-commutative for
turns out to be semi-commutative for .
.
For general n, we have the following theorem which is the main result of the present paper.
Theorem 1. The multi-component differential operators 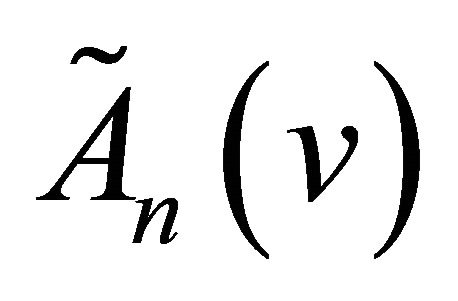 and
and 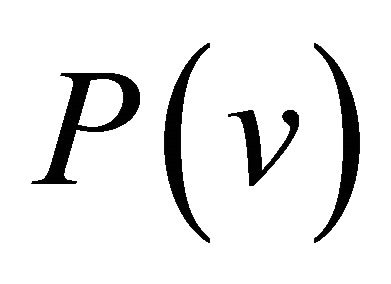 are semi-commutative, i.e.,
are semi-commutative, i.e., 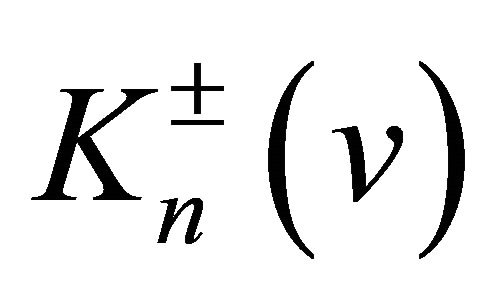 are the multiplicative operators, and they coincide with each other, i.e., the equality
are the multiplicative operators, and they coincide with each other, i.e., the equality
 (25)
(25)
hold for all n. Moreover, if we denote them as , then the identities
, then the identities
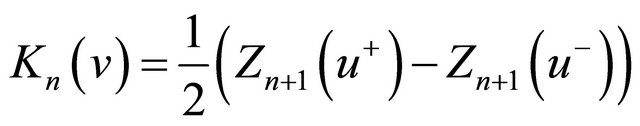 (26)
(26)
hold for all .
.
If the potential v depends also on the time variable t, i.e.,  , the evolution equation
, the evolution equation
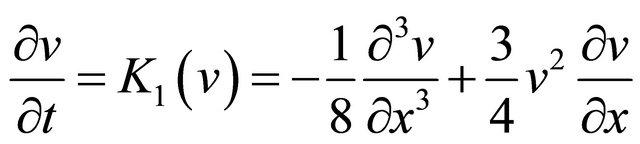
is nothing but the mKdV (−) equation. Hence, we call the differential polynomials ,
, 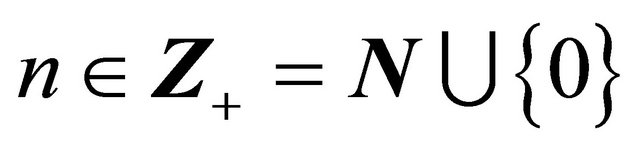 the mKdV (−) polynomials.
the mKdV (−) polynomials.
4. The Proof of Theorem 1
We prove the theorem by induction. Firstly, for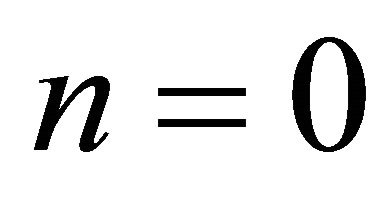 , one verifies
, one verifies
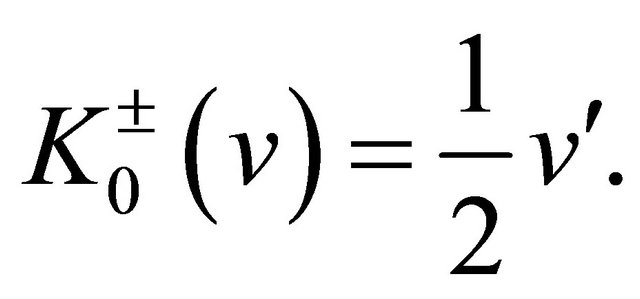
On the other hand, by (10), we have

Secondly, for , we assume that
, we assume that
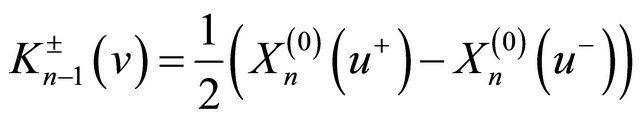
holds. Then, for , we have
, we have
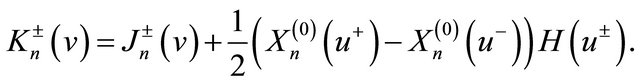
From (21) and (23), we have

This implies that 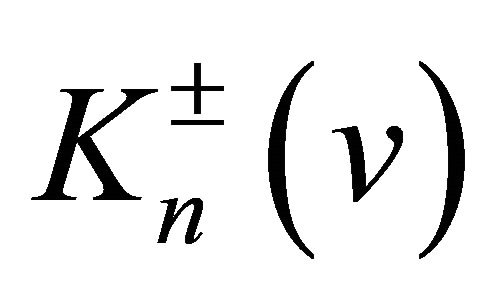 are the multiplicative operators, i.e.,
are the multiplicative operators, i.e.,  and
and 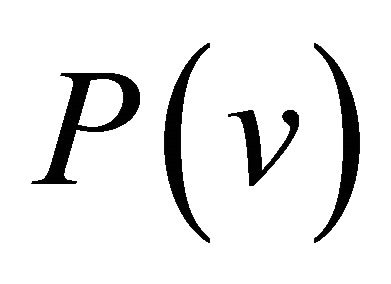 are semi-commutative.
are semi-commutative.
Similarly, by induction, we can show that 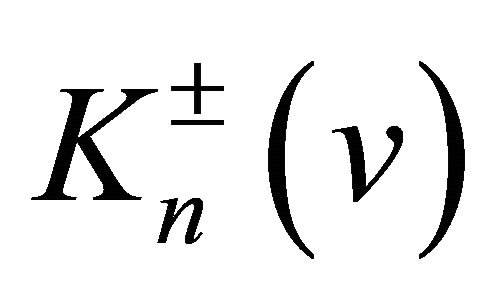 coincide with each other.
coincide with each other.
Next we show the identity (26). By straightforward calculation, one can show
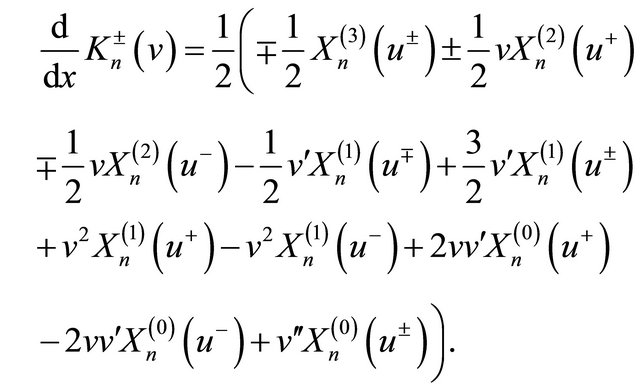 (27)
(27)
Put

then, by (27), we have

where we used the relation
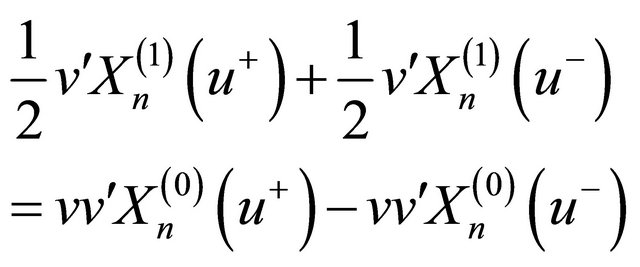
which are derived immediately from (22).
Thus, we have
 (28)
(28)
By (7), we have
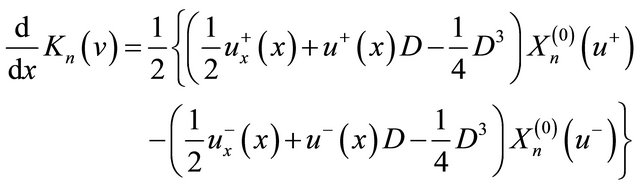
By (12) which is the definition of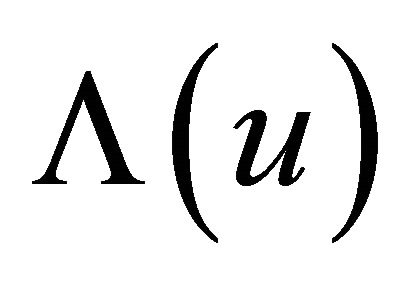 , we have
, we have

This completes the proof of Theorem 1.
5. The Recursion Operator
In the preceding section, we have shown the relation

hold for all n. Therefore, by (28), we have

Then, by (22), we have
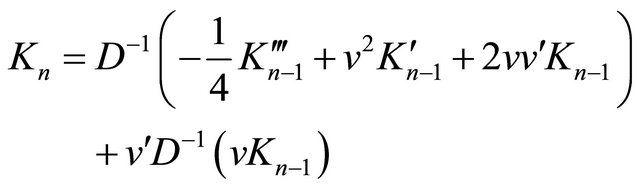 (29)
(29)
The relation (29) defines the recursion operators of
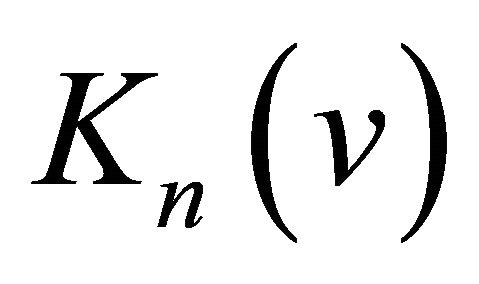 . Therefore, we have the following theorem.
. Therefore, we have the following theorem.
Theorem 2. The formal pseudo-differential operator 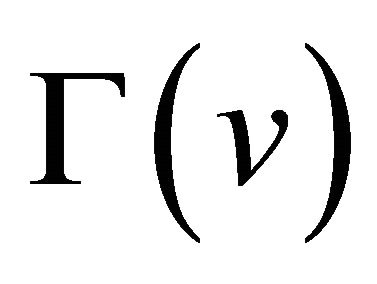 defined by
defined by

is the recursion operator associated with the mKdV (−) polynomials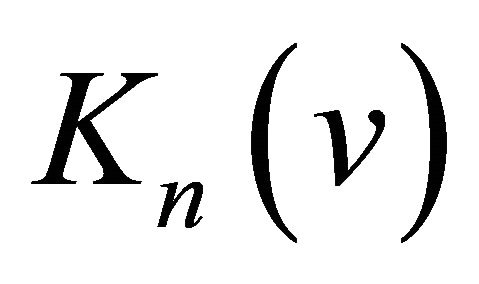 ,
,  , i.e.,
, i.e.,
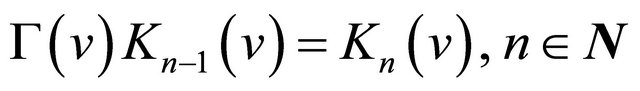
hold.
Using this recursion operator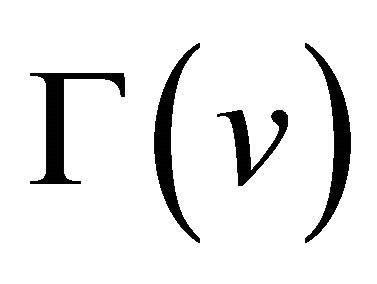 , one can calculate easily the hierarchy of the mKdV (−) polynomials.
, one can calculate easily the hierarchy of the mKdV (−) polynomials.
REFERENCES
- R. M. Miura, “Korteweg—De Vries Equation and Generalizations. I. A Remarkable Explicit Nonlinear Transformation,” Journal of Mathematical Physics, Vol. 9, No. 8, 1968, pp. 1202-1204. doi:10.1063/1.1664700
- M. Ohmiya, “Spectrum of Darboux Transformation of Differential Operator,” Osaka Journal of Mathematics, Vol. 36, No. 4, 1999, pp. 949-980.
- M. Ohmiya, “KdV Polynomials and Λ-Operator,” Osaka Journal of Mathematics, Vol. 32, No. 2, 1995, pp. 409- 430.
- M. Ohmiya and Y. P. Mishev, “Darboux Transformation and Λ-Operator,” Journal of Mathematics/Tokushima University, Vol. 27, 1993, pp. 1-15.
- M. Matsushima and M. Ohmiya, “An Algebraic Construction of the First Integrals of the Stationary KdV Hierarchy,” Proceeding of ICNAAM: Numerical Analysis and Applied Mathematics, Vol. 1, 2009, pp. 168-172.
NOTES
*Corresponding author.
1This work was supported by JSPS KAKENHI Grant Number 2354- 0255.

