Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24390,5 pages DOI:10.4236/apm.2012.26061
Uniqueness of Radial Solutions for Elliptic Equation Involving the Pucci Operator*
Department of Mathematics and Physics, North China Electric Power University, Beijing, China
Email: liuyong@ncepu.edu.cn
Received July 28, 2012; revised August 30, 2012; accepted September 21, 2012
Keywords: Pucci Operator; Radial Solution; Uniqueness; Super Linear
ABSTRACT
The solution of a nonlinear elliptic equation involving Pucci maximal operator and super linear nonlinearity is studied. Uniqueness results of positive radial solutions in the annulus with Dirichlet boundary condition are obtained. The main tool is Lane-Emden transformation and Koffman type analysis. This is a generalization of the corresponding classical results involving Laplace operator.
1. Introduction
We study the nonlinear elliptic equation
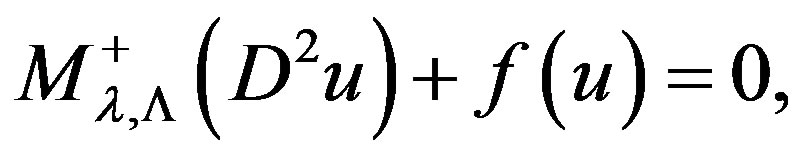 (1)
(1)
where 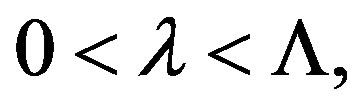
 is Pucci maximal operator, the potential f is super linear with some further constraints. Using
is Pucci maximal operator, the potential f is super linear with some further constraints. Using 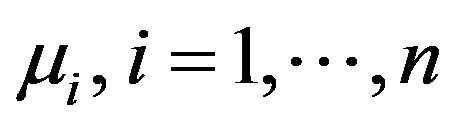 to denote the eigenvalues of
to denote the eigenvalues of 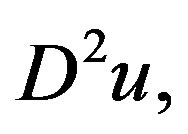 then explicitly, the Pucci operator
then explicitly, the Pucci operator 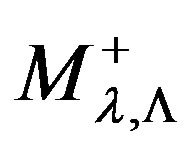 is given by
is given by
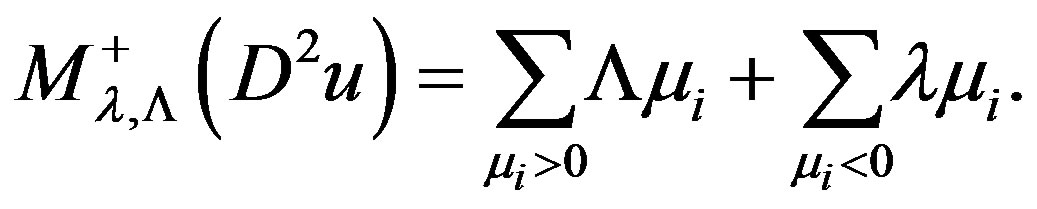
For more detailed discussion, see for example [1,2]. This equation has been extensively studied, see [3-5], etc. and the references therein.
Normalize  to be
to be  for simplicity. We will in this paper investigate the uniqueness of
for simplicity. We will in this paper investigate the uniqueness of  positive radial solution of (1) in the annulus
positive radial solution of (1) in the annulus
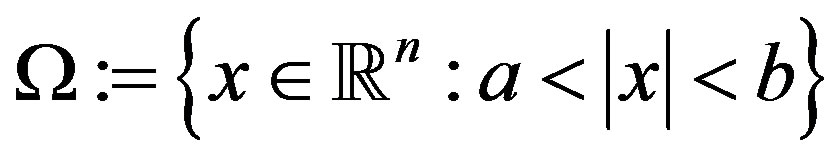
with Dirichlet boundary condition. In this case, Equation (1) reduces to
 (2)
(2)
where

Throughout the paper, we assume 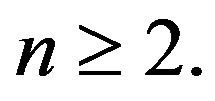 Note that
Note that 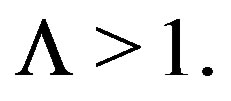 Now we could state our main results.
Now we could state our main results.
Theorem 1. Suppose  is small enough and
is small enough and
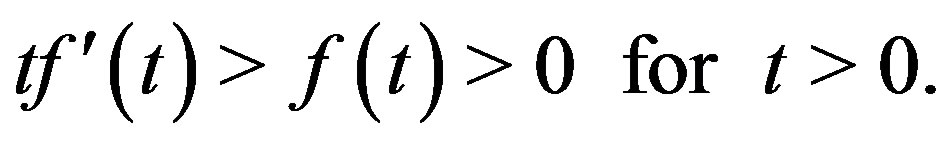
Then (2) has at most one positive solution with Dirichlet boundary condition.
If instead of the smallness of 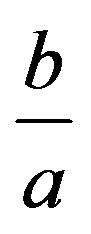 we assume further growing condition on
we assume further growing condition on 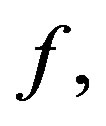 then we have the following Theorem 2. Suppose that for
then we have the following Theorem 2. Suppose that for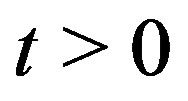 ,
,
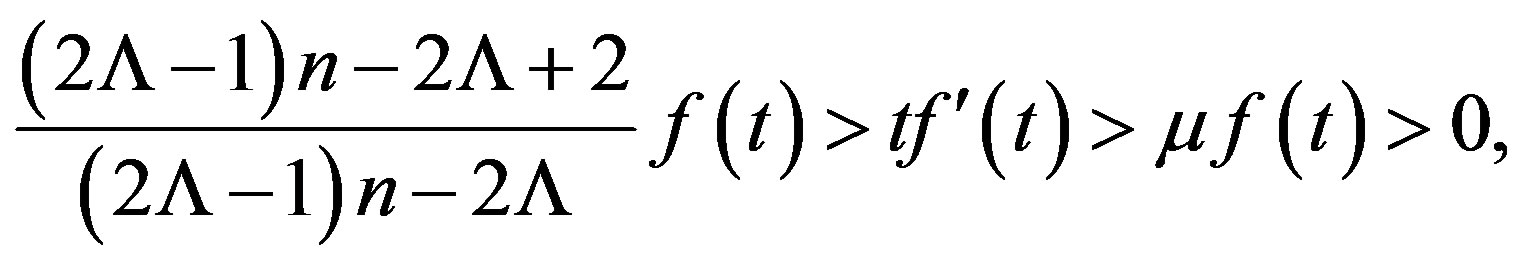
where
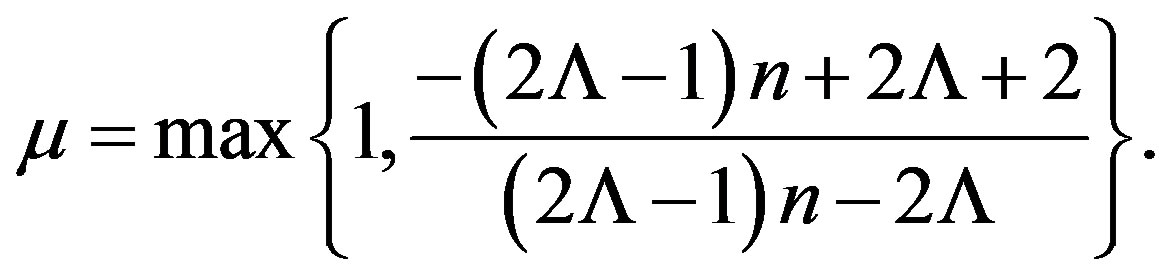
Then (2) has at most one positive solution with Dirichlet boundary condition.
In the case 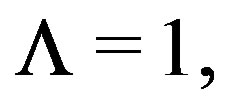 the Pucci operator reduces to the usual Laplace operator, and the corresponding unique results are proved by Ni and Nussbaum in [6].
the Pucci operator reduces to the usual Laplace operator, and the corresponding unique results are proved by Ni and Nussbaum in [6].
We also remark that the above theorems could be generalized to nonlinearities 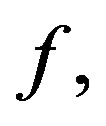 which also depends on
which also depends on 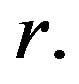 We will not pursue this further in this paper.
We will not pursue this further in this paper.
2. Lane-Emden Transformation and Uniqueness of the Radial Solutions
2.1. Proof of Theorem 1
We shall perform a Lane-Emden type transformation to Equation (2). Let us introduce a new function
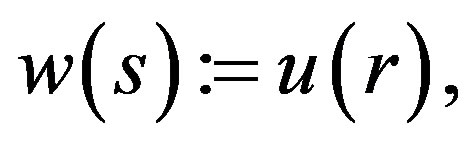
where 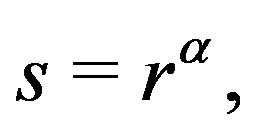 with
with

Then 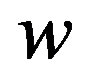 satisfies
satisfies
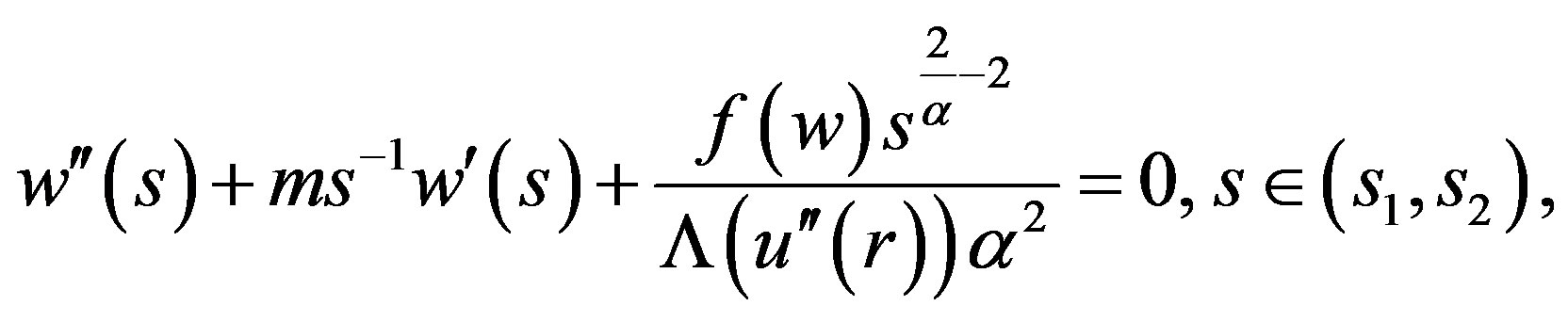 (3)
(3)
where we have denoted

and  Note that m may not be continuous at the points where
Note that m may not be continuous at the points where 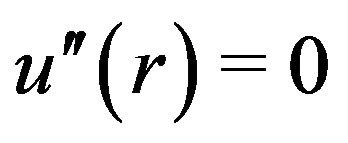 or
or 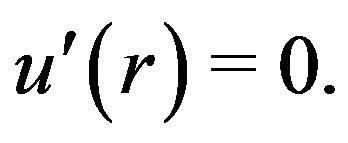 Additionally, if
Additionally, if 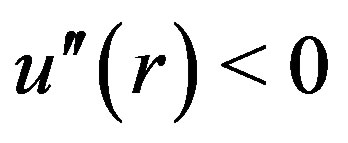 and
and  then
then 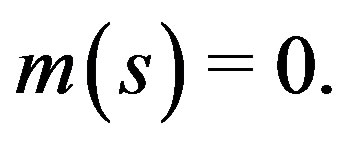
Lemma 3. Let w be a positive solution of (3) with 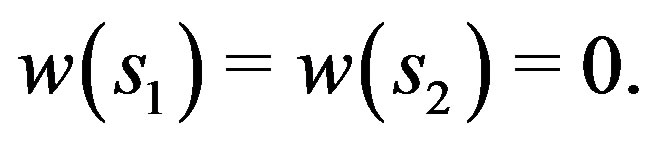 Then there exists
Then there exists 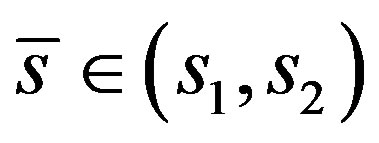 such that
such that 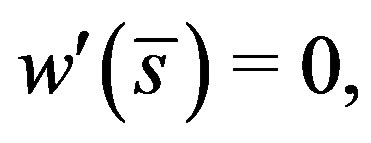 and
and
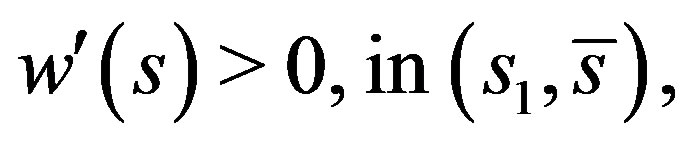

Proof. If 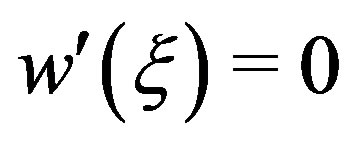 for some
for some 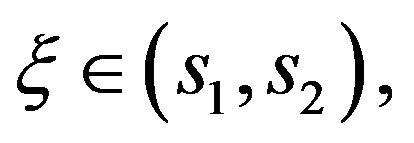 then
then

The conclusion of the lemma follows immediately from this inequality. ■
Given 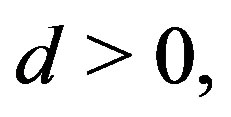 the solution of (3) with
the solution of (3) with  and
and 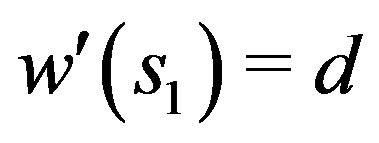 will be denoted by
will be denoted by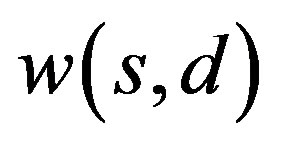 . Let
. Let
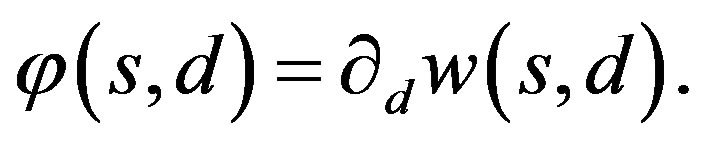
By standard argument, we know that positive solution of (3) with Dirichlet boundary condition is unique if we could show that
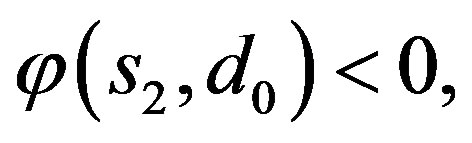
whenever 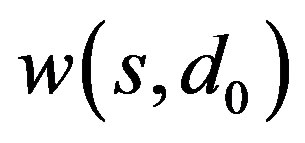 is a positive solution to (3) with
is a positive solution to (3) with 
The functions  and
and 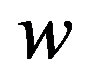 satisfy the following equations:
satisfy the following equations:
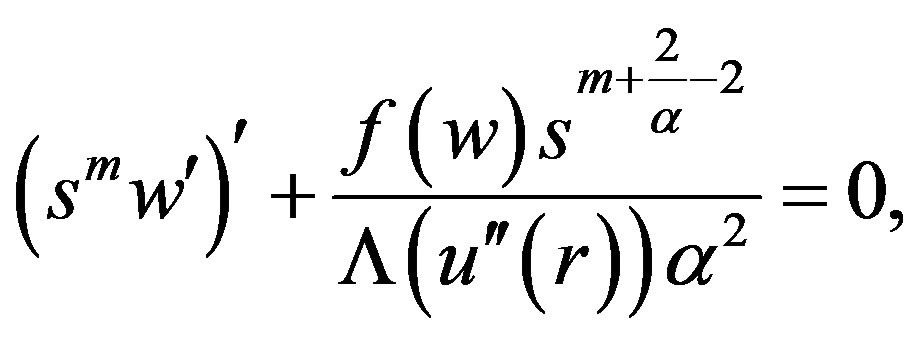
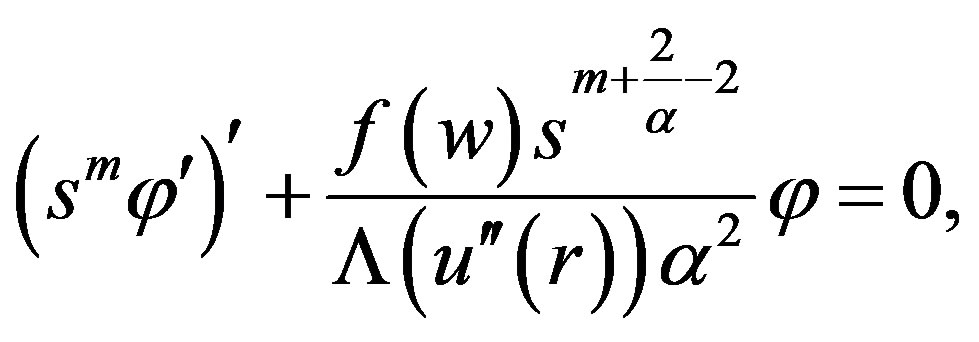
The initial condition satisfied by  is:
is: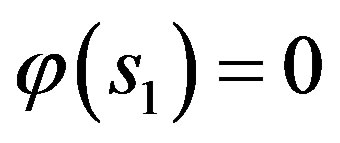 ,
,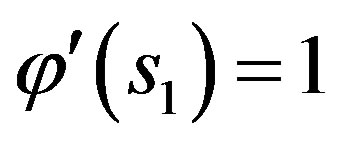 .
.
Now let 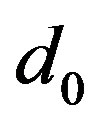 be a positive constant such that
be a positive constant such that 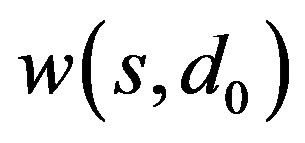 is a positive solution to (3) with
is a positive solution to (3) with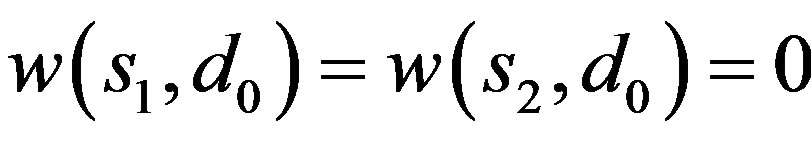 . To show that
. To show that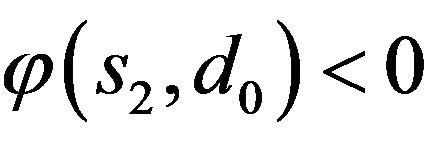 , let us first prove that
, let us first prove that 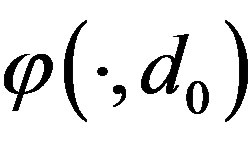 must vanish at some point in the interval
must vanish at some point in the interval 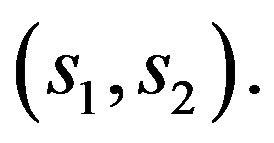 In the following, we write
In the following, we write 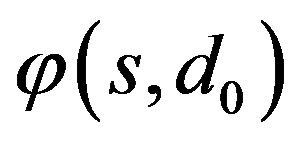 simply as
simply as 
Lemma 4. There exists 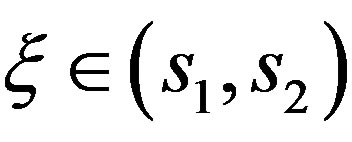 such that
such that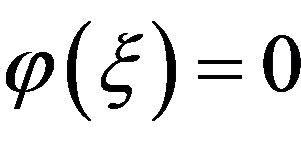 .
.
Proof. Let us consider the function
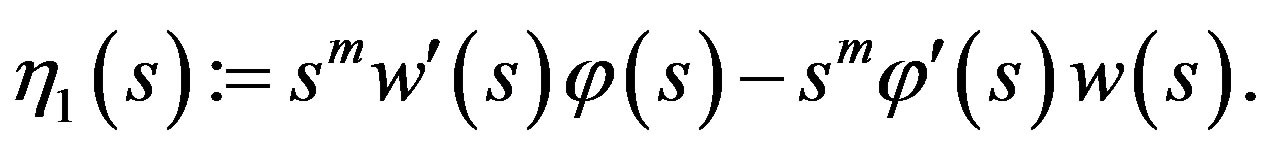
We have

We remark that  is indeed not everywhere differentiable, since m is not continuous. It however could be shown that the jump points of m are isolated. Here by
is indeed not everywhere differentiable, since m is not continuous. It however could be shown that the jump points of m are isolated. Here by , we mean the derivative of
, we mean the derivative of  at the point where it is differentiable. The same remark applies to the functions
at the point where it is differentiable. The same remark applies to the functions  and
and 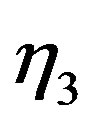 below.
below.
Now if 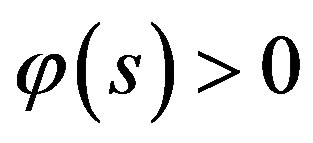 for
for 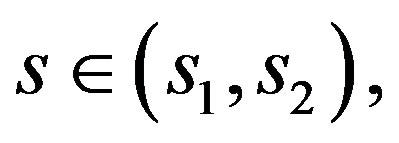 then
then
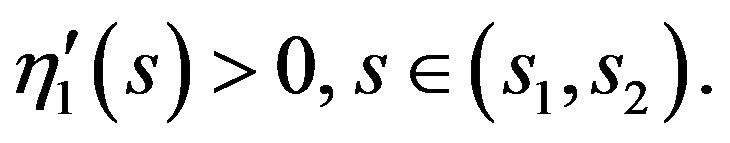
Since  we infer that
we infer that

It follows that

This is a contradiction, since 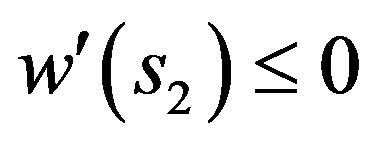 and
and 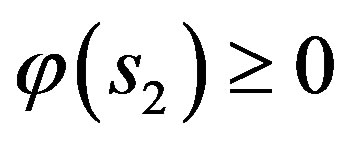 . ■
. ■
With the above lemma at hand, we wish to show that in the interval 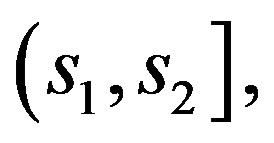
 vanishes at only one point ξ. For this purpose, let us define functions
vanishes at only one point ξ. For this purpose, let us define functions 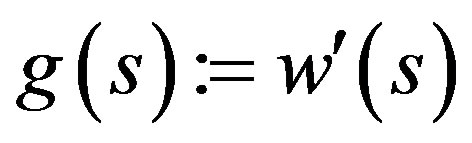 and
and  Put
Put
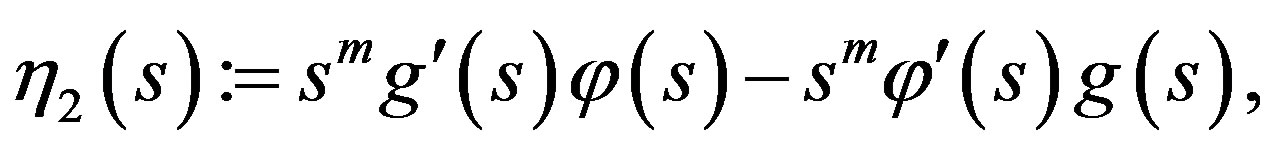
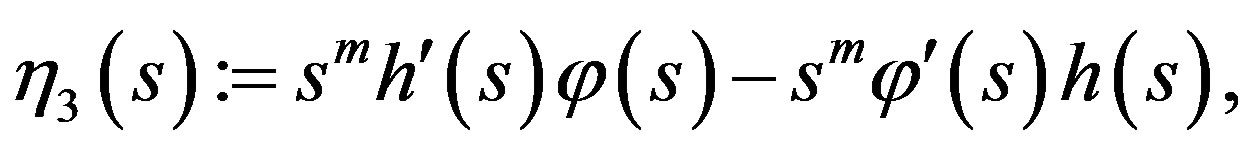
and

Lemma 5. We have
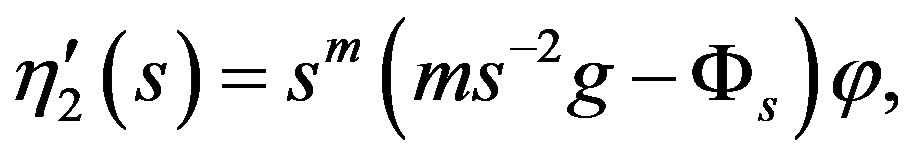 (4)
(4)
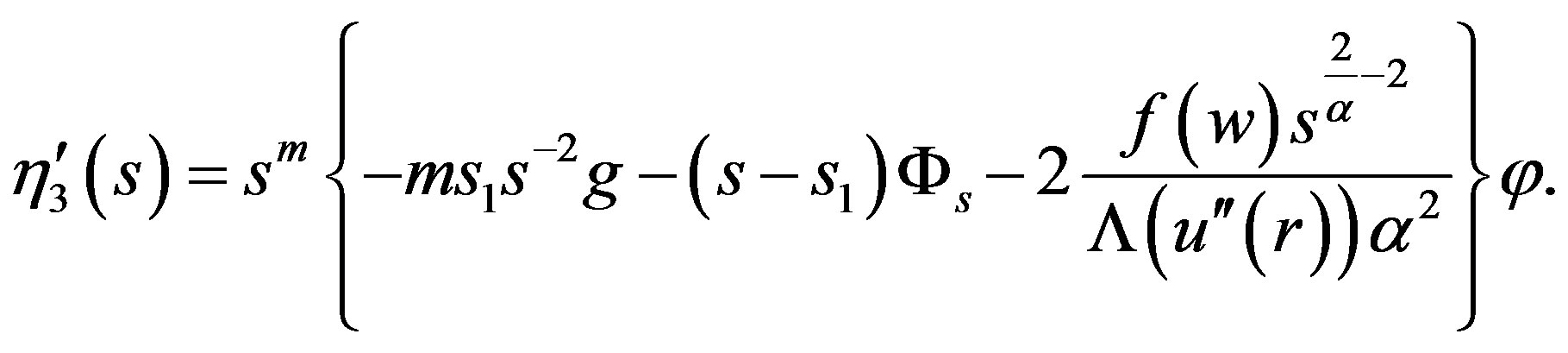 (5)
(5)
Proof. Differentiate the Equation (3) with respect to s gives us
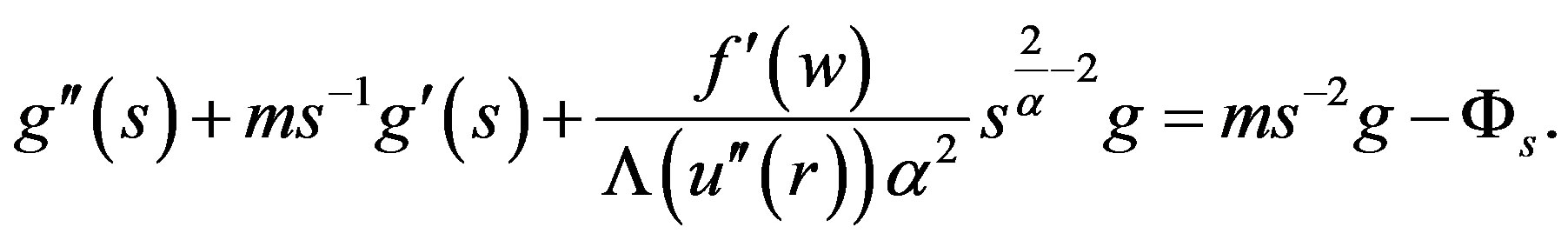 (6)
(6)
Hence

As to the function h, there holds
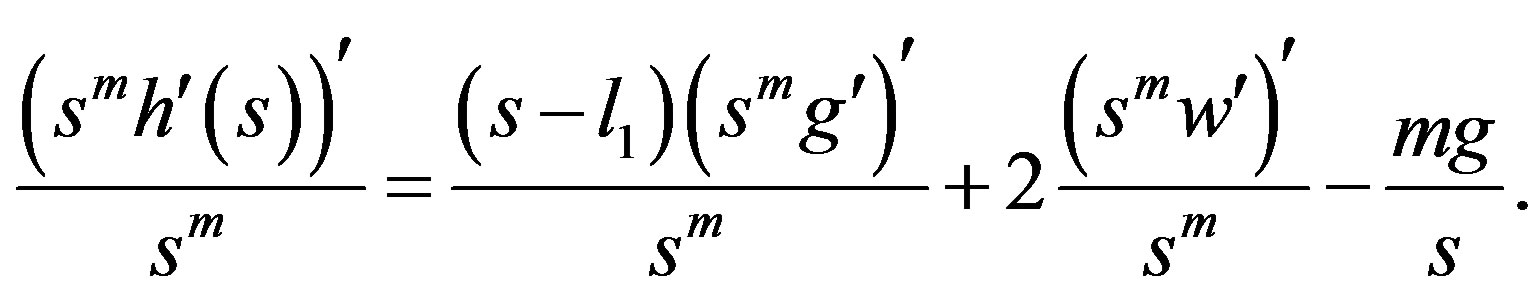
Combining this with (3) and (6) we get
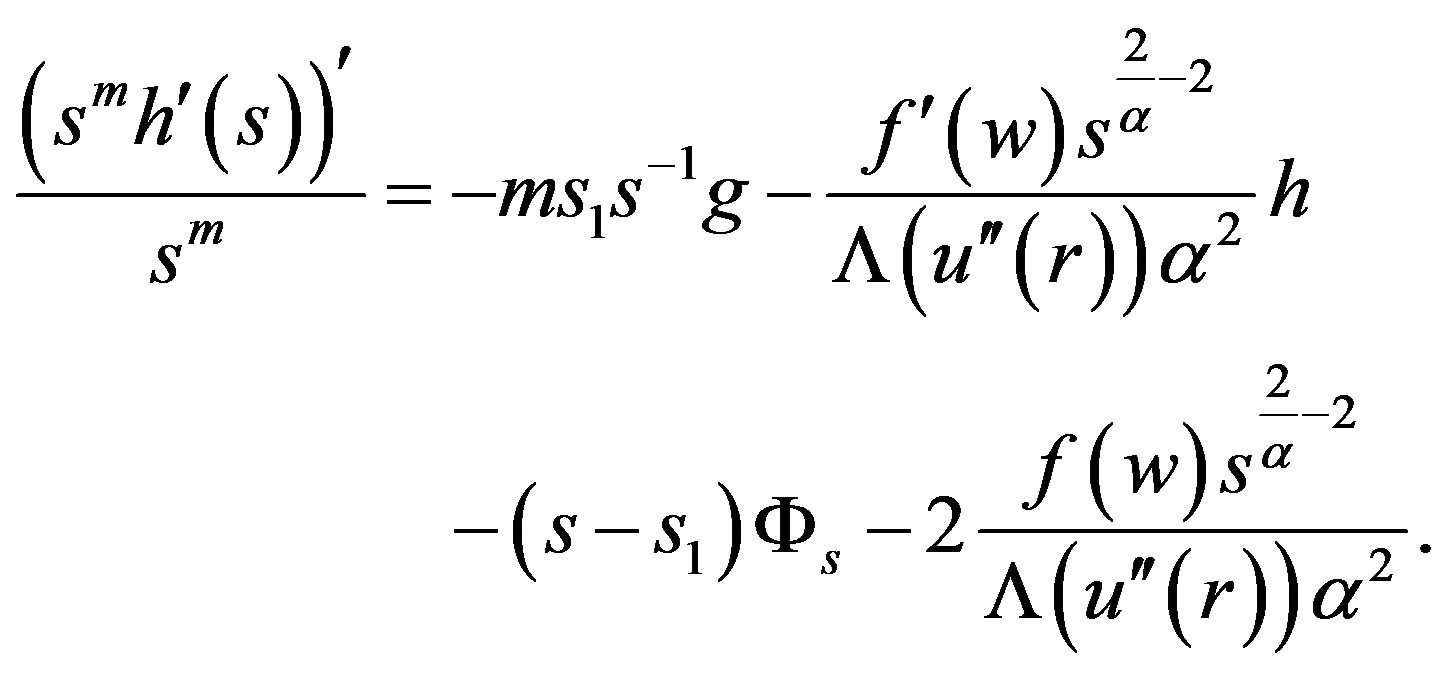
It follows that
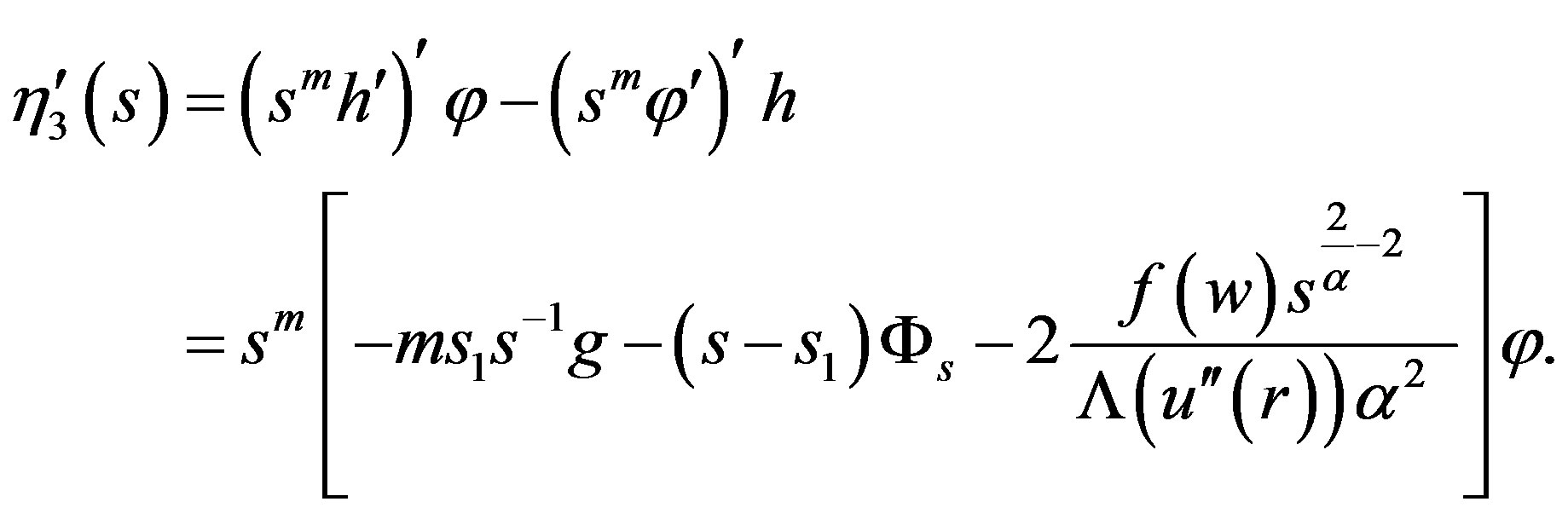
■
Now we are ready to prove Theorem 1.
Proof of Theorem 1. We need to show that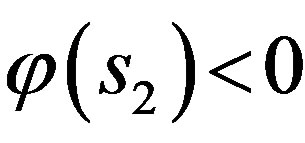 .
.
We first of all claim that the first zero  of
of  in
in 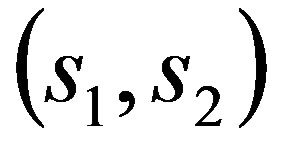 must stay in the interval
must stay in the interval 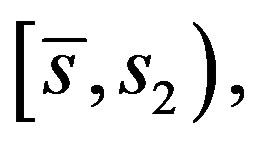 where
where 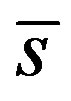 is given by Lemma 3. Suppose to the contrary that
is given by Lemma 3. Suppose to the contrary that
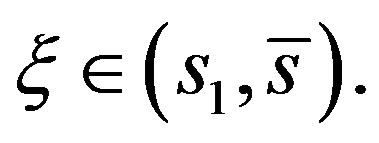 By (5) using the fact that
By (5) using the fact that  we find that if
we find that if 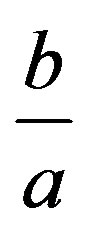 is small enough, then in the interval
is small enough, then in the interval 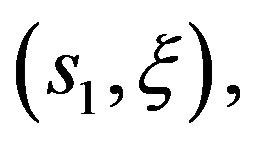
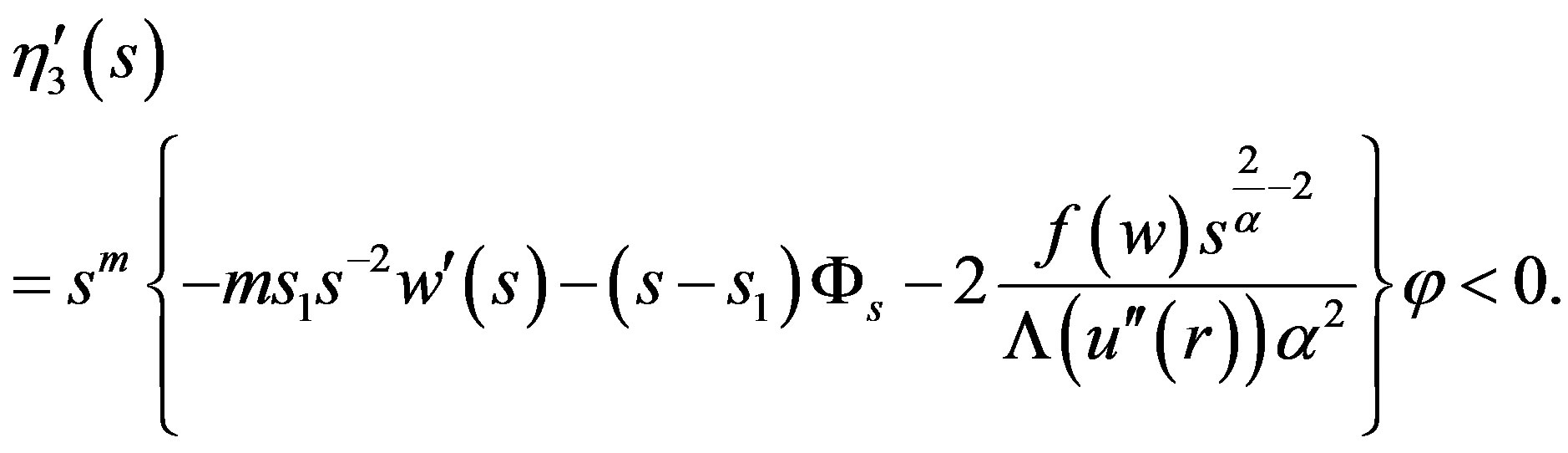
Since  we find that
we find that
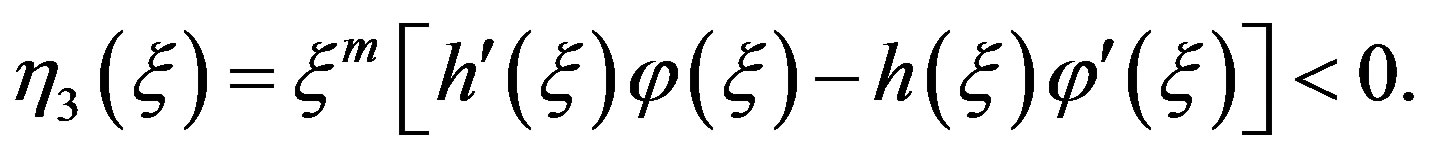
Therefore
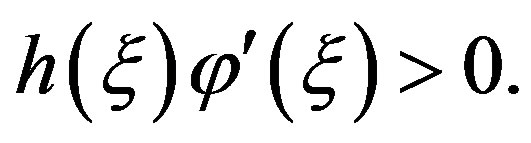
This is a contradiction, since 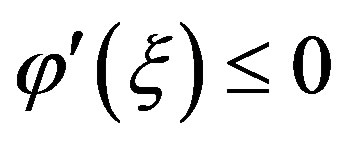 and
and 
Now the first zero  of
of  lies in
lies in 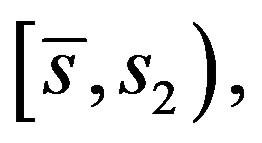 If
If 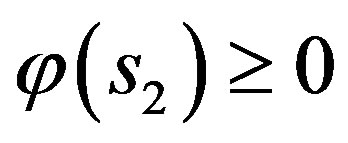 then the second zero
then the second zero 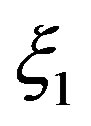 of
of  lies in
lies in  Note that in
Note that in 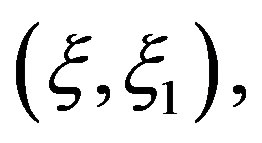
 Therefore, by identity (4)
Therefore, by identity (4)
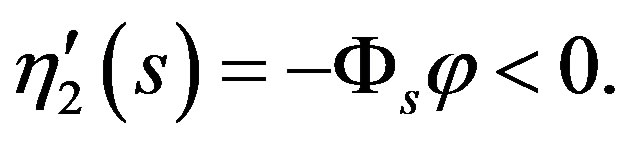
This together with
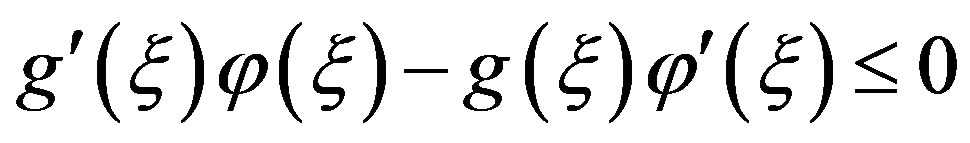
implies that

but this contradicts with ,
, 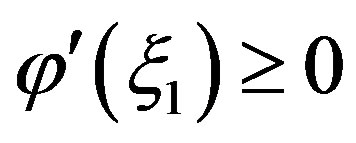 , and
, and  This finishes the proof. ■
This finishes the proof. ■
2.2. Proof of Theorem 2
Similar arguments as that of Theorem 1 could be used to prove Theorem 2. In this case, we shall make the following transform:

where
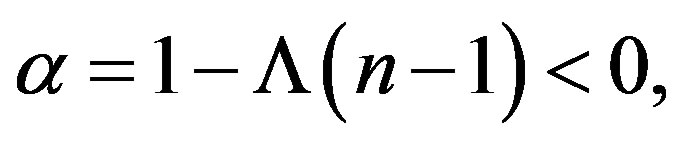
and 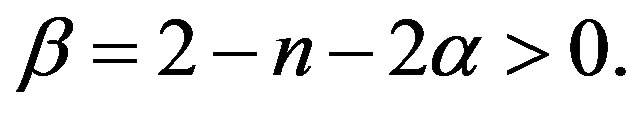 Then
Then
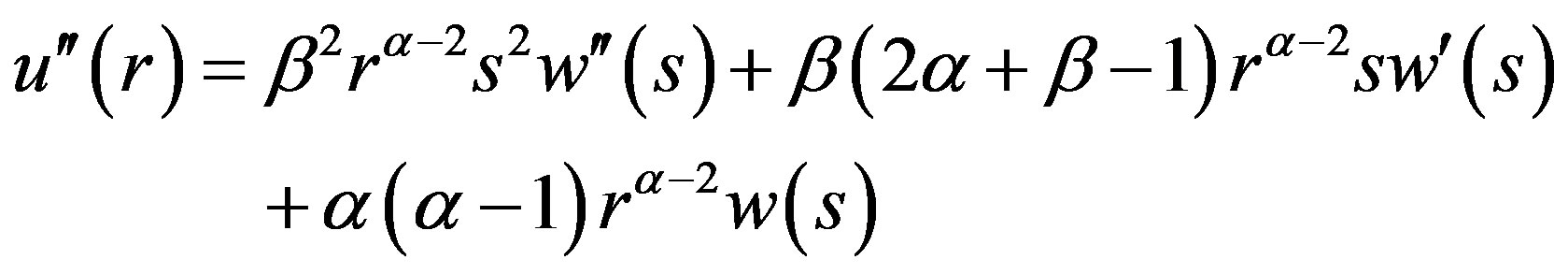 (7)
(7)
With this transformation, in the interval 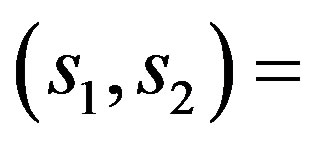
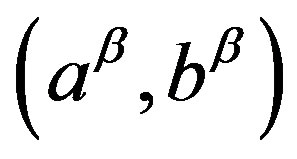 , w satisfies
, w satisfies
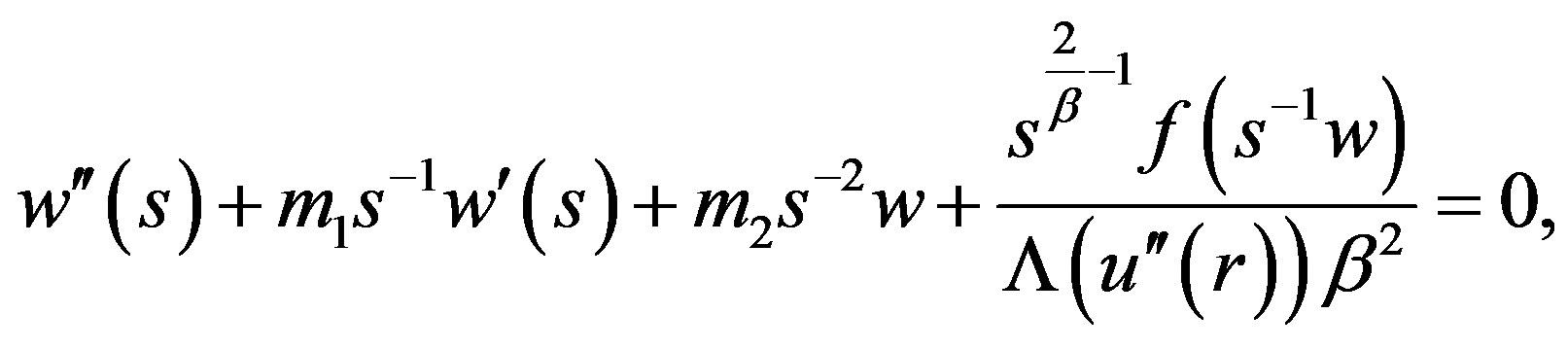 (8)
(8)
where
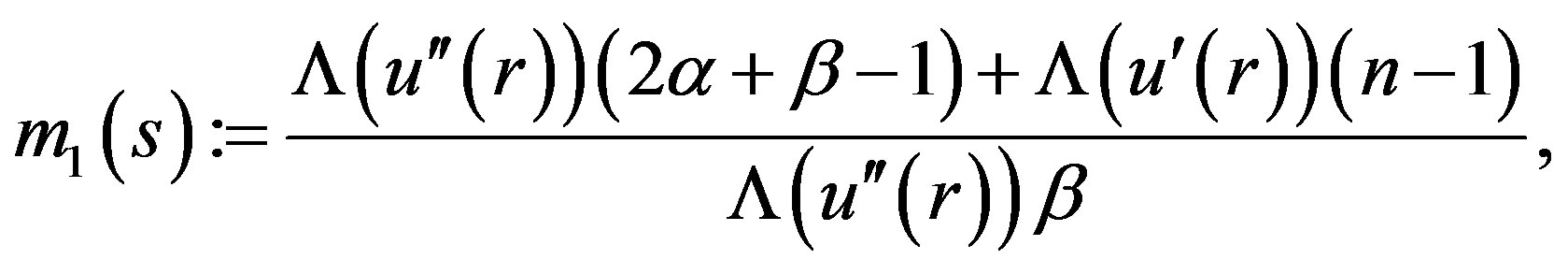
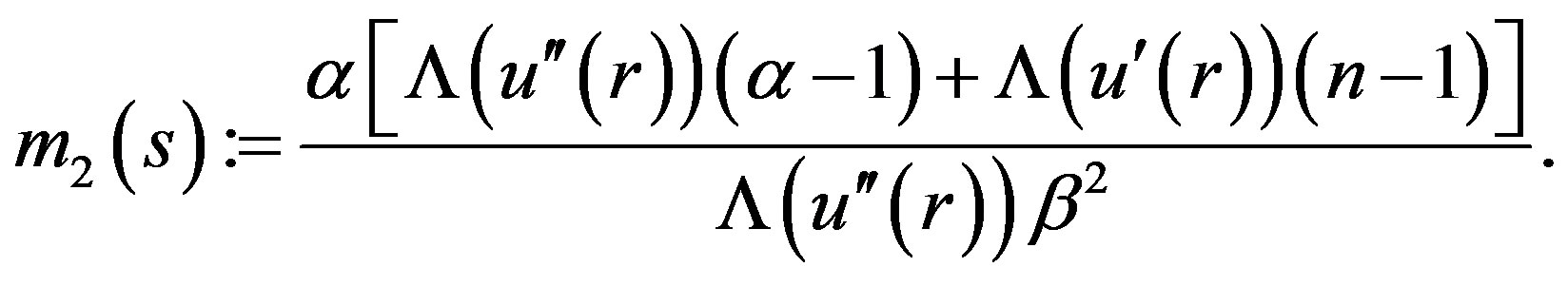
By the definition of  one could verify that
one could verify that  Note that
Note that 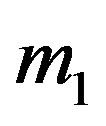 and
and 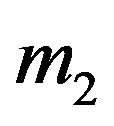 are step functions and not continous.
are step functions and not continous.
Let 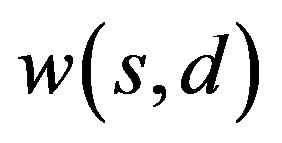 be the solution of (8) with
be the solution of (8) with 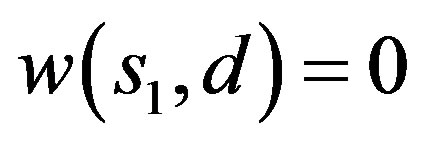 and
and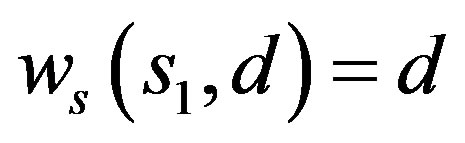 . Now similar as in the proof of Theorem 1, we suppose
. Now similar as in the proof of Theorem 1, we suppose 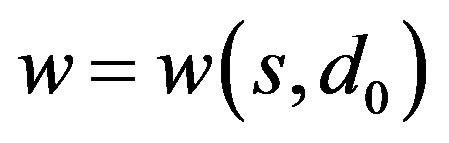 is a positive solution with Dirichlet boundary condition and
is a positive solution with Dirichlet boundary condition and . We have the following lemma, whose proof will be omitted.
. We have the following lemma, whose proof will be omitted.
Lemma 6. There exists 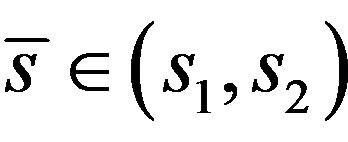 such that
such that 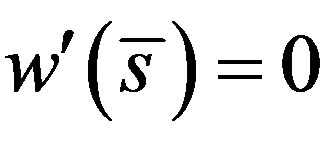 , and
, and

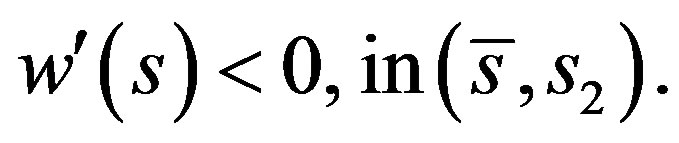
With this lemma at hand, we observe that by (8)

This combined with (7) tells us that 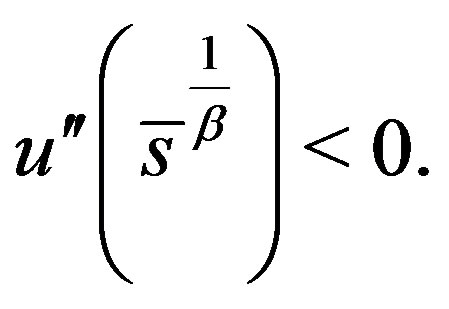 Then it is not difficult to show that for
Then it is not difficult to show that for 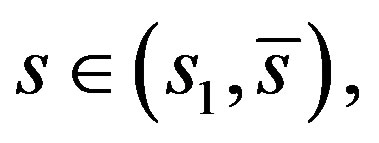
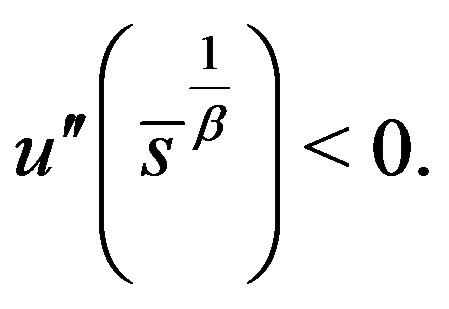 and
and 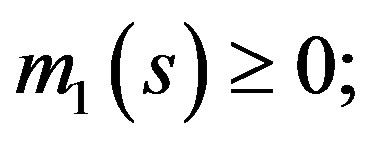 while for
while for 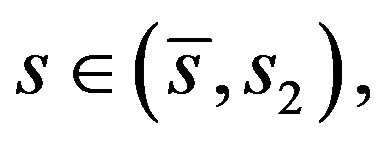

Recall that  satisfies
satisfies
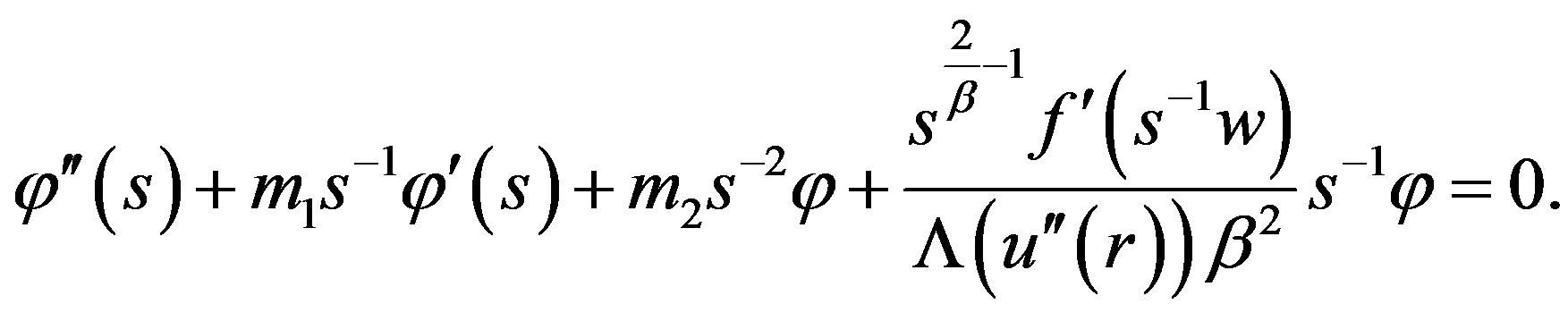
Consider the function 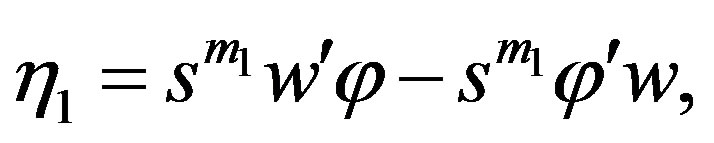 then
then
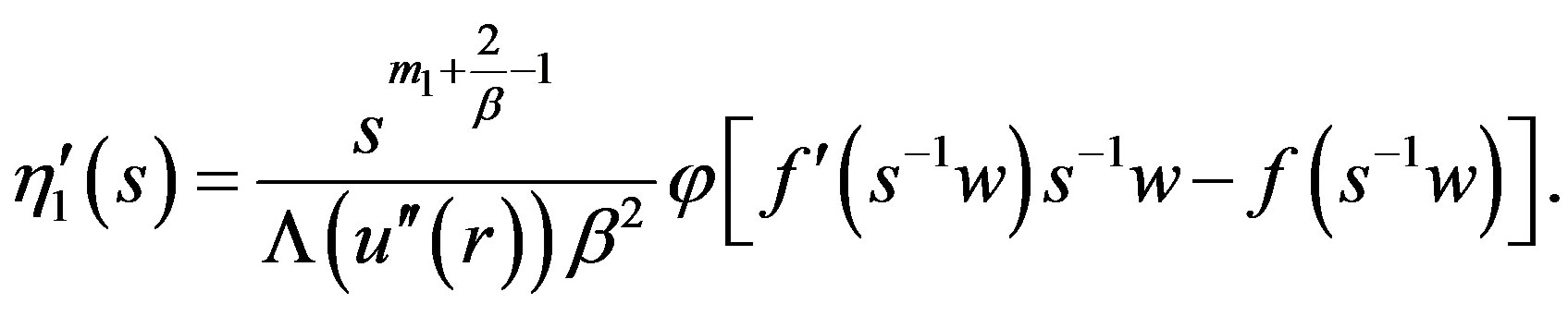
From this we infer that the function  must change sign in the interval
must change sign in the interval 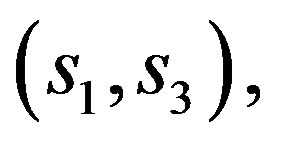 similar as that of Theorem 1.
similar as that of Theorem 1.
Now let us define
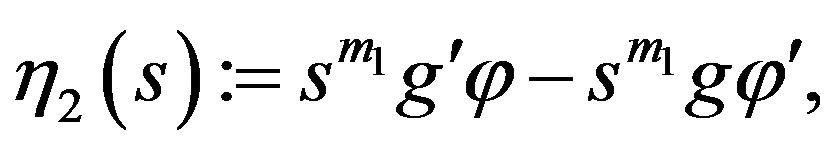
and
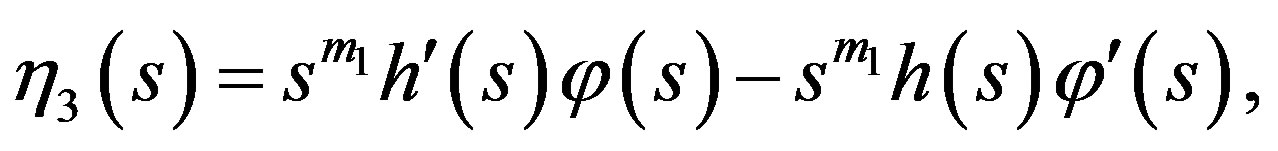
where 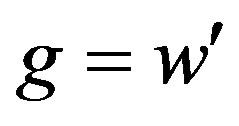 and
and 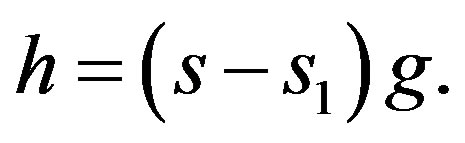 Moreover, denote
Moreover, denote
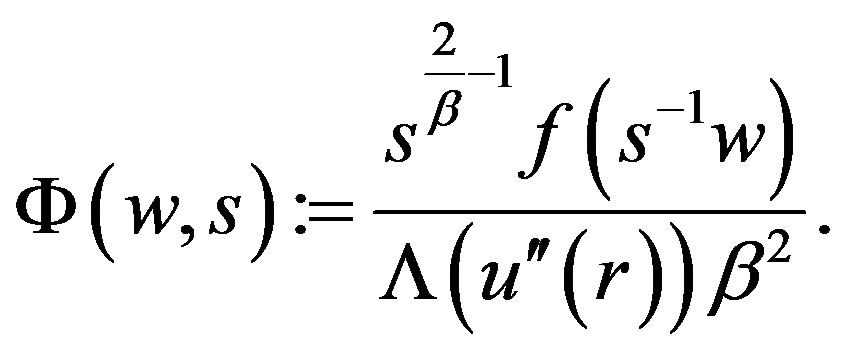
Lemma 7. There holds
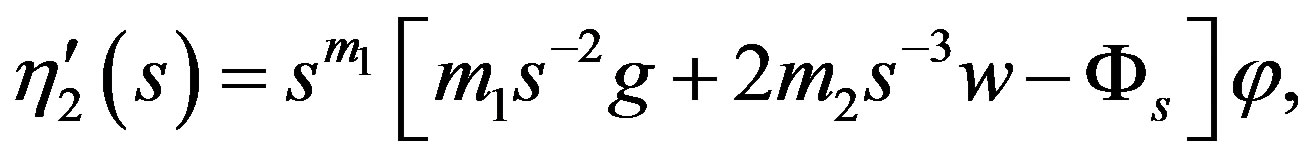

Proof. Direct calculation shows
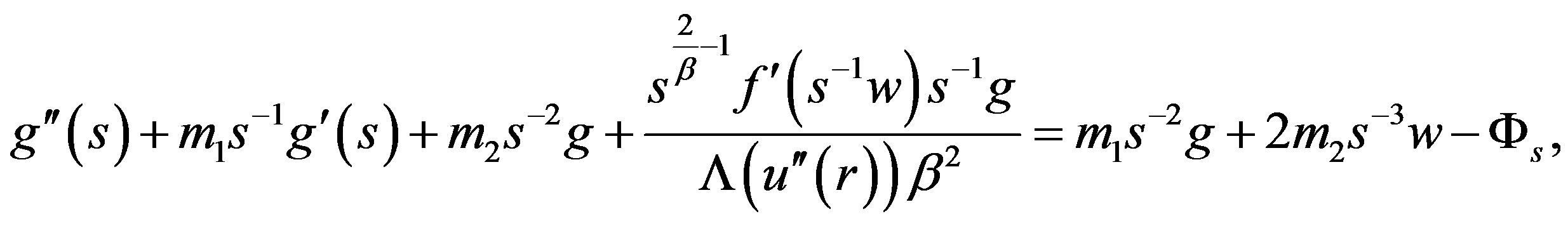
and
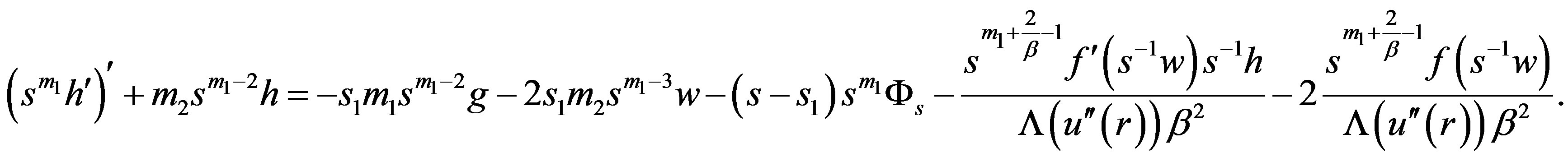
This then leads to the desired identity. ■
Now with the help of this lemma, we could prove Theorem 2.
Proof of Theorem 2. First we show the first zero  of
of  is in the interval
is in the interval 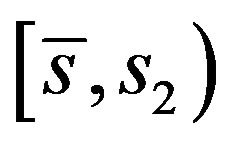 Otherwise, since
Otherwise, since
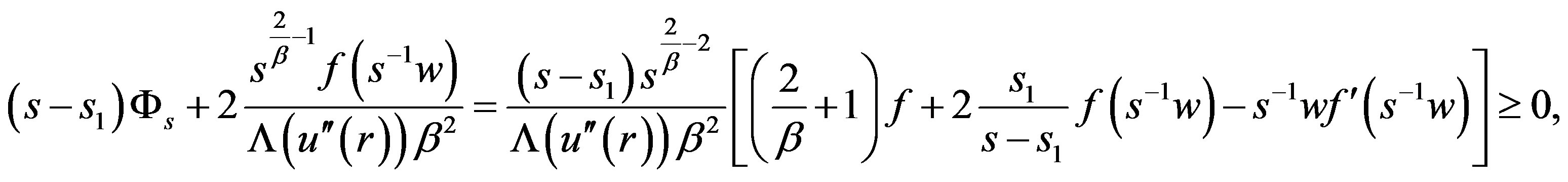
one could then use the fact that  in
in 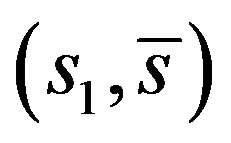 and
and 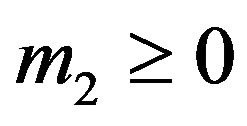 to deduce that in
to deduce that in 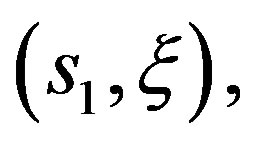

But this contradicts with 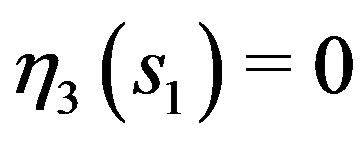 and
and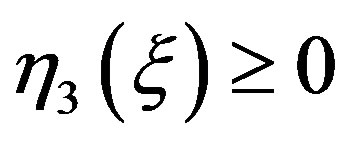 .
.
Now if the second zero  of
of  is in
is in 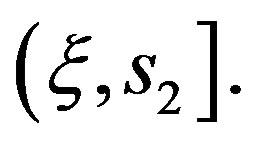 Then since
Then since
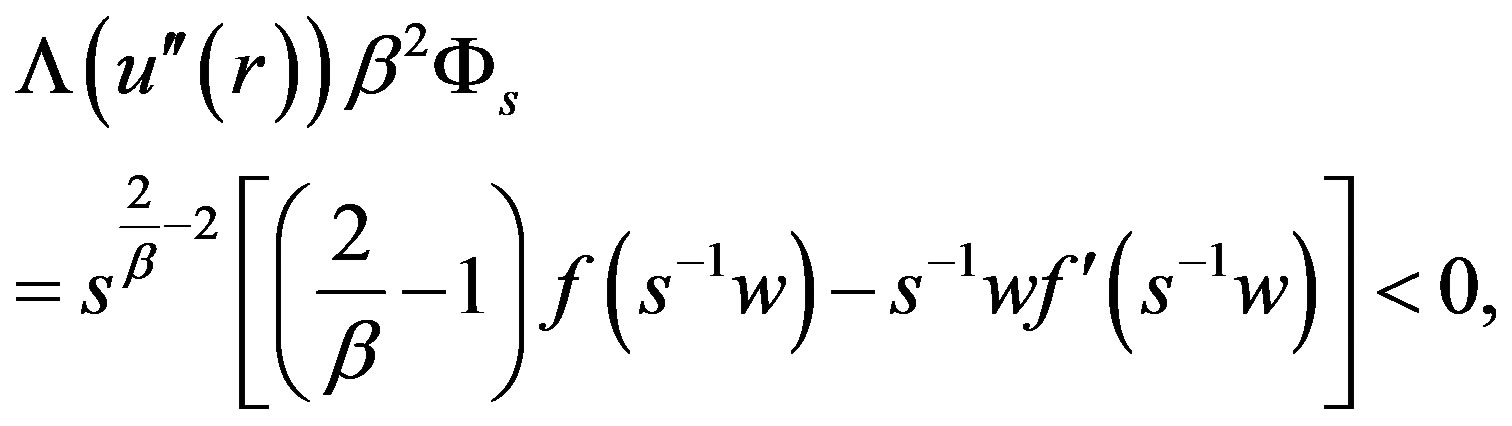
one could use 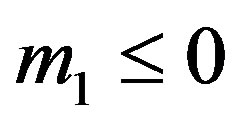 in
in 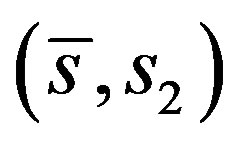 to deduce that
to deduce that 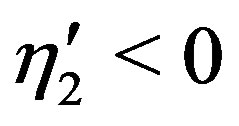 in
in 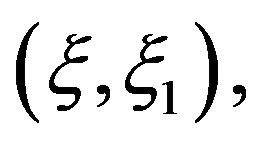 which contradicts with
which contradicts with 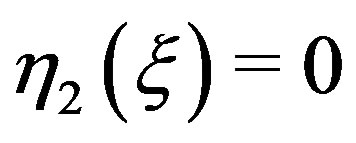 and
and 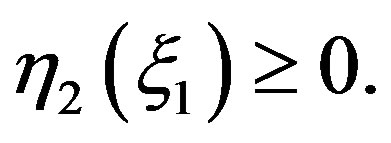 ■
■
3. Acknowledgements
The author would like to thank Prof. P. Felmer for useful discussion.
REFERENCES
- D. Gilbarg and N. S. Trudinger, “Elliptic Partial Differential Equations of Second Order,” Springer-Verlag, Berlin, 2001.
- L. A. Caffarelli and X. Cabre, “Fully Nonlinear Elliptic Equations,” American Mathematical Society Colloquium Publications, Providence, 1995.
- D. A. Labutin, “Removable Singularities for Fully Nonlinear Elliptic Equations,” Archive for Rational Mechanics and Analysis, Vol. 155, No. 3, 2000, pp. 201-214.
- P. L. Felmer and A. Quaas, “Critical Exponents for Uniformly Elliptic Extremal Operators,” Indiana University Mathematics Journal, Vol. 55, No. 2, 2006, pp. 593-629.
- P. L. Felmer and A. Quaas, “On Critical Exponents for the Pucci’s Extremal Operators,” Annales de l’Institut Henri Poincaré, Vol. 20, No. 5, 2003, pp. 843-865.
- W. M. Ni and R. D. Nussbaum, “Uniqueness and Nonuniqueness for Positive Radial Solutions of
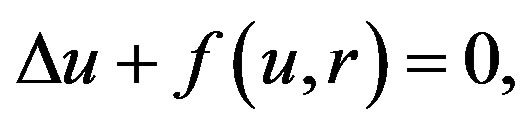 ” Communications on Pure and Applied Mathematics, Vol. 38, No. 1, 1985, pp. 67-108.
” Communications on Pure and Applied Mathematics, Vol. 38, No. 1, 1985, pp. 67-108.
NOTES
*The author is supported by NSFC under grant 11101141; SRF for ROCS, SEM; DF of NCEPU.

