World Journal of Condensed Matter Physics
Vol.4 No.3(2014), Article
ID:49397,21
pages
DOI:10.4236/wjcmp.2014.43022
Functionals and Functional Derivatives of Wave Functions and Densities
A. Gonis
Physical and Life Sciences, Lawrence Livermore National Laboratory, Livermore, USA
Email: gonis1@llnl.gov
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 May 2014; revised 2 July 2014; accepted 28 July 2014
ABSTRACT
It is shown that the process of conventional functional differentiation does not apply to functionals whose domain (and possibly range) is subject to the condition of integral normalization, as is the case with respect to a domain defined by wave functions or densities, in which there exists no neighborhood about a given element in the domain defined by arbitrary variations that also lie in the domain. This is remedied through the generalization of the domain of a functional to include distributions in the form of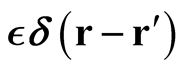 , where
, where 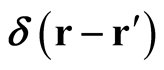 is the Dirac delta function and
is the Dirac delta function and 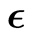 is a real number. This allows the determination of the rate of change of a functional with respect to changes of the independent variable determined at each point of the domain, with no reference needed to the values of the functional at different functions in its domain. One feature of the formalism is the determination of rates of change of general expectation values (that may not necessarily be functionals of the density) with respect to the wave functions or the densities determined by the wave functions forming the expectation value. It is also shown that ignoring the conditions of conventional functional differentiation can lead to false proofs, illustrated through a flaw in the proof that all densities defined on a lattice are
is a real number. This allows the determination of the rate of change of a functional with respect to changes of the independent variable determined at each point of the domain, with no reference needed to the values of the functional at different functions in its domain. One feature of the formalism is the determination of rates of change of general expectation values (that may not necessarily be functionals of the density) with respect to the wave functions or the densities determined by the wave functions forming the expectation value. It is also shown that ignoring the conditions of conventional functional differentiation can lead to false proofs, illustrated through a flaw in the proof that all densities defined on a lattice are 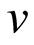 -representable. In a companion paper, the mathematical integrity of a number of long-standing concepts in density functional theory are studied in terms of the formalism developed here.
-representable. In a companion paper, the mathematical integrity of a number of long-standing concepts in density functional theory are studied in terms of the formalism developed here.
Keywords:Functional, Functional Derivative, Functional Derivative of Wave Functions, Functional Derivatives with Respect to Wave Functions, Functional Derivatives with Respect to Density, Rate of Change of a Functional, Rate of Change of Expectation Values, Rate of Change of a Wave Function

1. Introduction
Functionals and functional derivatives [1] [2] exhibit a ubiquitous presence in mathematical physics, from the calculus of variations to field theories. At the same time, this seems to generate the impression that the concept of functional differentiation applies only to functionals, as indeed that of ordinary differentiation applies to functions of coordinates. In the latter case, clearly one does not have a derivative unless one has present a function to which the procedure of differentiation can be meaningfully applied. The central result of this paper is that functional differentiation can also be interpreted as the rate of change of any quantity, the (dependent variable), that depends on a function of coordinates, the (independent variable), regardless of whether or not the dependent variable satisfies the rigorous definition of a functional of the independent variable.
Functional or not, the rate of change defines the change induced in the dependent variable with respect to a change at a single point in the domain of its independent variable and in this interpretation can be applied to a single pair,  , where
, where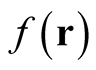 , the independent variable, is a function of coordinates, and
, the independent variable, is a function of coordinates, and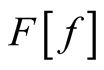 , the dependent variable, is determined through knowledge of
, the dependent variable, is determined through knowledge of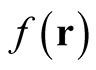 . In this form, the formalism developed here is applicable to a wave function or a single expectation value of an operator with respect to a wave function even if the wave function and expectation values are not parts of functionals.
. In this form, the formalism developed here is applicable to a wave function or a single expectation value of an operator with respect to a wave function even if the wave function and expectation values are not parts of functionals.
Indeed, the concept of the derivative as rate of change is well known from the calculus: The derivative of a function, say , at a given point,
, at a given point, 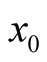 , in its domain of definition gives the rate of change of the function at
, in its domain of definition gives the rate of change of the function at  with respect to changes in its domain in the neighborhood of
with respect to changes in its domain in the neighborhood of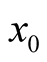 . In this case, the only way a change can be induced in the function is through a change in the variable (parameter), and the derivative takes the usual form of a limit,
. In this case, the only way a change can be induced in the function is through a change in the variable (parameter), and the derivative takes the usual form of a limit,
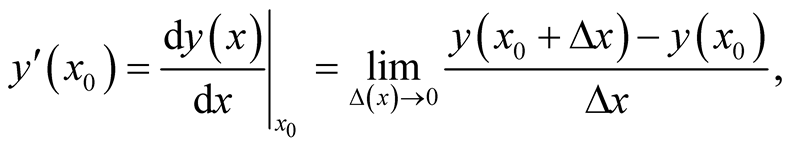 (0.1)
(0.1)
of the ratio of the difference in the function corresponding to two different points in the domain, to the difference between the two corresponding points in the domain, as the latter difference is allowed to vanish. In this case, the rate of change is synonymous with that of derivative. This exhibits the requirement that every point in the domain of  is surrounded by a possibly small but finite neighborhood throughout which the function is continuously and uniquely differentiable. In the absence of such a neighborhood, the function may not possess a derivative (
is surrounded by a possibly small but finite neighborhood throughout which the function is continuously and uniquely differentiable. In the absence of such a neighborhood, the function may not possess a derivative ( where
where  is an integer, positive, negative or zero is a case in point), and the concept of rate of change, as well as of the derivative, becomes moot.
is an integer, positive, negative or zero is a case in point), and the concept of rate of change, as well as of the derivative, becomes moot.
A characteristic feature of the derivative is the connection through the definition in (0.1) of the value of the function at  to its value at
to its value at 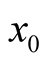 through the first order term in a Taylor series expansion, in the limit,
through the first order term in a Taylor series expansion, in the limit, 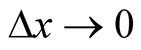 ,
,
 (0.2)
(0.2)
Analogously to a function, a functional is defined as a set of ordered pairs, 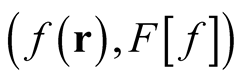 , that maps the independent variable,
, that maps the independent variable,  , an element of a normed linear space of functions (a Banach space),
, an element of a normed linear space of functions (a Banach space), 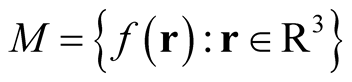 , to the field of real or complex numbers, through a well-defined mathematical procedure, e.g., an integral,
, to the field of real or complex numbers, through a well-defined mathematical procedure, e.g., an integral,
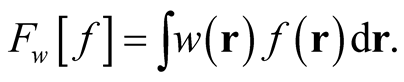 (0.3)
(0.3)
As for ordinary functions, the collection of first entries,  , forms the domain of the functional, while the set of second entries,
, forms the domain of the functional, while the set of second entries, 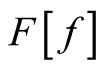 , forms its range. Examples of more general definitions of the range of a functional are given in the following. We consider only single-valued functionals in which no two elements in the range correspond to the same element in the domain.
, forms its range. Examples of more general definitions of the range of a functional are given in the following. We consider only single-valued functionals in which no two elements in the range correspond to the same element in the domain.
Again in analogy with ordinary differentiation, the functional derivative, 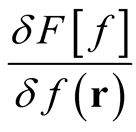 is given through the limiting procedure [3] ,
is given through the limiting procedure [3] ,
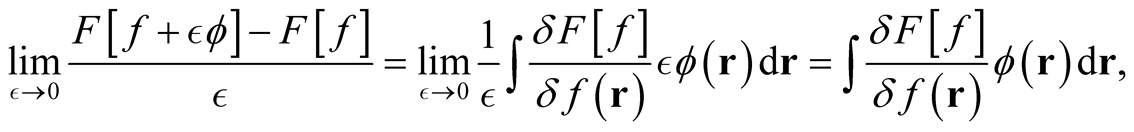 (0.4)
(0.4)
where  is arbitrary and
is arbitrary and 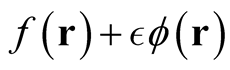 is an element of the domain of definition of
is an element of the domain of definition of 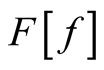 for all
for all . This definition hinges upon the existence of a small, albeit finite neighborhood of functions,
. This definition hinges upon the existence of a small, albeit finite neighborhood of functions, 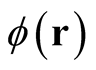 , about each point (function),
, about each point (function), 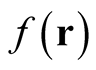 , in the domain of the functional such that every function,
, in the domain of the functional such that every function, 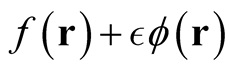 , belongs to the domain. Designating the domain of a functional with the symbol,
, belongs to the domain. Designating the domain of a functional with the symbol,  , we fave that for any
, we fave that for any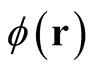 ,
,
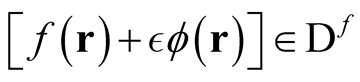 . (The concept of arbitrary
. (The concept of arbitrary  is understood under the obvious requirement that all relevant integrals must be well-defined.)
is understood under the obvious requirement that all relevant integrals must be well-defined.)
The need for arbitrariness of the test function, 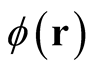 , and the consequences of its absence are discussed in Appendix.
, and the consequences of its absence are discussed in Appendix.
This formalism is immediately applicable to functionals of the form,
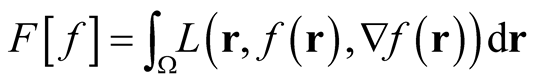 (0.5)
(0.5)
written as explicit functions of the coordinates, the independent variable and its derivative. For reference purposes and to distinguish such functionals from more general structures that enter the discussion in this paperwe will refer to them as functionals of form. In the integral above,  is the volume of a cube of side,
is the volume of a cube of side,  that, in general, can become arbitrarily large.
that, in general, can become arbitrarily large.
Beginning with the next section, we examine the analytic properties of derivatives of functionals as compared to those of a function.
2. Functional Derivatives
In view of (0.4), the change in the functional under a continuous change in the independent variable, takes the form
 (0.6)
(0.6)
implying that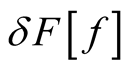 , the total change in
, the total change in 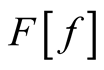 upon variation of the function,
upon variation of the function, 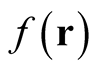 , throughout its domain is a linear superposition of the changes at each point,
, throughout its domain is a linear superposition of the changes at each point, 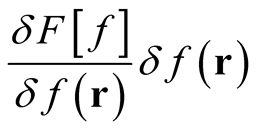 , summed (integrated point by point) over the whole range of
, summed (integrated point by point) over the whole range of 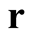 values [2]. It follows that
values [2]. It follows that 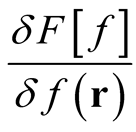 is the rate of change of the functional,
is the rate of change of the functional, 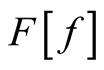 , with respect to the change in the independent variable at each point in its domain. This rate of change multiplied by a change at each point,
, with respect to the change in the independent variable at each point in its domain. This rate of change multiplied by a change at each point, 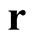 , of the independent variable that lies in the domain of the functional,
, of the independent variable that lies in the domain of the functional,
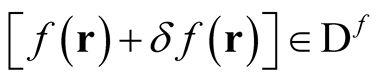 , leads to the change in the functional,
, leads to the change in the functional,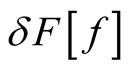 .
.
This is analogous to the change in a function, 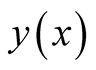 , induced by a small (infinitesimal) change in the independent variable,
, induced by a small (infinitesimal) change in the independent variable, 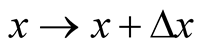 , that from (0.2), (first term in the Taylor series of a differentiable function), takes the form,
, that from (0.2), (first term in the Taylor series of a differentiable function), takes the form,
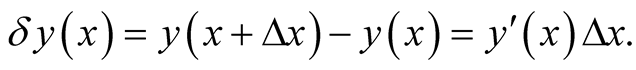 (0.7)
(0.7)
The change in the function at  equals its rate of change at
equals its rate of change at  times a difference between two points in its domain at
times a difference between two points in its domain at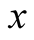 .
.
The analogous feature in the case of functionals rests on the existence of a small neighborhood of functions about a value (a function) in the domain of the functional in which the functional is uniquely and continuously differentiable through (0.4). In that case, there exists a neighborhood defined by small but arbitrary changes in the independent variable that are elements of the domain of the functional, so that the procedure in (0.4) is well-defined. As in the case of a function, the change in the functional induced by change in the independent variable takes the form, (first term in a Taylor series-like expansion of the functional),
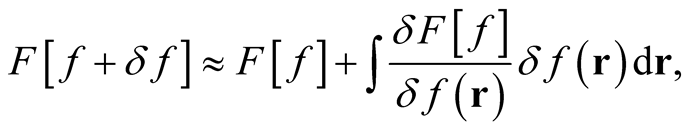 (0.8)
(0.8)
where 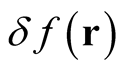 is an arbitrary (albeit small) change in the function
is an arbitrary (albeit small) change in the function 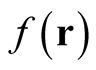 that is defined throughout space such that
that is defined throughout space such that  belongs to the domain of
belongs to the domain of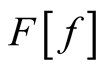 .
.
2.1. Functionals over Domains Constrained by Normalization
In the study of interacting N-particle systems, a density, 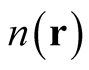 , describes the probability of a particle found at position,
, describes the probability of a particle found at position,  , and consequently must be non-negative,
, and consequently must be non-negative, 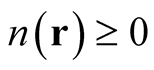 , and exhibit integral normalization,
, and exhibit integral normalization,
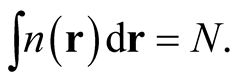 (0.9)
(0.9)
The normalization is also a formal requirement of the definition of the density in terms of the wave function describing the configurations of the system. For the case of electrons, our interest in this work, the system of 
particles is described by a wave function, 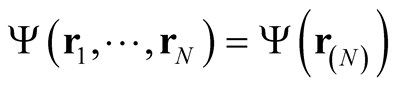 , of
, of 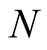 single-particle coordinates that is antisymmetric with respect to interchange of any coordinate pair (and spins, for electrons). In terms of a wave function, the density takes the form,
single-particle coordinates that is antisymmetric with respect to interchange of any coordinate pair (and spins, for electrons). In terms of a wave function, the density takes the form,
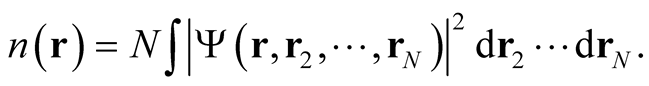 (0.10)
(0.10)
Under the general condition of unit normalization for the wave function,
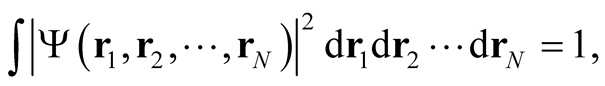 (0.11)
(0.11)
the normalization condition, Equation (0.9), follows. We now examine the determination of functional derivatives of functionals over the domain of densities, i.e., whose elements are subject to the condition of integral normalization.
2.2. Derivatives with Respect to the Density
As an illustrative example, consider the linear functional, of Equation (0.3), defined over the set of densities normalized to ,
,
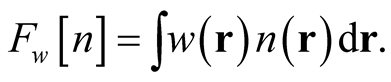 (0.12)
(0.12)
Assuming the existence of an arbitrary function, 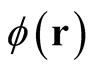 , such that
, such that 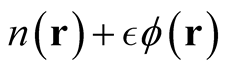 is a also a density normalized to
is a also a density normalized to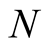 , the definition in (0.4),
, the definition in (0.4),
 (0.13)
(0.13)
leads to the identity, (see also Appendix),
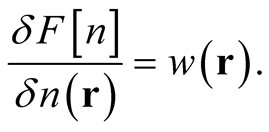 (0.14)
(0.14)
Unfortunately, in the present case, the derivation of the last equality is invalid.
When the domain of the functional is constrained to integral normalization, the test function, 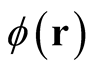 , cannot be arbitrary, but must satisfy the condition,
, cannot be arbitrary, but must satisfy the condition,
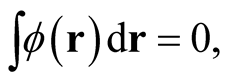 (0.15)
(0.15)
or the changed function,  , can fail the condition of integral normalization and thus lies outside the domain of the functional. In this case, neither the derivative nor its associated rate of change can seemingly be defined. Crucially, it is no longer possible to obtain the value of a functional at a function,
, can fail the condition of integral normalization and thus lies outside the domain of the functional. In this case, neither the derivative nor its associated rate of change can seemingly be defined. Crucially, it is no longer possible to obtain the value of a functional at a function, 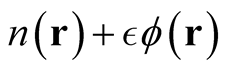 , from its value at
, from its value at 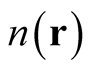 through a functional Taylor series of the type indicated in (0.8).
through a functional Taylor series of the type indicated in (0.8).
The difficulties associated with functional derivatives with respect to the density under the condition of integral normalization of the differentiating quantity have already been noted in the literature [4] (and references therein), with an attempt made at rectification. The formalism rests on attempts to obtain the change in the functional under a change in the independent variable through a modified functional Taylor-series-like expression. The formalism overlooks the cases in which the derivative is sought for isolated cases of a dependent variable and its associated independent variable in which the vary concept of a Taylor series become inapplicable.
Although the condition in (0.15) is characteristic of domains restricted to integral normalization, the rate of change of functionals defined over such domains can still be rigorously defined.
2.3. Inherent Property of Rate of Change
For reasons mentioned below, it is instructive to consider the identity functional,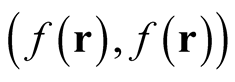 . Based on the properties of the Dirac delta function,
. Based on the properties of the Dirac delta function, 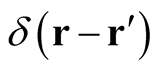 , the identity functional can be viewed as the mapping of the values of the function,
, the identity functional can be viewed as the mapping of the values of the function,  , onto itself, by means of the relation,
, onto itself, by means of the relation,
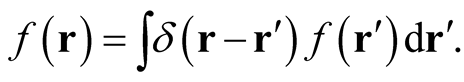 (0.16)
(0.16)
A particular interpretation of the last expression is useful: We view the quantity, 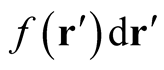 , as a perturbation of constant value,
, as a perturbation of constant value, 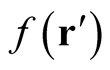 , throughout the (infinitesimal) volume
, throughout the (infinitesimal) volume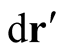 , producing the response,
, producing the response, 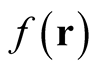 , at point,
, at point, 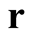 , given by the integrant in the last expression. In this sense, the Dirac delta function can be viewed as a response function, or susceptibility of free space, connecting the response of a medium (here coordinate space) to a perturbation distributed over the space.
, given by the integrant in the last expression. In this sense, the Dirac delta function can be viewed as a response function, or susceptibility of free space, connecting the response of a medium (here coordinate space) to a perturbation distributed over the space.
Now, using the definition of the functional derivative, Equation (0.4), and for general domains, unconstrained by normalization, we obtain,
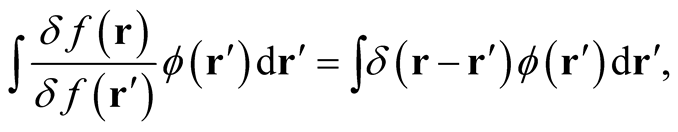 (0.17)
(0.17)
from which follows the result,
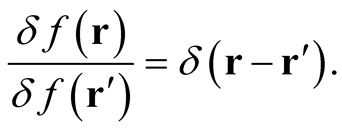 (0.18)
(0.18)
We note that the identical result is obtained through the procedure,
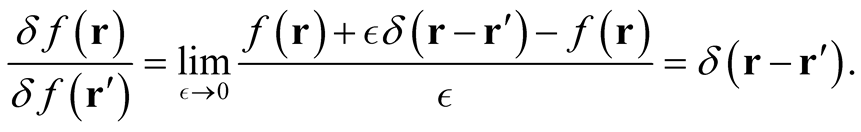 (0.19)
(0.19)
Before turning to the justification for this definition of the functional derivative, and its associated rate of change, we note some important properties: The rate of change of the identity functional is independent of the particular function in the domain of the functional and is thus an inherent property of the functional. Most importantly, the rate of change (the ratio, 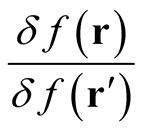 , of the change,
, of the change,  , at
, at , induced through a change,
, induced through a change,
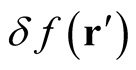 , at
, at ) is independent of
) is independent of 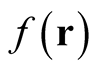 and hence requires no knowledge of a particular function, or of a different function in the domain of the functional. The functional derivative (interpreted as the rate of change) is thus an inherent property of the function at each point of the domain of the identity functional, and provides no connection to the change at a different point of the functional through a Taylor-series-like expansion. Consequently, the rate of change concept emerges as a fundamental, inherent property of functionals that may be obtained through conventional functional differentiation but exists even in cases where such differentiation is blocked. Specifically, it is applicable to each function in the domain of the functional, removing the need for the use of a test function.
and hence requires no knowledge of a particular function, or of a different function in the domain of the functional. The functional derivative (interpreted as the rate of change) is thus an inherent property of the function at each point of the domain of the identity functional, and provides no connection to the change at a different point of the functional through a Taylor-series-like expansion. Consequently, the rate of change concept emerges as a fundamental, inherent property of functionals that may be obtained through conventional functional differentiation but exists even in cases where such differentiation is blocked. Specifically, it is applicable to each function in the domain of the functional, removing the need for the use of a test function.
We can now write the general expression,
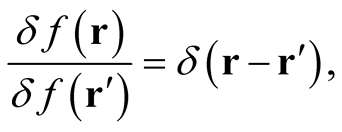 (0.20)
(0.20)
for all cases, irrespective of normalization requirements. Appendix establishes this general result along intuitive grounds.
It remains to establish that the definition of Equation (0.19) indeed corresponds to the derivative of the identity functional.
2.4. Functionals Over Delta-Function Distributions
In formal mathematics, the Dirac delta function is an example of a distribution (or generalized function) that lies outside the realm of ordinary functions [5] . The Dirac delta function cannot be obtained as the difference between two functions, or generally as a linear superposition of ordinary functions. Alternatively, no difference between two functions can be confined to a single point (a set of zero measure). Yet, functional derivatives, even in the conventional sense, encode the relative response of the functional due to a change at a single point of the function in the domain of the functional. This discussion motivates the following generalization of the domain of any functional that leads to the direct determination of a rate of change, irrespective of whether or not this can be obtained through conventional functional differentiation.
This is accomplished by extending the domain, 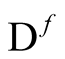 , to the set,
, to the set,
 (0.21)
(0.21)
the union of the domain of the functional and distributions proportional to the Dirac delta function. A schematic representation of this generalization is given in figure 1.
Let one of the axes in a three-dimensional Cartesian coordinate system represent the functions in 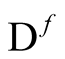 and let an axis perpendicular to it represent the values of a functional,
and let an axis perpendicular to it represent the values of a functional,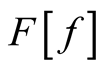 . The third axis represents the distributions,
. The third axis represents the distributions, 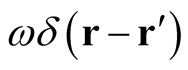 , where
, where 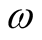 is a real number and the coordinates,
is a real number and the coordinates, 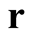 and
and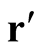 , are arbitrary. The value,
, are arbitrary. The value, 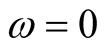 , designates the domain,
, designates the domain,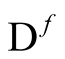 . The identity functional now takes the generalized form,
. The identity functional now takes the generalized form,
 (0.22)
(0.22)
The generalized identity functional can be expressed in the language of a function mapped onto itself,
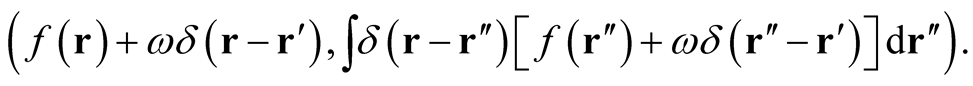 (0.23)
(0.23)
where the integral is evaluated through the recursion relation for delta functions [6] ,
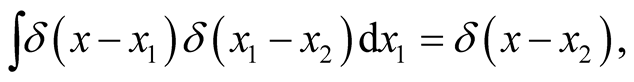 (0.24)
(0.24)
along with the property, 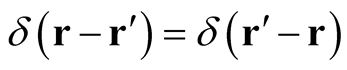 , and
, and 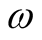 is a real number associated with a single-point,
is a real number associated with a single-point, 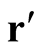 , in space. This feature is often described by replacing
, in space. This feature is often described by replacing 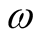 with the infinitesimal,
with the infinitesimal,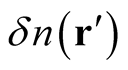 . Note that now, the constraint of integral normalization no longer applies to the identity functional. Thus, in the domain that includes distributions, we have,
. Note that now, the constraint of integral normalization no longer applies to the identity functional. Thus, in the domain that includes distributions, we have,
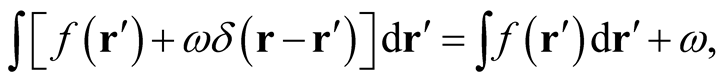 (0.25)
(0.25)
that is generally non-integral, even if the integral over 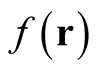 is confined to an integer. It follows that
is confined to an integer. It follows that 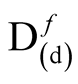 is the domain of the identity functional in the sense of a functional that maps a function in its domain onto itself.
is the domain of the identity functional in the sense of a functional that maps a function in its domain onto itself.
The derivative of the identity functional at any point in the plane defined by 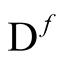 and
and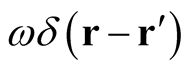 , takes the
, takes the

Figure 1. Schematic representation of functionals over distributions. The axis, 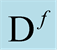 , contains the domain of a functional consisting of ordinary functions in three-dimensional space, the axis labeled,
, contains the domain of a functional consisting of ordinary functions in three-dimensional space, the axis labeled, 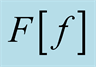 , encodes the values of the functionals (in a schematic representation), and the third axis labels continuously the amount of a distribution (the Dirac delta function) associated with any element of
, encodes the values of the functionals (in a schematic representation), and the third axis labels continuously the amount of a distribution (the Dirac delta function) associated with any element of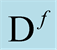 . The “plane” defined by
. The “plane” defined by  and
and  is a generalization of the domain,
is a generalization of the domain, 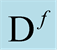 , that includes distributions.
, that includes distributions.
form,
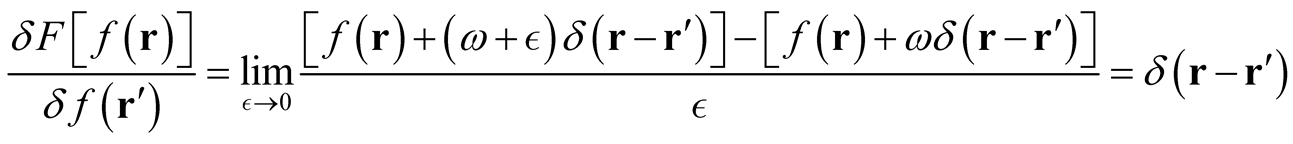 (0.26)
(0.26)
where 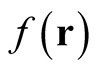 remains fixed. The main property of this result is that it is independent of
remains fixed. The main property of this result is that it is independent of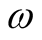 , so that it can be applied to the axis
, so that it can be applied to the axis 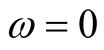 designating the domain of the functional,
designating the domain of the functional,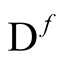 . At any point on that axis (i.e., for any
. At any point on that axis (i.e., for any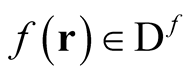 ), the derivative defining the rate of change of any functional over a domain, irrespective of normalization restrictions, now takes the following equivalent forms,
), the derivative defining the rate of change of any functional over a domain, irrespective of normalization restrictions, now takes the following equivalent forms,

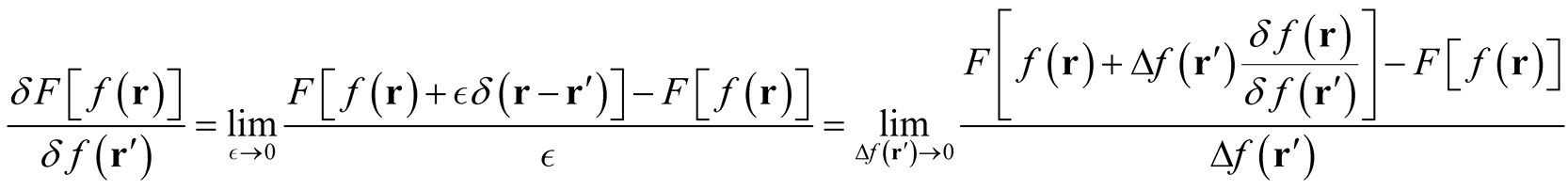 (0.27)
(0.27)
where 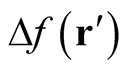 is an infinitesimal (but generally a real number). The definition in (0.27) remains valid in all cases, even when the domain of a functional,
is an infinitesimal (but generally a real number). The definition in (0.27) remains valid in all cases, even when the domain of a functional, 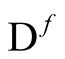 , is required to satisfy the condition of integral normalization.
, is required to satisfy the condition of integral normalization.
The general validity of this definition follows because the derivative of any function with respect to itself is not a function, but a distribution. As such it lies outside the domain of functions (that may be constrained by normalization). By writing 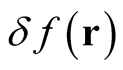 not explicitly as a difference of two functions, but rather as the derivative with respect of a function with respect to itself times a vanishing infinitesimal, we accomplish the variation of the functional without the need to consider differences of functions in its conventional domain.
not explicitly as a difference of two functions, but rather as the derivative with respect of a function with respect to itself times a vanishing infinitesimal, we accomplish the variation of the functional without the need to consider differences of functions in its conventional domain.
Furthermore, the definition is applicable to all functionals of form because the derivative in these cases can be expressed as the ordinary derivative of a differentiable function times the functional derivative of the identity. In fact, it is applicable to isolated single pairs of the form (independent variable, dependent variable) that may not form part of a functional (collection of pairs). The significance of these results is highlighted below.
2.5. Derivatives of Differentiable Functionals
The following is a well-known property of functional differentiation. Let a functional of form, 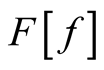 , correspond to a function of the parameter,
, correspond to a function of the parameter, 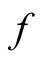 , that is differentiable in the ordinary sense with respect to
, that is differentiable in the ordinary sense with respect to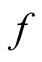 , so that the quantity,
, so that the quantity, 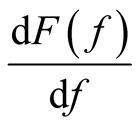 , is well defined. Then, the functional derivative takes the form,
, is well defined. Then, the functional derivative takes the form,
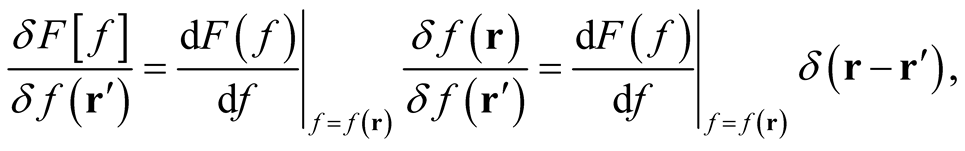 (0.28)
(0.28)
which justifies the general result in (0.27).
Although the formalism just completed provides a justification of the derivative given by (0.27), this result is already freely used in the literature [7] .
A simple example illustrates the point. Given the functional, 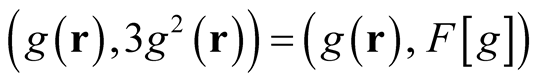 , using the rule established in (0.28), we obtain,
, using the rule established in (0.28), we obtain,
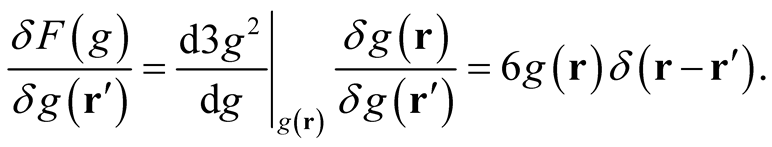 (0.29)
(0.29)
This is an example of the rule of parametric differentiation that leads to the rate of change of any functional of form (that is written explicitly in terms of the independent variable): Differentiate the function, 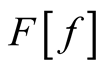 , with
, with 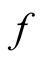 treated as a parameter, evaluate the derivative at
treated as a parameter, evaluate the derivative at  and affix the Dirac delta function to the result. The rule is readily extended to compound functions of a function, as well to cases when such functions occur in expressions under integral signs.
and affix the Dirac delta function to the result. The rule is readily extended to compound functions of a function, as well to cases when such functions occur in expressions under integral signs.
2.6. Summary
The rate of change of a functional with respect to the change of the independent variable at one point in space is an inherent property of a single point in the functional (a single ordered pair, (independent variable, dependent variable)), and in every case can be defined without reference to the value of the functional, or the independent variable, at different ordered pairs. As shown below, this allows the definition of the rate of change of quantities dependent on functions even if the dependence extends only to a single pair,  , that may or may not be part a functional.
, that may or may not be part a functional.
However, a Taylor-series like representation of the functional at at points close to a given independent variable can only be defined through the integral in (0.8) if the domain of the functional admits all possible infinitesimal neighborhoods about each point in the domain that differ arbitrarily from that point and throughout which the functional is continuously differentiable. In that case, the rate of change can be used to determine the value of the dependent variable at points (functions) near the function where the rate of change has been defined.
At the same time, the lack of a Taylor series representation is of no consequence in cases where the functional consists of a single pair of independent variable and its associated dependent variable, where the concept of a Taylor series becomes moot. As pointed out in the following discussion, far from being a limitation, this feature is consistent with the analytic properties of wave functions as well as with the manner in which the study of nature proceeds in terms of non-interacting systems (see following sections and comment in the Discussion section).
3. Functionals of Wave Functions and Densities
We consider the case in which the domain of a functional is required to satisfy a set of additional conditions such as that of normalization to an integer, as in the case of the wave functions of a many-particle Hilbert space and the corresponding densities obtained from them, Equations (0.9), (0.10) and (0.11).
Now, there exists no neighborhood about a particular density such that arbitrary variations of the form, 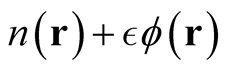 , define another density for arbitrarily chosen test function,
, define another density for arbitrarily chosen test function,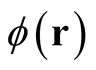 . (For example, with
. (For example, with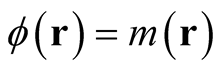 , where
, where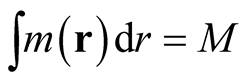 , the quantity
, the quantity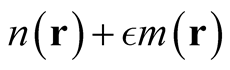 , is normalized to a fractional number failing the definition of a density.)
, is normalized to a fractional number failing the definition of a density.)
In this case, however, the concept of functional derivative as a rate of change remains valid and applicable where it retains all the properties attending to the rate of change such as assessments of the value of a quantity at a particular point with respect to its minimum based on the value of the rate of change at that point. The remainder of the paper is devoted to the exploitation of this feature and the derivation of formal results resting on it.
Two more advantages emerge. First, the rate of change of an expression such as an expectation value of an operator with respect to a wave function (defining the expectation value), or the density (defined by the wave function) can be obtained irrespective of whether or not the expectation value is a functional of the wave function or the density.
The second advantage is concerned with expressions, possibly functionals of wave functions or the density, that do not exhibit explicitly the independent variable, but are non-the-less dependent on it. Such expressions are not defined as mere functions of the independent variable, functionals of form, but rather by means of a procedure based on the independent variable (see Section 7.2). We shall refer to such functionals as functionals of process and in the following, we develop the general formalism for their derivatives (rates of change).
We generalize the concept of independent and dependent variable to apply to any ordered pair of the form,
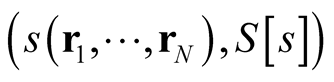 , where
, where 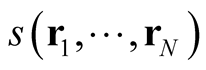 is a function of a multi-dimensional coordinate space, such as a wave function or a density, and
is a function of a multi-dimensional coordinate space, such as a wave function or a density, and 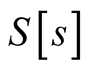 is a quantity that is determined through a procedure that depends exclusively on
is a quantity that is determined through a procedure that depends exclusively on  but may not necessarily be written explicitly in terms of
but may not necessarily be written explicitly in terms of .
.
In all that follows, we seek to determine the rate of change of functionals (or generally expectation values that are not necessarily functionals over wave functions or densities) with respect to changes at one point of the independent variable. We identify cases in which , the dependent quantity can be expressed as a mere function of its independent variable,
, the dependent quantity can be expressed as a mere function of its independent variable, 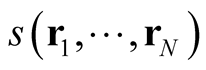 , and differentiate based on the procedure of parametric differentiation derived from the identity in (0.29). In each case, we express the dependent quantity (functional or not) in terms of the independent variable and proceed to obtain its rate of change with respect to that variable at a given, fixed independent variable.
, and differentiate based on the procedure of parametric differentiation derived from the identity in (0.29). In each case, we express the dependent quantity (functional or not) in terms of the independent variable and proceed to obtain its rate of change with respect to that variable at a given, fixed independent variable.
4. Functional Derivatives with Respect to Potential
The first demonstration of parametric differentiation (functional differentiation through (0.29)), is to determine the derivative, 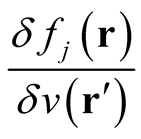 , where
, where  is an eigensolution of the single-particle Schrödinger equation for a potential,
is an eigensolution of the single-particle Schrödinger equation for a potential, 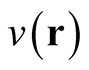 ,
,
 (0.30)
(0.30)
where 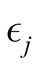 is the corresponding eigenvalue. The evaluation of the derivative is most conveniently carried out on the basis of the integral representation of the Schrödinger equation, the Lippmann-Schwinger equation at energy,
is the corresponding eigenvalue. The evaluation of the derivative is most conveniently carried out on the basis of the integral representation of the Schrödinger equation, the Lippmann-Schwinger equation at energy,  ,
,
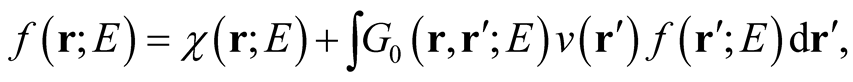 (0.31)
(0.31)
where  is the solution in the absence of the potential, and
is the solution in the absence of the potential, and 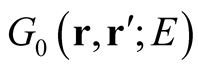 encodes the boundary conditions (behavior at infinity). We bypass the question whether or not these solutions define functionals of the potential; we use only the fact that they are parametrically dependent on it, and we seek the rate of change of the solution with respect to the change in the potential at a given point. The parametric dependence of the solution on the potential is exhibited through the iterative solution of the Lippmann-Schwinger equation,
encodes the boundary conditions (behavior at infinity). We bypass the question whether or not these solutions define functionals of the potential; we use only the fact that they are parametrically dependent on it, and we seek the rate of change of the solution with respect to the change in the potential at a given point. The parametric dependence of the solution on the potential is exhibited through the iterative solution of the Lippmann-Schwinger equation,
 (0.32)
(0.32)
Analogously, the evaluation of  is obtained as an iterative solution of the expression,
is obtained as an iterative solution of the expression,
 (0.33)
(0.33)
leading to the series,
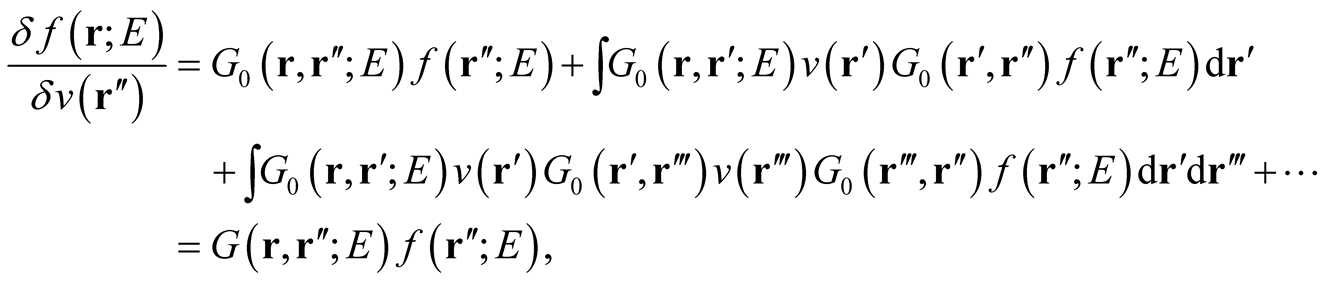 (0.34)
(0.34)
where,

 (0.35)
(0.35)
is the single-particle Green function in the presence of the potential. The Green function can also be written in the form of a resolvent,
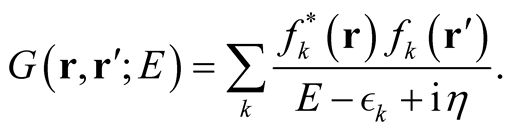 (0.36)
(0.36)
In the limit,  , we obtain,
, we obtain,
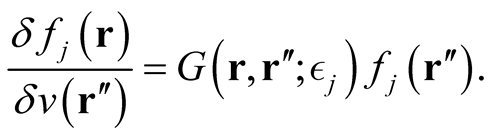 (0.37)
(0.37)
It is worth emphasizing that the last expression for the derivative (the rate of change of 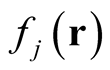 at a point,
at a point, 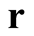 with respect to a change in the potential at
with respect to a change in the potential at ) is obtained strictly in terms of the solution for the given potential, with no requirement of considering the solutions at different potentials.
) is obtained strictly in terms of the solution for the given potential, with no requirement of considering the solutions at different potentials.
Consistent with the result established above, the functional derivative in (0.37) is confined to a single Hilbert space, the Hilbert space defined by the potential, 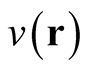 (and the number of particles under
(and the number of particles under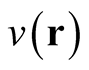 ).
).
5. Derivatives of Expectation Values
Consider a generally complex, many-particle wave function,  , in multidimensional coordinate space, subject to the normalization condition,
, in multidimensional coordinate space, subject to the normalization condition,
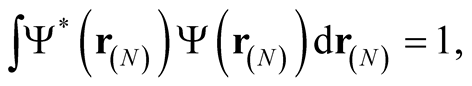 (0.38)
(0.38)
and the expectation value,
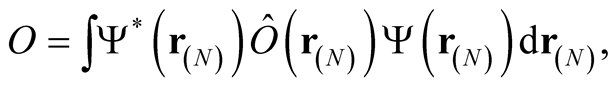 (0.39)
(0.39)
for an operator, 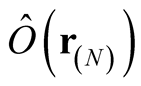 , in the space.
, in the space.
For a fixed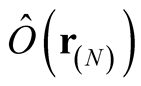 , the integral in (0.39) defines a functional of
, the integral in (0.39) defines a functional of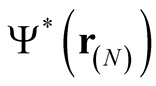 , or of
, or of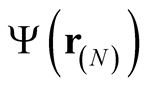 , a set of ordered pairs,
, a set of ordered pairs, 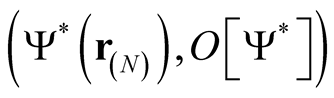 , or equivalently of
, or equivalently of , in which the independent variable,
, in which the independent variable, 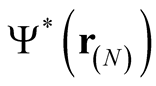 , ranges over all multidimensional functions that obey the normalization condition in (0.38) and for which the integral in (0.39) is well defined.
, ranges over all multidimensional functions that obey the normalization condition in (0.38) and for which the integral in (0.39) is well defined.
We seek to determine the functional derivative,  , of
, of 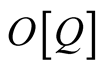 with respect to
with respect to 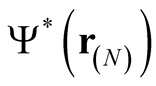 at a fixed multidimensional point,
at a fixed multidimensional point,  , through the conventional definition of functional differentiation,
, through the conventional definition of functional differentiation,
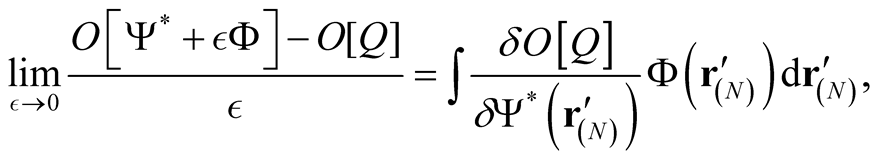 (0.40)
(0.40)
where  is arbitrary. At this point, however, the operation of conventional functional differentiation runs into an insurmountable barrier.
is arbitrary. At this point, however, the operation of conventional functional differentiation runs into an insurmountable barrier.
Even though the functional is one of form, exhibiting explicitly the independent variable, the requirement of arbitrariness may cause the quantity,  , to violate the condition of normalization thus failing to satisfy the definition of a many-particle wave function.
, to violate the condition of normalization thus failing to satisfy the definition of a many-particle wave function.
The functional derivative interpreted as a rate of change can now be obtained, however, through a generalization of the concept of parametric derivative to multi-dimensional space. In this procedure, using the definition of the multidimensional Dirac function and its properties under integration, and where 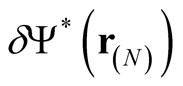 is an infinitesimal, (a number) we have,
is an infinitesimal, (a number) we have,
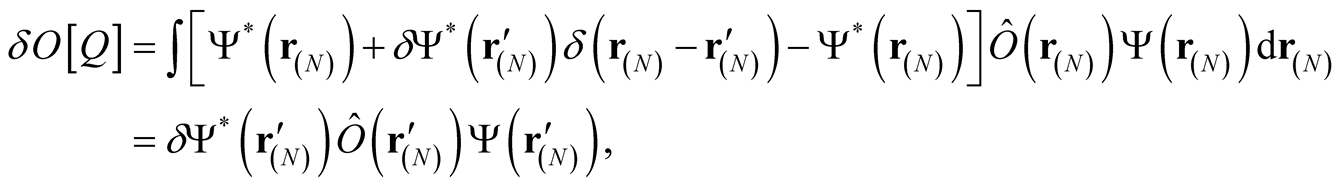 (0.41)
(0.41)
so that
 (0.42)
(0.42)
The feature that allows differentiation of expectation values is clear: The quantity, 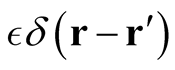 , can be interpreted as the difference between two elements in the domain of the functional obtained at a single (possibly multi-dimensional) point! In this sense, the use of the Dirac delta function yields the correct functional derivative (or, parametric derivatives are functional derivatives when interpreted as rates of change).
, can be interpreted as the difference between two elements in the domain of the functional obtained at a single (possibly multi-dimensional) point! In this sense, the use of the Dirac delta function yields the correct functional derivative (or, parametric derivatives are functional derivatives when interpreted as rates of change).
6. Derivation of the Time-Dependent Schrödinger Equation
The derivation of the time-dependent Schrödinger equation proceeds from the consideration of the action integral,
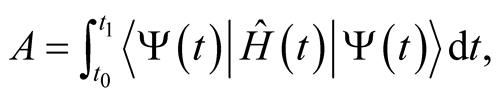 (0.43)
(0.43)
evaluated at the state (wave function), 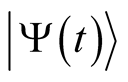 , that causes it to vanish, and obtain the derivative with respect to
, that causes it to vanish, and obtain the derivative with respect to
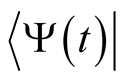 at the vanishing point. From the result in (0.41), and with the operator
at the vanishing point. From the result in (0.41), and with the operator 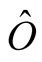 identified with the timedependent Hamiltonian,
identified with the timedependent Hamiltonian,
 (0.44)
(0.44)
we have (in operator form),
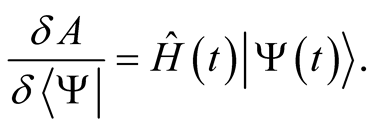 (0.45)
(0.45)
Setting the derivative in (0.45) equal to zero yields the TDSE,
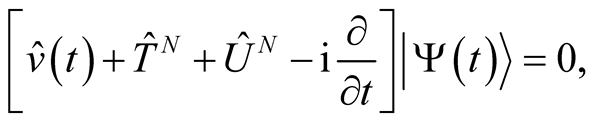 (0.46)
(0.46)
to be solved under some initial condition. This is none other than the well-known condition determining the TDSE as the vanishing of the derivative of the action at its stationary point. In this case, the TDSE is derived through the vanishing of the rate of change of the action with respect to changes in the wave function at points in multidimensional space.
7. Functionals of the Density and their Derivatives
We recall that in a many-particle system described by a wave function, 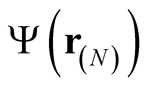 , a density,
, a density, 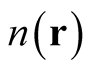 , describes the probability of finding a particle at
, describes the probability of finding a particle at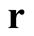 , and is given by means of the relation,
, and is given by means of the relation,
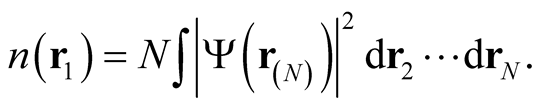 (0.47)
(0.47)
Consequently, a density function satisfies the conditions of positive semi-definiteness, 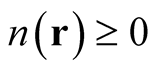 , and, because of the unit normalization of wave functions, normalization to an integer,
, and, because of the unit normalization of wave functions, normalization to an integer,
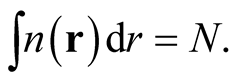 (0.48)
(0.48)
As a direct result of the normalization condition, conventional functional differentiation, requiring the value of a functional,  , at the point,
, at the point,  , is formally blocked: For arbitrary
, is formally blocked: For arbitrary , the function,
, the function, 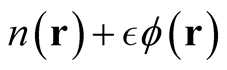 , may fail normalization and hence lies outside the domain of definition of
, may fail normalization and hence lies outside the domain of definition of . We inquire as to the possibility of differentiating functionals of the density that may not exhibit the presence of the independent variable explicitly. Such functionals arise through procedures (functionals of process) that are based on a density but are not mere functions of the density.
. We inquire as to the possibility of differentiating functionals of the density that may not exhibit the presence of the independent variable explicitly. Such functionals arise through procedures (functionals of process) that are based on a density but are not mere functions of the density.
We consider the set, 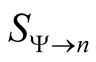 , the multivalued functional consisting of all N-particle coordinate anti-symmetric wave functions (in the following we suppress spin),
, the multivalued functional consisting of all N-particle coordinate anti-symmetric wave functions (in the following we suppress spin),  , that lead to a given density,
, that lead to a given density, 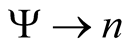 , through the relation in (0.47). Cioslowski [8] -[10] has described a formal procedure that generates the functional,
, through the relation in (0.47). Cioslowski [8] -[10] has described a formal procedure that generates the functional,
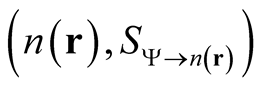 . Given a density, each element of
. Given a density, each element of 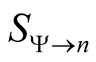 is expressed as a linear superposition of Slater determinants, each constructed form
is expressed as a linear superposition of Slater determinants, each constructed form 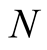 elements of an orthonormal and complete basis,
elements of an orthonormal and complete basis,  , based on
, based on
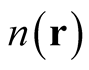 . Cioslowski also shows that each element of this basis depends parametrically on the density and possesses a well-defined functional derivative with respect to the density. This derivative is obtained through knowledge of the density alone, with no reference made to wave functions leading to other densities.
. Cioslowski also shows that each element of this basis depends parametrically on the density and possesses a well-defined functional derivative with respect to the density. This derivative is obtained through knowledge of the density alone, with no reference made to wave functions leading to other densities.
The set of all possible expectation values of many-particle operators with respect to the elements of 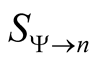 forms also a multivalued functional of the density.
forms also a multivalued functional of the density.
Although rigorous, Cioslowski’s formal procedure for the derivative is computationally out of reach. Here, we develop an equally rigorous alternative technique for differentiating the elements of 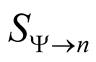 with respect to the density. Not unexpectedly, the method rests on the concept of parametric differentiation.
with respect to the density. Not unexpectedly, the method rests on the concept of parametric differentiation.
We recall the basic requirement of parametric differentiation of one function by another: The symbol,
 , encodes the relative rate of change of
, encodes the relative rate of change of 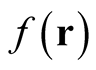 at a point,
at a point,  , induced through the change of the function
, induced through the change of the function
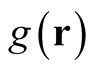 at a generally different point. The expression,
at a generally different point. The expression,  , does not refer to the difference between two functions throughout space; rather it is a number (an infinitesimal that is allowed to vanish in a limiting process) describing the change in a given function at a given point. A similar description applies to
, does not refer to the difference between two functions throughout space; rather it is a number (an infinitesimal that is allowed to vanish in a limiting process) describing the change in a given function at a given point. A similar description applies to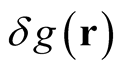 .
.
Therefore, as stated above, the expression, 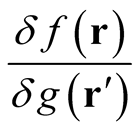 , has manifest meaning if and only if the coordinate dependence of the function
, has manifest meaning if and only if the coordinate dependence of the function 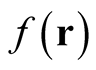 can be mapped onto an analytic (differentiable) function of
can be mapped onto an analytic (differentiable) function of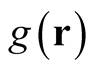 , (e.g.,
, (e.g.,
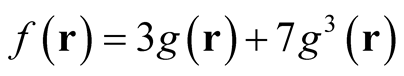 , say). In that case, the derivative,
, say). In that case, the derivative, 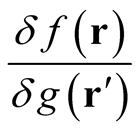 , proceeds by applying the expression for the derivative of the functional identity, (0.18), to the expression providing an exact representation of
, proceeds by applying the expression for the derivative of the functional identity, (0.18), to the expression providing an exact representation of  throughout space in therms of its parametrization by
throughout space in therms of its parametrization by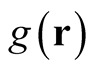 .
.
The following point is possibly both self-evident as well as subtle: There is nothing in the form of a function (its dependence on coordinates) that betrays its functional dependence on a particular density. A given function, (e.g.,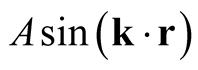 ), can be part of the orbitals forming various Slater determinants (an infinite number), each leading to a different density. In determining the functional derivative (parametric derivative) of an expectation value with respect to one of these densities, the derivative of the particular function must be obtained with respect to the density associated with that determinant. Whether or not the derivative of this function exists with respect to a different density, associated with a different Slater determinant and a different expectation value is inconsequential to the proceedings confined to a given density [11] , so that the various parametric derivatives with respect to different densities are unrelated to one another, and cannot be connected through parametric differentiation.
), can be part of the orbitals forming various Slater determinants (an infinite number), each leading to a different density. In determining the functional derivative (parametric derivative) of an expectation value with respect to one of these densities, the derivative of the particular function must be obtained with respect to the density associated with that determinant. Whether or not the derivative of this function exists with respect to a different density, associated with a different Slater determinant and a different expectation value is inconsequential to the proceedings confined to a given density [11] , so that the various parametric derivatives with respect to different densities are unrelated to one another, and cannot be connected through parametric differentiation.
Now, in the case in which a function is to be differentiated with respect to a given density, there exists an immediate and exact mapping of its dependence on coordinates to an analytic, differentiable form that explicitly exhibits the density. It is an expansion in the equidensity basis [12] .
7.1. Equidensity Basis
For the sake of completeness, in this subsection, we introduce the spin variable [13] [14] .
An exact mapping of a function,  (say an orbital arising from the solution of a single-particle Schrödinger equation), onto an analytic (differentiable) expression can be had in terms of the expansion of the function in terms of the equidensity basis. Namely, for each orbital,
(say an orbital arising from the solution of a single-particle Schrödinger equation), onto an analytic (differentiable) expression can be had in terms of the expansion of the function in terms of the equidensity basis. Namely, for each orbital, 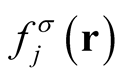 , that as an element of a Slater determinant contributes to the formation of a density,
, that as an element of a Slater determinant contributes to the formation of a density,
 (0.49)
(0.49)
with the sum ranging over some collection of orbitals, we write,
 (0.50)
(0.50)
with
 (0.51)
(0.51)
being the elements of an orthonormal and complete basis [15] [16] [12] , the equidensity basis, where
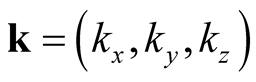 denote a set of three signed integers, the
denote a set of three signed integers, the  are expansion coefficients, and the vector
are expansion coefficients, and the vector
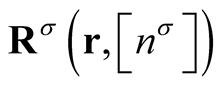 is defined by the expressions,
is defined by the expressions,
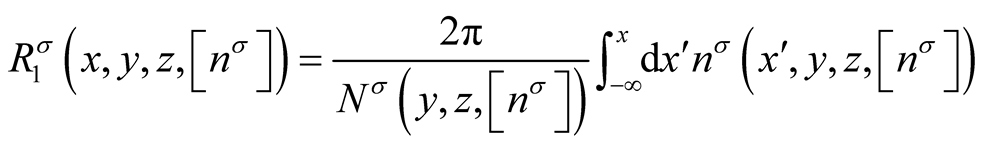
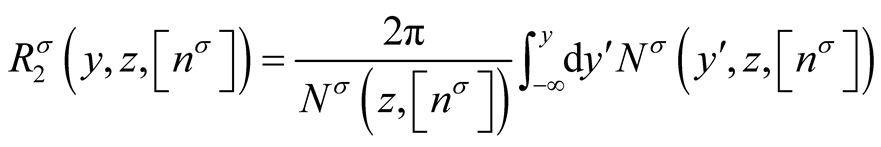
 (0.52)
(0.52)
with
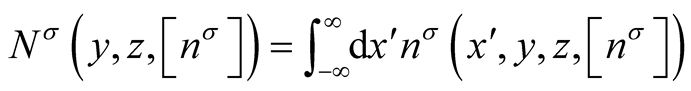
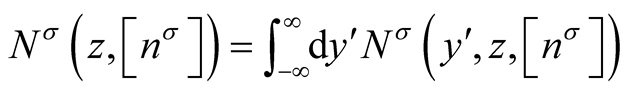
 (0.53)
(0.53)
where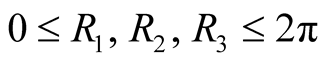 . The transformation,
. The transformation, 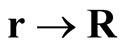 , maps [12] three-dimensional coordinate space onto the volume of a cube of side
, maps [12] three-dimensional coordinate space onto the volume of a cube of side 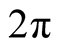 with the points at infinity mapped onto the surface of the volume [12] . Note that the
with the points at infinity mapped onto the surface of the volume [12] . Note that the 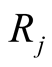 are written explicitly in terms of the density through a function of the density that is uniquely differentiable in terms of the densety based on (0.18) that now takes the form,
are written explicitly in terms of the density through a function of the density that is uniquely differentiable in terms of the densety based on (0.18) that now takes the form,
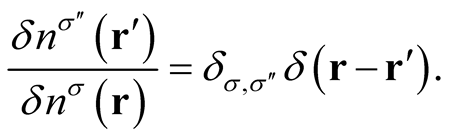 (0.54)
(0.54)
In accordance with the closing remarks in the previous section, an orbital may contribute to a number of different densities (in principle an infinite number) ant thus possesses unique parametric derivatives with respect to each of these densities.
The particular choice of 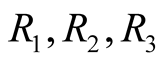 displayed above is not unique, with other choices, e.g. permuting coordinates or other coordinate systems, being possible [17] as well. However, given the uniqueness of the derivative, the different choices lead to identical results. In the following we use the definitions given in equations (0.52) and (0.53).
displayed above is not unique, with other choices, e.g. permuting coordinates or other coordinate systems, being possible [17] as well. However, given the uniqueness of the derivative, the different choices lead to identical results. In the following we use the definitions given in equations (0.52) and (0.53).
The coefficients, 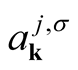 , are given as the overlap integrals,
, are given as the overlap integrals,
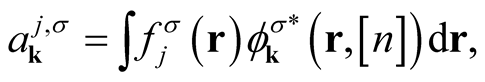 (0.55)
(0.55)
and are generally complex numbers. These coefficients change according to the density used to construct the equidensity basis. That density, on the other hand, is uniquely chosen as the density to which a given orbital may be contributing through (0.49), with no connection existing between the coefficients at one expansion (some density) to those at another. (It may be tempting to think of the equidensity basis as a functional of the density concluding that the coefficient for a given orbital at one density may be connected through functional differentiation to coefficients of the same orbital of another density. Recall, however, that the very concept of conventional functional differentiation is disallowed over the domain of densities, and the only differentiation available is that of parametric differentiation confined to the space of given density. Furthermore, any general function of coordinates, one that is not necessarily a solution of a Sxhrödinger equation and hence not a functional of a density can be expanded in terms of the equidensity basis for any density, each expansion defined in terms of coefficients that have no functional connection to those at another density. It follows that the question of the derivatives of the coefficients is mathematically moot.)
Finally, the parametric derivative of an expectation value with respect to a density formed by a wave function that leads to that density can be determined through the parametric derivative of the expansion of the wave function in the equidensity basis for that density. No connection of that derivative to that at another density that may contain the same orbital exists, or can be sought in terms of functional derivatives of the coefficients of the expansions.
Explicit examples of such derivatives of the Coulomb potential energy determined with respect to Slater determinants leading to a density are given in other work [14] .
7.2. Wave Functions Leading to a Density
Cioslowski [8] -[10] has given a formal procedure for determining the set of antisymmetric N-particle wave functions leading to a given density normalized to 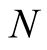 through the relation,
through the relation,
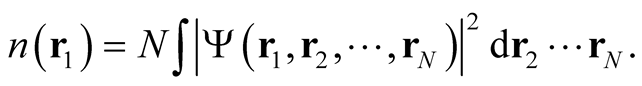 (0.56)
(0.56)
Suppressing spin, a brief summary of the procedure is given below, with details to be found in the original papers [8] -[10] .
Any antisymmetric N-particle wave function can be written as a linear superpositions of mutually orthonormal Slater determinants (in Einstein summation notation),
 (0.57)
(0.57)
where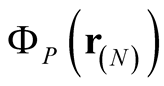 , with
, with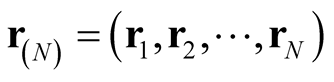 , is a Slater determinant of order
, is a Slater determinant of order 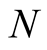 constructed from
constructed from 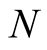 elements (orbitals),
elements (orbitals), 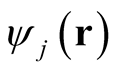 , that form a complete and orthonormal basis in single-particle, three-dimensional coordinate space. The orbitals,
, that form a complete and orthonormal basis in single-particle, three-dimensional coordinate space. The orbitals, 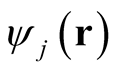 , are constructed so that the modulus of the wave function,
, are constructed so that the modulus of the wave function,  squared and integrated over all coordinates but one yields the density through (0.56).
squared and integrated over all coordinates but one yields the density through (0.56).
This property follows from the form of the orbitals (see [8] ),
 (0.58)
(0.58)
where the functions, 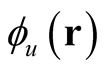 , form a complete but not necessarily orthonormal basis in three-dimensional coordinate space, the matrix,
, form a complete but not necessarily orthonormal basis in three-dimensional coordinate space, the matrix, 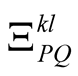 , is defined by the integral over all coordinates but one of two Slater determinants,
, is defined by the integral over all coordinates but one of two Slater determinants,
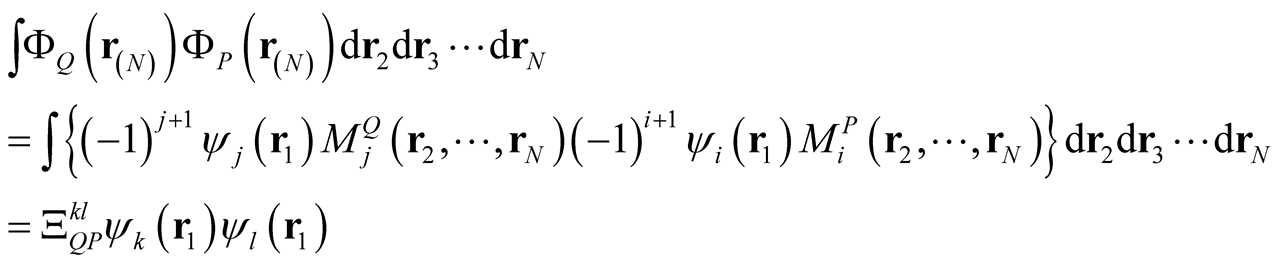 (0.59)
(0.59)
where in the second line we have used the expansion of a determinant along its first row, 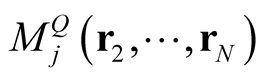 is the minor of
is the minor of 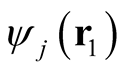 in
in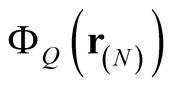 , and the matrix
, and the matrix 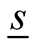 is defined as the square root of a matrix,
is defined as the square root of a matrix,
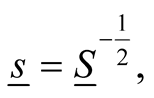 (0.60)
(0.60)
whose elements are given by the integrals,
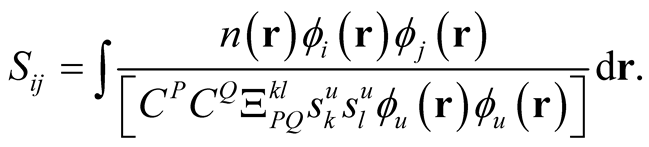 (0.61)
(0.61)
The non-linear nature of the transformation, 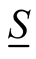 , between the set of functions,
, between the set of functions, 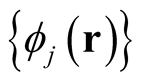 and
and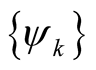 , is clear.
, is clear.
The existence and convergence of 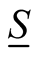 has been demonstrated by Cioslowski [9] [10] .
has been demonstrated by Cioslowski [9] [10] .
Cioslowski [8] shows that the set of orbitals, 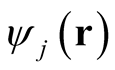 , that form the Slater determinant,
, that form the Slater determinant, 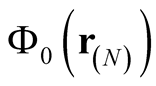 , are given by the expression,
, are given by the expression,
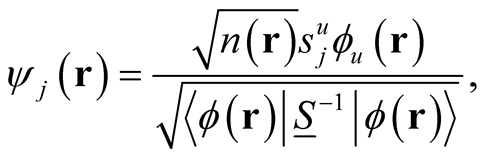 (0.62)
(0.62)
where,
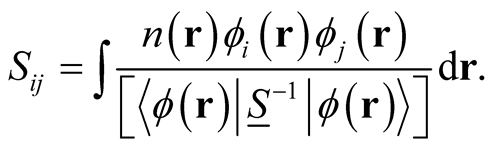 (0.63)
(0.63)
In the last two expressions, a vector-matrix notation is used, so that
 .
.
We now examine the properties of the orbitals defining , keeping in mind the parametric dependence of the matrix
, keeping in mind the parametric dependence of the matrix 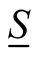 on the density.
on the density.
Clearly, the set, 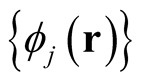 , is arbitrary and hence not a functional of the density. Because of this, the matrix,
, is arbitrary and hence not a functional of the density. Because of this, the matrix,
 , whose value depends on
, whose value depends on 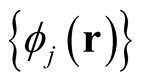 is not a functional of the density either, and consequently neither are the orbitals,
is not a functional of the density either, and consequently neither are the orbitals,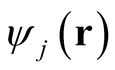 . However, in the absence of degeneracy, the set of orbitals forming
. However, in the absence of degeneracy, the set of orbitals forming 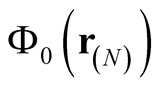 are a uniquely defined functional of the density regardless of the choice of
are a uniquely defined functional of the density regardless of the choice of  (the determination of
(the determination of  and other fuctionals in terms of procedures based on the density—functional of process—is given in detail in the paper following this one).
and other fuctionals in terms of procedures based on the density—functional of process—is given in detail in the paper following this one).
Cioslowski also shows that near its converged limit, 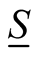 can ne solved by iteration,
can ne solved by iteration,
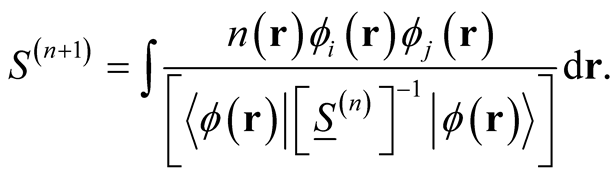 (0.64)
(0.64)
Because of the explicit presence of the density at each iteration step, the matrix, 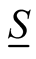 , possess a unique parametric derivative with respect to the density,
, possess a unique parametric derivative with respect to the density,
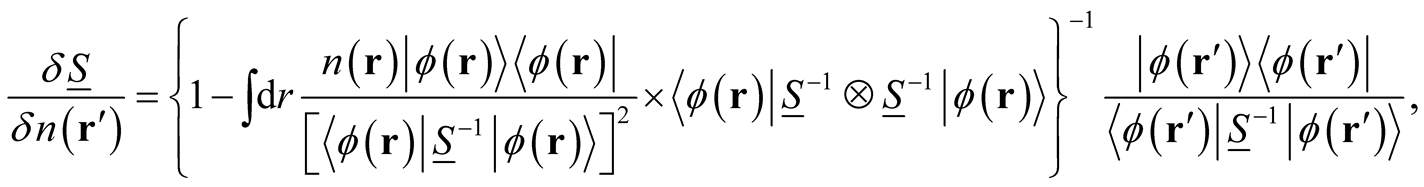 (0.65)
(0.65)
where the tensor product,  , is defined with respect to three operators (matrices) in the form,
, is defined with respect to three operators (matrices) in the form,
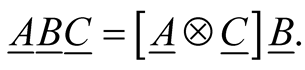 (0.66)
(0.66)
Expressions for the parametric derivative of  (under the conditions just stated) in the general case beyond the determinantal form are given by Cioslowski [10] and the reader is referred to that work for details (It is to be noted that Cioslowski’s [8] -[10] deliberations are based on a single density with no connection made to any other density).
(under the conditions just stated) in the general case beyond the determinantal form are given by Cioslowski [10] and the reader is referred to that work for details (It is to be noted that Cioslowski’s [8] -[10] deliberations are based on a single density with no connection made to any other density).
The orbitals contributing to 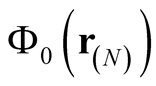 are unique and independent of the choice of the states,
are unique and independent of the choice of the states, 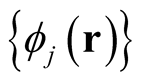 , (and the corresponding values of
, (and the corresponding values of ). Because each
). Because each 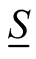 has a parametric derivative with respect to the density, the orbitals, given as the linear combination in Equation (0.62), have a unique parametric (functional) derivative with respect to
has a parametric derivative with respect to the density, the orbitals, given as the linear combination in Equation (0.62), have a unique parametric (functional) derivative with respect to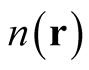 .
.
To summarize: Each density, 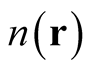 , defines its own space of parametric (functional) differentiation of individual orbitals used to construct the antisymmetric, N-particle wave functions,
, defines its own space of parametric (functional) differentiation of individual orbitals used to construct the antisymmetric, N-particle wave functions,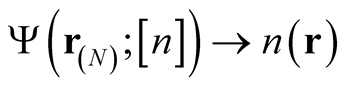 . The parametric derivatives of constrained search functionals, or general expectation values of operators, with respect to these wave functions can be obtained by means of the parametric derivatives of the orbitals under the integral signs defining the expectation value. They, in turn, can be obtained by the rigorous means of expanding in the equidensity basis and differentiating the expansion.
. The parametric derivatives of constrained search functionals, or general expectation values of operators, with respect to these wave functions can be obtained by means of the parametric derivatives of the orbitals under the integral signs defining the expectation value. They, in turn, can be obtained by the rigorous means of expanding in the equidensity basis and differentiating the expansion.
8. Functional Derivatives of Ensembles
Ensembles, or mixed states, are described by a density matrix [3] ,
 (0.67)
(0.67)
with, . Through the expression in (0.47), each of the states in the ensemble,
. Through the expression in (0.47), each of the states in the ensemble, 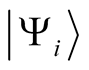 , gives rise to a density,
, gives rise to a density, 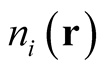 , each normalized to an integral value,
, each normalized to an integral value,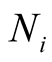 . The density of the ensemble takes the form,
. The density of the ensemble takes the form,
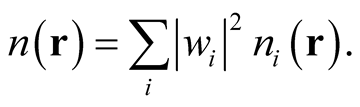 (0.68)
(0.68)
The expression in (0.67) describes a system that is known to occupy a state, 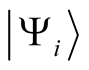 , with classical probability,
, with classical probability,
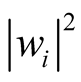 . Expectation values of operators,
. Expectation values of operators,  , are given by means of the trace rule,
, are given by means of the trace rule,
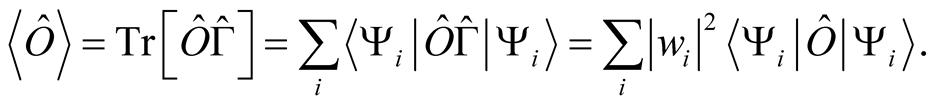 (0.69)
(0.69)
The functional derivative of 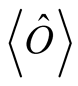 with respect to the density is given through the parametric derivative, by applying the universal, density-independent change,
with respect to the density is given through the parametric derivative, by applying the universal, density-independent change, 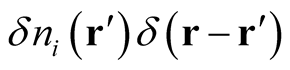 , where
, where 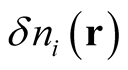 is an infinitesimal independent of
is an infinitesimal independent of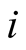 , to each of the terms in (0.69), and obtain the derivative with respect to the densities defined by each of the individual wave functions,
, to each of the terms in (0.69), and obtain the derivative with respect to the densities defined by each of the individual wave functions,
 (0.70)
(0.70)
In the last expression, each differentiation is performed at the density defined by the individual states,  , through expansions of corresponding orbitals in terms of the equidensity basis at that particular density, and subsequent (parametric) differentiation of the expansion. In short, the functional derivative (rate of change) of an ensemble of states is the ensemble of the rates of change of each of the states in the ensemble.
, through expansions of corresponding orbitals in terms of the equidensity basis at that particular density, and subsequent (parametric) differentiation of the expansion. In short, the functional derivative (rate of change) of an ensemble of states is the ensemble of the rates of change of each of the states in the ensemble.
9. The v-Representability of Densities Defined on a Lattice
In a well-known paper [18], Kohn purports to show that a density defined on a lattice is 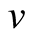 -representable, i.e., it can always be obtained from the wave function of the ground state of an interacting system defined on a discrete set of points (lattice) confined into a box, with vanishing conditions on the potential and the density on the sides of the box.
-representable, i.e., it can always be obtained from the wave function of the ground state of an interacting system defined on a discrete set of points (lattice) confined into a box, with vanishing conditions on the potential and the density on the sides of the box.
Kohn’s proof relies on the following theorem:
If 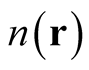 is a v-representable density, then so is
is a v-representable density, then so is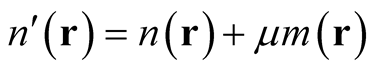 , where
, where 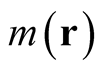 is arbitrary [except for the trivial conditions
is arbitrary [except for the trivial conditions ,
, 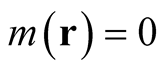 on the boundary], provided that
on the boundary], provided that  is small enough.
is small enough.
The proof hinges on the existence of a small neighborhood around a given density throughout which derivatives with respect to the density can be uniquely obtained in a continuously differentiable manner.
The existence of such a neighborhood guarantees the existence of uniquely defined Frèchet derivatives. As already stated above, however, no such neighborhood exists for the case of domains defined in terms of functions that satisfy the definition of a density.
The flaw in the proof is evident in the expression of the theorem. The function, 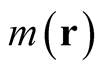 , cannot be both arbitrary and also required to integrate to zero. Clearly, unless it has this property, then
, cannot be both arbitrary and also required to integrate to zero. Clearly, unless it has this property, then 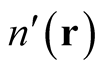 is not a density, but if it does, then
is not a density, but if it does, then 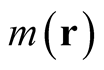 is not arbitrary. The condition,
is not arbitrary. The condition, 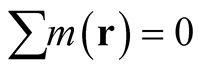 , the analogue of
, the analogue of 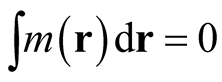 is not only non-trivial, it precludes the carrying out of functional differentiation altogether and negates the proof of the theorem. (This does not, necessarily, disprove the theorem, however, which may indeed be true but would require an alternative proof.)
is not only non-trivial, it precludes the carrying out of functional differentiation altogether and negates the proof of the theorem. (This does not, necessarily, disprove the theorem, however, which may indeed be true but would require an alternative proof.)
10. Discussion
The central result of this paper is the use of the Dirac delta function, rather than an arbitrary test function defined over an extended domain in coordinate space, as in the conventional formulation, in the determination of functional derivatives of quantities whose determination depends on a function of coordinates. In this procedure, the formalism leads to the rate of change of a dependent variable with respect to the change at one point of the independent variable (a function) in all cases, even when the function is constrained to integral normalization, thus blocking conventional formulations of the functional derivative.
In the case of general functionals, whose domains are free of conditions of normalizations, conventional functional derivatives coincide with parametric derivatives and Equation (0.6) remains valid. In the presence of externally imposed conditions, such as fixed normalization, for example, conventional functional differentiation becomes inapplicable whereas rates of change can still be readily evaluated through parametric differentiation.
This feature is particularly useful when a functional is known to exhibit an extremum (e.g., a minimum). Then, the rate of change at the minimum vanishes, while that at any other point is non-zero (signifying that the value of the functional is higher than that at its minimum, for example).
The paper provides a rigorous, exact procedure for the functional differentiation of expectation values of operators in quantum mechanics with respect to wave functions or the densities obtained from the wave functions entering the determination of the expectation value in question. Emphasis is placed on derivatives with respect to the density, especially since wave functions generally are not written explicitly in terms of the density. In this case, the dependence of the wave function on coordinates can be mapped exactly onto that of the density by means of an expansion in an orthonormal and complete basis (the equidensity basis at the density of the discussion) [12], allowing parametric differentiation to proceed unimpeded.
Finally, a comment on the absence of a Taylor-series-like expression that connects expectation values at one density to those at another, possibly nearby density. There are both mathematical as well as fundamental, physical reasons for this absence.
First, as mentioned in the text, a density defines a unique functional as the set of all antisymmetric wave functions that lead to the density. There is, however, no one-to-one correspondence between the elements of the sets defined by two different densities, and no functional of the form,  , where the dependent variable is a single wave function, can be established. In this case, the very concept of Taylor series connection between different wave function corresponding to different densities becomes moot.
, where the dependent variable is a single wave function, can be established. In this case, the very concept of Taylor series connection between different wave function corresponding to different densities becomes moot.
Second, recall that a density may correspond to the ground state of a many-particle system and thus belong to the Hilbert space determined by the potential acting on, and number of particles of, the system. This Hilbert space is separate and disjoint from that of any other system that is independent of (non-interacting with) the one in question. Consequently, there exists no connection between the spaces provided by the properties (quantum states or functional derivatives) of either system separately.
11. Acknowledgements
Discussions with colleagues at LLNL and ORNL provided motivation for this work. I am also grateful to the referees whose comments significantly improved the paper. Work supported by the US DOE under Contract DE-AC52-07NA27344 with LLNS, LLC.
References
- Courant, R. and Hilbert, D. (1953) Methods of Mathematical Physics. Vol. 1, Interscience Publishers, New York.
- Giaquinta, M. and Hildebrandt, S. (1996) Calculus of Variations 1. The Lagrangian Formalism, Grundlehren der Mathematischen Wissenschaften 310. Springer-Verlag, Berlin.
- Parr, R.G. and Yang, C.Y. (1989) Density Functional Theory of Atoms and Molecules. Oxford University Press, Oxford.
- Gál, T. (2001) Differentiation of Density Functionals That Conserves the Normalization of the Density. Physical Review A, 63, Article ID: 022506. http://dx.doi.org/10.1103/PhysRevA.63.022506
- Friedlander, G. and Joshi, M. (1998) Introduction to the Theory of Distributions. 2nd Edition, Cambridge University Press, UK.
- The recursion relation can be interpreted in terms of a susceptibility, whose inverse is defined by the relation, from which follows that the Dirac delta function is its own inverse.
- Trott, M. Functional Derivative. From MathWorld—A Wolfram Web Resource, Created by Eric W. Weisstein. http://mathworld.wolfram.com/FunctionalDerivative.html
- Cioslowski, J. (1988) Density Functionals for the Energy of Electronic Systems: Explicit Variational Construction. Physical Review Letters, 60, 2141-2143. http://dx.doi.org/10.1103/PhysRevLett.60.2141
- Cioslowski, J. (1988) Density Driven Self-Consistent Field Method. I. Derivation and Basic Properties. The Journal of Chemical Physics, 89, 4871-4874. http://dx.doi.org/10.1063/1.455655
- Cioslowski, J. (1989) Density Driven Self-Consistent Field Method. II. Construction of All One-Particle Wave Functions That Are Orthonormal and Sum up to a Given Density. International Journal of Quantum Chemistry, 36, 255262.
- Consider all two-particle densities of the form, where denotes the ground state of the one-dimensional harmonic oscillator and on of its excited states (an infinite number). The orbital, can be developed in a power series of an equidensity basis (see following subsection) in terms of any of the densities, and differentiated within the space of that density through parametric differentiation of the elements of the basis. Each such differentiation gives the rate of change of a single orbital with respect to a particular density. But the rate of change at one density is not connected to that at another density. Although the coefficients of the expansion depend on the density, there is no functional derivative of the expansion coefficients. Indeed, they cannot be said to depend functionally on the density. In the expansion of in terms of plane waves, for example, the coefficients have no association with any particular density, (remember this one orbital contributes to an infinite number of densities). Furthermore, consider the (infinite) number of densities for the ground states of systems of N particles, with. The reader may wish to consider which of these densities is the independent variable whose functional is the orbital, Which of these densities would be reflected in the coefficients of a plane-wave expansion of At the same time, the rate of change of this orbital with respect to a given density depends only on that density and can be obtained through expansion of the orbital in the equidensity basis for that density
- Zumbach, G. and Maschke, K. (1983) New Approach to the Calculation of Density Functionals. Physical Review A, 28, 544-554. http://dx.doi.org/10.1103/PhysRevA.28.544
- Gonis, A., Dane, M., Nicholson, D.M. and Stocks, G.M. (2012) Computationally Simple, Analytic, Closed Form Solution of the Coulomb Self-Interaction Problem in Kohn-Sham Density Functional Theory. Solid State Communications, 152, 771-774. http://dx.doi.org/10.1016/j.ssc.2012.01.048
- Dane, M., Gonis, A., Nicholson, D.M. and Stocks, G.M. (2013) On the Solution of the Self-Interaction Problem in Kohn-Sham Density Functional Theory. arXiv:1302.4809 [cond-mat.mtrl-sci]
- Macke, W. (1955) Zur wellenmechanischen Behandlung von Vielkorperproblemen. Annalen der Physik, 452, 1-9.
- Harriman, J.E. (1981) Orthonormal Orbitals for the Representation of an Arbitrary Density. Physical Review A, 24, 680-682. http://dx.doi.org/10.1103/PhysRevA.24.680
- Ludena, E.V. and López-Boada, R. (1996) Local-Scaling Transformation Version of Density Functional Theory: Generation of Density Functionals. Topics in Current Chemistry, 180, 169-224.
- Kohn, W. (1983) v-Representability and Density Functional Theory. Physical Review Letters, 51, 1596. http://dx.doi.org/10.1103/PhysRevLett.51.1596
Appendix
12. Need for Arbitrariness
The procedure of conventional differentiation, outlined in Section 2, relies on the existence of a small neighborhood about each point, 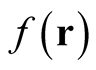 , in the domain of a functional,
, in the domain of a functional,  , defined by arbitrary changes in the domain,
, defined by arbitrary changes in the domain, 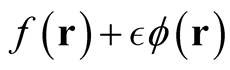 , that belong to the domain of the functional,
, that belong to the domain of the functional,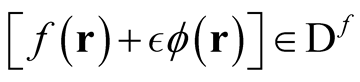 . We examine the reason for this condition and the consequences of its violation.
. We examine the reason for this condition and the consequences of its violation.
Consider the simple example of the linear functional,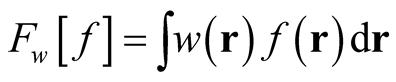 . From the conventional definition of functional derivative, we obtain the relations,
. From the conventional definition of functional derivative, we obtain the relations,
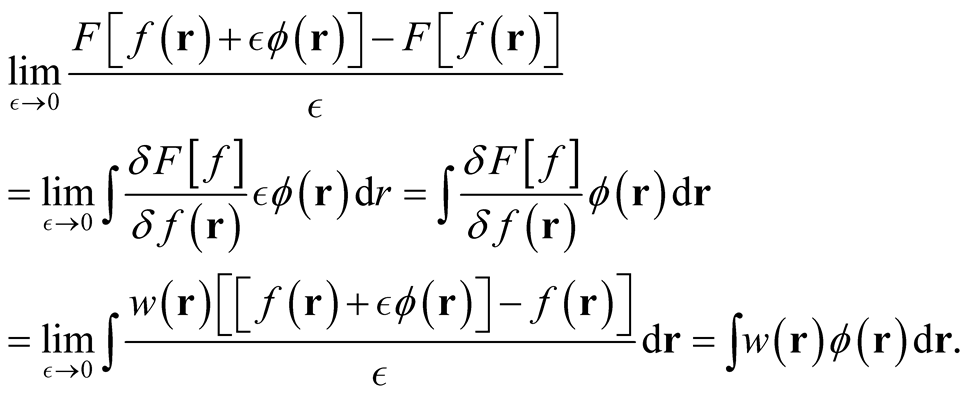
Provided that 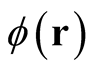 is arbitrary, the last expression in the second line and the expression in the last line give,
is arbitrary, the last expression in the second line and the expression in the last line give,
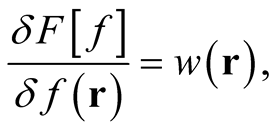 (0.71)
(0.71)
as follows from the well-known theorem on equality of integrants when two functions integrated agains any arbitrary function yield identical results, i.e., if
 (0.72)
(0.72)
for any (sufficiently well-defined) function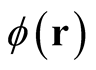 , then
, then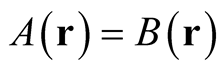 .
.
For the sake of completeness, this theorem is proven below. At this point we expose its content, beginning with a counterexample:
Suppose that 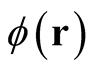 is not arbitrary but constrained by some condition, such as
is not arbitrary but constrained by some condition, such as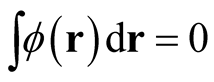 . In that case the last equality does not follow. For example,
. In that case the last equality does not follow. For example,  , and
, and  but this does not allow the conclusion that 1 = 2.
but this does not allow the conclusion that 1 = 2.
We now prove the theorem:
If for any two continuous and differentiable functions the equality,
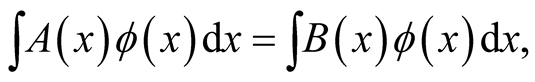 (0.73)
(0.73)
holds for all arbitrarily chosen, that is unconstrained, 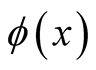 , then
, then  (where the equality means identity).
(where the equality means identity).
The theorem implies that the equality holds for any and all specific choices of  only if
only if .
.
(The contrapositive statement that if 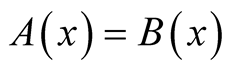 then the equality holds is trivially true.)
then the equality holds is trivially true.)
Choose as 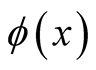 a Lorenztian centered at some point,
a Lorenztian centered at some point, 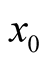 , with unit normalization, and allow the width to approach zero while the normalization is preserved. In the limit of vanishing width the Lorentzian assumes the form of a delta function while the equality in (0.73) continues to hold, so that,
, with unit normalization, and allow the width to approach zero while the normalization is preserved. In the limit of vanishing width the Lorentzian assumes the form of a delta function while the equality in (0.73) continues to hold, so that,
 (0.74)
(0.74)
implying,
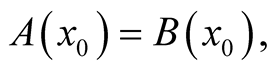 (0.75)
(0.75)
for every (arbitrary) point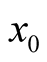 . This proves the theorem.
. This proves the theorem.
Constraining Arbitrariness
It can be readily shown that if the function 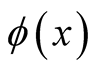 is constrained to satisfy an additional condition, such as
is constrained to satisfy an additional condition, such as
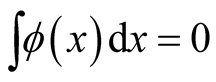 , the theorem just established fails. In that case,
, the theorem just established fails. In that case, 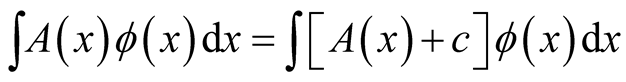 so that
so that
 . Under the condition that the test functions must integrate to zero, functional derivatives can be determined only modulo an arbitrary constant. This has immediate consequences in the determination of functional derivatives: Contrary to the demands of Frèchet differentiation, it leads to arbitrariness in the derivative defined conventionally with respect to an arbitrary test function [3].
. Under the condition that the test functions must integrate to zero, functional derivatives can be determined only modulo an arbitrary constant. This has immediate consequences in the determination of functional derivatives: Contrary to the demands of Frèchet differentiation, it leads to arbitrariness in the derivative defined conventionally with respect to an arbitrary test function [3].
13. The Identity Functional
In the case of the identity function,  , we have,
, we have, 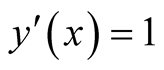 , so that the function at a given point,
, so that the function at a given point,  , in terms of its derivative at a given point,
, in terms of its derivative at a given point,  , is given by the expression,
, is given by the expression,
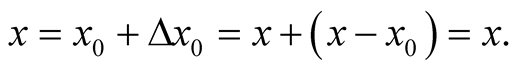 (0.76)
(0.76)
It is useful to inquire as to the analogous relation for the case of functionals.
We seek to determine the rate of change, 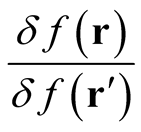 , of the identity functional,
, of the identity functional,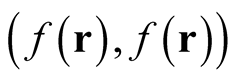 . It is useful to examine first the somewhat simpler case of functions defined on a lattice of distinct points,
. It is useful to examine first the somewhat simpler case of functions defined on a lattice of distinct points,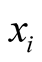 .
.
Given a change, 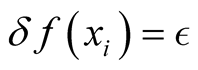 , in the function,
, in the function, 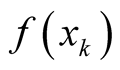 , at a point
, at a point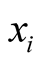 , the ratio of the change,
, the ratio of the change,  , at some point,
, at some point,  , to the change at
, to the change at , takes the form,
, takes the form,
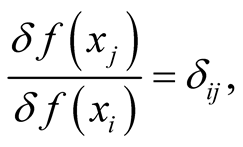 (0.77)
(0.77)
where  is the Kronecker delta, and the last relation follows because the change at all points,
is the Kronecker delta, and the last relation follows because the change at all points, 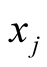 , vanishes except when
, vanishes except when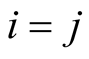 , where
, where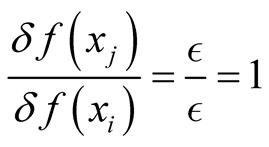 . This rate of change exhibits two important features: First, it remains valid regardless of the manner in which the change in the function at one of its points was introduced, either arbitrarily or as the difference at a single point between the function
. This rate of change exhibits two important features: First, it remains valid regardless of the manner in which the change in the function at one of its points was introduced, either arbitrarily or as the difference at a single point between the function 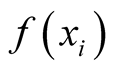 and another function,
and another function,  such that,
such that,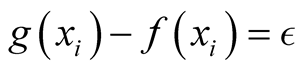 . In other words, the last relation is an inherent property of the function and is independent of the properties or existence of functions numerically in the vicinity of
. In other words, the last relation is an inherent property of the function and is independent of the properties or existence of functions numerically in the vicinity of . Second, we have,
. Second, we have,
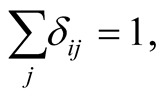 (0.78)
(0.78)
since each term in the sum vanishes except when the indices coincide where it equals unity.
In the continuum case, we set,
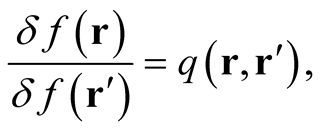 (0.79)
(0.79)
and once again we demand that,
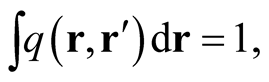 (0.80)
(0.80)
since the change in the function at all points other than  vanishes (the change is confined to a single point,
vanishes (the change is confined to a single point, ), and around the point
), and around the point 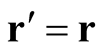 the quantity,
the quantity, 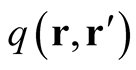 , must be such that a vanishing volume element multiplied by the height of
, must be such that a vanishing volume element multiplied by the height of  must yield unity (the ratio of two equal numbers denoting the change at
must yield unity (the ratio of two equal numbers denoting the change at ). By definition of the Dirac delta function, we set,
). By definition of the Dirac delta function, we set,
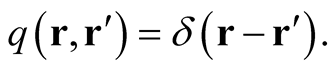 (0.81)
(0.81)
Therefore, a function can be changed in terms of a distribution (the Dirac delta function), so that,
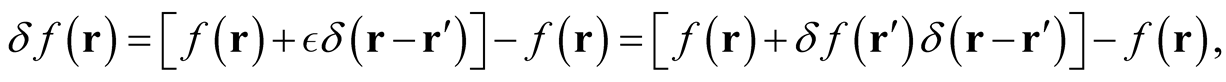 (0.82)
(0.82)
an expression that is intended to make clear that  is an infinitesimal change applied to point
is an infinitesimal change applied to point , and can be associated with a change of any function, rather than the difference between two functions at
, and can be associated with a change of any function, rather than the difference between two functions at .
.
The Dirac delta function is an example of a distribution, or generalized function [5]. It can also be viewed as a response function, or susceptibility, encoding the relative rate of change of a function at  induced through a change in the same function at
induced through a change in the same function at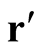 . From this viewpoint, it is seen that the rate of change of a function with respect to itself is an inherent property of the function and independent of the existence of other functions.
. From this viewpoint, it is seen that the rate of change of a function with respect to itself is an inherent property of the function and independent of the existence of other functions.

