Atmospheric and Climate Sciences
Vol.07 No.01(2017), Article ID:73798,10 pages
10.4236/acs.2017.71009
An Analysis of the Spectral Energetics for a Planet Experiencing Rapid Greenhouse Gas Emissions
André Ferreira Aranha1, José Augusto P. Veiga2
1UNINORTE Laureate International Universities, Manaus, Brazil
2Department of Meteorology, Institute of Technology, Amazonas State University, Manaus, Brazil

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 5, 2016; Accepted: January 21, 2017; Published: January 24, 2017
ABSTRACT
So far, energetics studies related to climate change have focused on the disturbed and undisturbed kinetic and potential energies, as well as their transformations, without dealing with the energetics involved in the phenomena of different spatial scales. Thus, the present work reports the first analysis of the spectral energetics for a condition of climate change, followed by the high-range emission scenario, RCP8.5, which originated from the new Max Planck Institute Earth System Model (MPI- ESM). The results showed that both types of generation (Go and Gn), baroclinic processes (Co and Cn), kinetic energies (Ko and Kn) and the barotropic process, Mn, significantly increase in the condition of a warming climate. Moreover, the results still reveal that in the most components of the energetics, is the planetary scale waves that are the most impacted under a climate change scenario. These results highlight that global warming can have different impacts on particular types of motions.
Keywords:
Energetics, Global Energetics, Spectral Energetics, Climate Change, MPI-ESM Model

1. Introduction
Quantifying the atmospheric energetics is a key element in understanding the dynamical behavior of the environment in a broad range of spatial and temporal scales of motion. This knowledge is achieved through the calculation of the potential (energy related to gravity and altitude) and kinetic (energy related to motions) energies, as well as their generation (energy source), transformation and dissipation (energy sink) pro- cesses. Furthermore, since the potential and kinetic energies can be divided into zonal, stationary and transient-related motions, the energetics of a particular type of atmospheric motion can be assessed [1] [2] . In addition, the energetics of all types of these atmospheric modes can be determined, either for the entire atmosphere or for only a part of it [3] [4] [5] [6] [7] .
Currently, a considerable number of studies have focused on the quantification of the global and local atmospheric energetics under increasing greenhouse gas emission scenarios [8] [9] [10] [11] [12] . However, the effect of accelerated greenhouse gas emissions on the atmospheric energetics in the spectral view is still minimal. This kind of study can reveal important characteristics related to the energetics of a particular scale of motion, which is the main focus of the present work.
For example, based on a 10-year numerical simulation with the Canadian Centre for Climate Modeling and the Analysis Model, Boer [8] found significant reduction in the baroclinic instability (quantified by the conversion between potential and kinetic energy of eddy-related motion) for the Northern Hemisphere’s winter season in the case of double CO2 concentration. According to the author, the consequent decreasing in pole- to-equator and land/ocean lower troposphere temperature gradients deplete the mid- latitude baroclinicity. This scenario produces a 12% reduction in the atmosphere’s rate of working (the rate of generation of available potential energy and its conversion to kinetic energy and subsequent dissipation) relative to 2 ´ CO2 simulation. In addition, the author found a reduction in the available potential energy of the zonal and eddy motions, followed by a decrease in their conversion to kinetic energies.
To assess the impact of the doubled CO2 in the atmosphere on the global energetics, Hernández-Deckers and von Storch [9] carried out an equilibrium and transient simulation using the ECHAM model. The results demonstrated that the total conversion rate of potential into kinetic energies is strongly shrieked. The reduction in the intensity of the Lorenz energy cycle was attributed to the decrease in the conversions from potential to kinetic energies. Moreover, as a response to the increasing barotropic conversion (measured in terms of zonal kinetic energy changes at the expense of eddy kinetic energy), they found a growth in the values of the zonal kinetic energy reservoir.
The authors still noticed a twofold role in the warming pattern of the atmosphere: an increase of AZ in the upper troposphere followed by a robust weakening of AZ in the lower levels. The double response, characterized by the strengthening in the upper troposphere and a weakening below, is concerning, mainly due to the transient eddy terms, with the stationary eddies having only a secondary importance. Veiga and Ambrizzi [12] showed that the intensity of the energetics depletes as the concentration of greenhouse gases increases. Moreover, they stressed that the RCP85 scenario drives the strongest decrease. For both the global and hemispherical domains, the zonal kinetic energy is the only energy reservoir that increases in a warmed environment, whereas the barotropic conversion is the only energy flux that also augments. They highlighted the importance of processes like the vertical and horizontal eddy-transports of momentum to the increase of barotropic conversion.
As noted, preceding works have not yet applied the spectral energy analysis in addressing the impacts of a warming planet on the broad range of atmospheric motions. Furthermore, some basic questions are still unanswered, for example: Are the available potential energy and kinetic energy of different scales of motion equally affected in a warming planet? In this way, the main purpose of the present work is to quantify the spectral energetics of the atmosphere under the condition of a planet experiencing rapid greenhouse gas emissions.
The paper is organized as follows: The data and methodology are discussed in Section 2, and the main results are presented in Section 3, with a discussion regarding the energetics of the basic state and the spectral energetics. A follow-up discussion is presented in Section 4, commenting on new insights and perspectives brought forth by the results.
2. Methodology
A set of two experiments that originated from the coupled atmosphere-ocean ECHAM/ MPI-ESM-MR general circulation model [13] is evaluated. This model has a spatial resolution equivalent to 1.875˚ × 1.875˚ degrees, and 31 levels in the vertical. In this work, we have used one future projection that is characterized by specific greenhouse gas concentrations consistent with a high-range emission scenario, RCP8.5 (Radiative Concentration Pathway). This RCP achieves a radiative stabilization of 8.5 W/m2 by the end of 2100 yr [14] .
For comparison purposes, a control experiment that covers much of the industrial period from the mid-19th century to the near-present is used [15] . The mean daily atmospheric data of the zonal and meridional components of the horizontal wind vector, air temperature, and vertical components of wind velocity and geopotential height are used in the computation of the spectral energetics [16] . The atmospheric variables were integrated from the lowest model level, considered to be 1000 hPa, up to 1 hPa. The analysis covers two specific ranges: 1980 to 1999 and 2080 to 2099, hereafter called L20C (late 20th century) and L21C (late 21st century), respectively.
The integral calculations of the energy terms were performed at each daily mean time step for the global domain. The set of energetic equations used here is based on the spectral formalism [16] , and is summarized below:
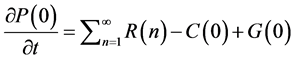 (1)
(1)
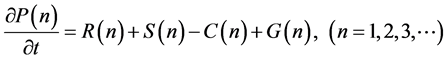 (2)
(2)
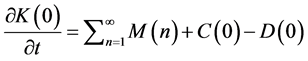 (3)
(3)
 (4)
(4)
This set of equations describes Saltzman’s [16] wave number formulation and accounts for the balance equations of the available potential energy (P) and kinetic energy (K). All of the quantities produced by these equations are relative to the total mass integrals of the atmosphere. Due to limit constraints, detailed mathematical expressions of all of the components of the energy budget, as described by Equations (1)-(4), are not presented here. The subscripts o and n denote zonal and wave components, respectively.
C(0,n), G(0,n), D(0,n) denote, respectively, the conversion between potential to kinetic energy of the basic state (wave number n), the generation of zonal potential energy (wave number n) and the dissipation of zonal kinetic energy (wave number n). Rn, Mn, Sn and Ln, represent, respectively, the conversion from Po to Pn, the conversion from Kn to Ko, the available potential energy transfer from eddies off all wave numbers to eddies of wave number n and the kinetic energy transfer from eddies off all wave numbers to eddies of wave number n.
In summary, the spectral energetics may provide information about the distribution of energy associated with different spatial scales of atmospheric motion, for instance, planetary and synoptic scales. Furthermore, depending on the data resolution, the spectral energetics may provide important information about the sub-synoptic scale, wave number greater than 31. However, the problem in achieving quantifications in order to express the energetics of these kinds of waves resides in the fact that the atmosphere is not considered to be in hydrostatic balance, which limits the use of the technique. Thus, from this methodology, it is possible to quantify the impact that a warming Earth imposes on the pattern of kinetic and potential energies, as well as on the rate of energy conversion in a wave number perspective. To achieve the purpose of this work, the annual mean averages are calculated for all of the dataset for the L20C and L21C cases.
3. Results and Discussions
3.1. Energetics of the Basic State
The two-box diagram of the energy cycles for the L20C (blue) and L21C (red) periods is presented in Figure 1. The values displayed in this figure are representative of the annual mean climatology. The results show that the increasing greenhouse gases in turn increase the generation of potential energy, the conversion between potential and kinetic energies, the kinetic energy and the dissipation process. In contrast, the potential energy is slightly reduced during the L21C period.
These results suggest an environment with stronger temperature and heating contrast, and consequently, a greater production of potential energy. Moreover, stronger temperatures and heating gradients yield strong conversions of potential energy into kinetic energy. This condition provoked ~38% more Ko during the LC21 period, followed by an increase in Do. The Po values present a slight decrease. However, the
Figure 1. The annual mean climatology of the Lorenz energy cycle for the basic state. The values in blue represent the L20C period and the red values correspond to the L21C period. Go, Po, Co, Ko and Do, represent, respectively, the generation of zonal available potential energy, the zonal available potential energy, the conversion between Po and Ko, the zonal kinetic energy and the dissipation of Ko. The units are 105 J/m2 for energy reservoirs and W/m2 for conversion terms.
decrease is not statistically significant, suggesting that there are no expressive changes in Po under a strong greenhouse gas emission scenario.
Although the two-box diagram of the energy cycle can illustrate important features of the general circulation, it limits the energetics’ interpretation associated with particular features of the atmospheric motions (for instance, the role of eddies). When using only this frame of reference, it is not possible to explain, for example, the increasing in the values of Ko (or the decrease in Po). In other words, the augment observed in the Ko values is not just provoked by increasing Co during the L21C period. Thus, key features of the atmospheric energetics can be found when dealing with spectral modes, which are presented in the next section.
3.2. Spectral Energetics
Figure 2 presents the energy reservoirs and conversion terms as functions of the zonal wave number. As Figure 2(a) illustrates, the conversion from Po to Pn (Rn) is significantly reduced for wave numbers less than 10 for the L21C period. For wave numbers greater than 10, there are no significant values. This is also true for the other energy and conversion terms that are presented latter.
The diminished energy transfer can be tied to the reduction of the potential energy of the basic state, as commented previously. In contrast, Pn is fed by the generation term (Gn), which acts as an additional source of potential energy (Figure 2(b)). The results still show significant increasing of Gn during the L21C period. Under the conditions of source (Gn) and sink (Rn), Pn is reduced, mainly in the case of planetary waves, indicating a spatial scale dependence of the energetics (Figure 2(c)). In addition, the integrated Pn difference (see bars) is higher for planetary waves than for synoptic scale waves (considered here as wave numbers greater than five).
These results suggest that there will be less potential energy available to kinetic energy, mainly for the planetary scale than for the synoptic scale waves. However, the results show significant increasing of the baroclinic process, represented by the Cn term, and less availability of potential energy in a warmed climate condition (Figure 2(d)), suggesting that these kinds of waves will undergo significant changes in their energetics. The most significant increasing of the energy conversion is observed for planetary scale waves (see the differences in the bars relative to other spectra).
These results show that the kinetic energy of planetary scale waves seems to be more robustly fed by the potential energy reservoir than for the intermediate and synoptic scale waves during the L21C period. It becomes immediately obvious from this result that Cn will impact directly the quantity of energy related to the motions of different scale waves.
The results demonstrate that the kinetic energy is significantly altered for the L21C period, mainly the kinetic energies of the planetary scale waves (see Figure 2(e)). Although the wave numbers 1 and 2 don’t appear to be significantly altered, their kinetic energy is raised in the scenario of a warmed climate, suggesting an important influence of greenhouse gas emissions on the energetics of the planetary scale waves. Furthermore, the results still show high impacts of climate change on synoptic scale waves. It is suggestive of a future scenario with planetary waves (like Ross by waves, for example) and synoptic waves (like troughs and ridges) with more energy related to its flow, which can directly impose significant variations in the climate were these phenomena are frequently observed.
Besides that, additional kinetic energy of these waves can alter the thin balance between the energy transfer between them and the basic state reservoir. To account for such a connection, or the energy transfer from the eddies to the basic state kinetic
Figure 2. The annual mean climatology of conversion from Po to Pn, Rn, (a), generation of available potential energy, Gn, (b), available potential energy, Pn, (c), conversion between potential and kinetic energy, Cn, (d), kinetic energy, Kn, (e) and conversion between Kn and Ko, Mn, (f) as a function of the zonal wave number. The values displayed in this figure are relative to the L20C (blue line) and L21C (red line) periods. The blue and red bars represent the sum of the energy accumulated in 1 - 4 and 5 - 31 wave-spectra, respectively for, L20C and L21C. To avoid axis overlapping, the values of the bars are multiplied by 10−1. Error bars indicating 95% confidence intervals for the mean are superposed on the lines. The units are W/m2 for Rn, Gn, Cn and Mn, and are 105 J/m2 for Pn and Kn.
energies, Figure 2(f) is presented. This figure shows that there are significant augments in the energy transfer from Kn to Ko (Mn), indicating that a broad range of atmospheric scale waves (planetary and synoptic scale waves) strengthen the basic state’s kinetic energy. These results help us to understand the increasing of kinetic energy of the basic state, as observed in Figure 1. Thus, it was observed that the Ko reservoir has two sources of energy: one from the basic state potential energy reservoir, accounted for with the term Co, and another one from the planetary and synoptic scale waves, via the barotropic processes. Thus, although the results presented here bring attention to a possible expressive change in the energetics of the planetary and synoptic scale waves, it is not possible to affirm anything about the rising or falling in their occurrence frequency. However, the results point to a future with a more hostile climate.
4. Concluding Remarks
In this paper, we present a spectral global energetic preliminary analysis from a set of two experiments that originated from the coupled atmosphere-ocean ECHAM/MPI- ESM-MR general circulation model: a control experiment (L20C) and one based on the RCP8.5 scenario (L21C). The main purpose of this study was to assess the impact of greenhouse gas emissions over the atmospheric motions using different spatial scales, which cannot be directly achieved from other types of energetic techniques. The results were based on the annual mean climatology analyses of the main components of basic and perturbed state energetics.
Relative to the basic state energetics, our results show increases in the values of Go, Co, Ko and Do, while the Po is slightly decreased during the L21C period. This anomalous energetics condition provoked ~38% (~3%) more (less) Ko (Po) during the LC21 period. These two important energy reservoirs can impact or be impacted by the perturbed state reservoirs, Pn and Kn, throughout the process of energy conversion (barotropic and baroclinic), as well as by the spatial scale of the perturbation.
Using the spectral energetics perspective, our results revealed that the energy conversion from Po to Pn is significantly reduced, while Gn acts as a source of energy to Pn. Under these two contrasting conditions, Pn is reduced. However, in a warmed climate condition, Pn anomalously fed Kn through a baroclinic process. Furthermore, the most significant increase of the energy conversion is for the planetary scale wave, with wave numbers from 1 - 4. These results show that the kinetic energy of the planetary scale waves seems to be more robustly fed by the potential energy reservoir than for the synoptic scale waves. In addition, Kn increases, especially for planetary scale waves, showing important features in the energetics of the atmosphere.
An important result observed in this study has to do with the action of Kn into Ko. Part of the increase in the values of Ko comes from the planetary and synoptic scale waves, via the barotropic processes. However, the planetary scale waves seem to be more important, as the accumulated energy of these spectra is higher than that of the synoptic one. Furthermore, the Ko reservoir had two sources of energy: one from the potential energy reservoir, accounted for with the term Co, and another one from the planetary and synoptic scale waves.
In brief, both types of generation (Go and Gn), conversion from potential to kinetic energy (Co and Cn) and kinetic energies (Ko and Kn) are increased in a warmed climate scenario. In the case of the perturbed state, the planetary and synoptic waves present an important role, with the former having been impacted more. Physically, the impact on the generation terms has to do with the strengthening of the horizontal heating gradient. The increase in the values of Co and Cn is a consequence of the Go and Gn augmentation, respectively, as strengthening in the horizontal gradient of heating produces a greater warmed air ascent and cooled air descent. In addition, as a consequence of the Co and Cn increasing, we see an augmentation in the Ko and Kn values. The other two branches of the energetics, Rn and Mn, presented, respectively, a reduction and an increase, with the former contributing to the increase of the basic state kinetic energy. The results of the present study highlight the fact that global warming can have different impacts over particular types of motions, with planetary scales experiencing the greatest impact.
Cite this paper
Aranha, A.F. and Veiga, J.A.P. (2017) An Analysis of the Spec- tral Energetics for a Planet Experiencing Rapid Greenhouse Gas Emissions. Atmospheric and Climate Sciences, 7, 117-126. http://dx.doi.org/10.4236/acs.2017.71009
References
- 1. Lorenz, E.N. (1955) Available Potential Energy. Tellus, 7, 157-167.
https://doi.org/10.1111/j.2153-3490.1955.tb01148.x - 2. Peixoto, J.P. and Oort, A.H. (1974) The Annual Distribution of Atmospheric Energy on a Planetary Scale. Journal of Geophysical Research, 20, 2149-2159.
https://doi.org/10.1029/JC079i015p02149 - 3. Ulbrich, U. and Speth, P. (1991) The Global Energy Cycle of Stationary and Transient Atmospheric Waves: Results from ECMWF Analyses. Meteorology and Atmospheric Physics, 45, 125-138.
https://doi.org/10.1007/BF01029650 - 4. Marques, C.A.F., Rocha, A. and Corte-Real, J. (2011) Global Diagnostic Energetics of Five State-of-the-Art Climate Models. Climate Dynamics, 36, 1767-1794.
https://doi.org/10.1007/s00382-010-0828-9 - 5. Pezza, A.B., Veiga, J.A.P., Simmonds, I., Keay, K. and Mesquita, M.D.S. (2010) Environmental Energetics of an Exceptional Highlatitude Storm. Atmospheric Science Letters, 11, 39-45.
- 6. Black, M.T. and Pezza, A.B. (2013) A Universal, Broad-Environment Energy Conversion Signature of Explosive Cyclones. Geophysical Research Letters, 40, 452-457.
https://doi.org/10.1002/grl.50114 - 7. Veiga, J.A.P., Pezza, A.B. and Ambrizzi, T. (2013) The Energy Cycle Associated to the Pacific Walker Circulation and Its Relationship to ENSO. Atmospheric and Climate Sciences, 3, 627-642.
https://doi.org/10.4236/acs.2013.34065 - 8. Boer, J. (1995) Some Dynamical Consequences of Greenhouse Gas Warming. Atmosphere-Ocean, 33, 731-751.
https://doi.org/10.1080/07055900.1995.9649551 - 9. Hernández-Deckers, D. and von Storch, J.-S. (2010) Energetics Responses to Increases in Greenhouse Gas Concentration. Journal of Climate, 23, 3874-3887.
https://doi.org/10.1175/2010JCLI3176.1 - 10. Hernandez-Deckers, D. and von Storch, J.-S. (2011) The Energetics Response to a Warmer Climate: Relative Contributions from the Transient and Stationary Eddies. Earth System Dynamics, 2, 105-120.
https://doi.org/10.5194/esd-2-105-2011 - 11. Veiga, J.A.P. and Ambrizzi, T. (2013) A Global and Hemispherical Analysis of the Lorenz Energetics Based on the Representative Concentration Pathways Used in CMIP5. Advances in Meteorology, 2013, Article ID: 485047.
- 12. Veiga, J.A.P., Ambrizzi, T. and Pezza, A.B. (2013) A Space Domain Energetics Study for CO2 Increasing Based on SRES-A2 Emission Scenario. Advances in Meteorology, 2013, Article ID: 697105.
https://doi.org/10.1155/2013/697105 - 13. Stevens, B.M., Giorgetta, M., Esch, M., et al. (2012) Atmospheric Component of the MPI-M Earth System Model: ECHAM6. Journal of Advances in Modeling Earth Systems, 5, 146-172.
https://doi.org/10.1002/jame.20015 - 14. Riahi, K., Rao, S., Krey, V., et al. (2011) RCP 8.5—A Scenario of Comparatively High Greenhouse Gas Emissions. Climatic Change, 109, 33-57.
https://doi.org/10.1007/s10584-011-0149-y - 15. Karl, E.T., Ronald, J.S. and Meehl, G.A. (2012) An Overview of CMIP5 and the Experiment Design. Bulletin of the American Meteorological Society, 93, 485-498.
https://doi.org/10.1175/BAMS-D-11-00094.1 - 16. Saltzman, B. (1957) Equations Governing the Energetics of the Large Scales of Atmospheric Turbulence in the Domain of Wave Number. Journal of Meteorology, 14, 513-523.
https://doi.org/10.1175/1520-0469(1957)014<0513:EGTEOT>2.0.CO;2




