Atmospheric and Climate Sciences
Vol.05 No.04(2015), Article ID:60565,8 pages
10.4236/acs.2015.54036
Characterization of the Atmospheric Dynamics in Riobamba City Using the Chaos Theory
Arquímides Haro1,2, Cecilia Limaico1,2, Yolanda Llosas3
1Physics and Mathematics School, Polytechnic School of Chimborazo, Riobamba, Ecuador
2Faculty of Engineering, National University of Chimborazo, Riobamba, Ecuador
3Department of Automatic Control, East University, Santiago, Cuba
Email: arquimidesharo@yahoo.es, cecitere_ln@hotmail.com, yolanda@fie.uo.edu.cu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 June 2015; accepted 23 October 2015; published 26 October 2015
ABSTRACT
Chaos studies all that is messy, disorganized and incoherent; mathematically the chaos is a dynamic system governed by nonlinear differential equations. Chaos has an unpredictable behavior; its dynamical is very sensitive to the initial conditions. Atypical chaotic system is the atmosphere; this limits the knowledge about its behavior; but with the advance in the computers, the results that are obtained with the chaos theory improved significantly; the description of atmosphera and its results have extended to other fields of the science, as the economy, health and others. The object of this work was to determine the atmospheric dynamics in the Riobamba city using the theory of chaos, with meteorological data of the meteorological station of the ESPOCH of one year (2010) of data that were processed with model TISEAN. The results determine a hyperchaotic system, according to the coefficients of Lyapunov.
Keywords:
Chaos Theory, Atmospheric Variables, Coefficients of Lyapunov, Dynamics, Entropy

1. Introduction
Chaos and the fractals are part of a bigger topic, dynamics. Dynamics began by the middle of 1600, when Isaac Newton invented the differential equations; he discovered the movement laws and the general gravitation. The following generations of mathematical and physicist treated problems of three bodies, but they realized that they were much more difficult than the problem of two bodies, until the point of considering them impossible [1] .
The history of chaos begins when the high-speed computers were invented (1950). In 1963 Edwar Lorenz worked in some equations (the equations worldwide well-known as equations of Lorenz) that predicted the time in the atmosphere, and he saw the behavior of its equations graphically. Although they were called high-speed computers in this time, now they are very slow [2] [3] .
The 1970s was the boom of chaos. In 1971, David Ruelle and Takias proposed a new theory for the turbulence of fluids based on a strange attractor. Years later they found case examples in repeated maps of population. He discovered that there are specific universal laws that differentiate the transition between regular behavior and chaos. That is, if it is possible that two systems evolve in a chaotic behavior like.
This work has taken a set of meteorological data (meteorological station, ESPOCH, 2010), which are pro- cessed, beginning with noise reduction, then, it determined the delay coordinates, the embedding parameters, which help determine the reconstruction of data in the space of the phases, to establish its dynamic estimated coefficients of Lyapunov, fractal dimension and entropy was also to do a prediction of the data based on the characteristics found and an analysis of actual and predicted data.
2. Material and Methods
2.1. Chaos Theory
Chaos theory is a field of study of the mathematics. It studies the behavior of dynamical systems that are highly sensitive to the initial conditions. Small differences in initial conditions (such as those due to rounding errors in numerical computation) this produce in diverging outcomes for such systems dynamic, it does long-term predictions impossibles [4] .
2.2. Dynamical Systems
A dynamic system can be represented by ordinary differential equations, Equation (1).
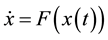 (1)
(1)
or in discrete time 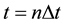 by maps of the form, Equation (2).
by maps of the form, Equation (2).
 (2)
(2)
However, chaotic systems do not respond to these equations, but now is possible to use the chaos theory; it follows procedures that go: from the reconstruction of the data series to the phases space, the determination of the degree of chaos and reaching the prediction of the systems [5] .
2.3. Delay Coordinates
A time series can then be thought of as a sequence of observations . Since the (usually scalar) sequence
. Since the (usually scalar) sequence 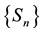 in itself does not properly represent the (multidimensional) phase space of the dynamical system, one has to employ some technique to determine the multidimensional structure of the data.
in itself does not properly represent the (multidimensional) phase space of the dynamical system, one has to employ some technique to determine the multidimensional structure of the data.
The most important phase space reconstruction technique is the method of delays. Vectors in a new space, the embedding space, are formed from time delayed values of the scalar measurements, Equation (3):
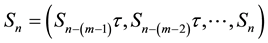 (3)
(3)
The number m of elements is called the embedding dimension; the time 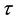 is generally referred to as the delay or lag. Celebrated embedding theorems by Takens [6] and by Sauer et al. [7] state that if the sequence
is generally referred to as the delay or lag. Celebrated embedding theorems by Takens [6] and by Sauer et al. [7] state that if the sequence 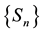 does indeed consist of scalar measurements of the state of a dynamical system, then under certain genericity assumptions, the time delay embedding provides a one-to-one image of the original set
does indeed consist of scalar measurements of the state of a dynamical system, then under certain genericity assumptions, the time delay embedding provides a one-to-one image of the original set , provided m is large enough.
, provided m is large enough.
Time delay embedding is used in almost all methods described [4] . The implementation is straightforward and does not require further explanation. If N scalar measurements are available, the number of embedding vectors are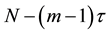 . This has to be kept in mind for the correct normalization of averaged quantities. There is a large literature on the “optimal” choice of the embedding parameters m and τ. These results provide the applied software.
. This has to be kept in mind for the correct normalization of averaged quantities. There is a large literature on the “optimal” choice of the embedding parameters m and τ. These results provide the applied software.
2.4. Embedding Parameters
A method to determine the minimal sufficient embedding dimension m was proposed by Kennel et al. [8] . It is called the false nearest neighbor method. The idea is quite intuitive. Suppose the minimal embedding dimension for a given time series  is m0. This means that in a m0 dimensional delay space the reconstructed attractor is a one-to-one image of the attractor in the original phase space. Especially, the topological properties are preserved. Thus the neighbors of a given point are mapped onto neighbors in the delay space. Due to the assumed smoothness of the dynamics, neighborhoods of the points are mapped onto neighborhoods again. Of course the shape and the diameter of the neighborhoods is changed according to the Lyapunov exponents. But suppose now you embed in an m-dimensional space with m < m0. Due to this projection the topological structure is not longer preserved. Points are projected into neighborhoods of other points to which they wouldn't belong in higher dimensions. These points are called false neighbors. If now the dynamic is applied, these false neighbors are not typically mapped into the image of the neighborhood, but somewhere else, so that the average “diameter” becomes quite large [6] .
is m0. This means that in a m0 dimensional delay space the reconstructed attractor is a one-to-one image of the attractor in the original phase space. Especially, the topological properties are preserved. Thus the neighbors of a given point are mapped onto neighbors in the delay space. Due to the assumed smoothness of the dynamics, neighborhoods of the points are mapped onto neighborhoods again. Of course the shape and the diameter of the neighborhoods is changed according to the Lyapunov exponents. But suppose now you embed in an m-dimensional space with m < m0. Due to this projection the topological structure is not longer preserved. Points are projected into neighborhoods of other points to which they wouldn't belong in higher dimensions. These points are called false neighbors. If now the dynamic is applied, these false neighbors are not typically mapped into the image of the neighborhood, but somewhere else, so that the average “diameter” becomes quite large [6] .
The idea of the algorithm false_nearest is the following. For each point 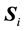 in the time series look for its nearest neighbor
in the time series look for its nearest neighbor 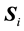 in am-dimensional space. Calculate the distance
in am-dimensional space. Calculate the distance . Iterate both points and compute, Equation (4).
. Iterate both points and compute, Equation (4).
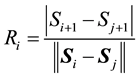 (4)
(4)
If  exceeds a given heuristic threshold
exceeds a given heuristic threshold

The introduction of the false nearest neighbors concept and other ad hoc instruments was partly a reaction to the finding that many results obtained for the genuine invariants, like the correlation dimension, has been spurious due to caveats of the estimation procedure. In the latter case, serial correlations and small sample fluctuations can easily be mistaken for nonlinear determinism. It turns out, however, that the ad hoc quantities basically suffer from the same problems―which can be cured by the same precautions. The implementation false_nearest therefore allows to specify a minimal temporal separation of valid neighbors.
2.5. Attractor
The attractor of a dynamic system is the region of space of the phases, in which the path is drawn, tending the movement after a time of adjustment to the attractor. A vast class of dissipative dynamical systems, has the re-
Figure 1. The fraction of false nearest neighbors as a function of the embedding dimension for noise free Lorenz (blue) and Hénon (red) time series, as well as a Hénon time series (green) corrupted by 10% of noise.
markable property of possessing an attractor, which is the place of routes after a long enough career points. A simple example is that of the pendulum swinging in the air, the amplitude of oscillation is progressively attenuated and all paths regardless of the initial conditions are approaching stable fixed point which is the attractor [10] .
In the case of chaotic systems, in which it has a strong dependence of the initial coordinates, the attractor is not in fact a regular object, but rather has a very complicated structure, then called him strange attractor (Rulle) [11] , which can have a fractal structure.
2.6. Noise Reduction
This noise reduction scheme is implemented quite easily. First an embedding has to be chosen. Except for extremely oversampled data, it is advantageous to choose a short time delay. The program always uses unit delay. The embedding dimension m should be chosen somewhat higher than that required by the embedding theorems. Then for each embedding vector {Sn}, a neighborhood 





Then complete around the series of time, all the measures 

2.7. Lyapunov Exponents
Chaos arises from the exponential growth of infinitesimal perturbations, together with global folding mechanisms to guarantee boundedness of the solutions. This exponential instability is characterized by the spectrum of Lyapunov exponents [13] . If one assumes a local decomposition of the phase space into directions with different stretching or contraction rates, then the spectrum of exponents is the proper average of these local rates over the whole invariant set, and thus consists of as many exponents as there are space directions. The most prominent problem in time series analysis is that the physical phase space is unknown, and that instead the spectrum is computed in some embedding space. Thus the number of the exponents depends on the reconstruction, and might be larger than in the physical phase space.
Chaos arises of the exponential growth of the infinitesimal interferences, the exponents of Lyapunov (λ) that quantify are to guarantee the analysis of this uncertainty as much as they go away two trajectories [14] .

With l(t) semi axis bigger than an ellipse, r small radio initial and t big time, in general settles down:
Variables that allow to characterizing an attractor, this way:
a) For a fixed point the 
b) In a cycle limit 


c) In the movement of a dimensional Torous n, 


d) In a chaotic system at least one Lyapunov exponent is negative.
The computation of the full Lyapunov spectrum requires considerably more effort than just the maximal exponent. An essential ingredient is some estimate of the local Jacobians, i.e. of the linearized dynamics, which rules the growth of infinitesimal perturbations. One either finds it from direct fits of local linear models of the type


From this result can define Kolmogorov entropy-Sinai.

Or the dimension fractal of Kaplan. Yorke (1979)

With j positive Lyapunov coefficients [5] .
2.8. Predicting Time Series
The basic functions used are Gaussians, with center points chosen to be data from the time series. The variance of Gaussians are set to the average distance between the centers [15] .
The pattern predicts the series of data using the following relationship:

where xn is the n-th delay vector and fi is a gaussian centered at the i-th center point and a constants.
2.9. Atmospheric Dynamics
The atmospheric time, besides being a dynamic system, is very sensitive to the changes in the initial variables, it is a transitive system and its periodic orbits are also dense, that makes of it an appropriate system to work with chaotic mathematics. The precision of the meteorological predictions is relative, and the announced percentages have not much meaning without a detailed description of the approaches used to judge the accuracy of the prediction.
Before the appearance of the Theory of Chaos, it was thought that the climate ended up being predicted with a Newton like accuracy. It was not more than a matter of introducing variables more and more in a computer sufficiently potent to process them. However, of some few variables of only some decades ago, now, they has considerate hundreds of thousands of variables without getting the prospective predictability, recently it has been proven that the chaotic character of the atmospheric time has to do with the geometric properties group of evolution of the climatic terrestrial system. These results suggest a practical impossibility to predict weather in the medium and long term. The climate is sensitive to small variations in the initial conditions and the determination of the initial conditions exactly is doomed to failure because of the Heisenberg uncertainty principle. In these days it is possible to demonstrate the dependability of the predictions with the theory of chaos for periods of up to five days thanks to the density among the periodic orbits of the system, and some successes have been achieved in the prediction of abnormal variations of some variables for periods of up to 30 days [15] .
3. Results and Discussion
3.1. Calculation of the Delay Time and Embedding Dimension
To perform the calculation has been used TISIAN model, in first instance you proceeds to determine the time of retard to reconstruct the series of meteorological data taken in the space of the phases and the embedding dimensions for to data series with noise reduction (Table 1).
3.2. Calculation of the Spectrum of Lyapunov
In each case (Figure 2), it is observed that there are two coefficients of Lyapunov that which indicates that the system is hypercaotic, the precipitation series he/she didn't also find correlation among the data for what you could not determine these coefficients.
Figure 2. Graph of the spectrum of Lyapunov of the meteorological data with noise reduction.
Table 1. Determined delay time (first minimum) function for the different parameters.
It is observed that for each case the dimension fractal, in the first place is not whole and it overcomes the three dimensions reaching the highest value the humidity, the same as the entropy that would indicate that it is the system with more disorder of the four that could be this values.
3.3. Prediction of the Meteorological Variables
Table 8 Hypothesis test with distribution Z for half zero with significance level 0.01 to two lines (theoretical Z this among 2.58 and 2.58).
4. Conclusions
The studied systems are chaotic and hyperchaotic, according to the Theory of the Chaos (Figure 2) (they present positive bigger coefficients to one of Lyapunov), to exception of the precipitation in whose data correlation has not been determined in the used pattern.
The level of calculated (entropyvalue) chaoticity reaches higher values in the parameters of humidity, diminishing gradually respectively toward the pressure, temperature and speed of the wind.
The dimensions of the parameters are fractional that go diminishing from the humidity in the same order of the entropy (3.765), pressure (3.461), temperature (3.177) and speed of the wind (3.155) (Table 2).
Various atmospheric parameters with high correlation and low absolute deviations between predicted and actual data with the exception of the precipitation which shows no correlation can be predicted (Tables 3-7).
The data predicted generally tend to differ much more in time with respect to the real data (Figures 3-7 and Tables 3-7).
The data are statistically same, and given the results seen previously one can say that they have the same behavior whit the 99% of precision (Table 8).
Figure 3. Comparison graph between real data and predictors of ambient temperature during 24 and 72 hours.
Figure 4. Comparison graph between real data and predictors of humidity during 24 and 72 hours.
Figure 5. Comparison graph between real data and predictors of speed of wind during 24 and 72 hours.
Figure 6. Comparison graph between real data and predictors of pressure during 24 and 72 hours.
Figure 7. Comparison graph between real data and precipitation predicted during 24 and 72 hours.
Table 2. The fractal dimension and the entropy of each of the parameters values.
Table 3. Correlation of the real data and prediction of temperature.
Table 4. Correlation of the real data and predicted of humidity.
Table 5. Correlation of the real data and predicted of speed of the wind.
Table 6. Correlation of the real data and predicted of atmospheric pressure.
Table 7. Correlation of the rainfall real and predicted data.
Table 8. Hypothesis test with distribution Z for half zero with significance level 0.01 to two lines (theoretical Z this among 2.58 and 2.58).
It is a method that works properly despite the conditions of the city of Riobamba, by its geographical position and height with respect to the level of the sea, being able to recommend its use as an alternative to the traditional ones that do not work precisely in these conditions and hardly have access.
Acknowledgements
Thanks to the alternative energy group of the ESPOCH for help our whit meteorological data and the Tisean software.
Cite this paper
ArquímidesHaro,CeciliaLimaico,YolandaLlosas, (2015) Characterization of the Atmospheric Dynamics in Riobamba City Using the Chaos Theory. Atmospheric and Climate Sciences,05,441-449. doi: 10.4236/acs.2015.54036
References
- 1. Alligood, K.T. (1996) Chaos an Introduction to Dynamical Systems. Springer-Verlag, New York.
- 2. De Souza Cavalcante, H.L.D., Oria, M., Sornette, D., Ott, E. and Gauthier, D.J. (2013) Predictability and Suppression of Extreme Events in Complex Systems. arXiv:1301.0244.
- 3. Field, C.B., Barros, V., Stocker, T.F. and Dahe, Q. (2012) Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. Cambridge University Press, UK.
http://dx.doi.org/10.1017/CBO9781139177245 - 4. Ruelle, D. (2013) Early Chaos Theory. Physics Today, May 2013, 27.
- 5. Alligood, K.T., Sauer, T. and Yorke, J.A. (1996) Chaos: An Introduction to Dynamical Systems. Springer-Verlag, New York.
- 6. Takens, F. (1981) Detecting Strange Attractors in Turbulence. Lecture Notes in Math. Vol. 898, Springer, New York.
http://dx.doi.org/10.1007/bfb0091924 - 7. Sauer, T., Yorke, J. and Casdagli, M. (1991) Embedology. Journal of Statistical Physics, 65, 579.
http://dx.doi.org/10.1007/BF01053745 - 8. Richter, M. and Schreiber, T. (1998) Phase Space Embedding of Electrocardiograms. Physical Review E, 58, 6392.
http://dx.doi.org/10.1103/PhysRevE.58.6392 - 9. Kennel, M.B., Brown, R. and Abarbanel, H.D.I. (1992) Determining Embedding Dimension for Phase-Space Reconstruction Using a Geometrical Construction. Physical Review A, 45, 3403.
http://dx.doi.org/10.1103/PhysRevA.45.3403 - 10. Rasband, N. (1990) Chaotic Dynamics of Nonlinear Systems. John Wiley & Sons, New York.
- 11. Mandelbrot, B.B. (1997) La Geometría Fractal de la Naturaleza. Tusquets Editores SA. Barcelona.
- 12. Schreiber, T. (1993) Extremely Simple Nonlinear Noise Reduction Method. Physical Review E, 47, 2401.
http://dx.doi.org/10.1103/PhysRevE.47.2401 - 13. Eckmann, J.-P. and Ruelle, D. (1985) Ergodic Theory of Chaos and Strange Attractors. Reviews of Modern Physics, 57, 617. http://dx.doi.org/10.1103/RevModPhys.57.617
- 14. Freedman, D.H. (1998) Chaos Theory. Boston Inc., Boston.
- 15. Palmer, T. and Hagedorn, R. (2006) Predictability of Weather and Climate. Cambridge University Press, UK.
http://dx.doi.org/10.1017/CBO9780511617652














