Atmospheric and Climate Sciences
Vol.4 No.1(2014), Article ID:41753,6 pages DOI:10.4236/acs.2014.41009
Detection of Approximate Potential Trend Turning Points in Temperature Time Series (1941-2010) for Asansol Weather Observation Station, West Bengal, India
1Department of Geography, Presidency University, Kolkata, India
2Department of Geography, Egra S.S.B College, Egra, India3Department of Geography and Environment Management, Vidyasagar University, Midnapore, IndiaEmail: scgeovu@yahoo.co.in, dbisai@gmail.com, khanansargeo@gmail.com
Copyright © 2014 Soumendu Chatterjee et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Soumendu Chatterjee et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 22, 2013; revised November 15, 2013; accepted November 25, 2013
Keywords:Sequential Version of Mann-Kendall Test Statistic; Temperature Trends; Turning Points
ABSTRACT
Researches are being carried out world-wide to understand the nature of temperature change during recent past at different geographical scales so that comprehensive inferences can be drawn about recent temperature trend and future climate. Detection of turning points in time series of meteorological parameters puts challenges to the researches. In this work, the temperature time series from 1941 to 2010 for Asansol observatory, West Bengal, India, has been considered to understand the nature, trends and change points in the data set using sequential version of Mann-Kendall test statistic. Literatures suggest that use of this test statistic is the most appropriate for detecting climatic abrupt changes as compared to other statistical tests in use. This method has been employed upon monthly average temperatures recorded over the said 70 years for detection of abrupt changes in the average temperature of each of the months. The approximate potential trend turning points have been calculated separately for each month (January to December). Sequential version of Mann-Kendall test statistic values for the months of July and August is significant at 95% confidence level (p < 0.05). The average temperature for most of the other months has shown an increasing trend but more significant rise in July and August temperature has been recognized since 1960s.
1. Introduction
In the background of global climate change and under local anthropogenic stresses many regions in the world have been suffering from different and frequent climatic problems. Atmospheric temperature is one of the major significant factors of weather and climate as it largely regulates the atmospheric phenomena irrespective of climate types. Thermal responses of global climate change constitute the most important component of climate assessment. The trend analysis and change point detection for any meteorological parameter owe to active lines of investigation that seek to identify the climatic change in a particular region. The assumption of stationarity, or timeinvariant characteristics of a climatological time series under consideration, seems to be invalid as a result of anthropogenic influences and the natural variability of the climate system [2]. Therefore, trend analysis and change point detection in temperature time series are crucial for understanding regional climate and planning resource management. There are several recent studies on climatologic temperature time series trends and detection of change points, which conclude about temperature related complex functions of the climatic environment [3]. Researchers have unfolded many harsh realities regarding global warming and its multifarious impacts, particularly on human society. This has instigated more and more studies in this field. In its Fourth Assessment Report, IPCC (2007) has pointed out that the mean surface temperature of the planet has risen by 0.74˚C over the 100 years between 1996 and 2005, 0.13˚C per decade being the rate during last 50 years. Between 1995 and 2006 the global communities have experienced 11 warmest years out of 12 since 1850 [4]. It has also been estimated that, by the end of this century Earth’s temperature will continue to increase between 1.4˚C and 5.8˚C. Similar results have been obtained from analyses of long term temperature time series at regional and local scale. During the last 100 years China has experienced a warming by 0.79˚C at the rate of 0.08˚C per decade with local level disparities in warming [5-7]. Large volume of literature has been produced on surface air temperature variation that includes research works to confirm global warming by use of a variety of methods [8-11]. It has been argued that daily minimum temperature exhibits more associations with global warming phenomenon rather than daily maximum [10].
The purpose of this study is to detect the change points and span of homogeneity in trends of temperature data set over the period from 1941 to 2010, for Asansol, India. Sequential version of Mann-Kendall test statistic has been adopted to identify the change point or break points in the considered time series data set. We think that, all the detected change points may be some outcome of potential trend turning points in time series. The serviceable data set has been employed according to forward temporal scale and at most four change points can be detected for a month.
2. Study Area
Asansol (23˚40'48"N and 86˚59'24"E), the second largest agglomeration in West Bengal, India, following Kolkata, is located between the rivers Ajoy and Damodar of Chottonagpur plateau fringe. The region sites on seams of coal. Asansol has a large history of coal mining and industrial activities related primarily to Iron and Steel production over more than 150 years. As such, the area has seen rapid experiencing urbanization with remarkable growth of population. According to Koppen’s classification (1884) the area belongs to Tropical Savanna Climate (denoted as “Aw”) sub type. Mean annual temperature of Asansol in slightly above 32˚C but in summer during April-May, the average daily temperature often goes beyond 40˚C while in winter months the lowest temperature goes even below 10˚C. During December to January, the average monthly minimum temperature remains around 12˚C. The area receives more than 1400 of mm rainfall annually much (80%) of which occurs during June-September, June and July being the rainiest and December being the driest month. In some years of the last decade Asansol and its surrounding weather observatories (e.g. Panagarh, Durgapur) have recorded highest summer temperatures and lowest winter temperatures within the last century. Expansion of large scale industries and installation of sponge iron factories in innumerable number may have been responsible for local temperature change that have bearing upon the local weather phenomena like smog, small scale thunderstorm, occurrence of Norwester etc. These observations really create research interest in temperature trend analysis of Asansol.
3. Data Base and Method
3.1. Data Base
This analysis has been carried on the lower atmospheric temperature data collected from Indian Meteorological Department (IMD), Kolkata (Alipore), recorded at Asansol weather observation station for the period from 1941 to 2010. Mean monthly maximum and mean monthly minimum temperature for each of the months over the 70 years has been considered. The data series is continuous and homogeneous without any gap in its sequence. Month-wise mean maximum and mean minimum temperatures are averaged to get mean monthly temperature year-wise. Finally, the monthly average data sets were employed for statistical analysis. In order to identify discontinuities and detection of change point thereby, sequential version of Mann-Kendall (Seq.MK) test statistic is applied. It is a valid method suggested by many investigators.
3.2. Method
Sequential Version of Mann-Kendall Test Statistic
The sequential version of Mann-Kendall test statistic [1, 12] when applied on time series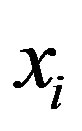 , detects approximate potential trend turning points in long term data. The Sequential Mann-Kendall test is computed using ranked values
, detects approximate potential trend turning points in long term data. The Sequential Mann-Kendall test is computed using ranked values 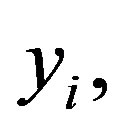 of the original values
of the original values , in analysis. The magnitudes of
, in analysis. The magnitudes of 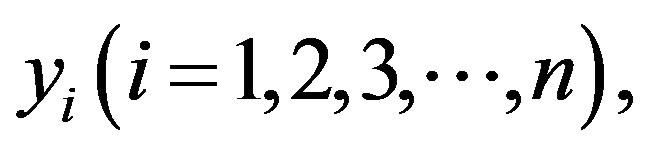 are compared with
are compared with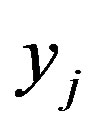 ,
, . For each comparison, the cases where
. For each comparison, the cases where  are counted and denoted by
are counted and denoted by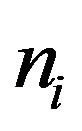 . A statistic
. A statistic 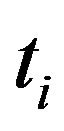 can therefore, be defined as [11].
can therefore, be defined as [11].
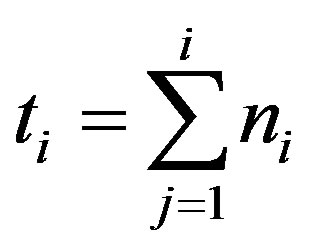 (1)
(1)
The distribution of test statistic 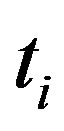 , has a mean as
, has a mean as
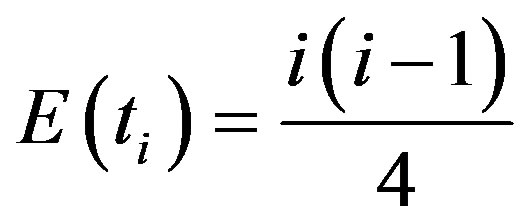 (2)
(2)
and variance as
 (3)
(3)
The sequential values of a reduced or standardized variable, called statistic 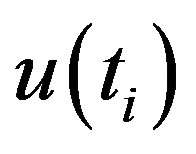 is calculated for each of the test statistic variable
is calculated for each of the test statistic variable 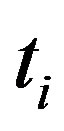 as follows:
as follows:
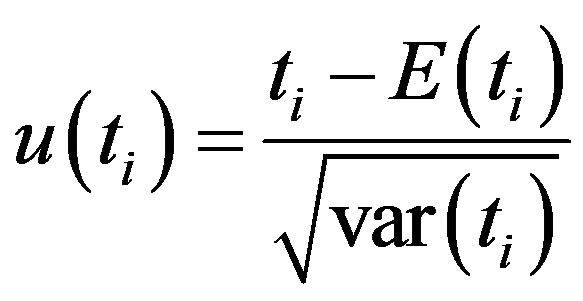 (4)
(4)
While the forward sequential statistic,  is estimated using the original time series
is estimated using the original time series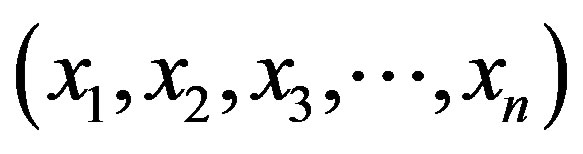 , values of the backward sequential statistic,
, values of the backward sequential statistic, 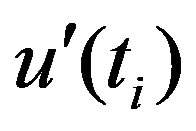 are estimated in the same manner but starting from end of the series. In estimating
are estimated in the same manner but starting from end of the series. In estimating 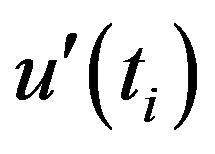 the time series is resorted so that last value of the original time series comes first
the time series is resorted so that last value of the original time series comes first .
.
The sequential version of Mann-Kendall test statistic allows detection of approximate beginning of a developing trend. When 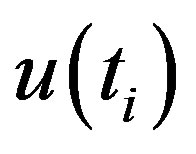 and
and 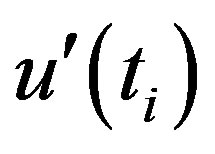 curves are plotted, the intersection of the curves
curves are plotted, the intersection of the curves  and
and 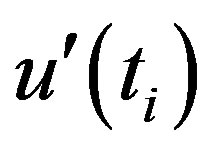 locates approximate potential trend turning point. If the intersection of
locates approximate potential trend turning point. If the intersection of 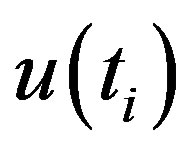 and
and 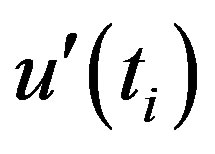 occur within
occur within  (5% level) of the standardized statistic, a detectable change at that point in the time series can be inferred. Moreover, if at least one value of the reduced variable is greater than a chosen level of significance of Gaussian distribution the null hypothesis (H0: Sample under investigation shows no beginning of a new trend) is rejected.
(5% level) of the standardized statistic, a detectable change at that point in the time series can be inferred. Moreover, if at least one value of the reduced variable is greater than a chosen level of significance of Gaussian distribution the null hypothesis (H0: Sample under investigation shows no beginning of a new trend) is rejected.
4. Results and Discussion
Sequential Version of Mann-Kendall test statistic calculated for monthly average temperature data set of Asansol station clearly detects the statistically significant turning points in yearly trend of monthly temperature. Yearly plots of  and
and  values for each of the months of a year have been shown in Figure 1. In case of the month of January, an apparently decreasing trend from 1957 to 2010 is observed. Though the curves intersect each other at 1973 but it cannot be recognized as a significant turning point as the associated probability value is much higher than the accepted level of significance (p < 0.05) in Table 1. Furthermore, although the
values for each of the months of a year have been shown in Figure 1. In case of the month of January, an apparently decreasing trend from 1957 to 2010 is observed. Though the curves intersect each other at 1973 but it cannot be recognized as a significant turning point as the associated probability value is much higher than the accepted level of significance (p < 0.05) in Table 1. Furthermore, although the 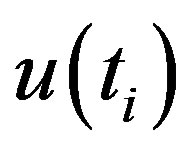 and
and 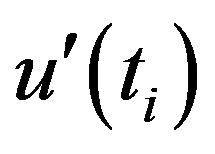 do not clearly cut each other but are closer to each other in 1992 where from they begin to diverge, indicating a starting point of an abrupt change in Figure 1(a). For the month of February,
do not clearly cut each other but are closer to each other in 1992 where from they begin to diverge, indicating a starting point of an abrupt change in Figure 1(a). For the month of February, 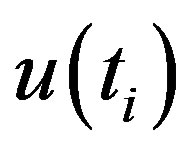 plot (Figure 1(b)) shows an increasing trend during 1945 and 1957, and 1980-2003, and a decreasing trend during 1941- 1944, and 1958-1979, then the curve gradually rises upward to indicate an increasing trend. Though less significant, 2003 can be identified as a turning point in the temperature trend of February.
plot (Figure 1(b)) shows an increasing trend during 1945 and 1957, and 1980-2003, and a decreasing trend during 1941- 1944, and 1958-1979, then the curve gradually rises upward to indicate an increasing trend. Though less significant, 2003 can be identified as a turning point in the temperature trend of February. 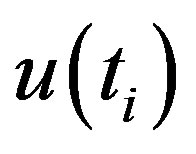 and
and 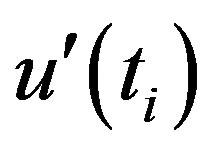 plots for the month of March in Figure 1(c), intersect each other for several times which indicates that there is no recognizable trend in the March temperature data set [11]. Sequential Mann-Kendall plots for April temperature has been given in Figure 1(d). It shows that, the
plots for the month of March in Figure 1(c), intersect each other for several times which indicates that there is no recognizable trend in the March temperature data set [11]. Sequential Mann-Kendall plots for April temperature has been given in Figure 1(d). It shows that, the 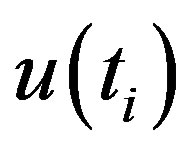 and
and  curves diverge since 1953 where they have taken
curves diverge since 1953 where they have taken

Table 1. Change points detection by sequential version ofMann-Kendall test for Asansol observatory (values significant at p < 0.05*).
a value of 0.387. Hence, for the April data set a less significant turning point can be detected at 1953. The 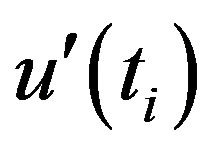 plot also helps to understand that April temperature at Asansol has increased since 1954 and afterward it has stabilized.
plot also helps to understand that April temperature at Asansol has increased since 1954 and afterward it has stabilized.
 plots for the month of May in Figure 1(e) and June in (f), indicates less significant trend turning point at the beginning of the 6th decade of the last Century. The May temperature had a decreasing trend prior to the abrupt change and slightly increasing trend after that change. On the contrary, the June temperature had a decreasing trend before the abrupt change and has almost stabilized after the change.
plots for the month of May in Figure 1(e) and June in (f), indicates less significant trend turning point at the beginning of the 6th decade of the last Century. The May temperature had a decreasing trend prior to the abrupt change and slightly increasing trend after that change. On the contrary, the June temperature had a decreasing trend before the abrupt change and has almost stabilized after the change.
Most significant turning points in month wise temperature time series over the period from 1941 to 2010 for Asansol station have been found for the months of July in Figure 1(g) and August in (h) in 1962 and 1969 respectively.  plots for those two months alsoexhibit an initial spell of uniformity in average temperature up to1962 and 1969, respectively and increasing trends thereafter. The temperature series for the September and October shows increasing trend over the period considered in Figures 1(i) and (j), abrupt changes for these two months have been found to have occurred since 1986 and 1989, respectively.
plots for those two months alsoexhibit an initial spell of uniformity in average temperature up to1962 and 1969, respectively and increasing trends thereafter. The temperature series for the September and October shows increasing trend over the period considered in Figures 1(i) and (j), abrupt changes for these two months have been found to have occurred since 1986 and 1989, respectively.  and
and 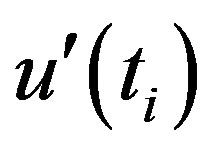 statistic values for the month of November converge gradually to intersect each others in 1998 and they diverge thereafter indicating a turning point at 1998, though at considerably low level of significance in Figure 1(k).
statistic values for the month of November converge gradually to intersect each others in 1998 and they diverge thereafter indicating a turning point at 1998, though at considerably low level of significance in Figure 1(k).  plot for the December temperature time series indicates a turning in the temperature trend since 1957 in Figure 1(l).
plot for the December temperature time series indicates a turning in the temperature trend since 1957 in Figure 1(l).
5. Conclusion
The sequential version of Mann-Kendall test statistic has been employed, in this analysis on year wise data of

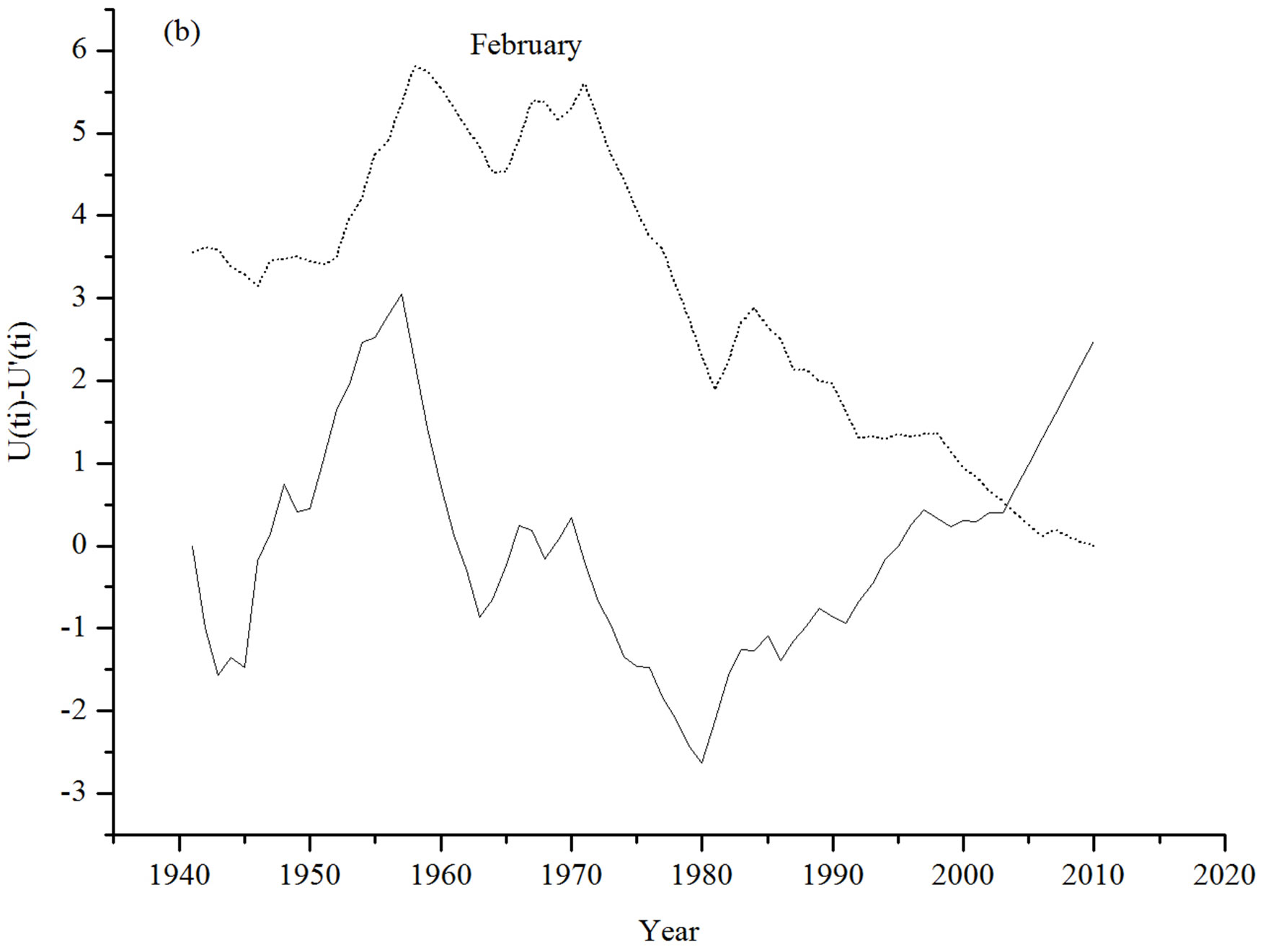
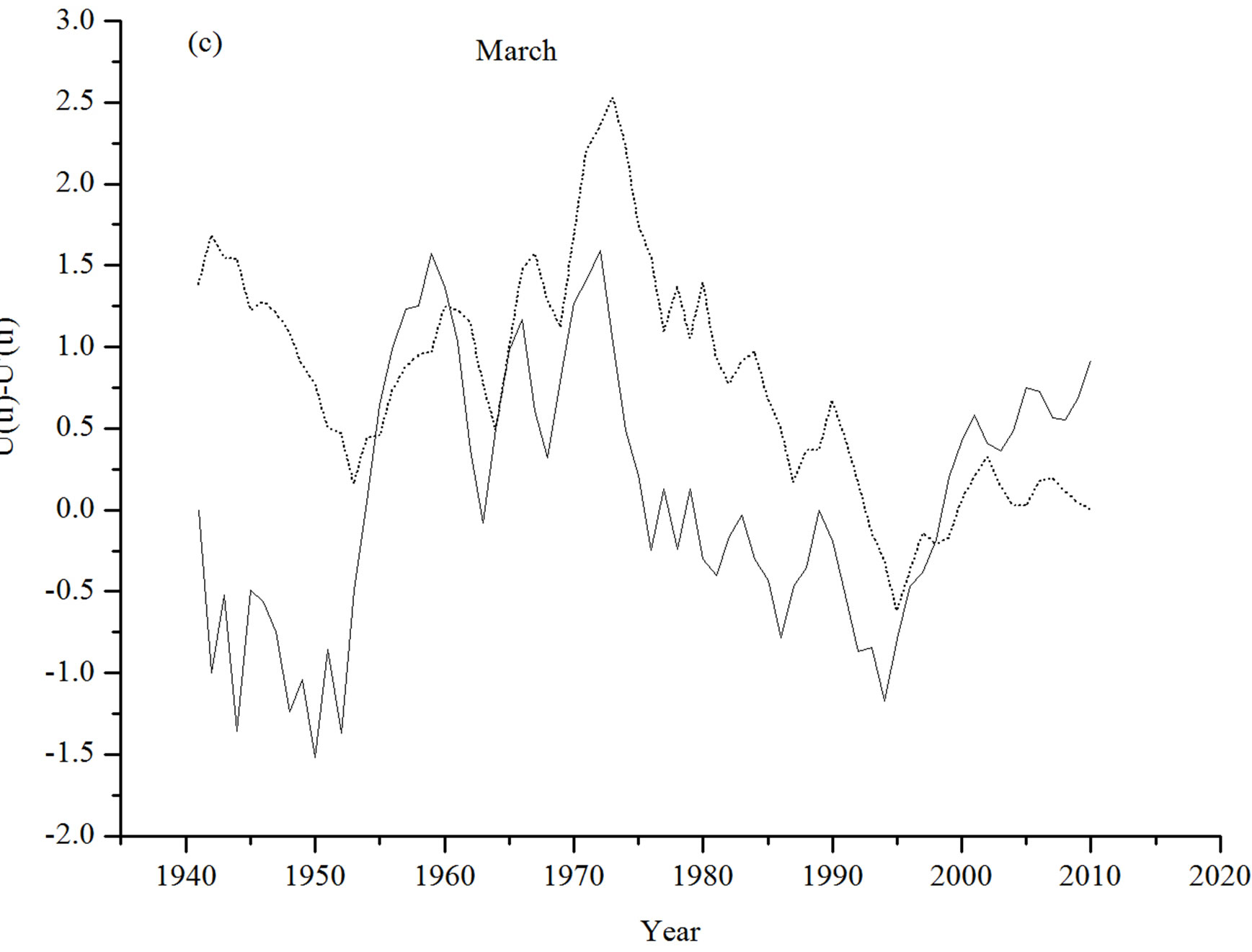
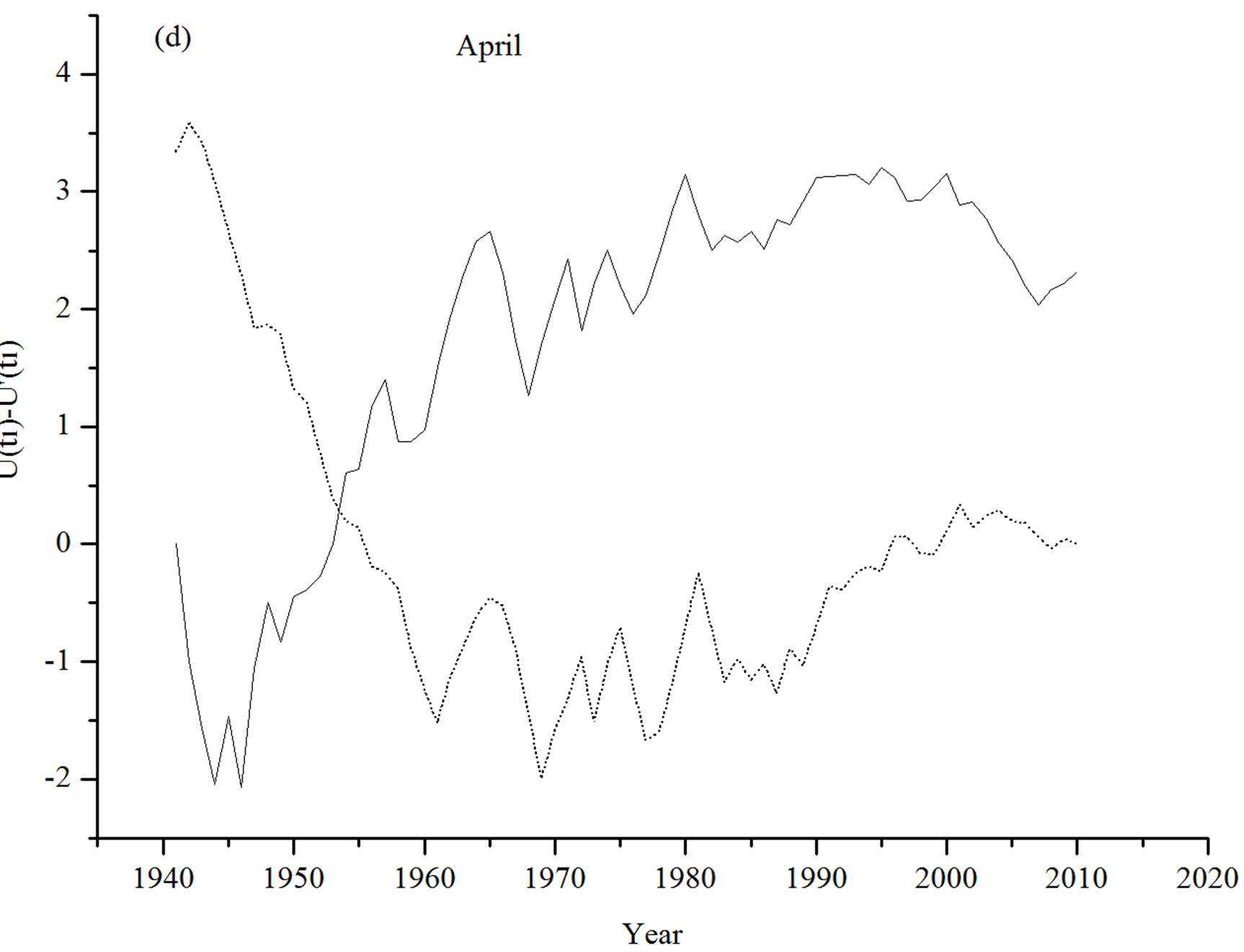

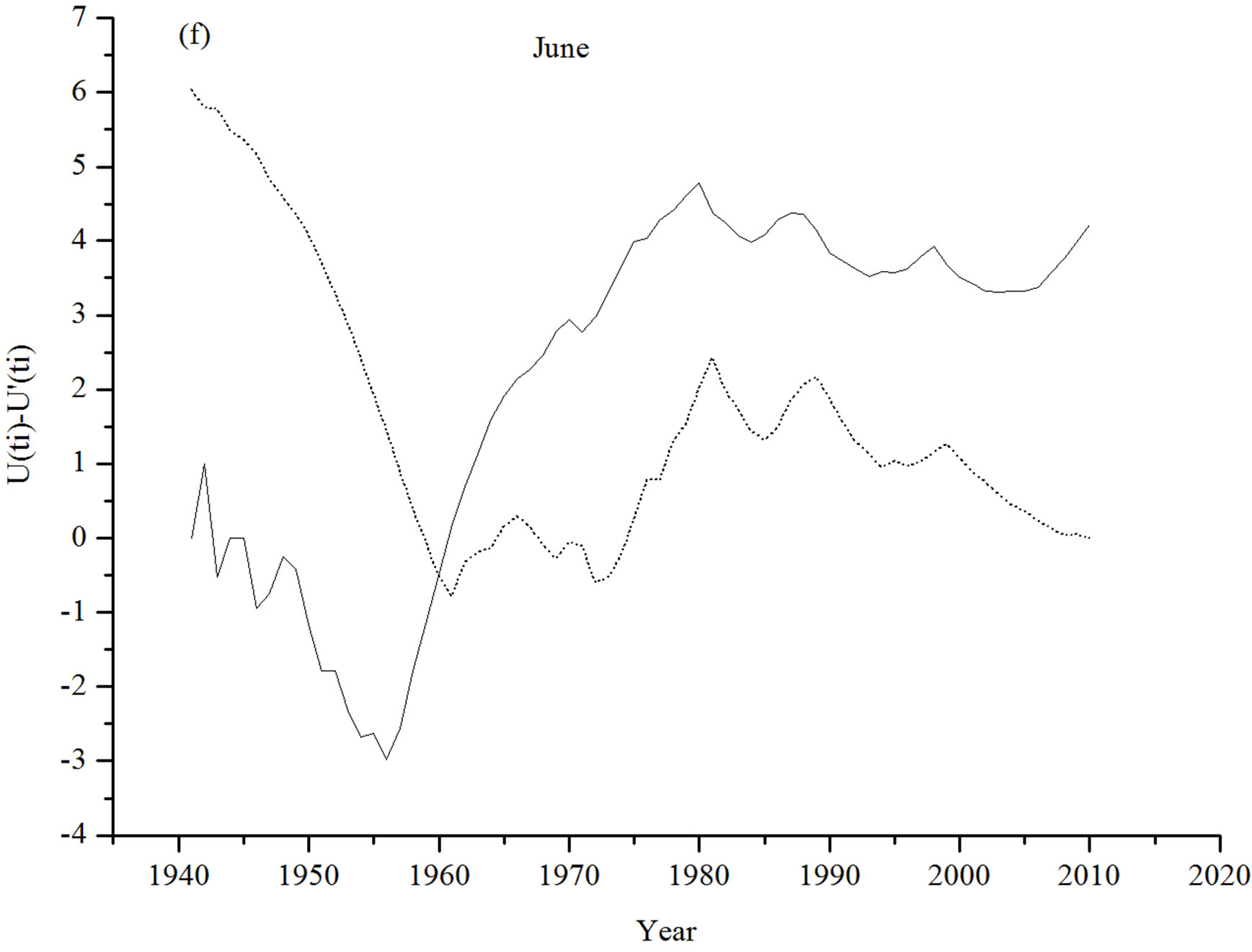


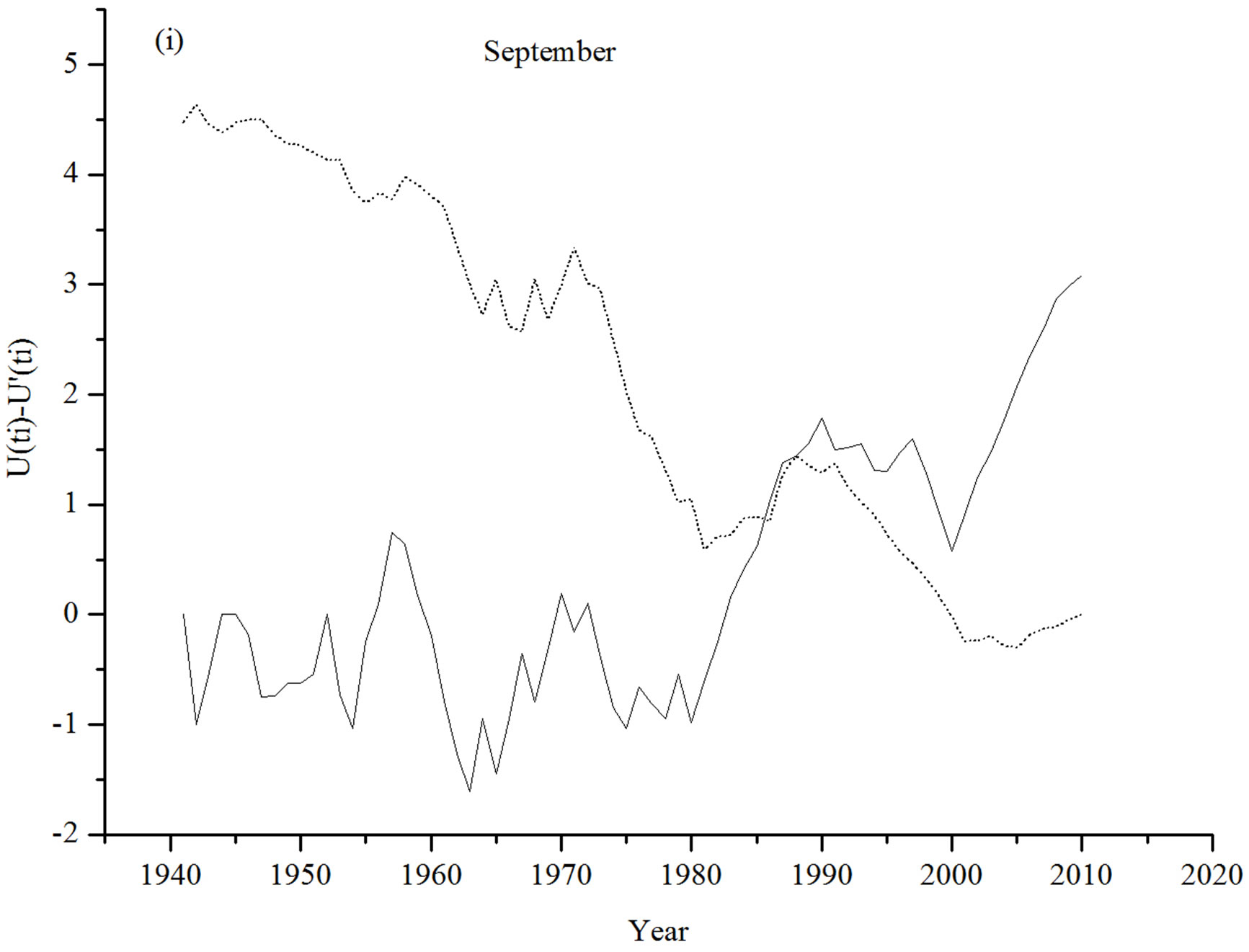
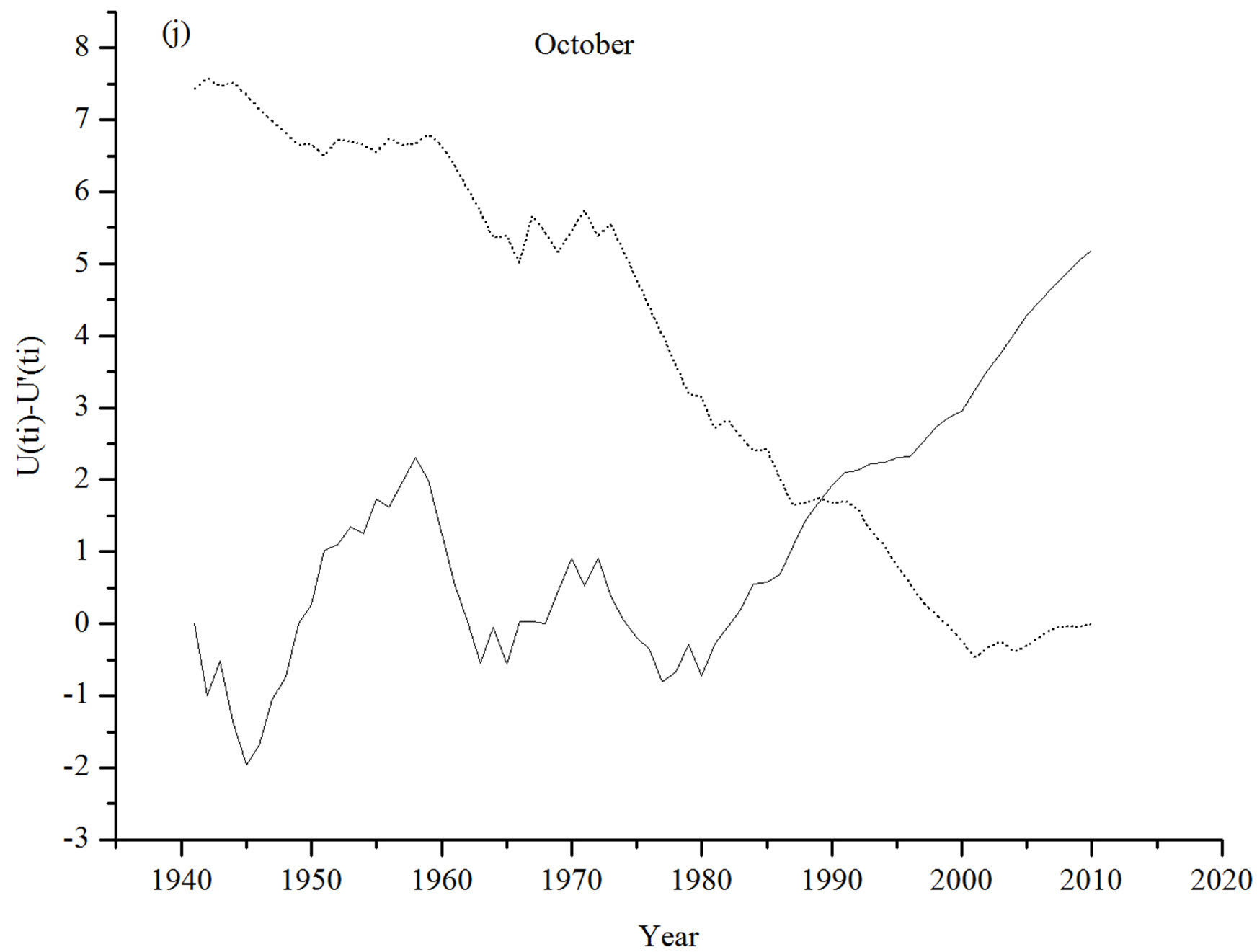
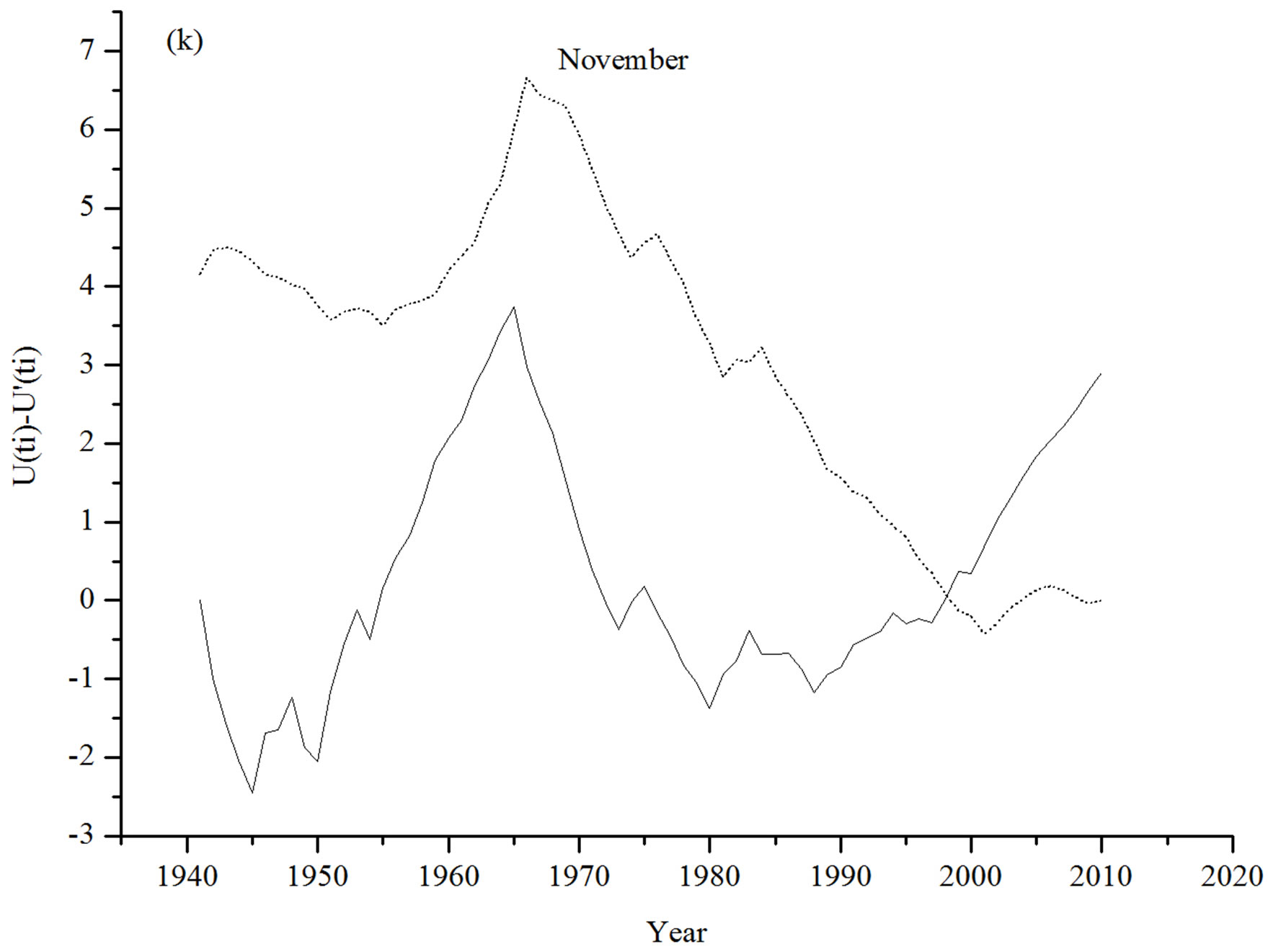
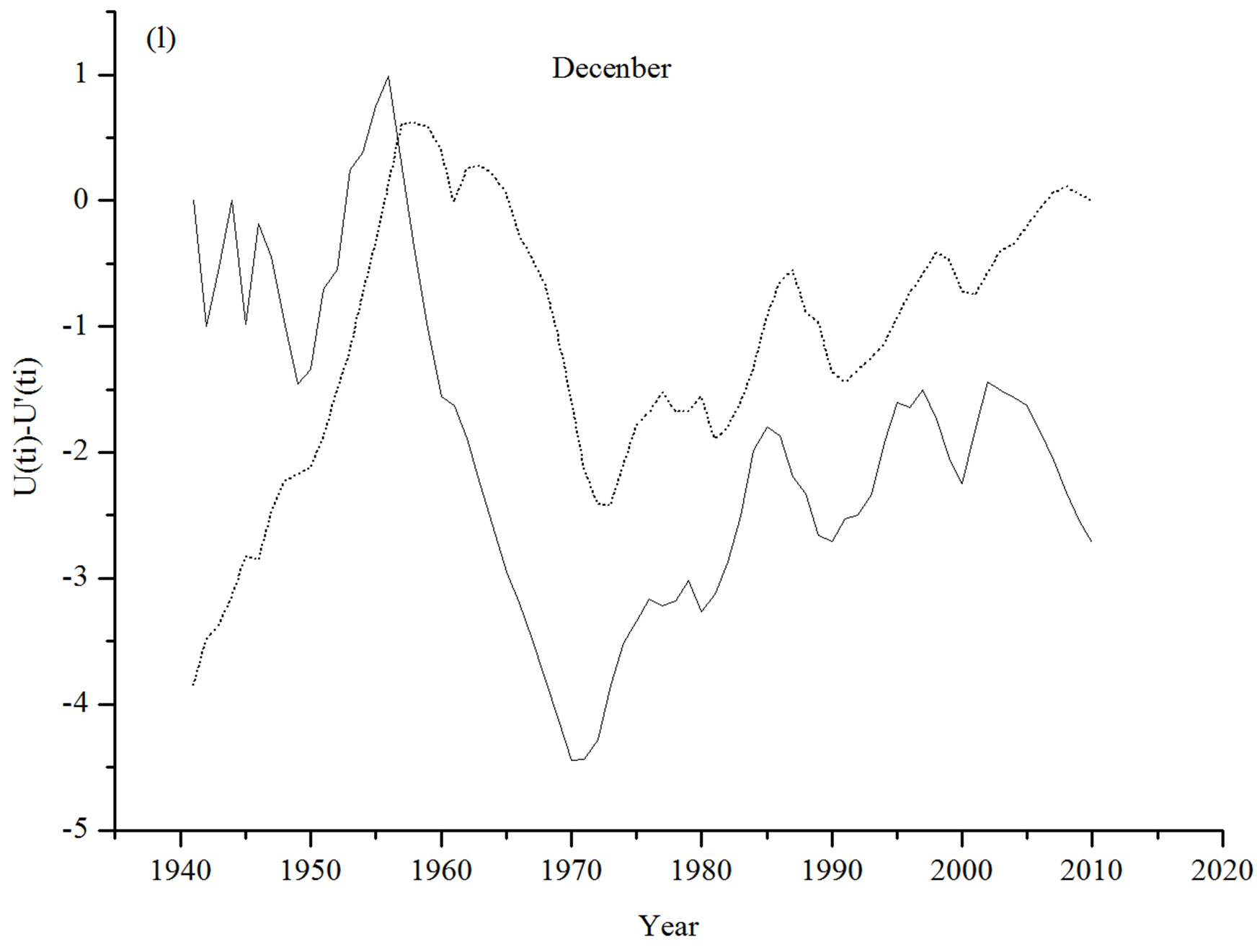
Figure 1. Abrupt changes in average monthly temperature as derived from sequential version of Mann-Kendall test statistic, u(ti) forward sequential statistic drawn in solid line and u'(ti) backward sequential statistic drawn in dotted line.
mean temperature for the each of months for the period from 1941 to 2010, in the case of Asansol Weather Observation Station, West Bengal, India. The study reveals that mean monthly temperatures for most of the months have increased since different time points within the time period considered. Though all such turning points in the temperature time series have been found to be statistically significant but highly significant changes have occurred in the case of July and August. It is important to note that these two months fall within the monsoon season and increase of average temperature may have significant bearing on the functionality of monsoon weather system over this area. Hence, findings of the present study invite initiatives for further investigation on effect of increase in mean monthly temperature during monsoon season in modifying pattern of rainfall over the area under study.
REFERENCES
- R. Sneyres, “On the statistical Analysis of Time Series of Observation,” Technical Note No. 143, World Meteorological Organisation, Geneva, 1990.
- S. Jain and U. Lall, “Magnitude and Timing of Annual Maximum Floods: Trends and Large Scale Climate Associations of the Blacksmith Rock River, Utha,” Water Resources Research, Vol. 36, No. 12, 2000, pp. 3641-3651. http://dx.doi.org/10.1029/2000WR900183
- D. K. Karpouzos, S. Kavalieratou and C. Babajimopoulos, “Trend Analysis of Precipitation Data in Pieria Region (Greece),” European Water, Vol. 30, 2010, pp. 31-40.
- IPCC, “Climate Change 2007: Synthesis Report,” In: R. K. Pachauri and A. Reisinger, Eds., Contribution of Working Group I, II. and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), Cambridge University Press, Cambridge, 2007.
- L. L. Ren, W. Zhang, C. H. Li and M. R. Wang, “Impacts of Human Activity on River Runoff in the Northern Area of China,” Journal of Hydrology, Vol. 261, No. 1-4, 2002, pp. 204-217. http://dx.doi.org/10.1016/S0022-1694(02)00008-2
- W. Qian and X. Linx, “Regional Trends in Recent Precipitation Indices in China,” Meteorology and Atmospheric Physics, Vol. 90, No. 3-4, 2005, pp. 193-207. http://dx.doi.org/10.1007/s00703-004-0101-z
- X. L. Wang, “Comments on Detection of Undocumented Change Points: A Revision of the Two Phase Regression Model,” Journal of Climate, Vol. 16, No. 20, 2003, pp. 3383-3385. http://dx.doi.org/10.1175/1520-0442(2003)016<3383:CODOUC>2.0.CO;2
- R. C. Balling, J. A. Skindlow and D. A. Philips, “The Impacts of Increasing Summer Mean Temperature on Extreme Maximum and Minimum Temperature in Phoenix, Arizona,” Journal of Climate Vol. 3, No. 12, 1990, pp. 1491-1494. http://dx.doi.org/10.1175/1520-0442(1990)003<1491:TIOISM>2.0.CO;2
- D. R. Easterling, L. G. Evans, P. Y. Groisman, T. R. Karl K. E. Kunkel and P. Ambenze, “Observed Variability in Trends in Extreme Climate Events: A Brief Review,” Bulletin of American Meteorological Society, Vol. 81, No. 3, 2000, pp. 417-425. http://dx.doi.org/10.1175/1520-0477(2000)081<0417:OVATIE>2.3.CO;2
- D. R. Easterling, B. Horton, P. D. Jones, T. C. Peterson, T. R. Karl, D. E. Parker, M. J. Salinger, V. Razuvayev, N. Plummer, P. Jamason and C. K. Folland, “Maximum and Minimum Temperature Trends For The Globe,” Science, Vol. 277, No. 5324, 1997, pp. 364-366. http://dx.doi.org/10.1126/science.277.5324.364
- B. Safari, “Trend Analysis of Mean Annual Temperature in Rwanda during Last Fifty Two Years,” Journal of Environmental Protection, Vol. 3, No. 6, 2012, pp. 538-551. http://dx.doi.org/10.4236/jep.2012.36065
- T. Mohsin and W. A. Gough, “Trend Analysis of LongTerm Temperature Time series in the Greater Toronto Area (GTA),” Theoretical and Applied Climatology, Vol. 98, 2009, pp. 3-4.

