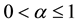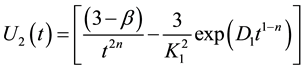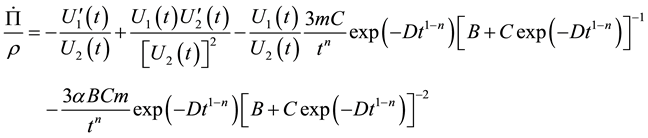International Journal of Astronomy and Astrophysics
Vol.05 No.03(2015), Article ID:59986,13 pages
10.4236/ijaa.2015.53025
Bulk Viscous Bianchi Type V Space-Time with Generalized Chaplygin Gas and with Dynamical G and L
Shubha S. Kotambkar1, Gyan Prakash Singh2, Rupali R. Kelkar3
1Department of Applied Mathematics, Laxminarayan Institute of Technology, Rashtrasant Tukadoji Maharaj Nagpur University, Nagpur, India
2Department of Mathematics, Visvesvaraya National Institute of Technology, Nagpur, India
3Department of Applied Mathematics, S. B. Jain Institute of Technology, Management and Research, Nagpur, India
Email: shubha.kotambkar@rediffmail.com, gpsingh@mth.vnit.ac.in, rupali.kelkar@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 March 2015; accepted 25 September 2015; published 28 September 2015
ABSTRACT
In this paper, bulk viscous Bianchi type V cosmological model with generalized Chaplygin gas, dynamical gravitational and cosmological constants has been investigated. We are assuming the condition on metric potential . To obtain deterministic model, we have considered physically plausible relations like
. To obtain deterministic model, we have considered physically plausible relations like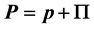 ,
, 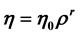 and the generalized Chaplygin gas is described by equation of state
and the generalized Chaplygin gas is described by equation of state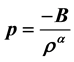 . A new set of exact solutions of Einstein’s field equations has been obtained in Eckart theory, truncated theory and full causal theory. Physical behavior of the models has been discussed.
. A new set of exact solutions of Einstein’s field equations has been obtained in Eckart theory, truncated theory and full causal theory. Physical behavior of the models has been discussed.
Keywords:
Bianchi Type V, Gravitational Constant, Cosmological Constant, Bulk Viscosity, Chaplygin Gas

1. Introduction
Recent cosmology is on Fridman-Lemaitra-Robertson-Walkar (FLRW) which is completely homogeneous and isotropic. But it is widely believed that FLRW model does not give a correct matter description in the early stage of universe. The theoretical argument [1] and the recent experimental data support the existence of an anisotropic phase, which turns into an isotropic one during the evolution of the universe. Anisotropic model plays significant role in description of evolution of the early phase of the universe and also helps in finding more general cosmological models than the isotropic FRW models. This motivates researcher for obtaining exact anisotropic solution for Einstein’s field equations as a cosmologically accepted physical models for the universe (in the early stages). The study of Bianchi type V cosmological model being anisotropic generalization of open FRW models is important to study old universe. A number of authors have investigated Bianchi type V cosmological model in general relativity in different context [2] - [15] . Rajbali and Seema Tinkar have discussed Bianchi type V bulk viscous Barotropic fluid cosmological model with variable G and L. Recently Yadav and Sharma [16] and Yadav [17] have discussed about transit universe in Bianchi type V space-time with variable G and L.
It has been widely discussed in the literature that during the evolution of the universe, bulk viscosity can arise in many circumstances and can lead to an effective mechanism of galaxy formation [18] . It is known that real fluids behave irreversibly and therefore it is important to consider dissipative processes both in cosmology and in astrophysics. To consider more realistic models, one must take in to account the viscosity mechanism. Bulk viscosity leading to an accelerated phase of the universe today has been studied by Fabris et al. [19] . Very recently Kotambkar et al. [20] have investigated anisotropic cosmological models with quintessence considering the effect of bulk viscosity.
A wide range of observations strongly suggest that the universe possesses non zero cosmological term [21] . The astronomical observations [22] [23] support that the expansion of the universe is accelerated. It suggests that there exists a new component in universe named as dark energy with negative pressure. A natural explanation for the accelerated expansion is due to a positive small cosmological constant. An attention has been paid to cosmological models with non zero cosmological term L [21] [24] , whose existence is favored by supernovae SNe Ia observations (refer to [22] [23] ) which are consistent with the recent anisotropy measurements of the cosmic microwave background (CMB) made by the WAMAP experiment [25] . Sahni and Starobinski [26] have presented detailed discussion on current observational situation focusing on cosmological tests on L.
Time varying G has many interesting consequences in astrophysics. Cunuto and Narlikar [27] have shown that G-varying cosmology is consistent with what so ever cosmological observations available at present. A new approach is appealing; it assumes the conservation of the energy momentum tensor which consequently gives G and L as coupled fields similar to the case of G in original Brans-Dicke theory. The cosmological model with variable G and L has been investigated by several researchers [28] - [32] . A number of researchers have discussed various anisotropic cosmological models with variable G and L [33] - [37] .
According to recent observational evidence, the expansion of the universe is accelerated, which is dominated by a smooth component with negative pressure, the so called dark energy. To avoid problems associated with L and quintessence models, recently, it has been shown that Chaplygin gas may be useful. The unification of the dark matter and dark energy component creates a considerable theoretical interest, because on the one hand, model building becomes reasonably simpler, and on the other hand such unification implies existence of an era during which the energy densities of dark matter and dark energy are strikingly similar. For representation of such a
unification, the generalized Chaplygin gas (GCG) with exotic condition of state 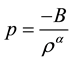 is considered, where
is considered, where
constant B and 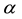 satisfy B > 0 and
satisfy B > 0 and 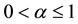 respectively. Due to observational evidence, cosmological models based on CG-EOS are very encouraging. Chaplygin gas and generalized Chaplygin gas cosmological models are first time proposed by Kamenshchik et al. [38] . WMAP constraints on the generalized Chaplygin gas model have been investigated by Bento et al. [39] .
respectively. Due to observational evidence, cosmological models based on CG-EOS are very encouraging. Chaplygin gas and generalized Chaplygin gas cosmological models are first time proposed by Kamenshchik et al. [38] . WMAP constraints on the generalized Chaplygin gas model have been investigated by Bento et al. [39] .
Motivated by above work we thought that it was worthwhile to study bulk viscous Bianchi type V space-time with generalized Chaplygin gas and dynamical G and L.
2. Metric and Field Equations
The spatially homogeneous and anisotropic space-time metric is given by
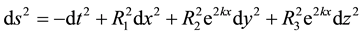 (1)
(1)
where  are functions of t alone.
are functions of t alone.
Einstein field equation with time dependent L and G may be written as
 (2)
(2)
where G and L are time dependent gravitational and cosmological constants. 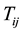 is energy momentum tensor of cosmic fluid in the presence of bulk viscosity defined as
is energy momentum tensor of cosmic fluid in the presence of bulk viscosity defined as
 (3)
(3)
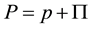 (4)
(4)
where p is equilibrium pressure, 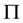 is bulk viscous stress together with
is bulk viscous stress together with .
.
Einstein’s field Equation (2) for the metric (1) takes form
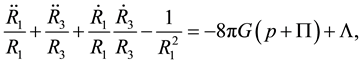 (5)
(5)
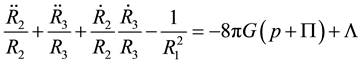

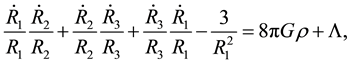
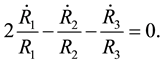
By the divergence of Einstein’s tensor i.e. 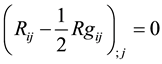
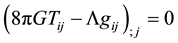

The energy momentum conservation equation 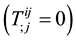
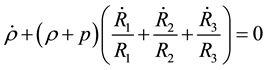
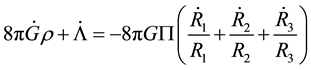
For the full causal non-equilibrium thermodynamics the causal evolution equation for bulk viscosity is given by [40]
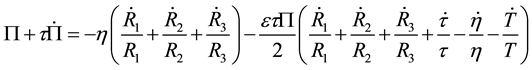

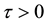
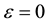
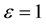
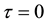
3. Cosmological Solutions
It can be easily seen that we have five Equations (5)-(9) with eight unknowns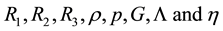
3.1. Case I: Non-Causal Cosmological Solution
For non causal solution
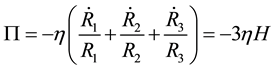
To find the complete solution of the system of equations, following relations are taken into consideration.
The power law relation for bulk viscosity is taken as

where 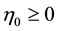
We consider an exotic background fluid, the Chaplygin gas, described by the equation of state
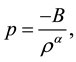
where B is constant and
To obtain the deterministic scenario of the universe, we assume the condition
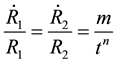
From Equation (9) and (17), one can get
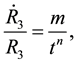
From Equations (17)-(18), one can easily calculate
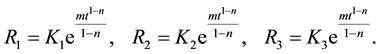
Using Equations (17) and (18), Equation (11) yields
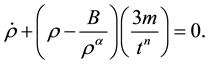
By solving Equation (20), we get
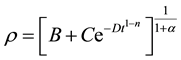
where 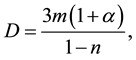

From Figure 1 one can easily see that energy density is decreasing with evolution of the universe.
On differentiating Equation (21), we get

Figure 1. This figure shows variation of energy density 
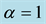
Now with the help of Equations (17)-(19) and (21), Equation (8) becomes
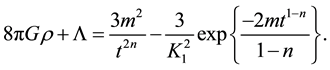
Which on differentiation yields

With the help of Equations (12), (14), (17)-(18) and (21), Equation (24) becomes
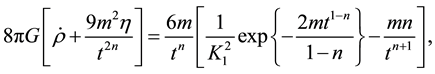
By use of Equations (15), (21) and (22) in Equation (25), we get
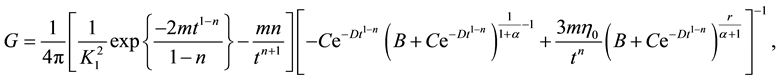
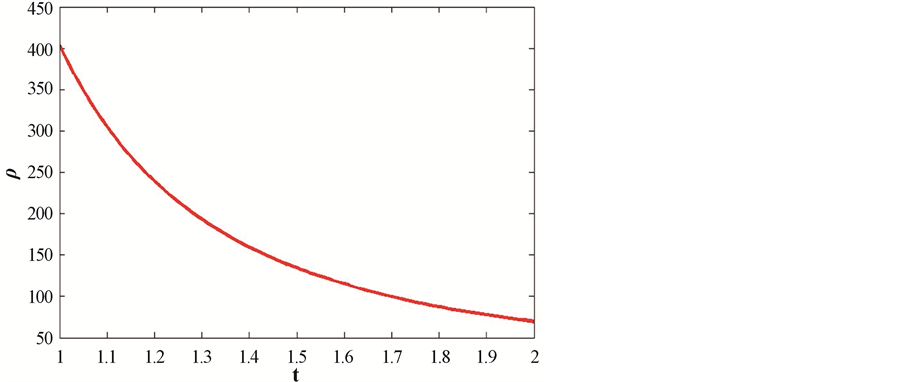
From Figure 2 it can be seen that G is increasing with evolution of the universe.
Now using Equations (21) and (26) in Equation (23) gives
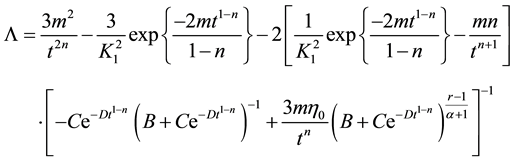
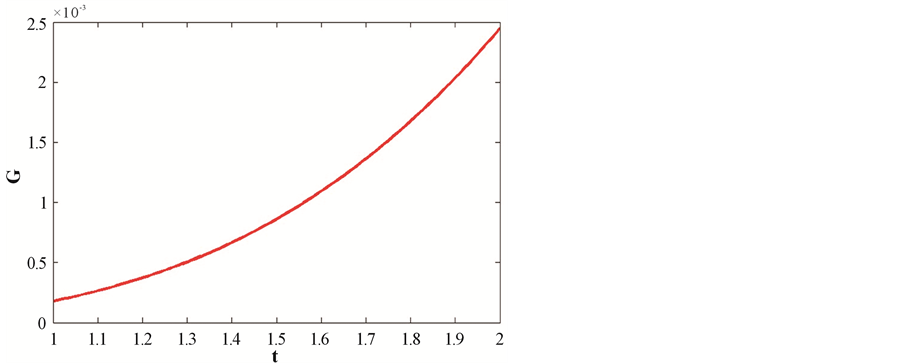
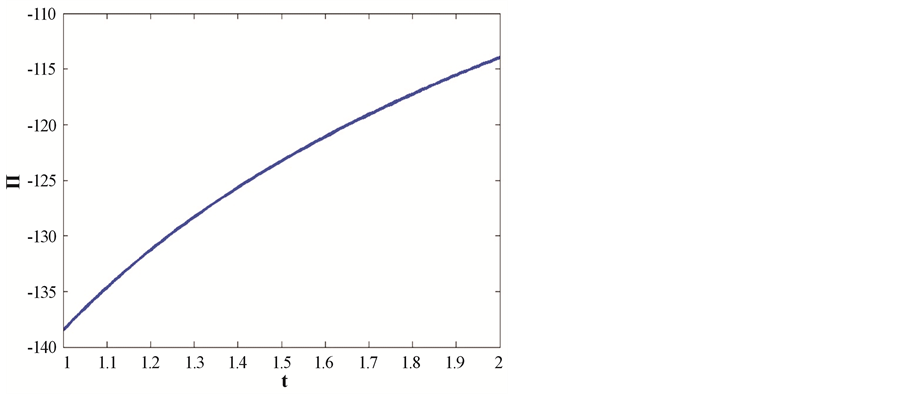
Figure 3 shows that cosmological constant is decreasing with the evolution of the universe.
On solving Equations (21) and (15) we can obtain the expression for bulk viscosity coefficient as

Figure 2. This figure shows variation of gravitational constant with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2, 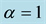
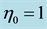
Figure 3. This figure shows variation of cosmological constant with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2, 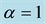

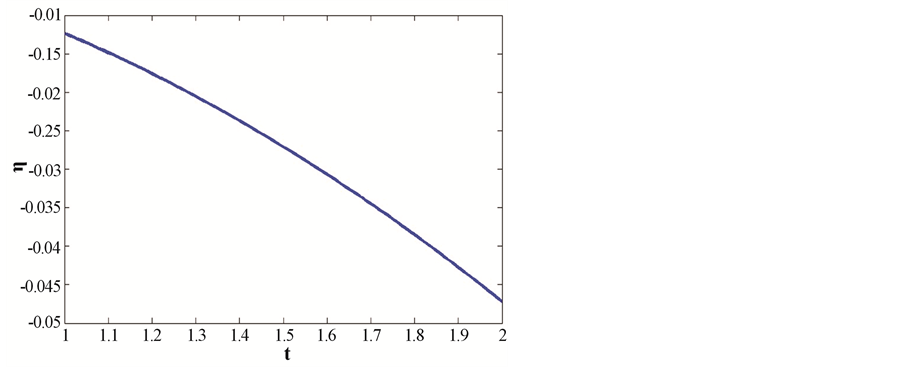
Figure 4 shows that bulk viscosity coefficient is decreasing with evolution of the universe.
Thus the metric (1) reduces into the form
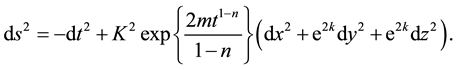
The deceleration parameter is given by
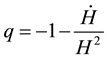
Figure 4. This figure shows variation of bulk viscosity coefficient with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2, 

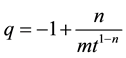
Expansion scalar, Shear coefficient, relative anisotropy for this model is given by
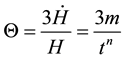
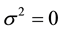
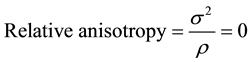
The critical energy density and the critical vacuum energy density are respectively given by
for the anisotropic Bianchi type V model can be expressed respectively as


Mass density parameter and the density parameter of the vacuum are given by
for the anisotropic Bianchi type V model can be expressed respectively as

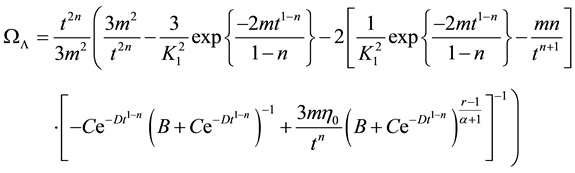
The State finder parameters 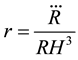
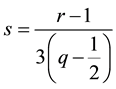
For this model
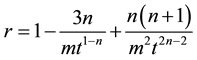
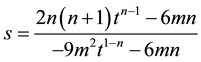
3.2. Case II: Causal Cosmological Solution
In addition to physically plausible relations (15)-(17), in this case we assume
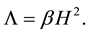
where H is Hubble parameter, given by

From Equation (17)-(19) and (41), the Hubble parameter is given by

Using equations (17)-(19), (40) and (42) in equation (8), we get
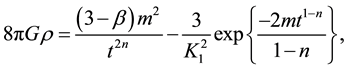
From Equations (21) and (43),
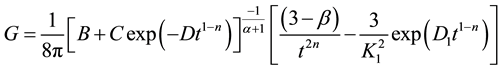
where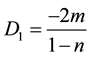
From Figure 5 one can easily see that gravitational constant is increasing with cosmic time.
Substitute the values from Equations (17)-(19), (40) and (44) in Equation (5), we get
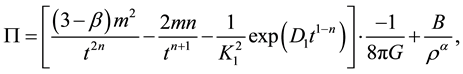
By use of Equation (21), Equation (44) gives
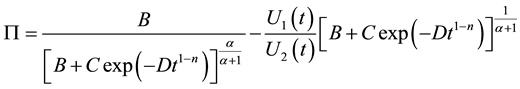
where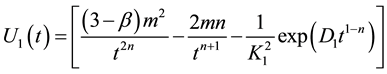
Figure 6 shows that bulk viscous stress is decreasing with the evolution of the universe.
3.2.1. Sub Cease (i): Evaluation of Bulk Viscosity in Truncated Causal Theory
Now we study variation of bulk viscosity coefficient 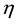
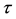

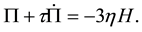
In order to have exact solution of the system of equations one more physically plausible relation is required.
Thus, we consider the well known relation
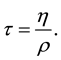
Using Equations (17)-(19), (46) and (48) in Equation (47) one can obtain coefficient of bulk viscosity as
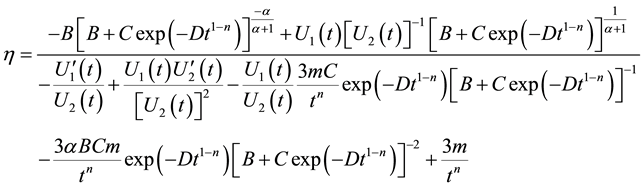
Figure 5. This figure shows variation of gravitational constant with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2,
Figure 6. This figure shows variation of bulk viscous stress with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2, 
Figure 7. This figure shows variation of bulk viscosity coefficient with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2,
From Figure 7 one can see that bulk viscosity coefficient is decreasing with time.
3.2.2. Sub Caese (ii). Evaluation of Bulk Viscosity in Full Causal Theory
It has already been mentioned that for full causal theory 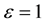
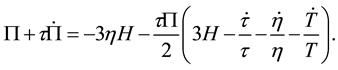
On the basis of Gibb’s inerrability condition, Maartens [40] has suggested the equation of state for temperature as
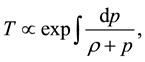
which with the help of Equation (21) gives
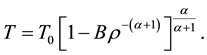
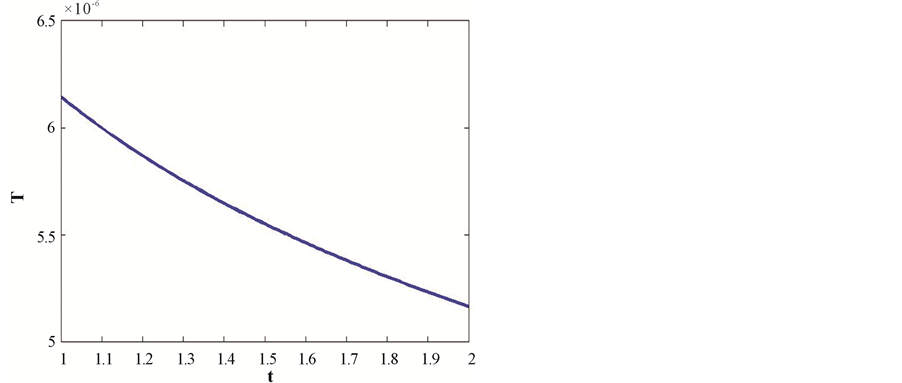
Figure 8 shows that temperature is decreasing with evolution of the universe.
using Equations (21), (42), (48) and (52) in Equation (50) one can obtain
which on simplification yields the expression for bulk viscosity as

where
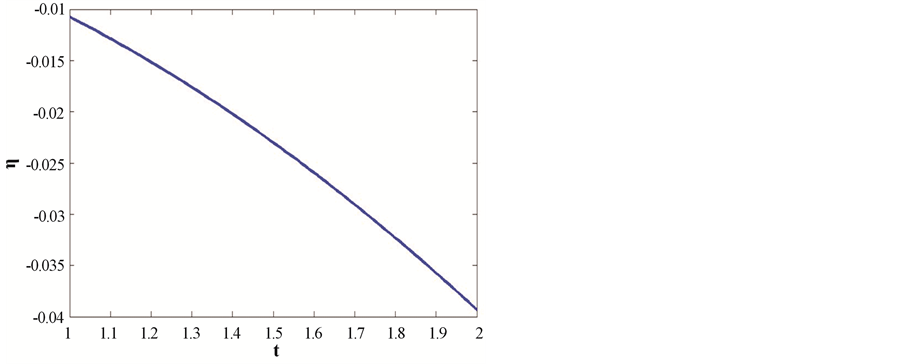
Figure 9 shows that bulk viscosity coefficient decreasing with evolution of universe.
4. Conclusion
In this paper, we have studied bulk viscous Bianchi type V space-time geometry with generalized Chaplygin gas and varying gravitational and cosmological constants. We have obtained a new set of exact solutions of
Einstein’s equations by considering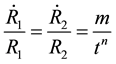
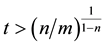
When 
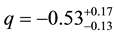
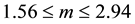
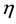
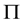
Figure 8. This figure shows variation of temparature with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2 and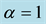
Figure 9. This figure shows variation of bulk viscosity coefficient with respect to cosmic time t. Here we consider B = 1, C = 1, n = 1.5, m = 2,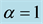
have clear idea of variation in behavior of cosmological parameters, relevant graphs have been plotted; all
graphs are in fair agreement with cosmological observations.
Cite this paper
Shubha S.Kotambkar,Gyan PrakashSingh,Rupali R.Kelkar, (2015) Bulk Viscous Bianchi Type V Space-Time with Generalized Chaplygin Gas and with Dynamical G and Λ. International Journal of Astronomy and Astrophysics,05,208-221. doi: 10.4236/ijaa.2015.53025
References
- 1. Misner, C.W. (1968) The Isotropy of the Universe. Astrophysical Journal, 151, 431-457.
http://dx.doi.org/10.1086/149448 - 2. Farnsworth, D.L. (1967) Some New General Relativistic Dust Metrics Possessing Isometries. Journal of Mathematical Physics, 8, 2315.
http://dx.doi.org/10.1063/1.1705157 - 3. Collins, C.B. (1974) Tilting at Cosmological Singularities. Communications in Mathematical Physics, 39, 131-151.
http://dx.doi.org/10.1007/BF01608392 - 4. Maartens, R. and Nel, S.D. (1978) Decomposable Differential Operators in a Cosmological Context. Communications in Mathematical Physics, 59, 273-283.
http://dx.doi.org/10.1007/BF01611507 - 5. Wainwright, J., Ince, W.C. and Marshman, W. (1979) Spetially Himigeneous and Inhomogeneous Cosmologies with Equation of State p = μ. General Relativity and Gravitation, 10, 259-271.
http://dx.doi.org/10.1007/BF00759860 - 6. Roy, S.R. and Singh, J.P. (1983) LRS Bianchi Type-V Universes Filled with Matter and Radiation. Astrophysics and Space Science, 96, 303-312.
http://dx.doi.org/10.1007/BF00651674 - 7. Banerjee, A. and Sanyal, A.K. (1988) Irrotational Bianchi Type V Viscous Fluid Cosmology with Heat Flux. General Relativity and Gravitation, 20, 103-113.
http://dx.doi.org/10.1007/BF00759320 - 8. Coley, A.A. (1990) Conformal Killing Vectors and FRW Spacetimes. General Relativity and Gravitation, 22, 241-251.
http://dx.doi.org/10.1007/BF00756274 - 9. Roy, S.R. and Prasad, A. (1994) Some L.R.S. Bianchi Type V Cosmological Models of Local Embedding Class One. General Relativity and Gravitation, 19, 939-950.
http://dx.doi.org/10.1007/BF02106663 - 10. Nayak, B.K. and Sahoo, B.K. (1989) Bianchi Type V Model with the Matter Distribution Admitting Anisotropic Pressure and Heat Flow. General Relativity and Gravitation, 21, 211-225.
http://dx.doi.org/10.1007/bf00764095 - 11. Bali, R. and Meena, B.L. (2004) Conformally Flat Tilted Bianchi Type-V Cosmological Models in General Relativity. Pramana: Journal of Physics, 62, 1007-1014.
- 12. Bali, R. and Yadav, M.K. (2005) Bianchi Type-IX Viscous Fluid Cosmological Model in General Relativity. Pramana: Journal of Physics, 64, 187-196.
- 13. Bali, R. and Singh, D.K. (2005) Bianchi Type V Bulk Viscous Fluid String Dust Cosmological Model in General Relativity. Astrophysics and Space Science, 300, 387-394.
- 14. Bali, R. and Tinker, S. (2009) Bianchi Type III Bulk Viscous Barotropic Fluid Cosmological Models with Variable G and Lambda. Chinese Physics Letters, 26, Article ID: 029802.
http://dx.doi.org/10.1088/0256-307X/26/2/029802 - 15. Rajbali, S.T. (2008) Bianchi Type V Bulk Viscous Barotropic Fluid Cosmological Models with Variable G and Lambda. Chinese Physics Letters, 25, 3090-3093.
http://dx.doi.org/10.1088/0256-307X/25/8/095 - 16. Yadav, A.K. (2013) Anisotropic Massive Strings in the Scalar Tensor Theory of Gravitation. Research in Astronomy and Astrophysics, 13, 772-782.
http://dx.doi.org/10.1088/1674-4527/13/7/002 - 17. Yadav, A.K., Pradhan, A. and Singh, A.K. (2012) Bulk Viscous LRS Bianchi Type I Universe with Variable G and Lambda. Astrophysics and Space Science, 337, 379-385.
http://dx.doi.org/10.1007/s10509-011-0814-7 - 18. Ellis, G.F.R. (1979) In: Schas, R., Ed., General Relativity and Cosmology, Enrico Fermi Course, Academic Press, New York, 47. Misner, C.W. (1968) The Isotropy of the Universe. Astrophysical Journal, 151, 431.
- 19. Fabris, J.C., Concalves, S.V.B. and de Sa’Ribeiro, R. (2006) Bulk Viscosity Driving the Acceleration of the Universe. General Relativity and Gravitation, 38, 495-506.
http://dx.doi.org/10.1007/s10714-006-0236-y - 20. Kotambkar, S., Singh, G.P. and Kelkar, R.K. (2014) Anisotropic Cosmological Models with Quintessence. International Journal of Theoretical Physics, 53, 449-460.
http://dx.doi.org/10.1007/s10773-013-1829-3 - 21. Krauss, L.M. and Turner, M.S. (1995) The Cosmological Constant Is Back. General Relativity and Gravitation, 27, 1137-1144.
http://dx.doi.org/10.1007/bf02108229 - 22. Riess, A.G., Filippenko, A.V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P.M., et al. (1998) Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal, 116, 1009-1038.
http://dx.doi.org/10.1086/300499 - 23. Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R.A., Nugent, P., Castro, P.G., et al. (1999) Measurements of Omega and Lambda from 42 High Redshift Supernovae. The Astronomical Journal, 517, 565-586.
http://dx.doi.org/10.1086/307221 - 24. Lima, J.A.S. and Trodden, M. (1996) Decaying Vacuum Energy and Deflationary Cosmology in Open and Closed Universe. Physical Review D, 53, 4280-4286.
http://dx.doi.org/10.1103/physrevd.53.4280 - 25. Bennett, C.L., Halpern, M., Hinshaw, G., Jarosik, N., Kogut, A., Limon, M., et al. (2003) First Year Wilkinson Microwave Anisotropy Prob (WMAP) Observations—Preliminary Maps and Basic Results. Astrophysical Journal Supplement, 148, 1-27.
- 26. Sahni, V. and Starobinski, A. (2000) The Case for a Positive Cosmological Lambda Term. International Journal of Modern Physics D, 9, 373-444.
- 27. Canuto, V.M. and Narlikar, J.V. (1980) Cosmological Tests of the Hoyle-Narlikar Conformal Gravity. The Astrophysical Journal, 236, 6-23.
http://dx.doi.org/10.1086/157714 - 28. Singh, G.P. and Kotambkar, S. (2001) Higher Dimensional Cosmological Model with Gravitational and Cosmological “Constants”. General Relativity and Gravitation, 33, 621-630.
http://dx.doi.org/10.1023/A:1010278213135 - 29. Singh, G.P. and Kotambkar, S. (2003) Higher Dimensional Dissipative Cosmology with Varying G and Lambda. Gravitation and Cosmology, 9, 206-210.
- 30. Singh, G.P., Kotambkar, S. and Pradhan, A. (2008) A New Class of Higher Dimensional Cosmological Models of Universe with Variable G and Lambda Term. Romanian Journal of Physics, 53, 607-618.
- 31. Pradhan, A. and Pandey, P. (2006) Some Bianchi Type I Viscous Fluid Cosmological Models with a Variable Cosmological Constant. Astrophysics and Space Science, 301, 127-134.
Pradhan, A., Singh, A.K. and Otarod, S. (2007) FRW Universe with Variable G and Lambda Term. Romanian Journal of Physics, 52, 445-458. - 32. Singh, C.P. and Kumar, S. (2006) Bianchi Type II Cosmological Models with Constant Deceleration Parameter. International Journal of Modern Physics D, 15, 419-438.
http://dx.doi.org/10.1142/s0218271806007754 - 33. Singh, C.P., Kumar, S. and Pradhan, A. (2007) Early Viscous Universe with Variable Gravitational and Cosmological Constant. Classical and Quantum Gravity, 24, 455-474.
http://dx.doi.org/10.1088/0264-9381/24/2/011 - 34. Singh, J.P. and Tiwari, S.K. (2008) Perfect Fluid Bianchi Type I Cosmological Constant Models with Time Varying G and Lambda. Pramana, 70, 565-574.
- 35. Singh, G.P. and Kale, A.Y. (2009) Anisotropic Bulk Viscous Cosmological Models with Variable G and Lambda. International Journal of Theoretical Physics, 48, 1177-1185.
http://dx.doi.org/10.1007/s10773-008-9891-y - 36. Bali, R. and Tinkar, S. (2009) Bianchi Type III Bulk Viscous Barotropic Fluid Cosmological Models with Variable G and Lambda. Chinese Physics Letters, 26, Article ID: 029802.
http://dx.doi.org/10.1088/0256-307X/26/2/029802 - 37. Verma, M.K. and Ram, S. (2011) Spatially Homogeneous Bulk Viscous Fluid Models with Time-Dependent Gravitational Constant and Cosmological Term. Advanced Studies in Theoretical Physics, 5, 387-398.
- 38. Kamenshchik, A., Moschella, U. and Pasquier, V. (2001) An Alternative to Quintessence. Physics Letters B, 511, 265-268.
http://dx.doi.org/10.1016/S0370-2693(01)00571-8 - 39. Bento, M.C., Bertolami, O. and Sen, A.A. (2003) WMAP Constraints on the Generalized Chaplygin Gas Model. Physics Letters B, 575, 172-180.
http://dx.doi.org/10.1016/j.physletb.2003.08.017 - 40. Maartens, R. (1995) Dissipative Cosmology. Classical and Quantum Gravity, 12, 1455-1465.
http://dx.doi.org/10.1088/0264-9381/12/6/011