Advances in Chemical Engineering and Science
Vol. 2 No. 1 (2012) , Article ID: 16707 , 8 pages DOI:10.4236/aces.2012.21009
Hydrodynamics of Liquid Film in Helical Tubes
Chemical Engineering Department, Higher Colleges of Technology, Sharjah, United Arab Emirates
Email: *mhameed@hct.ac.ae
Received August 23, 2011; revised September 30, 2011; accepted November 21, 2011
Keywords: Liquid Film; Flow in Helical Tube; Film Hydrodynamic
ABSTRACT
Hydrodynamic experiments on a liquid film are carried out using water in both straight and helical tubes at angles of inclination ranging between 2.5˚ and 5˚ and on three different coil diameters (23.86 cm, 32.74 cm and 41.13 cm) for film Reynolds numbers ranging from 100 to 2000. The film thickness is measured by two micrometers, arranged to measure vertical and horizontal distances within the cross section of the tube. The results of film thickness are related to the hydraulic radius to characterize the film flow in both types of tube. Momentum transfer rates are shown to be higher in helical tubes than in the straight incline tube. An empirical correlation is presented for film thickness in the helical tube in terms of NT (coil tube)/NT (straight tube) for film Dean number ranging from 1 to 1000.
1. Introduction
The occurrence and applications of film flow in chemical engineering processes are numerous; among them are absorption, extraction, heat transfer, humidification and distillation. The Wetted-wall column, a well know film flow technique, is frequently used for the experimental determination of mass transfer coefficients.
The presence of curves or bends is unavoidable in the design of open channel [1] thus producing spiral current and cross-waves in addition to the unique features of super elevation produced by centrifugal force.
Throughout the last century research work was mainly focused on film flow over flat surfaces or channels and over vertical tubes. Since 1960, extensive literature has been published dealing with wavy gas-liquid interfaces and concentrating mainly on the conditions under which waves exist and their effect on the processes of heat, mass and momentum transfer.
Hopf (cited in [2]) conducted experiments in a rectangular channel of slope ranging from 0.5˚ to 3.5˚ and noted the influence of turbulence between the critical film Reynolds numbers (Re¦, crit) ranging from 250 to 300. He found that wall roughness has no effect on Re¦,crit except for the smallest depths. Nusselt (cited in [3]) gave a theoretical treatment for smooth, laminar and two dimensional film flows and stated that:
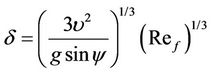 (1)
(1)
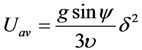 (2)
(2)
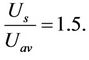 (3)
(3)
 (4)
(4)
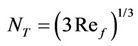 (5)
(5)
Jefferys [4] conducted experiments in channels at small slopes for a large range of Re¦. He confirmed the applicability of Equation (3) for the laminar region while the ratio of velocities decreases to 1.06 for the turbulent region. Cooper and Willey [5] determined experimental data for dilute sulfuric acid inside vertical tube and together with other workers found that up to Re¦ equal to 350, the data are in excellent agreement with Equation (3). While Kirkbride’s data [6] on film flowing outside a vertical tube deviated positively from the theoretical film thickness.
Fiend (cited in [2]) gave an experimental correlation for film flow of water and aqueous solutions with counter-current air in vertical tubes in turbulent region (Re¦ > 400) as:
 (6)
(6)
Brauer (cited in [2]) gave an empirical equation for turbulent flow as:
 (7)
(7)
while Fulford [2] related the falling film thickness by dimensional analysis for channel flow, of slopes between 7.5˚ - 9.0˚, over the range 30 < Re¦ < 300, in the form:
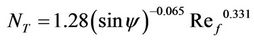 (8)
(8)
The equations mentioned above can be applied for quasi parallel-sided film i.e. for small film thickness flow inside or outside vertical tubes. While in straight inclined tubes and spiral tubes larger film thickness is expected but they differ in effect of centrifugal force on film in spiral tubes.
Most of the recent published works on helical pipes were mainly related to fully filled fluid flow in pipes and hardly any work was found dealing with film flow.
The latest work is concerned with the pipe flow belonging to Yamamoto and co-workers [7-9]. They studied the laminar and turbulent flow through helical coils. Their numerical and experimental data concluded a negligible effect of torsion on the flow within the range of their experimental data.
Several other workers investigated the emergence of turbulence region in flow through coiled pipes, both experimentally [8-11] and numerically [12,13]. The coil curvature seems to increase the value of the Reynolds number required to attain fully turbulence flow. Difficulties were experienced in locating the transition region in the fully filled flow in helical pipes.
Vashisth et al. [14] published an intensive review on the performance of curved tubes for heat and mass transfer for fully filled flow.
Gupta et al. [15] studied the effect of coil pitch and coil diameter on the friction factor for five types of fully filled coils with different radii variation developed for Newtonian fluid. They formulated an empirical Equation (9) based on their experimental data.
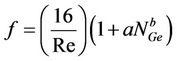 (9)
(9)
where a & b are constants and NGe is the Germano number that is equal to Re multiplied by coil curvature.

They concluded that Equation (9) predicts the observed coil friction factor values to within ±10%.
Film flow in curved tubes has not been given any attention in recent literature. The present work studies the thin film flow in curved tubes and extends its findings to large film thickness. The investigation covers experimental and theoretical film flow in both straight inclined and spiral tubes and how the two systems can be related. The work also discusses the case of film flow over flat surfaces.
2. Experimental Design
The apparatus used in this work is shown schematically in Figure 1, the system consists mainly of a constant head tank A, transparent flexible tube B, storage tank C and centrifugal pump D to circulate the distilled water in the system.
The testing part is made of flexible tube B having an elliptic cross section with an inside minor axis of 1.510 cm and inside major axis of 1.888 cm and a thickness of 0.412 cm.
It is known from literature that films are practically smooth for angles of inclination less than 5˚ over a wide range of Re¦ and would have limited ripples at higher range of Re¦. For this purpose, angles of inclination between 2.5˚ - 5˚ were studied.
In straight inclined tube experiments, the flexible tube is mounted on a flat steel plate. The far end of the tube away from the entrance is supported on a horizontal stand. It can be moved up or down to a suitable distance that can be conveniently measured by a traveling microscope in order to set the required include angle (2.5˚, 3˚, 5˚).
5˚).
The length of the developing region was estimated to be about 20 film thickness [16].
Hence, the film thickness is measured at 50 cm distance away from the entrance of the tube to insure that all measurements are made in the fully developed region.
A special micrometer, as shown in Figure 2, is used to
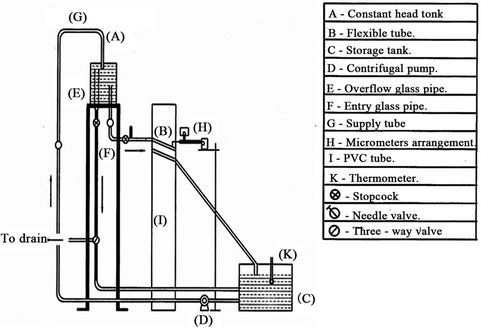
Figure 1. Chematic diagram of the apparatus used in film thickness measurement.
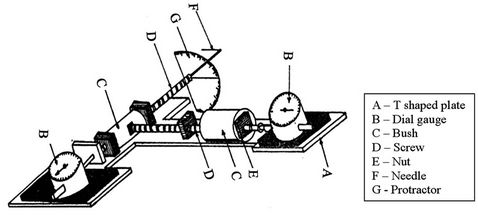
Figure 2. Micrometers arrangement.
measure the film thickness through holes in upper part of the flexible tube B. It consists of two micrometers arranged so that the vertical and horizontal distances of the cross sectional area of the flow can be measured. The whole arrangement is supported by a vertical stand, which allows the two micrometers to move to the required position near the system.
In spiral tube experiments, the helical is made up by wrapping the flexible tube B around the PVC tube I. Three tubes I of different diameters are selected. The flexible tube B is wrapped at the same angles of inclination as mentioned above. The curvature of the tube has a calming action, the developing region in curved tubes is expected to be shorter than that in straight tubes.
3. Theory and Model
3.1. Film Flow in Inclined Circular Tube
The cross section of circular tube and a liquid film are shown in Figure 3. It can be obtained from trigonometric relations that:
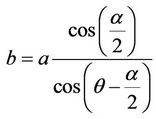 (10)
(10)
The Navier-Stokes equation in cylindrical coordinates for smooth, steady, laminar film flow can be reduced to the following equation:
 (11)
(11)
This differential equation can be solved by using the following boundary conditions:
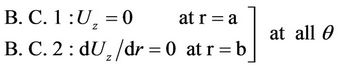
The solution below represents the known semi-parabolic relation in the r-direction.
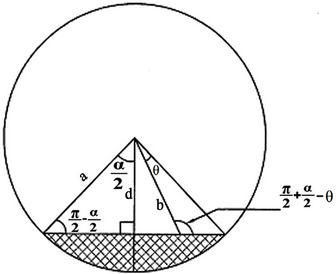
Figure 3. Liquid film in circular tube.
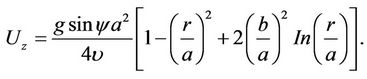 (12a)
(12a)
while the film surface velocity is represented by:
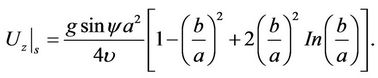 (12b)
(12b)
The average velocity is obtained from the following relationship:
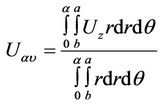 (13)
(13)
Submitting the expression of Uz in Equation (13) and carrying out the integration and then using the trigonometric identities would result in the following equation:
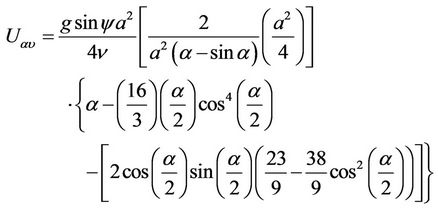 (14)
(14)
Since a2 (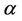 – sin
– sin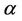 )/2 represent the cross-sectional area of the film, the volumetric flow rate can be given as:
)/2 represent the cross-sectional area of the film, the volumetric flow rate can be given as:
 (15)
(15)
By comparing Equation (2), which is for the average velocity in the conventional two dimensional film flows with the derived Equation (14) which is for the average velocity in the inclined tube, it can be considered from their identity that the film thickness in inclined tube is defined by Equation (16):
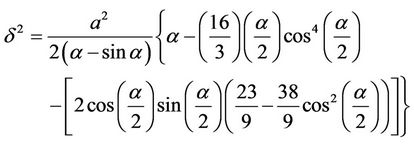 (16)
(16)
It is obvious that the film thickness is a function of both radius and central angle of the flow. Hence, the average velocity can be expressed as:
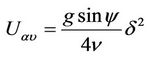 (17)
(17)
Further rearrangement of Equation (17) in terms of the dimensionless Nusselt film thickness and film Reynolds number would results in:
 (18)
(18)
As would be expected the flow in inclined circular tubes (Equation (18)) predicts higher Nusselt film thickness than in case of a flow over inclined flat plate (Equation (5)); since, the geometrical shape of the former offers higher wetted perimeter (HR/HD < 1) than in the latter case (HR/HD = 1) for the same free (exposed) surface.
It is more convenient to manipulate the experimental data for the flow in elliptic cross-section in terms of hydraulic radius rather than film thickness.
Applying the least squares fit to Equation (14) and the definition of hydraulic radius (refer to Figure 4) gives.
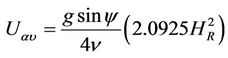 (19)
(19)
with a standard deviation of 4.578 × 10–3 and 0.94% average percentage error:
where
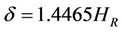 (20)
(20)
3.2. The Film Friction Factor
As the gas phase is practically stationary in the system, negligible drag force can be assumed at the free surface of the film. Therefore, the film weight is supported by the shear stress at the wall:
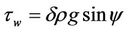 (21)
(21)
By substituting the value of d from Equation (17) and using the definition of Re¦, Equation (21) will be:
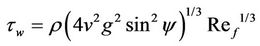 (22)
(22)
By defining the friction factor in the following form:
 (23)
(23)
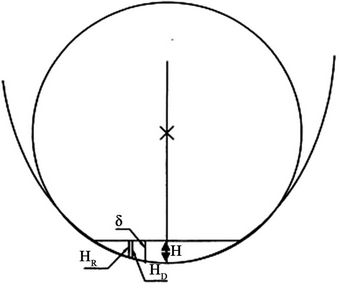
Figure 4. Hydraulic depth, hydraulic radius and film thickness at Ref = 303, angle of inclination 3˚.
and using the expression for Uav from Equation (17), the following equation is obtained:
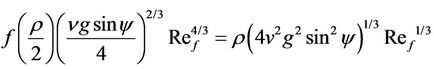 (24)
(24)
Simplifying the above equation will give a correlation relating the film friction factor and film Reynolds number:
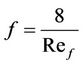 (25)
(25)
This is similar to the equation for laminar flow in a closed pipe. Equation (25) predicts a higher friction factor than would be predicted for liquid film falling on an inclined flat plate. Here again, the difference is due to the higher wetted perimeter for circular tubes than that of flat plates for the same free surface which would result in a higher drag force.
4. Results and Discussion
4.1. Inclined Tube
Figure 5 shows the variation of Nusselt film thickness versus film Reynolds number. Results show that laminar and turbulent regions fall within Re¦ ranging from 480 to 600. The transition region is reconfirmed at about the same Re¦ in Figure 6 in which the film friction factor, calculated from Equations (21) and (23), is plotted against the film Reynolds number.
In the laminar region (Re¦ < 480) (see Figure 5), most of the experimental points lie above the theoretical line of Equation (18) with the maximum deviation falling between +30% to –7%. The least-squares fit of the experimental data gives the empirical equation:
 (26)
(26)
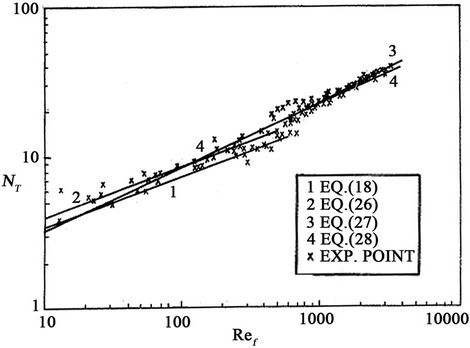
Figure 5. Inclined tube Nusselt number versus Reynolds number.

Figure 6. Film friction factor versus Reynolds number (inclined tube).
with standard deviation = 0.158 and average % error = 10.33.
While for the turbulent region (Re¦ > 600), the following empirical equation is obtained:
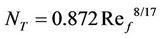 (27)
(27)
with standard deviation = 6.43 × 10–2 and average % error = 0.503.
Considering the whole experimental range of the film Reynolds number the following empirical equation is obtained:
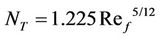 (28)
(28)
with standard deviation = 0.164 and average % error = 9.64.
The three above empirical equations, are shown in Figure 7 together with Nusselt, Fiend and Brauer equations for film flow over flat surfaces. For film flow in inclined circular tubes a higher Nusselt film thickness for both the laminar and turbulent regions is predicted.
Ripple inception is observed to occur at Ref ranging from 260 to 300 within all range of the angles of inclinations used in the experimental runs. Thomas, et al. [17] observed a ripple inception at lower range of Ref i.e. between 80 - 130 for the central region of the film in a wide channel. This difference in behavior may be due to the relatively narrow tube used in this study, where surface tension would have greater influence on the flow.
4.2. Helical Tube
A flexible transparent plastic tube is wrapped around a plastic cylinder at a predetermined angle of inclination, as in Figure 1. During the experimental runs, it was observed that the instability in film behavior increases with film flow rate and helix curvature.
As the flow rate is reduced, small cross waves were observed moving from the inner to the outer walls of the tube. These cross-waves disappear at lower flow rates and are replaced by small random ripples. At this stage four to five readings were recorded for film thickness.
First and second order polynomials were used to represent surface profile of the film and to extrapolate the surface shape near the inner and outer walls of the tube.
Most of the results suggested that first order polynomial correlation applied especially at low surface gradient. A typical representation of experimental runs is shown in Figure 8, which shows the unaxisymmetrical behavior of the film in helical tubes.
For each run the hydraulic radius, hydraulic depth and cross-sectional area of the flow are calculated. When the surface of the film was inclined, the surface length and the cross-sectional area of the flow were calculated using the analytic integration method for the surface equation.
In Figures 9 and 10, Nusselt film thickness is plotted against film Reynolds number. The transition region is not so distinguished as an inclined tube. In the helical tube gradual change of flow behavior confuses the limits of the transition region. This behavior is similar to itscounter part of a full pipe flow.
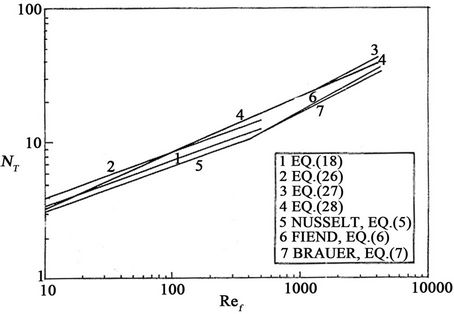
Figure 7. Comparison of present relation of film flow in inclined tube with that of inclined flat plate.
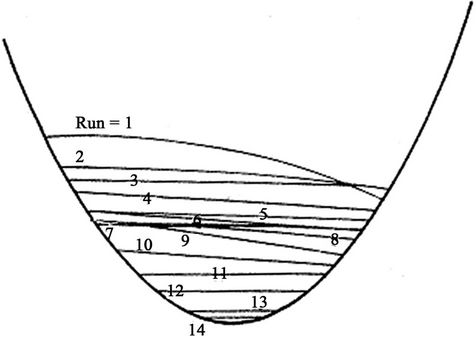
Figure 8. Film surface profile in elliptic cross sectional tube (polynomial approximation).
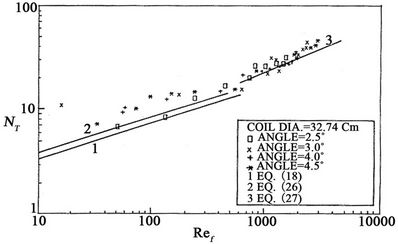
Figure 9. Helical tube Nusselt number versus Reynolds number (pitch effect at constant curvature).
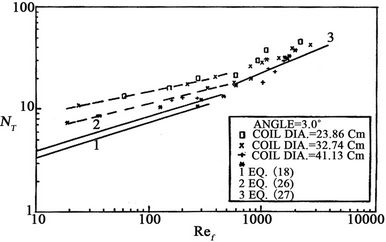
Figure 10. Helical tube Nusselt number versus Reynolds number (Curvature effect at constant pitch of 300 angle).
In the laminar region, the effect of pitch (angle of inclination) is clearly evident (see Figure 9) at certain film Reynolds number.
For turbulent flow, the action of coil diameter (curvature) and the action of centrifugal force would mostly reduce by inertia force and by the development of eddies. The effect of higher curvature can be observed while the pitch effect is overlapped by other effects.
In Figures 11 and 12, the Nusselt film thickness is plotted against the Dean number (De¦) which combines the effects of both curvature and film Reynolds number. The figures reveal that the spread in the experimental results is reduced as compared to Figures 9 and 10.
In order to relate Nusselt film thickness for coiled tubes to that of straight tubes, Figures 13 and 14 are plotted in terms of 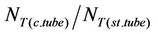 versus film Dean number. Equation (28) is applied to calculate NT(st.tube). It can be observed that most of the experimental points lie between value of
versus film Dean number. Equation (28) is applied to calculate NT(st.tube). It can be observed that most of the experimental points lie between value of  of 1 - 2. This ratio tends to decrease gradually with the increase of De¦ at certain coil diameter.
of 1 - 2. This ratio tends to decrease gradually with the increase of De¦ at certain coil diameter.
By the least squares fit, the following empirical correlation is obtained:
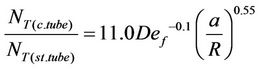 (29)
(29)
with Standard Deviation = 0.106 and average % error = 9.56.
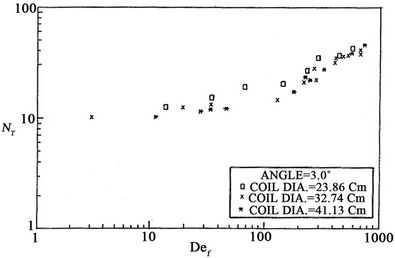
Figure 11. Helical tube Nusselt number versus Dean number (curvature effect at constant pitch of 3.00 angle).

Figure 12. Helical tube Nusselt number versus Dean number (curvature effect at constant pitch of 4.00 angle).

Figure 13. Ratio of Nusselt number of helical tube over Nusselt number (curvature effect at constant pitch of 3.00 angle).
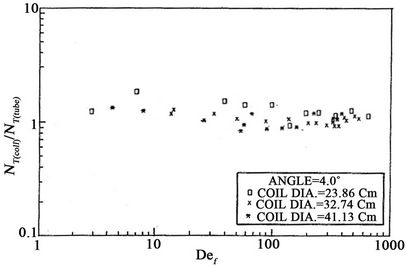
Figure 14. Ratio of Nusselt number of helical tube over Nusselt number (curvature effect at constant pitch of 4.00).
5. Conclusions
1) Systems that have their film thickness vary peripherally can be characterized by some average film thickness. This is a function of hydraulic radius defined by the film boundary.
2) In helical tubes, the film thickness increases with the increased curvature accompanied by a reduction in average velocity. Within the range of the obtained data, coiling effect may account for the maximum increase in film thickness of 70% over that of the inclined tube. But, this increase diminishes gradually in the turbulent region, where the secondary flow intensity is small relative to axial flow intensity.
3) Pitch within two to three tube diameters in length has no appreciable effect on film thickness at low tube curvature.
4) The transition region in a straight inclined tube is marked between Re¦ = 480 - 600, which is higher than the reported range for vertical tubes (Re¦ = 350 - 500). In helical tubes, the transition region is not so distinct (within experimental data) as it is in inclined tube 5) Results are correlated empirically for the cases of straight inclined and helical tubes. The former is expressed in terms of NT as function of Re¦ in the laminar and turbulent regions. While for the latter the empirical correlation is represented in terms of the ratio of NT to coil over NT for straight inclined tubes as function of Def.
REFERENCES
- V. T. Chov, “Open-Channel Hydraulic,” McGraw-Hill, Kogakusha, 1959.
- G. D. Fulford and T. B. Drew, “Advances in Chemical Engineering,” Academic Press, New York, Vol. 5, 1964.
- R. B. Bird, W. E. Steward and E. N. Lightfoot, “Transport Phenomena,” John Wiley, New York, 1960.
- H. Jefferys, “The Flow of Water in an Inclined Channel of Rectangular Section,” Philosophical Magazine, Vol. 49, 1925.
- C. M. Cooper, T. B. Drew and W. H. McAdams, Transactions of the American Institute of Chemical Engineers, Vol. 30, 1934.
- C. G. Kirkbride, Industrial & Engineering Chemistry Research, Vol. 26, 1934.
- K. Yamamoto, S. Yanase and T. Yoshida, “Torsion Effect on the Flow in a Helical Pipe,” Fluid Dynamics Research, Vol. 14, 1994, pp. 259-273. doi:10.1016/0169-5983(94)90035-3
- K. Yamamoto, T. Akita, H. Ikeuchi and Y. Kita, “Experimental Study of the Flow in a Helical Circular Tube,” Fluid Dynamics Research, Vol. 16, No. 4, 1995, pp. 237-249. doi:10.1016/0169-5983(95)00022-6
- K. Yamamoto, A. Aribowo, Y. Hayamizu, T. Hirose, K. Kawahara, “Visualization of the Flow in a Helical Pipe,” Fluid Dynamics Research, Vol. 30, No. 4, 2002, pp. 251-267. doi:10.1016/S0169-5983(02)00043-6
- D. R. Webster and J. A. C. Humphrey, “Experimental Observation of Flow Instability in a Helical Coil,” Fluid Engineering, Vol. 115, 1993, pp. 436-443. doi:10.1115/1.2910157
- A. Cioncolini and L. Santini, “An Experimental Investigation Regarding the Laminar to Turbulent Flow Tansition in Helically Coiled Pipes,” Experimental Thermal and Fluid Science, Vol. 30, No. 7, 2006, pp. 367-380. doi:10.1016/j.expthermflusci.2005.08.005
- T. J. Hüttl and R. Friedrich, “Influence of Curvature and Torsion on Turbulent flow in helically Coiled Pipes,” International Journal of Heat and Fluid Flow, Vol. 21, No. 3, 2000, pp. 345-353.
- T. J. Hüttl and R. Friedrich, “Direct Numerical Simulation of Turbulent Flows in Curved and helically Coiled Pipes,” Computers & Fluids, Vol. 30, No. 5, 2001, pp. 591-605. doi:10.1016/S0045-7930(01)00008-1
- V. Vashisth, V. Kumar and K. D. P. Nigam, “A Review on That Potential Applications of Curved Geometries in Process Industry,” Industrial & Engineering Chemistry Research, Vol. 47, No. 10, 2008, pp. 3291-3337. doi:10.1021/ie701760h
- R. Gupta, R. K. Wanchoo and T. R. M. J. Ali, “Laminar Flow in Helical Coils: A Parametric Study,” Industrial & Engineering Chemistry Research, Vol. 50, No. 2, 2011, pp. 1150-1157. doi:10.1021/ie101752z
- B. Atkinson and R. L. McKee, Chemical Engineering Science, Vol. 19, 1964.
- W. J. Thomas, M. S. Ray and E. W. Palmer, “Physical Absorption of Carbon Dioxide in Water Flowing in an Inclined Cell,” Chemical Engineering Communications, Vol. 2, No. 3, 1976, pp. 121-134. doi:10.1080/00986447608960454
Nonmenclatures

NOTES
*Corresponding author.

